现代战斗机对飞机的机动性和敏捷性有极高的要求,过失速机动作为两者的集中体现更是战斗机的必备能力之一。过失速机动是飞机超过失速迎角进行的迅速改变飞机速度矢量和机头指向的一种可控的机动飞行(例如“眼镜蛇机动”、“Herbst机动”等)。过失速机动飞行与常规机动相比,具有飞行迎角大、飞行速度低、三轴角速率大、飞机速度/方向/高度大幅度且变化突然等显著特征。
鸭式布局作为现代战斗机的一种先进的气动布局,在气动方面成功地利用了旋涡分离流构型的设计理念。特别是近距耦合鸭式布局飞机以其优良的气动性能越来越受到各国重视,是现代战斗机的常见布局之一。近距耦合鸭式布局中的鸭翼充分有效地利用旋涡气动力,不仅提供了正的配平升力,在其他操纵面的配合下还可以实现飞行姿态的直接力控制,从而使布局在大迎角下具有极强的控制能力[1]。因而这种有利干扰在战斗机大迎角机动和过失速机动过程中的作用尤为重要。
为了在实际应用中掌握这种有利干扰的规律,早期的鸭式布局研究多从纯工程应用的角度出发,通过测力实验研究鸭翼后掠角、上反角对布局纵向和横向气动特性的影响[1],通过改变鸭翼与主翼的几何外形、相对位置改变气动特性[2],或者在跨声速下研究布局的压力分布特性[3-4]等。结果表明鸭式布局的气动力主要受鸭翼与主翼的几何形状(后掠角、展弦比等)和相对位置、鸭翼偏角等影响,布局的增升起始迎角随着主翼后掠角的增大而提高,在小后掠的主翼上增升效果更为明显。
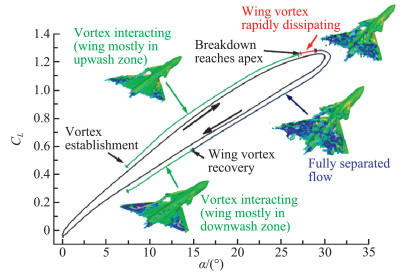
对于近距耦合鸭式布局而言,机动飞行中涉及的流动主要体现在大迎角下鸭翼涡与主翼涡的复杂干扰和破裂演变。刘沛清、陈名乾[5]数值模拟研究了带机身鸭式布局的类正弦俯仰运动(如图 1),结果表明:鸭式布局在大迎角俯仰过程中,主翼流场中存在主翼涡的产生、主翼涡与鸭翼涡相互干扰、涡破裂形成死水区、涡量重新卷积恢复并重新与鸭翼涡相互干扰的过程。伴随着涡系的产生与发展,上仰过程中升力相比静态状态有所提高,下伏过程中升力相比静态状态有所降低。气动力的迟滞和鸭式布局中涡系发展与演化的迟滞现象有关,不同的俯仰频率和迎角范围会对各阶段的产生与转变产生影响,从而决定迟滞环的大小。Davari[6]等在鸭式布局小迎角范围内的周期性俯仰运动实验中也发现了涡系间干扰的迟滞与布局气动特性的迟滞有明显的关联性。
|
图 1 鸭式布局俯仰运动的升力变化和流场状态[5] Fig.1 CL and flow field variation during canard configuration pitching movement[5] |
与此同时,研究中也发现由于鸭翼位于主翼之前,受主翼的上洗影响,容易引起鸭翼失速,由此可能带来以下问题:(1)在中小迎角下,主翼部分区域处于鸭翼流场的下洗区,降低了主翼升力;(2)在大迎角下鸭翼失速会给飞机的平衡能力带来问题,增大配平阻力;(3)大迎角下鸭翼前缘涡的破裂与机翼涡的干扰可能引起很大的纵向静不稳定;(4)在大迎角下鸭翼的尾流将影响垂尾和主翼,可能带来横侧向不稳定性[7-9]。
由于以上问题的产生均与布局的流动有关,因此对布局进行流动控制不失为一种合理的考虑。现代飞机的流动控制方法按飞行姿态可划分为三种:稳定流动控制、临界流动控制和湍尾流控制。稳定流动控制对应普通飞行状态,迎角范围在0°~15°之间,在此区域飞行器流场中涡系发展稳定,因而控制效果有限,只能小幅提高气动性能;临界流动控制对应大迎角机动状态,迎角范围在15°~30°之间,由于飞行器流场涉及破裂涡系的发展和演变,飞行器可能面临大迎角机动、抖振和失控等问题,通过流动控制可以比较容易的改变涡系状态,从而可实现气动性能的提高;湍尾流控制对应过失速机动状态,迎角范围在30°~70°之间,在此区域内飞行器流场处于大尺度分离流的状态,飞行器面临过失速机动中可能出现的初期尾旋问题,流动控制难度极大,耗能极高。当迎角大于70°,飞行器因流场处于完全分离状态而可能发展为尾旋,此时流动控制很难产生效果。鉴于此,考虑到控制技术的可行性和实用性,在大迎角下开展临界流动控制研究是切实可行的。
为了充分探讨近距耦合鸭式布局在大迎角机动飞行中的气动特点和控制技术,本文通过总结大量的流动显示和测力测压实验,首先探讨了大迎角下鸭翼涡和主翼涡的干扰机理,在此基础上开展了大迎角下鸭式布局涡系控制研究,旨在提出一种有效可行的大迎角飞行中的鸭翼涡控制技术。
1 大迎角下鸭翼涡与主翼涡干扰机理鸭式布局在不同迎角范围内涡系干扰的机理有所不同。在中小迎角下(18°以下)布局以附着流态为主,鸭翼与主翼的前缘涡较弱,涡系干扰以洗流作用为主[10-11]。OelKer等[1-11]通过实验和数值模拟,研究了小迎角下的共面鸭式布局流动,发现在鸭翼涡和主翼涡均未发生破裂的情况下,鸭翼涡距离主翼壁面很近,会与主翼边界层融合,主翼的剪切层会被卷入鸭翼涡中,鸭翼涡在主翼内段的强下洗作用下会导致主翼涡的外移,从而使主翼涡形成非锥形涡,同时小迎角时主翼内段受到下洗使得有效迎角减小,造成了升力的损失,但整体布局的升力通过鸭翼得到了弥补。Samimi等[12]也通过测压实验证明了鸭翼的洗流作用对主翼的重要作用。
大迎角下,Er-El[13]通过测压实验研究了涡系干扰对主翼上表面压力分布的影响,研究表明涡系干扰能明显改变主翼吸力峰。其机理主要分两部分:第一是鸭翼在主翼根部前端产生下洗,第二是之后两涡之间相互的诱导作用。不同迎角下二者作用的强弱区别导致了鸭翼对主翼有增升和减升的差异,同时也受鸭翼位置和鸭翼后掠角带来的鸭翼涡强弱的影响。Howard和O′Leary[14]利用物面油流及空间截面压力测量法,对鸭式布局翼身组合体在大迎角下的流动特征及旋涡干扰机理进行了研究,发现鸭翼涡在主翼的内段产生下洗,使原本分离的流动发生再附,形成主翼涡,这种再附作用是主翼涡破裂延迟的主要原因,也是鸭式布局在大迎角下增升的关键。Ponton等[15]对鸭式布局在30°~40°大迎角下的流场进行了分析,发现鸭式布局在鸭翼涡和主翼涡都发生破裂的情况下仍然具有增升作用,这种增升作用依然主要通过下洗实现。
刘沛清、魏园[16]通过激光片光诱导荧光技术在水洞中针对无机身的共面简化鸭式布局模型开展了一系列流动显示实验,结果清晰地显示了鸭翼涡和主翼涡的相互干扰作用。实验中采用的70°后掠角鸭翼、40°后掠角主翼的构型简称W40C70。从实验结果来看,根据涡系的强弱可以分为四个大类:
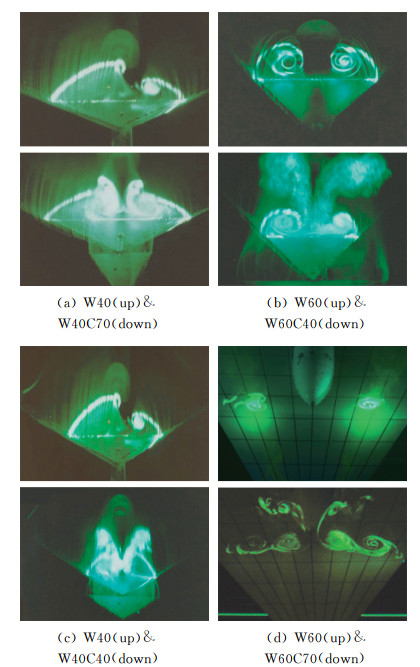
1) 强鸭翼涡与弱主翼涡干扰。以图 2(a)中单三角翼(上)和鸭式布局(下)的前缘涡流向片光截面为例,可以看出:在24°迎角下,单三角翼构型的前缘涡已经破裂且呈现出一定的不对称性;鸭式布局构型中鸭翼涡在内侧位置与破裂的主翼涡相互卷绕,虽然主翼涡不能恢复到破裂前的集中状态,但破裂的主翼涡有所集中且基本呈对称分布,流场稳定性得到提高。可以预见,在略低于24°迎角状态下,鸭翼涡可以推迟主翼涡的破裂,改善主翼的气动特性。
|
图 2 三角翼和鸭式布局涡系激光片光流动显示对比[16] Fig.2 Comparison of laser sheet flow visualization between delta and canard configuration[16] |
2) 弱鸭翼涡与强主翼涡干扰。以图 2(b)为例可以看出:24°迎角下,三角翼前缘涡具有很强的结构形态,鸭式布局中的弱鸭翼涡呈现为破碎的集中涡团,位于主翼涡的上方,且部分涡量从内侧卷入主翼涡中。在这种情况下,由于鸭翼涡强度较低且距离主翼涡较远,无法直接作用于强主翼涡上,但是弱鸭翼涡的下洗对主翼前缘流场仍有影响。
3) 弱鸭翼涡与弱主翼涡干扰。以图 2(c)为例,可以看出:相比于三角翼不对称的前缘涡分布,鸭式布局中弱鸭翼涡位于主翼涡的上方,部分涡量和主翼涡卷绕掺混。虽然弱鸭翼涡同样无法直接作用于弱主翼涡上,但是在弱鸭翼涡的下洗作用下,主翼上的附着流动有所改善,流动恢复对称性且分离区的面积有所减小,表明鸭翼涡的存在仍然可以推迟分离的发生。
4) 强鸭翼涡与强主翼涡干扰。以图 2(d)为例,可以看出:三角翼的前缘涡虽然相对比较集中,但涡系结构散乱,表明前缘涡已经开始向破裂发展。鸭式布局中主翼涡的结构清晰,相比三角翼布局更靠近前缘。鸭翼涡位于主翼涡内侧,尺寸和主翼涡相当,同时外部涡量在鸭翼涡的作用下从内侧进入鸭翼涡和主翼涡构成的双涡系统。鸭翼涡和主翼涡的相互作用明显。相比于三角翼构型,鸭式布局中鸭翼涡的下洗作用不仅改善了主翼涡的结构,对主翼涡的位置也产生了明显影响。
以上流动显示表明,对于不同的鸭式布局构型(鸭翼和主翼后掠角的不同),由于翼面上涡系干扰方式不同,增升规律也有所差别。为了系统研究鸭翼对主翼的增升规律,刘沛清、温瑞英[17]针对后掠角为40°、50°和60°的主翼进行了不同后掠角鸭翼的静态测力实验。
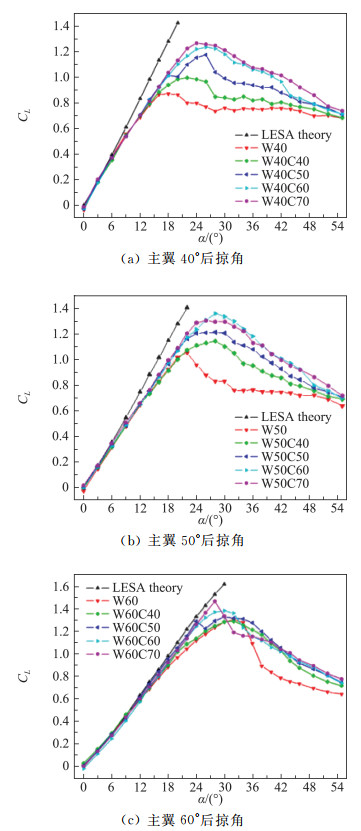
从测力实验结果来看(图 3),在主翼后掠角相同的情况下,16°~30°迎角范围内鸭式布局升力明显高于三角翼布局。对于相同后掠角的主翼,增升的效果与鸭翼后掠角在60°范围内呈正相关趋势。鸭翼对W60构型的增升结果略微复杂于前两者。W60C40的失速前升力系数只略高于W60构型,但失速后升力曲线与其他鸭式布局重合,明显高于三角翼布局。W60C50的升力曲线在迎角小于24°时和W60C60、W60C70基本重合,均明显高于W60和W60C40,之后突变到与W60C40曲线附近,这表明流场中鸭翼涡和主翼涡的相互作用方式可能发生了变化。相比于W60C70升力曲线在28°左右出现陡降,W60C60构型的升力曲线变化要缓和许多,表明W60C60构型中由鸭翼涡和主翼涡组成的双涡结构存在相对稳定的演化、破裂过程。对比不同的布局升力曲线可以看出,鸭式布局在中等后掠角的组合下相比三角翼可以获得比较明显的气动性能提升。
|
图 3 机翼后掠角分别为40°、50°和60°的鸭式布局升力系数[17] Fig.3 CL of canard configurations with different sweepback angles[17] |
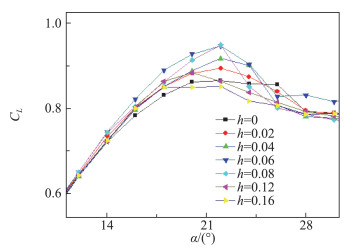
樊文博[18]研究了基于W40C40构型的非共面鸭式布局气动性能。测力结果(图 4)表明鸭翼位于主翼上方的布置可以提高布局最大升力,且存在最佳的高度位置可以使鸭翼对主翼的有利干扰最大化。虽然对失速迎角的影响不大,但鸭翼高度的增加会加快失速后升力的下降速度,导致在更大的迎角下升力低于共面布局。当迎角大于28°,布局完全失速后升力系数的差异基本消失。
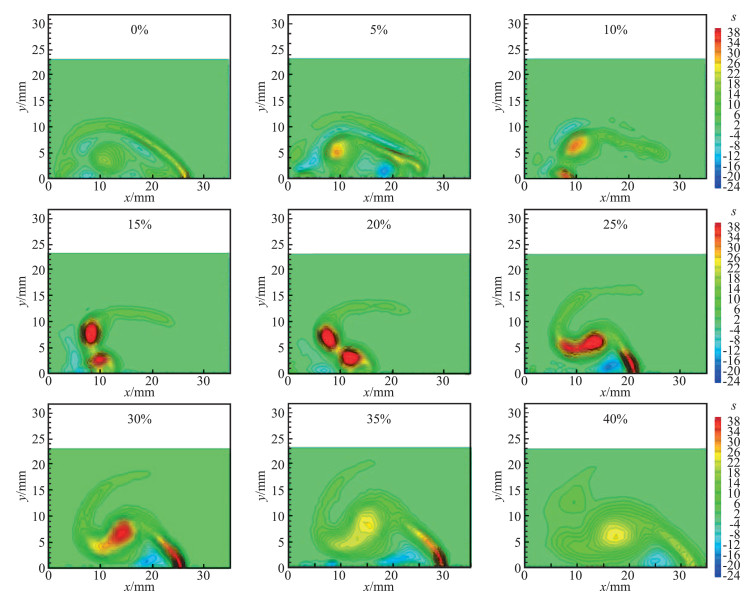
毛磊[19]通过PIV研究了W50C50布局中的鸭翼涡和主翼涡的干扰过程。实验结果(图 5)表明,对于中等后掠角的鸭式布局构型,鸭翼涡和主翼涡存在相互卷绕、融合的现象,这一现象在Bergmann和Humme[20]的研究中也得到类似结果。王亚平等[21]针对该构型进行了数值模拟研究,获得了与实验相近的结果(图 6),进一步表明,在大迎角下鸭翼涡和主翼涡存在复杂的相互诱导、卷绕行为。
|
图 5 W50C50布局20°迎角截面涡量分布[19] Fig.5 Vorticity distributions at different stream wise positions of W50C50 configuration under 20°angle of attack[19] |

|
图 6 W50C50布局22°迎角空间流线分布[21] Fig.6 Stream traces of W50C50 configuration under 22°angle of attack[21] |
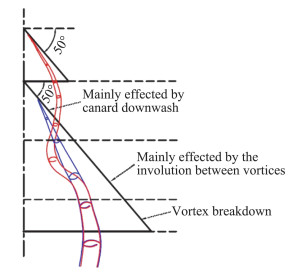
以上实验和数值模拟结果表明,鸭翼涡与主翼涡的干扰与演变机理虽然复杂,但总体上可看作分为诱导(上洗、下洗)和卷绕(增大涡强)两种形态,最终达到延迟涡破裂的结果。刘杰[22]通过系统的数值模拟研究发现,在大迎角下,鸭翼涡和主翼涡之间的干扰方式以相互卷绕为主(见图 7),属于涡系之间的直接作用,靠近主翼顶点附近的机翼流场受到鸭翼流场的下洗影响,在向下游发展过程中通过相互卷绕逐渐融合成单一稳定的集中涡,最终发展为集中涡的破裂。具体来说,鸭式布局涡系干扰过程可以分为涡系诱导、涡系卷绕、涡系融合和涡量扩散四个阶段。涡系诱导阶段,鸭翼涡对主翼产生“下洗”的诱导,抑制主翼涡的形成;涡系卷绕阶段,主翼涡快速卷起并增强,对鸭翼涡产生强诱导,使得鸭翼涡出现明显的位置和形状改变,并且两涡涡核距离快速减小;涡量融合阶段,鸭翼涡核与主翼涡核充分接近,只有唯一的最大涡量区域,呈现非对称性,随着涡量的融合最终形成对称性较好的单一涡;在涡量扩散阶段,合并的单一涡涡量迅扩散直至涡破裂。
|
图 7 大迎角下鸭式布局瞬时涡系干扰示意图[22] Fig.7 Sketch map of vortices interactions of canard configuration under high angle of attack[22] |
鸭式布局涡系干扰的复杂机理表明,通过控制气动面分离涡的复杂干扰,能够改善布局的气动性能,提高大迎角气动特性和过失速机动能力。因此开展在大迎角下通过控制鸭翼涡和主翼涡干扰行为的研究,从而达到改善布局气动特性的目的,是十分必要的。
2 大迎角下鸭翼涡主动控制技术传统的战斗机流动控制包括主翼展向吹气[23-28]、前缘襟翼[27]、边条[25]等,都对布局气动特性的提升有一定效果。展向吹气技术最早由Dixon等[28-31]首先提出,在此之后得到了广泛的研究[30-34]。Campbell[23-25]、Erickson[26-27, 35-36]对多种平面形状的机翼进行了展向吹气实验研究,结果表明展向吹气在中等迎角以上可以显著提高升力系数,延迟失速。Brandly和Wray [32-33]的流动显示研究结果表明,展向吹气可以改变前缘涡的位置、增强前缘涡的强度。Theisen等[37]对吹气喷管的位置做了大量的实验研究,发现吹气喷管距离翼面的最佳高度和喷管的出口直径有关,比较认同的说法是喷管距翼面的高度为喷管直径的1~2倍较好。秦燕华[38]在J-7、J-8、JH-7、双三角翼等气动布局上进行了展向吹气对大迎角气动特性的影响研究,发现喷管的弦向位置是影响气动收益最敏感的参数,喷嘴太靠近前缘时吹气的效果不如在较远的位置好。
针对鸭翼实施控制,可以明显提高鸭式布局飞机大迎角机动飞行的升力和操纵效率、改善失速性能、提高机动性。目前提出的一些主要措施有:全动鸭翼、鸭翼边条、鸭翼襟翼、鸭翼与主翼襟翼联合操纵。
采用全动鸭翼,可以通过改变鸭翼偏角来控制鸭翼涡系的发展,延迟鸭翼涡的破裂,提高鸭翼的控制效率,但存在配平阻力大、偏角控制范围小的缺点。Wibowo等[39]通过流动显示表明鸭翼偏转可以延迟主翼涡的破裂和布局的失速。Gloss[1]在鸭翼上加边条可以增强鸭翼涡的强度,延迟了鸭翼涡的破裂,但布局失速迎角有所降低。Re和Capone[40]在鸭翼上设置前缘/后缘襟翼并与鸭翼偏转一起操纵,实验结果表明,该方法可以提高鸭翼的升力和控制鸭翼的分离与涡破裂,明显提高飞机的抬头力矩和鸭翼的操纵效率,但控制规律十分复杂,需要大量的实验获得最优配置。Wei等[41]在风洞中测试了鸭翼加装格林襟翼对布局气动力的效果,发现三角形的鸭翼格林襟翼对布局的升力和抬头力矩的增加效果明显,但对鸭翼偏转效率会造成不利影响。
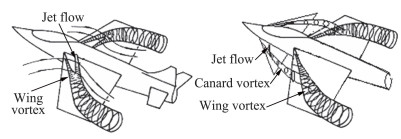
由于鸭翼涡和主翼涡的相互作用在气动力上有明显的关联,因此可以设想在大迎角下把鸭翼作为一种涡发生器,通过控制鸭翼涡与主翼涡的干扰作用,达到间接控制主翼涡的目的。Jenkins等[42]在近耦合鸭式布局鸭翼上进行吹气,发现鸭翼展向吹气改善了鸭翼的操纵效率,这对提高鸭翼的配平能力和大迎角的操纵性能都有利,并且发现鸭翼展向吹气需要较小的吹气量就可以达到增强鸭翼前缘涡的目的,从而对机翼产生较大的有利气动干扰。在此基础上,刘沛清、温瑞英[17]、樊文博[18]、曹硕[43]针对鸭翼展向吹气进行了系统的研究。刘沛清提出一种机翼涡间接涡控技术的新思路(如图 8所示),主要通过在大迎角下控制鸭翼涡的发展,进而改变鸭翼涡与主翼涡的干扰耦合状态,达到对机翼涡的间接控制,从而实现延迟机翼涡破裂、提高升力系数和失速迎角的目的。
|
图 8 鸭式布局机翼涡间接涡控技术示意图[17] Fig.8 Sketch map of vortex-control technology of canard-spanwise blowing of canard configurations[17] |
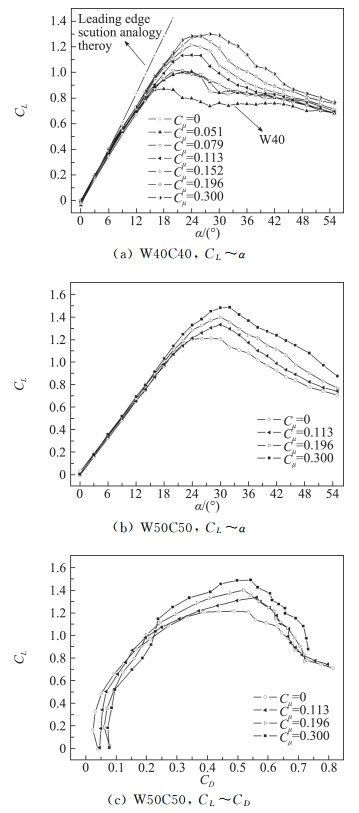
温瑞英[17]针对共面鸭式布局开展了鸭翼展向连续吹气实验,研究了包括吹气动量系数(Cμ)、布局后掠角等参数对气动特性的影响。其实验结果(图 9)表明,当吹气动量系数小于临界值时对布局没有增升作用,超过临界值后增升效果随吹气动量系数的增大而增大,但增升效果可能存在上限。W50C50布局的极曲线表明,中小迎角下展向吹气增加了布局阻力,但大迎角下展向吹气可以在更低的迎角下获得更大的升力同时降低阻力,从而改善了极曲线,提高了布局的升阻比。
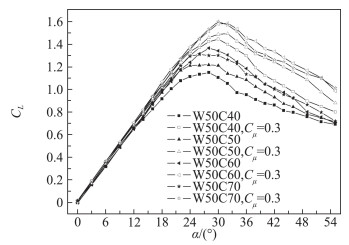
通过固定主翼后掠角和吹气动量系数,温瑞英[17]研究了鸭翼后掠角对鸭翼展向吹气增升效果的影响规律。在Cμ=0.3时选用W50构型的主翼搭配后掠角为40°、50°、60°和70°鸭翼的鸭式布局, 进行连续展向吹气测力实验(图 10)结果表明,对于中大后掠角范围内的鸭翼(40°到60°之间),不论有无流动控制,最大升力系数均随鸭翼后掠角增大而增大,失速也相应延迟;而对于大后掠角的鸭翼(70°或者以上),在没有展向吹气的情况下除了在失速迎角附近的小部分区域升力较大,其余部分升力与60°后掠鸭翼构型相差不大;与此同时,展向吹气增升效果出现的迎角也随着后掠角的增大而增大。
|
图 10 W50的不同鸭式布局在有无吹气情况下的升力系数[17] Fig.10 CL of canard configurations with and without canard-spanwise blowing[17] |
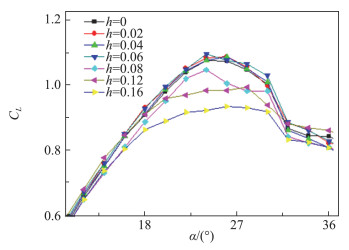
曹硕[43]在非共面的W40C40布局上研究了不同鸭翼高度下鸭翼展向吹气对布局升力的影响规律(见图 11)。对比图 4中的未吹气曲线可以看到,在一定高度差下,鸭翼展向射流可以使布局获得相同的升力系数,当鸭翼与主翼的高度差超过临界值时布局升力有所下降。在临界高度差范围内,固定吹气动量系数下鸭翼的升力基本保持不变,因此重合的升力系数曲线表明在展向吹气作用下,主翼的升力也基本不随鸭翼高度变化。这一结果表明,鸭翼对主翼的有利干扰可能存在上限。在射流的作用下鸭翼对主翼的有利干扰得到了极大增强,甚至远超主翼所能吸收的范围;当高度超过临界值时,鸭翼涡系和尾流对主翼涡系的卷绕和下洗作用因距离增加而减弱,因此布局升力降低。对比在未吹气情况下的升力系数曲线可以看出,未吹气情况下,鸭翼和主翼存在最优高度差以获得最优增升效果;而在鸭翼展向吹气的作用下,最优高度差从固定值拓宽为固定区域,从而可以拓宽布局气动设计的参数范围,有利于战斗机布局的总体设计。
|
图 11 W40C40在Cμ=0.3时不同鸭翼高度下局部升力系数[43] Fig.11 CL of W40C40 with varions canard vertical positions when Cμ=0.3[43] |
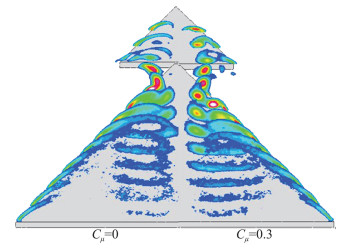
冯晓伟[44]在水槽中针对W50C50共面鸭式布局开展了鸭翼展向射流实验研究,通过PIV测量了各个截面的涡量分布(见图 12)。流场测量结果显示,鸭翼展向射流会使鸭翼涡远离对称面,导致鸭翼涡对主翼前缘的下洗作用增强,下洗作用区域增加,延迟主翼涡的产生。由于主翼涡的卷起被推迟,主翼对鸭翼涡的诱导能力减弱,同时由于射流增加了鸭翼涡的轴向速度,鸭翼涡的高度相比无展向射流的情况有所增加。鸭翼涡高度的增加延迟了鸭翼涡系和主翼涡系的卷绕融合,增大了主翼涡在发展过程中的强度,增强了涡系对翼面的诱导,也延缓了涡系的破裂。
|
图 12 W50C50在22°迎角有无展向射流的截面涡量分布[44] Fig.12 Vorticity distribution of W50C50 at α=22°with and without canard-spanwise blowing[44] |
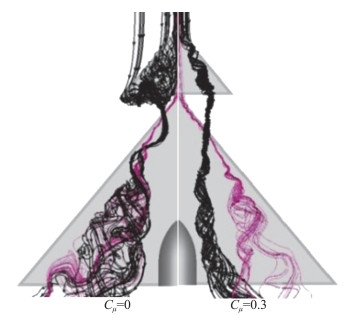
杨磊[45]数值模拟研究了鸭式布局在鸭翼展向吹气作用前后的流场状态。大迎角下的数值结果(见图 13)表明,展向吹气使得鸭翼涡的强度增加,尺寸变小,轴向速度大幅提高,不仅在鸭翼诱导出大面积的低压区,发展到主翼尾缘附近的涡系也可以诱导出低压区产生升力。对主翼流场而言,展向吹气使大迎角下鸭翼涡和主翼涡由相互卷绕变为相互分离,鸭翼涡的下洗作用强度得到增强和区域得以扩大,来流的有效迎角相应所降低,从而在延缓主翼涡的生成与发展的同时,减小了主翼涡初始阶段涡核的轴向速度、压强系数和总压损失,提高了前缘涡的稳定性。鸭翼涡的下洗也使得主翼涡距离翼面的高度更低,在翼面上可以诱导出更高的吸力峰。当鸭翼涡位于主翼涡内侧时,鸭翼涡的上洗作用对前缘涡的发展有促进作用。
|
图 13 W50C50在28°迎角有无展向吹气流场[45] Fig.13 Stream traces of W50C50 at α=28°with and without canard-spanwise blowing[45] |
鸭翼展向连续吹气实验结果表明,对鸭翼展向吹气在大迎角下可以有效延迟主翼涡的破裂,有很好的增升减阻作用。展向吹气在中等后掠角组合的鸭式布局上可以获得更好的效果,且随着吹气动量系数的增加而增强,在一定范围内可以减小鸭翼和主翼高度差对气动特性的影响。对中等后掠角组合的鸭式布局,在大迎角下鸭翼涡和主翼涡主要通过诱导和卷绕相互作用,展向吹气可以通过改变涡系的诱导、卷绕状态,增加主翼涡的强度,延迟涡破裂,从而增大主翼面吸力,提高升力。
2.2 鸭翼展向脉冲吹气涡控技术为了减小展向吹气的引气量,提高鸭翼展向吹气的控制效率和实用性,温瑞英[17]和曹硕[43]在连续吹气的基础上开展了鸭翼展向脉冲吹气涡控技术实验研究。
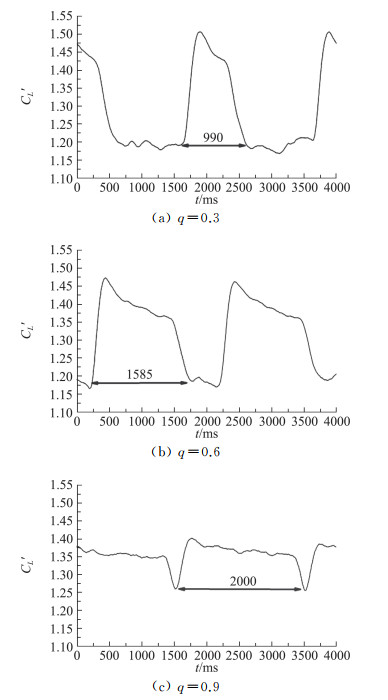
鸭翼展向脉冲吹气的增升效果主要受吹气动量系数、脉冲频率和脉冲占空比的影响。为了说明占空比的控制规律,以28°迎角下W50C50布局在Cμ=0.3、脉冲频率f=0.5 Hz的工况为例[17],图 14给出了占空比为0.3、0.6、0.9的瞬时升力系数曲线。可以看到,当占空比较小时(q=0.3, 0.6),占空比的变化对增升的时长有明显提高,瞬时最大、最小升力系数变化不大;当占空比较大时(q=0.9),相比前两者,瞬时最大升力系数明显降低,最小升力系数明显提高。这种变化表明,在占空比较低的情况下,上翼面流动在脉冲消失后可以恢复到近似于无吹气的状态;而占空比较高的情况下,一个周期内流动在恢复到无吹气状态之前就被下一次吹气改变。最大瞬时升力值在低占空比下较高,可能是由于脉冲开始的时刻流动处于无吹气状态,射流对流态的改变较大,因此流场对射流能量的吸收更多、利用率更高。
|
图 14 W50C50在28°迎角下、Cμ=0.3、f=0.5 Hz、展向吹气时不同q值下的瞬时升力系数[17] Fig.14 Instantaneous CL of W50C50 at α=28°with canard spanwise blowing of Cμ=0.3, f =0.5 Hz and different q values[17] |
在瞬时升力系数随时间变化的基础上,定义TL为射流作用下布局增升时间,即瞬时升力系数从无吹气状态开始增加到再次恢复的时间;定义TP为脉冲时间,即一个脉冲周期内射流持续的时间,相应的升力延迟时间Td为TL与TP的差值。占空比较高的情况下由于升力不能恢复到未吹气状态而不予考虑。
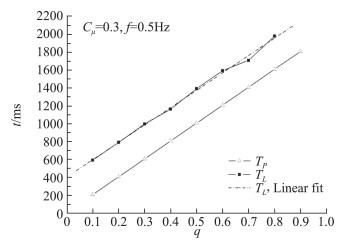
占空比对升力延迟时间的变化曲线如图 15所示。升力延迟时间Td基本呈线性增加,且始终高于射流持续时间TL,表明吹气的增升效果在吹气结束后可以保持一段时间,这种迟滞效应应该是脉冲吹气可以节省吹气量的关键原因。此外,TP和TL的斜率基本保持一致,表明迟滞时间为一近似常量,升力延迟时间和脉冲宽度无关。
|
图 15 W50C50在28°迎角下脉冲时间与涡生存时间随占空比的变化曲线[17] Fig.15 TP and TL of W50C50 at α=28°with different q values[17] |
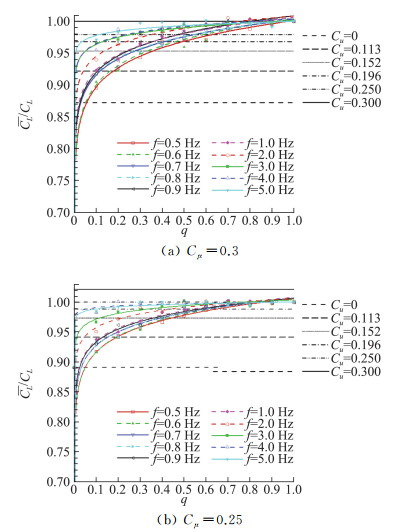
为了衡量脉冲吹气的增升效果,图 16给出了W50C50布局在28°迎角下、吹气动量系数Cμ=0.3和0.25时、不同脉冲频率下,占空比与升力系数比值的变化曲线。其中CL为连续吹气的升力系数,CL为脉冲吹气下的平均升力系数,两者比值为1表示脉冲吹气达到连续吹气的增升效果。实验结果表明,在一定的吹气动量系数下,对同一频率的脉冲吹气控制,增加占空比可以在前期迅速提高升力,但增升效果低于连续吹气。当占空比大于0.6后,增升效果放缓。继续增加展向吹气的占空比,会得到逐渐近似于连续吹气的增升效果。对比不同频率的曲线可以看到,占空比越低,吹气频率对展向吹气的增升效果越明显;当占空比大于0.6后吹气频率的增加对展向吹气升力的提升效果放缓。对比不同吹气动量系数下的曲线,以f=5 Hz曲线为例,Cμ=0.25时可以在更小的q值下获得更接近连续吹气的增升效果。因此,提高吹气动量系数、脉冲频率或占空比都对控制效果的提升有促进作用。
|
图 16 W50C50在28°迎角、Cμ=0.3和0.25时、不同频率下的CL/CL随脉冲宽度的变化曲线[17] Fig.16 Variations of CL/CL with q for W50C50 at α=28°, Cμ=0.3、0.25[17] |
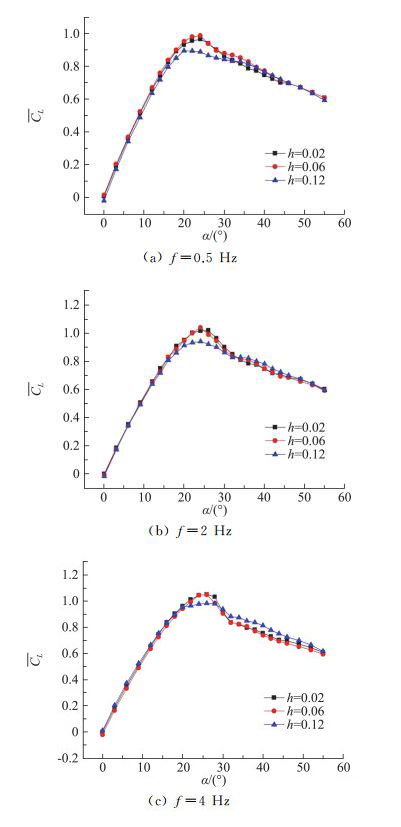
曹硕[43]关注了鸭翼高度对脉冲吹气增升效果的影响(见图 17),发现鸭翼高度对脉冲吹气和连续吹气具有相似的作用规律。即在一定的范围内,鸭翼相对主翼的高度对脉冲吹气的布局升力基本不产生影响,当超过临界值后增升效果在大迎角下变差。对比不同脉冲频率下的曲线变化趋势可以看出,随着脉冲频率的增加,h=0.12的曲线与其他较低高度差的曲线逐渐靠近,表明随着脉冲频率的增加,临界值可能会有所提高。
|
图 17 W40C40在q=0.2、Cμ=0.3、不同脉冲频率下的平均升力系数随鸭翼高度变化曲线[43] Fig.17 CL of non-coplanar W40C40 with canard-spanwise blowing of Cμ=0.3, q=0.2 and different frequency values[43] |
为了研究脉冲展向吹气的效率,温瑞英[17]统计了在获得相同升力情况下连续吹气与脉冲吹气所需吹气量的值,并进行了对比。
在28°迎角下,固定Cμ=0.3和脉冲吹气频率f=0.5 Hz,通过调节脉冲的占空比q,改变升力的大小的工况。表 1给出了该情况下达到其他连续吹气动量系数的升力值时所需的q值,进而可以估算出平均吹气动量系数和所节省的最小吹气量。可以看到,在达到目标升力的情况下,脉冲吹气所需的占空比均明显小于1,随着目标升力值的降低所需占空比逐渐下降,因此所需的平均吹气动量系数也逐渐下降。且对比以Cμ=0.113连续吹气的情况,节省的最小吹气量较多。
| 表 1 28°迎角下、Cμ=0.3、f=0.5 Hz时,达到连续吹气升力值时对应的参数[17] Table 1 α=28°, the corresponding q of pulse blowing of Cμ= 0.3, f=0.5 Hz to achieve the same CL of continuous blowing[17] |
|
|
此外,图 16表明通过提高吹气频率和占空比在不同的吹气动量系数下获得相同的增升效果。为了比较相同吹气动量系数下的效率,统计Cμ=0.3脉冲吹气时达到Cμ=0.25连续吹气时相同升力值下对应的射流频率f和占空比q, 如表 2所示。从表中数据看出,在达到Cμ=0.25连续吹气升力系数的情况下,当脉冲频率为0.5 Hz时对应的占空比为0.64,节省的吹气量为23.2%,但当脉冲平率为5 Hz时,所需占空比下降到0.2,节省的吹气量却上升到76%。数据表明,随着脉冲频率的增加,所需的脉冲占空比逐渐降低,节省的吹气量逐渐增加。
| 表 2 28°迎角下Cμ=0.3脉冲吹气达到Cμ = 0.25连续吹气升力值时所对应的f、q组合[17] Table 2 α=28°, the corresponding f & q for pulse blowing of Cμ=0.3 to achieve the same CL of continuous blowing with Cμ=0.25[17] |
|
|
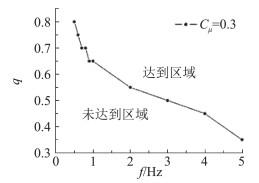
将表 2中的数据以脉冲频率和对应占空比作图,可得到脉冲吹气达到连续吹气效果的组合区域图(图 18)。图中在曲线上方的区域表示脉冲吹气在该区域内的f、q组合能够超过目标升力下连续吹气的升力值,且越靠近右侧节省的吹气量越大,脉冲吹气效率越高;而曲线下方区域内的f、q组合则不能达到目标升力。可以预见,图 18中曲线在f=0处q=1,表示鸭翼展向连续吹气控制;当f继续增大时,q的值将持续趋近与0,同时表示所需的平均吹气动量系数也趋近于0,表示零质量射流的吹气控制。
|
图 18 脉冲吹气达到目标连续吹气效果的f、q组合区域图[17] Fig.18 f & q combinations for pulse blowing to achieve the considerable effect of continuous blowing[17] |
本文通过调研近距耦合鸭式布局在大迎角下机动飞行的相关文献,总结了鸭式布局增升和控制的机理,并对鸭翼展向吹气流动控制研究进行了系统的梳理和总结。结果表明:
1) 在大迎角下鸭翼涡和主翼涡之间的干扰方式以相互卷绕为主,属于涡系之间的直接作用。具体相互作用方式从空间发展上可分为三个阶段:靠近主翼顶点附近的主翼流场受到鸭翼流场的下洗效应影响,在向下游发展过程中通过相互卷绕逐渐融合成单一稳定的集中涡,最终发展为集中涡的破裂。可以通过鸭翼涡对主翼涡施加影响,从而间接改变涡系干扰状态,进而达到流动控制的目的。
2) 对鸭翼展向连续吹气,在大迎角下可以有效延迟主翼涡的破裂,有很好的增升减阻作用。尤其在中等后掠角组合的鸭式布局上,展向吹气可以改变涡系的诱导和卷绕作用,延迟主翼涡破裂,提高升力,且在一定的高度差下能很好地维持非共面布局的气动特性。
3) 鸭翼展向脉冲吹气有效地利用了展向吹气的迟滞效应,可以通过提高占空比、脉冲频率,通过较低的引气量达到连续吹气下的目标升力提升效果。且脉冲频率越高,节省的吹气量越大。同样在一定的高度差下能很好地维持非共面布局的气动特性。
鸭式布局作为一种高机动、高敏捷布局,在过去的研究中主要集中在基于静态布局气动性能的优化和控制,对布局流动和控制机理的认识也达到了一定的高度。在进一步的工作中,研究对象应该从静态向动态扩展,积极开展包括改变来流速度、布局动态俯仰/摇滚/侧滑等因素的非定常气动特性研究,尤其需要关注布局非定常机动过程中的气动力、力矩、飞行稳定性、舵面操纵性等参数的变化,以及各种流动控制手段对相关因素的影响规律和作用机理,为鸭式布局飞机在复杂状态下的操纵和优化提供理论和数据支持。
| [1] |
GLOSS B B. Effect of wing planform and canard location and geometry on the longitudinal aerodynamic characteristics of a close-coupled canard wing model at subsonic speeds[R]. NASA TN-D-7910, 1975.
|
| [2] |
GLOSS B B. Effect of canard location and size on canard-wing interference and aerodynamic center shift related to maneuvering aircraft at transonic speeds[R]. NASA TN-D-7505, 1974.
|
| [3] |
GLOSS B B, KAREN E. Washburn. A study of canard-wing interference using experimental pressure data at transonic speeds[R]. NASA TP-1355, 1979.
|
| [4] |
GLOSS BB, WASHBURN K E. Load distribution on a close-coupled wing canard at transonic speeds[J]. Journal of Aircraft, 1978, 15(4): 234-239. DOI:10.2514/3.58347 |
| [5] |
陈名乾.近距耦合鸭式布局动态机动中涡系干扰机理的数值研究[D].北京: 北京航空航天大学, 2014. CHEN M Q. Numerical study on the mechanism of dynamic vortex interaction on a maneuvering close-coupled canard configuration[D]. Beijing: Beihang University, 2014. (in Chinese) |
| [6] |
DAVARI A R, ASKARI F, SOLTANI M R. canard flow improvement in a splitcanard configuration[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2015, 229(6): 1076-1087. DOI:10.1177/0954410014544180 |
| [7] |
方宝瑞. 飞机气动布局设计[M]. 北京: 航空工业出版社, 1997.
|
| [8] |
郑遂.鸭式布局先进战斗机研究进展[R].国防科研报告, GF-87282, 1995.
|
| [9] |
马宝峰, 刘沛清, 邓学蓥. 近距耦合鸭式布局气动研究进展[J]. 空气动力学学报, 2003, 21(3): 320-329. MA B F, LIU P Q, DENG X Y. Research advances on a close-coupled canard wing configuration[J]. Acta Aerodynamica Sinica, 2003, 21(3): 320-329. DOI:10.3969/j.issn.0258-1825.2003.03.009 (in Chinese) |
| [10] |
HUMMEL D, OELKER H C. Low-speed characteristics for the wing-canard configuration of the international vortex flow experiment[J]. Journal of Aircraft, 1994, 31(4): 868-878. DOI:10.2514/3.46573 |
| [11] |
OELKER H C, HUMMEL D. Investigations on the vorticity sheets of a close-coupled delta-canard configuration[J]. Journal of Aircraft, 1989, 26(7): 657-666. DOI:10.2514/3.45817 |
| [12] |
SAMIMI S, DAVARI A R, SOLTANI M R. canard-wing interactions in subsonic flow[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2013, 37(M2): 133. |
| [13] |
ER-EL J. Effect of wing/canard interference on the loading of a delta wing[J]. Journal of Aircraft, 1988, 25(1): 18-24. DOI:10.2514/3.45535 |
| [14] |
HOWARD R M, O'LEARY J F. Flowfield study of a close-coupled canard configuration[J]. Journal of Aircraft, 1994, 31(4): 908-914. DOI:10.2514/3.46578 |
| [15] |
PONTON A, LOWSON M, BARRETT R. The evaluation of canard couplings at high angles of attack[C]//Proc of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1992. DOI: 10.2514/6.1992-281
|
| [16] |
魏园.近距耦合鸭式布局涡系干扰方式及效果的实验研究[D].北京: 北京航空航天大学, 2004.
|
| [17] |
温瑞英.近耦合鸭式布局鸭翼展向吹气涡控技术实验研究[D].北京: 北京航空航天大学, 2008. WEN R Y. Experimental study on vortex-control technology of canard-spanwise blowing of close-coupled canard wing configurations[D]. Beijing: Beihang University, 2008. (in Chinese) |
| [18] |
樊文博.非共面鸭式布局鸭翼涡控制技术实验研究[D].北京: 北京航空航天大学, 2010. FAN W B. Experiment study on canard vortex-control technology of non-coplanar canard wing configurations[D]. Beijing: Beihang University, 2010. (in Chinese) |
| [19] |
毛磊.鸭式布局大迎角复杂涡系干扰与破裂机理实验研究[D].北京: 北京航空航天大学, 2011. MAO L. Experiment study on mechanism of vortex-interaction and vortex breakdown over canard configuration at high angles of attack[D]. Beijing: Beihang University, 2011. (in Chinese) |
| [20] |
BERGMANN A, HUMMEL D. Aerodynamic effects of canard position on a wing body configuration in symmetrical flow[C]//Proc of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. DOI: 10.2514/6.2001-116
|
| [21] |
刘沛清, 王亚平, 刘杰, 等. 近距耦合鸭式布局复杂涡系的干扰机理[J]. 北京航空航天大学学报, 2012, 38(7): 873-876, 881. LIU P Q, WANG Y P, LIU J, et al. Vortex interaction mechanism over close-coupled canard configuration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 873-876, 881. DOI:10.13700/j.bh.1001-5965.2012.07.014 (in Chinese) |
| [22] |
刘杰.近距耦合鸭式布局鸭翼涡控制数值研究[D].北京: 北京航空航天大学, 2010. LIU J. Numerical study of vortex-control technology of the close-coupled canard wing configuration[D]. Beijing: Beihang University, 2010. (in Chinese) |
| [23] |
CAMPBELL J F. Effects of spanwise blowing on the pressure field and vortex-lift characteristics of a 44 deg swept trapezoidal wing[R]. NASA TN-D-7907, 1975.
|
| [24] |
CAMPBELL J F. Augmentation of vortex lift byspanwise blowing[J]. Journal of Aircraft, 1976, 13(9): 727-732. DOI:10.2514/3.58703 |
| [25] |
CAMPBELL J F, ERICKSON G E. Effects of spanwise blowing on the surface pressure distributions and vortex-lift characteristics of a trapezoidal wing-strake configuration[R]. N79-16803, 1979.
|
| [26] |
ERICKSON G E. Effect ofspanwise blowing on the aerodynamic characteristics of the F-5E[J]. Journal of Aircraft, 1979, 16(10): 695-700. DOI:10.2514/3.58591 |
| [27] |
ERICKSON G E, CAMPBELL J F. Flow visualization of vortices locked by spanwise blowing over wings featuring a unique leading-and trailing-edge flap system[R]. NASA TMX-72788, 1975.
|
| [28] |
DIXON C J. Lift augmention by lateral blowing over a lifting surface[R]. AIAA 69-193, 1969.
|
| [29] |
CORNISH Ⅲ J J. High lift applications of spanwise blowing[R]. ICAS Paper 70-09, 1970.
|
| [30] |
DIXON C. Lift and control augmentation byspanwise blowing over trailing edge flaps and control surfaces[C]//Proc of the 4th Aircraft Design, Flight Test, and Operations Meeting, Los Angeles, CA, USA. Reston, Virigina: AIAA, 1972. DOI: 10.2514/6.1972-781
|
| [31] |
THEISEN J G, SCRUGGS R M, DIXON C J. Theoretical and experimental investigations of vortex lift control byspanwise blowing. volume 2. three-dimensional theory for vortex-lift augmentation[R]. Defense Technical Information Center, 1973. DOI: 10.21236/ad0771304
|
| [32] |
BRADLEY R G, WRAY W O. A conceptual study of leading-edge-vortex enhancement byblowing[J]. Journal of Aircraft, 1974, 11(1): 33-38. DOI:10.2514/3.60318 |
| [33] |
BRADLY R G, WRAY W O, SMITH C W. An experimental investigation of leading-edge-vortex augmentation by spanwise[R]. NASA CR-132415, 1974.
|
| [34] |
HUFFMAN J K, HAHNEF D E, JOHNSON T D Jr. Aerodynamic effects of distributedspanwise blowing on a fighter configuration[J]. Journal of Aircraft, 1987, 24(10): 673-679. DOI:10.2514/3.45506 |
| [35] |
ERICKSON G E, CAMPBELL J F. Improvement of maneuver aerodynamics by spanwise blowing[R]. NASA TP-1065, 1977.
|
| [36] |
ERICKSON G, SCHREINER J, ROGERS L. canard-wing vortex interactions at subsonic through supersonic speeds[C]//Proc of the 17th Atmospheric Flight Mechanics Conference, Portland, OR. Reston, Virginia: AIAA, 1990 DOI: 10.2514/6.1990-2814
|
| [37] |
THEISEN J G, SCRUGGS R M, DIXON C J. Theoretical and experimental investigations of vortex lift control by spanwise blowing. Volume 2: Three-dimensional theory for vortex-lift augmentation[R]. Defense Technical Information Center, 1973. DOI: 10.21236/ad0771304
|
| [38] |
秦燕华.展向射流与机翼前缘涡相互干扰机理的实验研究[D].北京: 北京航空航天大学, 1993.
|
| [39] |
WIBOWO, BEKTI S, ROHMAT T A. Water tunnel flow visualization due to canard deflection effect on aircraft to improve stall delay performance[C]//4th International Conference on Science and Technology (ICST). IEEE, 2018.
|
| [40] |
RE R J, CAPONE F J. Longitudinal aerodynamic characteristics of a fighter model with a close-coupled canard at Mach nmuber from 0.40 to 1.20[R]. NASA TP-1206, 1978.
|
| [41] |
WEI Z C, ZHAN J X, HE X, et al. Influence of Gurney flaps on aerodynamic characteristics of a canard-configuration aircraft[J]. Aircraft Engineering and Aerospace Technology, 2019, 91(4): 700-707. DOI:10.1108/aeat-08-2017-0181 |
| [42] |
JENKINS M, MEYER R. A large-scale low-speed tunnel test of a canard configuration with spanwise blowing[C]//Proc of the Aircraft Systems and Technology Meeting, Los Angeles, CA, USA. Reston, Virigina: AIAA, 1975. DOI: 10.2514/6.1975-994
|
| [43] |
曹硕.非共面鸭式布局鸭翼涡控制技术实验研究[D].北京: 北京航空航天大学, 2010. CAO S. Experiment study on canard vortex-control technology of non-coplanar canard wing configurations[D]. Beijing: Beihang University, 2010. (in Chinese) |
| [44] |
冯晓伟.鸭翼展向射流间接涡控技术PIV实验研究[D].北京: 北京航空航天大学, 2012. FENG X W. PIV experiment study of canard spanwise-blowing indirect vortex control technique[D]. Beijing: Beihang University, 2012. (in Chinese) |
| [45] |
杨磊.鸭式布局鸭翼展向吹气间接涡控制机理数值研究[D].北京: 北京航空航天大学, 2011. YANG L. Numerical study on indirect-vortex-control technology of canard-spanwise blowing on canard wing configuration[D]. Beijing: Beihang University, 2011. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38