对流场施加控制可以起到增强/减弱流动稳定性、推迟/加速转捩、抑制/促进流动分离等作用,进而实现飞行器的增升、减阻、降噪、减振等效果。对流场采取高效的流动控制技术,不仅在飞行器设计中具有重要的工程意义,也成为当前流体力学领域的前沿和热点问题。按照是否需要能量注入,流动控制可以分为被动控制技术和主动控制技术[1]。常见的被动流动控制技术有涡流发生器、粗糙带、减阻杆等,具有结构简单、结构可靠等优点,在工程上得到了广泛应用。但是一旦偏离设计工况,反而会影响控制效果,更可能会给飞行器带来不利影响。主动流动控制技术具有工作频域宽、适应性强等特点,合成射流作为主动流动控制技术之一,以其结构简单、设计紧凑、稳定性高而备受关注[2]。
“合成剪切流动”最早是由Coles[3]提出并开展了实验验证。Glezer等人[2]在1998年提出了零质量射流概念,指出零质量射流的本质是振动膜的往复运动使得腔内流体产生周期性的吹吸,流体在出口处的剪切作用下形成的一系列非定常涡环。明晓教授也在同一时期发现了声学整流效应中的零质量射流现象[4]。
压电式合成射流本质上也是零质量射流的一种,它是通过压电陶瓷在变化的电信号下产生振动,压缩/膨胀腔内流体进而产生非定常射流。压电式激励器的结构相对简单、响应快,并且易于微小型化,在低速流场中得到了广泛的应用。但是在高速流场中,由于膜片两侧压力不同,会存在压载失效问题,罗振兵等人创新性地将振动膜片两侧同时处于受控流场中,发明了合成双射流激励器[5]。该激励器不仅解决了上述问题,同时能量效率和工作频率也得以倍增[6],已经在流动分离控制、掺混增强、防/除冰、小空间散热等方面得到了广泛应用[7]。
相对于合成射流,合成双射流的两股射流交替形成,并在向下游的演化过程中相互卷积吸引,涡对发生旋转变形,流场结构更为复杂,需要采用降维方法对流场做降阶处理,从大量数据中提取出流场的特征结构。本征正交分解(POD)是从海量数据、高维数据中提取分析低维近似流场结构的强大工具,其通过各阶模态的能量贡献率,将高维度非线性系统做线性降阶处理,利用少量模态数据即可得到流场的大尺度特征结构并能够对流场实施重构。本文拟采用POD方法对合成双射流的PIV实验数据进行处理,提取流场中的大尺度流动结构,分析流场的模态特征,以期进一步了解合成双射流的流场特性。
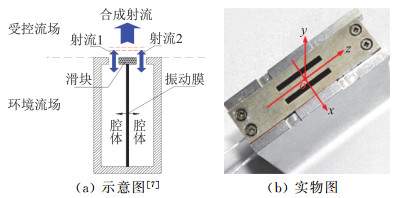
1 实验装置 1.1 合成双射流激励器合成双射流激励器装置示意图如图 1(a)所示[7]。该种设计的典型特点是振动膜两侧同时处于受控流场中,膜片两侧的压力相同,解决了压载失效问题,同时又具有两个出口,能够交替形成两股相位差为180°的射流,提高激励器的能量效率和工作频率。
|
图 1 合成双射流激励器示意图与实物图 Fig.1 Schematicand physical picture of dual synthetic jets actuator |
实验所用的合成双射流激励器采用了矩形出口(如图 1(b)所示),出口尺寸为20 mm×2 mm,出口深度为4 mm,两出口间距为5 mm。振动膜片的直径为23 mm,腔体的体积为24.6×103 mm3。坐标原点位于两出口的中间位置,x方向为横向,y方向为流向。实验中,激励器的电压信号为正弦波,频率为400 Hz,幅值为220 V。根据文献[6-7]可知,此时合成双射流的频率也为400 Hz。
1.2 PIV流场显示技术图像粒子测速(Particle Image Velocimetry, PIV)是20世纪80年代发展起来的一种新的非接触式流动显示技术,具有抗干扰能力强、响应快、测速范围宽、测量范围广等优点[8],已经得到了广泛的应用。
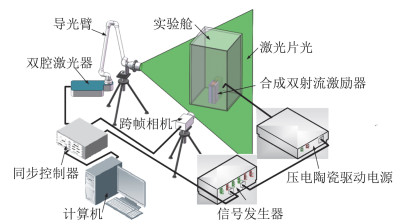
PIV系统主要由激光器、同步控制器、CCD相机图像采集卡和系统软件等组成,如图 2所示[9]。PIV的基本原理是,向流场中均匀播撒粒子,激光器在极短的时间间隔Δt内两次照亮观测区域,利用粒子对激光的散射作用,获取粒子在两次片光照亮时的位置信息,同时采用同步发生器对相机进行协同工作,获取两帧流场图像,采用自相关算法求得粒子在Δt时间间隔内的位移量,进而求得粒子的速度。由于粒子具有很好的跟随性,且时间间隔Δt极短,则认为得到的粒子速度就是粒子的瞬时速度,也即流场的速度。本文实验中采用平均粒径小于5 μm的烟作为示踪粒子,前人已开展相关实验验证其具有良好的跟随性[10]。
实验所用PIV系统由200 mJ的双腔激光器、导光臂、24 mmF/2.8镜头、分辨率为2456 pixel×2058 pixel的CCD相机、同步发生器等组成。激光器的工作频率为10 Hz,对应的CCD相机的拍摄频率也为10 Hz,查问区域的尺寸为32 pixel×32 pixel,重叠区域尺寸为16 pixel×16 pixel。粒子的固有计算位移误差为±0.1 pixel,图像与流场之间的放大系数为0.0964,粒子的位移误差约为0.01 mm,而跨帧时间为15 μs,则对应的速度测量不确定度≤0.7 m/s。
2 POD模态分解方法POD最早由Lumley[11-12]提出并应用于剪切流动中大尺度分离涡结构的提取。随后,众多学者将其用于对湍流的研究中,如有限长钝头平板边界层流动分离[13]、圆柱尾迹流动[14]、零质量射流流场结构[15-16]等。
POD最基本的思想是寻找一组最优正交基
| $ u\left( {x, t} \right) = \sum\limits_{i = 1}^N {{a_i}\left( t \right){\phi _i}\left( x \right)} $ | (1) |
其中
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}&{......}&{{u_N}} \end{array}} \right] $ | (2) |
基于此,计算速度场的自协方差矩阵:
| $ \mathit{\boldsymbol{C = }}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}} $ | (3) |
通过求解上述矩阵的特征值,即可求得POD的最优分解。具体步骤如下:
| $ \mathit{\boldsymbol{C}}{A_i} = {\lambda _i}{A_i} $ | (4) |
其中,λ是特征值,A是与之对应的特征向量。将求解出来的特征值按大小进行降序排列:
| $ {\lambda _1} > {\lambda _2} > ... > {\lambda _N} = 0 $ | (5) |
这样,分解出来的前几阶模态就会占有较大的能量。构建POD模态:
| $ {\phi _i} = \frac{{\sum\limits_{n = 1}^N {A_n^{^i}{u_n}} }}{{\left\| {\sum\limits_{n = 1}^N {A_n^{^i}{u_n}} } \right\|}}, {\rm{ }}\;\;\left( {i = 1, 2, \ldots , N} \right) $ | (6) |
其中,Ani为对应第i阶特征值的特征向量的第n阶分量。
将N阶POD模态表示为:
| $ \mathit{\boldsymbol{\psi }} = \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _2}}& \ldots &{{\phi _N}} \end{array}} \right] $ | (7) |
则时间系数ai可以表示为:
| $ {a_i} = {\mathit{\boldsymbol{\psi }}^{\rm{T}}}{u_n} $ | (8) |
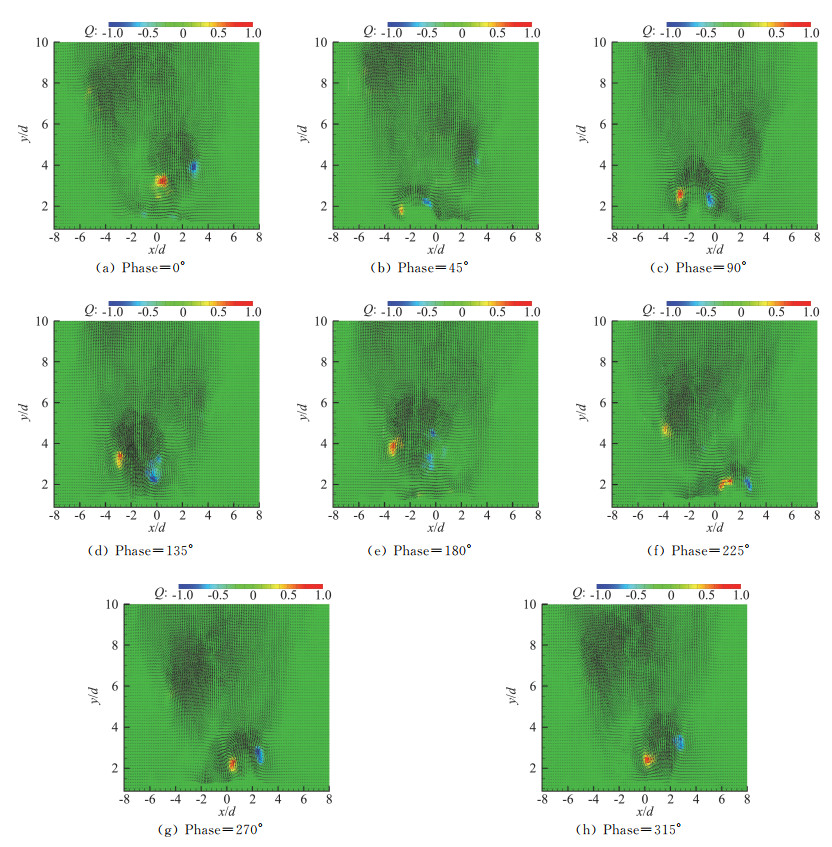
以激励器左边出口的射流涡刚从出口脱落时刻为0°相位,图 3给出了合成双射流一个周期内8个不同相位时刻的速度矢量与无量纲涡结构云图,其中涡结构采用的是Jeong和Hussain[18]提出的速度梯度张量的第二不变量Q识别方法。以激励器的出口宽度d作为参考量对坐标值进行无量纲化,则两个射流出口分别位于x轴上x=(1.25, 2.25)和x=(-1.25, -2.25)处。从图中可以看出,在Phase=0°相位点,左边的腔体开始压缩,射流剪切涡对从出口处脱落;随着时间的发展,射流涡向下游逐步迁移,同时会受到右侧腔体吸气过程导致的低压作用而略微向右侧倾斜(Phase=45°),在Phase=90°相位点,左侧处于最大压缩状态;此后,振动膜片将开始向右侧运动,但由于左侧依然处于压缩状态,所以射流涡强度依然较强并持续向下游推移(Phase=135°);在Phase=180°相位点,振动膜片回到中间位置并向右运动,右侧腔体开始压缩状态,右侧出口的射流即将脱离;此后右侧射流涡将经历左侧射流涡的同样过程,而左侧的射流则在涡对的自诱导速度下进一步向下游迁移,涡量逐渐减小,最终耗散在环境流场中(Phase=225°,Phase=270°,Phase=315°),此时合成双射流完成一个工作周期。下一个周期,射流又将重复此行为。由此可见,合成双射流的工作频率为合成射流的两倍,它能够在一个工作周期内通过左右腔体的交替压缩两次向外输出射流涡,不断向工作流场注入涡量与动量。
|
图 3 合成双射流相位平均流场 Fig.3 Phase averaged flow field of dual synthetic jets |
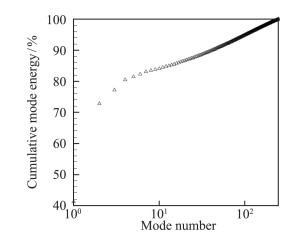
将激励器的一个工作周期等分为250个相位点,利用PIV的锁相控制技术对每个相位点流场进行测试,记录24对相关图像,采集了6000个流场样本,并通过相位平均得到相应各相位的流场结果。通过比对6000个流场样本与采用相位平均方法得到的250个相位平均样本,发现得到的POD分解模态特征基本一致,因此采用250个等时间间隔的流场流向速度和横向速度数据进行POD模态分解分析。图 4给出了POD分解各阶模态对湍动能的累积贡献率,从图中可以看出,第一阶模态的能量贡献率占据大约41%的能量,前两阶累计达到了72.7%,前四阶的累积贡献率为80.5%,占据了大部分的能量,第五阶模态以后的各阶模态贡献率均较低,表明前四阶模态所表征的是流场中的主要流动结构,湍流结构的尺度较大,而高阶模态展现的是更为破碎的小尺度涡结构。
|
图 4 POD模态累积贡献率 Fig.4 Cumulative mode energy of POD modes |
图 5具体给出了前四阶POD模态速度矢量与涡量云图,具体数值采用了每幅云图中的最大值做了无量纲化处理。图示表明,Mode 1和Mode 2关于射流出口中心轴线大致成对称分布,而Mode 3和Mode 4则呈现反对称分布。这是因为POD分解的模态是成对分布的,每对模态之间互为补集,所包含的能量相近、流动结构相似,但存在一定的相位差。具体分析来看,Mode 1主要体现了激励器出口附近由于两股射流相互卷吸干扰形成的大尺度旋涡结构,涡量的最大值出现在激励器两出口的中间位置,无量纲流向高度在2.2到2.4之间,同时在涡量核心区的两侧又有一组涡量为负的涡对;在Mode 1的基础上,Mode 2中的三个涡结构沿流向发展了1个无量纲高度,涡的强度有所降低,同时,在出口附近又形成了一组涡量为正且强度较高的涡对;Mode 3和Mode 4中,沿着射流流向分布着一系列正负涡量交替出现的小尺度涡结构,在两出口之间也有一对涡量相反的小尺度涡结构,并且,Mode 4也是在Mode 3的基础上发展了1个无量纲高度。
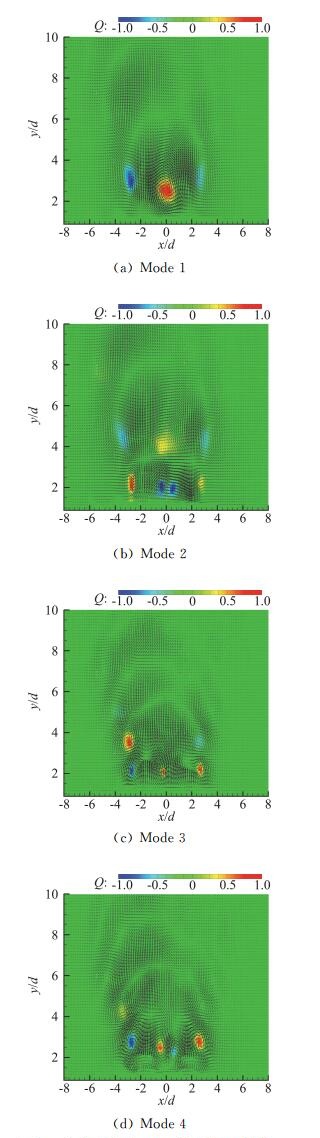
|
图 5 合成双射流POD分解前四阶模态 Fig.5 First four POD modes of dual synthetic jets |
分析认为,POD分解的本质就是对不同涡结构依据其能量大小进行排序,而涡结构的能量往往与其旋涡尺度有关。合成双射流的大尺度湍流结构主要是在激励器出口位置以及射流卷吸与相互作用较强的出口中间位置,这与Mode 1和Mode 2所展现的结果相一致。而随着模态阶数的增加,反映的涡结构的尺度也随之减小,由于与环境流场存在剪切、卷积与能量传递作用,大尺度涡结构逐渐破碎分解为能量较低的小尺度涡结构,湍动能分布更加扩散,逐步呈现在高阶模态中(Mode 3与Mode 4),直到全部耗散在流场中(更高阶模态)。
前四阶模态的时间系数曲线都呈现近似正弦变化的周期性特征(如图 6(a)所示),对时间系数做频谱分析,可以观察到各阶模态的频率特征(图 6(b)),其中,Mode 1和Mode 2的频率为400 Hz,与激励器的工作频率相同,对应的功率谱密度值也相对较高;Mode 3和Mode 4的频率则为二阶谐频800 Hz,这是因为随着模态阶数的增加,其所表征的流动结构尺度有所减小,相应的时间尺度也有所减小;同时其对应的功率谱密度值也相对前两阶模态小了一个数量级,这也与图 4中特征值减小这一结果相互印证。
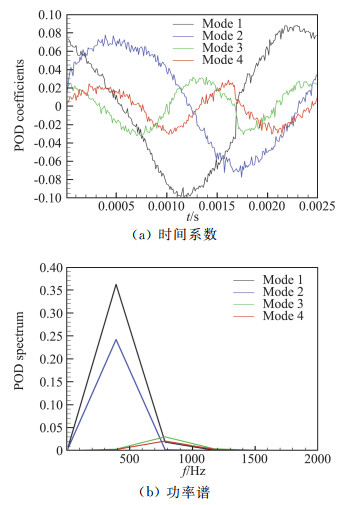
|
图 6 前四阶POD模态时间系数及其功率谱 Fig.6 Time coefficients and power spectrum of the first four POD modes |
图 7和图 8直观地给出了合成双射流速度场POD分解前四阶模态的横向模态和流向模态云图。图中做了归一化处理,红色部分代表正的速度,蓝色部分代表负的速度。从图中可以看出,对于横向模态,Mode 1和Mode 2关于激励器射流出口中心线呈对称分布,其中Mode 2是在Mode 1的基础上向下游发展了一个无量纲高度,流动的结构尺度也有所发展;Mode 3和Mode 4则呈反对称分布特征,Mode 4也是在Mode 3的基础上向下游发展了一个无量纲高度;并且横向模态的分布特征与图 5中射流的涡量场分布特征十分相似。而对于流向模态则恰好相反,此时前两阶模态呈反对称分布,而后两阶模态则呈对称分布特征。这与Liran等人[19]针对单个圆形出口的合成射流进行POD分解得到的结果相一致。
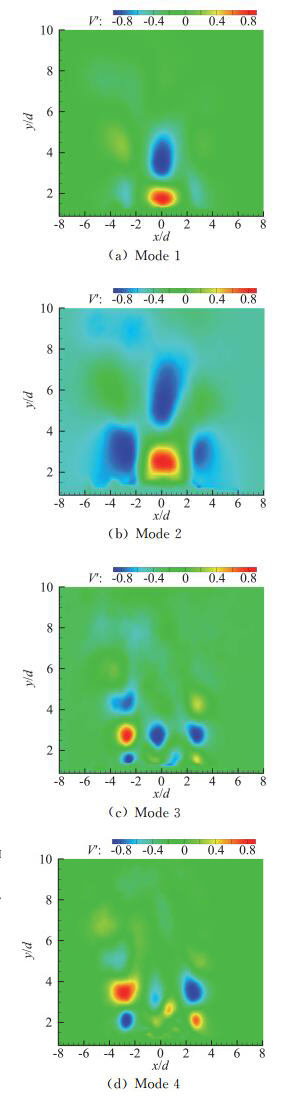
|
图 7 合成双射流POD分解前四阶横向模态 Fig.7 Transverse direction of the first four POD modes |
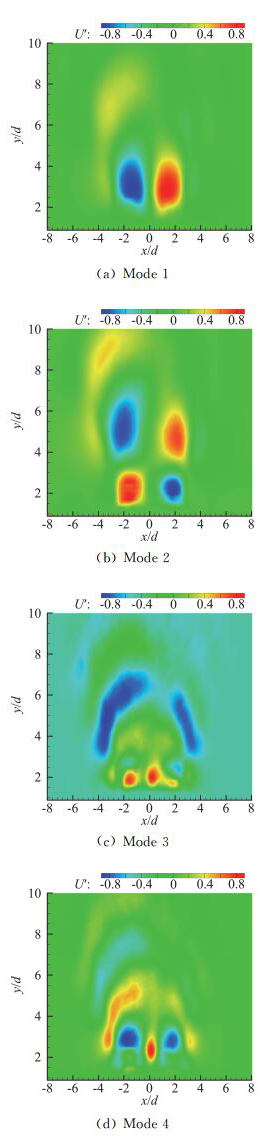
|
图 8 合成双射流POD分解前四阶流向模态 Fig.8 Streamwise direction of the first four POD modes |
采用PIV流场显示技术对静止环境中合成双射流进行了实验研究,并基于POD方法分析了合成双射流的流场特性,得出以下结论:
1) 在一个工作周期内,合成双射流的两个出口交替形成两股相位差为180°、相互卷积吸引的射流,不断向流场输入动量和涡量。
2) POD分析的结果表明,模态阶数越高,所表征的流动结构尺度越小,占据的能量也越小,前四阶模态占据了流场绝大部分的能量(80.5%)。
3) 前两阶POD横向模态呈对称分布,后两阶呈反对称分布;而前两阶流向模态则呈反对称分布,后两阶呈对称分布,表明合成双射流流场具有高度对称性。
后续将进一步深入对合成双射流流场特征结构的研究,采用流场拉格朗日特征分析方法来捕捉射流的涡环运动轨迹特征。
| [1] |
CATTAFESTA L N Ⅲ, SHEPLAK M. Actuators for active flow control[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 247-272. DOI:10.1146/annurev-fluid-122109-160634 |
| [2] |
GLEZER A, AMITAY M. Synthetic jets[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 503-529. DOI:10.1146/annurev.fluid.34.090501.094913 |
| [3] |
SAVAS Ö, COLES D. Coherence measurements in synthetic turbulent boundary layers[J]. Journal of Fluid Mechanics, 1985, 160: 421-446. DOI:10.1017/s0022112085003548 |
| [4] |
明晓, 戴昌晖, 史胜熙. 声学整流效应的新现象[J]. 力学学报, 1992, 24(1): 48-54. MING X, DAI C H, SHI S X. A new phonomenon of acoustic streaming[J]. Acta Mechanica Sinica, 1992, 24(1): 48-54. (in Chinese) |
| [5] |
罗振兵, 夏智勋, 刘冰.单膜双腔双口合成射流激励器: CN1818399[P]. 2006-08-16. LUO Z B, XIA Z X, LIU B. Synthetic jetting excitor with single-membrane, double openings and double cavities: CN1818399[P]. 2006-08-16.(in Chinese) |
| [6] |
LUO Z B, XIA Z X, LIU B. New generation of synthetic jet actuators[J]. AIAA Journal, 2006, 44(10): 2418-2420. DOI:10.2514/1.20747 |
| [7] |
罗振兵, 夏智勋, 邓雄, 等. 合成双射流及其流动控制技术研究进展[J]. 空气动力学学报, 2017, 35(2): 252-264. LUO Z B, XIA Z X, DENG X, et al. Research progress of dual synthetic jets and its flow control technology[J]. Acta Aerodynamica Sinica, 2017, 35(2): 252-264. DOI:10.7638/kqdlxxb-2017.0053 (in Chinese) |
| [8] |
WESTERWEEL J, ELSINGA G E, ADRIAN R J. Particle image velocimetry for complex and turbulent flows[J]. Annual Review of Fluid Mechanics, 2013, 45(1): 409-436. DOI:10.1146/annurev-fluid-120710-101204 |
| [9] |
彭磊, 罗振兵, 邓雄, 等. 水下合成双射流流场特性与推力特性实验研究[J]. 空气动力学学报, 2017, 35(2): 290-298. PENG L, LUO Z B, DENG X, et al. Experimental investigation on characteristics of flow field and propulsion of dual synthetic jets in water[J]. Acta Aerodynamica Sinica, 2017, 35(2): 290-298. DOI:10.7638/kqdlxxb-2016.0183 (in Chinese) |
| [10] |
DENG X, XIA Z X, LUO Z B, et al. Vector-adjusting characteristic of dual-synthetic-jet actuator[J]. AIAA Journal, 2015, 53(3): 794-797. DOI:10.2514/1.j053415 |
| [11] |
LUMLEY J L. The structure of inhomogeneous turbulence[R]//YAGLOM A M, TARTARSKY V I, Eds. Atmospheric turbulence and wave propagation. Moscow: Nauka, 1967: 166-178.DOI: 10.1007/BF00271656
|
| [12] |
BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539-575. DOI:10.1146/annurev.fl.25.010193.002543 |
| [13] |
ZHANG Q S, LIU Y Z. Influence of incident vortex street on separated flow around a finite blunt plate:PIV measurement and POD analysis[J]. Journal of Fluids and Structures, 2015, 55: 463-483. DOI:10.1016/j.jfluidstructs.2015.03.017 |
| [14] |
FENG L H, WANG JJ, PAN C. Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control[J]. Physics of Fluids, 2011, 23(1): 014106. DOI:10.1063/1.3540679 |
| [15] |
LE CLAINCHE S, VEGA J M, SORIA J. Higher order dynamic mode decomposition of noisy experimental data:The flow structure of a zero-net-mass-flux jet[J]. Experimental Thermal and Fluid Science, 2017, 88: 336-353. DOI:10.1016/j.expthermflusci.2017.06.011 |
| [16] |
LIU Q, LUO Z B, DENG X, et al. Numerical investigation on flow field characteristics of dual synthetic cold/hot jets using POD and DMD methods[J]. Chinese Journal of Aeronautics, 2020, 33(1): 73-87. DOI:10.1016/j.cja.2019.07.004 |
| [17] |
MEYER K E, PEDERSEN J M, ÖZCAN O. A turbulent jet in crossflow analysed with proper orthogonal decomposition[J]. Journal of Fluid Mechanics, 2007, 583: 199-227. DOI:10.1017/s0022112007006143 |
| [18] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285: 69. DOI:10.1017/s0022112095000462 |
| [19] |
LIRAN O, EPHRAIM G. Turbulent characteristics of axisymmetric and non-circular synthetic jets[R]. AIAA 2010-1261.
|
 2020, Vol. 38
2020, Vol. 38