高超声速飞行器边界层流场发生转捩时,飞行器表面热环境及飞行器气动特性发生显著变化。正确预测转捩位置,对于优化飞行器热防护设计、提升飞行器性能具有十分重要的工程意义[1-2]。
影响高超声速边界层转捩的因素众多,包括转捩雷诺数、边界层边缘马赫数、壁面温度、攻角、头部钝度等[1-5],且作用机理复杂,许多问题尚未解决。因此,高超声速边界层转捩是当前流体力学领域一个前沿和难点问题,受到广泛关注。
壁面温度是影响高超声速转捩的一个重要因素。通常情况下,地面风洞试验中壁温与来流总温比高,而天上真实飞行条件下的壁温与来流总温比低,地面试验无法模拟天上真实飞行的壁温条件,这是造成天地差异的一个重要因素。因此,研究壁面温度条件对边界层流动稳定性及转捩的影响十分重要。
Gary[6]研究表明,转捩雷诺数随着壁温比的降低而增大。Stetson[7]则通过热线试验发现,冷壁的转捩雷诺数(约3.2×106)低于正常壁温下的转捩雷诺数(约4.8×106)。Malik[8]采用eN法分析了5°尖锥的边界层流场稳定性特征,发现对于绝热壁边界层,在来流马赫数低于7时为第一模态导致转捩,而对于冷却壁,在较低马赫数时已变为第二模态导致转捩。Gasperas[9]研究分析了平板和尖锥在不同壁温下的稳定性特征,认为表面温度沿流向线性降低时,扰动增长率和N值明显小于绝热壁。尚庆等[10]研究表明,壁温升高会使壁面热流下降,速度边界层变厚,剖面不饱满,更易发生流动分离。苏彩虹、周恒[11]研究了0°攻角高超声速钝锥边界层,表明绝热壁边界层的转捩位置比等温壁边界层靠后。曹伟[12]研究发现,壁面温度条件对是第一模态还是第二模态波决定转捩位置有很大关系。刘志勇、杨武兵等[13]研究了一定来流工况下的平板边界层,发现壁温升高,初始推迟转捩,随后变化趋势发生反转。Liang等[14]研究了壁温对马赫数7.99的钝锥边界层流动稳定性影响,研究表明不同壁温比条件显著影响了边界层广义拐点和压力梯度分布,导致不同稳定性特征,同时在绝热壁条件下,扰动波增长不再只依赖于第二模态扰动波。王振清,唐小军等[15]研究表明,冷壁总体上加速了钝楔边界层高频不稳定模态的发展。Eppink等[16]通过对比试验和线性PSE结果表明,壁温对横流行波增长率影响很大,将显著改变N值分布。
以往关于高超声速边界层转捩壁温影响的研究多基于二维平板或轴对称的钝锥等简单外形,研究结果表明了壁面温度条件对转捩影响的复杂性。然而,对于采用升力体外形的高超声速飞行器来说,其三维几何特征明显,包括钝化的端头和翼前缘、大后掠角的翼面形状、较扁平的迎风面构型等。平板钝三角翼外形具有钝化的钝头、钝化的翼前缘、大的翼后掠角,有攻角下,其迎风面为简单的平板构型。显然,平板钝三角翼相比二维平板和轴对称钝锥更能表征升力体外形的高超声速流动,包括横流效应、前缘效应和熵层效应等,研究平板钝三角翼外形壁温条件对边界层流动稳定性及转捩的影响既具有学术价值,也具有工程价值。但是,对此类外形的相关研究工作很少,为此,有必要开展相关的壁温影响研究,为高超声速飞行器的转捩分析与预示奠定理论基础。
本文针对平板钝三角翼外形,围绕典型高超声速风洞试验状态开展流场数值计算和线性稳定性分析,研究不同壁温条件下该外形边界层的流动稳定性特征,并采用eN法获取不同壁温条件下平板钝三角翼表面的N值分布,研究壁温条件对边界层转捩的影响。
1 计算方法 1.1 控制方程采用可压缩N-S方程进行基本流场的数值模拟。若直角坐标系为(
| $ \frac{{\partial \mathit{\boldsymbol{\hat Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{\hat E}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \zeta }} = \frac{{{\rm{ }}\partial \mathit{\boldsymbol{\hat E}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \zeta }} $ | (1) |
式中,
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat Q}} = \mathit{\boldsymbol{JQ}}}\\ {\mathit{\boldsymbol{\hat E}} = \mathit{\boldsymbol{J}}({\xi _x}\mathit{\boldsymbol{E}} + {\xi _y}\mathit{\boldsymbol{F}} + {\xi _z}\mathit{\boldsymbol{G}})}\\ {\mathit{\boldsymbol{\hat F}} = \mathit{\boldsymbol{J}}({\eta _x}\mathit{\boldsymbol{E}} + {\eta _y}\mathit{\boldsymbol{F}} + {\eta _z}\mathit{\boldsymbol{G}})}\\ {\mathit{\boldsymbol{\hat G}} = \mathit{\boldsymbol{J}}({\zeta _x}\mathit{\boldsymbol{E}} + {\zeta _y}\mathit{\boldsymbol{F}} + {\eta _z}\mathit{\boldsymbol{G}})}\\ \begin{array}{l} {{\mathit{\boldsymbol{\hat E}}}_v} = \mathit{\boldsymbol{J}}({\eta _x}{\mathit{\boldsymbol{E}}_v} + {\zeta _y}{\mathit{\boldsymbol{F}}_v} + {\zeta _z}{\mathit{\boldsymbol{G}}_v})\\ {{\mathit{\boldsymbol{\hat F}}}_v} = \mathit{\boldsymbol{J}}({\eta _x}\mathit{\boldsymbol{E}}v + {\eta _y}{F_v} + {\eta _z}{\mathit{\boldsymbol{G}}_v}) \end{array}\\ {{{\mathit{\boldsymbol{\hat G}}}_v} = \mathit{\boldsymbol{J}}({\zeta _x}{\mathit{\boldsymbol{E}}_v} + {\zeta _y}{\mathit{\boldsymbol{F}}_v} + {\zeta _z}{\mathit{\boldsymbol{G}}_v})} \end{array} $ |
N-S方程数值求解中,采用有限体积法,对流项采用三阶迎风Roe-FDS格式离散,黏性项采用中心差分格式离散,时间推进为AF-LU隐式方法。
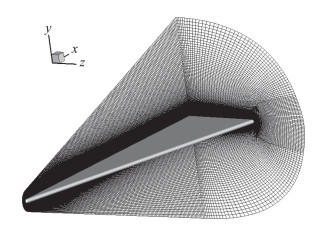
不考虑对底部流场的模拟,物面采用无滑移边界条件,出口设为超声速外插边界条件。计算域为半模,网格量为201×281×137,如图 1,法向网格布置点数较多,原因在于后续稳定性分析需要较为精细的边界层流场。
|
图 1 计算域及网格 Fig.1 Computational domain and mesh |
根据线性稳定性理论,二维局部平行流假设下,分析O-S方程可将小扰动表示为行进波形式:
| $ q(x, y, z, t) = \hat q(y){{\rm{e}}^{{\rm{i}}(\alpha x + \beta z{\rm{ - }}\omega t)}} + {\rm{c}}{\rm{.c}}. $ | (2) |
对于空间模式,式(2)中波数α、β一般为复数,其虚部的负值-αi、-βi分别为扰动在x向、z向的空间增长率,ω为扰动波频率。
扰动向下游传播时增长率将发生变化。目前工程上常用的一种转捩预测方法eN法[17-19]就是基于线性稳定性理论,将增长率沿扰动传播路径积分, 得到扰动幅值放大因子N:
| $ N\left( {\omega , x, z} \right) = \int_{({x_0}, {z_0})}^{(x, z)} { - ({\alpha _i}{\rm{d}}x + {\beta _i}{\rm{d}}z)} $ | (3) |
式中,(x0, z0)为频率为ω的扰动波开始失稳处(αi、βi由正转负的中性点),其位置在中性曲线上;增长率-αi、-βi取当地频率为ω的最不稳定扰动波(增长率最大)的增长率,扰动传播路径方向即该扰动波的群速度方向。
预设转捩判据为Ntr(通常由经验给出),即对于不同频率ω的扰动波,若在(xtr, ztr)处幅值放大因子达到Ntr,预示转捩发生。不同频率扰动波达到Ntr的位置不同,一般取最上游位置作为转捩发生位置,对应N值称为包络N值。转捩位置曲线应满足:
| $ N\left( {x, z} \right) \equiv \mathop {{\rm{max}}}\limits_\omega N\left( {\omega , x, z} \right) = {N_{{\rm{tr}}}} $ | (4) |
文献[20]针对HIFiRE-1飞行工况进行了数值模拟,钝锥半锥角7°,头部半径2.5 mm,计算工况如表 1,壁面条件取恒温壁Tw=410 K (Tw/T0, ∞=0.168)。
| 表 1 算例工况 Table 1 Freestream conditions of numerical example |
|
|
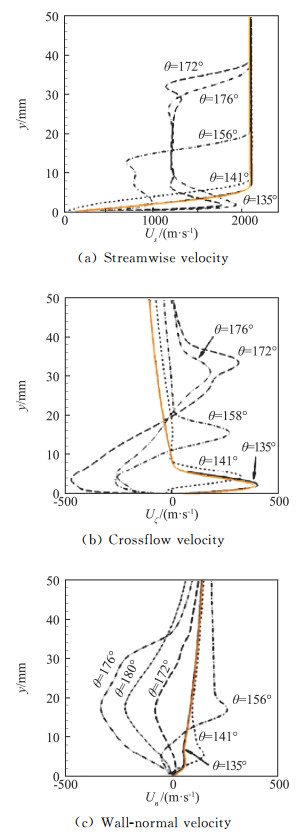
为考核三维流场计算的可靠性,特别是边界层流场和横流效应,本文采用前述计算方法对文献[20]中算例进行了计算,得到的流向x=850 mm、背风面θ=135°位置点的基本流速度剖面与文献[20]结果比较如图 2所示,其中橘色速度剖面为计算结果,与算例基本相符,验证了边界层流场计算的正确性。
|
图 2 算例对比 Fig.2 Comparison of numerical example |
几何模型为一平板钝三角翼外形[21],长度取400 mm,钝度半径3 mm,后掠角75°。定义坐标系原点O为钝三角板顶点,x、z轴指向如图 3所示,y轴符合右手坐标系。

|
图 3 平板钝三角翼外形及坐标系示意图 Fig.3 Modal and coordinate system of flat plate blunt delta wing |
基本的计算工况选取典型的地面高超声速风洞试验条件:单位来流雷诺数Re∞=7.12×106/m,马赫数M∞=6,总温T0, ∞=420 K,攻角、侧滑角均为0°。选取壁温条件时,考虑了以下四种典型情况:
1) 真实飞行状态下,来流总温高,壁温比小,约为0.3;2)在飞行器再入段,由于前期的气动加热和随后的飞行速度降低,有些情况下会出现真实壁温高于绝热壁温的情况,即壁面向流场放热,此时壁温比很高,超过绝热壁温比;3)高超声速风洞试验中,来流总温较低,壁温比通常为0.7左右;4)在温敏漆等试验中,由于采用非金属材料,壁面条件可看作是绝热壁。于是,本文选取了四个典型的壁温条件,包括一个绝热壁条件和三个等温壁条件(150 K,300 K,400 K)。不同壁温条件下,壁温与来流总温比如表 2所示。
| 表 2 不同壁温条件下壁温与来流总温比 Table 2 Ratios of wall temperature to total temperature of freestream for different wall conditions |
|
|
为便于比较,本文结果分析采用如下的无量纲化形式:
| $ \begin{array}{l} {x^*} = x/{L_x}, {z^*} = z/{L_z}, y_n^* = {y_n}/\delta , \\ {V^*} = V/{V_{∞}}, {T^*} = T/{T_{0, ∞}} \end{array} $ |
式中,Lx、Lz分别为钝三角翼外形的长度和底部半宽度,δ为当地边界层厚度,V∞为来流速度(860.838 m/s),T0, ∞为来流总温(420 K)。
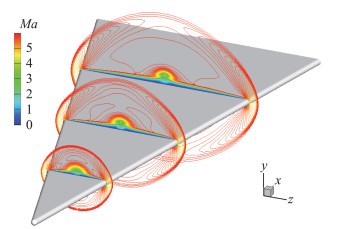
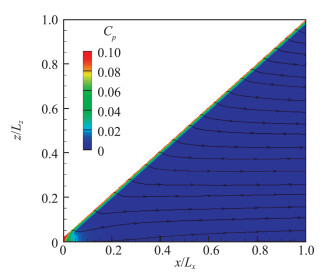
图 4为绝热壁条件下平板三角翼不同流向位置处的马赫数分布云图,由于工况为0°攻角状态,迎/背风流场对称,同一流向截面上从侧前缘至中心子午线发展,边界层逐渐增厚,并在中心区域形成流向涡结构。图 5为三角翼表面压力系数及壁面极限流线分布,图 6为无量纲最大横流速度分布,图中Z/Lz=0对应对称中心线位置,Z/Lz=1对应钝三角翼底部最大展向位置。可知除中心子午线流向涡区域和侧前缘区域外,翼身上壁面极限流线方向基本平行,无复杂流场结构。
|
图 4 不同流向位置处的马赫数云分布 Fig.4 Mach number contours at different streamwise locations |
|
图 5 表面压力系数分布及流线 Fig.5 Limiting surface streamlines |

|
图 6 横流速度分布 Fig.6 Cross flow velocity contours |
由于中心对称线区域流动复杂,存在大尺度流向涡结构,流场变化剧烈,因此,后续采用线性稳定性理论分析时应避开该区域,且平板三角翼外形需考虑三维效应,故基于绝热壁状态流场,特别是中心流向涡尺度特征和边界层横流流动特征(如图 6),选择当地流线近乎平行、横流效应较弱位置Point1(x*=0.88,z*=0.2),和靠近前缘、横流效应较强点Point2(x*=0.88,z*=0.8)两点进行研究,分析不同壁面温度条件对不同模态流动稳定性特征影响。
绝热壁条件下除头部和前缘区域外,其它位置的绝热壁温均处于300~400 K之间,两点当地绝热壁温分别为Taw, 1=330 K、Taw, 2=339 K,与来流总温比分别为Taw, 1 *=0.786、Taw, 2 *=0.807,暂将绝热状态视为等温壁状态Tw*=0.714和0.952中间一临界状态。
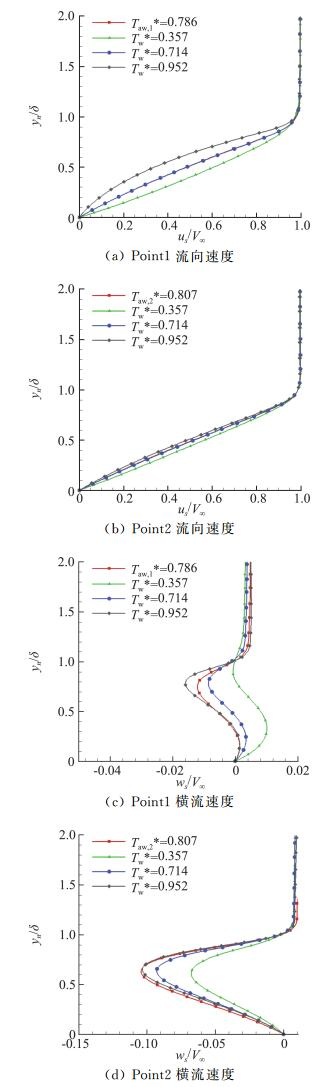
Point1、Point2处不同壁温条件下速度剖面的对比如图 7,其中图 7(a)、图 7(b)为流向速度剖面,图 7(c)、图 7(d)为横流速度剖面。由图 7(a)、图 7(b)可知,Tw*=0.357时较其它三种壁面温度条件下流向速度剖面更加饱满,绝热条件下两点速度剖面与Tw*=0.714几乎重合。由图 7(c)、图 7(d)可知,Point1处横流速度比Point2处小一个量级,且图 7(d)表明,壁温比越高,横流速度越大。
|
图 7 速度剖面 Fig.7 Velocity profiles |
在获取各壁温条件基本流流场的基础上,针对平行性较好的流动区域(中心流向涡区域和侧前缘区域除外)开展了线性稳定性分析计算,获得了边界层流动的稳定性特征。
高超声速边界层内存在局部超声速扰动区域,此时无黏不稳定性占主导地位,广义速度拐点

|
图 8 广义速度梯度 |
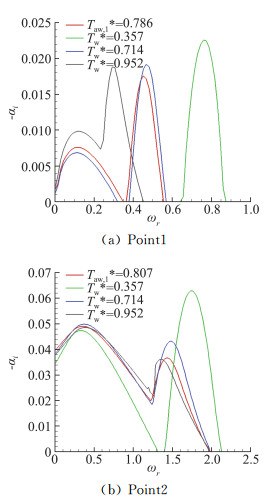
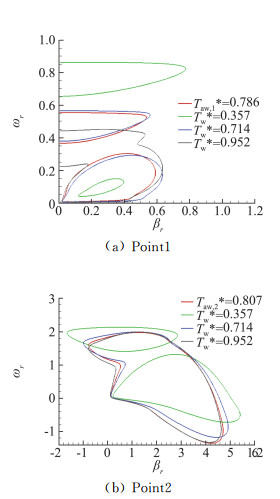
图 9、图 10分别为不同壁面温度条件下Point1和Point2两点当地每个频率的最大增长率分布和中性曲线。图中,低频和高频两个分支分别对应第一模态和第二模态的扰动。ωr为扰动波的无量纲频率,βr为扰动波的展向波数。
|
图 9 增长率分布 Fig.9 Distributions of amplification rate |
|
图 10 中性曲线 Fig.10 Neural Curve |
分析比较Point1点的稳定性特征(图 9(a)和图 10(a))可知,低壁温比(Tw*=0.357)状态下,第一模态的扰动很弱;随着壁温比Tw*的上升,第一模态扰动的频域和展向波数范围逐渐扩张,对应的扰动增长率峰值也逐渐升高,第二模态扰动的频域和展向波数范围则逐渐缩小,扰动增长率峰值也逐渐降低;第二模态曲线逐渐向第一模态靠拢,对于Tw*=0.952状态,出现了中性曲线相交。
Point2靠近钝三角翼前缘,边界层横流速度较大。分析图 9(b)和图 10(b)可知,对应横流驻波(ωr=0)的扰动增长率在高壁温比(Tw*=0.807和0.952)时,高于第二模态最大扰动增长率;随着壁温比Tw*的升高,横流驻波(ωr=0)的展向波数范围略微缩小,扰动增长率有所增大。无论是第一模态还是第二模态。扰动增长率的量值均明显高于Point1,且除Tw*=0.357外,第一模态的最大扰动增长率均大于第二模态。对于Tw*=0.357,相比Point1,第一模态和第二模态彼此更为靠近,而对于Tw*=0.714、0.807和0.952,第一模态和第二模态彼此相交。
由图 8可知,低壁温比状态(Tw*=0.357)下存在两个广义拐点,其它状态则只存在一个广义拐点。而从图 9看,低壁温比状态下第二模态的扰动增长率明显更高。由此推测,两者之间可能存在关联,即第二广义拐点的出现可能促进第二模态失稳。
综上分析,可知:
1) 壁温比Tw*对不同模态的影响存在差异。壁温比Tw*升高促使第一模态波的增长,抑制第二模态波的增长,对第二模态的影响强于对第一模态影响(增长率分布、频域和波数范围),并促使模态相交出现。
2) 由于钝三角翼存在复杂的三维边界层流动,不同展向位置的边界层稳定性特征不同,壁温的影响也出现差异,这与二维平板和0°攻角轴对称钝锥不同。Point2(靠近前缘区域)的横流模态扰动增长率与第二模态增长率幅值相当,且当地扰动增长率明显高于Point1(靠近对称中心线),并先于Point1出现模态相交现象。
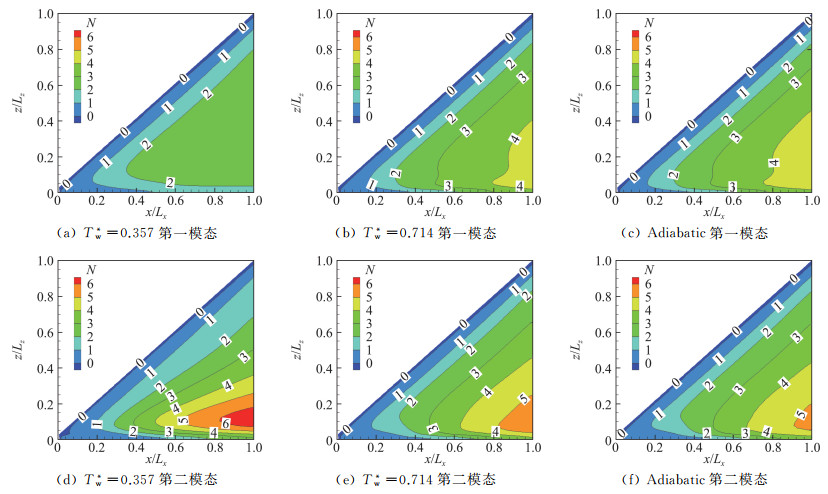
3.3 包络N值及转捩分析图 11为不同壁温比条件(Tw*=0.357和0.714,绝热壁)下平板钝三角翼表面不同模态包络N值分布(由于半模计算带来的边界效应和中心涡结构的影响,对称中心线附近的N值是失真的)。由于Tw*=0.952时三角翼中心区域不同模态中性曲线明显相交,已无法明确区分第一、二模态N值,在此就不对其进行分析。
|
图 11 不同模态包络N值分布 Fig.11 N-factor contours for different mode disturbances |
比较可知,在钝三角翼表面,等温壁Tw*=0.357和0.714条件下,第二模态N值的最大值明显大于第一模态,即低壁温比下主要是第二模态诱发转捩,而绝热壁条件下,两者的量值是相当的。从随壁温比的变化规律看,随着壁温比Tw*升高,第一模态包络N值的最大值逐渐增大,而第二模态包络N值的最大值逐渐减小,表明壁温比的升高会加速第一模态失稳,抑制第二模态失稳,这与文献[6]和文献[15]的结论相同。
四种壁温条件下整体包络N值在钝三角翼表面的分布情况见图 12。
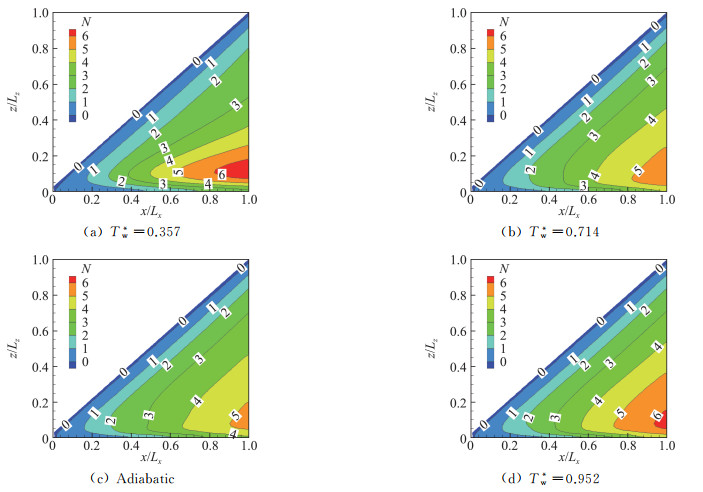
|
图 12 整体包络N值分布 Fig.12 Total N-factor contours |
比较可知,随着壁温比Tw*升高,包络N值的最大值先减小后逐渐增大。暂取N=4.5作为转捩Ntr值,则不同壁温比条件下转捩位置如图 13所示。可知,随着壁温比Tw*增大,流向上转捩阵面先向后推移,达到一定临界壁温比条件(本例中在绝热壁条件附近)后,转捩阵面转而前移,出现转捩反转,且Tw*=0.357的转捩阵面形状明显不同于其他三种壁温比条件。文献[11]指出,绝热壁边界层的转捩位置比等温壁边界层的靠后,这与本文结果一致,但由于文献[11]仅考虑了壁温低于绝热壁温的情况,没有预示出转捩反转。文献[13]中采用eN法预示出了转捩反转,但未从机理上对该现象进行分析。

|
图 13 转捩判据为Ntr=4.5时转捩线位置 Fig.13 Transition locations at Ntr=4.5 |
为探讨转捩反转现象的内在机理,下面分析过Point1点最不稳定扰动波沿势流方向的变化情况。
首先提取不同壁温条件下Point1点处的包络N值及对应该包络N值的扰动波频率(本文称之为Point1点的最不稳定波频率)和扰动增长率,如表 3所示。
| 表 3 Point1点当地最不稳定扰动波参数 Table 3 The most unstable disturbance characters at Point1 |
|
|
过Point1点对应最不稳定波频率的扰动波其增长率沿势流方向的分布如图 14(a)所示,横轴ls*为无量纲势流方向距离。图 14(b)、图 14(c)分别为流向ls*≈0.0065位置(靠近扰动失稳起始点)和Point1点扰动增长率的频域分布,四个圆点分别为表 3中提取的Point1点的最不稳定波频率对应增长率。

|
图 14 对应最不稳定波频率的扰动特性 Fig.14 Character curves of the most unstable disturbance |
由图 14(a)可知,对应Point1点最不稳定波频率的扰动增长率沿势流方向明显具有两个峰值,ls*=0.0065点和Point1点则分别位于前后这两个峰值区域内。
第一个峰值区域位于钝三角翼的前缘附近,结合图 14(b)可知,该区域内边界层具有较强的横流效应,且横流模态波的增长率超过了第二模态波的增长率。由于在ls*=0.0065点附近Point1点最不稳定波频率处在当地的第一模态频域范围内,因此,此处的扰动属于第一模态扰动。随着壁温比Tw*的增大,该区域内的扰动增长率增大,同时峰值区域沿势流方向的范围也增大。
扰动波沿势流方向发展到Point1点时,结合图 14(c)可知,最不稳定波频率进入了当地的第二模态频域范围内,扰动转而属于第二模态扰动。扣除Tw*=0.952,随着壁温比Tw*的增大,扰动增长率降低。
不同壁温条件下N值沿势流方向的分布如图 15所示,其分布与变化受图 14(a)中两个增长率峰值区域的共同影响。壁温比小于等于绝热壁值时,壁温比对第二个增长率峰值区域的作用对N值产生的影响程度大,使得Point1点的N值随Tw*增大而减小;而壁温比超过绝热壁值时,壁温比对第一个增长率峰值区域的作用对N值产生的影响超过了对第二个增长率峰值区域的影响,而这种影响方向是相反的。综合的结果,使得Point1点的N值转而随壁温比Tw*的增大而增大。

|
图 15 N值分布 Fig.15 Distributions of N-factor |
由以上分析可知,转捩反转的内在机理在于大后掠角平板钝三角翼边界层流动独特的横流特征:在靠近前缘区域,横流效应强,扰动以横流模态和第一模态为主,形成一个扰动增长率峰值区域;而在靠近对称中心线的区域,横流效应弱,扰动以第二模态为主,形成另一个扰动增长率峰值区域。壁温比低于绝热壁值时,壁温比的增加主要影响第二个峰值区域,导致N值降低,转捩延迟;当壁温比超过绝热壁值后,壁温比对第一个峰值区域的影响超过了对第二个峰值区域的影响,导致N值增大,转捩前移。
4 结论本文研究了在地面风洞试验条件(M∞=6,Re∞=7.12×106/m,α=β=0°)下,壁面温度变化对大后掠角平板钝三角翼外形高超声速边界层流动稳定性及转捩的影响。所得结论如下:
1) 低壁温比下(Tw*=0.357),边界层速度剖面更饱满,出现第二个广义速度拐点。
2) 壁温条件的变化对不同模态的扰动产生显著影响。壁温比升高促进横流模态和第一模态扰动增长,同时第二模态的扰动受到抑制。
3) 随着壁温比的增加,受第一、第二模态联合作用影响,钝三角翼表面N值分布呈现先减小后增大的特点,预示存在转捩反转现象,反转点壁温比大约在绝热壁壁温比(约0.8)附近。
高超声速静风洞转捩试验中,来流总温低,壁温比的量值高(约0.7),不少试验采用非金属模型,壁面可视为绝热壁。而在实际的高超声速飞行试验中,来流总温高,壁温比的量值低(量级大致在0.3)。本文的研究结果表明,这两种状态的稳定性特征差异大,这预示着可能存在显著的天地差异。显然,直接基于地面的静风洞试验结果来预示飞行条件下的转捩可能是不合适的,需要开展相关的天地差异分析和天地相关性研究。
| [1] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. DOI:10.7638/kqdlxxb-2017.0030 (in Chinese) |
| [2] |
杨武兵, 沈清, 朱德华, 等. 高超声速边界层转捩研究现状与趋势[J]. 空气动力学学报, 2018, 36(2): 183-195. YANG W B, SHEN Q, ZHU D H, et al. Tendency and current status of hypersonic boundary layertransition[J]. Acta Aerodynamica Sinica, 2018, 36(2): 183-195. DOI:10.7638/kqdlxxb-2018.0011 (in Chinese) |
| [3] |
余平, 段毅, 尘军. 高超声速飞行的若干气动问题[J]. 航空学报, 2015, 36(1): 7-23. YU P, DUAN Y, CHEN J. Some aerodynamic issues in hypersonic flight[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 7-23. (in Chinese) |
| [4] |
BUSHNELL D M, YIP L P, YAO C S, et al. Reynolds number influences in aeronautics[R]. NASA TM-107730, 1993.
|
| [5] |
FEDOROV A V. Prediction and control of laminar-turbulent transition in high-speed boundary-layer flows[J]. Procedia IUTAM, 2015, 14: 3-14. DOI:10.1016/j.piutam.2015.03.017 |
| [6] |
CHAPMAN G T. Transition of the laminar boundary layer on a delta wing with 74° sweep in free flight at Mach numbers from 2.8 to 5.3[R].NASA TN-D-1066, 1961.
|
| [7] |
STETSON K, THOMPSON E, DONALDSON J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. V-Tests with a cooled model[C]//Proc of the 20th Fluid Dynamics, Plasma Dynamics and Lasers Conference, Buffalo, NY, USA. Reston, Virigina: AIAA, 1989. AIAA-89-1895. DOI: 10.2514/6.1989-1895
|
| [8] |
MALIK M. Prediction and control of transition in hypersonic boundary layers[C]//Proc of the 19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference, Honolulu, HI, USA. Reston, Virigina: AIAA, 1987. AIAA-87-1414. DOI: 10.2514/6.1987-1414
|
| [9] |
GASPERAS G. Effect of wall temperature distribution on the stability of the compressible boundary layer[C]//Proc of the 20th Fluid Dynamics, Plasma Dynamics and Lasers Conference, Buffalo, NY, USA. Reston, Virigina: AIAA, 1989. AIAA-89-1894. DOI: 10.2514/6.1989-1894
|
| [10] |
尚庆, 陈林, 李雪, 等. 高超声速钝双楔绕流流动转捩与分离流动的壁温影响[J]. 航空学报, 2014, 35(11): 2958-2969. SHANG Q, CHEN L, LI X, et al. Wall temperature effect on transition flow and separated flow in hypersonic flow around a blunt double wedge[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2958-2969. (in Chinese) |
| [11] |
苏彩虹, 周恒. 零攻角小钝头钝锥高超音速绕流边界层的稳定性分析和转捩预报[J]. 应用数学和力学, 2007, 28(5): 505-513. SU C H, ZHOU H. Stability analysis and transition prediction of hypersonic boundary layer over a blunt cone with small nose bluntness at zero angle ofattack[J]. Applied Mathematics and Mechanics, 2007, 28(5): 505-513. DOI:10.3321/j.issn:1000-0887.2007.05.001 (in Chinese) |
| [12] |
曹伟. 高超声速边界层的转捩问题[J]. 空气动力学学报, 2009, 27(5): 516-523. CAO W. A study of the transition prediction of hypersonic boundary layer on plane and wedgeflow[J]. Acta Aerodynamica Sinica, 2009, 27(5): 516-523. DOI:10.3969/j.issn.0258-1825.2009.05.003 (in Chinese) |
| [13] |
LIU Z Y, YANG W B, SHEN Q. Investigation on correlation between wind tunnel and flight test data for boundary layer transition[C]//Proc of the AIAA Flight Testing Conference, Washington, D.C. Reston, Virginia: AIAA, 2016. AIAA 2016-3980. DOI: 10.2514/6.2016-3980
|
| [14] |
LIANG X, LI X L, FU D X, et al. Effects of wall temperature on boundary layer stability over a blunt cone at Mach 7.99[J]. Computers & Fluids, 2010, 39(2): 359-371. DOI:10.1016/j.compfluid.2009.09.015 |
| [15] |
王振清, 唐小军, 孟祥男, 等. 壁温对来流脉冲波作用下钝楔高超声速边界层稳定性的影响[J]. 宇航学报, 2014, 35(4): 481-490. WANG Z Q, TANG X J, MENG X N, et al. Effect of wall temperature on the stability of hypersonic boundary layer over a blunt wedge under the action of pulse wave in incoming stream[J]. Journal of Astronautics, 2014, 35(4): 481-490. DOI:10.3873/j.issn.1000-1328.2014.04.016 (in Chinese) |
| [16] |
EPPINK J, WLEZIEN R. Data analysis for the NASA/Boeing hybrid laminar flow control crossflow experiment[C]//Proc of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, Hawaii. Reston, Virigina: AIAA, 2011. AIAA 2011-3879. DOI: 10.2514/6.2011-3879
|
| [17] |
周恒, 赵耕夫. 流动稳定性[M]. 北京: 国防工业出版社, 2004. ZHOU H, ZHAO G F. Hydrodynamic stability[M]. Beijing: National Defense Industry Press, 2004. (in Chinese) |
| [18] |
CEBECI T, STEWARTSON K. On stability and transition in three-dimensional flows[J]. AIAA Journal, 1980, 18(4): 398-405. DOI:10.2514/3.50772 |
| [19] |
唐登斌. 边界层转捩[M]. 北京: 科学出版社, 2015. TANG D B. Boundary layer transition[M]. Beijing: Science Press, 2015. (in Chinese) |
| [20] |
LI F, CHOUDHARI M, CHANG C L, et al. Stability analysis for HIFiRE experiments[C]//Proc of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, Louisiana. Reston, Virigina: AIAA, 2012. AIAA 2012-2961. DOI: 10.2514/6.2012-2961
|
| [21] |
BRAZHKO V N, VAGANOV A V, KOVALEVA N A, et al. Experimental investigation at Mach number M=7.5 of aerodynamic heating and laminar-turbulent transition on blunt delta wing[C]//ICMAR 2008.
|
 2020, Vol. 38
2020, Vol. 38


