圆柱绕流现象广泛存在于工程领域中,是引发研究者持续关注的重要原因。烟囱、建筑群、传输线、电缆、海上结构等领域均涉及对圆柱绕流的实际应用。在桥梁工程领域,如大跨度桥梁的斜拉索,也具有圆柱绕流现象,其引发的风致振动问题会对桥梁结构造成疲劳损伤和潜在威胁,因此斜拉索流动控制具有重大的工程实际意义。国内外学者提出了各种针对性的流动控制方法,其中在索表面布置螺旋式凸起与表面压痕[1]、设置辅助索系统[2-3]均可有效抑制索结构的风致振动。
普朗特开创了流动控制的先河,他采用抽吸气的方法来推迟流动分离[4],近年来,吸吹气控制方法也逐渐被应用于圆柱流动控制。Kim和Choi[5]设计了一种在圆柱体表面上下侧施加沿展向正弦变化的定常吸吹气控制方法,也称为分布力控制方法。当上下侧分布力是同相位时,在旋涡脱落过程中沿展向会产生相位失配,有效抑制甚至消除了旋涡脱落。Chen等[6-7]在圆柱分离点附近沿展向布置有限个吸气孔,发现有限个独立吸气孔使二维近尾流模式转变成强烈的三维近尾流模式。Feng和Wang[8-9]针对圆柱绕流场,提出了前、后驻点处合成射流的新型流动控制方法。研究发现,在前驻点采用合成射流时,增加吹气动量系数可明显增强虚拟气动外形效应;在后驻点采用合成射流时,可引发尾流涡脱模式的改变,当发生涡同步现象时尾流旋涡由交替脱落模式转变为对称脱落模式。Baek和Karniadakis[10]、Gao等[11]、Zhu等[12]在圆柱内部开槽形成内部流动通道;Chen等[13-14]通过在圆柱体表面安装中空的套环,套环外表面均匀分布若干气孔,在套环内部形成流动通道。研究表明,开槽或套环的控制方法均可以起到较好地抑制旋涡脱落、减小升力脉动的控制效果。
前人已开展了基于吸/吹气方法对圆柱流动进行控制的研究。一方面,开槽或者套环的被动控制方法具有无需额外的能量输入、设置简单、成本低的优点,在特定条件下可取得较好的控制效果,但控制效果有限,且开槽的控制方法对于要求结构完整的构件如桥梁的斜拉索或吊杆等并不适用。另一方面,现有的分布力、定常吸/吹气、合成射流等主动吸吹气方法也具有较好的控制效果,且可针对不同的实际应用场所进行不同的参数调整,但是针对在圆柱前后驻点采用吸吹气组合的研究较少。在此基础上,本文设计了在圆柱前后驻点吹气、前驻点吸气后驻点吹气、前驻点吹气后驻点吸气、前后驻点吸气四种定常吸吹气方案。通过对Re=300的二维无控圆柱及有控圆柱绕流进行大涡模拟,探究四种不同定常吸吹气控制方案的控制效果。同时,通过三维大涡模拟,进一步验证数值结果的准确性以及可靠性。
1 数值方法与验证 1.1 控制方程LES的主要思想是大尺度涡受流场影响较大,且几乎包含所有湍动能,而小尺度涡主要是耗散湍动能,且趋于各向同性。因此,在数值模拟中直接解析湍流中的大尺度涡,而小尺度涡对大尺度涡的影响则通过亚格子尺度模型体现在大尺度涡的瞬时动量方程中。
LES通过滤波函数将每个瞬时变量分成两部分,如瞬时速度分量ui(i=1, 2, 3), 有:
| $ {{u_i} = \overline {{u_i}} + {{u'}_i}} $ | (1) |
式中:ui为大尺度的平均分量,是滤波后的瞬时分量,也是在模拟时直接解析的部分;u′i为小尺度分量,需要通过模型来表现。
经滤波函数处理后,不可压缩流的瞬时控制方程表示为:
| $ {\frac{{\partial {{\overline u }_i}}}{{\partial {x_i}}} = 0} $ | (2) |
| $ {\frac{{\partial {{\overline u }_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {{{\overline u }_i}\;{{\overline u }_j}} \right) = - \frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + \nu \frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\overline u }_i}}}{{\partial {x_j}}}} \right) - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}} $ | (3) |
式中:带有上划线的量为滤波后的场变量。τij为亚格子尺度应力(简称SGS应力),它体现了小尺度涡的影响,其表达式为:
| $ {{\tau _{ij}} = \overline {{u_i}{u_j}} - {{\overline u }_i}\;{{\overline u }_j}} $ | (4) |
为使控制方程封闭,采用Smagorinsky-Lilly亚格子应力模型来构造SGS应力。其假定SGS应力具有如下形式:
| $ {{\tau _{ij}} - \frac{1}{3}{\tau _{kk}}{\delta _{ij}} = - 2{\mu _t}{{\overline S }_{ij}}} $ | (5) |
式中:μt为亚格子尺度的湍动黏度(也称涡黏系数),Sij为解析尺度的应变变化率张量。SGS应力的各向同性部分τkk附加到滤波后的静压项中,不加入亚格子应力模型。
在Smagorinsky-Lilly亚格子应力模型中,认为亚格子湍流具有混合长度型湍动黏度,可表示为:
| $ {{\mu _t} = \rho L_s^2{{\left( {2{{\overline S }_{ij}}{{\overline S }_{ij}}} \right)}^{\frac{1}{2}}}} $ | (6) |
式中:Ls为亚格子尺度的混合长度。其计算式为:
| $ {{L_s} = {\rm{min}}\left( {\kappa d, {C_s}\Delta } \right)} $ | (7) |
式中:κ为冯·卡门常数,d为到最近壁面的距离,Cs为Smagorinsky常数,取为0.1,Δ为网格尺寸,由计算单元的体积来计算Δ=V1/3。
1.2 数值方法与模型圆柱直径D=0.1 m,来流风速U=0.043 822 m/s,相应雷诺数为Re=300。前处理采用ICEM对计算域进行网格划分,采用Fluent 17.2进行数值计算。圆柱中心为坐标原点,圆柱中心到入口距离为10D,圆柱中心到出口距离为30D,计算域宽度为20D,三维模拟的展向长度为6D。计算域网格采用结构化网格,计算域内所用网格高度比不大于1.05,圆柱周围网格进行O型剖分,二维网格如图 1所示。
|
图 1 二维网格示意图 Fig.1 Schematic of the two-dimensional mesh |
数值计算入口采用速度入口边界条件,出口采用湍流充分发展的“outflow”边界条件,周围壁面设为对称边界条件,圆柱表面设为无滑移壁面,吸吹气位置采用速度入口边界条件,改变正/负值即可设定吹/吸气,时间步长Δt=0.04s。
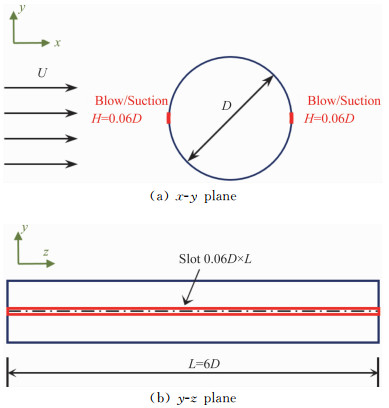
在圆柱前后驻点处进行主动吸吹气控制时,吸吹气高度为H=0.06D。根据前后驻点不同的吸吹气布置,分为前后吹气(BB)、前吸气后吹气(SB)、前吹气后吸气(BS)、前后吸气(SS)四种控制方案。有控圆柱示意图如图 2所示,对于三维工况,在圆柱前后驻点沿展向通长设置吸吹气槽。分别计算各控制方案在不同吸吹气风速(Us-b/U=0.1~1,增量0.1,共10种控制风速)的控制效果,同时,对三维的无控工况与Us-b/U=0.8时BB有控工况进行数值模拟。
|
图 2 有控圆柱示意图 Fig.2 Schematic of the controlled cylinder |
二维网格由疏至密设计3套网格(网格A、B、C),分别对Re=300的无控工况进行无关性计算。网格参数如表 1所示,其中,N代表网格总数,Nc代表圆柱周向节点数目,Δy/D为第一层网格高度与直径之比,Δz/D为三维网格展向高度与直径之比。无关性验证与结果如表 2所示,表中所示结果均由数值解达到稳定后的统计结果求得。CD mean为阻力系数平均值,CLrms为升力系数脉动值,Cpb为圆柱基底压力,St为斯托拉哈数。
| 表 1 网格参数 Table 1 Parameter of the mesh |
|
|
| 表 2 无关性验证与结果比对 Table 2 Mesh dependence study and result comparison |
|
|
经无关性计算发现,Re=300时随着网格逐渐加密,无量纲参数呈逐渐减小的变化趋势。网格B和C计算得到的阻力平均值和升力脉动值的误差分别为0.6%和2.0%,在5%的误差范围内,且和Jiang等[15]相同雷诺数下的二维DNS结果很接近,因此选用网格B进行其它有控工况下的数值模拟。三维工况的x-y平面网格和网格B完全相同。经比较,三维无控工况的结果与Jiang等[15]相同雷诺数下的三维DNS结果十分接近;同时,本文所采用网格沿壁面首层网格法线方向的无量纲高度y+=yuτ/ν < 1,其中y是首层网格的法向高度,uτ是摩擦速度,ν是流体的运动黏度,将首层网格的法向高度替换成其它两个方向的高度可对应求得x+ < 4、z+ < 10,因此充分验证了数值方法与网格划分的准确性和网格无关性。
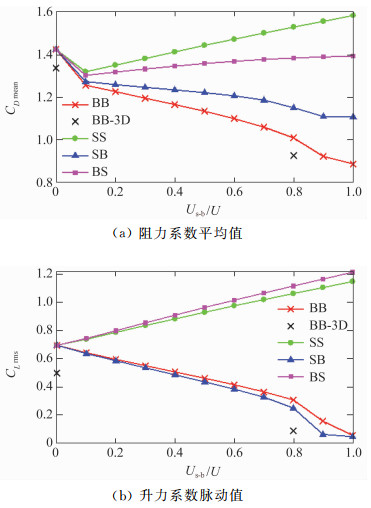
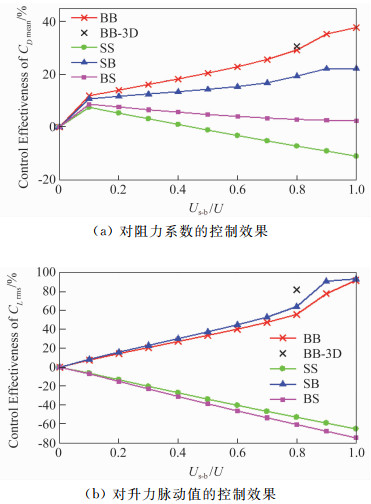
2 计算结果及分析 2.1 气动力参数BB、SB、BS、SS四种控制方案在Us-b/U=0.1~1(增量0.1),共10种控制风速下的CD mean和CLrms如图 3所示,其相应气动力参数的控制效果如图 4所示。气动力参数控制效果的定义如公式(8)所示,其中二维有控工况以二维无控工况作为对照组,三维有控工况以三维无控工况作为对照组:
| $ 气动力参数控制效果 = \frac{{对照组 - 有控组}}{对照组} \times 100\% $ | (8) |
|
图 3 有控工况的气动力参数 Fig.3 Aerodynamic coefficients of the controlled cylinder |
|
图 4 有控工况气动力参数的控制效果 Fig.4 Control effectiveness of the aerodynamic coefficients of the controlled cylinder |
由图 3和图 4可以看出,当Us-b/U=0.1时四种控制方法均达到约10%的减阻效果,随着Us-b增大,前后吹气和前吸后吹两种控制方案的减阻效果基本呈线性增加,而前后吸气和前吹后吸两种方案的减阻效果逐渐恶化。当Us-b/U≥0.9时,前吸后吹的减阻效果基本稳定在22%;而当Us-b/U=1时,前后吹气的减阻效果达到38%,且随着Us-b增大仍具有上升趋势。因此,从减阻的角度来衡量,前后吹气的方案具有更好的控制效果。
此外,四种方案的CLrms呈现出类似CD mean的控制效果。不同的是,对于所有的Us-b/U,前后吸气和前吹后吸两种方案均没有减小升力脉动。而前后吹气和前吸后吹两种控制方案的升力脉动基本呈线性减小,同样地,当Us-b/U≥0.9时,前吸后吹方案升力脉动减小值基本维持在无控圆柱的93.5%左右;而前后吹气方案在Us-b/U≤1时减小升力脉动的控制效果略小于前吸后吹方案,但从趋势来看,在Us-b/U>1时前后吹气具有更好的控制效果。
接下来,将从表面压力分布和流场特性两部分来分析主动吸吹气的控制机理。将前后吹气和前吸后吹方案在Us-b/U=0.8、1.0时的工况(工况BB0.8、BB1.0、SB0.8、SB1.0)、两种后驻点吸气方案在Us-b/U=0.8时的工况(工况SS0.8与BS0.8)与二维无控工况(工况BC)进行对比分析,探究其控制机理。同时,利用三维无控工况(BC-3D)与前后吹气方案的三维工况(BB0.8-3D)进一步对比验证。
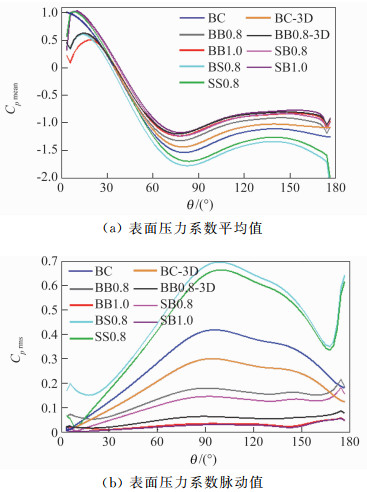
2.2 表面压力分布8种工况的表面压力分布如图 5所示,其中三维工况的表面压力分布取自跨中截面。
|
图 5 压力系数分布 Fig.5 Pressure coefficient distribution |
由图可以看出,对于后驻点吸气工况BS0.8、SS0.8,圆柱后部的平均压力比BC工况要小得多,而脉动压力也出现较大增长,这也就造成了更大的压差阻力和升力脉动。此外由图 5(a)可以看出,两种工况的分离点均向下游发生推移,因此推测其在近尾流处产生了更强的集中涡。
由BB0.8、BB1.0、SB0.8、SB1.0四个工况看出,由于后驻点吹气,圆柱后部压力系数平均值的分布类似,较BC工况平均压力均出现显著增加,且随着吹气风速增加,圆柱后部平均压力增加越大。对于工况BB0.8、BB1.0,由于前驻点吹气,前驻点附近压力系数平均值显著减小,且分别在15°和20°附近达到峰值0.63和0.51,这说明由于前驻点吹气使得在圆柱前部形成了近流线型的虚拟表面,且随着吹气风速增加,虚拟表面越大,使得圆柱前部更为接近流线型。而对于工况SB0.8、SB1.0,由于前驻点吸气,在吸气孔附近的压力系数平均值也显著减小,随后以较大的速率增加,分别在8°和10°重新到达1,这说明前驻点吸气的控制方法仅使得前驻点位置向两侧略微推移。这也就解释了虽然SB1.0工况在圆柱后部的平均压力比BB1.0工况要小,但是其正压区面积要显著大于BB1.0工况,所以BB1.0工况的阻力要比SB1.0工况小得多。
另外, BB0.8、BB1.0、SB0.8、SB1.0四个工况的表面压力脉动分布类似,较BC工况均有显著减小,且当Us-b/U=0.8时,SB0.8的表面压力脉动较BB0.8要小,而当Us-b/U=1.0时两者基本相等,这与上一节升力系数脉动值的结果一致。
对于二维工况和三维工况的对照组(BC与BC-3D、BB0.8与BB0.8-3D),其压力平均值和脉动值的分布趋势基本一致,只是在负压区内三维工况的压力平均值较二维工况要大,且其压力脉动整体要比二维工况小。Breuer[16]曾指出三维结构强烈影响着近尾流,这些三维结构包含着成对的相对旋转的流向涡,这是二维数值模拟所不能捕获到的。本文中二维模拟和三维模拟结果的些许差异,也间接证明了这一点。这表明当Re=300时,圆柱绕流已经表现出了一定的三维特性,但由于雷诺数较低,三维流场较弱,因此二维模拟仍可以获得较为可靠的数值结果。
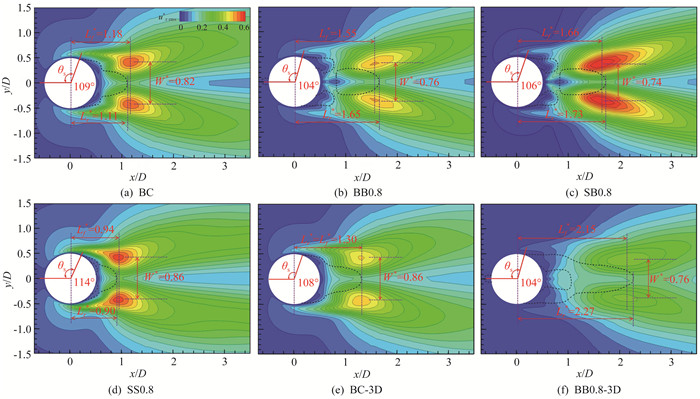
2.3 流场特性二维BC、BB0.8、SB0.8、SS0.8工况以及三维BC-3D、BB0.8-3D工况跨中截面的顺流向无量纲风速脉动值(ux, rms*)分布图如图 6所示。图中黑色的虚线为u=0的等值线,θs代表相应工况下的分离点,Lf*代表旋涡形成长度,Lr*代表回流区的顺流向长度,W*代表尾流宽度。
|
图 6 顺流向无量纲速度脉动值 Fig.6 Non-dimensional streamwise fluctuating velocity |
由图可以看出,相对于BC工况,BB0.8和SB0.8工况的分离角和尾流宽度均稍微减小,其回流区长度分别增加了0.54D和0.62D, 旋涡形成长度分别增长了0.37D和0.48D。由于尾流旋涡被拉长,升力脉动和涡脱频率也相应减小。而SS0.8工况,旋涡形成长度减小了0.24D, 且尾流宽度相应增加,这表明在圆柱后部存在能量强而集中的旋涡运动,直接导致圆柱升力脉动和阻力的增大。
根据二维和三维工况的对比发现,两者分布规律基本一致,明显不同的地方是三维工况的旋涡形成长度和回流区长度较二维工况偏大,这主要是因为二维模拟缺少流向涡的生成。另外,对于有控工况,两者的旋涡形成长度和回流区长度的差异更为明显,这也间接证明,对于相同有控工况三维模拟的控制效果比二维模拟更佳。
二维BC、BB0.8、SB0.8、SS0.8工况以及三维BC-3D、BB0.8-3D工况跨中截面的时均流线图如图 7所示。由图 7(a、b、e、f)可看出,BB0.8和BB0.8-3D工况由于前驻点吹出气流与来流方向相反,吹气区域两侧与周围气流间存在较强的剪切,因而在圆柱前部产生一对小驻涡,从而形成虚拟表面,使得圆柱前部接近流线型,起到虚拟气动外形效应,可以有效降低圆柱表面顺流向阻力作用;由于后驻点吹出的气流与圆柱后主旋涡的回流发生相互作用,在圆柱尾流处形成双回流区。受圆柱后主旋涡的影响,吹出气流向两侧流动并卷起形成一对旋涡,形成了上游回流区。在该回流区的下游,存在一对因圆柱固有流动分离产生的不断交替脱落的反向旋涡,即下游回流区。结果表明,由于吹出气流卷起旋涡的阻隔作用,圆柱主旋涡被推移到下游,旋涡形成长度显著增长,避免了尾流交替脱落旋涡直接作用在圆柱表面,因而有效减小了作用在圆柱表面的升力脉动。该双回流区与Gao等[11]、Feng等[9]中的描述相吻合。由图 7(b、c)比较可得,SB0.8和BB0.8工况的尾流时均流场分布基本一致,同时SB0.8工况由于前驻点吸气孔的吸气作用,圆柱前驻点向两侧发生偏移。

|
图 7 时均流线图 Fig.7 Time-averaged streamline |
由图 7(a、d)可看出,SS0.8工况由于后驻点吸气作用,使圆柱后的低压中心点更接近圆柱后部,这与SS0.8工况圆柱后半部分压力系数平均值降低相吻合,诱使两侧剪切层向圆柱后部靠拢,从而使得高强度的集中涡紧靠圆柱后部,显著增大圆柱的升力脉动与阻力大小。由于BS0.8工况与SS0.8工况的后驻点均为定常吸气,因此其尾流时均流场分布基本一致,而其圆柱前部应与BB0.8工况一样产生小驻涡,具有虚拟气动外形效应。
3 结论针对圆柱流动控制提出四种控制方案,分别为前后驻点吹气、前驻点吸气后驻点吹气、前驻点吹气后驻点吸气、前后驻点吸气,本文采用LES模拟分别对Re=300的圆柱绕流无控工况和有控工况进行二维模拟,并选择个别工况进行三维模拟验证。主要结论如下:
1) 根据模拟结果发现,后驻点吹气的两种工况(BB与SB)具有较好的控制效果。由于后驻点吹气孔吹出气流与圆柱主旋涡发生相互作用,两种方案在圆柱尾流处均形成双回流区,吹气孔吹出气流卷起的旋涡将圆柱主旋涡向下游推移,避免了尾流交替脱落旋涡的直接作用,因而显著抑制了作用在圆柱表面的升力脉动,当Us-b/U=1时升力脉动减小值均可达到92%以上。另外,对于BB控制方案,由于前驻点吹气在圆柱前部产生小驻涡,起到了虚拟气动外形效应,使圆柱正压区面积显著减小,当Us-b/U=1时阻力系数平均值减小了38%;对于SB方案,正压区表面压力仅在吸气孔附近明显减小,其正压区减小值比BB控制方案小得多,Us-b/U=1时阻力系数平均值减小了22%。从升阻力系数分布趋势来看,BB控制方案在Us-b/U>1时,其升阻力控制效果要优于SB方案。
2) 后驻点吸气的两种控制方案(BS与SS),由于后驻点吸气作用,圆柱后的低压中心点更接近圆柱后部,使得更强的集中涡紧靠在圆柱后部,控制效果是恶化的。
3) 根据二维模拟和三维模拟的对比发现,由于二维模拟缺少流向涡的生成,两者在流场分布上存在一定差异,但由于低雷诺数圆柱绕流的三维特性并不显著,整体分布趋势大致相同,因此本文可以为圆柱流动吸吹气控制提供参考。
4) 三维展向不同的吸吹气布置是接下来的研究侧重点,如沿展向布置定长的吸吹槽、有限个吸吹气孔等。
| [1] |
KATSUCHI I, YAMADA H, SAKAKI I, et al. Wind-tunnel investigation of the aerodynamic performance of surface-modification cables[J]. Engineering, 2017, 3(6): 817-822. DOI:10.1016/j.eng.2017.09.001 |
| [2] |
JING H Q, HE X H, ZOU Y F, et al. In-plane modal frequencies and mode shapes of two stay cables interconnected by uniformly distributed cross-ties[J]. Journal of Sound and Vibration, 2018(417): 38-55. |
| [3] |
HE X H, CAI C, WANG Z J, et al. Experimental verification of the effectiveness of elastic cross-ties in suppressing wake-induced vibrations of staggered stay cables[J]. Engineering Structures, 2018(167): 151-165. |
| [4] |
徐枫.结构流固耦合振动与流动控制的数值模拟[D].哈尔滨: 哈尔滨工业大学, 2009. XU F. Numerical simulation of fluid-solid coupling vibration and flow control of structures[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese) http://d.wanfangdata.com.cn/thesis/D257622 |
| [5] |
KIM J, CHOI H. Distributed forcing of flow over a circular cylinder[J]. Physics of Fluids, 2005, 17(3): 033103. DOI:10.1063/1.1850151 |
| [6] |
CHEN W L, LI H, HU H. An experimental study on a suction flow control method to reduce the unsteadiness of the wind loads acting on a circular cylinder[J]. Experiments in Fluids, 2014, 55(4): 1-20. DOI:10.1007/s00348-014-1707-7 |
| [7] |
CHEN W L, CAO Y, LI H, et al. Numerical investigation of steady suction control of flow around a circular cylinder[J]. Journal of Fluids and Structures, 2015, 59: 22-36. DOI:10.1016/j.jfluidstructs.2015.09.002 |
| [8] |
FENG L H, WANG J J. The virtual aeroshaping enhancement by synthetic jets with variable suction and blowing cycles[J]. Physics of Fluids, 2014, 26(1): 014105. DOI:10.1063/1.4861367 |
| [9] |
FENG L H, WANG J J. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point[J]. Journal of Fluid Mechanics, 2010, 662: 232-259. DOI:10.1017/S0022112010003174 |
| [10] |
BAEK H, KARNIADAKIS G E. Suppressing vortex-induced vibrations via passive means[J]. Journal of Fluids and Structures, 2009, 25(5): 848-866. DOI:10.1016/j.jfluidstructs.2009.02.006 |
| [11] |
GAO D L, CHEN W L, LI H, et al. Flow around a circular cylinder with slit[J]. Experimental Thermal and Fluid Science, 2017, 82: 287-301. DOI:10.1016/j.expthermflusci.2016.11.025 |
| [12] |
ZHU H J, ZHAO H L, ZHOU T M. Direct numerical simulation of flow over a slotted cylinder at low Reynolds number[J]. Applied Ocean Research, 2019, 87: 9-25. DOI:10.1016/j.apor.2019.01.019 |
| [13] |
CHEN W L, GAO D L, YUAN W Y, et al. Passive jet control of flow around a circular cylinder[J]. Experiments in Fluids, 2015, 56(11): 1-15. DOI:10.1007/s00348-015-2077-5 |
| [14] |
CHEN W L, WANG X J, GAO D L. Self-suction and self-jet control on wind loads and turbulent flow structures over a circular cylinder[J]. Journal of Aerospace Engineering, 2019, 32(1): 04018132. DOI:10.1061/(asce)as.1943-5525.0000965 |
| [15] |
JIANG H Y, CHENG L, DRAPER S, et al. Three-dimensional direct numerical simulation of wake transitions of a circular cylinder[J]. Journal of Fluid Mechanics, 2016, 801: 353-391. DOI:10.1017/jfm.2016.446 |
| [16] |
BREUER M. Numerical and modeling influences on large eddy simulations for the flow past a circular cylinder[J]. International Journal of Heat and Fluid Flow, 1998, 19(5): 512-521. DOI:10.1016/S0142-727X(98)10015-2 |
 2020, Vol. 38
2020, Vol. 38

