2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000;
3. 北京航空航天大学 国家计算流体力学实验室, 北京 100191
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China;
3. National Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, China
高速的空腔流动会产生强烈的振动与噪声,是航空航天领域中一类受到广泛关注的流动问题[1-3]。数值模拟是研究空腔流动机理与振动/噪声控制方法的重要手段。从流动分离的角度来看,空腔流动是一类典型的具有固定分离点(空腔的前缘点)的大范围分离流动,其分离区的特征尺度与空腔尺寸相当。在较高雷诺数条件下,空腔流动中既包含由外形引起的大尺度三维旋涡结构,又包含随机无序的小尺度的湍流涡旋,这使得在高雷诺数条件下很难获得高速空腔流动的高保真数值模拟结果。
直接数值模拟(DNS)和大涡模拟(LES)[4-6]能够较为精确地分辨空腔流动中包含大范围分离的多尺度湍流,但需要消耗很大的计算资源(尤其是在高雷诺数情况下),目前很难大范围地用于高雷诺数空腔流动的预测。雷诺平均Navier-Stokes(RANS)方法通过半经验的模型来模化所有的湍流脉动,只对最大尺度的平均流进行求解,其计算量相对较小,但现有的RANS方法在含有大范围分离的流动中难以给出准确的预测结果。
近年来RANS-LES混合方法(Hybrid RANS-LES method, HRLM)在大范围分离流动的模拟中获得了广泛的关注[7-9]。这种方法一般是仅在远离壁面的大尺度分离区分辨大涡并采用LES进行模拟,而在其他区域(如附体的湍流边界层内)采用RANS来模拟,从而对于高雷诺数壁面湍流的模拟兼具了RANS的高效率和LES的湍流模拟能力。根据混合方式可分为分区混合方法和非分区混合方法[10]。
非分区混合方法通过建立依赖网格尺度和流动参数的经验关系式来决定RANS和LES的区域,其流场中没有明确的RANS和LES的区分界面,如Speziale[11]构造的模型。而在分区混合方法中,需要基于对流动机理的认识人为确定交界面,并在两侧分别使用RANS和LES,如Embedded LES[12]。
无论是否人为分区,RANS解和LES解之间的匹配区域在HRLM中是普遍存在的,即所谓的“灰区”题。一般情况下,HRLM计算的可靠性由LES决定,因此从RANS解向LES解过度导致的“灰区”也是HRLM中关注最广泛的问题,在这个过程中分辨的湍流脉动与模化的湍流应力是不匹配的,虽然混合方法进入了LES的分支,但是数值解并不能正确的给出可分辨的“大涡”与相应的亚格子应力,这就需要有一段适应区域以供LES逐步建立起真实的湍流脉动成分。
分区或非分区HRLM均能适用于高雷诺数空腔流动的模拟,例如文献[13, 14]中的Embedded LES和文献[15]中的脱体涡模拟(DES)。由于来流边界层的分离点及分离区域的位置是固定的,因此HRLM的“灰区”通常位于分离点附近(分区模拟时人为确定的分界面位于接近空腔前缘的上游位置)。
在分区模拟的交界面上添加人工合成的湍流脉动能够有效地减小下游适应区的长度以使LES尽快完成真实亚格子应力的恢复。在使用HRLM对附体的湍流边界层流动或中/小范围分离湍流进行模拟时,合成湍流能够有效减小“灰区”的不利影响[16],但是对于类似空腔流动的大范围分离湍流,关于合成湍流对HRLM模拟的影响并没有明确的结论。直观上看,来流边界层中添加合理的脉动有助于更真实地描述分离后的初始剪切层中固有的Kelvin-Helmholtz不稳定性,但是Sagaut等[17]认为流动中绝对主导的自持振荡机制使得是否精细地描述来流边界层中的真实湍流结构对模拟结果的影响十分有限。在文献[13]中的Embedded LES中,交界面设置在空腔前缘位置导致了初始剪切层仍然以二维的旋涡结构为主。Lawson等[18]通过添加合成涡(SEM)[19-20]给出了来流脉动对Rossiter模态的影响,但其计算采用的展向对称边界条件可能掩盖剪切层中的展向失稳模态。
本文对马赫数0.6的空腔流动开展了分区和非分区RANS-LES混合模拟,具体计算采用基于S-A模型的改进的延迟DES(IDDES)方法[21],IDDES作为DES的一种改进,具备同时模拟附体边界层和大范围分离流动的能力,其在高速高雷诺数空腔流动的模拟中已经得到的广泛的应用[22-23]。当来流边界层中含有合适的湍流脉动时,IDDES模拟等同于Wall-Modeled LES(壁面模型由RANS部分提供),因此IDDES也能够用于大范围分离湍流的分区模拟(类似Embedded LES)[16]。分区模拟的交界面上添加了人工合成的湍流脉动,主要目的即在于给出有/无合成湍流(Synthetic Turbulence,ST)时所得到空腔流动的时均特性和动态特性,通过详细地对比分析明确来流边界层中ST对空腔流动HRLM模拟结果的影响。
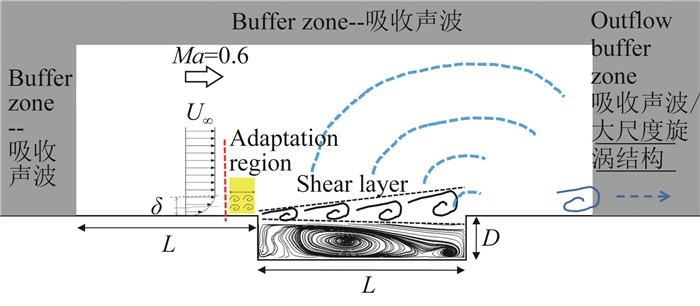
1 计算设置 1.1 空腔外形与计算条件本文模拟采用的空腔外形参考文献[2]中的风洞实验,空腔的长度(L)、深度(D)和宽度(W)之间的比值为L :D :W=6 :1 :2,在空腔上游设置有一段长度等于空腔长度(L)的平板(如图 1)。来流马赫数Ma=0.6,基于来流参数的雷诺数ReL=ρ∞U∞L/μ∞ =2.46×106。
|
图 1 空腔流动计算设置示意图 Fig.1 Schematic of the case-setup of the cavity flow |
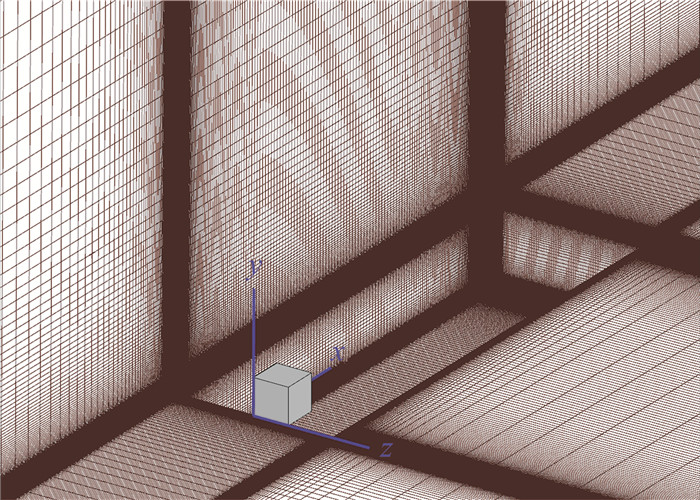
计算采用多块对接网格(如图 2所示),在腔内包括369×181×185个点(分别对应x、y、z方向),空腔外部包括585×181×301个点,整个网格共计含有4.42×107个网格点,网格分布在各个壁面及空腔开口处的剪切层附近加密,壁面第一层网格对应壁面单位约为1.0。
|
图 2 计算网格示意图 Fig.2 Schematic of the computational grids |
本文针对可压缩Navier-Stokes方程进行求解,其在三维笛卡尔坐标系(x, y, z)下的无量纲守恒形式为:
| $ \frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}} = \frac{{\partial {\mathit{\boldsymbol{E}}_v}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial y}} + \frac{{\partial {\mathit{\boldsymbol{G}}_v}}}{{\partial z}} $ | (1) |
式中,Q=[ρ, ρu, ρv, ρw, e]为守恒变量,ρ为密度、p为压力、u =(u, v, w)为速度矢量,总能e可表示为:
| $ e = \frac{p}{{\gamma - 1}} + \frac{1}{2}\rho ({u^2} + {v^2} + {w^2}) $ | (2) |
E、F、G表示空间各个方向上的无黏通量,Ev、Fv、Gv 表示黏性通量,各通量的具体表达式参见文献[24]。
基于S-A模型的IDDES输运方程为:
| $ \begin{array}{l} \frac{{\partial \rho \tilde \nu }}{{\partial t}} + \nabla \cdot (\rho \tilde \nu \mathit{\boldsymbol{u}}) = S + \frac{1}{{ Re \sigma }}\nabla \cdot \\ [\rho (\nu + (1 + {C_{b2}})\rho \tilde \nu )\nabla \tilde \nu ] - \frac{1}{{ Re \sigma }}{C_{b2}}\rho \tilde \nu {\nabla ^2}\tilde \nu \end{array} $ | (3) |
式中,ν为分子运动黏性系数,
| $ {S = {C_{b1}}\rho \varOmega \tilde \nu - \frac{1}{{ Re }}{C_{w1}}{f_w}\rho {{\left( {\frac{{\tilde v}}{{{{\tilde l}_{{\rm{ IDDES }}}}}}} \right)}^2}} $ | (4) |
| $ {{{\tilde l}_{{\rm{ IDDES }}}} = {f_d}(1 + {f_e}){d_w} + (1 - {f_d}){l_{{\rm{ LES }}}}} $ | (5) |
dw表示最小壁面距离,lLES为对应亚格子模型的长度尺度,模型的涡黏性系数为μT=ρ
壁面边界采用无滑移绝热边界条件;对于除固壁外的其他各个开边界(包括来流边界、出口边界、远场边界),为了抑制声波虚假反射对模拟结果的“污染”,本文采用文献[26]的特征边界处理,并在开边界与流动区域之间额外添加了一层边界缓冲区,缓冲区内的控制方程添加了人工阻尼项,从而确保旋涡等大尺度流动结构顺利流出边界而不会造成反射[27-28]。
为了对比人工合成湍流对流动模拟结果的影响,本文设置了两个算例,在第一个算例中使用文献[29]提出的ST构造方法(记为“Case 0: ST-on”),即在选定的交界面上添加湍流速度脉动u′,其计算方式为:
| $ {\mathit{\boldsymbol{u}}^\prime } = \mathit{\boldsymbol{A}} \cdot {\mathit{\boldsymbol{\hat u}}^\prime }(\mathit{\boldsymbol{x}},t) $ | (6) |
矩阵
| $ \begin{array}{*{20}{l}} {\hat A = [{a_{ij}}] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\sqrt {{R_{11}}} }&0&0\\ {{R_{21}}/{a_{11}}}&{\sqrt {{R_{22}} - a_{21}^2} }&0\\ {{R_{31}}/{a_{11}}}&{({R_{32}} - {a_{21}}{a_{31}})/{a_{22}}}&{\sqrt {{R_{33}} - a_{31}^2 - a_{32}^2} } \end{array}} \right]} \end{array} $ | (7) |
雷诺应力Rij由交界面上的IDDES(等同于RANS)解近似给出。辅助矢量
| $ {\mathit{\boldsymbol{\hat u}}^\prime }(\mathit{\boldsymbol{x}},t) = \sqrt 6 \sum\limits_{n = 1}^N {\sqrt {{q^n}} } [{\mathit{\boldsymbol{\sigma }}^n}{\rm{cos}}({k^n}{\mathit{\boldsymbol{d}}^n} \cdot {\mathit{\boldsymbol{r}}^\prime } + {\varphi ^n})] $ | (8) |
其中,上标“n”表示第n个模态的参数,q是由当地的von Karman模型能谱近似给出的模态幅值,k n=k· d n为三维的波数矢量,k表示波数矢量的模,d为均匀分布于单位半径的球面上的随机方向矢量,σ为随机生成的、与d垂直的单位矢量,φ是均匀分布于[0, 2π]区间的随机相位,r ′为表征扰动传播的位置矢量。该ST构造方法具有效率高、鲁棒性强的优点,更具体的细节参见文献[29]。此时数值模拟相当于分区HRLM。ST添加的流向位置在空腔上游距离前缘0.5D处(如图 1中红色虚线所示),根据此处的边界层厚度估算,0.5D的流向长度能够保证足够的适应区距离。在第二个算例中不添加任何人工脉动(记为“Case 1: ST-off”),此时全场使用IDDES进行计算,相当于非分区HRLM。
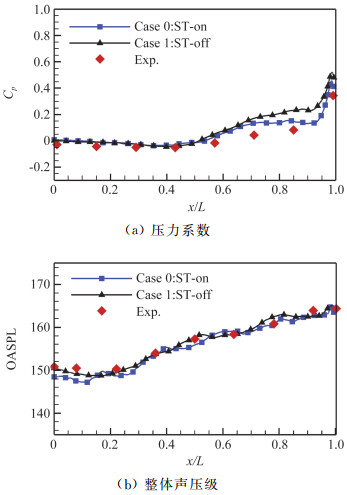
图 3中给出了底面中线(z=0)上的平均压力系数Cp和整体声压级OASPL分布。可以看出两种情况下计算得到的底面中线上的Cp在前半部分与实验结果符合较好,而在x/L>0.6的范围内两组计算的结果均略高于实验值,其中Case 0与实验值更接近,这将在后面结合流场结构进一步分析;两个算例的OASPL与实验结果具有较好的一致性。整体来说,数值模拟与实验结果的对比证明了本文计算的可靠性。
|
图 3 底面中线上的平均压力系数和整体声压级分布 Fig.3 Distributions of mean pressure coefficient and overall sound pressure level along the middle line of the bottom wall |
本节从流动的时均特性和动态特性两方面分析添加ST对HRLM计算结果的影响。
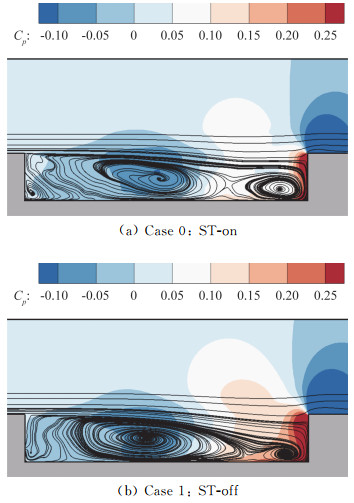
2.1 流动时均特性对比分析通过对非定常流动进行时间平均,可以对流场结构的主要特征进行分析。图 4中给出了展向中截面上的流线分布(背景云图为压力系数),可以看出中截面上的流动由两个环流区构成,其中较大的环流区靠近前壁面,其流向尺度占据了空腔长度的一半以上,较小的环流区靠近于后壁。当有ST时,后壁环流的尺寸明显大于无ST的结果,且具有更强的涡量,较强的涡量会导致更低的压力分布,这也解释了图 3(a)中的时均压力系数分布在后壁附近出现的差别。
|
图 4 时均场展向中截面(z=0)的流线分布,背景云图为压力系数 Fig.4 Time-averaged stream line on the middle spanwise plane, background contours are colored by pressure coefficient |
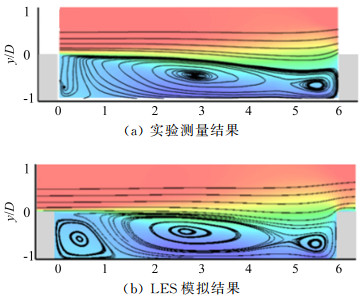
Zhang等[30]对相近工况下(Ma=0.6,L/D=6)的空腔流动开展了实验和LES模拟研究,其雷诺数分别为ReL, exp=1.875×106以及ReL, LES=6×104,与本文有所不同,但是一般认为雷诺数对空腔流动中主控的自持振荡的影响较小。图 5中给出了Zhang等[30]得到的展向截面上时均流线分布,其中计算和实验均体现了与本文结果相似的主要环流结构,本文的计算结果相比于文献中的LES模拟更接近实验,而未添加合成湍流的后壁环流区略微偏小。
|
图 5 实验和计算中Ma=0.6,L/D=6空腔流动的展向截面流线分布[30] Fig.5 Time-averaged streamlines on the spanwise plane obtained by the experiment and computation on the cavity flow of Ma=0.6, L/D=6[30] |
剪切层在空腔流致振荡中扮演了重要角色,基于平均场可以得到剪切层的涡量厚度δ和动量厚度θ,用来考察剪切层的定量特性。二者的定义分别为:
| $ {\delta = \frac{{{U_1} - {U_2}}}{{{{[{\rm{d}}U/{\rm{d}}y]}_{{\rm{max}}}}}}} $ | (9) |
| $ {\theta = \int_{{y_1}}^{{y_2}} {\frac{{\rho U}}{{{\rho _\infty }{U_\infty }}}} \left( {1 - \frac{U}{{{U_\infty }}}} \right){\rm{d}}y} $ | (10) |
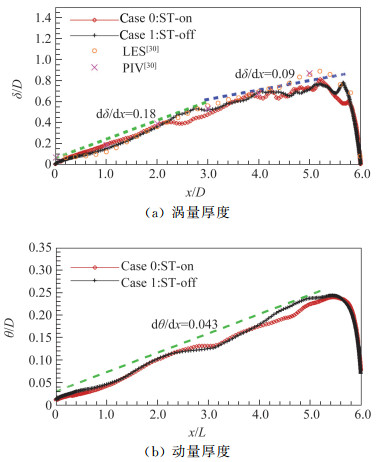
式中y1、y2、U1、U2的定义见文献[31, 32]。图 6中给出了δ和θ沿流向的变化,可以看出有无ST对剪切层平均厚度的影响很小,涡量厚度曲线大致可分为两段线性增长的区域,这与Beresh等[32]和Larcheveque等[31]的结果类似,两个区域的线性增长率分别为dδ/dx≈0.18和dδ/dx≈0.09,略低于Beresh等[32]得到的结果。图 6(a)中,本文结果与Zhang等的计算和实验数据[30]取得了较好的一致性。动量厚度近似以dθ/dx≈0.043的斜率线性增长。添加ST使Case 0得到的动量厚度在4 < x/D < 5.5的区间内略低于Case 1,这与文献[18]中图 11的结果一致。
|
图 6 剪切层涡量和动量厚度沿流向的分布 Fig.6 Streamwise distributions of the vorticity and momentum thicknesses of the shear layer |
|
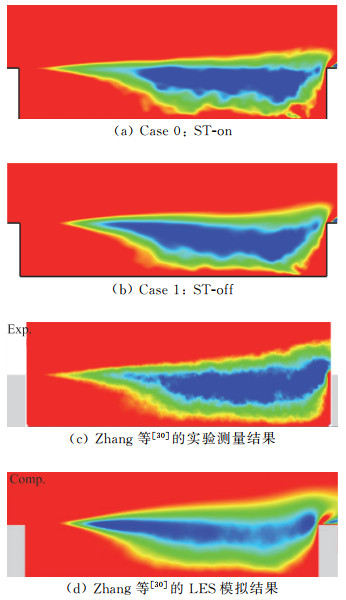
图 11 展向中截面雷诺剪切应力τxy分布云图 Fig.11 Contours of the Reynolds' shear τxy stress on the middle spanwise plane |
为了估计在剪切层内三维涡结构的平均对流速度,我们沿着剪切层中心线(y=0,z=0),计算了时空自相关函数,其定义为:
| $ {C_{vv}}({r_x},{r_t}) = \frac{{\langle v(x + {r_x},t + {r_t})v(x,t)\rangle }}{{\langle {v^2}\rangle }} $ | (11) |
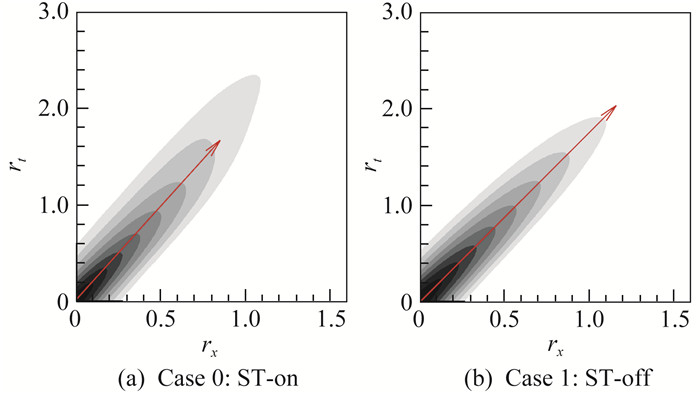
其中〈*〉表示时间平均,v表示法向脉动速度(能较好的反映对流效应),自相关函数具有较大值的位置代表流动结构在时空平面内的运动轨迹,该轨迹的斜率drx/drt近似代表了剪切层内流动结构的平均对流速度。图 6中给出了两个算例中自相关函数在rx-rt平面内的分布,可以估算出Case 0中对流速度约为drx/drt=0.539,而Case 1中对流速度约为drx/drt =0.571,基本符合Rossiter公式中表征对流速度的常数取值(0.55~0.57)。二者之间的差异说明上游添加的ST使剪切层涡结构的平均对流速度略有降低,在剪切层厚度变化(图 5)非常接近的前提下,ST对对流速度的影响可能是通过改变上游的流动三维机制引入的,这一点将在后文进一步阐述。
|
图 7 沿剪切层中心的时空自相关函数 Fig.7 Spatial-temporal auto-correlation along the center of the shear layer |
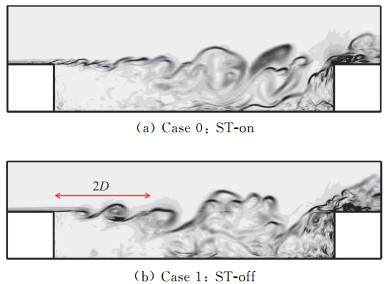
在图 8和图 9中分别给出了由Q准则表示的瞬时旋涡结构和展向中间截面(z=0)上的瞬时涡量分布。在图 8(a)中可以清楚的看到与上游边界层中所添加的ST对应的三维旋涡结构。ST对结果的影响主要集中在剪切层中。在Case 1中,来流边界层仅由RANS给出了平均剖面(图 8(b)),进入剪切层区域后,在初始阶段迅速形成展向近似均匀的涡结构,经过一定的发展距离流动的三维特性逐渐增强,并开始出现明显的流向涡结构。从图 9中也能看出,两个算例在剪切层初始阶段的流动结构尺度上存在差别,经过大约2D的流向距离,这种定性上的差别逐渐变得不明显。

|
图 8 Q准则显示的瞬时旋涡结构 Fig.8 Instantaneous vortical structures displayed by the Q-criterion |
|
图 9 展向中截面瞬时密度梯度分布图 Fig.9 Instantaneous contours of the density gradient on the middle spanwise plane |
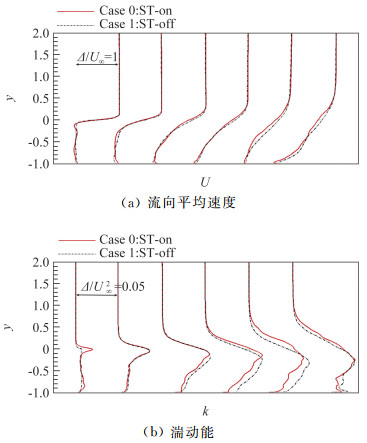
图 10中定量对比了6个不同的流向站位上(分别为x/D=0.5、1.5、2.5、3.5、4.5、5.5)平均流向速度U和湍动能k(
|
图 10 不同流向站位上的平均流向速度和湍动能剖面 Fig.10 Profiles of the mean streamwise velocity and turbulent kinetic energy at different streamwise locations |
图 11中给出了展向中截面的雷诺剪切应力τxy的分布,并与Zhang等[30]的计算和实验结果进行了对比。在剪切层靠近前缘的位置,Case 0添加合成湍流的计算结果更符合实验,而Case 1以及文献[30]中的LES结果在此处分辨的τxy剪切应力的绝对值偏小,体现了来自“灰区”的耗损,这也与湍动能的比较体现了类似的差异(见图 10(b))。在剪切层的后部,本文计算结果与实验测量的结果取得了很好的一致。
Zhang等所开展的LES模拟在入口添加了随机Fourier模态扰动,但是从模拟结果可以看出剪切层初始阶段的流动结构仍然以大尺度展向涡为主(见文献[30]中图 9),说明边界层/剪切层中的小尺度湍流结构并未得到充分的激发,入口附近仍存在“灰区”。可以认为文献[30]中的LES模拟结果与实验测量结果之间的差异也部分地来源于剪切层初始阶段的小尺度湍流结构。
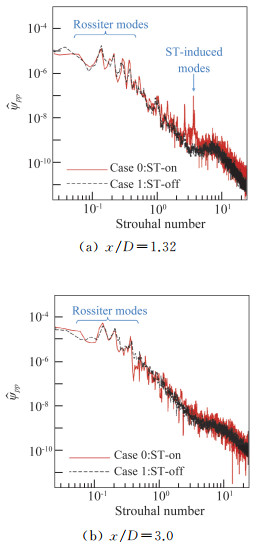
图 12中给出了空腔底面中线上x/D=1.32、3.0位置上的压力脉动的功率谱密度,通过对比可以看出添加ST对Rossiter模态(图 12中较低Strouhal数的峰值)的影响很小。在x/D=1.32位置的高频区域(图 12(a)),Case 0的结果相比于Case 1出现了额外的高频峰值(Strouhal数约为3.645处),这也对应着来流边界层中的ST对腔内流动的诱导作用;而在更下游的x/D=3.0位置,高频区域Case 0中的峰值消失。
|
图 12 底部采样点上的压力脉动功率谱密度 Fig.12 Power spectral densities of pressure fluctuations on the bottom sample points |
结合2.1节中关于平均特性的对比分析结果,可以发现ST对模拟结果的直接影响主要表现为增强剪切层初始阶段的脉动量,而随着流动的发展,有无ST对中下游位置的剪切层的影响非常微小,且图 12中的对比也说明二维平面内的自持振荡机制并没有因添加ST而改变,说明两个算例在后壁附近的环流区域出现的差异并不是由二维机制导致的。
为了定量考察流动结构的三维特性,可定义剪切层湍流脉动的展向波数谱为:
| $ {S_z} = \frac{1}{{2l}}\int_{ - l}^l w (x,y,z,t){{\rm{e}}^{ - {\rm{i}}\xi z}}{\rm{d}}z $ | (12) |
其中,w(x, y, z, t)表示非定常展向速度,ξ为展向波数,积分限取为l=0.9D,以排除侧壁对展向均匀性的影响。
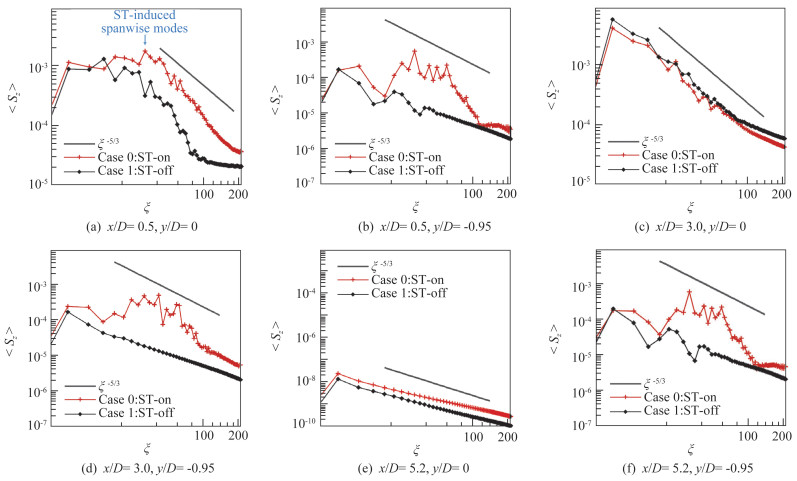
图 13中给出了x-y平面内六个不同位置上时间平均的〈Sz〉。在剪切层中心(y/D=0),Case 0在最上游的x/D=0.5位置上(图 13(a))得到的波数谱上明显出现了在ξ≈31.6处的峰值,而Case 1的结果中没有,说明该波数的产生与上游添加的ST有关(在图中记为“ST-induced spanwise modes”),而随着流动向下游发展,在x/D=3.0和x/D=5.2位置上,两个算例得到的展向波数谱变得非常接近。
|
图 13 不同位置上的时间平均展向波数谱 Fig.13 Time-averaged spanwise wavenumber spectra at different locations |
在接近底面的不同流向位置上(图 13(b、d、f)),Case 0的展向波数谱也表现出了上述展向模态,说明ST改变了对腔内流动三维机制的模拟结果,而这种变化并未出现在对下游位置剪切层的模拟结果中。综合以上分析可以认为有无ST所导致的HRLM模拟结果的差异主要来自于三维流动的区别,而主导的自持振荡(本质上为二维机制)并未受到明显影响。根据与实验数据的对比,可以认为添加ST使空腔流动HRLM模拟结果更符合实际流动。
3 结论本文对马赫数0.6的空腔流动开展了分区及非分区的RANS-LES混合模拟,对比了在分离点上游添加合成湍流对剪切层以及腔内的分离区模拟产生的影响:
1) 在剪切层初始阶段,合成湍流显著增加了湍动能的大小,旋涡结构具有一定的展向波数,而未添加合成湍流时,剪切层初始阶段的结果主要呈现出展向近似均匀的涡结构。
2) 对于腔内的流动,添加合成湍流增大了后壁附近环流区的尺寸,进而降低了靠近后壁区域的剪切层动量厚度和平均压力分布。在添加合成湍流情况下,底面靠近后壁区域的压力系数更加接近实验数据。
3) 合成湍流的添加未对主导流动的自持振荡机制产生明显的影响,而腔内流动模拟结果差别主要来源于合成湍流改变了腔内流动的三维机制。
| [1] |
万振华, 周林, 孙德军. 方腔流致振荡及噪声的数值研究[J]. 空气动力学学报, 2012, 30(3): 291-298. WAN Z H, ZHOU L, SUN D J. Numerical investigation of flow-induced oscillations and noise from a rectangular cavity[J]. Acta Aerodynamica Sinica, 2012, 30(3): 291-298. (in Chinese) |
| [2] |
杨党国, 刘俊, 王显圣, 等. 典型构型空腔模型设计与流动/噪声特性研究[J]. 空气动力学学报, 2018, 36(3): 432-439, 448. YANG D G, LIU J, WANG X S, et al. Analysis of design method and aeroacoustics characteristics inside typical cavity[J]. Acta Aerodynamica Sinica, 2018, 36(3): 432-439, 448. (in Chinese) |
| [3] |
王显圣, 杨党国, 刘俊, 等. 空腔可压缩流致噪声问题研究进展[J]. 实验流体力学, 2018, 32(3): 1-16. WANG X S, YANG D G, LIU J, et al. Progress of research on noise induced by compressible flow over cavities[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 1-16. (in Chinese) |
| [4] |
SAGAUT P. Large eddy simulation for incompressible flows[M]. Berlin, Heidelberg: Springer, 2001. DOI:10.1007/978-3-662-04416-2
|
| [5] |
张兆顺, 崔桂香, 许春晓. 湍流理论与模拟[M]. 北京: 清华大学出版社, 2005. ZHANG Z S, CUI G X, XU C X. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2005. (in Chinese) |
| [6] |
GARNIER E, ADAMS N, SAGAUT P. Large eddy simulation for compressible flows[M]. Dordrecht, Netherlands: Springer, 2009. DOI:10.1007/978-90-481-2819-8
|
| [7] |
肖志祥, 罗堃宇, 刘健. 宽速域RANS-LES混合方法的发展及应用[J]. 空气动力学学报, 2017, 35(3): 338-353. XIAO Z X, LUO K Y, LIU J. Developments and applications of hybrid RANS-LES methods for wide-speed-range flows[J]. Acta Aerodynamica Sinica, 2017, 35(3): 338-353. (in Chinese) |
| [8] |
徐佳敏, 宋文滨. 分区LES/DES混合方法及缝翼三维流场模拟[J]. 空气动力学学报, 2014, 32(5): 668-674. XU J M, SONG W B. Zonal LES/DES method and its application in slat flow field simulation[J]. Acta Aerodynamica Sinica, 2014, 32(5): 668-674. (in Chinese) |
| [9] |
张露, 李杰. 基于RANS/LES方法的超声速底部流场数值模拟[J]. 航空学报, 2017, 38(1): 47-58. ZHANG L, LI J. Numerical simulations of supersonic base flow field based on RANS/LES approaches[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 47-58. (in Chinese) |
| [10] |
FRÖHLICH J, VON TERZI D. Hybrid LES/RANS methods for the simulation of turbulent flows[J]. Progress in Aerospace Sciences, 2008, 44(5): 349-377. DOI:10.1016/j.paerosci.2008.05.001 |
| [11] |
SPEZIALE C G. Turbulence modeling for time-dependent RANS and VLES:A review[J]. AIAA Journal, 1998, 36: 173-184. DOI:10.2514/3.13796 |
| [12] |
KÖNIG D, MEINKE M, SCHRÖDER W. Embedded LES-to-RANS boundary in zonal simulations[J]. Journal of Turbulence, 2010, 11: N7. DOI:10.1080/14685241003698159 |
| [13] |
KOJIMA Y, HASHIMOTO A, KAMEDA M. Effects of inflow turbulence on cavity flow simulation with embedded-LES method[C]//Proc of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018. doi: 10.2514/6.2018-1090
|
| [14] |
ANUPINDI K, SANDBERG R D. Implementation and evaluation of an embedded LES-RANS solver[J]. Flow, Turbulence and Combustion, 2017, 98(3): 697-724. DOI:10.1007/s10494-016-9787-5 |
| [15] |
PENG H S. Simulation of turbulent flow past a rectangular open cavity using DES and unsteady RANS: AIAA 2006-2827[R]. Reston: AIAA, 2006.
|
| [16] |
PROBST A, SCHWAMBORN D, GARBARUK A, et al. Evaluation of grey area mitigation tools within zonal and non-zonal RANS-LES approaches in flows with pressure induced separation[J]. International Journal of Heat and Fluid Flow, 2017, 68: 237-247. DOI:10.1016/j.ijheatfluidflow.2017.08.008 |
| [17] |
SAGAUT P, GARNIER E, TROMEUR E, et al. Turbulent inflow conditions for large-eddy-simulation of compressible wall-bounded flows[J]. AIAA Journal, 2004, 42(3): 469-477. DOI:10.2514/1.3461 |
| [18] |
LAWSON S J, BARAKOS G N. Computational fluid dynamics analyses of flow over weapons-bay geometries[J]. Journal of Aircraft, 2010, 47(5): 1605-1623. DOI:10.2514/1.C000218 |
| [19] |
JARRIN N, BENHAMADOUCHE S, LAURENCE D, et al. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations[J]. International Journal of Heat and Fluid Flow, 2006, 27(4): 585-593. DOI:10.1016/j.ijheatfluidflow.2006.02.006 |
| [20] |
JARRIN N, PROSSER R, URIBE J C, et al. Reconstruction of turbulent fluctuations for hybrid RANS/LES simulations using a Synthetic-Eddy Method[J]. International Journal of Heat and Fluid Flow, 2009, 30(3): 435-442. DOI:10.1016/j.ijheatfluidflow.2009.02.016 |
| [21] |
SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 |
| [22] |
XIAO L H, XIAO Z X, DUAN Z W, et al. Improved-delayed-detached-eddy simulation of cavity-induced transition in hypersonic boundary layer[J]. International Journal of Heat and Fluid Flow, 2015, 51: 138-150. DOI:10.1016/j.ijheatfluidflow.2014.10.007 |
| [23] |
LUO K Y, ZHU W Q, XIAO Z X, et al. Investigation of spectral characteristics by passive control methods past a supersonic cavity[J]. AIAA Journal, 2018, 56(7): 2669-2686. DOI:10.2514/1.J056689 |
| [24] |
HOFFMANN K A, CHIANG S T. Computational fluid dynamics, Volume Ⅱ[M]. 4th ed.. Wichita, Kansas: Engineering Education System, 2000.
|
| [25] |
GUO Q L, SUN D, LI C, et al. A new discontinuity indicator for hybrid WENO schemes[J]. Journal of Scientific Computing, 2020, 83(2): 28. DOI:10.1007/s10915-020-01217-w |
| [26] |
GUO Q L, LI Q, ZHANG H X. Investigations on the boundary condition of the acoustic computation[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(S): 127-131. |
| [27] |
BODONY D J. Analysis of sponge zones for computational fluid mechanics[J]. Journal of Computational Physics, 2006, 212(2): 681-702. DOI:10.1016/j.jcp.2005.07.014 |
| [28] |
MANI A. Analysis and optimization of numerical sponge layers as a nonreflective boundary treatment[J]. Journal of Computational Physics, 2012, 231(2): 704-716. DOI:10.1016/j.jcp.2011.10.017 |
| [29] |
SHUR M L, SPALART P R, STRELETS M K, et al. Synthetic turbulence generators for RANS-LES interfaces in zonal simulations of aerodynamic and aeroacoustic problems[J]. Flow, Turbulence and Combustion, 2014, 93(1): 63-92. DOI:10.1007/s10494-014-9534-8 |
| [30] |
ZHANG Y, SUN Y Y, ARORA N, et al. Suppression of cavity flow oscillations via three-dimensional steady blowing[J]. AIAA Journal, 2015, 57(1): 90-105. DOI:10.2514/1.J057012 |
| [31] |
LARCHEVÊQUE L, SAGAUT P, LÊ T H, et al. Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number[J]. Journal of Fluid Mechanics, 2004, 516: 265-301. DOI:10.1017/s0022112004000709 |
| [32] |
BERESH S J, WAGNER J L, CASPER K M. Compressibility effects in the shear layer over a rectangular cavity[C]//46th AIAA Fluid Dynamics Conference, Washington, DC. Reston, Virginia: AIAA, 2016 doi: 10.2514/6.2016-3313
|
 2020, Vol. 38
2020, Vol. 38

