舰载直升机以其高度的灵活性和机动性,逐渐成为海军舰船的标准配置[1],是海洋战场上夺取和保持制空权、制海权的重要力量。直升机舰面起降极具挑战性,它必须适应复杂的海上飞行和舰载作业的环境,包括甲板空间的限制、舰船的随机六自由度运动和钝体流动分离引起的尾流扰动等[2],因此舰船气流场是影响舰载直升机起降安全的重要因素之一。直升机着舰时,旋翼尾流受地面阻塞效应影响会向上卷起旋涡[3],并与舰船流场产生干扰,这种非定常耦合流场效应会在旋翼桨叶上产生不稳定力,使得旋翼系统的气动载荷因涡流影响发生显著改变,出现桨叶挥舞等现象,甚至可能使直升机进入相当危险的“涡环状态”[4],直接影响直升机的控制裕度、飞行员的工作负荷和功率余量。
国内外关于孤立舰船流场的研究已有50多年的历史。20世纪60年代,美国海军从CV61“突击者”号开始,对多架航母的气流场进行了实船测量,并将测量结果作为风洞试验的补充[5]。前苏联在设计“戈尔什科夫”号时,利用风洞试验对舰船模型的上层建筑和甲板附近的流场进行了研究,其分析结果为实船设计提供了参考[6]。随着计算机技术的飞速发展,数值计算方法逐渐被引入到舰船流场研究中,20世纪90年代后期,人们开始应用CFD数值模拟预测舰船尾流,它可以用来计算全尺寸的解[7],得出气流场的基本形态和各参数分布,可控性好且成本较低。
然而,这些研究多集中于孤立舰船流场的研究,或者是通过简单叠加法得到的单向耦合流场,即把孤立舰船的流场信息提取出来,再添加到旋翼流场的计算当中[8],忽略了直升机与舰船流场之间的相互作用,因此其仿真结果难以为直升机的舰面操纵提供准确的指导。为了增强舰载直升机与舰船的动态适配性,人们开始对机舰耦合流场展开深入的研究,其难点主要在于如何准确捕捉旋翼尾迹。研究旋翼气动特性的方法主要包括:动量理论、叶素理论和基于滑移网格或嵌套网格的非定常数值模拟方法。动量理论的核心是将桨叶模型假想成有无限多叶片的薄桨盘,桨叶对来流的作用力等于桨盘单位时间通过动量的增量,因此可以通过添加动量源项来模拟桨盘受力。该方法的优点在于旋翼结构得到简化,忽略了桨叶附近细致的流动特征,但仍能对旋翼的远场尾迹进行较准确的计算。Rajagopalan[9]和Chaffin[10]等先后采用动量源的方法对旋翼流场进行了数值模拟并取得了一定成果。叶素理论把桨叶看成由无限多的桨叶叶素构成,每个桨叶剖面作为一个二维翼型来产生气动作用,相比于只考虑了桨叶轴向效应的动量理论,叶素理论还考虑了旋转效应,且叶素理论从更微观的角度对基于动量理论的载荷近似分布进行了完善。基于滑移网格或嵌套网格的非定常数值模拟方法需要在桨叶周围生成比较密的贴体网格,计算量较大但准确性较高。Park[11]等采用滑移网格方法模拟了直升机悬停和前飞过程中的旋翼流场,结果显示该方法对于复杂的非定常旋翼流场的预测具有高效性和鲁棒性。
20世纪末,Wakefield等用动量源法对旋翼进行等效替代,将桨盘对流体施加的向下作用力以动量源项的形式添加到控制方程中[12],使用CFX解算器获得了旋翼与舰船耦合流场解,并验证了动量盘源法的合理性[13]。2014年,Crozon等对加拿大巡逻护卫舰进行了数值模拟并考虑了旋翼的影响[14],首先采用稳态的动量源项法进行了计算,结果表明,当舰载直升机在舰船表面近距离作业时,耦合效应对舰船尾流和旋翼涡流的影响非常重要,从而证明了叠加法的无效性。为了更好地捕捉旋翼尾迹涡等流场细节,他们还运用滑移网格法在桨叶周围生成贴体网格,更真实地模拟旋翼的高速旋转,计算结果与试验数据吻合度很高,说明这种数值模拟方法为确定安全飞行包线提供了可能性。国内苏大成等基于雷诺平均N-S方程对直升机/舰船耦合流场进行数值模拟,直升机旋翼等旋转部件的模拟使用动量源模型,仿真结果显示:相对孤立舰船而言,耦合流场下旋翼涡与舰尾涡产生较强的干扰[15],这种干扰和舰面效应的共同作用下,会使得旋翼拉力产生显著振荡;对全机状态下的耦合流场进行模拟后发现,直升机的机身和尾桨对舰尾流场的影响不大,可将直升机全机简化为旋翼。
目前,关于机舰耦合流场的研究大多是用动量源项法对旋翼进行替代,无法捕捉旋翼螺旋式桨尖涡等流场细节。本文针对SFS2简化护卫舰模型[16],运用重叠网格法模拟旋翼的高速旋转(忽略机身的影响),计算了正顶风下直升机在甲板上悬停和垂直降落过程中的耦合流场,通过观察流线图、云图及流场参数随时间的变化等,详细分析了舰船尾流与旋翼涡流的耦合“涡-涡”干扰效应,并结合旋翼拉力系数的变化情况,对直升机的舰面安全操作提出了建议。
1 数值计算方法 1.1 数值计算方法本文通过重叠网格方法来模拟旋翼旋转,采用可压缩的N-S方程作为主控制方程,具体表达式见式(1):
| $ \frac{\partial }{\partial t}\iiint_{V}{\boldsymbol{W}\text{d}V+}\iint_{\partial V}{({{\boldsymbol{F}}_{c}}-{{\boldsymbol{F}}_{v}})\text{d}S}+\iiint_{v}{\boldsymbol{T}\text{d}V=0} $ | (1) |
其中,W、Fc和Fv分别为守恒变量、对流通量和黏性通量,T为旋转源项,表达式如式(2、3)。
| $ \boldsymbol{W} = \left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{array} \right],{\mathit{\boldsymbol{F}}_c} = \left[ \begin{array}{l} \;\;\;\;\;\rho (\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_b})\\ \rho u(\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_b}) + {n_x}p\\ \rho v(\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_b}) + {n_y}p\\ \rho w(\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_b}) + {n_z}p\\ \rho H(\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_b}) + {q_b}p \end{array} \right] $ | (2) |
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_v} = \left[ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;0\\ {n_x}{\tau _{xx}} + {n_y}{\tau _{xy}} + {n_z}{\tau _{xz}}\\ {n_x}{\tau _{yx}} + {n_y}{\tau _{yy}} + {n_z}{\tau _{yz}}\\ {n_x}{\tau _{zx}} + {n_y}{\tau _{zy}} + {n_z}{\tau _{zz}}\\ {n_x}{\mathit{\Phi }_x} + {n_y}{\mathit{\Phi }_y} + {n_z}{\mathit{\Phi }_z} \end{array} \right],\\ \mathit{\boldsymbol{T}} = \left[ \begin{array}{l} \;\;\;\;\;\;0\\ \rho {\left( {\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{q}}} \right)_x}\\ \rho {\left( {\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{q}}} \right)_y}\\ \rho {\left( {\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{q}}} \right)_z}\\ \;\;\;\;\;\;0 \end{array} \right] \end{array} $ | (3) |
式中:ρ和p分别为流体密度和压强;E和H分别为单位流体内能和总焓;(u, v, w)为流体绝对速度q在旋转坐标系下的分量;qb为控制体表面的绝对速度;(nx, ny, nz)为控制面的单位外法向矢量n的三个分量;ω为旋翼转动角速度矢量;τ为黏性应力;Φ为黏性力和热传导对流体的功。
通过Fluent对流场进行数值计算,运用mesh motion对部件网格的旋转运动进行设置,采用k-ε湍流模型、密度基耦合隐式求解器,通量格式为Roe-FDS格式,时间推进为双时间步迭代法,时间步长为0.0004s,最大内迭代步数为30。
直升机与舰船耦合流场所需计算的速度场跨度很大,包含舰船表面的低速不可压流及旋翼旋转的高速可压流,而密度基求解器在求解低速问题时,由于流体速度与声速的量级相差过大会使得N-S方程具有很强的刚性,导致收敛速度非常慢。因此对时间导数进行预处理[17],重新标度了所解方程的声速,从而减轻了低马赫数和不可压流动中数值刚性的影响。
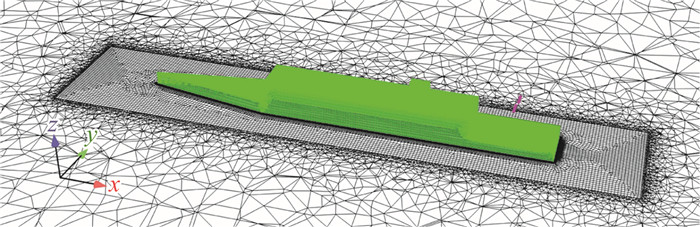
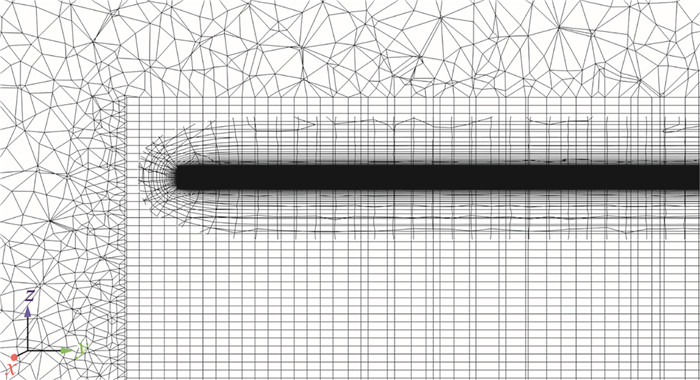
1.2 计算网格如图 1所示,舰船计算模型采用SFS2简化护卫舰模型,旋翼(两片桨叶、直径10 m)位于后甲板正上方10 m高度处,计算域设置的尽量大以满足阻塞率的要求,网格采用混合非结构网格,总网格数约1300万,旋翼网格与背景网格的重叠如图 2所示。
|
图 1 计算网格模型 Fig.1 Computational mesh model |
|
图 2 旋翼重叠网格细节图 Fig.2 Details of overset mesh around rotors |
传统的动网格在处理大幅度运动时,常常由于网格的大变形导致计算不收敛,且无法处理旋转类的问题[18]。重叠网格法适用于任何无规则的运动,对于运动的部件,在重叠区域单独生成部件重叠网格,它可以相对于背景网格独立运动且不会对其产生干扰,信息传递则是通过将背景网格的边界单元变量信息插值到重叠网格的边界单元来实现,因此无需对网格进行重构,节省计算时间。
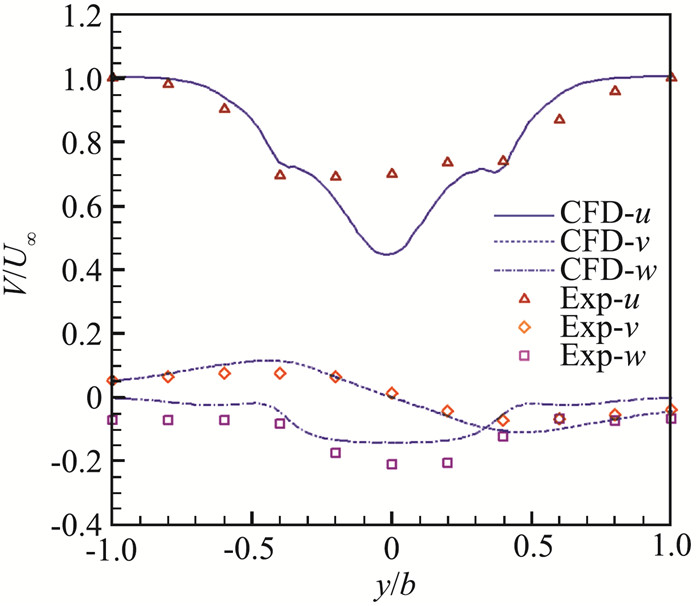
2 验证计算 2.1 孤立舰船流场验证为了验证数值模拟计算结果的正确性,将正顶风下SFS2孤立舰船流场的数值计算结果与试验数据进行了比较,图 3为CFD计算的飞行甲板上空直线上的速度分布曲线与文献[19]的对比结果,所测量的直线位于与机库等高的飞行甲板中央的z平面内。图中横轴表示y坐标与甲板宽度的比值,纵轴表示各方向的无量纲化速度。可以看出计算结果呈现出比较好的对称性,由于采用的是RANS模型,甲板中央处v方向速度与试验结果偏差略大,但仍可以接受的误差允许范围之内。
|
图 3 飞行甲板上空无量纲速度与实验结果对比 Fig.3 Comparison between numerical calculation results and experimental results of dimensionless velocity over flight deck |
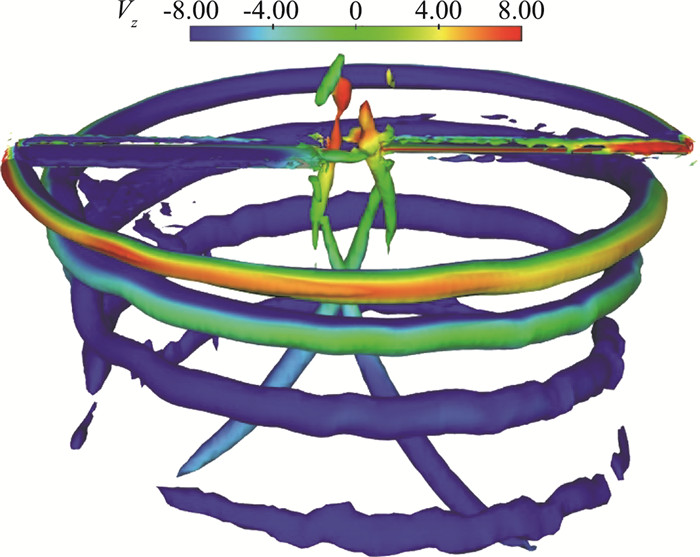
Caradonna-Tung旋翼模型的实验数据被广泛用于检验旋翼数值模拟的可靠性,该模型由两片桨叶组成,桨叶外形轮廓采用无扭转的NACA0012翼型,桨盘半径为1.143 m。针对桨距角θc=8.0°、转速Ω=1250 r/min、翼尖马赫数Mtip=0.439的基础算例[20]利用重叠网格法进行了验证计算。图 4为数值模拟得到的桨尖涡分布图,可以很清晰地看到随着旋翼的高速旋转,沿着桨叶后缘脱出一圈圈螺旋状的桨尖涡。
|
图 4 桨尖涡示意图 Fig.4 Sketch map of tip vortex |
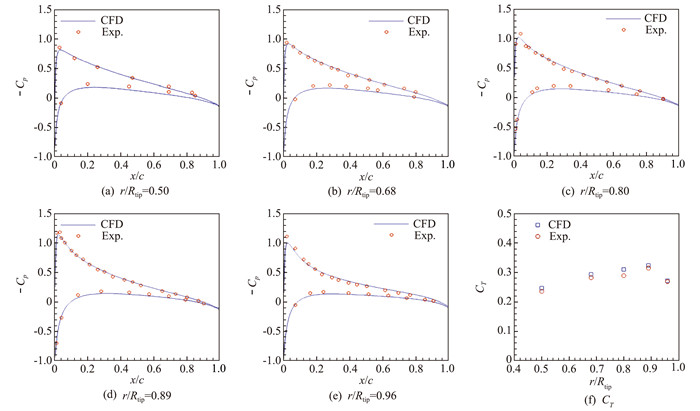
为了验证算法的正确性,将数值计算得到的沿桨叶不同位置剖面的压力系数与试验结果进行比较。如图 5(a~e)所示,图中横坐标为弦线上的点到前缘的距离与弦长之比,结果显示,数值计算的上下翼面压力系数与实验结果基本吻合。图 5(f)是计算得到的沿桨叶展向不同剖面拉力系数与实验结果的比较。数值计算所得旋翼总拉力系数为0.00457(实验值为0.00460),误差仅为0.65%,可以看到桨叶沿展向拉力分布与试验结果均有良好的一致性,说明用重叠网格法模拟旋翼转动是可行的。
|
图 5 Mtip=0.439时Cp的数值计算结果与实验结果的比较 Fig.5 Comparison between numerical calculation results and experimental results of pressure coefficient when tip Mach number is 0.439 |
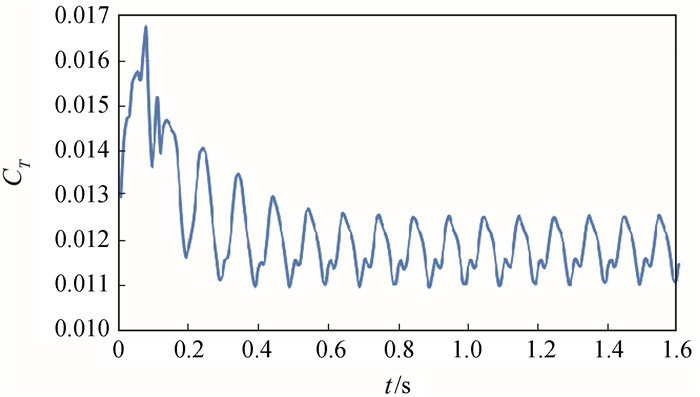
通过Fluent计算了正顶风下来流风速20 m/s、直升机悬停于甲板上方的机舰耦合流场,旋翼转速为300 r/min。以定常的计算结果作为初始流场进行非定常续算,重叠网格对时间步长的要求非常严格,本文计算采取的时间步长为0.0004s。图 6为旋翼拉力系数随时间变化曲线,可以看到当悬停0.6s即旋翼转过三圈之后,拉力系数逐渐收敛并呈现稳定的周期性波动,由于采用的是双桨叶刚性旋翼,因此周期为0.1s,与实际情况相符。
|
图 6 旋翼拉力系数随悬停时间变化曲线 Fig.6 Variation of thrust coefficient with hovering time |
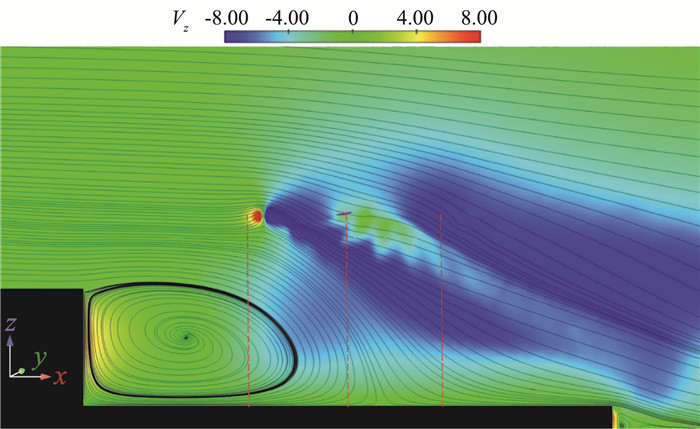
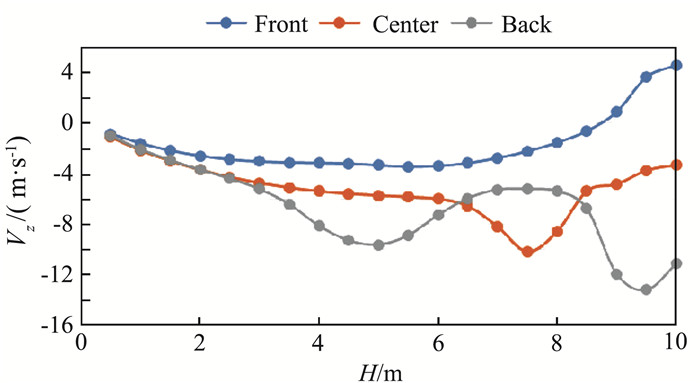
图 7为悬停1.6s的纵向中心截面垂向速度云图和流线图。在机库后方为典型的后台阶绕流现象,气流沿机库边缘发生分离后形成马蹄涡附着于飞行甲板面,该回流区内存在大量流动分离。旋翼高速旋转产生强烈的下洗流,影响范围可以扩散到甲板上方2.5 m处,正顶风使得下洗流被吹向舰尾,但仍然有部分下洗流受到回流区的影响。在起降点中心以及其前、后各5 m位置作垂直于甲板面的直线(见图 7中虚线),沿三条直线对垂向速度沿甲板高度的变化进行测量,如图 8所示。由于旋翼的下洗流是成两股被吹向后方,所以离甲板面不同高度上,靠后的位置可能分别受到两股下洗流的影响,垂向速度沿高度会发生突变,而不是离甲板越近下洗流一直衰减。
|
图 7 纵向中心截面垂向速度云图和流线图 Fig.7 Contours of z-velocity and streamlines in a longitudinal plane through center of the ship |
|
图 8 垂向速度沿甲板高度的变化曲线 Fig.8 Variation of z-velocity along the height of deck |
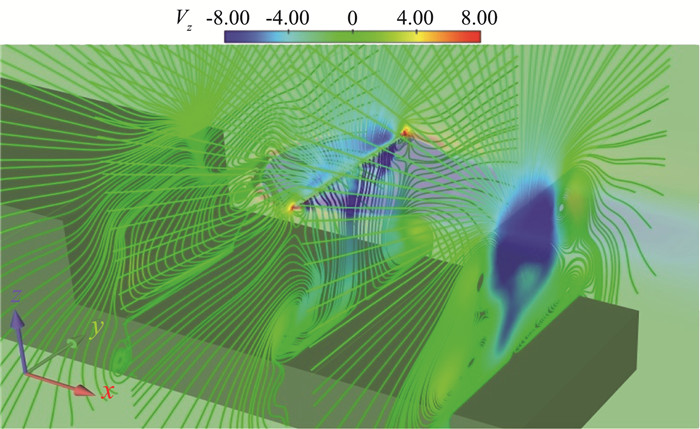
图 9中展示的是甲板不同位置的横向截面流线图并用垂向速度对旋翼所在平面进行着色。旋翼下洗流受到地面阻塞效应影响向上卷起,且回流区内的低压效应使得甲板两侧下方的气流被吸到舰面上方形成一对反向旋转的舷涡,下游的下洗流强度明显强于上游,旋翼脱出的尾迹涡在舰尾有非常大的影响,涡核直径可达3 m,且尾迹涡逐渐向下发展的过程中与舷涡发生耦合。
|
图 9 甲板不同位置横向截面流线图 Fig.9 Streamlines in different transverse planes along the deck |
通过λ2等值面绘制旋涡示意图并用湍动能着色,湍动能计算公式(4)如下:
| $ k=\frac{3}{2}{{({{u}_{\text{avg}}}I)}^{2}} $ | (4) |
其中uavg为平均速度,I为湍流强度,且I=0.16Re-1/8。
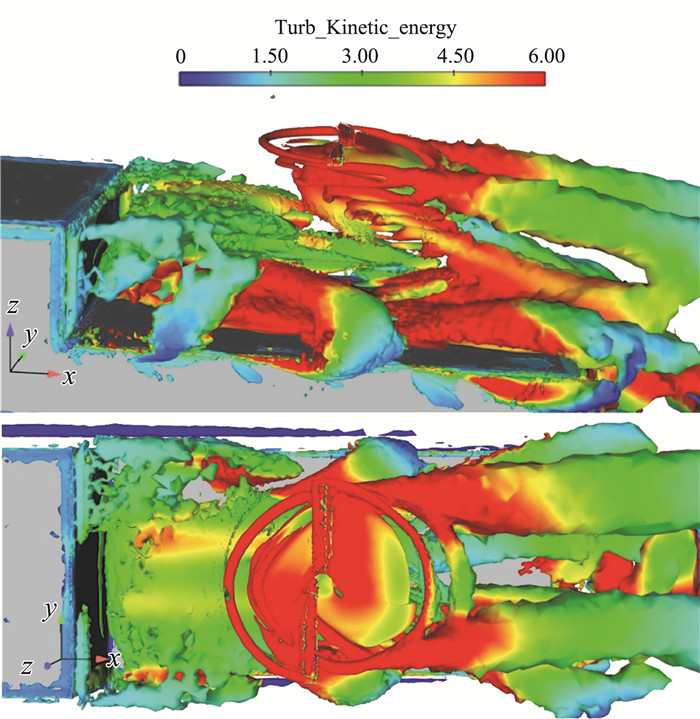
如图 10所示,能明显地看到旋翼旋转过程中,桨叶拖出的尾迹迅速卷起强集中涡并向下游发展,沿桨叶后缘桨尖涡呈螺旋状一圈圈脱落,不仅在桨盘平面内诱导强烈的下洗流,且逐渐与回流区旋涡及舷涡发生干扰。英国民航局CAA(Civil Aviation Authority)制定的CAP437标准中规定,满足安全起降的气流垂向速度标准差应小于1.75 m/s,数值模拟中假设湍流应力各向同性,则该条件可转化为:湍动能k < 6 m2/s2。图中红色表示湍动能超限区域,回流区旋涡、舷涡及桨尖涡的湍动能均已超出安全条件,三者携带着巨大湍动能的旋涡的耦合干扰,使得旋翼下方的流场变得极其复杂,大大增加了流场湍流度,且这种影响一直持续到舰尾。
|
图 10 λ2等值面图(上:侧视图,下:俯视图) Fig.10 Isosurface of λ2(The above is the side view while the below is the top view) |
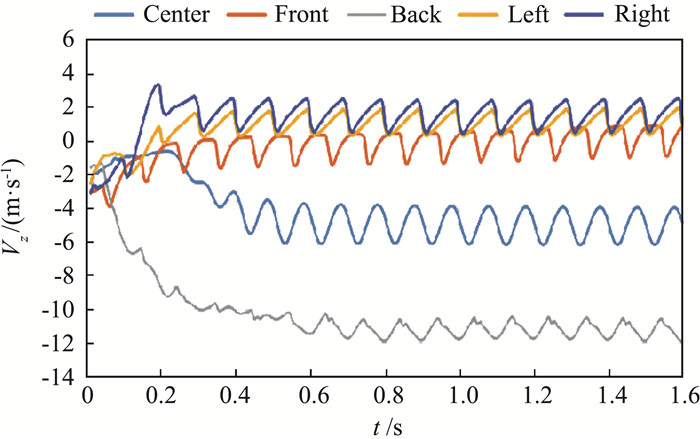
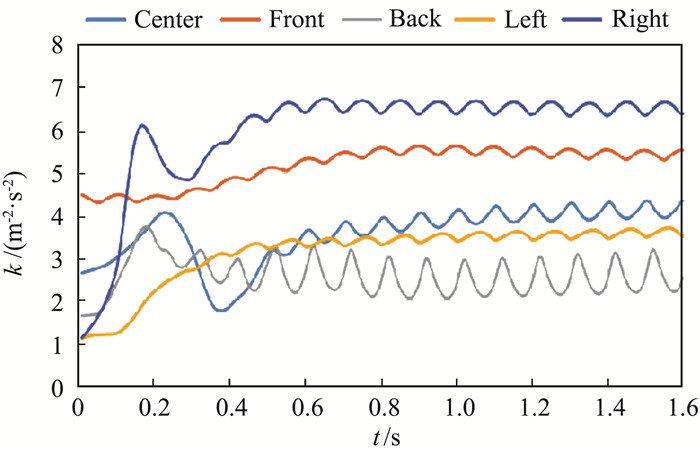
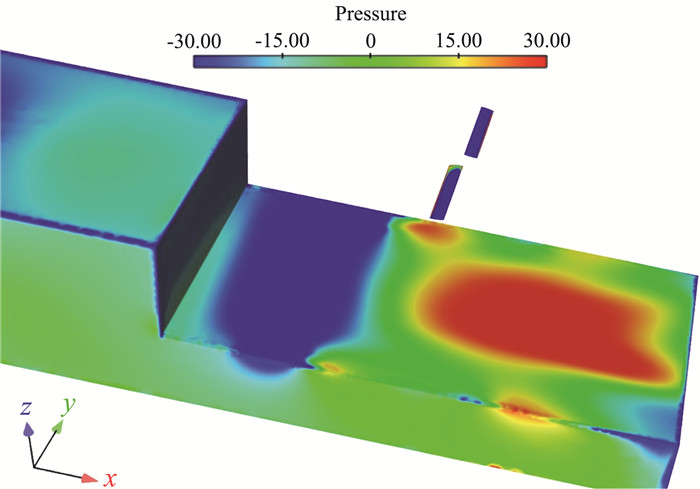
为了更直观地了解旋涡对流场参数随时间变化的影响,在旋翼正下方1 m高度处的中心、前、后、左、右位置共取了五个观测点。图 11和图 12为各观测点垂向速度和湍动能随悬停时间的变化曲线。一开始处于流场的建立过程,所以速度波动较大。可以看到各观测点的垂向速度大致在0.6 s之后成有规律的周期性波动,波动范围大约为2 m/s,且这个波动周期与旋翼旋转周期是一致的,说明虽然桨尖涡向下游传播过程中与舰船尾流发生碰撞,但由于直升机悬停高度离甲板较远,这种耦合作用并不会对直升机的高空悬停产生大的影响。中轴线上的三个测点从前往后下洗流速度逐渐增强,尤其是后测点的下洗流速度达到-11 m/s,这使得前后速度差较大,直接影响旋翼和机身受到的力和力矩,加大了驾驶员的操作难度;左、右测点则呈现轻微上洗且二者垂向速度基本重合,对直升机的操作影响不大。旋翼下方1 m处只有右测点的湍动能超出限制,而且左测点的湍动能只有右测点的一半,说明当直升机以逆时针方向(俯视图)旋转时,旋翼下方右侧流场的湍流度大于左侧。由图 13中1.6s时刻甲板表面压力分布可知,旋翼产生的强下洗流受来流影响被吹向舰尾,所以在甲板中后方形成大范围的高压区,而甲板前方回流区内的流体流速高、静压低,这种“前低后高”的压力分布使得直升机会受到向前的推力,容易发生“前冲”事故,需要引起重视。
|
图 11 观测点垂向速度随悬停时间变化曲线 Fig.11 Variation of z-velocity with hovering time at observation points |
|
图 12 观测点湍动能随降落时间变化曲线 Fig.12 Variation of turbulent kinetic energy with landing time at observation points |
|
图 13 甲板表面压力分布 Fig.13 Pressure distribution on the deck surface |
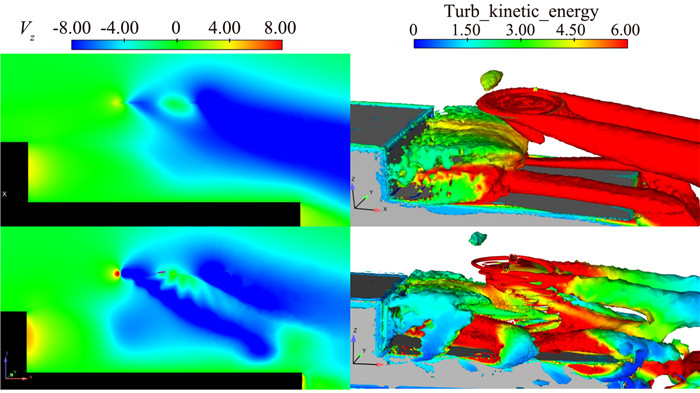
最后,将动量源项法得到的计算结果与重叠网格法的计算结果进行比较,动量源项分布采用的是径向载荷三角形近似分布形式,已知桨尖半径R0,桨毂半径R1,设载荷峰值ΔPr位于a(R0-R1)处(本文采取a=0.75),径向载荷分布满足下列函数:
| $ \Delta P\left( r \right)=\left\{ \begin{align} & \frac{\Delta {{P}_{r}}}{a{{R}_{0}}-{{R}_{1}}}(r-{{R}_{1}}), {{R}_{1}}<r \le {{R}_{0}} \\ & -\frac{\Delta {{P}_{r}}}{{{R}_{0}}-a{{R}_{0}}}(r-{{R}_{0}}), a{{R}_{0}}<r <{{R}_{0}} \\ \end{align} \right. $ | (5) |
由
|
图 14 两种方法结果对比(上:动量源法,下:重叠网格法) Fig.14 Comparison between the two methods(above: momentum source method, below: overset mesh method) |
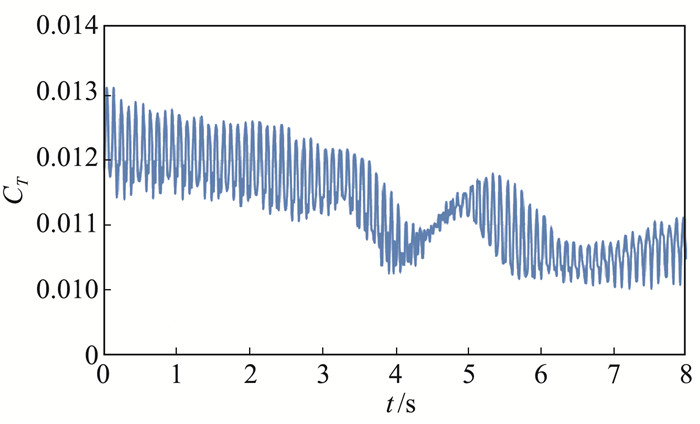
在悬停计算结果稳定的基础上,让旋翼以0.5 m/s的速度垂直下降,降落时间为8 s即降落至与机库等高的位置。如图 15所示为降落过程中旋翼拉力系数随时间的变化曲线,随着直升机的降落,旋翼涡流与回流区的干扰变得更加剧烈,拉力系数出现显著的振荡,但整体呈现下降的趋势。在3.5 s后拉力系数陡然下降并很快回升后又再次下降,这种突变产生的原因是此刻上游旋涡刚好发展到后甲板上方并打在旋翼上,影响到旋翼的载荷分布。可以看到,拉力系数总体变化幅度已达到15%。
|
图 15 旋翼拉力系数随降落时间变化曲线 Fig.15 Variation of thrust coefficient with landing time |
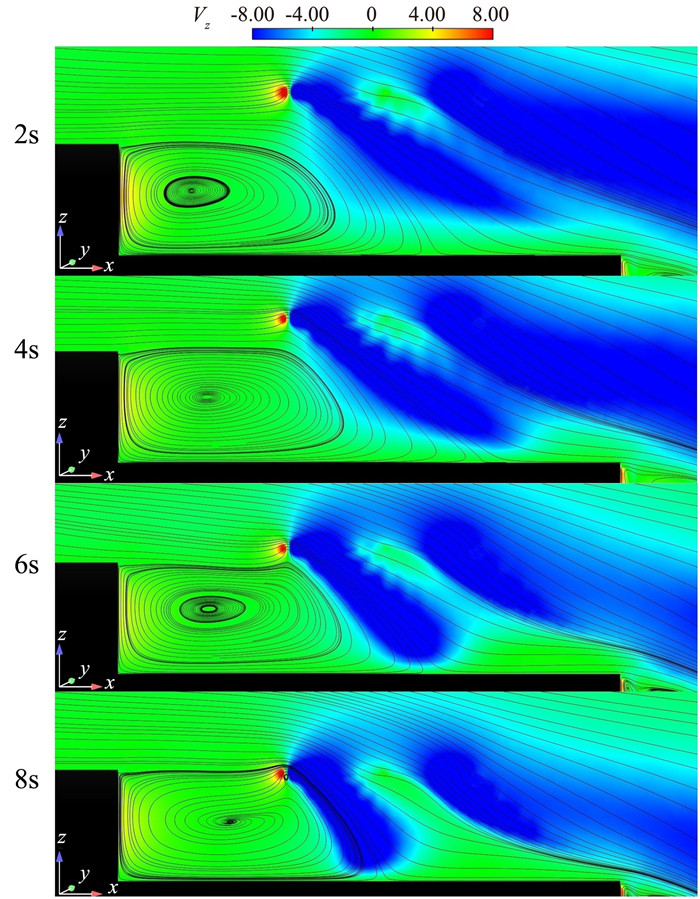
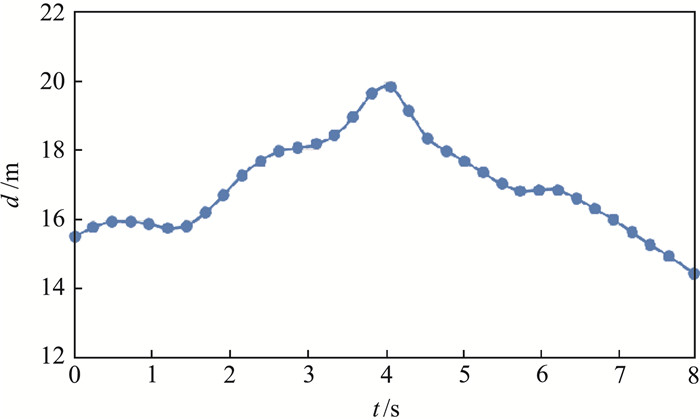
截取了下降2s、4s、6s、8s时刻的纵向中心截面垂向速度云图和流线图,如图 16所示。随着旋翼的下降,回流区受到挤压,再附点位置发生明显的移动,靠近机库一侧的强下洗流逐渐被吸向回流区,而靠近舰尾一侧的下洗流强度和影响范围削弱。对再附点的移动进行了测量,结果如图 17所示。再附点先向远离机库方向移动,然后向靠近机库方向移动,最远可达20 m,最近约14.4 m。再附点位置的变化直接反映回流区尺寸的变化,降落初期旋翼离回流区还有一定距离,所以脱落的桨尖涡只影响到回流区的上部,致使其下部的尺寸被拉长,再附点后移;随着旋翼的继续下降至4s之后,整个回流区完全受到旋翼桨尖涡的挤压,长度和高度都有所减小,8s时桨尖已经完全处于回流区内部。
|
图 16 不同时刻纵向中心截面垂向速度云图和流线图 Fig.16 Contours of z-velocity and streamlines in a longitudinal plane through center of the ship at different landing time |
|
图 17 再附点到机库的距离随降落时间变化曲线 Fig.17 Variation of distance between reattachment point and hangar with landing time |
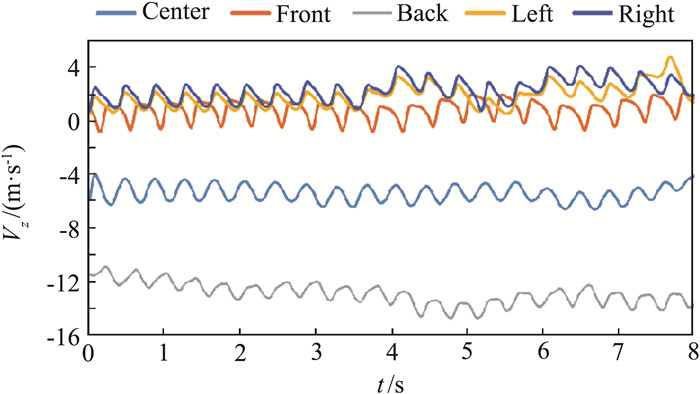
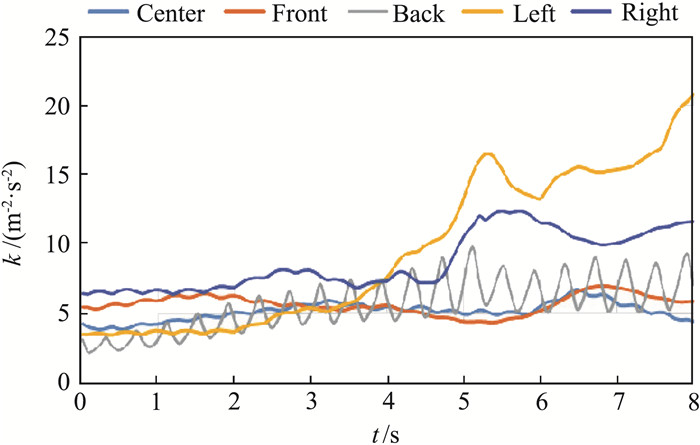
图 18和图 19分别给出了观测点垂向速度和湍动能随降落时间的变化曲线,与悬停状态不同,垂向速度的周期性被破坏,尤其到了降落的中后期,测点的无规则振荡变得明显。随着直升机的降落,前测点转变为弱上洗,而后测点的下洗流强度持续增加最大可达到-14 m/s,这种前后巨大的速度差可能使直升机后仰,对维持直升机的俯仰稳定性来说是巨大的挑战。对比表 1悬停与降落过程中观测点垂向速度标准差可以发现,旋翼下降过程中其下方流场的波动变大,尤其是后测点的垂向速度标准差约为悬停时的2倍,说明随着直升机的降落,旋翼尾涡与舰船尾涡的干扰变强。同时降落过程中,左、右测点的湍动能在4 s后急剧上升,最高甚至超过了20 m2/s2,这也从另一个方面反映了旋翼涡与舰船尾涡干扰的增强,使得流场变得非常紊乱。前、中、后三个测点的湍动能虽然也略微超出限制,但相比左、右测点而言波动小了很多,所以直升机降落过程中应当尽量保持机身对称面与舰船对称面重合,来减少左右两侧湍流对起降安全性造成的影响。
|
图 18 观测点垂向速度随降落时间变化曲线 Fig.18 Variation of z-velocity with landing time at observation points |
|
图 19 观测点湍动能随降落时间变化曲线 Fig.19 Variation of turbulent kinetic energy with landing time at observation points |
| 表 1 悬停与降落过程中观测点垂向速度标准差对比(单位:m/s) Table 1 Comparison of z-velocity standard deviationat observation points during hovering and landing (unit: m/s) |
|
|
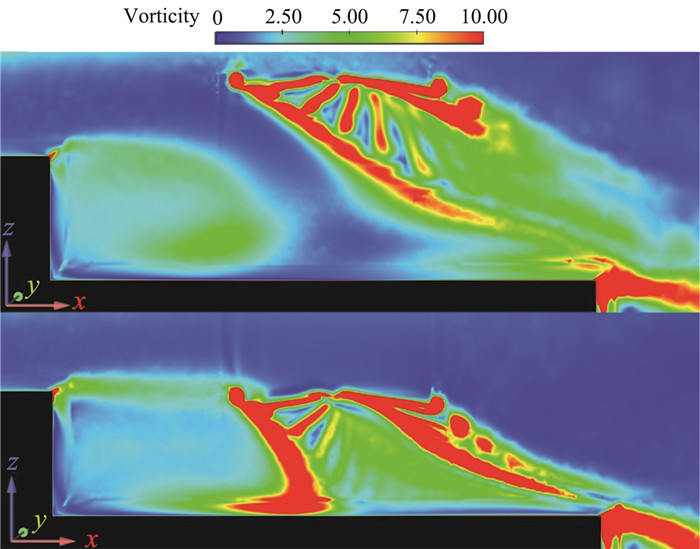
对比初始时刻和终了时刻的涡量云图(图 20),可以发现,当旋翼下降8 s后,舰面流场与旋翼流场耦合“涡-涡”干扰加剧,且旋翼流场受地面效应的影响变得非常明显,使得流场紊流度增加,红色强涡流区域的影响范围明显扩大,尤其是桨尖涡与回流区的耦合效应可以非常清晰地从涡量图中反映出来。
|
图 20 纵向中心截面涡量云图(上:0 s,下:8 s) Fig.20 Contours of vorticity in a longitudinal plane through center of the ship(The above is at time of 0 s while the below is at time of 8 s) |
本文运用重叠网格法动态模拟旋翼的旋转,对直升机与舰船的耦合流场进行了数值分析计算,得出以下结论:
1) 在计算资源条件允许的情况下,运用重叠网格法能够真实地还原旋翼高速旋转的动态过程,且可以捕捉到起降区空气流场的细节。
2) 直升机在甲板上空悬停的过程中,旋翼拉力系数逐渐收敛并呈现稳定的周期性波动,桨尖涡脱落与回流区、舷涡发生“涡-涡”干扰,但并不会对直升机的高空悬停产生大的干扰,值得注意的是旋翼下方前后流场存在较大垂向速度差,可能对机身的俯仰稳定性产生影响。
3) 直升机着舰过程中,这种耦合涡干扰越来越剧烈,尤其是当旋翼开始进入到回流区内部时,流场湍流度和旋涡强度急剧增加,严重影响旋翼的载荷分布与直升机的受力平衡,加重了驾驶员的操纵负担。同时由于舰面效应的增强使得旋翼下方左右两侧的耦合流场变得极其紊乱,所以出于安全性考虑,直升机着舰时应当尽量保持机身对称面与舰船对称面重合。
| [1] |
杨俊. 舰船机库大门对直升机起降特性影响研究[J]. 飞行力学, 2017, 35(4): 10-13. YANG J. Study of influence of warship hangar door on helicopter's take-off and landing characteristics[J]. Flight Dynamics, 2017, 35(4): 10-13. DOI:10.13645/j.cnki.f.d.20170504.005 (in Chinese) |
| [2] |
SHI Y J, HE X, XU Y, et al. Numerical study on flow control of ship airwake and rotor airload during helicopter shipboard landing[J]. Chinese Journal of Aeronautics, 2019, 32(2): 324-336. DOI:10.1016/j.cja.2018.12.020 |
| [3] |
SHUKLA S, SINHA S S, SINGH S N. Ship-helo coupled airwake aerodynamics:a comprehensive review[J]. Progress in Aerospace Sciences, 2019, 106: 71-107. DOI:10.1016/j.paerosci.2019.02.002 |
| [4] |
NEWMAN S. The phenomenon of helicopter rotor blade sailing[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 1999, 213(6): 347-363. DOI:10.1243/0954410991533070 |
| [5] |
曲飞, 陆超, 姜治芳, 等. 舰船舰面空气流场的CFD数值模拟探讨[J]. 中国舰船研究, 2009, 4(5): 23-27. QU F, LU C, JIANG Z F, et al. CFD numerical simulation of ship air-wake[J]. Chinese Journal of Ship Research, 2009, 4(5): 23-27. (in Chinese) |
| [6] |
耿雪.直升机旋翼与舰船甲板复合流场研究[D].大连: 大连海事大学, 2014. GENG X. The study of composite flow field of the helicopter rotor and ship deck[D]. Dalian: Dalian Maritime University, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10151-1014264300.htm |
| [7] |
POLSKY S. A computational study of unsteady shipairwake[C]//40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV. Reston, Virginia: AIAA, 2002. doi: 10.2514/6.2002-1022 https://www.researchgate.net/publication/269212852_A_computational_study_of_unsteady_ship_airwake
|
| [8] |
宗昆, 宗伟, 李海旭, 等. 舰载直升机起降区空气流场模拟方法研究[J]. 舰船科学技术, 2018, 40(2): 124-130, 139. ZONG K, ZONG W, LI H X, et al. Research of simulation methods on landing flow field for shipborne helicopters[J]. Ship Science and Technology, 2018, 40(2): 124-130, 139. DOI:10.3404/j.issn.1672-7649.2018.02.024 (in Chinese) |
| [9] |
RAJAGOPALAN R G, MATHUR S R. Three dimensional analysis of a rotor in forward flight[J]. Journal of the American Helicopter Society, 1993, 38(3): 14-25. DOI:10.4050/jahs.38.14 |
| [10] |
CHAFFIN M S, BERRY J D. Navier-Stokes simulation of a rotor using a distributed pressure disk method[C]//Proceedings of 51st Annual Forum of American Helicopter Society, 1995, 25-45. https://vtol.org/store/product/navierstokes-simulation-of-a-rotor-using-a-distributed-pressure-disk-method-374.cfm
|
| [11] |
PARK Y, KWON O J. Simulation of unsteady rotor flow field using unstructured adaptive sliding meshes[J]. Journal of the American Helicopter Society, 2004, 49(4): 391-400. DOI:10.4050/JAHS.49.391 |
| [12] |
WAKEFIELD N H, NEWMAN S J, WILSON P A. CFD predictions of the influence of external airflow on helicopter operations when operating from ship flight decks[C]//Proceedings of the RTO Applied Vehicle Technology Panel Symposium, Research and Technology Organization, Neuilly sur Seine, France, 1999, 1-10. https://www.researchgate.net/publication/313154875_CFD_predictions_of_the_influence_of_external_airflow_on_helicopter_operations_when_operating_from_ship_flight_decks
|
| [13] |
WAKEFIELD N H, NEWMAN S J, WILSON P A. Helicopter flight around a ship 's' superstructure[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2002, 216(1): 13-28. DOI:10.1243/0954410021533391 |
| [14] |
CROZON C, STEIJL R, BARAKOS G N. Numerical study of helicopter rotors in a ship airwake[J]. Journal of Aircraft, 2014, 51(6): 1813-1832. DOI:10.2514/1.C032535 |
| [15] |
苏大成, 史勇杰, 徐国华, 等. 直升机/舰船耦合流场的数值模拟[J]. 航空学报, 2017, 38(7): 75-86. SU D C, SHI Y J, XU G H, et al. Numerical simulation of coupled flow field of helicopter/ship[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 75-86. DOI:10.7527/S1000-6893.2017.120853 (in Chinese) |
| [16] |
ROPER D M, OWEN I, PADFIELD G D, et al. Integrating CFD and piloted simulation to quantify ship-helicopter operating limits[J]. The Aeronautical Journal, 2006, 110(1109): 419-428. DOI:10.1017/s0001924000001329 |
| [17] |
WEISS J, SMITH W A. Preconditioning applied to variable and constant density flows[J]. AIAA Journal, 1995, 33(11): 2050-2057. DOI:10.2514/3.12946 |
| [18] |
杨爱明, 刘金花, 翁培奋. 基于重叠网格技术和多重网格算法的悬停旋翼黏性绕流数值模拟[J]. 空气动力学学报, 2009, 27(1): 5-10. YANG A M, LIU J H, WENG P F. Navier-Stokes computation about a helicopter rotor in hover using chimera grids and multigrid acceleration[J]. Acta Aerodynamica Sinica, 2009, 27(1): 5-10. DOI:10.3969/j.issn.0258-1825.2009.01.002 (in Chinese) |
| [19] |
FORREST J S, OWEN I. An investigation of ship airwakes using detached-eddy simulation[J]. Computers & Fluids, 2010, 39(4): 656-673. DOI:10.1016/j.compfluid.2009.11.002 |
| [20] |
CARADONNA F X, TUNG C. Experimental and analytical studies of a model helicopter rotor in hover[J]. Vertica, 1981, 5(2): 149-161. |
 2020, Vol. 38
2020, Vol. 38


