2. 中国科学技术大学 近代力学系, 合肥 210000
2. Department of Modern Mechanics, University of Science and Technology of China, Hefei 210000, China
流体经过物体表面空腔或者缺口时,由于腔外剪切层和腔内流动的相互作用会形成方腔自激振荡,并伴随有强烈的压力、速度脉动,且会辐射出低频高幅值噪声[1]。这一现象广泛存在于军用和民用航空领域[2],属于典型的声-涡干扰类流致噪声问题。
从20世纪中叶开始,由于飞行器的速度不断提高,起落架舱等构件产生的噪声引起人们的重视。到70年代,随着战斗机巡航速度进一步提高,武器舱等方腔结构对飞行性能的影响凸显。武器舱内高达170 dB的压力脉动对结构产生强动态载荷,造成疲劳损伤,损坏电子设备[3],更重要的是影响武器的安全分离和精确投递。起落架舱噪声会影响航空运输器乘坐的舒适性[4],并且破坏气动性能[5]。随着最近愈发强调轻盈紧凑型智能武器的存储分离,低阻力安全投放成为战斗机的一项重要的性能标准[6]。总之,随着航空运输业的持续发展以及乘客对舒适性的要求逐渐提高,气动噪声已经成为航空业亟待解决的问题,其噪声水平直接关系到飞行适航证的获取[7]。航空运输业的可持续发展,愈发关注环境友好型飞行器,噪声控制技术在航空器的设计和研发中日益重要。
飞行器气动噪声控制的一个难点是噪声与流动分离、阻力等其他特性紧密耦合[5]。深入认识流动的内在物理机制是实现流动控制的关键,噪声控制更需如此。传统的被动控制技术多通过抬升剪切层来减弱剪切层与后拐角的相互作用来抑制噪声,如前缘采用导流装置[8-9]、改变后壁面形状[10]或者设置子腔[11]等。这种控制技术需要改变方腔外形,虽然能够抑制振荡噪声,但是会破坏流动特性,甚至增加阻力等。
方腔噪声控制根据是否有能量注入分为主动和被动控制,其中主动控制又根据是否存在反馈环被分为开环和闭环控制。主动控制通过增加剪切层和激励器的相互作用改变剪切层特性来削弱涡角相互作用,比如在前缘布置质量射流激励器[12]或零质量射流激励器[13]等,或者构成闭环反馈回路抑制自激振荡[14]。但是,实际流动问题中非线性相互作用强,增加了开环主动控制的难度,并降低了其适用范围。因此,考虑流动动态特性的控制问题需要进行主动闭环控制,即引入优化控制策略。
Gharib[15]最早实验研究了方腔流动的主动控制,在方腔上游边界层内激发Tollmein-Schlichting波抑制了剪切层内的速度脉动。Shaw[16]通过带通滤波器的反馈信号调整脉冲射流激励器,基于迭代搜索的控制方式实现了压力脉动的有效控制。Micheau[17]通过方腔底部的压力脉动的反馈信号驱动方腔后缘的震动表面来打破自持机制以抑制压力脉动。Debiasi[18]设计了自适应算法,通过动态调整控制的频率以达到最好的抑制效果。Williams[13]通过手动调节控制参数,实现了方腔扰流的动态反馈控制。虽然能够取到很好的控制效果,但是设计控制律非常困难。因此,需要发展一种计算量与控制参数无关的优化控制手段。
伴随方法通过求解控制方程的伴随方程,能够很快地得到目标函数对控制参数的梯度,且该过程的计算量不依赖于控制参数数目。国内研究中,伴随方法被成功应用到机翼优化设计[19]、圆柱绕流[20]等气动优化工作中,尚未应用到方腔流动中。Liu[21]通过不可压缩三维方腔的结构敏感性分析发现, 能够通过改变构型形状抑制三维剪切层不稳定性的位置。Bewley[22]首次基于伴随方法开展了流动优化的控制研究,通过在边界施加零质量射流控制湍流边界层。基于伴随的不可压缩流动优化控制技术成功应用到剪切层噪声控制[23]、射流噪声[24]和尾缘噪声控制[25]等。Yamouni等[26]基于伴随方法求解可压缩方腔流动。Javier[27]首次基于伴随方法开展了二维方腔流动的优化控制研究,通过改变传感器位置研究对流动控制的影响。Xiao等[28]首次开展了长时域边界层流动转捩的非线性优化控制研究,得到了最优的壁面激励。
目前,长时域非线性问题的优化过程不易收敛,基于伴随的非定常可压缩流动控制研究仍不多见。本文主要研究二维方腔构型,基于伴随方法实现参数化控制。在方腔前缘附近施加时空随机激励,以压力脉动的时空积分作为目标函数,采用BFGS算法优化控制过程,并结合时域滚动技术开展长时域方腔流动噪声的优化控制研究。
1 控制方程与离散方法 1.1 控制方程方腔流动的可压缩Navier-Stokes方程可以写成向量形式为:
| $ {\frac{{\partial \rho }}{{\partial t}} = - \nabla \cdot (\rho \mathit{\boldsymbol{u}})} $ | (1) |
| $ {\frac{{\partial \rho \mathit{\boldsymbol{u}}}}{{\partial t}} = - \nabla \cdot (\rho \mathit{\boldsymbol{u}} \otimes \mathit{\boldsymbol{u}}) - \nabla p + \frac{1}{{Re}}\nabla \cdot \mathit{\boldsymbol{\tau }}} $ | (2) |
| $ {\frac{{\partial \rho E}}{{\partial t}} = - \nabla \cdot (\rho \mathit{\boldsymbol{u}}E) - \nabla \cdot (p\mathit{\boldsymbol{u}}) + \frac{1}{{ Re }}\nabla \cdot (\mathit{\boldsymbol{\tau }} \cdot \mathit{\boldsymbol{u}}) - \nabla \cdot \mathit{\boldsymbol{Q}}} $ | (3) |
其中:ρ是密度,速度向量u =(u, v),⊗表示张量积,压力为p,基于方腔深度的雷诺数Re=ρuD/μ。特征速度为远场声速c∞,特征压力为ρ∞c∞2,特征时间为D/c∞。总能E表示为:
| $ E = \frac{1}{2}\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}} + \frac{p}{{\rho (\gamma - 1)}} $ | (4) |
比热比γ=1.4,τ和Q分别表示黏性应力张量和热通量向量,表示为:
| $ {\mathit{\boldsymbol{\tau }} = \lambda (\nabla \cdot \mathit{\boldsymbol{u}}) + \mu (\nabla \mathit{\boldsymbol{u}} + \nabla {\mathit{\boldsymbol{u}}^{\rm{T}}})} $ | (5) |
| $ {\mathit{\boldsymbol{Q}} = - \kappa \nabla T} $ | (6) |
动力学黏性系数μ是温度函数,λ=-2μ/3,理想气体的热传导系数κ=μ/[Pr·Re·(γ-1)],空气介质的Pr数为0.72。上述方程组通过状态方程完成封闭:
| $ p = \rho RT $ | (7) |
基于伴随的优化控制研究,其优势是梯度求解过程的计算量和控制参数数目无关。为了简化,控制方程重写为:
| $ \frac{{\partial \mathit{\boldsymbol{q}}}}{{\partial t}} + N(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{F}} $ | (8) |
其中q = [ρ u v p] T。引入状态变量的小扰动q ′,对方程(8)进行Fréchet推导可以得到线化方程:
| $ {\mathit{\boldsymbol{\dot q}}^\prime } + {N^\prime }(\mathit{\boldsymbol{q}}){\mathit{\boldsymbol{q}}^\prime } = 0 $ | (9) |
其中N′(q)是线化N-S算子。
引入伴随算子N′(q)†,通过下面式子作用在伴随状态q†=[ρ† u† p†]上:
| $ \langle {N^\prime }(\mathit{\boldsymbol{q}}){\mathit{\boldsymbol{q}}^\prime },{\mathit{\boldsymbol{q}}^\dagger }\rangle = \langle {\mathit{\boldsymbol{q}}^\prime },{N^\prime }{(\mathit{\boldsymbol{q}})^\mathit{\dagger }}{\mathit{\boldsymbol{q}}^\dagger }\rangle + BT $ | (10) |
BT是边界条件相关项,时空域的内积形式为:
| $ \langle a,b\rangle = \int_0^T {\int_\varOmega a } \cdot b{\kern 1pt} {\kern 1pt} {\rm{d}}\mathit{\boldsymbol{x}}{\kern 1pt} {\rm{d}}t $ | (11) |
对式(10)分部积分,将q′的微分算子转到q†上,线性扰动控制方程可以推导为:
| $ {N^\prime }{(\mathit{\boldsymbol{q}})^\dagger }{\mathit{\boldsymbol{q}}^\dagger } = \left( {\mathit{\boldsymbol{T}}\frac{\partial }{{\partial t}} + \mathit{\boldsymbol{X}}\frac{\partial }{{\partial x}} + \mathit{\boldsymbol{Y}}\frac{\partial }{{\partial y}} + \frac{{Ma}}{{Re}}\mathit{\boldsymbol{D}}} \right){\mathit{\boldsymbol{q}}^\dagger } $ | (12) |
其中,Ma为来流马赫数,相关矩阵分别为:
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} u&{{u^2}}&{uv}&{\frac{{{u^2} + {v^2}}}{2}u}\\ \rho &{2\rho u}&{\rho v}&{\frac{\gamma }{{\gamma - 1}}p + \frac{\rho }{2}(3{u^2} + {v^2}) + \frac{{5Ma}}{{3Re}}\frac{{\partial v}}{{\partial y}}}\\ 0&0&{\rho u}&{\rho uv - \frac{{5Ma}}{{3Re}}\frac{{\partial u}}{{\partial y}}}\\ 0&1&0&{\frac{{\gamma u}}{{\gamma - 1}}} \end{array}} \right] $ | (13) |
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} v&{uv}&{{u^2}}&{\frac{{{u^2} + {v^2}}}{2}v}\\ 0&{\rho v}&0&{\rho uv - \frac{{5Ma}}{{3Re}}\frac{{\partial v}}{{\partial x}}}\\ \rho &{\rho u}&{2\rho v}&{\frac{\gamma }{{\gamma - 1}}p + \frac{\rho }{2}(3{u^2} + {v^2}) + \frac{{5Ma}}{{3Re}}\frac{{\partial v}}{{\partial x}}}\\ 0&0&1&{\frac{{\gamma v}}{{\gamma - 1}}} \end{array}} \right] $ | (14) |
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&u&v&{\frac{{{u^2} + {v^2}}}{2}}\\ 0&\rho &0&{\rho u}\\ 0&0&\rho &{\rho v}\\ 0&0&0&{\frac{1}{{\gamma - 1}}} \end{array}} \right] $ | (15) |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&{ - \frac{{\gamma p}}{{ Pr (\gamma - 1){\rho ^2}}}\left( {\frac{{{\partial ^2}}}{{\partial x}} + \frac{{{\partial ^2}}}{{\partial y}}} \right)}\\ 0&{\frac{{4{\partial ^2}}}{{3\partial x}} + \frac{{{\partial ^2}}}{{\partial y}}}&{\frac{{{\partial ^2}}}{{3\partial xy}}}&{u\frac{{4{\partial ^2}}}{{3\partial x}} + u\frac{{{\partial ^2}}}{{\partial y}} + v\frac{{{\partial ^2}}}{{3\partial xy}}}\\ 0&{\frac{{{\partial ^2}}}{{3\partial xy}}}&{\frac{{{\partial ^2}}}{{\partial x}} + \frac{{4{\partial ^2}}}{{3\partial y}}}&{v\frac{{{\partial ^2}}}{{\partial x}} + v\frac{{4{\partial ^2}}}{{3\partial y}} + u\frac{{{\partial ^2}}}{{3\partial xy}}}\\ 0&0&0&{\frac{\gamma }{{ Pr (\gamma - 1)\rho }}\left( {\frac{{{\partial ^2}}}{{\partial x}} + \frac{{{\partial ^2}}}{{\partial y}}} \right)} \end{array}} \right] $ | (16) |
为了控制噪声,将噪声相关的目标函数定义为长时间压力脉动的平均量:
| $ J(\mathit{\boldsymbol{f}}) = \frac{1}{{2T}}\int_\varOmega {\mathop \smallint \nolimits_0^T } {[p(\mathit{\boldsymbol{f}},\mathit{\boldsymbol{x}},t) - \bar p]^2}{\rm{d}}t{\kern 1pt} {\rm{d}}\mathit{\boldsymbol{x}} $ | (17) |
T代表优化时域长度,p是控制前时均压力,p是施加了控制f的压力。
引入Lagrange函数L(q, q′, q†)求解最小值问题:
| $ L(\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{q}}^\prime },{\mathit{\boldsymbol{q}}^\dagger }) = J(\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{q}}^\prime }) + \langle {\mathit{\boldsymbol{q}}^\dagger },{\mathit{\boldsymbol{\dot q}}^\prime } + {N^\prime }(\mathit{\boldsymbol{q}}){\mathit{\boldsymbol{q}}^\prime }\rangle $ | (18) |
其中,q†是伴随乘子。Lagrange函数对q′和q†的偏微分为:
| $ {\frac{{\partial L(\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{q}}^\prime },{\mathit{\boldsymbol{q}}^\dagger })}}{{\partial {\mathit{\boldsymbol{q}}^\prime }}} = 0} $ | (19) |
| $ {\frac{{\partial L(\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{q}}^\prime },{\mathit{\boldsymbol{q}}^\dagger })}}{{\partial {\mathit{\boldsymbol{q}}^\dagger }}} = 0} $ | (20) |
Lagrange函数对伴随算子的偏分是直接系统的控制方程:
| $ \frac{{\partial L(\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{q}}^\prime },{\mathit{\boldsymbol{q}}^\dagger })}}{{\partial {\mathit{\boldsymbol{q}}^\dagger }}} = 0 \Rightarrow {\mathit{\boldsymbol{\dot q}}^\prime } + {N^\prime }(\mathit{\boldsymbol{q}}){\mathit{\boldsymbol{q}}^\prime } = 0 $ | (21) |
梯度信息被用来更新式(8)右侧的控制力:
| $ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} - {\alpha ^k}{(\nabla J)^k} $ | (22) |
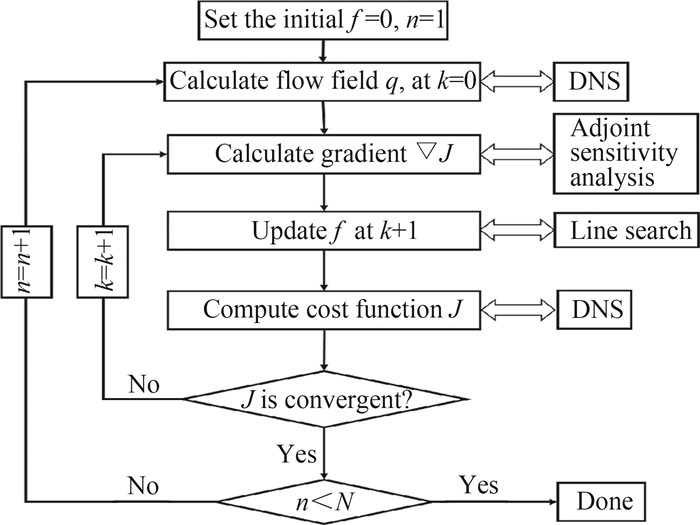
k是优化迭代步数,α是f空间内的步长, 用于控制激励在给定方向上的前进距离,采用Quasi-Newton法的Broyden-Fletcher-Goldfarb-Shanno (BFGS)算法优化控制力 f 。图 1给出了基于伴随方法的方腔流致噪声优化控制的流程。
|
图 1 伴随优化控制的整个流程图 Fig.1 The entire flow chart of adjoint-based optimizations |
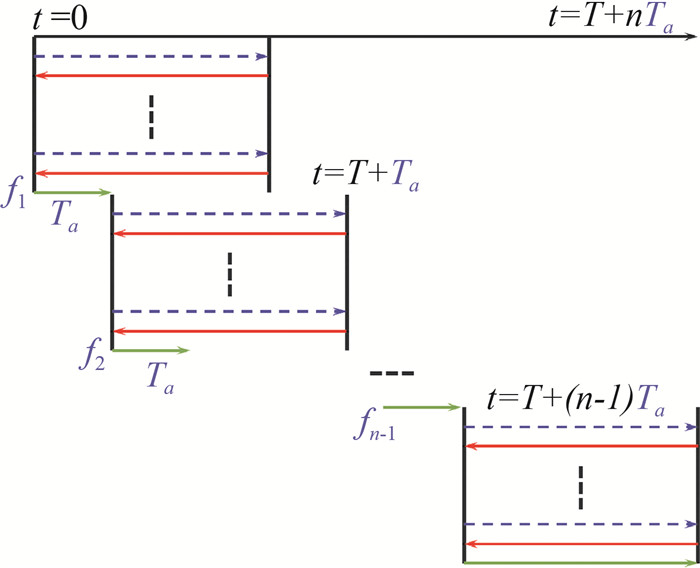
由于方腔流动中强非线性效应的影响,控制时域过长时会导致计算的敏感性难以收敛甚至得到错误的结果。为了克服这个问题,本文采用Model Predictive Control方法把长时域分解为多个短时域进行模拟[28],即滚动时域技术,如图 2所示, 其中Tα为迭代递进步长。
|
图 2 滚动时域方法的示意图 Fig.2 Schematic plot of the receding horizon framework |
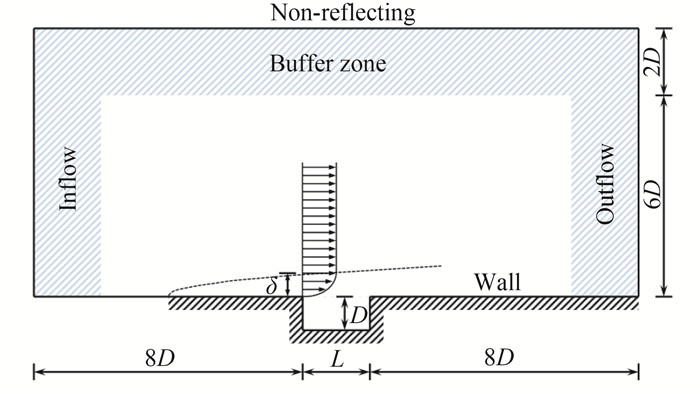
本文主要研究层流流经长深比L/D=2的开式方腔流动,来流马赫数Ma=0.5,基于方腔深度的雷诺数Re=3000,方腔前缘处的动量厚度δ=1/52.8L,如图 3所示。空间离散格式采用7点色散关系保持格式(DRP),时间推进采用4阶Runge-Kutta方法。伴随过程和直接过程中,每个时间步内在全方向上采用十阶显式滤波格式来保证数值计算过程的稳定性。上游来流、下游出流和远场采用无反射边界条件,方腔来流经过一段无滑移边界后过渡到黏性等温壁面。为了抑制声波在远场边界的反射,在远场边界附近采用了缓冲区技术。计算域上游最远距离方腔前缘8D,下游最远距离后拐角8D,法向最远处距离方腔唇口8D,远场缓冲区宽度为2D。DNS和伴随过程采用同样的数值格式,时间推进的步长取为Δtc∞/D=0.002。短时域优化时长为Tc∞/D=20,优化推进5个短时域,迭代递进步长Ta=1/2T,总优化时域tc∞/D=60。
|
图 3 方腔流动模拟的构型(虚线表示黏性边界层,阴影表示缓冲区) Fig.3 Configuration of the cavity flow simulation(Dashed lines represent the edge of boundary layer, and the shadow areas represent the buffer zone) |
数值模拟使用的网格在壁面附近和剪切层内加密,为了保证数值解是收敛的,采用了三套网格验证收敛性,网格设置如表 1所示。为了更方便地显示网格收敛性,采用监测点A(0, 0.14)和B(2, 0.14)处压力脉动的时均值
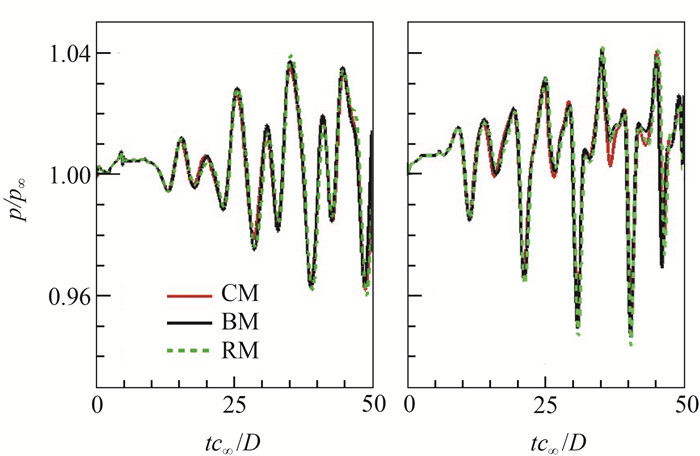
表 1中的定量结果表明,加密网格(RM)后,监测点A(0, 0.14)和B(2, 0.14)处的压力脉动时均值变化相对粗网格(CM)明显减少。如图 4所示,加密网格的压力时程曲线没有发生明显的变化,说明当前网格(BM)下得到的数值解是收敛的,模拟结果不依赖于网格。
| 表 1 网格收敛性及误差分析 Table 1 Grid convergence and error analysis |
|
|
|
图 4 网格收敛性验证:监测点A(左)、B(右)位置的压力时程曲线 Fig.4 Grid convergence verification: Evolution of pressure at the point A (left) and B (right) |
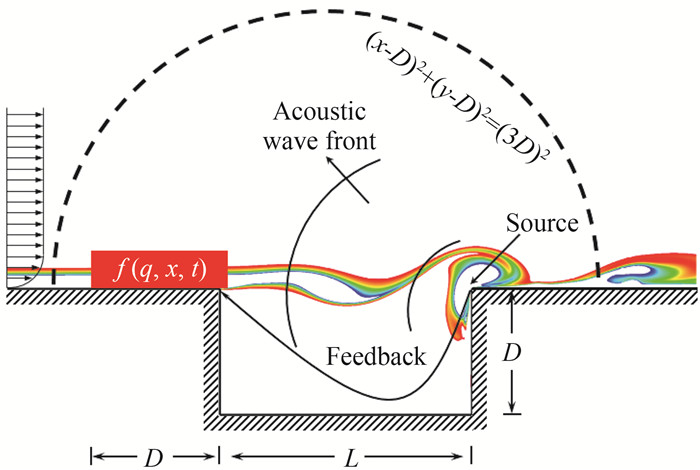
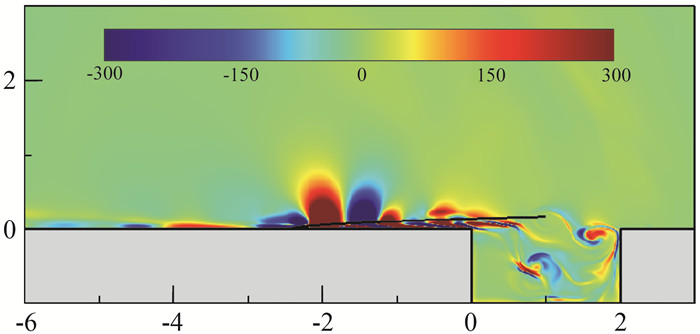
方腔自持振荡发声主要是由于来流边界层在方腔前缘分离,剪切层的旋涡撞击到方腔后拐角后向外辐射噪声,如图 5所示。首先,为了确定控制激励施加的最优位置,开展了方腔流动对方腔后拐角附近激励的敏感性分析。图 6给出一个瞬时方腔流动对后拐角激励的敏感性分布,可以看出最敏感位置集中在方腔前缘附近。基于敏感性分析结果,我们在方腔前缘附近区域施加体积力f(x, y, t)以抑制方腔辐射噪声远场目标区域内的噪声,控制激励布置在区域[(-1, 0), (1.015, 0.3)]内。目标区域布置在一段弧线(x-D)2+(y-D)2=9D2上,能够有效地涵盖所有辐射方向上的噪声,如图 5虚线所示。
|
图 5 方腔优化控制示意图(红色区域为激励施加位置,弧线为目标区域) Fig.5 Schematic diagram of optimized noise control of cavity flow(The red block indicates the position excitation is applied, The dash lines represent the target line) |
|
图 6 方腔流动对后拐角激励的敏感性分布 Fig.6 Sensitivity distribution of cavity flow to the excitation near the rear corner |
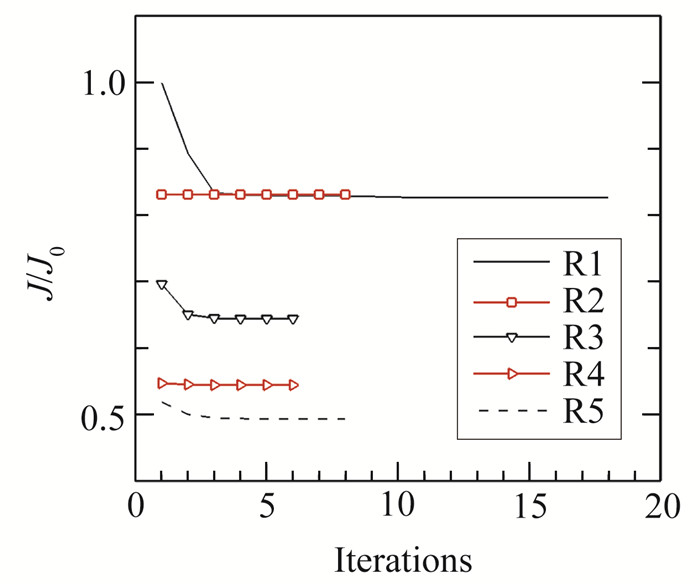
当前整个优化过程需要求解46次目标函数,即总共需要50次DNS迭代优化激励使目标函数最小(每个时域迭代收敛后进行一次DNS更新时域间的激励)。所有迭代完成后,总体目标函数收敛了52.1%。表 2详细给出了各个滚动时域内DNS次数和目标函数收敛情况,其中伴随方程的求解次数和DNS相同。用未控制的目标函数J0将目标函数归一化,图 7给出了所有滚动时域的目标函数的收敛情况。在第一个滚动时域R1内,前3个优化迭代过程中优化激励作用明显,目标函数迅速收敛。第三、五滚动时域内也出现相同现象,这主要是进入时域内的初始激励和最优激励偏差较大导致。
| 表 2 滚动时域内优化迭代次数和目标函数变化量 Table 2 The number of iterations and change in cost function for the receding horizons |
|
|
|
图 7 滚动时域内目标函数J的演化过程 Fig.7 Evolution of the cost function J for the receding horizons |
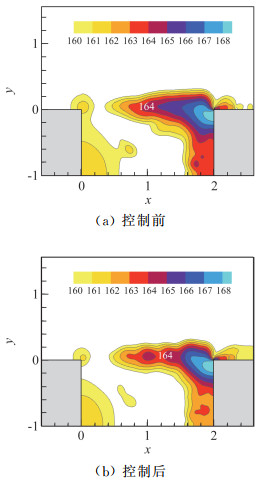
图 8给出了控制前和控制后方腔内总声压级(OASPL)分布情况。可以清晰地看出无论是否进行控制,后拐角附近的声压都是最强的,这表明方腔后拐角发生的涡角相互作用是辐射噪声的主要来源。优化后的前缘和后缘附近的同幅值的声压级分布区域变小,表明噪声强度被削弱。另外,对比控制前后的结果发现,前缘引入的控制激励主要改变了压力剪切层内的压力振荡分布,同时,方腔后半部分主回流区内的压力振荡也得到了一定程度的减弱,这表明控制可能减弱了剪切层内的旋涡与回流区相互作用。
|
图 8 控制前后方腔流动近场总声压级分布云图 Fig.8 ontours of OASPL in the near field of cavity flow for uncontrolled case and controlled case |
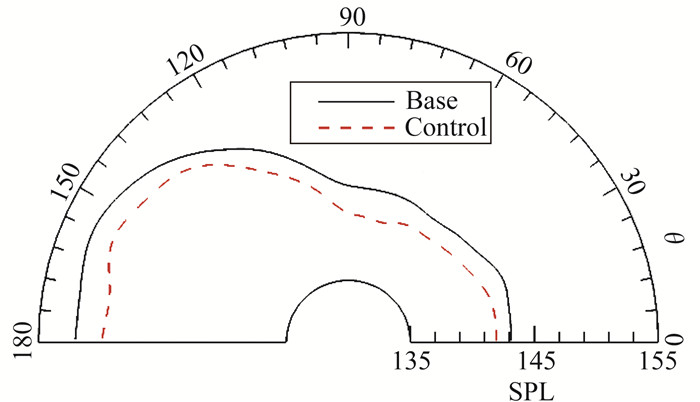
图 9给出了目标区域内的不同角度上的总体声压级(OASPL)分布。相比控制前的总声压级分布情况,可以看出优化后的噪声在目标区域内全辐射方向上均被抑制,其中噪声最强的方向上抑制噪声2 dB。当前研究结果表明基于伴随的优化控制可以得到高质量的梯度信息,其可以用于更新控制激励信号。需要指出的是,当前研究中选择的目标区域虽然能够反映出全方向上的噪声辐射信息,但是,对于方腔噪声控制而言,这样的目标函数取法是否能取得最优效果仍有待于进一步深入研究。
|
图 9 目标区域总声压级(0°和180°分别表示下游和上游方向,黑色、红色线段分别表示控制前后的声压级) Fig.9 Overall sound pressure levels on the target line(0° and 180° denote the upstream and downstream directions. The black and red line show the OASPL for the uncontrolled and controlled cases, respectively) |
本文通过采用长时域控制技术,基于连续伴随方法的优化控制算法初步实现了非定常可压缩方腔流致噪声的主动反馈控制,并且在所有辐射方向上削弱了噪声的总声压级,其中辐射最强方向上总声压级减小约2 dB。
为了控制更有效果,一般需要在敏感性幅值较强的区域布置外部激励,因此,本文首先进行了敏感性分析,最后将外部激励布置在了方腔前缘边界层附近。为了实现长时间的反馈控制,本文采用了滚动时域技术,在优化迭代46次后,目标函数趋于收敛。对比控制前后的结果发现后拐角是辐射噪声的主要来源,控制后主要是方腔上方的剪切层的总声压级分布被改变,目标控制区总声压级下降。
值得注意的是,虽然当前的伴随控制取得了效果,但是其是否是全局最优以及如何选取最优目标函数等问题仍然需要进一步深入研究。
| [1] |
万振华, 周林, 孙德军. 方腔流致振荡及噪声的数值研究[J]. 空气动力学学报, 2012, 30(3): 291-298. WAN Z H, ZHOU L, SUN D J. Numerical investigation of flow-induced oscillations and noise from a rectangular cavity[J]. Acta Aerodynamica Sinica, 2012, 30(3): 291-298. DOI:10.3969/j.issn.0258-1825.2012.03.003 (in Chinese) |
| [2] |
BRUGGEMAN J C, HIRSCHBERG A, VAN DONGEN M E H, et al. Self-sustained aero-acoustic pulsations in gas transport systems:experimental study of the influence of closed side branches[J]. Journal of Sound and Vibration, 1991, 150(3): 371-393. DOI:10.1016/0022-460X(91)90893-O |
| [3] |
KOOK H, MONGEAU L, BROWN D V, et al. Analysis of the interior pressure oscillations induced by flow over vehicle openings[J]. Noise Control Engineering Journal, 1997, 45(6): 223. DOI:10.3397/1.2828444 |
| [4] |
ROVIG G W, BOHNKER B K, PAGE J C. Hearing health risk in a population of aircraft carrier flight deck personnel[J]. Military Medicine, 2004, 169(6): 429-432. DOI:10.7205/MILMED.169.6.429 |
| [5] |
MCGREGOR O W, WHITE R A. Drag of rectangular cavities in supersonic and transonic flow including the effects of cavity resonance[J]. AIAA Journal, 1970, 8(11): 1959-1964. DOI:10.2514/3.6032 |
| [6] |
STANEK M, RAMAN G, KIBENS V, et al. Control of cavity resonance through very high frequency forcing[C]//6th Aeroacoustics Conference and Exhibit, Lahaina, HI. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-1905 https://www.researchgate.net/publication/268467072_Control_of_cavity_resonance_through_very_high_frequency_forcing
|
| [7] |
YU Y H. Measurements of sound radiation from cavities at subsonic speeds[J]. Journal of Aircraft, 1977, 14(9): 838-843. DOI:10.2514/3.58863 |
| [8] |
COMTE P, DAUDE F, MARY I. Simulation of the reduction of unsteadiness in a passively controlled transonic cavity flow[J]. Journal of Fluids and Structures, 2008, 24(8): 1252-1261. DOI:10.1016/j.jfluidstructs.2008.08.001 |
| [9] |
杨党国, 刘俊, 王显圣, 等. 典型构型空腔模型设计与流动/噪声特性研究[J]. 空气动力学学报, 2018, 36(3): 432-439, 448. YANG D G, LIU J, WANG X S, et al. Analysis of design method and aeroacoustics characteristics inside typical cavity[J]. Acta Aerodynamica Sinica, 2018, 36(3): 432-439, 448. DOI:10.7638/kqdlxxb-2017.0201 (in Chinese) |
| [10] |
VIKRAMADITYA N S, KURIAN J. Pressure oscillations from cavities with ramp[J]. AIAA Journal, 2009, 47(12): 2974-2984. DOI:10.2514/1.43068 |
| [11] |
LEE Y, KANG M, KIM H, et al. Passive control techniques to alleviate supersonic cavity flow oscillation[J]. Journal of Propulsion and Power, 2008, 24(4): 697-703. DOI:10.2514/1.30292 |
| [12] |
SAROHIA V, MASSIER P F. Control of cavity noise[J]. Journal of Aircraft, 1977, 14(9): 833-837. DOI:10.2514/3.58862 |
| [13] |
WILLIAMS D, FABRIS D, IWANSKI K, et al. Closed-loop control in cavities with unsteady bleed forcing[C]//38th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-470
|
| [14] |
CATTAFESTA L, ALVI F, WILLIAMS D, et al. Review of active control of flow-induced cavity oscillations (invited)[C]//33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, Florida. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-3567
|
| [15] |
GHARIB M. Response of the cavity shear layer oscillations to external forcing[J]. AIAA Journal, 1987, 25(1): 43-47. DOI:10.2514/3.9576 |
| [16] |
SHAW L, NORTHCRAFT S. Closed loop active control for cavity acoustics[C]//5th AIAA/CEAS Aeroacoustics Conference and Exhibit, Bellevue, WA. Reston, Virginia: AIAA, 1999 doi: 10.2514/6.1999-1902
|
| [17] |
MICHEAU P, CHATELLIER L, LAUMONIER J, et al. Active control of a self-sustained pressure fluctuation due to flow over a cavity[C]//10th AIAA/CEAS Aeroacoustics Conference, Manchester, GREAT BRITAIN. Reston, Virginia: AIAA, 2004 doi: 10.2514/6.2004-2851
|
| [18] |
DEBIASI M, SAMIMY M. Logic-based active control of subsonic cavity flow resonance[J]. AIAA Journal, 2004, 42(9): 1901-1909. DOI:10.2514/1.4799 |
| [19] |
高昌, 张小庆, 贺元元, 等. 连续伴随方法在二维高超声速进气道优化中的应用[J]. 空气动力学学报, 2020, 38(1): 21-26. GAO C, ZHANG X Q, HE Y Y, et al. Applications of continuous adjoint method in 2D hypersonic inlet optimization[J]. Acta Aerodynamica Sinica, 2020, 38(1): 21-26. DOI:10.7638/kqdlxxb-2018.0214 (in Chinese) |
| [20] |
范宝春, 张辉, 陈志华, 等. 圆柱绕流的优化控制[J]. 空气动力学学报, 2007, 25(s2): 97-101. FAN B C, ZHANG H, CHEN Z H, et al. Adjoint-based optimal control of flow aroud cylinder[J]. Acta Aerodynamica Sinica, 2007, 25(s2): 97-101. (in Chinese) |
| [21] |
LIU Q, GÓMEZ F, THEOFILIS V. Control of flow instabilities in an open aircraft bay model cavity[C]//46th AIAA Fluid Dynamics Conference, Washington, D.C.. Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-3317
|
| [22] |
BEWLEY T, MOIN P, TEMAM R. DNS-based predictive control of turbulence:an optimal benchmark for feedback algorithms[J]. Journal of Fluid Mechanics, 2001, 447: 179-225. DOI:10.1017/S0022112001005821 |
| [23] |
WEI M, FREUND J B. A noise-controlled free shear flow[J]. Journal of Fluid Mechanics, 2005, 546(-1): 123-152. DOI:10.1017/S0022112005007093 |
| [24] |
KIM J, BODONY D J, FREUND J B. Adjoint-based control of loud events in a turbulent jet[J]. Journal of Fluid Mechanics, 2014, 741: 28-59. DOI:10.1017/jfm.2013.654 |
| [25] |
SCHULZE J, SESTERHENN J. Optimal distribution of porous media to reduce trailing edge noise[J]. Computers & Fluids, 2013, 78: 41-53. DOI:10.1016/j.compfluid.2011.12.022 |
| [26] |
YAMOUNI S, SIPP D, JACQUIN L. Interaction between feedback aeroacoustic and acoustic resonance mechanisms in a cavity flow:a global stability analysis[J]. Journal of Fluid Mechanics, 2013, 717: 134-165. DOI:10.1017/jfm.2012.563 |
| [27] |
OTERO J. Development and application of an adjoint-based optimal flow control framework for compressible direct numerical simulations[D]. University of Southampton, 2017. https://www.researchgate.net/publication/319542622_Development_and_application_of_an_adjoint-based_optimal_flow_control_framework_for_compressible_direct_numerical_simulations
|
| [28] |
XIAO D, PAPADAKIS G. Nonlinear optimal control of transition due to a pair of vortical perturbations using a receding horizon approach[J]. Journal of Fluid Mechanics, 2019, 861: 524-555. DOI:10.1017/jfm.2018.919 |
 2020, Vol. 38
2020, Vol. 38


