捕获轨迹试验(CTS)是一种测量外挂物分离后相对载机轨迹的先进试验方法,能有效评估外挂物分离的安全特性,获得与全尺寸飞行数据基本相当的试验结果,广泛应用于外挂物投放/发射的地面模拟测量[1]。国外从20世纪50年代就已着手捕获轨迹试验的研究,先后在风洞中建立了CTS试验系统[2-8],用于机弹相容性研究以及分离安全性评估,为机载武器的研制提供了技术支撑。国内中国空气动力研究与发展中心自1980年就开始相继研究用于1 m和2 m量级亚跨和超声速风洞中的CTS系统[9-12],并得到了较大发展。CTS试验系统通常由计算机及程序、六自由度运动机构、载弹测力天平、载机支撑系统、测控系统等组成,其中六自由度运动机构是其核心组件,现有的CTS试验系统中六自由度机构普遍采用串联的形式,存在机构刚度较弱以及关节误差积累导致的定位精度差等不足。
近年来,随着并联机构的发展,研究人员逐渐认识到并联机构的优势,并联形式的六自由度机构在风洞中已逐步得到应用,主要应用在风洞中提供模型支撑进行飞机模型动态试验等方面[13-17]。在风洞中采用并联机构构型的优势有:1)定位精度高,相比串联机构各关节存在的误差累计效应来说,并联机构多支链同时操作末端机构可以避免关节的积累误差;2)机构刚度高,机构采用六个固定杆长的并联机构构型,保证了高的机构刚度,受风载时变形小,模型不会出现剧烈抖动现象,保证风洞试验过程中的定位精度;3)机构承载能力强,能够承受高马赫数时风洞开关车产生的大冲击载荷。
为克服现有的基于串联六自由度机构的CTS试验技术的不足,本文将并联机构应用到CTS风洞试验技术中,对基于并联机构构型的CTS风洞试验技术进行研究,并进行风洞试验验证。
1 总体技术方案如图 1所示,CTS试验系统以专用的风洞试验段为基础,所有部件集成安装到该试验段。半臂迎角机构安装到试验段上方,用来支撑载机模型,迎角范围为-5°~15°。载弹模型支撑机构采用固定杆长的并联机构构型形式,具有6个运动自由度(3平动+3转动)。为了实现六自由度机构大的滚转运动空间,满足武器分离投放模拟的要求,在并联机构的前端连接模型的位置串联了一个滚转驱动机构,可以实现导弹±180°范围的滚转姿态模拟。六自由度机构在流场中阻塞度 < 1%。

|
图 1 六自由度运动机构 Fig.1 Six-degree of freedom (DOF) mechanism |
CTS试验测控系统由信号采集系统、载弹轨迹生成程序、并联式六自由度机构反解程序以及伺服电机控制程序组成,系统工作流程如图 2所示,试验时根据载弹的气动力以及其动力学参数通过载弹轨迹生成程序得到载弹某一个时刻的位姿,通过六自由度机构的反解程序得到伺服电机需要的运动位置。

|
图 2 CTS系统工作流程图 Fig.2 Work flow diagram of CTS system |
并联六自由度机构基本构型如图 3所示,包括六组直线驱动单元(A1、A2、…、A6),动平台、六组连接杆以及之间的运动副。在不影响机构分析的基础上,可将连接杆AiCi(i=1, 2, …, 6)两侧的铰链形式简化为球关节,并在滑块Ai所在平面中心设置基座原点O,并设定其x轴方向垂直于左右两侧平面,y轴方向平行于左右两侧平面。同时,在动平台中心设置动系原点P,其坐标方向在初始状态与O系保持平行。

|
图 3 六自由度并联机构示意图 Fig.3 Schematic diagram of 6-DOF parallel mechanism |
将上层杆件(A1C1和A4C4)的杆长记作L1,将中层杆件(A2C2和A5C5)的杆长记作L2,将下层杆件(A3C3和A6C6)的杆长记作L3,两侧直线导轨中心线之间的距离为D,动平台各铰链点与yp轴夹角分别记作θ、φ和ψ,铰链点的外接圆半径记作RC。同时设定六组驱动的驱动量为q1、q2、…、q6。
给定六自由度并联机构的基本参数,具体数值如表 1所示。
| 表 1 六自由度并联机构基本参数 Table 1 Basic parameters of 6-DOF parallel mechanism |
|
|
并联机构的位姿反解是试验系统中测控软件的基础,位姿反解过程为:给定载弹的分离位姿,需要解算出直线驱动单元对应的驱动量。
动坐标系{P}与动平台固接,显然,动坐标系中任意向量都能在定坐标系{O}中表示:
| $\boldsymbol{R}=[\boldsymbol{T}] \boldsymbol{R}+\boldsymbol{P} $ | (1) |
其中,[T]是动平台姿态方向余弦矩阵,应用zyx型欧拉角进行表示,P是选定点在定坐标系{O}中的位置矢量,可表示为P=(xp yp zp)。
各个铰链点Ci和Ai(i=1, 2, …, 6)在各自坐标系的坐标可以通过给定结构参数求得,通过公式(1)可以求出各个铰链点在固定坐标系{O}中的坐标值。六个连接杆矢量CiAi在{O}系可以表达式为:
| $C_{i} A_{i}=C_{i}-A_{i} $ | (2) |
同时,根据各个连接杆Li长度恒定的几何关系,通过对公式(2)展开后进行求模计算,有|CiAi|=Li,即可得出各驱动量qi的函数表达式:
| $q_{i}=\sqrt{\left|L_{i}\right|^{2}-\left(\mathrm{A}_{i x}-C_{i x}\right)^{2}-\left(\mathrm{A}_{i y}-C_{i y}\right)^{2}}-q_{0} $ | (3) |
其中,q0表示驱动中间位置,为恒定值。
2.2 六自由度机构工作空间分析六自由度机构的工作空间是CTS试验载弹模型的活动范围,该范围会直接约束投放试验的地面模拟能力。分析工作空间时考虑了各关节转角的约束、各杆直线运行空间的约束、机构各构件的干涉及构件与风洞洞壁的干涉等情况。实际运行中并联机构执行除滚转外的5个自由度,滚转运动由并联机构前端的滚转机构单独实现,其角度范围为:-180°≤θ≤180°。
1) 静平台运行空间约束:Axmini≤Axi≤Axmaxi。Axmini和Axmaxi分别表示第i杆静铰链直线运行空间的最小值和最大值。
2) 铰链转角限制:δPi≤δPmax、δBi≤δBmax。δPmax和δBmax分别表示静平台铰链和动平台铰链的最大转角。
3) 机构各构件的干涉:dlmin≤Δ1、dmmin≤Δ2。dlmin和Δ1分别为运行中杆件和铰链中心的最小距离和设计最小距离;dmmin和Δ2分别为运行中不同杆件之间的最小距离和设计最小距离。
4) 构件与洞壁的干涉:ymin≤Pyi≤ymax、zmin≤Pzi≤zmax。Pyi和Pzi分别为动平台第i铰链中心的坐标值。
根据机构干涉条件可计算构型的工作空间,垂直于气流方向的工作截面如图 4所示。
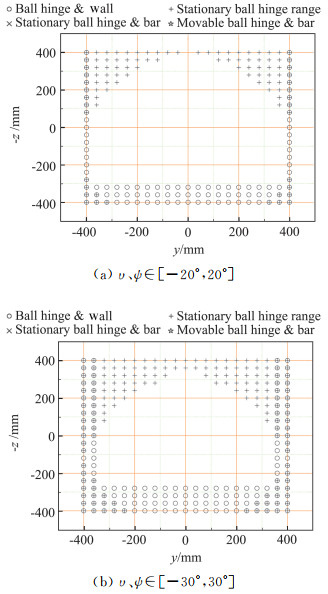
|
图 4 工作空间截面图 Fig.4 Sectional diagram of work space |
从工作空间截面图可见,影响工作空间的因素主要是动平台铰链点与风洞洞壁的干涉及静铰链的角度范围限制;机构的工作范围与动平台姿态角耦合,随着动平台姿态的增加,机构的工作范围逐渐缩小。
在姿态角范围在±30°内时,机构的工作空间可如表 2所示,在该空间中可满足常规分离试验的风洞模拟。
| 表 2 机构工作范围 Table 2 Workspace of the mechanism |
|
|
串联机构和并联机构的刚度矩阵普遍采用如下形式:
| $\boldsymbol{K}=[\boldsymbol{J}]^{\mathrm{T}} \boldsymbol{K}[\boldsymbol{J}] $ | (4) |
其中,K表示CTS机构的主刚度对角矩阵,为恒定值,可将其设定为单位矩阵。J为机构的雅克比矩阵。
根据方向刚度定义,刚度分为转动刚度和移动刚度,其中移动刚度为主要刚度,取f为三个外力矢量方向上的单位矢量,则移动方向刚度可表示为:
| $K_{F}=f^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}} \boldsymbol{f} $ | (5) |
通过建立移动方向刚度KF的拉格朗日函数,求解其极值,并选取所有特征值中的极小值与极大值的比值
| $\varepsilon=\frac{\int \frac{\sqrt{\chi_{\min }}}{\sqrt{\chi_{\max }}} \mathrm{d} W}{\iint_{\mathrm{d} W}} $ | (6) |
对并联机构的ε求解得到值为0.83,串联机构对比构型采用文献[18]中的参数,计算结果0.63。可以看出并联六自由度机构刚度较高。在相同机构阻塞度约束下,采用并联构型可以提高六自由度机构的刚度以及承载力。
2.4 六自由度机构地面测试利用便携式三坐标对六自由度机构空间位姿进行测量,测试现场照片如图(5)所示。便携式的三坐标测量仪采用的是ROMER绝对测量臂。

|
图 5 载弹模型位姿测量照片 Fig.5 Photograph of the attitude for the store model |
采用文献[19-22]中的运动学标定方法对研制的并联式六自由度机构进行运动学标定并对加工及装配带来的误差进行修正。把测量得到的位姿代入运动学位姿反解表达式(3)中,通过雅克比矩阵对非奇异性位姿进行辨识。利用辨识出的并联机构的结构参数修正测控系统中的参数以提高并联机构运动精度。
随机选取空间任意10组位姿进行定位精准度的测试,表 3给出了机构精准度的测试结果。并联机构的定位精度以及对确定位姿点的定位准度比较高,位置精度优于0.1 mm,角度精度优于0.05°。
| 表 3 机构各自由度的精准度 Table 3 Precision and accuracy of 6-DOF mechanism |
|
|
为了验证在风洞气流条件下六自由度机构的定位精准度以及机构运行的稳定性,进行了自由流条件下六自由度机构走迎角序列时导弹气动系数的测量。图 6是自由流对比试验结果,从结果中可以看出:CTS六自由度机构得到的结果重复性很好,说明机构在有风载下具有良好的定位精度;自由流试验数据与风洞中常规迎角机构得到试验结果一致性较好。图 7是六自由度机构自由流时不同马赫数下的试验结果,从图中可以看出不同马赫数下得到的试验结果规律性良好。
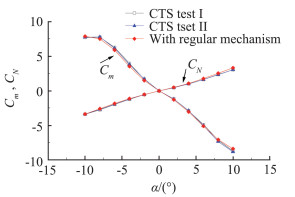
|
图 6 自由流对比试验结果 Fig.6 Comparisons of freestream data between regular mechanism and CTS system |
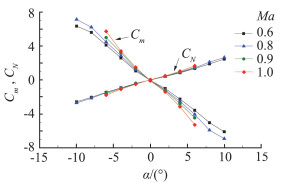
|
图 7 自由流下不同马赫数下试验结果 Fig.7 Feestream comparisons for different Mach numbers |
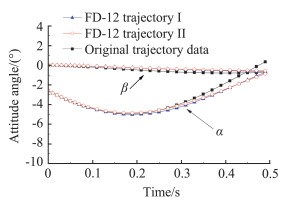
为了验证基于并联机构的CTS试验系统的可靠性,进行了带载机干扰的轨迹线验证试验,图 8和图 9是在相同工况下得到的轨迹线数据对比,从结果可以看出:FD-12风洞CTS系统轨迹线的重复性较好,与原有串联机构轨迹线的数据规律一致,数据相关性较好;只有在时间序列的后半段,俯仰角姿态出现分叉现象,主要是因为CTS试验方法中轨迹解算存在误差积累效应,串联机构会存在由于刚度不足导致的位姿定位精度误差,给试验结果带来累计效应,所以随时间的增加误差会增大。
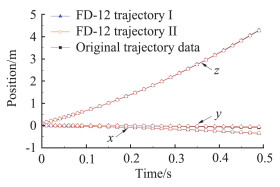
|
图 8 带载机干扰的轨迹线位置重复性对比 Fig.8 Comparisons of trajectory position repetitions with the carrier interference |
|
图 9 带载机干扰的轨迹线姿态角重复性对比 Fig.9 Comparisons of trajectory pose repetitions with the carrier interference |
本文将并联六自由度机构应用到1.2 m高速风洞CTS试验技术,在风洞尺寸约束下对六自由度机构构型以及结构参数进行了设计,并计算了机构的运动空间,进行了地面测试以及风洞试验验证,得到如下结论:
1) 高速风洞CTS试验系统中,采用固定杆长的并联六自由度机构可以提高试验系统的机构刚度、定位精准度以及机构的承载能力。机构位置精度优于0.1 mm,角度精度优于0.05°,满足CTS试验要求。
2) 自由流风洞试验数据重复性良好,与风洞常规迎角机构得到的数据一致性较好且不同马赫数下试验结果规律性良好;带载机干扰的CTS轨迹线试验数据重复性良好。
| [1] |
李周复. 风洞特种试验技术[M]. 北京: 航空工业出版社, 2010. LI Z F. Special wind tunnel test technique[M]. Beijing: Aviation Industry Press, 2010: 113-116. (in Chinese) |
| [2] |
GARCON F, TARAVEL P, RAFFIN J C. Recent developments in captive trajectory systems of the ONERAModane wind tunnels[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2001. doi: 10.2514/6.2001-579
|
| [3] |
ZILBERMAN M, SHAY M. The use of the Captive Trajectory system for computation of trajectories to the impact point[C]//17th Aerospace Ground Testing Conference, Nashville, TN. Reston, Virginia: AIAA, 1992. doi: 10.2514/6.1992-4031
|
| [4] |
CARMAN J, HILL J B, D W, et al. Store separation testing techniques at the Arnold engineering development center. volume 2. description of captive trajectory store separation testing in the aerodynamic wind tunnel (4T)[R]. Defense Technical Information Center, 1980. doi: 10.21236/ada087561
|
| [5] |
RAY E. Comparison of AEDC 4T and CALSPAN 8-ft wing tunnels for FA-18C/JDAM[R]. Defense Technical Information Center, 2000. doi: 10.21236/ada376031
|
| [6] |
VEAZEY D, HOPF J. Comparison of aerodynamic data obtained in the Arnold Engineering Development Center wind tunnels 4T and 16T[C]//20th AIAA Advanced Measurement and Ground Testing Technology Conference, Albuquerque, NM. Reston, Virginia: AIAA, 1998. doi: 10.2514/6.1998-2874
|
| [7] |
CENKO A, PHILLIPS K, M HOLMES I. Captive Trajectory System sting effects on store loads[C]//32nd Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1994. doi: 10.2514/6.1994-195
|
| [8] |
CENKO A, PIRANIAN A, RAY E. Freestream data effects on trajectory predictions[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, California. Reston, Virginia: AIAA, 2002. doi: 10.2514/6.2002-4417
|
| [9] |
于志松, 王发祥, 罗新福. 两种特殊CTS试验技术的研究[J]. 流体力学实验与测量, 2004, 18(4): 49-53. YUZ S, WANG F X, LUO X F. Investigation of two special CTS test techniques[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(4): 49-53. (in Chinese) |
| [10] |
黄叙辉, 罗新福, 于志松. FL-24风洞新型捕获轨迹系统设计与发展[J]. 空气动力学学报, 2008, 26(2): 145-149. HUANG X H, LUO X F, YU Z S. Design & development of a new captive trajectory simulation system in FL-24 wind tunnel[J]. Acta Aerodynamica Sinica, 2008, 26(2): 145-149. (in Chinese) |
| [11] |
黄叙辉, 庞旭东, 宋斌. 1.2 m跨超声速风洞新型捕获轨迹系统研制[J]. 实验流体力学, 2008, 22(2): 95-98. HUANG X H, PANG X D, SONG BIN. Development of a new captive trajectory simulation system in the 1.2 m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(2): 95-98. (in Chinese) |
| [12] |
李平, 黄叙辉, 周润, 等. 2 m×2 m超声速风洞CTS测控系统研制[J]. 实验流体力学, 2015, 29(4): 95-100. LI P, HUANG X H, ZHOU R, et al. Development of measurement and control system for CTS in 2 m×2 m supersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 95-100. (in Chinese) |
| [13] |
LOESER T, BERGMANN A. Development of the dynamic wind tunnel testing capabilities at DNW-NWB[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-453
|
| [14] |
HVBNER A R. Experimental and numerical investigations of unsteady aerodynamic derivatives for transport aircraft configurations[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-1076
|
| [15] |
LOESER T, BERGMANN A. Capabilities of deployment tests at DNW-NWB[M]. RTO-AVT-133, 2006: 13.
|
| [16] |
BERGMANN A, HUEBNER A, LOESER T. Experimental and numerical research on the aerodynamics of unsteady moving aircraft[J]. Progress in Aerospace Sciences, 2008, 44(2): 121-137. DOI:10.1016/j.paerosci.2007.10.006 |
| [17] |
谢志江, 孙小勇, 孙海生, 等. 低速风洞动态试验的高速并联机构设计及动力学分析[J]. 航空学报, 2013, 34(3): 487-494. XIE Z J, SUN X Y, SUN H S, et al. Mechanism design and dynamics analysis of high speed parallel robot for dynamic test in low speed wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 487-494. (in Chinese) |
| [18] |
缑双双, 蹇开林. 一种六自由度分离体机构运动学分析及仿真[J]. 重庆理工大学学报(自然科学), 2017, 31(5): 43-48. GOU SS, JIAN K L. Kinematics analysis and simulation of a 6-DOF separation mechanism[J]. Journal of Chongqing University of Technology (Natural Science), 2017, 31(5): 43-48. (in Chinese) |
| [19] |
陈晓光.双端虎克铰并联运动模拟器机构的分析[D].哈尔滨: 哈尔滨工业大学, 2011: 30-36. CHEN X G. Analysis of the hexaglide parallel mechanism with double-end universal joints in kinematics chains[D]. Harbin: Harbin Institute of Technology, 2011: 30-36. |
| [20] |
张学功, 邹怀武, 陈卫东. 并联六自由度对接平台运动学标定方法研究[J]. 宇航学报, 2007, 28(2): 273-277. ZHANG X G, ZOU H W, CHEN W D. The Research of kinematic calibration method of parallel 6-DOF dock platform[J]. Journal of Astronautics, 2007, 28(2): 273-277. (in Chinese) |
| [21] |
王浩.六自由度并联调整装置运动学标定研究[D].成都: 电子科技大学, 2013. WANG H. Study on kinematic calibration of the 6-DOF parallel adjustment device[D]. Chengdu: University of Electronic Science and Technology of China, 2013. |
| [22] |
于大泳.六自由度运动模拟器精度分析及其标定[D].哈尔滨: 哈尔滨工业大学, 2006. YU D Y.Accuracy analysis and calibration of six-DOF motion simulator[D]. Harbin: Harbin Institute of Technology, 2006. |
 2020, Vol. 38
2020, Vol. 38

