城市规划气候适应性设计需在城市形态的规划设计过程中综合考虑建筑密度、建筑高度等一系列技术指标对城市微气候(如风速、风向、温度、湿度等)的影响,对定量分析工具的时间、空间分辨率要求较高,故计算流体力学(Computational Fluid Dynamics,CFD)模拟技术被认为是最适合的分析工具之一[1-2]。然而,大多数城市微气候CFD模拟均是基于足尺模型,计算开销大且对计算硬件条件依赖性强。对于区域稍大的城市微气候问题,即使采用雷诺平均湍流模拟,网格数也在千万级以上[3-4]。例如,文献[5]所报道的对整个东京城区风速场和温度场的模拟,网格更是多达50亿。显然,这是目前一般小型计算机的内存和存储条件所难以满足的。因此,寻找和探索减少计算开销的方法就成为城市微气候CFD数值模拟迫切需要解决的问题之一。
根据相似理论的基本原理,只要维持足尺现象与计算模型之间的单值条件相似,并保证同名相似准则相等,则可以对计算模型进行尺度的缩小与放大、参数的提高和降低、介质性能的改变等操作而不改变其相似性[6]。因此,一些学者开始探索CFD缩尺模拟方法提高计算效益[7-12]。文献[7]采用了几何缩尺模型进行数值模拟,但依然采用实际流动介质,缩尺模拟结果不能达到与实际现象的完全相似。为了保证缩尺模拟的相似性,通常是根据实际流动的动力-热力过程确定关键相似准则,并以此指导设计实际缩尺或放尺模拟方案。例如,文献[8]基于弗劳德准则对道路隧道通风问题进行了缩尺模拟,结果显示缩尺模拟与足尺模拟之间有良好的相似性;文献[9]则根据阿基米德数相等的原则对室内热环境进行相似模拟,也证实了方法的可行性。但研究也显示[13]:在一些特定情况下,由于某些相似准则不易匹配会导致计算结果产生不同程度的失真。
综合文献分析可以发现:目前CFD相似模拟技术主要是通过移植物理相似试验原理发展起来的,即在几何缩尺的同时保留物理模型不变,通过控制关键相似准则达到相似要求。此类方法没有充分考虑计算机仿真的特殊性,它们还是在一种不完全相似的条件下进行的模拟,局限性没有得到解决。
本文从大气流动控制方程组出发,通过方程推导法推导出对应的相似准则,并通过构造满足相似准则的虚拟流动介质用于城市微气候CFD缩尺模拟计算,从而保证相似性得到严格的满足。这种缩尺模拟方法从本质上维持了缩尺模型和足尺模型的相似性,可以在保证较高精度的同时大幅减少计算开销。
1 CFD缩尺模拟方法根据相似第三定理[14]:如两个现象的单值条件相似,且由单值量组成的同名相似准则数值相同,则这两个现象相似。基于该相似定理,以下所构筑CFD缩尺模拟方法首先推导了相似流动的相似准则及边界条件,然后通过构造完全满足相似准则的虚拟流动介质用于缩尺模型数值计算,以保证缩尺数值计算与原型流动之间的相似性。
1.1 相似流动的相似准则假设大气为不可压缩的恒定流,在不考虑辐射传热引起的浮力影响情况下,大气流动可由以下控制方程组所描述[15]。
质量守恒方程:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 $ | (1) |
动量守恒方程(简称N-S方程):
| $ \begin{array}{*{20}{l}} {\frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\upsilon \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial p}}{{\partial {x_i}}} - \rho \beta (T - {T_{{\rm{ ref }}}}){g_i}} \end{array} $ | (2) |
能量守恒方程:
| $ \begin{array}{*{20}{c}} {{C_v}\rho \left( {\frac{{\partial T}}{{\partial t}} + {u_j}\frac{{\partial T}}{{\partial {x_j}}}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{k_d}\frac{{\partial T}}{{\partial {x_j}}}} \right) + }\\ {\frac{\partial }{{\partial {x_j}}}\left[ {\upsilon {u_j}\left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right]} \end{array} $ | (3) |
式中:下标i和j表示方向,xi是笛卡尔坐标,m;ui是速度分量,m/s;t为时间,s;ρ为空气密度,kg/m3;p是流体微元体上的压力,Pa;ν为运动粘滞系数,m2/s;gi为重力加速度,m/s2;β为体积膨胀率,1/K;T和Tref分别为瞬时温度和浮力参考温度,ΔT为两者的差值,K;Cv为定压比热容,J/(kg·K);kd为导热系数,W/(m·K)。
将原型(P)与模型(P′)的各物理量的相似比用CP表示,则有
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {\frac{{{x_i}}}{{x_i^\prime }} = \frac{{{x_j}}}{{x_j^\prime }} = \frac{l}{{{l^\prime }}} = {C_l},\quad \frac{\rho }{{{\rho ^\prime }}} = {C_\rho }}\\ {\frac{T}{{{T^\prime }}} = {C_T},\quad \frac{\beta }{{{\beta ^\prime }}} = {C_\beta },\quad \frac{{\Delta T}}{{\Delta {T^\prime }}} = {C_{\Delta T}}}\\ {\frac{{{u_i}}}{{u_i^\prime }} = \frac{{{u_j}}}{{u_j^\prime }} = \frac{u}{{{u^\prime }}} = {C_u}}\\ {\frac{p}{{{p^\prime }}} = \frac{{\rho {u^2}}}{{{\rho ^\prime }{u^{\prime 2}}}} = {C_\rho }C_u^2} \end{array}} \right.\\ \left\{ {\begin{array}{*{20}{l}} {\frac{t}{{{t^\prime }}} = \frac{{\frac{l}{u}}}{{\frac{{{l^\prime }}}{{{u^\prime }}}}} = \frac{{l{u^\prime }}}{{{l^\prime }u}} = \frac{{{C_l}}}{{{C_u}}},\frac{\upsilon}{{{\upsilon^\prime }}} = {C_\upsilon}}\\ {\frac{{{g_i}}}{{g_i^\prime }} = {C_g},\frac{{{k_d}}}{{k_d^\prime }} = {C_k},\frac{{{c_v}}}{{c_v^\prime }} = {C_c}} \end{array}} \right. \end{array} $ | (4) |
式中,l为特征长度,m;u为速度,m/s;其余各物理量概念与前文一致。
将式(4)代入控制方程(1)、(2)和(3),得
| $ \frac{{{C_u}}}{{{C_l}}}\frac{{\partial u_i^\prime }}{{\partial x_i^\prime }} = 0 $ | (5) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial ({\rho ^\prime }u_i^\prime )}}{{\partial {t^\prime }}} + \frac{{\partial ({\rho ^\prime }u_i^\prime u_j^\prime )}}{{x_j^\prime }} = \frac{{{C_\upsilon }}}{{{C_u}{C_l}{C_p}}}\frac{\partial }{{\partial {x_j}}}\left( {{\upsilon ^\prime }\frac{{\partial u_i^\prime }}{{\partial x_j^\prime }}} \right) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {p^\prime }}}{{\partial x_i^\prime }} - \frac{{{C_l}{C_{\Delta T}}{C_g}{C_\beta }}}{{C_u^2}}{\rho ^\prime }{\beta ^\prime }\Delta {T^\prime }g_i^\prime } \end{array} $ | (6) |
| $ \begin{array}{l} C_v^\prime {\rho ^\prime }\left[ {\frac{{\partial {T^\prime }}}{{\partial {t^\prime }}} + u_j^\prime \frac{{\partial {T^\prime }}}{{\partial x_j^\prime }}} \right] = \frac{{{C_k}}}{{{C_\rho }{C_c}{C_u}{C_l}}}\frac{\partial }{{\partial x_j^\prime }}\left( {k_d^\prime \frac{{\partial {T^\prime }}}{{\partial x_j^\prime }}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{C_\upsilon }{C_u}}}{{{C_\rho }{C_c}{C_l}}}\frac{\partial }{{\partial x_j^\prime }}\left[ {{\upsilon ^\prime }u_j^\prime \left( {\frac{{\partial u_i^\prime }}{{\partial u_j^\prime }} + \frac{{\partial u_j^\prime }}{{\partial x_i^\prime }}} \right)} \right] \end{array} $ | (7) |
使式(6)、(7)中每一项的相似比组合量彼此相等,则
| $ \frac{{{C_\upsilon }}}{{{C_u}{C_l}{C_p}}} = \frac{{{C_l}{C_{\Delta T}}{C_B}{C_\beta }}}{{C_u^2}} = \frac{{{C_k}}}{{{C_\rho }{C_c}{C_u}{C_l}}} = \frac{{{C_\upsilon }{C_u}}}{{{C_\rho }{C_c}{C_l}}} = 1 $ | (8) |
将相似变换式(4)代入式(8),可得:
| $ \frac{{{\rho ^\prime }{u^\prime }{l^\prime }}}{{{\upsilon ^\prime }}} = \frac{{\rho ul}}{\upsilon }\quad {\rm{ 或 }}\quad R{e^\prime } = Re $ | (9) |
| $ \frac{{\Delta {T^\prime }{l^\prime }g_i^\prime {\beta ^\prime }}}{{{u^{\prime 2}}}} = \frac{{\Delta Tl{g_i}\beta }}{{{u^2}}}\quad {\rm{ 或 }}\quad R{i^\prime } = Ri $ | (10) |
| $ \frac{{k_d^\prime }}{{{\rho ^\prime }c_v^\prime {u^\prime }{l^\prime }}} = \frac{{{k_d}}}{{\rho {c_v}ul}}\quad {\rm{ 或 }}\quad \frac{1}{{R{e^\prime }}}\frac{1}{{P{r^\prime }}} = \frac{1}{{Re}}\frac{1}{{Pr}} $ | (11) |
| $ \frac{{{u^\prime }{v^\prime }}}{{{\rho ^\prime }c_v^\prime {l^\prime }{T^\prime }}} = \frac{{u\upsilon }}{{\rho {c_v}lT}}\quad {\rm{ 或 }}\quad \frac{1}{{R{e^\prime }}}E{c^\prime } = \frac{1}{{Re}}Ec $ | (12) |
由此可以看出:在浮力影响下的相似大气流动中,必须在模型和原型之间严格维持雷诺数Re、理查德森数Ri、普朗特数Pr以及爱克特数Ec等相似准则彼此相等。
1.2 相似流动边界条件根据相似理论,缩尺模型和足尺模型满足相似性需要保证边界条件相似,包括流动边界条件和热力边界条件。
在不考虑辐射换热的稳态模拟中,足尺模型和缩尺模型之间流动边界条件相似需要在对应位置上平均风速等于给定的速度比、湍流强度保持相等,以及湍流积分尺度等于给定缩尺比;而热力边界条件相似只需流体温度及壁面温度维持不变即可。
1.3 虚拟流动介质构筑方法由式(9~12)可知,大气流动的相似准则有4个:雷诺数Re、理查德森数Ri、普朗特数Pr、爱克特数Ec;变量有10个:密度ρ、速度u、特征长度l、运动黏滞系数ν、温度差ΔT、重力加速度gi、体积膨胀率β、导热系数kd、比热容Cv、温度T。
在本文的模拟中,指定温度差ΔT、重力加速度gi、体积膨胀率β、温度T的相似比为1、速度u的相似比为2、特征长度l的相似比为4,根据同名相似准则相等的原则,即可根据式(8)确定密度ρ、运动黏滞系数ν、导热系数kd、比热容Cv等4个变量的相似比,将各相似比代入式(4)可得到严格满足相似条件的虚拟流动介质的物性参数。
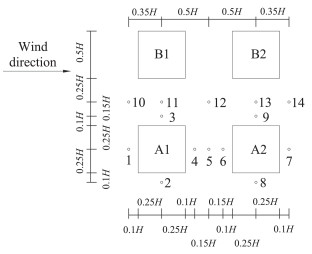
2 数值模拟与分析 2.1 计算模型与边界条件计算模型如图 1所示,模型中的建筑物布置两行两列,足尺模型的建筑物长L和宽B取20 m,高H取40 m,建筑物间距W取20 m。取缩尺比为1:4,对应的缩尺模型中L=B=5 m, H=10 m,W=5 m。在计算模型0.05H~0.95H的高度之间每隔0.1H作一平面,在每个平面上取14个采样点,计算模型及采样点平面位置如图 1所示。
|
图 1 计算模型和采样点位置平面示意图 Fig.1 Plane diagram of the calculation model and the locations of the sampling points |
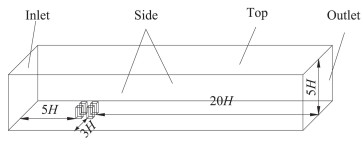
如图 2所示,模拟计算域以建筑高度H为参照,入流边界设置在建筑群迎风面前5H处,出流边界设置在背风面后20H处,侧流边界设置在距离建筑最近墙面3H处,计算域顶部边界离地5H。计算域采用非结构化四面体网格划分,足尺模型与缩尺模型网格划分对比如表 1所示。由表 1可知,缩尺模型网格数量约为足尺模型网格数量的0.5倍。
|
图 2 计算域示意图 Fig.2 Diagram of the computational domain |
| 表 1 足尺模型与缩尺模型网格划分对比 Table 1 Parameters of discretization |
|
|
足尺模型对应的物性参数[16]如表 2所示。根据虚拟流动介质构筑方法,由足尺模型的物性参数推导出缩尺模型的物性参数如表 2所示。
| 表 2 足尺模型与缩尺模型对应的物性参数 Table 2 Parameters of physical property |
|
|
湍流模拟采用商业软件Fluent中的SST k-ω模型,近壁区采用标准壁面函数,引入Boussinesq密度假设,足尺模型和缩尺模型的入流边界设置为Dirichlet边界条件、入流温度30 ℃,对应的平均风速剖面、湍流剖面设置如表 3所示,出流边界设置为自由出流边界条件、零梯度温度壁面,侧向边界及顶部边界设置为对称边界条件、热对称边界,固壁边界设置为无滑移光滑壁面、固壁恒温36 ℃。
| 表 3 足尺模型与缩尺模型对应的入流边界条件 Table 3 Boundary conditions of inlet |
|
|
解的收敛控制标准设为:各求解变量的残差不大于10-4,在求解域内整体不平衡率低于5%。
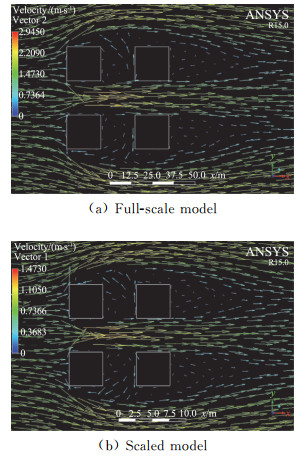
2.2 计算结果与分析 2.2.1 流动形态分析足尺模型和缩尺模型在离地0.5H平面的大气流动形态可由图 3看出:沿流动方向,在建筑物之间气流因巷道效应加速;前排建筑物背面产生回流腔区,腔区范围受后排建筑物限制;后排建筑物背面亦产生回流腔区,腔区尺度相对较大;腔区内流速较其他区域变慢。足尺模型和缩尺模型的平面流动形态具有良好的相似性。
|
图 3 0.5H高度处流动矢量图 Fig.3 Vector plot of the flow at the height of 0.5H |
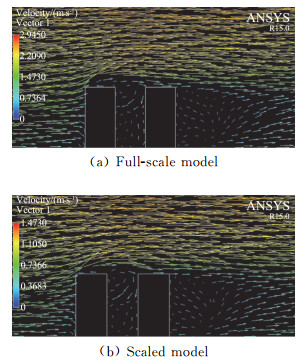
足尺模拟和缩尺模拟中A排建筑中心立面处的风速矢量图如图 4所示。从图 4(a)中可以看出:在足尺模型中,气流在前排建筑屋面前端产生分离,在绕流后,一部分气流下陷到建筑物之间形成上下两个旋转方向相反的旋涡结构;气流在前排建筑物屋面前端分离产生回流腔区,绕流后的气流附着到后排建筑物屋面,并在第二排建筑背面形成一个回流腔区。通过比较图 4(b)给出的缩尺模拟结果可以看出:两者之间的竖向流动形态在特征上也维持了较好的相似性。
|
图 4 垂直中心对称面上流动矢量图 Fig.4 Vector plot of the flow at the vertical center symmetry plane |
为了对本文模拟方法的精度进行说明,选取位于建筑物背风面低风速区的采样点5和顺风道高风速区的采样点12在不同高度处的风压和温度以及冠层内流动形态较复杂的0.75H高度处不同采样点的风压和温度情况进行分析。其他采样点因相似性更好,限于篇幅不在此一一展示。
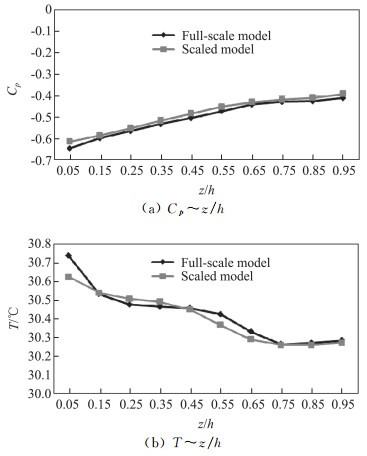
足尺模拟和缩尺模拟中采样点5和采样点12在不同高度处的风压系数
|
图 5 采样点5足尺模型与缩尺模型的比较 Fig.5 Comparision of the wind pressure coefficients and ambient temperatures between the full-scale model and the scale-down mode at the sample point 5# |
|
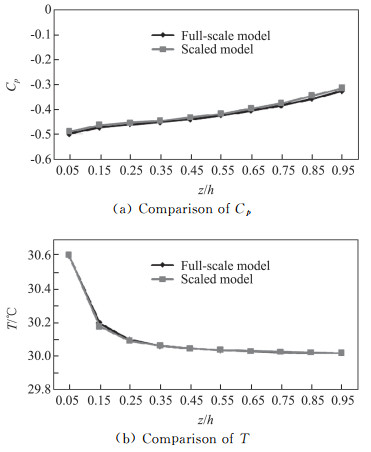
图 6 采样点12处足尺模型与缩尺模拟的比较 Fig.6 Comparision of the wind pressure coefficients and ambient temperatures between the full-scale model and the scale-down mode at the sample point 12# |
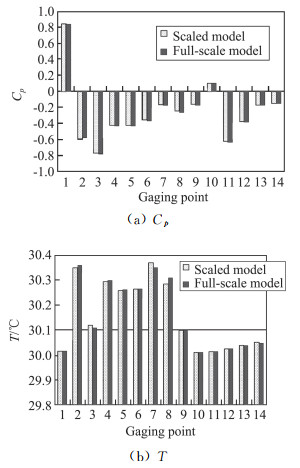
图 7柱状图比较了足尺模拟和缩尺模拟各采样点在0.75H高度处的风压系数和空气温度。从图中可以看出:缩尺模型上各采样点的风压系数和温度与足尺模型的吻合较好,缩尺模型与足尺模拟之间有很好的相似性。
|
图 7 不同采样点足尺和缩尺模拟的风压系数、温度柱状图 Fig.7 Column plot of wind pressure coefficients and ambient temperatures between the full-scale model and the scale-down model at different sample points |
由表 1可知,缩尺模型网格数量约为足尺模型网格数量的0.5倍。在相同的计算机配置及Fluent 15.0软件设置下,本次足尺模拟的计算时长约为100 min,缩尺模拟的计算时长约为60 min,仅为足尺模拟的0.6倍。可见,采用本文构筑的缩尺模拟方法能够在保证较高模拟精度的基础上,有效减少计算开销。
3 结论本文从城市环境下大气流动控制方程组出发,用方程推导法得出了相似流动所需满足的相似准则及边界条件,以此构筑出基于虚拟流动介质的CFD缩尺模拟方法。通过算例比较分析,证明所建立的CFD缩尺模拟方法可以完整地再现足尺流动的形态特征,其模拟精度与足尺模拟之间的相对误差小于5%,从而验证了本文所建立的基于虚拟流动介质的CFD缩尺模拟方法可以保证缩尺模拟的相似要求,并可达到有效减少计算开销的目的。另外,值得注意的是,本文仅就大气为不可压缩的恒定流且不考虑辐射传热引起的浮力影响情况下的缩尺模拟方法进行讨论,后续仍需结合城市微气候的动力-热力过程,对湍流、辐射、湿热交换过程的相似本质进行深入研究,以构筑城市微气候现象的完备的相似准则,为发展CFD缩尺模拟方法奠定坚实的理论基础。
| [1] |
蒋维楣, 王咏薇, 刘罡, 等. 多尺度城市边界层数值模式系统[J]. 南京大学学报(自然科学), 2007, 43(3): 221-237. JIANG W M, WANG Y W, LIU G, et al. Mutil-scale urban boundary layer modelling system[J]. Journal of Nanjing University (Natural Sciences), 2007, 43(3): 221-237. (in Chinese) |
| [2] |
李磊, 胡非, 刘京. CFD技术在我国城市气候环境微尺度问题中的应用[J]. 气象科技进展, 2015, 5(6): 23-30. LI L, HU F, LIU J. Application of CFD technique on micro-scale issues in urban climatic environment researches in China[J]. Advances in Meteorological Science and Technology, 2015, 5(6): 23-30. (in Chinese) |
| [3] |
王宝民, 刘辉志, 桑建国. 北京商务中心区大气环境的数值模拟[J]. 气候与环境研究, 2007, 12(5): 604-618. WANG B M, LIU H Z, SANG J G. Numerical simulation of atmospheric environment of the central business district in Beijing[J]. Climatic and Environmental Research, 2007, 12(5): 604-618. (in Chinese) |
| [4] |
WANG XX, LI Y G. Predicting urban heat island circulation using CFD[J]. Building and Environment, 2016, 99: 82-97. DOI:10.1016/j.buildenv.2016.01.020 |
| [5] |
ASHIE Y, KONO T. Urban-scale CFD analysis in support of a climate-sensitive design for the Tokyo Bay area[J]. International Journal of Climatology, 2011, 31(2): 174-188. DOI:10.1002/joc.2226 |
| [6] |
左东启. 相似理论20世纪的演进和21世纪的展望[J]. 水利水电科技进展, 1997, 17(2): 10-15. ZUO D Q. Development of the theory of similarity:its progress in the 20th century & new trends in the 21st century[J]. Advances in Science and Technology of Water Resources, 1997, 17(2): 10-15. (in Chinese) |
| [7] |
汪新, McNamara K F. 大涡模拟建筑物对近源大气污染物扩散的影响[J]. 应用力学学报, 2007, 24(2): 284-288. WANG X, MCNAMARA K F. Effects of buildings on pollutant dispersion from a nearby source by means of large-eddy simulation[J]. Chinese Journal of Applied Mechanics, 2007, 24(2): 284-288. (in Chinese) |
| [8] |
MUSTO M, ROTONDO G. CFD analysis of a realistic reduced-scale modeling equipped with axial jet fan[J]. Fire Safety Journal, 2015, 74: 11-24. DOI:10.1016/j.firesaf.2015.03.006 |
| [9] |
胡宇, 黄晨, 蔡宁. 大空间建筑及其相似放大建筑的室内热环境模拟分析[J]. 流体机械, 2012, 40(9): 67-71, 42. HU Y, HUANG C, CAI N. Numerical simulation for analyzing thermal environment of a large-scale building and its similar construction[J]. Fluid Machinery, 2012, 40(9): 67-71, 42. (in Chinese) |
| [10] |
WANG X, MCNAMARA K F. Numerical and wind tunnel simulation of pollutant dispersion in the near wake of buildings[J]. Wind and Structures, 2005, 8(6): 427-442. DOI:10.12989/was.2005.8.6.427 |
| [11] |
ZHANG X Y, CHEN H D. Numerical study on similarity of plume infrared radiation between reduced-scale solid rocket motors[J]. Chinese Journal of Aeronautics, 2016, 29(4): 924-933. DOI:10.1016/j.cja.2016.06.005 |
| [12] |
COUTINHO C P, BAPTISTA A J, DIAS RODRIGUES J. Reduced scale models based on similitude theory:a review up to 2015[J]. Engineering Structures, 2016, 119: 81-94. DOI:10.1016/j.engstruct.2016.04.016 |
| [13] |
WU G Y, WANG Q C, ZHANG K, et al. CFD simulation of hydrodynamics and heat transfer for scale-up of the jetting fluidized beds[J]. Powder Technology, 2016, 304: 120-133. DOI:10.1016/j.powtec.2016.08.021 |
| [14] |
王丰. 相似理论及其在传热学中的应用[M]. 北京: 高等教育出版社, 1990. WANG F. Similarity theory and its application in heat transfer[M]. Beijing: Higher Education Press, 1990. (in Chinese) |
| [15] |
VERSTEEG H K, MALALASEKERA W. An Introduction to computational fluid dynamics: the Finite Volume Method, second edition[M]. World Publishing Corporation, 2007.
|
| [16] |
赵冰春.基于相似理论的典型大气边界层流动的数值模拟研究[D].广州: 广东工业大学, 2016. ZHAO B C. Numerical simulation study on typical atmospheric boundary layer flow based on similarity theory[D]. Guangzhou: Guangdong University of Technology, 2016. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38


