雷诺数的变化主要影响边界层分离、旋涡流动、激波/边界层干扰、激波/旋涡干扰等黏性起支配作用的流动。风洞试验的雷诺数模拟不足,将会使上述流动现象发生变化,与真实飞行存在差异。目前风洞试验中实现高雷诺数的方法主要有降低总温、增加总压、采用重气体或者增大模型尺寸等方法,其中降低总温(即低温风洞)是最有前途的一种方法[1]。
因为低温风洞控制过程的复杂性,从低温风洞建设早期至今,国内外学者对其控制系统的设计进行了大量的研究。关于NASA的TCT、NTF这两座风洞,早期的文献表明其采用的是非线性增益调度PI控制[2-5]。欧洲的ETW风洞采用的是一种具有自学习能力的控制算法[6],并且取得了良好的控制效果,但是文献[6]并未给出算法的详细信息。近年来,上述这些风洞都不同程度地对其控制系统进行了改进,但是现有的已出版的资料并未披露过多的细节。传统的PI控制已经难以满足对低温风洞控制系统日益增高的性能要求,而现代控制理论以及智能控制由于其算法的复杂性,目前能够成功应用到低温风洞控制系统中的还很少[7]。
本文以NASA TCT风洞为研究对象,基于自抗扰控制(Active Disturbance Rejection Control,ADRC)原理设计了一种多变量控制系统实现该风洞温度、总压和马赫数的控制。ADRC中的扩张状态观测器(Extended State Observer,ESO)能够将温度、总压和马赫数三个通道之间的耦合、系统的外部扰动以及系统内部参数的摄动视为总扰动估算出来,补偿到误差反馈控制中,从而实现温度、总压和马赫数的解耦控制,并且兼具良好的抗干扰能力。
1 自抗扰控制原理ADRC是韩京清研究员基于PID控制技术并吸取现代控制理论成就,提出的一种不依赖被控对象精确模型的新型控制技术[8]。为了减少整定参数,便于工程应用,高志强教授提出了线性ADRC[9]。目前ADRC在许多工程领域获得了良好的控制效果。下面简要介绍ADRC原理。
考虑一个n阶非线性、参数不确定系统:
| $ {y^{(n)}}\left( t \right) = f(y,\dot y{\rm{ }}, \ldots ,{y^{(n - 1)}},w,u) + bu\left( t \right) $ | (1) |
式中,f(*)表示内部扰动和外部扰动综合特性,b为对象参数。为了获得系统扰动的估计值
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot Z}}(t) = \mathit{\boldsymbol{AZ}}(t) + \mathit{\boldsymbol{B}}u(t) + \mathit{\boldsymbol{L}}(y(t) - \hat y(t))\\ \hat y(t) = \mathit{\boldsymbol{CZ}}(t) \end{array} \right. $ | (2) |
式中,L为观测器待定系数矩阵,
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{Z}} = {{\left[ {\begin{array}{*{20}{c}} {{z_1}}&{{z_2}}& \ldots &{{z_{n + 1}}} \end{array}} \right]}^{\rm{T}}},}\\ {\mathit{\boldsymbol{B}} = {{\left[ {\begin{array}{*{20}{c}} 0& \ldots &0&b&0 \end{array}} \right]}^{\rm{T}}},}\\ {\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0& \ldots &0 \end{array}} \right],}\\ {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&0& \ldots &0\\ 0&0&1& \ldots &0\\ \vdots &{}&{}& \ddots &{}\\ \vdots &0&0& \cdots &1\\ 0&0&0& \cdots &0 \end{array}} \right].} \end{array} $ | (3) |
当ESO的系数矩阵L取值恰当时,
| $ u = ({u_0} - \hat f(*))/{b_0} $ | (4) |
式中,b0为b的估计值。将式(4)带入式(1),则原系统可转化如下的串联积分形式:
| $ {y^{(n)}} = f(*) - \hat f(*) + {u_0} \approx {u_0} $ | (5) |
上述系统可用如下简单的控制器律进行控制,即:
| $ {u_0} = {k_1}({y_{\rm{d}}} - {z_1}) - {k_2}{z_2} - \ldots - {k_n}{z_n} $ | (6) |
式中,yd为系统输出期望值,为控制器的系数矩阵。文献[7]采用带宽的概念对L和
| $ \mathit{\boldsymbol{L}} = {\left[ {C_{n + 1}^1{\omega _{\rm{o}}},C_{n + 2}^2\omega _{\rm{o}}^2, \ldots ,C_{n + 1}^{n + 1}\omega _{\rm{o}}^{n + 1}} \right]^{\rm{T}}} $ | (7) |
| $ \left[ {{k_1},{k_2}, \cdots ,{k_n}} \right] = {\left[ {C_n^n\omega _{\rm{c}}^n,C_n^{n - 1}\omega _{\rm{o}}^{n - 1}, \ldots ,C_n^1{\omega _{\rm{c}}}} \right]^{\rm{T}}} $ | (8) |
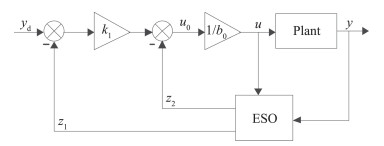
因此,ADRC需要整定的参数有三个:b0、ωo和ωc。ADRC的结构十分简单,当系统阶数n为1时,其结构示意图如图 1所示。
|
图 1 ADRC结构示意图 Fig.1 The structure of ADRC |
TCT是一座连续式跨声速低温风洞,试验段尺寸为0.33 m×0.33 m,马赫数范围0.2~1.35,雷诺数范围:3.28×106~4×108 /m,总压范围:1~6 atm(1 atm=101 325 Pa),温度范围:78~320 K。风洞洞体由铝合金材料构成,洞体外部覆盖绝热材料以隔绝风洞与环境之间的热交换。该风洞以氮气为介质,氮气气流由风机驱动。风机对氮气做功以及氮气与洞壁之间的摩擦会产生热量。该风洞采用向洞内喷射液氮的方式降低氮气的温度,但是这种冷却方式会导致洞体内氮气质量的增加,为了维持风洞压力,又需要将部分温度较高的氮气排出。
在设计该风洞流场控制系统时存在四个困难:1)精确的流场模型难以获得;2)系统参数随着风洞工况变化而变化,参数波动范围大;3)系统存在强烈的耦合;4)系统存在大时滞。
文献[3]采用机理建模法得到了TCT风洞流场的集中参数模型,其温度、马赫数和总压与液氮注入阀开度、压缩机转速和氮气排气阀开度的关系见式(9):
| $ \left[ {\begin{array}{*{20}{c}} T\\ M\\ p \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{K_{\rm{L}}}\left( {\alpha + \beta } \right)}}{\theta }\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{L}}}s}}}&{\frac{{{K_{\rm{F}}}\left( {\alpha + \beta } \right)}}{{{K_{\rm{m}}}\theta {{(1 + 0.2{M^2})}^3}}}\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{F}}}s}}}&{\frac{{{K_{\rm{g}}}p\alpha }}{{\sqrt T \theta }}\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{g}}}s}}}\\ 0&{\frac{1}{{{K_{\rm{m}}}\sqrt T }}\frac{{{{\rm{e}}^{ - {\tau _{\rm{a}}}s}}}}{{1 + {t_{\rm{p}}}s}}}&0\\ {{K_{\rm{L}}}p\left( \begin{array}{l} \frac{1}{{{W_{\rm{g}}}}}\frac{1}{s} + \\ \frac{{\alpha + \beta }}{{T\theta }}\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{L}}}s}} \end{array} \right)}&{\frac{{Mp}}{{{K_{\rm{m}}}\sqrt T }}\left( \begin{array}{l} b + \\ \frac{{{K_{\rm{F}}}Mp}}{{\sqrt T \theta {{(1 + 0.2{M^2})}^3}}}\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{F}}}s}} \end{array} \right)}&{\frac{{ - {K_{\rm{g}}}{p^2}}}{{\sqrt T }}\left( \begin{array}{l} \frac{1}{{{W_{\rm{g}}}}}\frac{1}{s} + \\ \frac{\alpha }{{T\theta }}\frac{{1 + {t_{\rm{m}}}s}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{g}}}s}} \end{array} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_{\rm{L}}}}\\ N\\ {{A_{\rm{g}}}} \end{array}} \right] $ | (9) |
式中,T为风洞温度,K;M为试验段马赫数;p为总压,atm;AL为液氮调节阀开度,0~100%;N为压缩机转速,r/min;Ag为氮气排气阀开度,0~100%;s为Laplace算子,式(9)中其余参数见表 1。
| 表 1 流场模型参数表 Table 1 The parameters of flow field model |
|
|
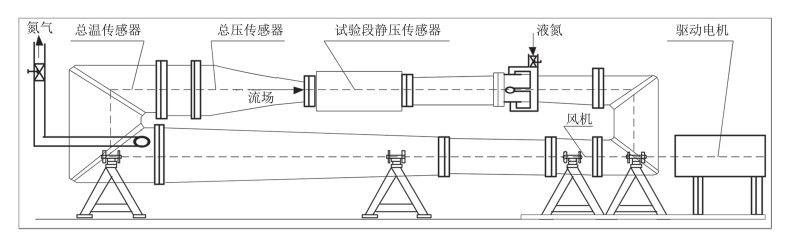
该风洞结构示意图见图 2。
|
图 2 0.3 m TCT风洞结构示意图 Fig.2 The structure of 0.3 m TCT wind tunnel |
考虑三输入三输出系统:
| $ \left\{ \begin{array}{l} {{\dot y}_1} = {f_1}\left( * \right) + {b_{11}}{u_1} + {b_{12}}{u_2} + {b_{13}}{u_3}\\ \dot y{_2} = {f_2}\left( * \right) + {b_{21}}{u_1} + {b_{22}}{u_2} + {b_{23}}{u_3}\\ \dot y{_3} = {f_3}\left( * \right) + {b_{31}}{u_1} + {b_{32}}{u_2} + {b_{33}}{u_3} \end{array} \right. $ | (10) |
将u2、u3对y1的影响看成扰动,y2和y3类似。则该系统可改写为:
| $ \begin{array}{l} {{\dot y}_1} = f_1^\prime \left( * \right) + {b_{11}}{u_1}\\ {{\dot y}_2} = f_2^\prime \left( * \right) + {b_{22}}{u_2}\\ {{\dot y}_3} = f_3^\prime \left( * \right) + {b_{33}}{u_3} \end{array} $ | (11) |
式中,
| $ \left[ {\begin{array}{*{20}{c}} T\\ M\\ p \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{K_{\rm{L}}}\left( {\alpha + \beta } \right)}}{\theta }{\rm{ }}\frac{{1 + {t_{\rm{m}}}s{\rm{ }}}}{{s(1 + {t_{\rm{g}}}s)}}{{\rm{e}}^{ - {\tau _{\rm{L}}}s}}}&0&0\\ 0&{\frac{1}{{{K_{\rm{m}}}\sqrt {T} }}\frac{{{{\rm{e}}^{ - {\tau _{\rm{a}}}s}}}}{{1 + {t_{\rm{p}}}s}}}&0\\ 0&0&{\frac{{ - {K_{\rm{g}}}{p^2}}}{{\sqrt T {\rm{ }}{W_{\rm{g}}}}}\frac{{1{\rm{ }}}}{s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_{\rm{L}}}}\\ N\\ {{A_{\rm{g}}}} \end{array}} \right] $ | (12) |
若忽略时滞环节,温度传递函数的阶数为2,可采用2阶ADRC控制器,马赫数和总压传递函数的阶数均为1,因此可采用1阶ADRC控制器。现以马赫数自抗扰控制的设计为例,对控制器的设计过程进行简要的说明。式(12)中,忽略时滞环节,并且将马赫数和转速之间的关系改用微分方程来表示,则有:
| $ \dot M = - \frac{M}{{{t_{\rm{p}}}}} + \frac{N}{{{t_{\rm{p}}}{K_{\rm{m}}}\sqrt T }} $ | (13) |
式中,将-M/tp也归结为扰动项,与式(1)类比可知,
|
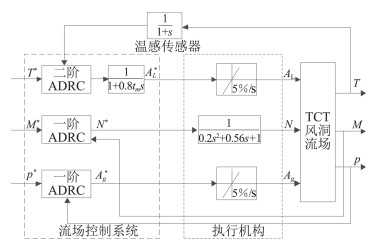
图 3 流场自抗扰控制框图 Fig.3 The structure of ADRC controller for flow field |
| 表 2 ADRC控制器参数 Table 2 The parameters of ADRC controller |
|
|
图 3中温度控制器与总压、马赫数控制器略有不同,主要是温度控制通道串联了一阶惯性环节1/(1+0.8tms),其原因是温度通道含有一个零点-1/tm,在TCT风洞的运行工况范围内,tm取值50~500,该零点较小,十分接近虚轴,严重影响温度的动态性能,为了改善温度的动态性能,给温度通道串联一个惯性环节。此外,温度传感器的响应时间较长,这里用1/(1+s)来模拟温度传感器的动态特性,压力传感器的响应时间相对来说很短,可以忽略不计。TCT风洞流场控制系统中有三个执行机构,即液氮注入阀、氮气排出阀以及风机转速调节系统。为了更真实地模拟流场系统,这里考虑执行机构的动态特性:风机转速调节系统的动态特性用二阶环节1/(0.2s2+0.56s+1)来表示,而阀门的开度变化率限定为5%/s。
表 2中,三个ADRC控制器的参数b0并非常数,与式(12)中传递函数系数有关,因此本文所设计的ADRC控制器是一种变增益控制器。在TCT风洞运行工况范围内,各系数取值范围:
在Matlab/Simulink平台按照式(9)和表 1搭建TCT风洞流场仿真模型,按照图 3和表 2搭建流场控制系统,对本文提出的流场控制方法进行仿真分析。
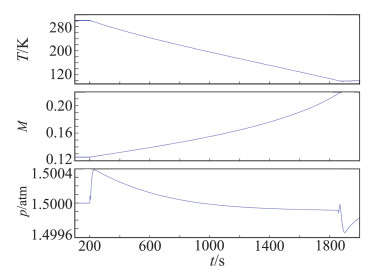
4.1 风洞降温仿真风洞氮气介质初始温度为300 K,将风机稳定在较低的转速1200 r/min,降温过程中风洞总压维持在1.5 atm。为了避免温度冲击,液氮注入阀门最大开度限定为12.5%。整个降温过程中温度、马赫数和总压曲线见图 4。氮气温度从300 K降至100 K所需时间约为30 min,期间马赫数从0.12上升至0.22,总压保持在1.5 atm左右。
|
图 4 风洞降温过程流场曲线图 Fig.4 Flow field curves of cooling process |
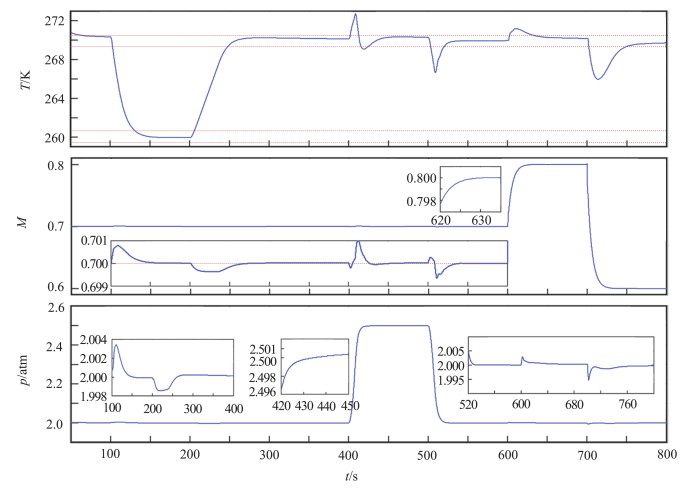
工况1:风洞初始条件为T=270 K,M=0.7,p=2 atm。t=100 s时,温度设定值降低10 K,风洞温度从270 K下降至260 K大概需要30 s。t=200 s时,温度设定值增加10 K,风洞升温所需时间约50 s。风洞升温速度主要由风机转速决定的:在低马赫数时,风洞升温较慢;高马赫数时,风洞升温较快。温度变化过程中,在自抗扰控制器的作用下马赫数和总压的波动都很小。t=400 s时,总压设定值增加0.5 atm;t=500 s时总压设定值减小0.5 atm。设定值变化时,总压稳定时间大概为20 s。t=600 s时,马赫数设定值增大0.1;t=700 s时,马赫数设定值减小0.2。马赫数稳定时间约为20 s。工况1下的仿真曲线见图 5。
|
图 5 工况1流场动态响应曲线 Fig.5 Dynamic response curves of flow field under condition 1 |
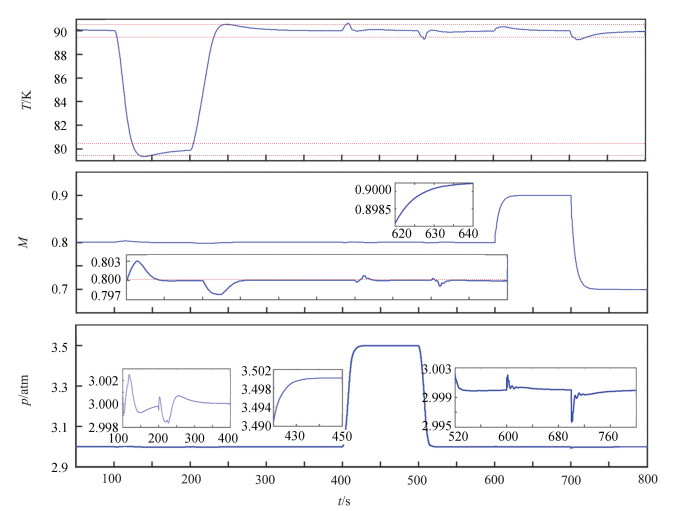
工况2:风洞初始条件为T=90 K,M=0.8,p=3 atm,执行类似的操作,流场曲线见图 6。工况2流场响应曲线与工况1相似。
|
图 6 工况2流场动态响应曲线 Fig.6 Dynamic response curves of flow field under condition 2 |
从仿真结果可以看出ADRC流场控制系统的稳态精度和响应速度都能满足风洞试验的需求。
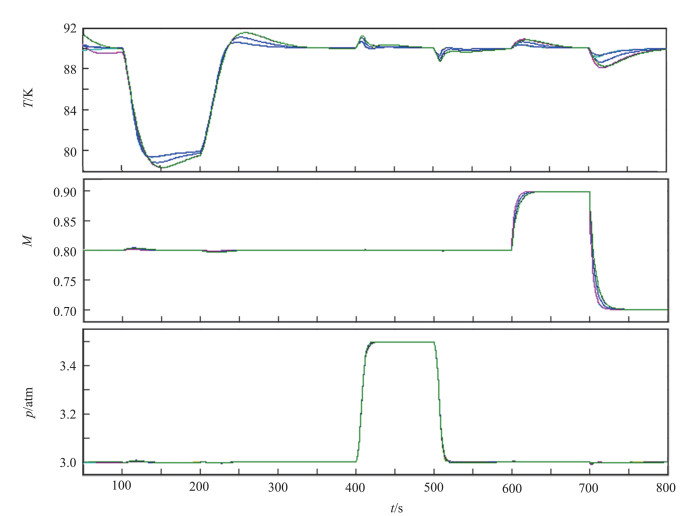
4.3 参数摄动仿真表 2中ADRC控制器的参数b0对流场模型依赖程度较大,因此b0对控制系统的鲁棒性影响较大。将三个ADRC控制器的参数b0分别在标称值基础上增加50%和降低50%,组合成8种情形,采用工况2的条件进行仿真,结果见图 7。可以看出b0的摄动对温度控制系统的动态响应速度和超调量有轻微的影响,而总压和马赫数控制系统则表现出十分优越的鲁棒性。
|
图 7 参数摄动情况下流场曲线 Fig.7 Flow field curves under parameter perturbation |
由于低温风洞运行包络较宽,本文无法对所有的运行工况进行仿真,因而只选取了降温过程、工况1和工况2这三种典型的工况进行了仿真分析。尤其是工况2,在总温较低的情况下,流场之间的耦合更强,滞后时间更大,充分体现出低温风洞流场的复杂性。从仿真结果来看,采用ADRC对低温风洞进行控制能够取得良好的控制效果。
ADRC所表现出的良好的控制性能,如不依赖被控对象的精确模型、较强的解耦能力和鲁棒性,本质上都可以归结于其抗干扰能力。ADRC将低温风洞流场的建模误差、流场的耦合、系统参数摄动等都视为扰动,只要扰动或者其变化率是有界的,则都可使用ESO进行估算,然后通过前馈补偿将扰动消除掉。而对于流场大时滞问题,则通过调节控制器的参数,适当削弱动态性能来提高系统的稳定性。
5 结论本文以0.3 m TCT风洞研究对象,基于自抗扰控制原理设计了该风洞的流场控制系统。通过仿真分析可以得到以下结论:
1) 采用自抗扰控制无需额外设计解耦器,通过ESO将总温、总压和马赫数三个耦合以及其他扰动估计出来并进行前馈补偿,即可实现低温风洞流场三个变量的解耦控制;
2) 自抗扰控制具有良好的鲁棒性和抗扰能力,能够适应低温风洞这种难以精确建模的、复杂的控制对象;
3) 自抗扰控制算法简单,需要调试的参数较少,便于工程应用。
本文仅完成了低温风洞自抗扰控制仿真研究工作,若将ADRC应用于实际风洞流场控制系统中还需要注意以下几个方面:
1) 时滞对ADRC性能的影响相对较大,如果通过调节参数仍无法达到令人满意的控制效果则需要采用其他措施来削弱时滞带来的不利影响[19-20];
2) 工程应用上,与PID类似,ADRC的参数也可通过调试进行整定,但是为了降低调试周期和提高控制性能,需要先期对流场进行辨识、建立数学模型[21],尤其是获取系统的相对阶次以及参数b是十分必要的;
3) ADRC的设计原则相对灵活,针对不同的控制对象需要进行适当调整,如对于信号噪声较大的场合,可考虑对部分已知的对象模型加以利用,在保持控制性能不变的情况下降低ESO带宽,减少噪声的放大。总之,目前ADRC还未应用到低温风洞控制系统中,因此还需要在引导风洞中开展进一步研究。
| [1] |
廖达雄, 黄知龙, 陈振华, 等. 大型低温高雷诺数风洞及其关键技术综述[J]. 实验流体力学, 2014, 28(2): 1-6, 20. LIAO D X, HUANG Z L, CHEN Z H, et al. Review on large-scale cryogenic wind tunnel and key technologies[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 1-6, 20. (in Chinese) |
| [2] |
THIBODEAUX J J, BALAKRISHNA S. Automatic control of a 0. 3 m cryogenic test facility[J]. Journal of Guidance Control and Dynamics, 1981, 4(4): 428-432. doi: 10.2514/3.56095
|
| [3] |
BALAKRISHNA S, GOGLIA G L. Automatic control of a liquid nitrogen cooled, closed-circuit, cryogenic pressure tunnel: NASA-CR-162636[R]. United States: NASA, 1980.
|
| [4] |
BALAKRISHNA S, GOGLIA G L. Synthesis of a control model for a liquid nitrogen cooled, closed circuit, cryogenic nitrogen wind tunnel and its validation: NASA-CR-162508[R]. United States: NASA, 1979.
|
| [5] |
BALAKRISHNA S, KILGORE W, THIBODEAUX J. Control of large cryogenic tunnels[C]//28th Joint Propulsion Conference and Exhibit, Nashville, TN. Reston, Virginia: AIAA, 1992. doi: 10.2514/6.1992-3930
|
| [6] |
GOBERT J. ETW control system: Design and first results[C]//25th Plasmadynamics and Lasers Conference, Colorado Springs, CO. Reston, Virginia: AIAA, 1994. doi: 10.2514/6.1994-2514
|
| [7] |
ZHU R S, YIN G F, TANG G S, et al. Temperature trajectory control of cryogenic wind tunnel with robust L1 adaptive control[J]. Transactions of the Institute of Measurement and Control, 2018, 40(13): 3675-3689. DOI:10.1177/0142331217728569 |
| [8] |
HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [9] |
GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, 2003, Denver, CO, USA. IEEE, 2003: 4989-4996. doi: 10.1109/ACC.2003.1242516
|
| [10] |
程赟, 陈增强, 孙明玮, 等. 多变量逆解耦自抗扰控制及其在精馏塔过程中的应用[J]. 自动化学报, 2017, 43(6): 1080-1088. CHENG Y, CHEN Z Q, SUN M W, et al. Multivariable inverted decoupling active disturbance rejection control and its application to a distillation column process[J]. Acta Automatica Sinica, 2017, 43(6): 1080-1088. (in Chinese) |
| [11] |
薛洪武, 吴爱国, 董娜. 制冷系统自抗扰解耦控制[J]. 西安交通大学学报, 2016, 50(9): 85-90. XUE H W, WU A G, DONG N. Active disturbance rejection decoupling control for refrigeration systems[J]. Journal of Xi'an Jiaotong University, 2016, 50(9): 85-90. (in Chinese) |
| [12] |
ZHAO C Z. Capability of ADRC for minimum-phase plants with unknown orders and uncertain relative degrees[C]//Proceedings of the 29th Chinese Control Conference, Beijing, China. IEEE, 2010: 6121-6126.
|
| [13] |
ZHAO C Z, LI D H. Control design for the SISO system with the unknown order and the unknown relative degree[J]. ISA Transactions, 2014, 53(4): 858-872. DOI:10.1016/j.isatra.2013.10.001 |
| [14] |
ZHAO S, GAO Z Q. Active disturbance rejection control for non-minimum phase systems[C]//Proceedings of the 29th Chinese Control Conference, Beijing, China. IEEE, 2010: 6066-6070.
|
| [15] |
TAN W, FU C F. Analysis of active disturbance rejection control for processes with time delay[C]//2015 American Control Conference (ACC), Chicago, IL, USA. IEEE, 2015: 3962-3967. doi: 10.1109/ACC.2015.7171948
|
| [16] |
DONG L, EDWARDS J. Active disturbance rejection control for an electrostatically actuated MEMS device[J]. International Journal of Intelligent Control and Systems, 2011, 16(3): 160-169. |
| [17] |
袁东, 马晓军, 曾庆含, 等. 二阶系统线性自抗扰控制器频带特性与参数配置研究[J]. 控制理论与应用, 2013, 30(12): 1630-1640. YUAN D, MA X J, ZENG Q H, et al. Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems[J]. Control Theory & Applications, 2013, 30(12): 1630-1640. (in Chinese) |
| [18] |
张鋆豪, 张文安. 磁悬浮球系统的线性自抗扰控制与参数整定[J]. 系统科学与数学, 2017, 37(8): 1741-1756. ZHANG J H, ZHANG W A. Linear active disturbance rejection control to magnetic levitation ball system and parameters tuning[J]. Journal of Systems Science and Mathematical Sciences, 2017, 37(8): 1741-1756. (in Chinese) |
| [19] |
ZHENG Q L, GAO Z Q. Predictive active disturbance rejection control for processes with delay[C]//32nd Chinese Control Conference, 2013: 4108-4113.
|
| [20] |
ZHAO S, GAO Z Q. Modified active disturbance rejection control for time-delay systems[J]. ISA Transactions, 2014, 53(4): 882-888. DOI:10.1016/j.isatra.2013.09.013 |
| [21] |
梁青, 王传榜, 潘金文, 等. 线性自抗扰控制参数b0辨识及参数整定规律[J]. 控制与决策, 2015, 30(9): 1691-1695. LIANG Q, WANG C B, PAN J W, et al. Parameter identification of b0 and parameter tuning law in linear active disturbance rejection control[J]. Control and Decision, 2015, 30(9): 1691-1695. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38

