2. 中国空气动力研究与发展中心, 绵阳 510700
2. China Aerodynamics Research and Development Center, Mianyang 510700, China
由于科技的进步,航空产业水平的提高,越来越多的研究者开始针对跨声速状态下的飞行器问题进行深入研究。一是因为跨声速飞行状态往往有着较高的飞行效率,适用于多用途飞行器的优化设计问题;二是因为跨声速流动复杂多变,又往往含有非线性特征,具有较高的学术研究价值。
跨声速抖振现象是在一定来流马赫数和迎角组合下出现的激波大幅自激现象,不仅激波位置会出现周期性的摆动,而且气动力响应也出现大幅震荡现象[1]。在跨声速状态下,由于激波与附面层的相互干扰引起的跨声速抖振问题具有复杂的非线性与非定常特征,极大制约了这类飞行器的飞行性能与飞行包线。所以跨声速抖振问题一直以来都是航空工程领域的研究难点和热点[2-3]。
抖振控制是跨声速抖振研究的重要内容之一,通过推迟或消除激波的自激振荡,进而提高流动的稳定性。现有的抖振控制主要分为被动控制与主动控制。被动控制主要通过改变附面层或者尾缘的局部形状,对激波附面层作用区和尾迹区流动进行干预[4]。研究中广泛采用的被动控制装置包括附面层凹槽[5-7],前缘涡流发生器[8-10]和控制鼓包(Shock Control Bump, SCB)[11-12]等。Abramova等对吹吸气抑制抖振的能力进行了研究,研究表明切向吹吸气抑制了激振引起的流体分离,增加了升力,并延迟了抖振的发生。而对尾迹区流动的控制大多采用主动控制方式,包括尾缘偏转装置(Trailing Edge Deflector, TED),射流襟翼(Fluidic Vortex Generator, FVG)[13]和尾缘舵面等。Abramova等[14]对吹吸气控制抖振的能力进行了研究,研究表明切向吹吸气抑制了激振引起的流体分离,增加了升力,并延迟了抖振的发生。Tian等[15]利用后缘偏转器的主动控制对抖振状态进行了研究,在二维环境下闭环主动控制驱动的后缘偏转器可以大大减少流动不稳定性并延迟抖振的发生。高传强[1]等研究了以升力系数为反馈的闭环控制策略,以尾缘15%弦长舵面为控制器执行机构,基于极点配置和LQR方法开展次优控制律设计。最近,任凯等[16]基于无模型自适应控制方法[17]对抖振抑制开展了研究,基于尾缘的主动作动提升流动稳定性,实现了较好的控制效果。
近些年针对抖振现象的研究发现[18],在结构刚度释放,结构的固有频率与流动抖振频率相近时,结构响应不再跟随气动力激励频率,而是锁定于结构固有频率,这一反常的现象被称为“锁频”现象。锁频的发生同时会伴随快速而剧烈的结构发散,结构振幅巨大,往往造成破坏性的结果。为了避免这一问题,在飞行器设计过程中往往只能牺牲其他方面的性能设计来减少锁频现象的发生。
因为锁频现象的复杂性, 目前机理不明确,针对这一结构失稳状态的流固耦合控制研究,大多集中在结构固定的纯抖振控制。而近年来,随着对锁频现象认识的提高,高传强等[19-20]利用降阶模型分析了锁频状态下的结构失稳主要是由结构模态与流动模态耦合导致的结构模态失稳造成,并且结合这一结果准确预测了结构锁频边界。这一发现给锁频状态下的流固耦合控制提供了思路:可以利用流固耦合效应,对结构模型进行稳定性抑制,达到流固耦合下锁频状态的控制[21]。
本文在抖振主动控制方法的基础上,首先通过引入结构反馈回路,实现对于结构释放下锁频状态的自适应抑制。紧接着通过对失稳模式的研究,提出了针对流固耦合控制的混合自适应控制模型。利用控制回路的切换,对锁频状态下已经出现失稳的流动、结构进行同步控制,并最终完全抑制锁频的产生。结果表明,这一方法对抖振流动下的流固耦合控制有着较好的控制效果。
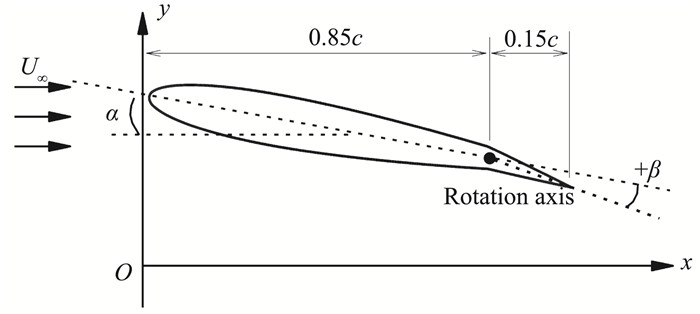
1 研究模型及方法 1.1 研究模型本文以抖振锁频状态下的二维NACA0012翼型为例进行流固耦合控制。控制器为舵面控制,包含翼型尾缘处15%弦长, 与文献[21]中的模型一致。
研究对象的物理模型示意图如图 1所示,参考文献[18]中的参数设定,模型释放单一旋转自由度,其刚度以kα给定,其中无量纲质量比μ=200。来流马赫数Ma=0.75、迎角α=5.5°、雷诺数Re=3×106。按照减缩频率的定义,无量纲化的俯仰支撑频率可以表示为ωαb=kαU∞,其中ωα为翼型俯仰支撑系统的固有频率,U∞是自由来流速度,b=c/2, c是翼型的弦长。计算环境下无量纲时间T=dt/(2b/a),其中dt为实际时间间隔,a为来流声速。研究针对这一抖振锁频下的典型状态进行控制律测试。
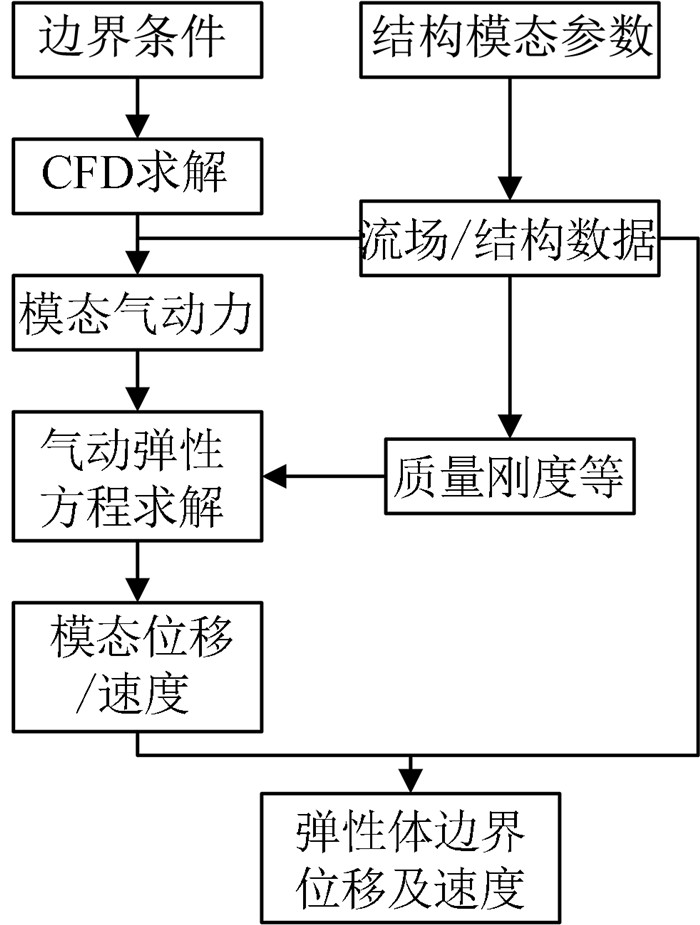
对于本文研究的气动弹性问题,虽然跨声速气动力表现为明显的非线性,但是所关心的结构运动的位移振幅却较小,结构载荷和变形近似满足线性关系。因此,时域仿真通过CFD方法获得非线性的非定常气动力,结构的弹性变形运动通过线性结构振动方程描述和求解,求解思路如图 2所示。
|
图 2 气动弹性数值模拟流程图 Fig.2 Flow chart of aeroelastic numerical simulation |
应用拉格朗日方程,基于模态坐标的气动弹性方程可以表示为式(1-2):
| $ {\mathit{\boldsymbol{M}}\ddot \xi + \mathit{\boldsymbol{G}}\dot \xi + \mathit{\boldsymbol{K}}\xi = \mathit{\boldsymbol{F}}} $ | (1) |
| $ {{F_i} = \int {\int\limits_s p } (x,y,t)\varPhi i(x,y,z){\rm{d}}s} $ | (2) |
其中,M为广义质量矩阵;G为结构阻尼矩阵;K为广义刚度矩阵;F为广义气动力(模态气动力)。非定常流场压力p(x, y, t)由非定常流场求解器直接提供,每个时间步逐步计算。
1.2 无模型自适应控制无模型自适应控制方法是候忠生1994年提出的自适应控制理论[17],这种无模型控制器只需要时域系统的输入输出数据,不需要任何模型的信息,而且计算量小,方程形式简单,不需要精确的数学建模。其基本思想是:对于离散时间的一般非线性系统,在每个工作时刻,基于伪偏导数(Pseudo Partial Derivative, PPD)的设计,可以用动态线性模型来逼近未知的复杂非线性系统,利用被控对象的输入输出数据求解系统当前时刻的伪偏导数项,从而实现无模型的非线性系统自适应控制。
一般的离散时间下的单输入、单输出非线性系统可表示为:
| $ \begin{array}{*{20}{l}} {y(k + 1) = f(y(k), \cdots ,y(k - {n_y}),u(k), \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u(k - {n_u}))} \end{array} $ | (3) |
其中,u(k)和y(k)分别代表了第k个时刻系统的输入和输出数据,nu、ny分别为输入、输出延迟阶数,f为形式未知的非线性函数。通过伪偏导数ϕc(k)构建无模型自适应控制方程。将系统线化得到:
| $ y(k + 1) = y(k) + {\phi _c}(k)\Delta u(k) $ | (4) |
| $ \begin{array}{*{20}{l}} {J(u(k)) = |{y_r}(k + 1) - y(k + 1){|^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda |u(k) - u(k - 1){|^2}} \end{array} $ | (5) |
其中,λ>0为加权因子,用来平衡输出误差与控制输入偏差,yr(k+1)是期望输出。将式(4)代入目标式(5)中,令
| $ \begin{array}{*{20}{l}} {u(k) = u(k - 1) + \frac{{\rho {\phi _c}(k)}}{{\lambda + |{\phi _c}(k){|^2}}} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{y_r}(k + 1) - y(k)]} \end{array} $ | (6) |
其中,ρ∈(0, 1]为步长因子,可以使算法获得更好的适应性。λ限制了控制输入u(k)的变化,可以控制输入,避免输入的剧烈变化,选取合适的λ还可以增强被控系统的稳定性。为了得到时变PPD参数ϕc(k),选取如下PPD估计函数:
| $ \begin{array}{*{20}{l}} {J({\phi _c}(k)) = |\Delta y(k) - {\phi _c}(k)\Delta u(k - 1){|^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu |{\phi _c}(k) - {{\hat \phi }_c}(k - 1){|^2}} \end{array} $ | (7) |
其中,μ>0为加权因子,令
| $ \begin{array}{*{20}{l}} {{{\hat \phi }_c}(k) = {{\hat \phi }_c}(k - 1) + \frac{{\eta \Delta u(k - 1)}}{{\mu + \Delta u{{(k - 1)}^2}}} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\Delta y(k) - {{\hat \phi }_c}(k - 1)\Delta u(k - 1)]} \end{array} $ | (8) |
其中,η∈(0, 1]为步长因子,可使控制方法获得更好的适应性,
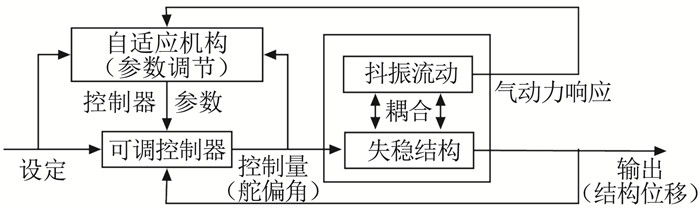
将传统无模型自适应控制方法与抖振锁频控制研究相匹配,需要同时考虑由于结构释放引起的结构响应失稳和抖振流动失稳。对式(5)中,yr(k+1)表示目标输出结果,通过引入俯仰幅值(结构位移)yr1与气动力响应yr2作为反馈,构建图 3所示系统,通过自适应求解控制舵偏角实时进行闭环控制。
|
图 3 自适应控制流程图 Fig.3 Framework of active control system |
| $ \begin{array}{l} J(u(k)) = |{y_{r1}}(k + 1) - y(k + 1){|^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _1}|u(k) - u(k - 1){|^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _2}|{y_{r2}}(k + 1) - y(k + 1){|^2} \end{array} $ | (9) |
为了平衡结构与气动之间的贡献,选择:
| $ {\lambda _2} = [{y_{r1}}(k + 1) - {y_1}(k)]/[{y_{r2}}(k + 1) - {y_2}(k)] $ | (10) |
这样通过构建两条控制回路,监控整个翼型的失稳过程,通过尾缘偏转进行控制,避免结构进入锁频发散环节。
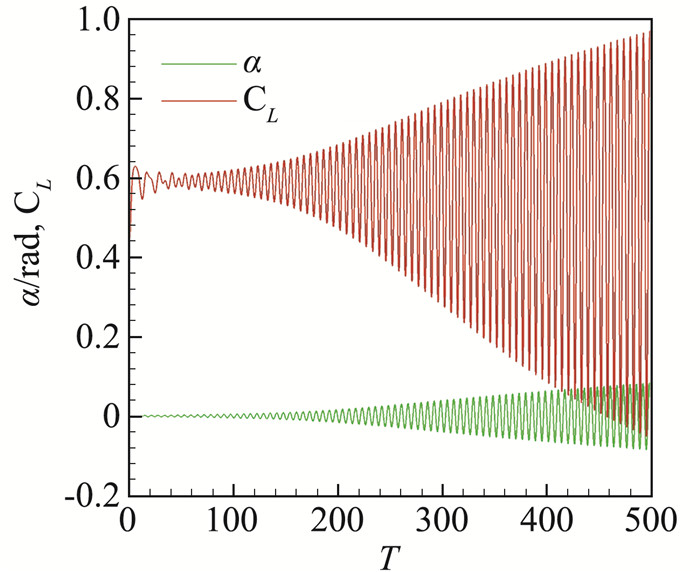
2 算例对比与结果分析针对来流马赫数Ma=0.75、α=5.5°、Re=3×106这一典型抖振状态进行流固耦合控制分析。图 4给出了研究状态下的结构和气动响应结果,T表示计算环境下的无量纲时间步,CL为升力系数。由于“锁频”的影响,结构和气动响应快速发散,并逐步到达极限环状态。这一状态对应抖振载荷最大的状态,对控制器的要求最高。因此,可以预见,当本文的研究策略对迎角5.5°有效时,实现其它抖振状态的控制将会更为有利。
|
图 4 结构自由响应与气动力抖振幅值 Fig.4 Structure free response and lift coefficient value |
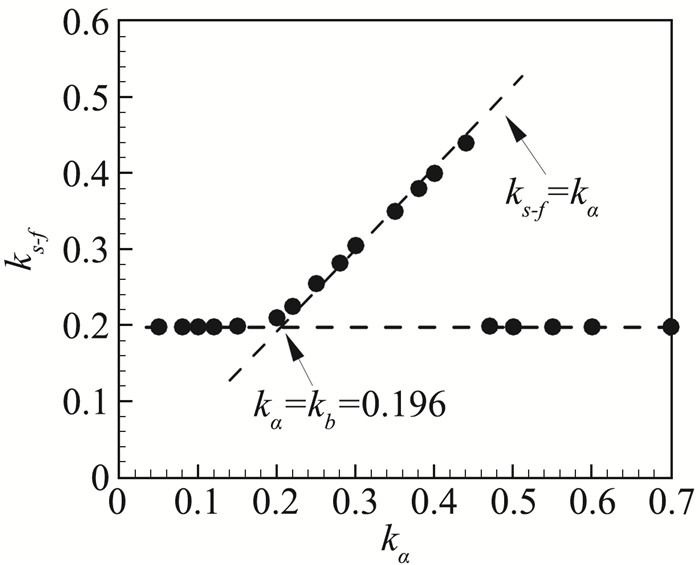
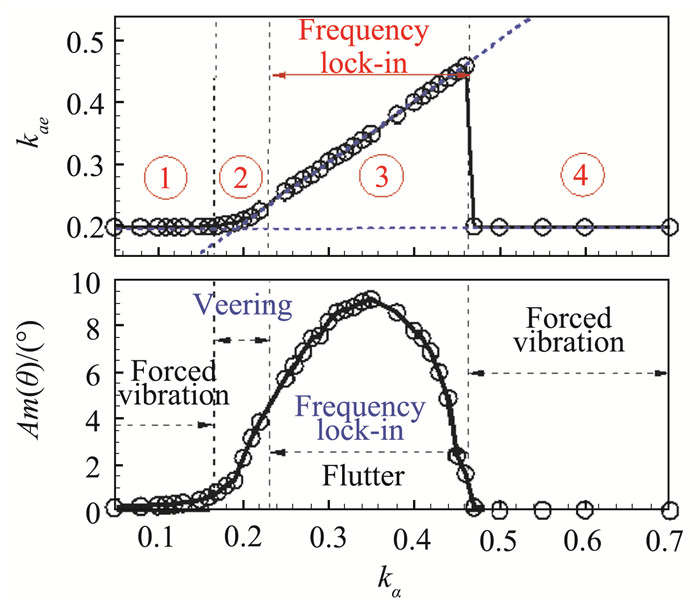
Gao[23]对这一状态下的锁频区间进行了详细的分析。图 5给出了系统耦合响应频率ks-f随结构频率kα的变化关系,其中流动频率kb=0.196。当0.21 < kα < 0.46时,耦合响应频率锁定于结构频率,发生锁频现象,图中虚线即表示ks-f=kα。如图 6所示,由于锁频引发的结构响应幅值随结构频率先增加后减少,其中kα=0.3~0.35是锁频最严重的区间,结构响应幅值最为剧烈。
|
图 5 系统耦合响应频率随结构频率的关系[23] Fig.5 Relationship between system coupling response frequency and structure frequency[23] |
|
图 6 系统耦合响应频率和响应幅值随结构频率的变化[23] Fig.6 System coupling response frequency and response amplitude change with structure frequency [23] |
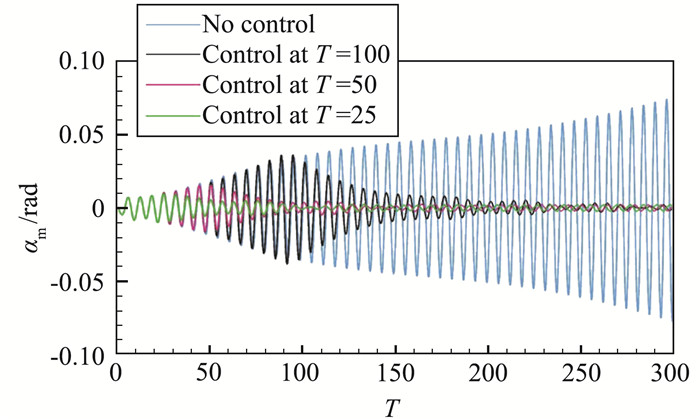
利用本文的控制方法,在仿真环境下进行抖振失稳控制。在不施加控制的状态下,由于锁频现象的出现,翼型俯仰角快速发散,并逐渐进入极限环状态。作为对比,算例依次选择在三个不同的失稳阶段(T=25, 50, 100)介入控制。图 7给出了在三个不同的时刻进行响应抑制的结果,图中αm代表由于结构发散造成的迎角增量。如图所示,本文的控制方法在算例中展示了较强的鲁棒性。特别是在T=100的时刻介入控制时,这种情况下结构的迎角已经发散了一定的程度,迎角范围已经达到5.5°±2.8°。这时,自适应控制方法依然有着较强的控制能力,在较短的时间内将结构幅值限定到指定状态。
|
图 7 kα=0.32下不同时刻控制结构响应图 Fig.7 Responding of strcture at different control time |
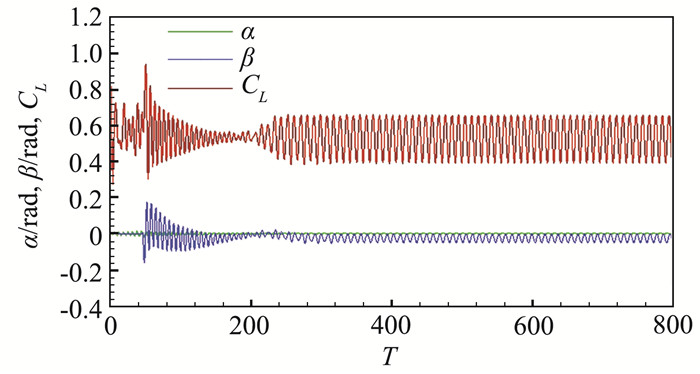
然而在研究过程中发现,不同于单纯的流动控制,随着控制的进行,当结构幅值抑制到一定范围后,由于流固耦合效应的减弱,流动会突然进入另一个失稳模式。如图 8所示,其中β是控制舵偏角。随着控制的进行,结构发散被一步步的抑制,升力脉动也一步步减弱,当时间步长到达200时,由于流固耦合效应的减弱,流动突然脱离控制而失稳。这一过程反映了流固耦合效应在气动弹性控制中的重要影响,流动、结构双双失稳的模式给抖振锁频下的控制带来了很大的挑战。
|
图 8 耦合系统控制结果,kα=0.32 Fig.8 Control results of the coupled system, kα= 0.32 |
通过对比在控制时间步200前后的流动频率与结构频率,可以看到两者有着明显的区别。为了解决这一失稳模型的转换对控制效率带来的影响,本文对控制器的回路进行设计,以结构俯仰幅值不超过0.01为阈值进行切换,通过在流动控制率与结构控制律之间的切换,确保流动与结构在合适的范围内,不再失稳发散。
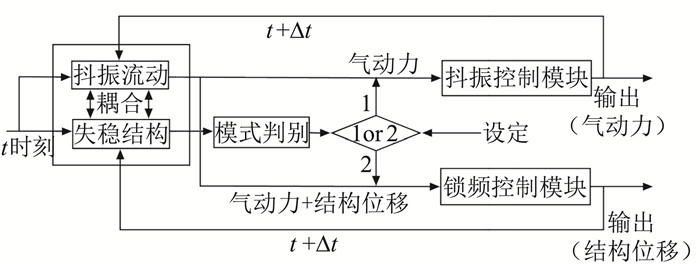
为了避免基于单一控制律设计只能控制一个失稳模式的尴尬境地,本文设计了基于失稳模式的控制律切换回路,见图 9。在这里,非锁频模块是单纯针对抖振流动的单输入单输出(Single Input Single Output,SISO)无模型自适应控制,它只采用气动力作为控制目标,具有较高的流动控制效率。而锁频控制模块,是针对气动力与结构位移的多输出自适应控制方法,本文依据结构俯仰幅值作为阈值以在这两种控制模式间切换,以同步抑制这两种失稳模式。
|
图 9 基于模式切换的耦合控制回路 Fig.9 Coupling control loop based on mode switching |
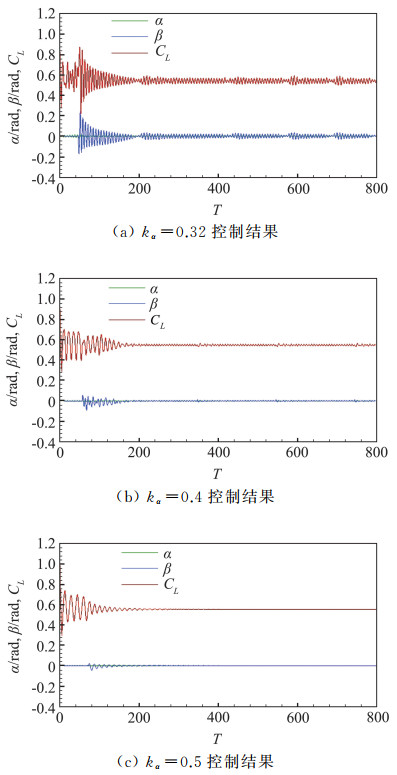
为了验证控制方法,选取了kα=0.32、kα=0.4、kα=0.5三种状态下的失稳进行控制,其中kα=0.32、kα=0.4为锁频状态,kα=0.5为单纯的抖振非锁频状态,在这里作为对照。
由于模式切换避免了无模型控制进入失效状态,在耦合系统的控制结果上有着明显的提升。如图 10所示,针对不同锁频程度下的控制结构都有了较大的提升,不仅避免了结构发散到极限环的失稳过程,而且通过模式切换避免了之前存在的流动突然失稳,将升力波动限制在了较小的幅值内。
|
图 10 基于失稳模式切换的耦合系统控制结果 Fig.10 Control results of coupled system based on instability mode switching |
基于模式切换的控制回路设计,对锁频状态下的双失稳模式有着较高的控制效率,可以在几乎不改变控制律的基础下,适应锁频以及非锁频状态下的多模式控制需求。
3 结论本文针对NACA0012翼型,通过CFD/CSD时域耦合仿真,对马赫数0.7、迎角5.5°这一典型抖振状态下的锁频失稳进行了主动控制研究。通过结合无模型自适应控制方法与控制律设计,提出了一种基于响应幅值的控制模式切换方法。通过在锁频与非锁频控制模式的切换,有效抑制了结构在锁频状态下的失稳,并且抑制了升力的大幅脉动。这种方法不受流动状态与结构参数的限制,具有较好的泛化能力。不同于单纯的流动控制方法,这一方法有效地利用了流固耦合系统的特性,在多失稳模式的控制中有着较好的应用前景。
目前的抖振控制依然依赖于较高频的尾缘作动,难以直接在工程中复现。未来的工作可能进一步考虑增加控制手段,提升控制效率,在锁频控制中研究对应失稳模式之间的物理机理与阈值选取过程,有可能进一步揭示锁频状态下的流固耦合特性及其控制方法。
| [1] |
GAO C Q, ZHANG WW, KOU J Q, et al. Active control of transonic buffet flow[J]. Journal of Fluid Mechanics, 2017, 824: 312-351. DOI:10.1017/jfm.2017.344 |
| [2] |
张伟伟, 高传强, 叶正寅. 机翼跨声速抖振研究进展[J]. 航空学报, 2015, 36(4): 1056-1075. ZHANG WW, GAO C Q, YE Z Y. Research advances of wing/airfoil transonic buffet[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1056-1075. DOI:10.7527/S1000-6893.2014.0213 (in Chinese) |
| [3] |
董圣华, 史爱明, 叶正寅, 等. 超临界翼型跨声速抖振CFD计算和POD分析[J]. 空气动力学学报, 2015, 33(4): 481-487. DONG S H, SHI A M, YE Z Y, et al. CFD computation and POD analysis for transonic buffet on a supercritical airfoil[J]. Acta Aerodynamica Sinica, 2015, 33(4): 481-487. DOI:10.7638/kqdlxxb-2013.0100 (in Chinese) |
| [4] |
LEE B H K. Oscillatory shock motion caused by transonic shock boundary-layer interaction[J]. AIAA Journal, 1990, 28(5): 942-944. DOI:10.2514/3.25144 |
| [5] |
RAGHUNATHAN S, MABEY D G. Passive shock-wave/boundary-layer control on a wall-mounted model[J]. AIAA Journal, 1987, 25(2): 275-278. DOI:10.2514/3.9618 |
| [6] |
SMITH A, BABINSKY H, FULKER J L, et al. Shock wave/boundary-layer interaction control usingstreamwise slots in transonic flows[J]. Journal of Aircraft, 2004, 41(3): 540-546. DOI:10.2514/1.11479 |
| [7] |
TITCHENER N, BABINSKY H. Shock wave/boundary-layer interaction control using a combination of vortex generators and bleed[J]. AIAA Journal, 2013, 51(5): 1221-1233. DOI:10.2514/1.J052079 |
| [8] |
MCCORMICK D C. Shock/boundary-layer interaction control with vortex generators and passive cavity[J]. AIAA Journal, 1993, 31(1): 91-96. DOI:10.2514/3.11323 |
| [9] |
CARUANA D, MIGNOSI A, CORRÈGE M, et al. Buffet and buffeting control in transonic flow[J]. Aerospace Science and Technology, 2005, 9(7): 605-616. DOI:10.1016/j.ast.2004.12.005 |
| [10] |
HUANG J B, XIAO Z X, LIU J, et al. Simulation of shock wave buffet and its suppression on an OAT15A supercritical airfoil by IDDES[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(2): 260-271. DOI:10.1007/s11433-011-4601-9 |
| [11] |
田云, 刘沛清, 彭健. 激波控制鼓包提高翼型跨声速抖振边界[J]. 航空学报, 2011, 32(8): 1421-1428. TIAN Y, LIU P Q, PENG J. Using shock control bump to improve transonic buffet boundary of airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1421-1428. (in Chinese) |
| [12] |
TIAN Y, GAO S Q, LIU P Q, et al. Transonic buffet control research with two types of shock control bump based on RAE2822 airfoil[J]. Chinese Journal of Aeronautics, 2017, 30(5): 1681-1696. DOI:10.1016/j.cja.2017.07.011 |
| [13] |
DANdoiS J, LEPAGE A, DOR J B, et al. Open and closed-loop control of transonic buffet on 3D turbulent wings using fluidic devices[J]. Comptes Rendus Mécanique, 2014, 342(6-7): 425-436. DOI:10.1016/j.crme.2014.01.015 |
| [14] |
ABRAMOVA K A, PETROV A V, POTAPCHICK A V, et al. Investigations of transonic buffet control on civil aircraft wing with the use of tangential jet blowing[C]//Perm, Russia. Author(s), 2016: 020017. doi: 10.1063/1.4963940
|
| [15] |
TIAN Y, LI Z, LIU P. Upper trailing-edge flap for transonic buffet control[J]. Journal of Aircraft, 2017, 55(1): 382-389. DOI:10.2514/1.C033134 |
| [16] |
REN K, CHEN Y, GAO C Q, et al. Adaptive control of transonic buffet flows over an airfoil[J]. Physics of Fluids, 2020. |
| [17] |
侯忠生.非线性系统参数辨识, 自适应控制及无模型学习自适应控制[D].沈阳: 东北大学, 1994.
|
| [18] |
RAVEH D E, DOWELL E H. Aeroelastic responses of elastically suspended airfoil systems in transonic buffeting flows[J]. AIAA Journal, 2014, 52(5): 926-934. DOI:10.2514/1.J052185 |
| [19] |
GAO C Q, ZHANG W W, LI X T, et al. Mechanism of frequency lock-in in transonic buffeting flow[J]. Journal of Fluid Mechanics, 2017, 818: 528-561. DOI:10.1017/jfm.2017.120 |
| [20] |
GAO C Q, ZHANG W W, YE Z Y. A new viewpoint on the mechanism of transonic single-degree-of-freedom flutter[J]. Aerospace Science and Technology, 2016, 52: 144-156. DOI:10.1016/j.ast.2016.02.029 |
| [21] |
GAO C Q, ZHANG W W, LI X T. Passive feedback control of transonic buffet flow[J]. Physics of Fluids, 2019, 31(4): 046103. DOI:10.1063/1.5087014 |
| [22] |
高传强, 张伟伟. 跨声速嗡鸣诱发机理及其失稳参数研究[J]. 空气动力学学报, 2019, 37(1): 99-106. GAO C Q, ZHANG W W. Study on the mechansim and instability parameters of transonic buzz[J]. Acta Aerodynamica Sinica, 2019, 37(1): 99-106. DOI:10.7638/kqdlxxb-2018.0204 (in Chinese) |
| [23] |
高传强.跨声速复杂气动弹性问题的诱发机理及控制研究[D].西安: 西北工业大学, 2018. GAO C Q. Research on the mechanism and control of complex aeroelastic problems in transonic flows[D]Northwestern Polytechnical University, 2018. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10699-1020706511.htm |
 2020, Vol. 38
2020, Vol. 38