由于传统布局的民用客机在增大载运量、提高升阻比、降低油耗等方面的提升空间有限,人们开始追求新的气动布局方案以提高载运量和经济性[1-3]。鉴于此,出现了诸如翼身融合(BWB)、联结翼以及多机身等气动效率更加高效的非常规布局形式[4]。经过国内外研究人员的多年探索,BWB布局被认为是最有可能取代传统布局的大型客机设计方案,该布局可大幅度减小浸润面积、降低阻力,从而提高升阻比,而且在安全性、舒适性及环境噪声等方面也具有潜在优势[5]。
常规布局飞机通常采用增大机翼弯度的方式增加起降升力,在不大的迎角下即可获得足够的升力,且其伴随产生的俯仰力矩可由大力臂的平尾(升降舵)消除。而BWB布局俯仰控制装置力臂较短,难以克服传统变弯增升装置产生的低头力矩,从而限制了传统增升装置能力的发挥,往往不得不采用增大迎角的方式获取升力,对于静安定的飞机,这进一步增大了飞机对抬头控制能力的需求。因此,探索能够同时增加升力和抬头力矩的新型增升装置,成为BWB布局工程化的迫切需求[6-7]。
按鸭翼与主翼面之间的距离可将鸭翼布局分为近距耦合和远距耦合两种[8]。近距耦合鸭翼布局由于具有良好的低速大迎角气动特性而成为先进气动布局研究中的重要内容。国内外针对鸭翼布局从尺寸优化、流动分析等方面开展了大量研究。包括研究鸭翼偏度、位置对气动特性的影响,鸭翼涡系结构的流动机理[9-11]等。但研究和应用的对象大多局限于前掠翼、盒式翼以及常规布局等领域[12-14],未见在BWB布局上的应用研究。
近年来随着计算流体力学的发展,研究人员开始越来越多地使用数值模拟技术开展气动特性分析工作。本文针对BWB布局利用CFD方法对近距耦合鸭翼开展数值模拟分析,研究其气动特性以及流动机理,并针对不同鸭翼高度及平面形状开展参数敏感性分析研究。
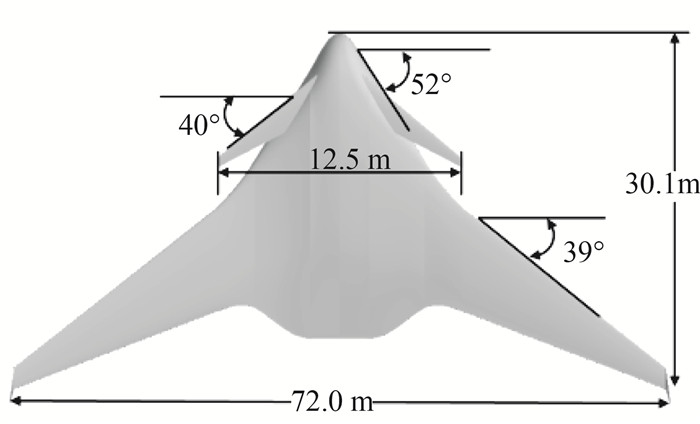
1 计算模型及方法 1.1 计算模型BWB布局采用具有中等展弦比和中等前缘后掠角的鸭翼,BWB本体外翼段采用超临界翼型,中央机身做适当修形以满足客货舱布置需要,鸭翼采用NACA-4系列低速翼型。其他主要参数包括:BWB机身长度30.1 m,展长72.0 m,展弦比6.50,中央机身前缘后掠角为52°,外翼段后掠角为39°;鸭翼展长12.5 m,展弦比为4.15,前缘后掠角为40°,鸭翼相对于机翼在垂直方向高0.8 m。力矩参考点取平均气动弦25%位置处,距离机头顶点16.4 m。
|
图 1 计算基本模型 Fig.1 BWB with canard wing configuration |
本研究主要针对BWB飞机起降状态下的纵向气动特性,计算来流马赫数Ma=0.23,单位长度雷诺数5.36×106/m,开展多迎角间隔计算。
数值模拟计算采用三维可压缩N-S方程,在直角坐标系下该方程的守恒形式可表示为:
| $ \iiint\limits_{\mathit{\Omega }}{\frac{\partial \boldsymbol{W}}{\partial t}\text{d}V}+\iint\limits_{\partial \mathit{\Omega }}{\boldsymbol{H}\cdot \boldsymbol{n}\text{d}S}=\iint\limits_{\partial \mathit{\Omega }}{{{\boldsymbol{H}}_{V}}\cdot \boldsymbol{n}\text{d}S} $ | (1) |
式中:W为守恒变量矢量,H和HV分别表示无黏和黏性通矢量。
在计算过程中采用SST湍流模型,利用有限体积法对控制方程进行离散化,计算所采用的非结构网格为保证精确模拟附面层内流动特征,在物面附近生成了各向异性的棱柱层网格。
为考察网格密度对计算结果的影响,生成三种密度的非结构网格,分别用C(Coarse)、M(Medium)和F(Fine)来表示,网格密度依次递增,对应的网格参数如表 1所示。除了对附面层网格分布加密外,M网格相对于C网格,F网格相对于M网格,均在展向与弦向方向节点数进行了适当增加。
| 表 1 不同密度网格参数 Table 1 Grid parameters with different density |
|
|
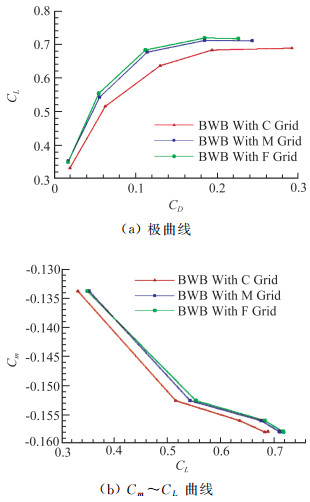
图 2给出了不同网格密度下的针对BWB本体的极曲线与俯仰力矩系数曲线,可看出不同密度网格对俯仰力矩模拟的结果差别量较小(俯仰力矩系数差量控制在0.002以内),但在升阻特性模拟上,M密度网格和F密度网格的极曲线计算结果一致性较好,而C密度网格与前两者有较大偏离。因此从精度和计算速度综合考虑,采用M密度网格(图 3)。全模网格节点数约950万,BWB本体及鸭翼表面均采用物面无滑移条件。
|
图 2 不同网格密度下的极曲线与俯仰力矩曲线 Fig.2 Pitch moment coefficient and polar curve |

|
图 3 三维计算网格(M,950万) Fig.3 Computational model and mesh(M, 9.5 million) |
为验证数值计算方法的可信度,选择已经过风洞试验的BWB布局飞机开展数值模拟验证,BWB风洞试验模型如图 4所示。计算来流马赫数Ma=0.40,基于试验模型的雷诺数为4.46×106。

|
图 4 用于计算方法验证的BWB模型 Fig.4 Experimental model of BWB |
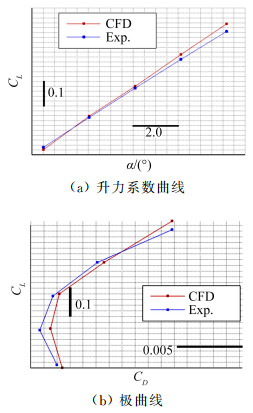
计算结果与试验数据对比如图 5所示,可以看出在该迎角范围内的升力数值模拟结果与试验数据基本吻合良好;阻力值计算有一定偏差,但处于可接受范围内,而且极曲线趋势一致。总体而言本文所采用的数值模拟方法具有与本研究相适应的可信度,可用于与BWB飞机相关的纵向气动特性分析。
|
图 5 计算结果与风洞试验数据对比(Ma=0.4) Fig.5 Comparison between calculated results with wind tunnel test (Ma=0.4) |
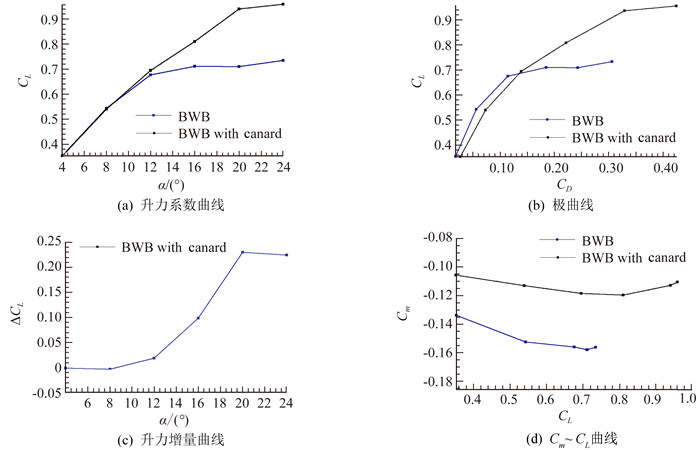
低速下带鸭翼和未安装鸭翼BWB飞机的气动特性曲线如图 6所示。从升力系数对比(图 6(a))可以看出,鸭翼在小迎角下对升力系数影响不大,但随着迎角的增加(大于12°),鸭翼对全机气动特性影响明显,延伸升力系数曲线线性段,将失速迎角从12°推迟至22°,最大升力系数也有显著增加。
|
图 6 带鸭翼BWB飞机的气动特性曲线 Fig.6 Aerodynamic characteristic curve of BWB aircraft with canard wing |
图 6(b)显示由于鸭翼的存在产生了额外的摩阻、诱导以及干扰阻力,导致在小升力系数下(小于0.7),BWB带鸭翼构型的升阻特性较差。随着迎角的增加,鸭翼增升的效果逐渐明显,推迟失速并极大降低了分离流动带来的压差阻力,抵消了由于安装鸭翼带来的阻力增量,升阻特性远优于没有安装鸭翼的BWB布局。
为更好观察鸭翼在不同迎角阶段的升力影响,图 6(c)给出了计算迎角范围内带鸭翼构型的升力系数增量曲线,可以看出在小迎角范围内鸭翼引起了较小的升力损失,在迎角8°附近,升力损失最大值约占总升力的0.6%,但随着迎角增加,受到推迟失速以及鸭翼自身升力贡献等因素的影响,相对于无鸭翼构型,施加鸭翼可产生30%以上的升力增量。
图 6(d)给出了俯仰力矩曲线对比,低速下本体存在较大的低头力矩。在安装鸭翼后,受到升力作用点前移,以及内翼段涡增升的影响,BWB模型的低头力矩得到有效的抑制,并产生0.03~0.04的抬头力矩增量,降低了BWB布局对低速起降状态下的抬头控制需求。
从图 6(a)的升力系数曲线可以看出,BWB本体在升力系数0.7附近即进入非线性段,逐渐开始出现下降趋势,安装鸭翼后,其线性段延伸,最终最大升力系数可达0.9以上;相对应的,图 6(d)的俯仰力矩曲线显示,受到鸭翼对分离抑制的影响,鸭翼的安装推迟了俯仰力矩曲线中“勺形区”的出现,将可用升力系数从0.7提升至0.8附近。
从图 6(d)可以看出,安装鸭翼后俯仰力矩曲线斜率降低,纵向静稳定裕度发生改变。若将当前的力矩参考点视为重心位置,则在升力系数0.4附近本体的纵向静稳定裕度为9.7%,而安装鸭翼后降低至3.8%。表明采用鸭翼会明显降低纵向静稳定裕度,鸭翼对稳定性的不利影响后期需进一步相关研究。
2.2 三维流态分析气动特性曲线显示在中小迎角范围内,安装鸭翼会造成一定的升力损失,并产生额外阻力,但随着迎角的增加,鸭翼优势逐渐明显,可以产生较大的升力增量,推迟失速并降低分离带来的压差阻力,使得升阻比明显提升,并增加了抬头力矩。可以看出鸭翼增升减阻以及抬头收益均发生在大迎角状态,为更好分析鸭翼的气动效果,对典型迎角下的三维流动形态展开分析。图 7给出了各个迎角下安装鸭翼前后的流场对比。
|
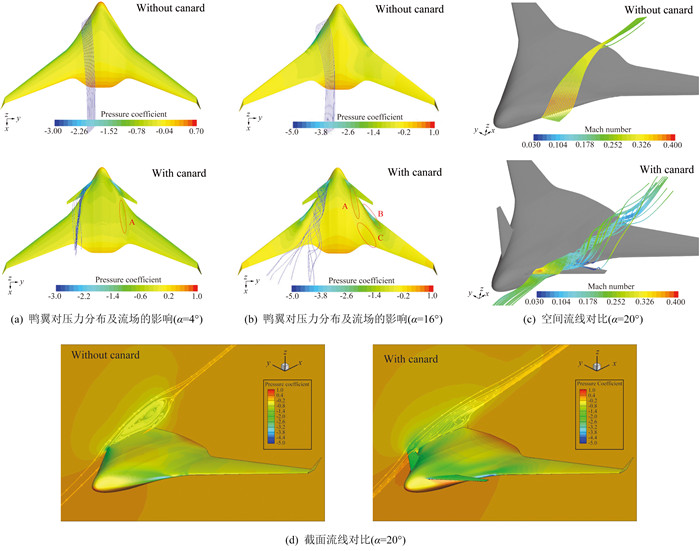
图 7 各个迎角下安装鸭翼前后的流场对比 Fig.7 Comparison of flow field with and wihtout canard at different angles of attack |
图 7(a、b)分别为典型中小迎角(α=4°)以及大迎角(α=16°)下安装鸭翼前后的表面压力分布及空间流线对比。观察α=4°的空间流线可以看出,未安装鸭翼时,BWB布局的内翼段全部为附着流动,安装鸭翼后鸭翼内侧前缘会脱出分离涡,该涡的加速效果在本体内翼段附近(A区)产生较为明显的低压区域,但该涡系在BWB内翼段未得到充分发展,因此涡增升效果较弱。同时受到鸭翼与本体之间相互干扰的影响,全机升力增量为负。
从图 7(b)可以看出,在大迎角下,鸭翼前缘内侧沿翼展方向的分离涡强度明显增加,分离涡在本体内翼段产生的加速诱导作用使位于涡下方的翼面上产生了明显的负压区域(A区及B区)。随着分离涡向后发展逐渐远离鸭翼附近的涡源,本体内翼段后方的分离涡强度逐渐降低,诱导作用减弱,因此在C区出现流动减速,产生高压区。从升力增量曲线可知,受到鸭翼本身的升力贡献以及鸭翼分离涡对本体的升力贡献双重作用的影响,BWB布局具有明显的增升效果。
为更好看出鸭翼分离涡对推迟失速的收益,图 7(c、d)给出了迎角20°下空间流线以及展向截面流线对比。从图 7(c)的空间流线对比可以看出,由于鸭翼脱出的分离涡强度较高,通过诱导作用[15]的有利影响,借助鸭翼分离涡的涡量输入,增强了对本体内翼段的流动控制能力。
图 7(d)显示在该迎角附近,未安装鸭翼的BWB布局内翼产生大范围的分离流动并影响到整个上翼面,造成升力损失并处于过失速状态。安装鸭翼后,上翼面完全被稳定的鸭翼涡控制,表面压力较低,产生了更大的升力,位于鸭翼后方的机翼的外翼段分离区域较小,并未出现明显的流动分离现象。
根据上述分析可知,受到分离涡强度的影响,在大迎角下,BWB安装近距耦合鸭翼后具有明显的气动优势。鸭翼产生的分离涡能让BWB本体内翼段形成稳定的集中涡,提高全机的失速迎角,并产生可观的升力及力矩收益。
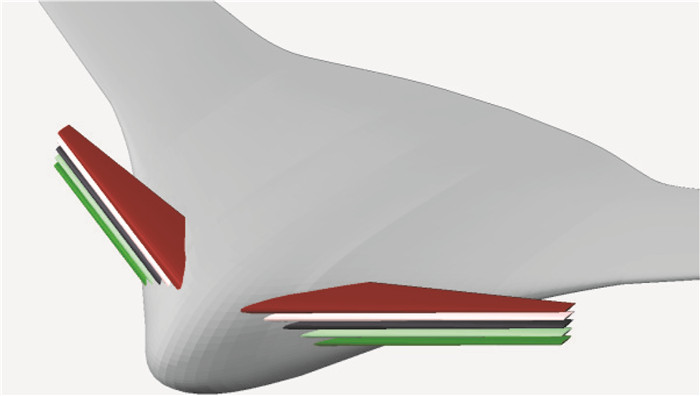
2.3 鸭翼高度的影响在基本构型的基础上,改变鸭翼高度以研究垂直位置对气动特性的影响,鸭翼相对于机翼前缘在垂直方向上的高度差分别为:-0.4 m、0 m、0.4 m、0.8 m、1.2 m,不同高度下的全机外形如图 8所示。图 9给出了不同高度鸭翼对应的BWB构型全机升力系数曲线对比。
|
图 8 不同鸭翼高度模型 Fig.8 Model with different canard position |
|
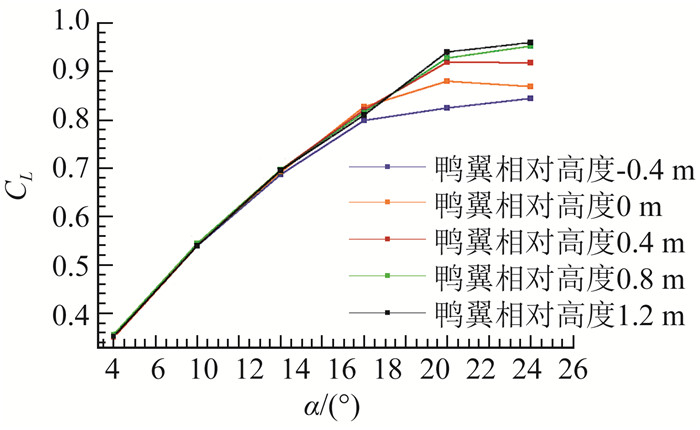
图 9 不同鸭翼高度下升力系数曲线 Fig.9 Lift coefficient curves at different canard heights |
对两个迎角阶段分别进行分析:
1) 在中小迎角下(α<12°)下:由于鸭翼涡系尚未完全成形,而且本体上翼面尚未产生明显分离流动,因此鸭翼与本体之间的相互干扰主要为鸭翼与机翼之间的洗流作用。随着鸭翼位置的增高,对机翼的下洗作用逐渐增强,减小了机翼局部迎角,导致机翼升力随着鸭翼位置的增高而减小。但同时机翼对鸭翼的上洗作用也随之增强,二者相互抵消导致在该迎角范围内,全机构型的升力特性相差不大,升力系数曲线基本重合。
(2) 在大迎角下(α>20°):鸭翼脱体涡系已形成,BWB本体内翼段在没有鸭翼的情况下已开始出现大范围的分离区,施加鸭翼后,鸭翼前缘涡的高能量气流抑制了本体内翼段上翼面的分离气流,减弱大迎角下的气流分离。而且高位鸭翼脱体涡对本体内翼段上翼面的影响强于低位,加速了气流流动。从图 9也可以看出,鸭翼相对高度越高,鸭翼的抑制失速和增升效果就越明显,鸭翼相对高度1.2 m构型较鸭翼相对高度0 m构型在α=24°下升力系数增加了6%,失速迎角也有相应增加。
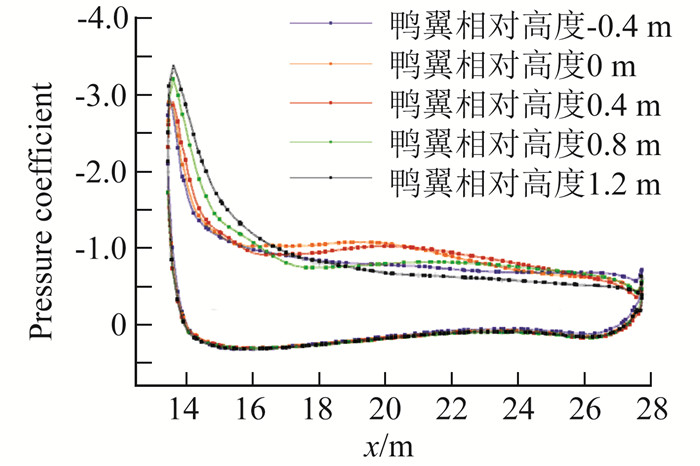
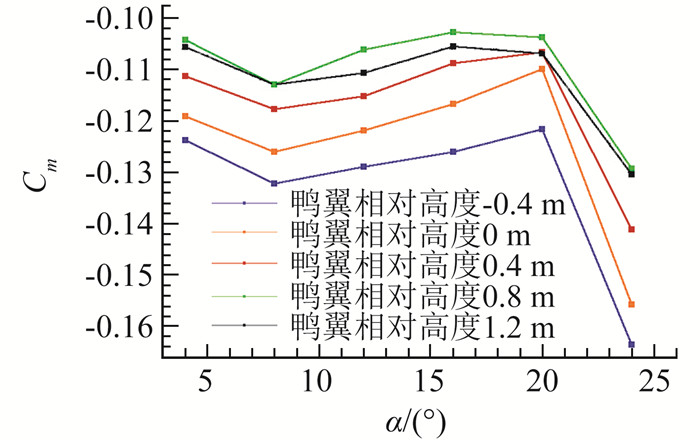
图 10给出了α=20°不同鸭翼高度位置下典型截面位置(距对称面9 m)的压力分布,鸭翼脱体涡加速了本体上翼面气流流动,本体升力随之上升。而且这种加速效果主要影响本体前缘附近区域,形成较大范围的低压区,鸭翼垂直位置越高,低压区峰值越大,气动作用点也随之前移,提高了抬头力矩。图 11给出了不同鸭翼高度下的俯仰力矩曲线,可以看出鸭翼相对高度越高,鸭翼脱体涡的影响就越明显,其抬头力矩收益越大,最多有20%的抬头力矩增量。鸭翼高于机翼1.2 m相对于鸭翼位于机翼下方0.4 m,其升力系数提高了13.6%,增量作用点位于重心之前,导致全机低头力矩降低了20.8%。
|
图 10 不同鸭翼高度对应的压力分布(α=20°) Fig.10 Pressure distribution at different canard heights (α=20°) |
|
图 11 不同鸭翼高度下俯仰力矩曲线 Fig.11 Pitch moment coefficient at different canard heights |
在上述计算分析结果的基础上,对不同平面形状的鸭翼开展数值模拟分析,在展弦比、稍根比以及面积相同的情况下,分析不同鸭翼前缘后掠角对气动特性的影响。
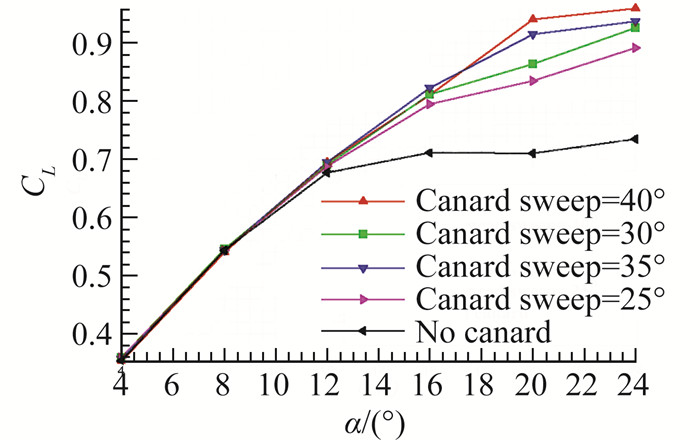
图 12显示全机升力系数随着鸭翼后掠角的增加而单调递增,α=20°状态下,鸭翼后掠40°的升力相对于35°、30°及25°后掠增加了3%~10%。主要由于随着后掠角的增加,鸭翼对本体内翼段的涡增升效果加强,本体内翼段前缘吸力峰增加,提高了本体的升力。与此同时,由于后掠降低了鸭翼自身的有效速度,因此鸭翼本身由于后掠增加带来了升力损失,但鸭翼对本体的涡增升效果大于鸭翼自身升力损失效果,因此全机升力系数随鸭翼后掠的增大而增加。
|
图 12 不同鸭翼后掠角下的全机升力系数 Fig.12 Variation of lift coefficient with canard sweep angles |
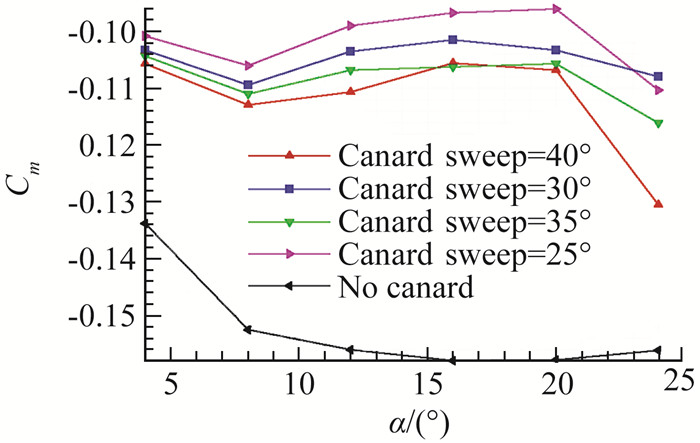
图 13为全机俯仰力矩曲线,可以看出与升力曲线的趋势不同,随着后掠角的增加,低头力矩增加。这主要是由于后掠角增加后,鸭翼自身升力贡献降低,由于鸭翼位置离重心较远,从而产生了较大的低头力矩,而且这种低头力矩无法被增升效果所抵消,从而导致抬头力矩收益降低。
|
图 13 不同鸭翼后掠角下的俯仰力矩系数 Fig.13 Variation of pitch moment coefficient with canard sweep angles |
1) 近距鸭翼可提高BWB布局飞机升力系数曲线线性段,且在大迎角下受到鸭翼脱离涡的影响,升阻及力矩特性远优于无鸭翼构型。观察不同高度及平面形状的鸭翼可知,设计合理的鸭翼可产生20%~35%的抬头力矩增量,提升可用升力系数范围,降低BWB布局纵向配平与操纵难度;
2) 鸭翼相对高度越高,脱体涡对本体内侧上翼面的影响就越明显,抑制失速的能力以及增升效果就越强,并增加抬头力矩收益;
3) 鸭翼后掠角越大,对本体内翼段涡增升效果就越强,并抵消了鸭翼本身的升力损失,全机升力随之增加;但由于鸭翼距重心位置较远,因此后掠增加引起的鸭翼升力损失会导致抬头力矩的收益降低;
需要注意的是,尽管鸭翼在低速下展现了较好的气动效果,但也会伴随产生一些问题,包括:纵向静稳定裕度的降低、安装机构对机身内部空间的挤占、鸭翼安装产生的额外的阻力与重量、分离流对前缘增升装置的不利干扰等,下一步将针对上述问题继续开展多专业的技术探索。
| [1] |
BERTON J J, BRIDGES J E, BURLEY C B, et al. Subsonic fixed wing N+1 noise goal study[C]//Acoustics Technical Working Group Meeting, Williamsburg, VA, September 23-24, 2008.
|
| [2] |
ENVIA E, BERTON J J, BRIDGES J E, et al. Progress toward SFW N+1 noise goal[C]//2nd Annual Fundamental Aeronautics Program Meeting, Atlanta, GA, October 7-9, 2008. https://core.ac.uk/display/10574735
|
| [3] |
ENVIA E, BERTON J J, BRIDGES J E, et al. N+1 Generation: noise and fuel burn reduction[C]//Fundamental Aeronautics Program, Subsonic Fixed Wing Project, 12-Month Program Review, Washington, D.C., November 5-6, 2008.
|
| [4] |
GREITZER E M, BONNEFOY P A, DELAROSABLANCO E, et al. N+3 aircraft concept designs and trade studies, Volume 1[R]. NASA/CR-2010-216794/VOL1.
|
| [5] |
PAMBAGJO T, NAKAHASHI K, OBAYASHI S, et al. Aerodynamic design of a medium size blended-wing-body airplane[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2001 doi: 10.2514/6.2001-129
|
| [6] |
BOWLUS J, MULTHOPP D, BANDA S, et al. Challenges and opportunities in tailless aircraft stability and control[C]//Guidance, Navigation, and Control Conference, New Orleans, LA. Reston, Virginia: AIAA, 1997 doi: 10.2514/6.1997-3830
|
| [7] |
WOOD R M, BAUER S X S. Advanced aerodynamic control effectors: AIAA-99-5619[R]. Reston: AIAA, 1999.
|
| [8] |
朱自强. 现代飞机的空气动力设计[M]. 北京: 国防工业出版社, 2011.
|
| [9] |
TU E. Effect of canard position on the longitudinal aerodynamic characteristics of a close-coupled canard-wing-body configuration[C]//Astrodynamics Conference, Hilton Head Island, SC. Reston, Virginia: AIAA, 1992. doi: 10.2514/6.1992-4632
|
| [10] |
HUMMEL D, OELKER H C. Low-speed characteristics for the wing-canard configuration of the International Vortex Flow Experiment[J]. Journal of Aircraft, 1994, 31(4): 868-878. DOI:10.2514/3.46573 |
| [11] |
OELKER H C, HUMMEL D. Investigations on the vorticity sheets of a close-coupled delta-canard configuration[J]. Journal of Aircraft, 1989, 26(7): 657-666. DOI:10.2514/3.45817 |
| [12] |
李岸一, 王旭, 刘文法, 等. 鸭翼涡与边条涡对前掠翼布局的增升研究[J]. 空军工程大学学报(自然科学版), 2010, 11(1): 19-22, 58. LI A Y, WANG X, LIU W F, et al. Study on lift-enhancement of canard vortex and strake vortex to configuration with forward-sweptwing[J]. Journal of Air Force Engineering University (Natural Science Edition), 2010, 11(1): 19-22, 58. (in Chinese) |
| [13] |
李其畅, 赵忠良, 杨海泳, 等. 边条翼和近距鸭翼布局模型动态气动特性分析[J]. 空气动力学学报, 2015, 33(2): 178-182. LI Q C, ZHAO Z L, YANG H Y, et al. Dynamic characteristics of hinged strake-wing and close-coupled wing-canard configuration fighter models[J]. Acta Aerodynamica Sinica, 2015, 33(2): 178-182. (in Chinese) |
| [14] |
任智静, 王旭, 刘文法. 前掠翼布局中鸭翼气动影响的数值模拟[J]. 航空学报, 2010, 31(7): 1318-1323. REN Z J, WANG X, LIU W F. Numerical simulation on aerodynamic influence of canard on forward-swept configuration[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1318-1323. (in Chinese) |
| [15] |
展京霞, 王晋军, 赵霞, 等. 近距鸭翼高度对鸭翼-前掠翼布局纵向气动特性影响的实验研究[J]. 实验流体力学, 2006, 20(2): 50-54. ZHAN J X, WANG J J, ZHAO X, et al. Investigation on the effects of the height of close canard wing on the aerodynamic characteristics of a forward-swept configuration[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(2): 50-54. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38

