空化是指液体内局部压强低于临界值时气泡的形成、发展和溃灭的动态过程[1]。空化现象最早发现于驱逐舰的螺旋桨上,空化气泡溃灭产生的冲击波和微射流作用在螺旋桨叶片上,对叶片产生冲击作用出现空蚀,损坏螺旋桨叶片表面,进而出现振动和噪声,影响推进效果[1]。近年来由于超声清洗技术[2]、空化污水处理技术[3]、激光空化强化技术[4]以及空化技术在军事上的广泛应用[5],国际国内兴起了一股空化应用的研究热潮[6]。
空化技术在生物医学上也有广泛用途,随着基因工程和分子生物学的发展,基因治疗[7]被认为是最有前景的癌症治疗方法之一。基因治疗的关键是找到一种安全高效的基因转染方法,而超声靶向微泡破坏技术(UTMD)[8]是其中最有发展潜力的一种。超声靶向微泡破坏技术利用微气泡在超声波场中的动力学响应,诱发细胞膜声孔效应来增加膜的通透性,进而有效促进大分子物质的胞内传输。Taniyama等[9]通过电镜观测到超声作用后,细胞膜上产生可恢复的孔洞,验证了超声靶向微破坏技术的可行性及其临床应用价值。但到目前为止超声作用下气泡溃灭如何增加细胞膜通透性的机理尚未有定论。
以往的近壁气泡空化溃灭研究往往关注气泡在刚性壁面附近溃灭时产生的射流及其对壁面的冲击作用,分析气泡尺寸和近壁距离等参数的定量影响[10]。近年来的研究发现,气泡在弹性壁面附近溃灭时存在与刚性壁面不一样的行为。Chen等[11]研究了超声作用下血管内的微气泡溃灭过程,发现溃灭射流并不是射向血管壁,而是射向血管中心,这与刚性壁面的结论正好相反,他们认为是壁面材料性质造成了射流反向。Brujan等[12]通过实验研究了激光空化气泡在弹性壁面附近的溃灭现象,发现弹性壁面的弹性模量较小时,气泡溃灭射流远离壁面;在弹性模量较大时,气泡溃灭射流朝向壁面。Ma等[13]发现在空化泡生长和溃灭过程中弹性壁面的被动变形使得附近微气泡的溃灭行为有别于刚性壁面。然而细胞与弹性壁面在弹性模量等性质上存在较大区别,而且由于细胞与气泡尺寸相当,当附近空化气泡溃灭时具有更丰富的动力学响应行为。
超吸水聚合物(super absorbent polymer,SAP)具有与癌细胞较为接近的密度和弹性模量[14],SAP弹性小球在空化气泡溃灭流场中具有较好的变形行为[14],能够较好地近似UTMD技术中细胞在附近微气泡溃灭时的动态响应过程。因此,本文拟采用激光诱导方法来生成单个可控空化气泡,研究SAP弹性小球在空化气泡膨胀与溃灭时的形变过程。
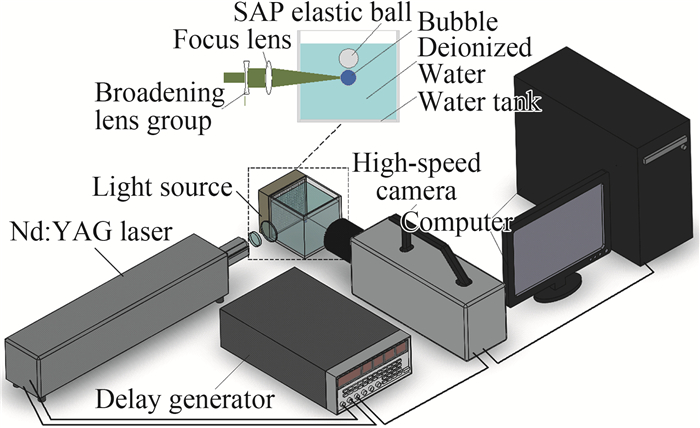
1 实验装置与方法实验系统如图 1所示,主要由固体激光器(镭宝Dawa-300)、延时触发器(美国Stanford DG645)、高速相机(NAC HX-6)、无频闪常亮光源、扩束-聚焦镜片组、滤波片和水箱等组成。高速相机和固体激光器由延时触发器通过BNC线分别连接控制,输出的触发信号先触发激光器发出波长为532 nm、能量可调的脉冲激光,然后再触发高速相机开始拍摄,以避免空化瞬间的高亮激光损伤相机感光芯片。
|
图 1 实验系统示意图 Fig.1 Schematic diagram of experimental system |
实验中,SAP弹性小球通过细铜丝悬挂于水箱的去离子水中,水箱放置于精密位移平台上,通过调整位移平台来控制激光空化气泡中心位于小球正下方,并且可以调整气泡中心与小球的距离。实验中的SAP弹性小球为高吸收性聚合物材料,可以吸收并保留大量液体,据文献中的实验测量数据,其泊松比v=0.49[15],杨氏模量E=21 kPa[14],密度ρ=1117 kg/m3。
实验中,固体激光器产生的脉冲激光经过扩束-聚焦镜片组后被聚焦至水箱的去离子水中,当聚焦点的激光功率密度超过去离子水的击穿阈值时,去离子水被电离击穿,产生等离子体并迅速膨胀形成空泡[4],类似微爆炸。激光聚焦点即为空化气泡中心,气泡尺寸可通过固体激光器能量耗散器调节。实验中气泡中心到水箱壁面的距离远大于气泡尺寸,因此认为壁面的影响可忽略不计[4]。实验中定义球泡间的无量纲距离为γ[16]:
| $ \gamma =\frac{L+r}{{{R}_{\max }}} $ | (1) |
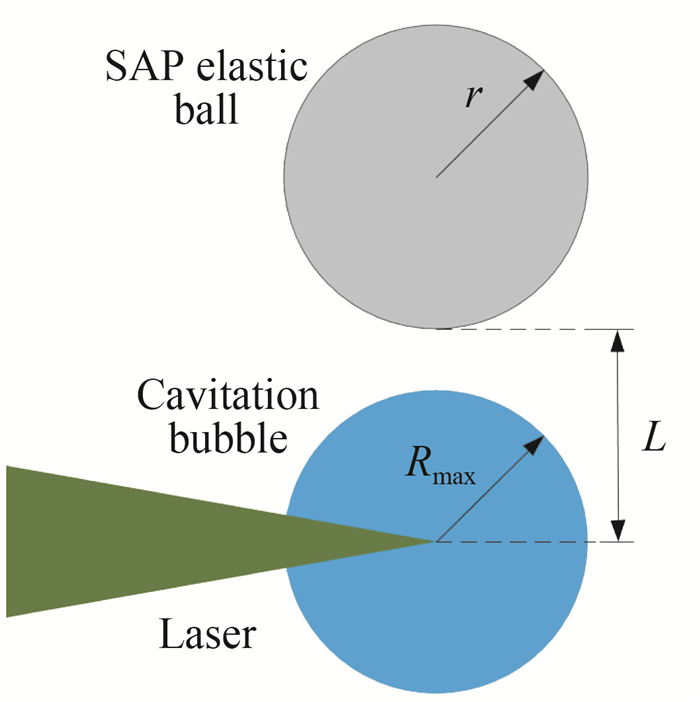
式中,Rmax为空化气泡膨胀到最大时的半径,r为SAP弹性小球的半径,L为气泡中心到弹性小球表面的最近距离,实验参数如图 2所示。
|
图 2 实验参数示意图 Fig.2 Schematic diagram of experiment parameters |
实验过程中,通过高速相机捕捉记录下完整的空化气泡膨胀与溃灭过程,使用无频闪常亮光源作补光。为保证图像清晰度,实验中高速相机的采样频率为50 000帧/秒,对应两张照片之间的时间间隔为20 μs,此时图像的分辨率为320 pixel×232 pixel。后期通过图像处理软件ImageJ来获得空化气泡的最大半径以及弹性小球变形参数。在实验中,由于高速相机帧率的限制,相机拍摄到的气泡最大半径很大概率不是空化气泡的实际最大半径。而且由于激光空化时的偶然性,在激光能量一致时也不能完全保证每次空化气泡大小的一致性。
2 空化气泡溃灭演化过程图 3给出了SAP弹性小球附近激光空化气泡的溃灭演化以及弹性小球的变形过程。实验中采用的弹性小球半径r=1.74 mm,激光空化气泡中心到小球中心距离L=0.4 mm,实验中生成的空化气泡的最大半径Rmax =1.59 mm,所以根据公式(1)计算可知,球泡无量纲距离γ=1.35。实验中,根据延时触发器设置,定义相机拍摄第一张照片为t=0 s。

|
图 3 气泡在SAP弹性小球附近的膨胀与溃灭过程 Fig.3 Process of bubble expansion and collapse near a SAP elastic ball |
从图 3可以看出,SAP弹性小球附近的激光空化气泡存在多次膨胀与溃灭过程。每次可以分为两个阶段:膨胀阶段和溃灭阶段。以第一次膨胀与溃灭过程为例,图 3(a~h)是气泡的一次膨胀阶段,持续140 μs左右。在气泡膨胀过程中,随着气泡的发展变大,弹性小球开始被挤压变形,在气泡达到最大体积时(图 3(h))弹性小球挤压变形也最大。另一方面,由于弹性小球的存在,气泡膨胀时形状也受到影响,与自由溃灭时的球形不一样,气泡呈现非球形。
当空化气泡达到最大体积之后,在内部气液相变和外部流体压力的共同作用下,气泡体积迅速变小,发生溃灭。图 3(h~n)是气泡的一次溃灭阶段,持续时间120 μs左右。气泡溃灭最后时刻,由于周围液体的瞬间冲击,会在气泡中心出现往四周传播的冲击波,但是在本实验中,由于相机时间分辨率和空间分辨率的限制,没有捕捉到冲击波现象。
气泡一次膨胀与溃灭总持续时间在260 μs左右,当气泡一次溃灭结束后,气泡体积又重新膨胀,进入二次膨胀(图 3(n~q))和二次溃灭(图 3(q~u))阶段,总持续时间在140 μs左右,二次膨胀最大体积小于一次膨胀时的最大气泡体积。当二次溃灭结束后,还存在三次膨胀与溃灭(图 3(u~x)),总持续时间在60 μs左右,而且气泡体积更小,溃灭强度更弱。实验中,由于相机时间分辨率和空间分辨率限制,气泡溃灭持续时间和气泡最大尺寸都存在一定的误差。当高速相机时空分辨率进一步提高时应该还会出现四次以及更高次的膨胀与溃灭阶段。
从图 3中还可以发现,与刚性壁面[17]和刚性小球[16]不一样的是,气泡在弹性小球附近溃灭时,并没有出现射向弹性小球的微射流。在刚性壁面和刚性小球附近,当气泡溃灭阶段周围液体往气泡中心汇聚时,由于壁面的存在,气泡靠近壁面侧的液体补充不及时,而远离壁面侧的液体往气泡中心运动时会穿过近壁面侧的气泡界面,形成了指向刚性壁面的微射流[16-17]。细胞也具有较大的可变形性,在超声靶向微泡破坏技术中,微气泡在细胞附近溃灭时,并不一定会出现射向细胞的微射流,溃灭微射流可能并不是造成气泡膜通透性增加的原因。
3 弹性小球变形分析及模拟 3.1 弹性小球变形分析在空化气泡的膨胀与溃灭过程中,附近弹性小球出现明显变形。从图 3中可以发现,在一次膨胀过程中,随着气泡迅速变大,弹性小球被挤压变形,在气泡达到最大体积时(图 3(h))弹性小球变形也最大。气泡一次溃灭时,周围液体迅速向气泡中心汇聚,速度较大,流体中存在较大的剪切,造成弹性小球被拉扯变形。在一次溃灭气泡体积最小时刻,弹性小球下部被拉扯出一个尖端,如图 3(n)所示,此时,弹性小球表面受到最大应力。
在气泡一次膨胀与溃灭过程的弹性小球变形中,溃灭阶段时间更短,而且变形存在奇点,因此有理由相信,在超声靶向微泡破坏技术中,超声作用下10微米量级的气泡在相同尺寸细胞附近溃灭时,细胞也会出现类似变形,从而增加了细胞膜的通透性,进而实现了达到基因转染的目的。
从图中还可以看出,二次溃灭和三次溃灭对气泡的挤压和拉扯作用较弱,在这两个阶段,SAP弹性小球在其自身弹性的作用,逐渐恢复其原来的球状。
气泡的膨胀与溃灭过程伴随着周围液体的运动,气泡溃灭时由于周围液体往气泡中心急速运动,会伴随着压力波的生成[1, 4]。在各向同性的均质物体中,压力波沿纵向直线传播,压力波的传播速度up由下式给出[18]:
| $ {{u}_{p}}=\sqrt{\frac{K+\frac{4}{3}G}{\rho }} $ | (2) |
式中K是体积模量,G是剪切模量,ρ是波传播介质密度。均质各向同性线弹性材料的弹性特性可由其中的任何两个模量唯一确定,给定任意两个可以计算其他弹性模量[18]:
| $ K=\frac{E}{3(1-2v)} $ | (3) |
| $ G=\frac{E}{2(1+v)} $ | (4) |
式中,E为弹性小球杨氏模量,v为弹性小球泊松比。
根据SAP弹性小球的泊松比[15]和杨氏模量[14],可以计算得知压力波在直径为3 mm的弹性小球内部传播的时间尺度为9.3 μs,而弹性小球受到气泡一次膨胀与溃灭时冲击作用时间约为260 μs,压力波在弹性小球内的传播速度远高于气泡溃灭引起弹性小球形变的速度,因此排除压力波对本实验的影响,这也解释了弹性小球形变主要在靠近气泡的下半球部分,而上半球部分几乎无形变的原因。
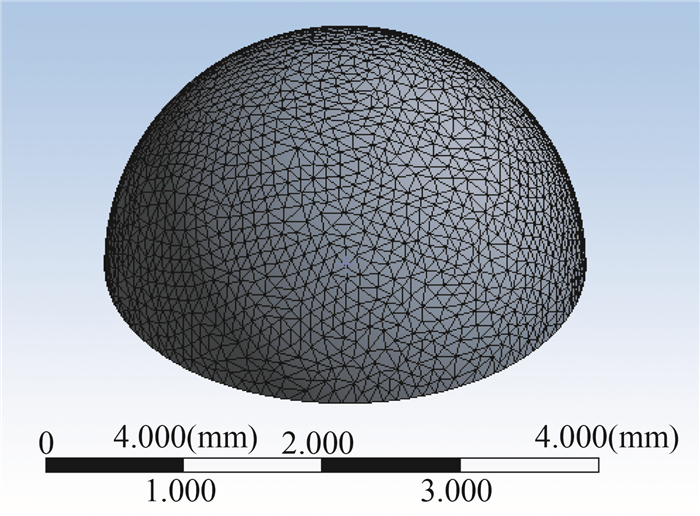
3.2 弹性小球变形模拟空化气泡膨胀与溃灭时和弹性小球的相互作用过程涉及到复杂的能量转换,为了分析弹性小球在气泡膨胀阶段的受力,模拟了弹性小球的受力变形过程。采用ANSYS Workbench里多体动力学分析中的瞬态动力学模块对弹性小球形变过程进行模拟,可以得到不同半径SAP弹性小球在不同压力荷载作用下的形变量。从图 3可以发现,弹性小球上半部分在空化气泡一次膨胀溃灭过程中几乎没有变化,因此采用如图 4所示的半球模型,通过在弹性半球上方放置平板并施加压力,观察弹性小球的形状变化情况。弹性球物性参数按照Goh等[14]的实验测量数据设置,弹性半球的半径根据该实验设置,采用5种小球(r=1.45、1.58、1.74、2.13、2.68 mm)。
|
图 4 弹性半球模型 Fig.4 Elastic hemisphere model |
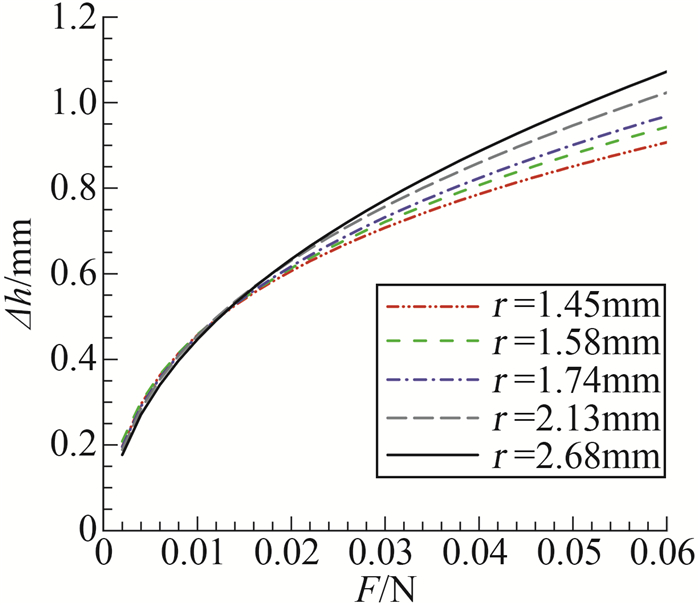
弹性半球的形变量Δh,定义为弹性球达到最大形变时高度方向的形变量。图 5给出了5种SAP弹性半球在不同外加载荷作用下的变形情况。随着外加压力的增加,弹性小球的形变量逐渐增大,但是变化趋势逐渐变慢。作用力比较小时,弹性小球半径越小,越容易变形。但是当形变量达到一定程度之后,相同作用力下半径越小的弹性小球形变量也越小。基于图 5中气泡膨胀阶段弹性小球的最大形变量与作用的压力荷载之间的F-Δh曲线,根据实验中测得的SAP弹性小球形变量,就可以获得作用在弹性小球上的作用力。图 6给出了5种SAP弹性小球在不同球泡距离γ时空化气泡膨胀阶段受到的最大挤压作用力。
|
图 5 SAP弹性半球在不同压力荷载下的变形情况 Fig.5 Deformation of SAP elastic hemisphere under different pressure loads |
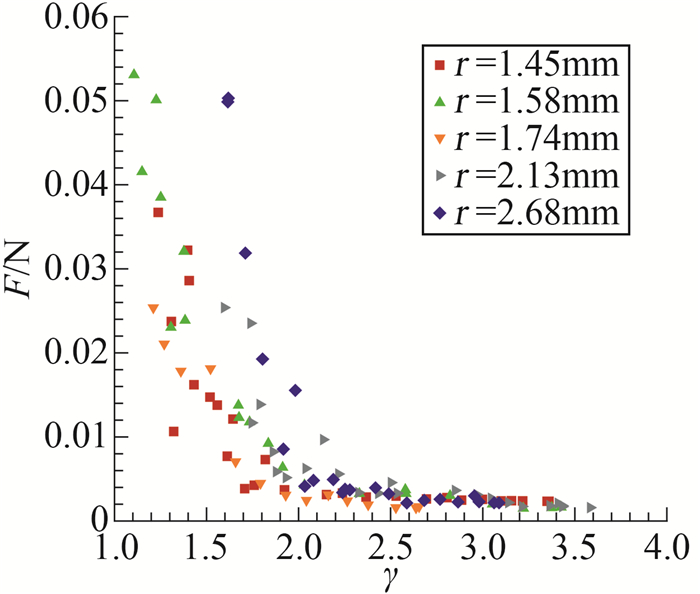
|
图 6 弹性小球受到的冲击压力随无量纲距离γ的变化 Fig.6 Variation of impact pressure on the elastic sphere with the dimensionless distance γ |
因为实验中激光空化气泡略小于弹性小球尺寸,按照方程(1)中无量纲距离γ的定义,气泡中心离弹性小球越近,无量纲距离γ越接近1;而气泡中心离弹性小球越远,无量纲距离γ也越大。从图中可以看出,对于给定尺寸的弹性小球,气泡中心离弹性小球越近,气泡膨胀阶段对弹性小球的挤压作用越大。当γ>2时,空化气泡一次膨胀时对气泡的挤压作用力小于0.01 N;而当γ < 1.5时,气泡对弹性小球的挤压作用力可达到0.05 N,气泡中心越靠近弹性小球,弹性小球受到的挤压作用越大。Zhang等[16]在研究刚性小球附近的气泡溃灭时,他们发现当无量纲距离γ>2.5时,附近气泡溃灭与壁面几乎相互无影响,而气泡在弹性小球附近溃灭时,此时气泡溃灭还会影响弹性小球变形。
4 结论本文研究了激光空化气泡膨胀和溃灭时对附近SAP弹性小球形变的影响,获得以下结论:
1) 通过高速相机获取的空化气泡与弹性小球的动态演化过程发现空化气泡存在多次膨胀与溃灭过程,一次膨胀与溃灭最剧烈,持续时间最长,二次和三次溃灭逐渐减弱。
2) 在气泡作用下,SAP弹性小球出现明显变形,在气泡膨胀阶段,弹性小球下半部分受迫挤压,在空化气泡达到最大体积时弹性小球变形最大。而当气泡一次溃灭时,由于受到流体强剪切的作用,弹性小球被剧烈拉扯,出现明显变形。气泡的二次和三次膨胀与溃灭过程对弹性小球变形影响较小。
3) 通过弹性小球形变过程的模拟,还获得了不同球泡无量纲距离γ时气泡溃灭时弹性小球受到的挤压作用。随着球泡无量纲距离变小,膨胀气泡对弹性小球的挤压作用增大。
4) 与刚性壁面和刚性小球不同的是,气泡在弹性小球附近溃灭时没有出现射流现象。
5) 根据SAP弹性小球在附近气泡膨胀与溃灭时的形状变化过程,我们认为超声靶向微泡破坏技术中,是空化气泡溃灭时强流体剪切引起的挤压和拉扯作用,而不是溃灭射流增加了细胞膜的通透性。由于细胞结构的复杂性,SAP弹性小球在附近气泡膨胀与溃灭时的动力学响应并不能完全揭示细胞膜通透性增加机理,细胞在超声靶向微泡破坏技术中的响应还有待进一步研究。
| [1] |
潘森森, 彭晓星. 空化机理[M]. 北京: 国防工业出版社, 2013. PAN S S, PENG X X. Physical mechanism of cavitation[M]. Beijing: National Defense Industry Press, 2013. (in Chinese) |
| [2] |
陈伟中. 声空化物理[M]. 北京: 科学出版社, 2014. CHEN W Z. Acoustic cavitation physics[M]. Beijing: Science Press, 2014. (in Chinese) |
| [3] |
DULAR M, GRIESSLER-BULC T, GUTIERREZ-AGUIRRE I, et al. Use of hydrodynamic cavitation in (waste) water treatment[J]. Ultrasonics sonochemistry, 2016, 29: 577-588. DOI:10.1016/j.ultsonch.2015.10.010 |
| [4] |
任旭东, 袁寿其. 激光诱导空泡空化强化理论与技术[M]. 北京: 科学出版社, 2017. REN X D, YUAN S Q. Laser induced cavitation enhancement theory and technology[M]. Beijing: Science Press, 2017. (in Chinese) |
| [5] |
姚熊亮, 汪玉, 张阿漫. 水下爆炸气泡动力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012. YAO X L, WANG Y, ZHANG A M. Bubble Dynamics of Underwater Explosions[M]. Harbin: Harbin Engineering University Press, 2012. (in Chinese) |
| [6] |
牟斌, 江雄, 王建涛. 空化流动隐式求解方法研究[J]. 空气动力学学报, 2017, 35(1): 27-32. MOU B, JIANG X, WANG J T. Investigation on implicit numerical method for cavitation flow[J]. Acta Aerodynamica Sinica, 2017, 35(1): 27-32. DOI:10.7638/kqdlxxb-2015.0027 (in Chinese) |
| [7] |
FERRARA K, POLLARD R, BORDEN M. Ultrasound microbubble contrast agents:fundamentals and application to gene and drug delivery[J]. Annual Review of Biomedical Engineering, 2007, 9(1): 415-447. DOI:10.1146/annurev.bioeng.8.061505.095852 |
| [8] |
NOBLE M L, KUHR C S, GRAVES S S, et al. Ultrasound-targeted microbubble destruction-mediated gene delivery into canine livers[J]. Molecular Therapy, 2013, 21(9): 1687-1694. DOI:10.1038/mt.2013.107 |
| [9] |
TANIYAMA Y, TACHIBANA K, HIRAOKA K, et al. Development of safe and efficient novel nonviral gene transfer using ultrasound:enhancement of transfection efficiency of naked plasmid DNA in skeletal muscle[J]. Gene therapy, 2002, 9(6): 372. DOI:10.1038/sj.gt.3301678 |
| [10] |
张阿漫, 姚熊亮. 近壁面气泡的运动规律研究[J]. 物理学报, 2008, 57(3): 1662-1671. ZHANG A M, YAO X L. The law of the bubble motion near the wall[J]. Acta Physica Sinica, 2008, 57(3): 1662-1671. DOI:10.3321/j.issn:1000-3290.2008.03.059 (in Chinese) |
| [11] |
CHEN H, KREIDER W, BRAYMAN A A, et al. Blood vessel deformations on microsecond time scales by ultrasonic cavitation[J]. Physical Review Letters, 2011, 106(3): 034301. DOI:10.1103/PhysRevLett.106.034301 |
| [12] |
BRUJAN E A, NAHEN K, SCHMIDT P, et al. Dynamics of laser-induced cavitation bubbles near elastic boundaries:influence of the elastic modulus[J]. Journal of Fluid Mechanics, 2001, 433: 283-314. DOI:10.1017/S0022112000003335 |
| [13] |
MA X, HUANG B, ZHAO X, et al. Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries[J]. Ultrasonics Sonochemistry, 2018, 43: 80-90. DOI:10.1016/j.ultsonch.2018.01.005 |
| [14] |
GOH B H T, GONG S W, OHL S W, et al. Spark-generated bubble near an elastic sphere[J]. International Journal of Multiphase Flow, 2017, 90: 156-166. DOI:10.1016/j.ijmultiphaseflow.2016.03.021 |
| [15] |
URAYAMA K, TAKIGAWA T, MASUDA T. Poisson's ratio of poly(viny1 alcohol) gels[J]. Macromolecules, 1993, 26(12): 3092-3096. DOI:10.1021/ma00064a016 |
| [16] |
ZHANG Y, CHEN F, ZHANG Y, et al. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle[J]. Experimental Thermal and Fluid Science, 2018, 98: 645-661. DOI:10.1016/j.expthermflusci.2018.06.014 |
| [17] |
YE L, ZHU X. Analysis of the effect of impact of near-wall acoustic bubble collapse micro-jet on Al 1060[J]. Ultrasonics sonochemistry, 2017, 36: 507-516. DOI:10.1016/j.ultsonch.2016.12.030 |
| [18] |
LOWRIE W. The Fundamentals of geophysics[M]. Cambridge University Press, 1997.
|
 2020, Vol. 38
2020, Vol. 38


