2. 上海理工大学 能源与动力工程学院, 上海 200093
2. University of Shanghai for Science and Technology, Shang hai 200093, China
空化是指在一定温度下液体内部局部压力低于汽化压力时发生汽化相变的物理现象。涡轮泵、螺旋桨、水轮机、高压喷嘴、滑动轴承等设备在特定的工况下会发生空化现象。空化的发生常带来负面的影响,使得设备内部流场不稳定,并产生大的压力脉动,从而引起设备性能下降、结构振动、产生噪声和材料空蚀破坏等。
空化一般要经历初生、发展和溃灭三个阶段。影响空化发生的主要因素包括几何模型因素、流场工况参数和水质条件。根据空化汽液界面的形状和相对于物体表面的尺寸不同,一般可分为游离泡空化、附着片状空化、云状空化和超空化。有研究表明[1-4],云空化溃灭引起的高压力脉冲是极具破坏性的,而云空化流动是一种含相变传质的非定常多相复杂湍流流动,对其开展研究涉及诸多方面。空蚀的力学过程可理解为空化结构溃灭产生巨大的压力脉冲冲击结构表面,在时间的积累下引起材料的疲劳破坏[2-4]。因此,分析云空化结构的产生、运动和溃灭过程,获取冲击载荷,并评估特定材料在冲击载荷作用下的抗冲击能力,这应是空蚀研究的基础性问题。
目前,已有学者针对云空化结构的溃灭和空蚀破坏开展了理论、数值和实验方面的研究工作。因此,非常有必要对该领域的研究进展进行梳理,并探讨今后可能的研究方向。
1 典型局部空化流动结构局部空化包括片空化和云空化,如图 1所示。片空化指在特定的工况条件下,物体表面最小压力点附近会生成较多的空化汽泡,附着在物体表面上呈现的层状现象。云空化则指当片空化发展到一定的程度,在其后端发生不稳定的破碎或断裂,形成大量空化汽泡聚集的现象[5]。一般片状空化比较稳定,而云空化中的空腔脱落和回射流再附着机制具有明显的周期性。当大量的云空化汽泡与物体表面相互作用而溃灭时,会对其产生较强的侵蚀作用。
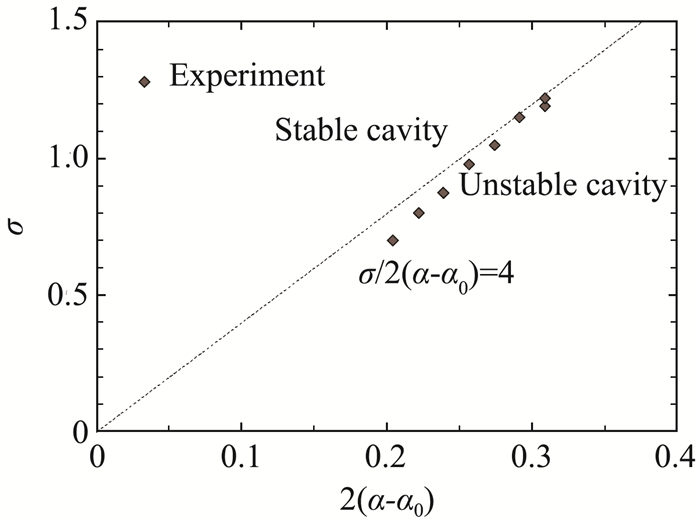
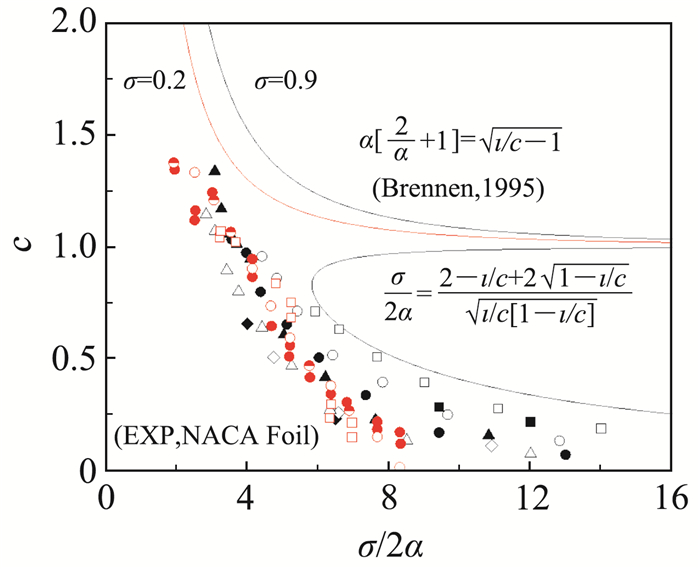
局部空化可能是稳定的,也可能是动力学多模态演化的。图 2为NACA66水翼表面空化流动结构的稳定性随来流迎角和空化数的分区[7-8],即实验观察发现σ/2(α-α0)=4为翼型表面稳定的片空化过渡到非稳定的脱落云空化的近似分界线。图 3为典型的绕流翼型空穴长度随空化数变化的L形曲线,其中实线为绕流平板水翼获得的理论解[9-10]。实验总结发现,当σ/2α < 4时,翼型表面空穴的长度大于弦长的一半,空化结构发生不稳定脱落进入云空化状态。
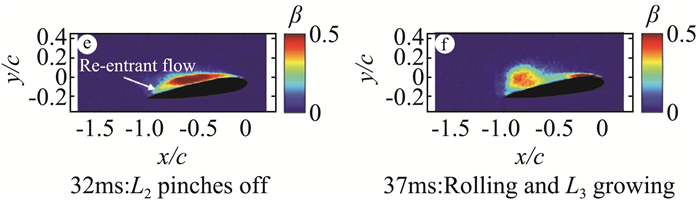
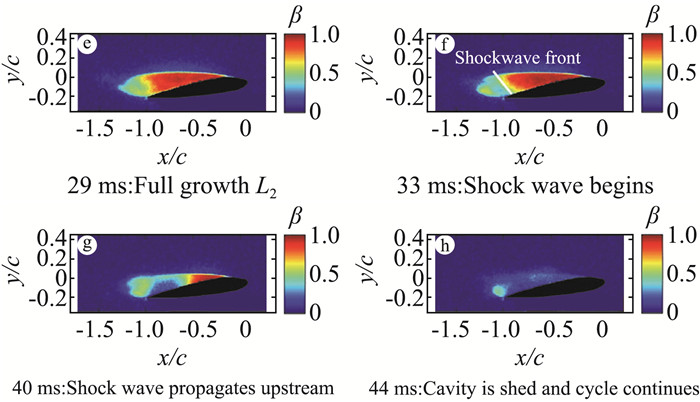
在云空化状态下,存在多种非稳定的空化流动结构,其中绕流物体表面附近比较典型的是回射流结构[11]和凝聚激波结构[3]。回射流机制被视为原始云空腔下游存在与流体相反的逆向流动,当这股反向流体再次与靠近前缘的汽-液界面相交时,引起空腔断裂产生一个新分离的腔体。图 4为NACA 0015对称翼型由回射流驱动的云空化结构的脱落过程,存在特征脱落频率(0.4),且分离、三维展向效应等会使得脱落边界和脱落云层呈现不同的形态,如新月型、U型和马蹄形等[11-13]。图 5为同一翼型在相对较低的空化数下,由凝聚激波机制诱导的空化结构演化过程[10]。凝聚激波本质上不同于空腔溃灭发出的冲击波。空腔溃灭引起的冲击压力上升时间短、振幅大[14]。相反,凝聚冲击与局部空腔回缩有关,作用时间长,相变过程压力上升幅值小(几千帕),凝聚激波向上游移动速度与对流速度相当,会导致前缘空化带断裂并脱落。与回射流相比,凝聚激波可能跨越空腔的整个高度,演化特征频率相对较低,而回射流为在片状空腔下面向上游运动的逆流薄层,诱导并形成大尺度脱落的空化云团[3]。
|
图 4 空化脱落回射流机制( |
|
图 5 空化结构演化凝聚激波机制( |
国内外学者针对不同简单构型的典型局部空化流动开展了大量的工作,下面将分别从实验和数值两个方面总结相关研究进展。
2.1 实验研究定量测量局部空化流动的流场信息十分困难,摄像或高速摄影是观察局部空化流动演化的主要手段。如Foeth和Terwisga[15]对三维扭曲水翼的高速摄影实验中发现了回射流展向分量诱导的三维云空化结构脱落现象。Callenaere[9]等在靠近薄板空化闭合的壁面上安装小凸起结构可以抑制云空化的发生,证明了回射流的存在。Wang等[16]通过高速摄影观察到典型的回射流诱导云空化脱落现象。最近,Simoa[3]、Wu[10]和Ganesh[17]等使用高速可视化技术和X射线光密度测定法,在较低空化数下,观察到楔形体空腔下游的空化云溃灭诱导了沿片状空腔传播的凝聚激波现象。
在流场定量测量方面,Laberteaux等[18]发展了一种多帧PIV系统,发现片空化尾部闭合区的流动呈现明显非定常性。Arndt等[19]则利用时间分辨PIV测量了NACA0015空化尾迹中的涡量场。Peng[20]等采用LDV测量了沿梢涡轨迹典型截面中的旋流场,并利用体PIV系统测量了速度和涡量分布。可见,受限于空化流动结构的非定常性、光学反射、示踪粒子跟随性等方面的制约,目前开展空化结构内的流场测量还存在较大困难。
人们还尝试采用图像法或直接测量的方法获得空化流动中汽(气)含率。很多学者研究了水中含气饱和度对空化初生的影响[21-22]。Stutz和Reboud[23]通过将光学探头放入楔型的非稳态空泡流中测量了时均汽含率。Evert等[24]使用X射线计算机断层摄影术来获得喷嘴中时均空隙率分布。Wan等[25]采用电阻探针系统对空化流动中汽含率进行了测量。此外,有关空化压力脉动和噪声的测量研究,将在空蚀实验部分介绍。
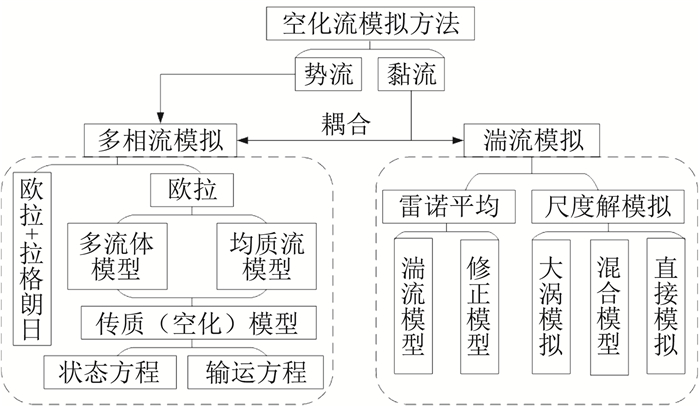
2.2 数值研究空化流是一种包含汽液相间质量传输的非定常多相湍流流动,因此空化流动的数值模拟非常复杂,将涉及多相流、相间质量输运(空化模型)和湍流模拟等方面。经过科技工作者多年的研究,基于不同的理论和假设,目前已发展了多种有效的空化流数值模拟方法,主要的方法概括如图 6所示。
|
图 6 空化流数值模拟方法 Fig.6 Simulation methods of cavitation flow |
研究者们采用上述空化流数值计算方法,针对不同的问题开展了大量的研究工作。
欧拉-拉格朗日是一种描述空泡流动中汽液两相流动的动力学与运动学耦合方法。Hsiao等[26]利用Level Set方法模拟宏观大尺度的空泡结构的界面,而低于网格分辨率的小尺度云泡则采用拉格朗日方法追踪,汽相的欧拉模拟和拉格朗日颗粒追踪可根据合适判据进行切换。Ghahramani等[27]在OpenFOAM中开发了一个欧拉-拉格朗日求解器,计算了水翼表面非稳态空化流动。近年来,一些学者尝试在欧拉框架下建立空泡流动的动力学与运动学统一模型。如Dumond[28]就通过耦合基于热力学状态方程的空化模型与随机场方法, 在计算宏观空化现象的同时,计算了流场中空泡直径的分布。De Giorgi[29]利用Sauer-Schnerr模型计算宏观空化流动,同时求解群体平衡方程研究空泡直径分布对空化流动演化的影响。
基于输运方程的欧拉均质流模拟方法是目前应用较为广泛的一种方法,其可以宏观上描述空化流动结构的非稳态过程。根据输运方程源项给定方式的不同可分为两类:一类是直接给定显式表达式描述汽泡的生成和扩散行为,如Merkle[30]、Kunz[31]等空化模型;另一类是以简化的Reyleigh-Plesset方程为基础给出表达式,一般包括局部压差作为驱动控制项,如Kubota[32]、Singhal[33]、Sauer & Schneer[34]和Zwart[35]等空化模型。质量输运方程模型由于存在相变率常数,实际空化流动模拟时一般需要标定。如Morgut[36]就以绕水翼空化流动的实验结果为参考,通过优化算法重新标定了Zwart模型、Singhal模型及Kunz模型中的常系数,提高了计算精度。Asnaghi等[37]则通过分析流动中的剪切力对相变的影响,定义了一种基于局部流动修正的相变率函数,该模型可以准确模拟扭曲水翼表面的压力分布,并成功捕捉由回射流引起的三维片空化到云空化的演化过程。
基于状态方程的空化模型可直接考虑流体的可压缩效应。一般假定混合介质的密度是压力的单值函数,汽液混合物的密度在两相过渡区内以一个大斜率曲线进行过渡。许多研究者基于正压状态假设提出了多种形式的空化模型,如Coutier-Delgosha和Reboud[38]采用水蒸汽的理想气体状态方程与液态水的Tait模型状态方程,混和区通过正弦函数连接水蒸汽与液态水的状态方程。Ventikos和Tzabiras[39]建立了一种考虑焓的空化模型,利用查表计算水汽混合物实验数据中密度与压力及焓的关系。Koukouvinis等[40]通过引入新的传质速率模型并考虑了混合物的可压缩效应,准确地预测了汽相结构的坍塌现象。Gnanaskandan等[41]采用可压缩数值计算方法对NACA66翼型的云空化不稳定性进行了分析,阐述了瞬态空化结构演变以及空腔溃灭引起的激波现象。虽然这种方法理论上可以直接描述空化流动结构的溃灭、压力波的生成和空间传播,但要准确描述压力波大小和传播则需要非常精细的时空尺度,需要消耗巨大的计算资源和时间。
由于大多数情况下非稳态片空化形成云空化的流动是湍流流动,因此湍流模型的选择也是准确把握空化流动的关键。研究者们越来越清晰地认识到雷诺平均方法具有强湍流黏性耗散性,逐渐尝试采用修正的湍流模型或直接采用含尺度解模型(如DES、LES、SAS、PANS、BES、FBM等)模拟非稳态的空化流动结构。如Ahn[42]等提出了一种修正湍流黏度模型用于预测空化流的方法,改进了两方程湍流模型由于湍流黏度过高而无法准确地预测非稳态云空化现象。Girimaji[43]等发展了一种基于k-ε模型的PANS方法,以较小的计算量提取湍流的重要非定常特征尺度。Roohi等[44]利用LES方法研究了Clark-Y水翼周围的云空化和超空化动力学。Chen等[45]使用可压缩的LES模型,捕捉了Delft扭曲水翼上的级联空化脱落结构。Ji等[46-47]用LES模拟了水翼上的空化-涡旋相互作用。由于亚格子应力和低阶格式数值截断误差相当,一些学者考虑直接利用数值格式误差的人工黏性代替亚格子应力模型,提出了一种隐式大涡模拟方法(ILES)。如Egerer等[48]应用ILES方法有效地模拟了湍流与空化结构的耦合效应。此外,一些学者认为空化流动的某些现象有时是由惯性力主导的,数值模拟时可以忽略流体黏性的影响。如Schmidt等[49]采用无黏可压缩的均质模型,研究了二维NACA0015翼型的云空化现象。Eskilsson等[50]采用可压缩的空化模型,比较了势流、雷诺平均和大涡模拟的结果,发现无黏模型同样可以捕捉凝聚激波现象。
3 空蚀风险预估 3.1 空蚀实验研究进展空蚀破坏过程一般可以分为潜伏孵化期、加速期、减速期和稳定破坏期,需要经历较长时间累积过程,但可通过在实验室模拟给定材料样本在空化工况下的响应,以缩短空蚀破坏的时间,并定量评估空蚀破坏程度。目前,这种加速空蚀实验测试装置主要包括超声振动杆、水射流、高速循环水槽和高速转盘等[51]。如Boyd等[52]通过超声换能器表面的振动将超声场引入到流体介质中,模拟了低频超声场中近壁空化泡的生长和溃灭现象,发现在空蚀形成的早期过程中通常可见从微米到毫米大小的个别凹坑;对于深坑或大面积侵蚀区域,主要是由集体大规模泡群溃灭造成的。Deplancke等[53]探索了聚合物涂层对表面空蚀的影响,发现采用高分子聚乙烯之类的涂层,会降低物体表面的损坏程度。
点蚀实验是一种描述空化溃灭强度或侵蚀性的方法。在空蚀早期潜伏孵化阶段,假设材料表面仅发生塑性变形形成点孔。随着表面分析技术的发展,人们可以定量测量点蚀位置的尺寸、深度和分布,以判断冲击载荷强弱。如Samir Chandra Roy和Jean-Pierre Franc[9]提出了一种基于测试目标材料本构属性和逆向有限元的方法以计算空蚀冲击载荷的思路,即通过样本材料的压缩实验、纳米压痕实验和霍普金森压杆实验,以确定材料本构模型参数;再根据点蚀实验获得的空蚀点变形参数,结合测得的目标材料本构,采用逆向有限元仿真获得冲击载荷的特征幅值和特征宽度。当样本材料从塑性变形阶段进入加速破坏阶段,通过测量样本材料质量损失随时间变化判断空蚀破坏程度。如Choi[54]针对不同的材料和工况条件,分别在超声振动杆和高压水射流装置中开展了空蚀实验,发现样本质量减少随空蚀时间变化曲线呈现典型的S形,且在选取特征长度和时间归一化后,不同的材料具有一致的标度率。
此外,采用压力传感器是一种评估冲击载荷的直接测量技术,但受限于压力传感器的尺寸、响应频率、量程、精度以及空蚀的随机性等,目前用于空蚀位置压力脉动的测量还存在困难[55]。PIV技术也可作为一种测量流场中瞬时空间压力分布的非侵入式方法。Liu[56]等利用双相机共四次曝光的PIV系统测量样本颗粒的加速度分布,假设不考虑黏性影响,根据测量的加速度场分布和已知边界参考压力,积分计算获得汽泡破碎过程的压力分布。最近,Sinibaldi等[57]尝试通过定制的光纤探针测量了激光诱导空泡溃灭过程引起的压力脉动。
工程上,目前主要采用油漆涂层破坏实验与图像拍摄相结合,定性评估实验模型表面的空化侵蚀程度,但这种方法无法揭示出更多侵蚀背后的物理机制。
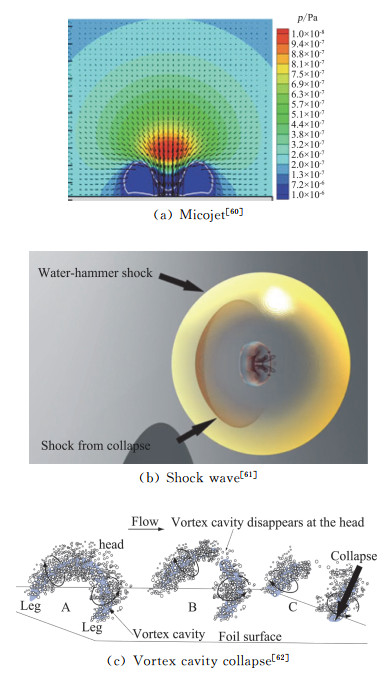
3.2 空蚀破坏的微观机理空蚀的核心事件是汽泡的溃灭,如图 7所示。早在1917年,Rayleigh指出汽泡破碎过程中产生的冲击波是空蚀主要原因[58]。Han等[59]实验观察了汽泡附近由于存在固体表面而引起流场的不对称性,导致塌陷时形成微射流现象,后来大量的实验证实了这一现象,并发现如果汽泡足够接近壁面,射流会直接撞击壁面,产生较大的水锤压力。围绕固体表面附近空泡溃灭产生冲击波和微射流现象,研究者们开展了大量的研究工作,进一步加深了对空蚀破坏的微观机理认识。
|
图 7 近壁空泡溃灭现象 Fig.7 Collapse of near-wall cavitation |
在微泡溃灭实验研究方面:早期实验一般采用火花放电方法产生汽泡。Tomita和Shima[63]测量到固体表面附近的空化汽泡破裂产生了几十兆帕的冲击压力,并发现壁面附近的汽泡会朝着壁面运动。随着科技的发展,目前采用非接触激光方法产生理想的球形汽泡,并结合高速摄影技术,在理解近壁汽泡破碎和空蚀方面取得了许多进展。如Brujan等[64]指出与固体表面直接接触的汽泡是造成局部侵蚀的最大原因。Zhang等[65]通过高速摄影研究了自由表面和刚性边界附近汽泡半径、汽泡脉动周期、射流速度和汽泡中心迁移的变化规律。
噪声和发光的测量也是研究空化汽泡溃灭过程的一种重要手段。Oweis[66]等指出如果汽泡被高度剪切变形,体积无法显著地实现加速变形,则基于球形汽泡动力学的传统方法会明显高估塌陷汽泡产生的噪声。Choi等[67]利用聚焦的激光脉冲在涡旋的中心产生一个核,对涡核内的单个空化汽泡的生长、分裂和溃灭过程进行了详细研究,发现在溃灭过程中产生的声脉冲比由于生长和分裂引起的噪声高出4个量级。Shamsborhan等[68]应用压力传感器和光学探头测量了高汽相体积分数空化流动中的声速,发现声速下降到了10 m/s以下,当地马赫数超过1.2。Supponen [69]等通过改变汽泡的大小、驱动压力和抛物线飞行重力的大小,测量了单个泡在均匀压力梯度下的变形和发光光谱,探索了从非球面到高度球形汽泡破裂过程。
在微泡溃灭数值研究方面:起初学者们主要基于势流理论的方法研究计算壁面附近汽泡的溃灭过程,后来逐渐开始考虑流体的黏性、表面张力、液体可压缩性效应和热效应等。但由于空泡溃灭物理过程的复杂性和时空尺度的广泛性,如何提高冲击波和界面处理的精度和计算稳定鲁棒性,研究者们开展了很多的工作。如Zhang[70]等假设汽相满足理想气体正压模型,液相为不可压流体,采用基于压力基的方法求解了多泡在压力驱动下的溃灭过程,得出中心汽泡的溃灭过程明显不同于单泡,存在总体溃灭延迟现象和后期加速现象。最近,Beig[61]采用高分辨率(9亿网格近似1/4球泡)的数值方法对单个汽泡在刚性表面附近溃灭过程进行分析,发现壁面的局部高温可能主要是由空泡溃灭冲击或水锤冲击引起的,何种机制主导取决于汽泡与壁面的初始距离以及驱动压力。Peng[71]等尝试使用格子Boltzmann方法模拟了两个相邻空化泡之间的弱、强相互作用以及空化泡群间的相互作用,发现外层汽泡对微射流具有屏蔽效应。
3.3 空蚀风险预估研究进展因空化流涉及的时、空尺度范围很广,而目前的计算能力不允许解析空化流中出现的所有尺度,因此构建大尺度空化结构的溃灭侵蚀预估模型是非常必要的。研究者们基于对不同空蚀机制的认识,开展了一些探索工作。其中,比较有代表性的是:Kato模型[72]假设云空化溃灭是发生空蚀的主要原因,指出只有在特定距离内才会对材料构成侵蚀威胁。由于该模型往往基于简化模型实验率定的关系式,还需要进一步的实验和理论支撑。Bark等[51]指出集聚空穴的溃灭对空蚀起主导作用,提供了依据图像观察分析空化结构的演化(发展、集聚和可能的微泡回弹)以评估侵蚀性的基本准则。但该方法只是基于宏观空化结构的实验观察或大尺度空穴的模拟结果进行定性分析,一般需要结合可视化分析、涂层测试以及可能补充高频区噪声测量进行综合评估。此外,由于该方法主要是基于对回弹腔的观测以估计溃灭强度,因此不适用于由不可压缩求解器获得的流场。Dular模型[73]假设壁面的空蚀是由近壁的单泡溃灭引起,此单泡的溃灭又主要是由云空泡溃灭产生的激波诱导,然后根据每个位置图像像素灰度水平评估空蚀的风险。该模型假设的空蚀物理过程与测定的空泡和泡云溃灭的声功率比较结果矛盾,且采用测量图像像素变化表征空化体积变化率不太恰当,主要原因是由于泡的自身尺寸存在差异也有可能引起图像灰度水平变化。
Hammitt [74]率先假设脱落空化结构中所含的势能与其初始体积以及环境压力与饱和蒸汽压之间的差成正比,一旦超过与材料属性相关的阈值,就会发生空化侵蚀破坏。自从空化结构势能的概念提出后,沿着该方向已经有了较多重要进展。Fortes Patella和Reboud[75]认为压力波的发射可能是由汽泡、涡空化结构溃灭以及微射流形成的,开发了一种基于汽泡破碎、压力波释放和邻近固壁之间能量平衡的方法来估计空化的侵蚀性。Franc和Michel[6]认为冲击波和微射流机制都会产生与一般金属屈服应力相当量级的高压脉冲;当云泡群破碎时,特定汽泡释放的压力波会增加相邻汽泡的溃灭速度,触发的能量级联机制使得对壁面施加侵蚀冲击的时间和幅度均会增强。Wang[76]等认为空腔溃灭期间的能量级联可简化为首先初始势能腔的能量转化为周围液体的动能,动能在空泡溃灭之前完成在空间的聚焦,最后在特定条件下瞬间转化成声能。最近,Schenke和Terwisga等[77]提出了一种空蚀冲击载荷预估模型,该模型的基本思想是假设空腔结构的初始势能在塌陷收缩时首先转化为界面附近的动能,该动能随着空腔体积的减小逐渐随界面向中心聚焦,当满足溃灭条件时,累积的能量以压力波能的方式释放出来,最后压力波能以辐射的方式投影到考察的壁面,从而获得对壁面的冲击载荷,但该模型忽略了能量在空间输运的耗散。能量传递过程参见图 8所示。

|
图 8 基于能量输运的空蚀冲击载荷预估模型 Fig.8 Cavitation erosion model based on energy transport |
可见,随着对微泡破碎过程的大量实验和数值研究的深入,人们逐渐意识到基于能量输运的空蚀模型由于无需考虑详细的溃灭过程,且建模的思想符合客观的空泡溃灭的物理过程,是非常适合用于建立空化结构破碎过程的能量传递和转换模型,以评估空化的侵蚀性。
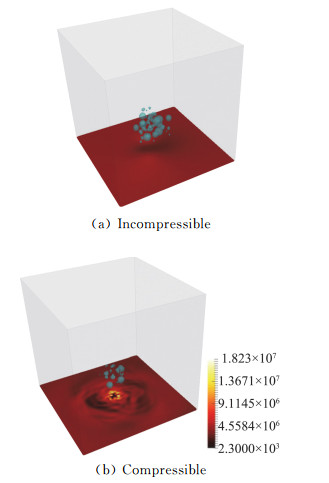
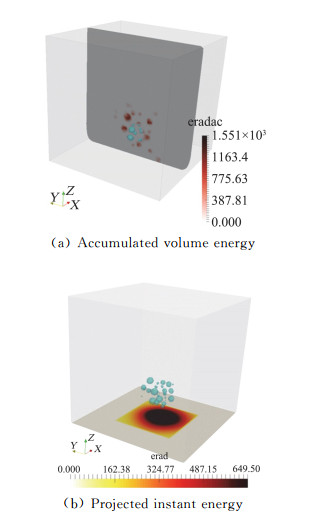
我们也基于能量输运、空间聚焦、辐射投射和壁面累积的思想,在空蚀方面也开展了一些研究工作。如图 9对比了采用不可压缩和可压缩方法计算空泡群溃灭时壁面压力分布,认为不可压方法仅可以捕捉到空泡溃灭引起的压力变化,但无法捕捉空泡溃灭压力大小和描述溃灭引起的压力波传播过程;而可压缩方法虽然可以详细描述空泡溃灭压力传播过程,但需要非常小的时空分辨率以提高捕捉的精度,而这需要非常巨大的计算资源。图 10为空泡溃灭过程空间能量的累积和空泡溃灭瞬间辐射能量对壁面的投影。针对NACA0015翼型由回射流主导的空化脱落工况,图 11为数值模拟得到的云空化脱落结构与实验结果对比。图 12为基于能量输运的空蚀风险预估区域与实验中翼型表面涂层破坏区域的对比。可见,虽然目前我们能够定性描述空泡能量输运过程和预估空蚀风险区域,但还存在很多问题值得深入研究:(1)初始势能还不能准确计算,因为能够有效驱动空腔溃灭的环境压力与流场中绝对局部压力是不同的,且在计算距离空腔溃灭中心一定距离处的局部峰值压力时,所得结果与数值计算采用的时空分辨率有很强的依赖关系,无法保证假设的初始势能在转化过程的守恒性;(2)不能真实反映空泡溃灭过程能量的时空输运机制,因为很多模型忽略了势能随着空化结构溃灭过程时空集聚效应;(3)尚不清楚初始势能的转化效率和溃灭能量向壁面输运的效率,缺乏从能量的观点出发,对空化结构溃灭能量的转化、占比和输运和耗散机制的系统研究;(4)空化结构溃灭能量释放的判据还不一致有效,因为适用于可压缩计算的压力判据不一定适用于不可压计算。
|
图 9 泡群溃灭过程壁面压力分布 Fig.9 Pressure distribution induced by bubbles collapse |
|
图 10 空泡溃灭过程空间能量累积和壁面投射 Fig.10 Accumulated volume energy and projected instant surface energy by bubbles collapse |

|
图 11 回射流机制诱导的翼型空化脱落和马蹄涡结构 Fig.11 Cavitation structures shedding by re-entrant jet and induced horse shore structure |

|
图 12 翼型表面空蚀破坏数值预测和实验对比 Fig.12 Damage pattern on the NACA0015 hydrofoil surface from experimental paint tests (a) and high erosion risk areaspredicted by simulation (b) |
1) 在空化结构溃灭和空蚀破坏机理探索方面,已有一些学者针对单泡或一定数量汽泡在近壁或自由面附近开展了研究工作,对空泡溃灭的发声、发热、发光效应和诱导的流场已有一定的认识。但仍有很多机理研究和数理建模工作需要深入开展,比如空泡、泡群和空化流动结构与湍流涡结构、边界层的相互作用,空化流动结构非稳定破碎和溃灭机制,空化结构溃灭时能量输运和转化机制,材料空蚀的微观过程及疲劳破坏等。
2) 在实验测试方面,已有很多学者做了大量的工作,如采用电火花放电、激光聚焦生成泡,研究泡的演化及与边界的相互作用;在水槽/水洞中针对一些简化模型,采用图像观测空化流结构的演化、测量空泡特征长度和体积分数,开展空化流速度场、压力场和声学信号的测量等;在模拟加速空蚀进程的实验测试装置中对样本材料开展点蚀实验,统计孔的数量、位置和样本材料的质量损失,测量孔的大小和孔深等;以及工程上利用表面油漆涂层定性评估实验模型表面的空化侵蚀程度等。但仍有很多工作需要深入开展,包括:三维空化流结构的空间重构;开发提高空化流场(速度、压力和体积分数等)测量精度和响应频率的测试技术;样本材料表面侵蚀力测量、统计和宏观建模;样本材料空蚀过程中微观结构演化测量等。
3) 在数值计算方面,鉴于空化流动包含非常宽泛的时空尺度,研究者们已经针对不同层级应用采用不同的数值计算方案,获得了一些与空化流动相互作用的流场信息,其中基于输运方程的欧拉均质流模型应用最为广泛,学者们也已采用一些包含更多物理信息的空化修正模型和更多尺度信息的湍流模型以提高数值计算的精度。为了能更加准确地获得空泡溃灭对壁面的冲击载荷,今后可尝试开展的研究包括:基于微观或介观模型的大规模泡群溃灭过程模拟;基于状态方程的空化流计算以考虑空化溃灭过程中压力波的传播;构建欧拉和拉格朗日耦合模型以考虑流动与空泡相互作用、空泡的生成和溃灭过程;开发空泡、空化结构溃灭与材料发生侵蚀的耦合计算方法;发展基于能量输运的空蚀风险预估模型;分析结构材料的空蚀破坏过程等。
| [1] |
XU C, WANG Y W, HUANG C G, et al. Cloud cavitating flow that surrounds a vertical hydrofoil near the free surface[J]. Journal of Fluids Engineering-Transactions of the Asme, 2017, 139(10). |
| [2] |
MIHATSCH M S, SCHMIDT S J, ADAMS N A. Cavitation erosion prediction based on analysis of flow dynamics and impact load spectra[J]. Physics of Fluids, 2015, 27(10). |
| [3] |
GANESH H, MÄKIHARJU S A, CECCIO S L. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities[J]. Journal of Fluid Mechanics, 2016, 802: 37-78. DOI:10.1017/jfm.2016.425 |
| [4] |
SCHMIDT S J, MIHATSCH M S, THALHAMER M, et al. Assessment of erosion sensitive areas via compressible simulation of unsteady cavitating flows[J]. Fluid Mechanics and its Applications, 2014, 106: 329-344. |
| [5] |
PELZ P F, KEIL T, GROß T F. The transition from sheet to cloud cavitation[J]. Journal of Fluid Mechanics, 2017, 817: 439-454. DOI:10.1017/jfm.2017.75 |
| [6] |
FRANC J P, MICHEL J M. Fundamentals of cavitation[J]. Fluid Mechanics and its Applications, 2005, 76(11): 1-46. |
| [7] |
LEROUX J B, COUTIER DELGOSHA O, ASTOLFI J A. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil[J]. Physics of Fluids, 2005, 17: 052101. DOI:10.1063/1.1865692 |
| [8] |
LEROUX J B, ASTOLFI J A, BILLARD J Y. An experimental study of unsteady partial cavitation[J]. Journal of Fluids Engineering, 2004, 126(1): 94-101. DOI:10.1115/1.1627835 |
| [9] |
CALLENAERE M, FRANC J P, MICHEL J M, et al. The cavitation instability induced by the development of a re-entrant jet[J]. Journal of Fluid Mechanics, 2001, 444: 223-256. DOI:10.1017/S0022112001005420 |
| [10] |
WU J, GANESH H, CECCIO S. Multimodal partial cavity shedding on a two-dimensional hydrofoil and its relation to the presence of bubbly shocks[J]. Experiments in Fluids, 2019, 60(4): 60. |
| [11] |
WU Q, HUANG B, WANG G Y, et al. The transient characteristics of cloud cavitating flow over a flexible hydrofoil[J]. International Journal of Multiphase Flow, 2017, 99. |
| [12] |
WU X C, WANG Y W, HUANG C G. Effect of mesh resolution on large eddy simulation of cloud cavitating flow around a three dimensional twisted hydrofoil[J]. European Journal of Mechanics-B/Fluids, 2016, 55: 229-240. DOI:10.1016/j.euromechflu.2015.09.011 |
| [13] |
PENG X X, JI B, CAO Y, et al. Combined experimental observation and numerical simulation of the cloud cavitation with U-type flow structures on hydrofoils[J]. International Journal of Multiphase Flow, 2016, 79: 10-22. DOI:10.1016/j.ijmultiphaseflow.2015.10.006 |
| [14] |
APAZIDIS N. Numerical investigation of shock induced bubble collapse in water[J]. Physics of Fluids, 2016, 28(4): 046101. DOI:10.1063/1.4944903 |
| [15] |
FOETH E J, VAN DOORNE C W H, VANTERWISGA T, et al. On the collapse structure of an attached cavity on a three-dimensional hydrofoil[J]. Journal of Fluids Engineering, 2008, 130(7): 071303. DOI:10.1115/1.2928345 |
| [16] |
YE B S, WANG Y W, HUANG C G. Numerical study of the pressure wave-induced shedding mechanism in the cavitating flow around an axisymmetric projectile via a compressible multiphase solver[J]. Ocean Engineering, 2019, 187: 106179. DOI:10.1016/j.oceaneng.2019.106179 |
| [17] |
MÄKIHARJU S A, GANESH H, CECCIO S L. The dynamics of partial cavity formation, shedding and the influence of dissolved and injected non-condensable gas[J]. Journal of Fluid Mechanics, 2017, 829: 420-458. DOI:10.1017/jfm.2017.569 |
| [18] |
LABERTEAUX K R, CECCIO S L. Partial cavity flows Part 2 cavities forming on test objects with spanwise variation[J]. Journal of Fluid Mechanics, 2001, 431: 43-63. DOI:10.1017/S0022112000002937 |
| [19] |
ARNDT R E A. Cavitation in vortical flows[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 143-175. |
| [20] |
PENG X X, XU L H, LIU Y W. Experimental measurement of tip vortex flow field with/without cavitation in an elliptic hydrofoil[J]. Journal of Hydrodynamics, Ser B, 2017, 29(6): 939-953. DOI:10.1016/S1001-6058(16)60808-9 |
| [21] |
GROß T, LUDWIG G, PELZ P F. Experimental and theoretical investigation of nucleation from wall-bounded nuclei in a laminar fflow[J]. Journal of Physics Conference Series, 2015, 656(1): 012034. |
| [22] |
GROß T F, LUDWIG G, PELZ P F. Experimental evidence of nucleation from wall-bounded nuclei in a laminar flow[J]. Journal of Physics Conference, 2015, 656(1): 012034. |
| [23] |
STUTZ B, REBOUD J L. Two-phase flow structure of sheet cavitation[J]. Physics of Fluids, 1997, 9(12): 3678-3686. DOI:10.1063/1.869505 |
| [24] |
EVERT S J, ROBERT W, POELMAA M C. Void fraction measurements in partial cavitation regimes by X-ray computed tomography[J]. International Journal of Multiphase Flow, 2019, 120: 103085. DOI:10.1016/j.ijmultiphaseflow.2019.103085 |
| [25] |
WAN C R, WANG B L, WANG Q, et al. Probing and imaging of vapor-water mixture properties inside partial/cloud cavitating flows[J]. Journal of Fluids Engineering, 2017, 139(3): 031303. DOI:10.1115/1.4035013 |
| [26] |
HSIAO C T, CHAHINE G L. Scaling of tip vortex cavitation inception noise with a bubble dynamics model accounting for nuclei size distribution[J]. Journal of Fluids Engineering, 2005, 127(1): 55-65. DOI:10.1115/1.1852476 |
| [27] |
GHAHRAMANI E, ARABNEJAD M H, BENSOW R. A hybrid model for simulation of cavitating flows[C]//12th OpenFOAM© Workshop, 2017.
|
| [28] |
DUMOND J, MAGAGNATO F, CLASS A. Stochastic-field cavitation model[J]. Physics of Fluids, 2013, 25(7): 94-98. |
| [29] |
MARIA GRAZIA DE GIORGI, ANTONIO FICARELLA, DONATO FONTANAROSA. Impact of population balance modeling on the prediction of cryogenic cavitation in aerospace propulsion systems[C]//2018 Joint Propulsion Conference, Cincinnati: 2018.
|
| [30] |
MERKLE C L, FENG J Z, BUELO P E O. Computational modeling of the dynamics of sheet cavitation[C]//In Proceedings of the 3rd International Symposium on Cavitation, France: 1998: 307-311.
|
| [31] |
KUNZ R F, BOGER D A, STINEBRING D R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]. Computers & Fluids, 2000, 29(8): 850-872. |
| [32] |
KUBOTA A, KATO H, YAMAGUCHI H A. New modeling of cavitating flows:a numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of Fluid Mechanics, 1992, 240: 59-96. DOI:10.1017/S002211209200003X |
| [33] |
SINGHAL A K, ATHAVALE M M, LI H, et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering, 2002, 124(3): 617-624. DOI:10.1115/1.1486223 |
| [34] |
SAUER J, SCHNERR G H. Unsteady cavitating flow-a new cavitation model based on modified front capturing method and bubble dynamics[C]//Proceedings of 2000 ASME Fluid Engineering Summer Conference, American Society of Mechanical Engineers, 2000: 11-15.
|
| [35] |
ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]//5th International Conference on Multiphase Flow, Japan: 2004.
|
| [36] |
MORGUT M, NOBILE E. Numerical predictions of cavitating flow around model scale propellers by CFD and advanced model calibration[J]. International Journal of Rotating Machinery, 2012, 1-11. |
| [37] |
ASNAGHI A, FEYMARK A, BENSOW R E. Improvement of cavitation mass transfer modeling based on local flow properties[J]. International Journal of Multiphase Flow, 2017, 93: 142-157. DOI:10.1016/j.ijmultiphaseflow.2017.04.005 |
| [38] |
COUTIER-DELGOSHA O, REBOUD J L, et al. Numerical simulation of the unsteady behaviour of cavitating flows[J]. International Journal for Numerical Methods in Fluids, 2003, 42(5): 519-530. |
| [39] |
VENTIKOS Y, TZABIRAS G. A numerical method for the simulation of steady and unsteady cavitating flows[J]. Computers & Fluids, 2000, 29(1): 63-88. |
| [40] |
KOUKOUVINIS P, MITROGLOU N, GAVAISES M, et al. Quantitative predictions of cavitation presence and erosion-prone locations in a high-pressure cavitation test rig[J]. Journal of Fluid Mechanics, 2017, 819: 21-57. DOI:10.1017/jfm.2017.156 |
| [41] |
GNANASKANDAN A, MAHESH K. Large eddy simulation of the transition from sheet to cloud cavitation over a wedge[J]. International Journal of Multiphase Flow, 2016(83): 86-102. |
| [42] |
AHN S H, XIAO Y X, WANG Z W, et al. Unsteady prediction of cavitating flow around a three dimensional hydrofoil by using a modified RNG k-ε model[J]. Ocean Engineering, 2018, 158: 275-285. DOI:10.1016/j.oceaneng.2018.04.005 |
| [43] |
GIRIMAJI, SHARATH S. Partially-averaged Navier-Stokes model for turbulence:a reynolds-averaged Navier-Stokes to direct numerical simulation bridging method[J]. Journal of Applied Mechanics, 2006, 73(3): 413-421. DOI:10.1115/1.2151207 |
| [44] |
ROOHI E, ZAHIRI A P, PASSANDIDEH-FARD M. Numerical simulation of cavitation around a two-dimensional hydrofoil using VOF method and LES turbulence model[J]. Applied Mathematical Modelling, 2013, 37(9): 6469-6488. DOI:10.1016/j.apm.2012.09.002 |
| [45] |
CHEN Y, CHEN X, LI J, et al. Large eddy simulation and investigation on the flow structure of the cascading cavitation shedding regime around 3D twisted hydrofoil[J]. Ocean Engineering, 2017, 129: 1-19. DOI:10.1016/j.oceaneng.2016.11.012 |
| [46] |
JI B, LUO X W, ARNDT R E A, et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil[J]. International Journal of Multiphase Flow, 2015, 68: 121-134. DOI:10.1016/j.ijmultiphaseflow.2014.10.008 |
| [47] |
LONG X P, CHENG H Y, JI B, et al. Large eddy simulation and Euler-lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil[J]. International Journal of Multiphase Flow, 2018, 100: 41-56. DOI:10.1016/j.ijmultiphaseflow.2017.12.002 |
| [48] |
EGERER C P, SCHMIDT S J, HICKEL S, et al. Efficient implicit LES method for the simulation of turbulent cavitating flows[J]. Journal of Computational Physics, 2016, 316. |
| [49] |
SCHNERRA G H, SEZAL I H, J S S. Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics[J]. Physics of Fluids, 2008, 20(4): 040703. DOI:10.1063/1.2911039 |
| [50] |
ESKILSSON C, BENSOW R E. A compressible model for cavitating flow: comparison between Euler, RANS and LES simulations[C]//29th Symposium on Naval Hydrodynamics, Gothenburg: Chalmers University of Technology, 2012: 1-13.
|
| [51] |
CHAHINE G L, KIM K H, FRANC J P, et al. Advanced experimental and numerical techniques for cavitation erosion prediction[J]. Fluid Mechanics and its Applications, 2014, 106. |
| [52] |
BOYD B, BECKER S. Numerical modeling of the acoustically driven growth and collapse of a cavitation bubble near a wall[J]. Physics of Fluids, 2019, 31(3): 032102. DOI:10.1063/1.5084729 |
| [53] |
TIANA DEPLANCKE, OLIVIER LAME, JEAN-YVES CAVAILLE, et al. Outstanding cavitation erosion resistance of Ultra High Molecular Weight Polyethylene (UHMWPE) coatings[J]. Wear, 2015, 328-329: 301-308. |
| [54] |
CHOI J K, ARVIND J, CHAHINE G L. Scaling of cavitation erosion progression with cavitation intensity and cavitation source[J]. 2012, 278-279: 53-61.
|
| [55] |
FRANC J P, RIONDET M, KARIMI A, et al. Impact load measurements in an erosive cavitating flow[J]. Journal of Fluids Engineering, 2011, 133(12): 1915-1920. |
| [56] |
LIU H L, LIU D X, WANG Y, et al. Experimental investigation and numerical analysis of unsteady attached sheet cavitating flows in a centrifugal pump[J]. Journal of Hydrodynamics, Ser B, 2013, 25(3): 370-378. DOI:10.1016/S1001-6058(11)60375-3 |
| [57] |
SINIBALDI G, OCCHICONE A, PEREIRA F A, et al. Laser induced cavitation:Plasma generation and breakdown shockwave[J]. Physics of Fluids, 2019, 31: 103302. DOI:10.1063/1.5119794 |
| [58] |
RAYLEIGH L. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine, 1917, 34(200): 94-98. |
| [59] |
HAN R, ZHANG A M, LI S, et al. Experimental and numerical study of the effects of a wall on the coalescence and collapse of bubble pairs[J]. Physics of Fluids, 2018, 30(4): 042107. DOI:10.1063/1.5024946 |
| [60] |
CHAHINE G L, HSIAO C T. Modelling cavitation erosion using fluid-material interaction simulations[J]. Interface Focus, 2015, 5(5): 20150016. DOI:10.1098/rsfs.2015.0016 |
| [61] |
BEIG S A, ABOULHASANZADEH B, JOHNSEN E. Temperatures produced by inertially collapsing bubbles near rigid surfaces[J]. Journal of Fluid Mechanics, 2018, 852: 105-125. DOI:10.1017/jfm.2018.525 |
| [62] |
KAWANAMI Y, KATO H, YAMAGUCHI H. Inner structure of cloud cavity on a foil section[J]. JSME International Journal Series B, 2002, 45(3): 655-661. DOI:10.1299/jsmeb.45.655 |
| [63] |
TOMITA Y, SHIMA A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse[J]. Journal of Fluid Mechanics, 1986, 169: 535-564. DOI:10.1017/S0022112086000745 |
| [64] |
BRUJAN E A, IKEDA T, YOSHINAKA K, et al. The final stage of the collapse of a cloud of bubbles close to a rigid boundary[J]. Ultrasonics Sonochemistry, 2011, 18(1): 59-64. DOI:10.1016/j.ultsonch.2010.07.004 |
| [65] |
ZHANG S, ZHANG A M, WANG S P, et al. Dynamic characteristics of large scale spark bubbles close to different boundaries[J]. Physics of Fluids, 2017, 29(9): 092107. DOI:10.1063/1.4986821 |
| [66] |
OWEIS G F, CHOI J, CECCIO S L. Dynamics and noise emission of laser induced bubbles in a vortical flow field[J]. Journal of the Acoustical Society of America, 2004, 115(3): 1049. DOI:10.1121/1.1646402 |
| [67] |
CHOI J, CECCIO S L. Dynamics and noise emission of vortex cavitation bubbles[J]. Journal of Fluid Mechanics, 2007, 575: 1-26. DOI:10.1017/S0022112006003776 |
| [68] |
HIVA SHAMSBORHAN, OLIVIER COUTIER-DELGOSHA, GUY CAIGNAERT, et al. Experimental determination of the speed of sound in cavitating flows[J]. Experiments in Fluids, 2010, 49(6): 1359-1373. DOI:10.1007/s00348-010-0880-6 |
| [69] |
SUPPONEN O, OBRESCHKOW D, KOBEL P, et al. Luminescence from cavitation bubbles deformed in uniform pressure gradients[J]. Physical Review E, 2017, 96(3): 033114. DOI:10.1103/PhysRevE.96.033114 |
| [70] |
张凌新, 闻仲卿, 邵雪明. 多泡相互作用对气泡溃灭的影响[J]. 力学学报, 2013, 45(6): 861-867. ZHANG L X, WEN Z Q, SHAO X M. Investigation of bubble-bubble interaction effect during the collapse of multi-bubble system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 861-867. (in Chinese) |
| [71] |
PENG C, TIAN S C, LI G S, et al. Single-component multiphase lattice Boltzmann simulation of free bubble and crevice heterogeneous cavitation nucleation[J]. Physical Review E, 2018, 98(2): 023305. DOI:10.1103/PhysRevE.98.023305 |
| [72] |
KATO H, KONNO A, MAEDA M, et al. Possibility of quantitative prediction of cavitation erosion without model test[J]. 1996, 118(3): 617-633.
|
| [73] |
DULAR M, COUTIER-DELGOSHA O. Numerical modelling of cavitation erosion[J]. International Journal for Numerical Methods in Fluids, 2009, 61(12): 1388-1410. DOI:10.1002/fld.2003 |
| [74] |
HAMMITT F G. Cavitation and multiphases flow phenomena[M]. New York: McGraw-Hill International, 1980: 423.
|
| [75] |
FORTES-PATELLA R, CHALLIER G, REBOUD J L, et al. Energy balance in cavitation erosion:from bubble collapse to indentation of material surface[J]. Journal of Fluids Engineering-Transactions of the Asme, 2013, 135(1): 011303. DOI:10.1115/1.4023076 |
| [76] |
WANG Y C, BRENNEN C E. Numerical computation of shock waves in a spherical cloud of cavitation bubbles[J]. Journal of Fluids Engineering, 1999, 121(4): 872-880. DOI:10.1115/1.2823549 |
| [77] |
SCHENKE, VAN TERWISGA S, TOM J C. An energy conservative method to predict the erosive aggressiveness of collapsing cavitating structures and cavitating flows from numerical simulations[J]. International Journal of Multiphase Flow, 2019, 111: 200-218. DOI:10.1016/j.ijmultiphaseflow.2018.11.016 |
| [78] |
MARTIJN VAN RIJSBERGEN, FOETH E J, FITZSIMMONS P. High-speed video observations and acoustic-impact measurements on a NACA 0015 foil[C]//Proceedings of the 8th International Symposium on Cavitation, Singapore: 2012.
|
 2020, Vol. 38
2020, Vol. 38