当液相介质中局部压力降至其饱和蒸气压以下时,液相中将产生大量充满气体和蒸汽的空穴,这些空穴是一些单个的球形空泡,或是多个空泡形成的空泡群以及外形不规则的空腔。这是一个复杂、不稳定、多尺度和多相的流动现象,即空化[1-2]。从力学的角度上看,空化是液体在足够大的应力作用下发生的一种断裂现象,因此空化亦可被认为是液体的一种力学破坏形式[3]。空化流动是高速水动力学的核心关键问题,具有明显的非定常特性,同时包含了多种复杂流动现象,如多相流、湍流和可压缩流动等[4],这也使得空化成为各种工程应用上一个极大的挑战。
空化涉及国民经济发展和国家安全等工程领域关键技术的突破,空化的发生会引起压力脉动、负载突变,改变系统性能、破坏过流部件表面和产生振动噪声,严重影响机械系统的高效安全运行。在水力机械领域,空化引起的振动是影响水电机组和大型排灌泵站安全运行的主要问题[5-6],梢涡空化是限制螺旋桨等水下推进装置高效航行的根本原因[7]。在水中兵器领域,为提高鱼雷和新型潜艇的综合性能,亟需解决空泡噪声这一关键问题[8]。在水下发射领域,潜射导弹在出水过程中,受到复杂水环境的影响,其运动速度和周围流场参数不断变化,弹体表面形成具有强非定常特性的空穴,伴随着空穴的发展、断裂和脱落,弹体所受载荷十分复杂[9]。在航空航天领域,需采用具有高功率密度的高转速涡轮泵输送液体燃料,提升涡轮泵及其前装诱导轮的空化性能对保障大功率火箭发动机安全具有重大意义[10]。另一方面,超空泡减阻技术在水中兵器领域的应用极大地改变了海洋作战局面,如超空泡鱼雷减阻技术,使鱼雷在高速运行过程中产生超空泡并包裹弹体,从而降低鱼雷摩擦阻力[11-12]。
综上所述,考虑水力机械内部的振动和噪声等问题、航行体和水下兵器的创新研制和隐蔽性问题以及其他领域的关键技术问题,对空化现象的研究具有重要的理论和工程应用价值。本文首先综述了空化流动现象的实验和数值研究现状,然后进一步对空化诱导结构振动特性及其与结构动态响应的耦合作用研究进行了综述,并对非定常空化流动及其诱导振动特性研究的发展趋势进行了展望。
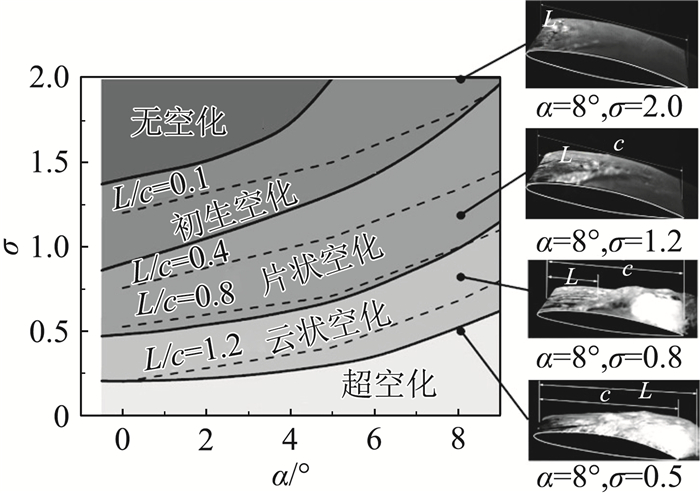
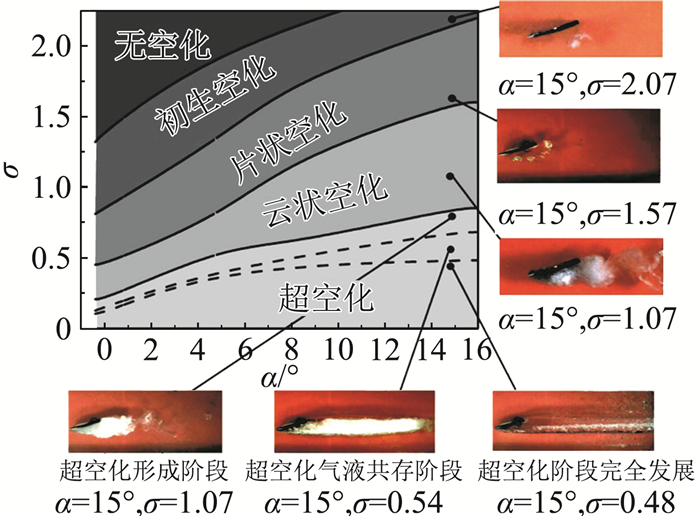
1 空化流动的研究现状 1.1 空化流动的试验研究实验研究一直是人们探索复杂空化现象与空化流动机理的基本方法。1896年Parsons建立第一个空化水洞,开始进行螺旋桨空化现象的观察研究[13]。Knapp[14]基于大量的空化实验观测,根据空化发生部位和动力特性将空化分为游移空化、固定空化、旋涡空化和振荡空化。Brennen[1]等按空化的发展阶段特征将其划分为初生空化、片状空化、云状空化和超空化。图 1给出了不同水翼迎角和流场空化数条件下,绕NACA66水翼的典型空化形态及平均空泡长度。初生空化阶段,水翼前缘吸力面开始出现游离状空泡,其发生和发展过程具有一定随机性。随着空化数的减小,水翼吸力面空泡区域增大,形成了相对稳定的附着型空穴,同时空穴尾部存在小尺度空泡的快速形成与脱落。当空化数进一步降低时,空化发展至云状空化阶段,附着型空穴断裂,大尺度云状空泡团形成并发生周期性脱落和溃灭现象。继续降低空化数时,绕水翼空化流动由云状空化发展至超空化阶段,空泡覆盖了整个翼型并保持较稳定的状态。在此基础上,Tulin[15]总结了超空化水翼的翼型,建立了超空化的理论基础,提出了一种Hydronautics低阻力超空化水翼。与一般水翼相比,Hydronautics超空化水翼是一种易于超空化产生的特殊的水翼,两种水翼的前后缘形状正好相反,Hydronautics超空化水翼的迎流面为一尖角,尾部为一钝剖面。Li等[16]采用高速全流场显示技术观测了绕Hydronautics超空化水翼的空化流动,如图 2所示。Zhang等[17]进一步采用欧拉和拉格朗日方法对空化流场旋涡结构进行了分析。对于一般绕水翼的片状空化,其头部即片状空穴前缘一般附着在翼型吸力面壁面上,而且位置基本不随时间的变化而变化。而由于具有尖锐前缘的超空化水翼为不良绕流体,实验中基本没有观察到此阶段空化的前缘附着现象,而是在尾流中出现两旋转方向相反的旋涡,上涡沿顺时针旋转,下涡为逆时针旋转。随着空化数的降低,空化涡街现象趋于明显。当空化数降至σ=0.87时,出现明显的云状空化。同一般水翼的附着型空化一样,空化开始充满整个吸力面,并形成周期性的空化云脱落。不同的是,其后部仍有上下涡配对之后形成的脱落。随着空化数的进一步降低形成超空化时,空泡的发展经历空穴形成、两相共存和完全发展阶段。
|
图 1 典型工况下绕NACA66水翼典型空化形态及其平均空泡长度[18] Fig.1 Cavity patterns and average cavity length for typical cavitation around NACA66 hydrofoil[18] |
|
图 2 典型工况下绕Hydronautics超空化水翼典型空化形态及其平均空泡长度[18] Fig.2 Cavity patterns and average cavity length for typical cavitation around Tulin hydrofoil[18] |
随着水洞、水池实验研究的大量开展以及各种先进测试设备与技术的出现,人们对空化现象的认识不断深入。Arakeri和Acosta[19]、Katz[20]分别基于纹影法和全息显示技术研究了绕回转体流动分离与初生空化流动,发现了空化初生与边界层流动的相互关系,结果表明空化发生在流动分离区域,且湍流再附着区域对空化初生有着较大影响。Guennoun等[21]采用微型压力传感器和高速摄像机同步测量技术研究了绕水翼泡状空化流场特性,揭示了游离型空泡的形成机理和周期性水动力特性。Kubota[22]采用高速摄像机和激光多普勒测速仪(Laser Doppler Velocimetry,LDV)观测了绕水翼云状空化流场结构的演变情况,基于条件采样技术发现了最大涡量分布与空化核的关系,初步探究了云状空化流动中空化与旋涡结构的相互作用关系。Liu等[23]利用氙气闪光灯和高速摄像机对绕二维Clark-Y型水翼空化流动进行了观测,并利用激光多普勒测速技术对流场空泡内外区域的液相速度进行了测量。结果表明,空泡内部的平均速度分布与边界层内单向流动的平均速度分布基本一致,但水翼近壁区域的反向射流具有强烈的波动性和间歇性。Stutz和Rebound[24-25]发展了一种双探针光学探头以测量流场空泡内部含气量、流速和空泡尺寸等空化流动参数,并应用此技术对文丘里管内不同空化数和雷诺数条件下的空化流动进行了研究,进一步阐明了空泡发展、近壁面反向射流和大尺度空泡团脱落的流动机理。Arndt[26]等应用数字式粒子图像测速(DPIV)技术,对绕NACA0015水翼单相流动的尾迹流域进行了测量,研究表明空化的发生显著改变流场结构,水翼尾缘低速尾迹区域明显扩大。张博[27]等采用动态应变仪与箔式中温电阻应变片组成测量电桥测量了空化流场中不同空化阶段水翼所受的升阻力,揭示了亚空化流动下的不同空化阶段的非定常水动力特性及其与空穴形态间的关系。Matthieu等[28]利用三维粒子测速技术(Stereo Particle Image Velocimetry,SPIV)对不同流速、迎角和间隙宽度工况下水翼下游三个平面内的来流速度场进行了测量,研究了不同来流工况的间隙泄漏涡结构特征,阐明了特定间隙宽度条件下的最大涡流强度及间隙涡空化流动机理。Che[29]用高速摄像机和压力测量装置同步观测了水翼在过渡空穴振荡时期空穴脱落和回射流现象。
综上所述, 由于非定常空化流动中水-汽自由表面的干扰和反光等问题,传统的实验观测仍局限于对空泡外围及尾流的观测。Wang等[30]基于高速全流场显示和瞬时粒子图像测量TR-PIV系统,发展了通气空泡内部流动结构的精细化测量技术,实现了对通气空泡流型、复杂湍流旋涡结构、运动特性的准确观测与测量。近年来,高时间分辨率的X光密度测量以及X光诱导的粒子相关测速技术已揭开了空泡内部流场结构测量的序幕,并已成为空化流动实验研究的主要发展方向。Ganesh[31]针对高雷诺数空化流场的瞬态密度测量,发展了一种采样频率在1kHz以上的X射线速度测量装置,获得了楔形体片状空泡内水蒸气体积分数的时空变化。
基于试验技术的综合应用,人们开始逐渐关注空穴的断裂及空泡的脱落行为及其对空化水动力特性的影响。Kubota等[22]阐明了空化的微观结构,确定了在空化的形成和发展过程中包含许多微小的气泡集中涡,并提出了近壁反向射流的存在是空穴尾部不稳定的原因。Leroux等[32-33]基于实验观测和压力测量等手段研究了非定常空化水动力稳定特性对空化发展及空泡断裂脱落现象的影响,揭示了不同来流迎角条件下两种不同的非定常空化流动水动力特性。Kjeldsen等[34]对空泡云团脱落和溃灭过程中的参数进行傅立叶变换分析,得到其频谱相关特性。张博等[35]通过测量水翼表面压力分布揭示了空穴在生长、断裂、脱落过程的非定常水动力特性,综合分析了水翼动力特性与空穴形态的内在关系。Kawanami等[36]应用高速摄像技术和压力传感器测压技术研究了云状空泡的非定常脱落机制,认为在云状空化的非定常发展过程中,反向射流引发空泡的断裂与脱落,并发现在附着空穴尾部区域放置障碍物可以抑制反向射流和大尺度云状空泡团的形成,从而大幅减小水翼结构的绕流阻力和流动噪声。图 3给出了云状空化反向射流及大尺度空泡团脱落现象。如图 3(a)所示,局部片状空化从水翼的前缘发展到x/c=0.5的位置。在空泡发展过程中,空泡在尾缘处形成回射流,并从空泡尾缘两侧向空泡前缘中心移动。De Lange[37]和Franc[38]研究指出,根据空泡边界动量守恒,回射流有垂直和沿空泡闭合线两个分量。如图 3(b)所示,随着云状空泡的脱落,这两束向上的流动相互碰撞,切断了空泡的下游部分,并在剩余的空泡后缘形成一个楔形孔。云状空泡继续向下游移动,最终溃灭,如图 3(c)所示。Yang等[39]研究表明,反向射流和水翼吸力面的展向速度是导致云状空化三维效应的主要因素。Foeth[40]指出,由于回射流对空泡脱落的重要影响,需要精确模拟回射流的方向和动量。
1.2 空化流动的数值模拟研究随着计算技术的发展,数值模拟成为空化研究的另一重要手段。最早的空化数值计算基于自由流线理论并应用速度图法进行求解,假设空泡表面为自由流线,将空泡内部压力视为常数,在求解过程采用空穴的闭合模型[42-43]。但该方法由于忽略空穴内部的流动,无法准确获得非定常空化流动数值计算结果。随后,大量学者针对空化流动的数值模拟开展研究,主要可分为两大类,一类是界面追踪法,另一类是基于Navier-Stokes(N-S)方程的数值计算求解法。
界面追踪法假设空穴内部压力恒等于汽化压力,在汽液两相界面应用运动学和动力学方程的边界条件,迭代计算获得界面位置。其中,边界元计算方法应用较为广泛[44-45],通常应用于定常附着型空化和超空化的流动计算,可以较好地预测空化流动的整体行为,但对空化形态的非定常变化和三维界面的追踪模拟准确度不高。
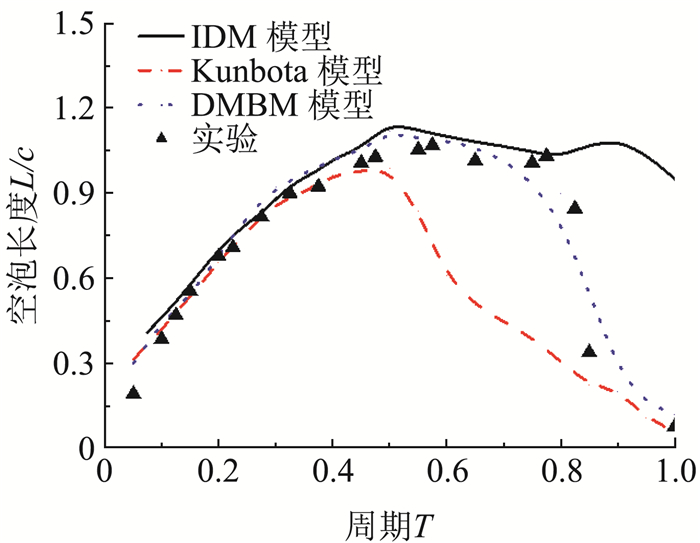
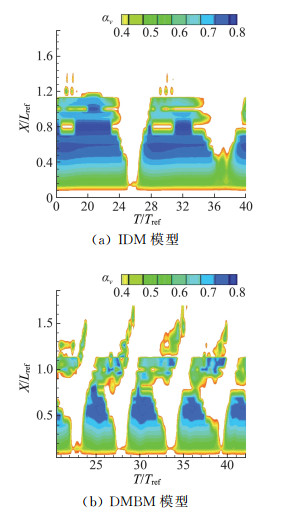
基于N-S方程的数值计算求解法,需要结合多相流模型、湍流模型和空化模型。在多相流模型的研究中,目前广泛应用的均相流模型认为整个空化流场由可变密度的单一流质组成,应用均质平衡流模型(HEM)建立一组偏微分方程来控制流体运动和状态。Delannoy[46]最早提出基于压力-混合密度耦合法对可变密度场进行定义,该方法对空穴附近的流场有一定效果,但由于忽略了气液相间输运方程,仅适于计算较稳定的附着型空化流场,无法捕捉空化流场中的复杂非定常湍流结构[47-48]。基于此,另一种处理方法是采用基于质量传输方程的模型来求解密度场,通过额外的传输模型求解流场中的汽相或液相的百分比,可以较好地模拟惯性力对空穴的生长、附着和发展的影响。考虑到空化流动的动力学特性、频繁的相间交换等,Rayleigh[49]早在1917年比较系统地提出了空化理论,建立了在无限理想不可压缩流体中球形空泡轴对称溃灭的控制方程。Plesset[50]进一步研究提出了Rayleigh-Plesset方程,形成了空泡动力学理论基础。再此基础上,Kubota等[51]通过建立质量传输与压强之间的关系提出了基于空泡动力学的质量传输方程,较好地描述了空泡生长和发展过程中的体积变化。国内外研究学者基于不同的假设,通过物理现象观察或经验方程式确定相应的蒸发与凝结系数控制相变化和传输强度,从而发展出不同的空化模型。大量学者基于Rayleigh-Plesset方程建立了表征质量传输与压强变化关系的空化输运方程,即相间传输率正比于饱和蒸汽压与当地压力之差的平方根。其中,Zwart[52]模型根据经验将空泡半径、空化核子等参数取为常数;Schnerr和Sauer[53]在模型中通过引入汽核体积分数考虑了单位体积内空化核子随含气率的变化;Singhal[54]综合考虑了流场流动特性(表面张力、湍流脉动等)对汽液相间质量传输过程的影响,提出了全空化模型;Gerber[55]、Frobenius[56]、牟斌等[57]也在此基础上结合经验公式提出了相应的空化模型。此外,Merkle[58]、Kunz[59]等基于量纲分析和实验现象观测结果推导建立了空化输运方程,结果表明相间质量传输率正比于饱和蒸汽压与当地压力之差的绝对值,并通过添加源项调节汽液相间传输,实现了水下航行体自然空化与通气超空化流动的数值求解。在此基础上,Senocak和Shyy[60-61]提出了基于空泡界面动力学的质量传输模型(Interfacial Dynamic Model,IDM),从理论上消除了Merkle和Kunz模型中经验系数对空化模型的影响,具有较高的精度。黄彪等[62]基于上述模型发展了一种基于混合密度分域的空化模型(Density modify based cavitation model,DMBM),在含汽量较大的区域内采用空泡界面动力学质量传输空化模型,以模拟空穴内部、汽液交界面的演变过程,而在含汽量较小的区域采用Kubota空化模型,以捕捉空泡团的旋涡脱落现象。图 4和图 5给出了不同模型预测的非定常空穴长度随时间的演化情况,可以看出Kubota模型过早预测了空穴的断裂,这是由于Kubota空化模型根据空泡动力学方程计算单个气泡体积的扩散速度,假设空泡是均匀的径向发展且不会相互作用。附着型空穴的发展和回缩、断裂过程可以视为无数空泡体积变化的整体行为,对空穴内部的流场结构的特征差异不能很好的体现。采用IDM空化模型所预测的附着空穴长度则一直比较稳定,相较而言,DMBM模型对空穴发展的两个典型阶段均有比较客观的描述,该模型结合了IDM与Kubota空化模型在模拟云状空化流动现象的优点,准确地模拟出附着在翼型前端稳定的含气量相对较大的空穴与翼型尾部含气量相对较低的不稳定的汽液两相区,两者动态界面非常明显;此外,DMBM空化模型合理地预测了空泡脱落时刻翼型尾部的不稳定脉动区,当反向射流发展到水翼前缘位置时,会切断附着型空穴,导致空穴长度的骤降,与实验观察有较好的一致性。
|
图 4 不同空化模型预测附着空穴长度随时间的变化过程(σ=0.80, α=8°, Re=7×105)[62] Fig.4 Evolution of attached cavity length predicted by different cavitation models (σ=0.80, α=8°, Re=7×105)[62] |
|
图 5 不同空化模型预测得到的云状空化水汽含量时空变化云图(σ=0.80, α=8°, Re=7×105)[62] Fig.5 Space-time evolution of water vapor volume fraction predicted by different cavitation models (σ=0.80, α=8°, Re=7×105)[62] |
空化流动几乎包含了所有复杂的流动现象,尤其是云状空泡团发展过程的强烈不稳定行为,往往与流场旋涡结构的运动密切相关。因此,对湍流的数值模拟是建立非定常空化流动数值计算方法的关键。目前对湍流的数值模拟主要有雷诺时均化湍流模型(Reynolds-Averaged Navier-Stokes,RANS)和大涡模拟(Large Eddy Simulations,LES)。
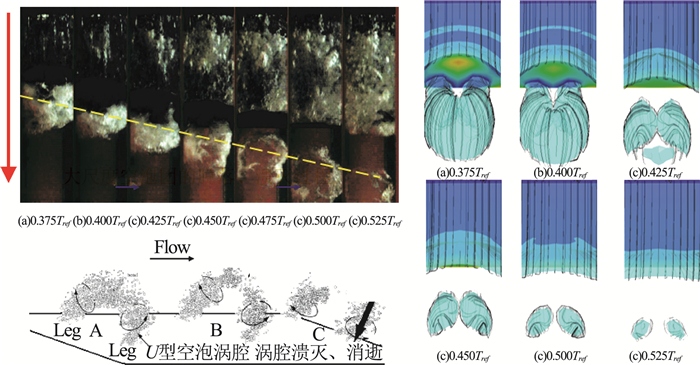
长期以来,建立在雷诺时均化Navier-Stokes方程(RANS)基础上的数值模拟方法是空化流动数值模拟的主要选择,湍流模型在很大程度上影响着对空化流动的精确预测。Launder和Spalding提出的标准k-ε模型[63]定义了涡黏系数与湍动能和湍动能耗散的关系,其稳定性、经济性、适用性以及一定的精度使之在目前的工业流动和热传递模拟中得到广泛的应用,但是该模型在处理多重湍流尺度决定的动力流动结构方面的缺陷使其在非定常流动计算中的应用受到了很大的限制。为了解决标准RANS模型在空化流动中对黏性系数过度预测的问题,Kinzel[64]采用DES模型对绕三维轴对称回转体的空化绕流现象进行了模拟,并与采用标准RANS模型得到的结果进行对比,研究表明DES模型对于空穴区域内的反向射流现象及大尺度空泡团的整体脱落有较好的模拟。Johansen等[65]、Wu等[66]、黄彪等[67]采用一种基于标准k-ε模型的滤波器湍流模型(Filter-based Model,FBM)对绕Clark-Y型水翼云状空化流动进行了数值计算,更准确地模拟出了云状空穴形态与空化区尾部涡团交替脱落的非定常细节。Yakhot[68]、Coutier-Delgosha[69]、Zhou和Wang[70]、Yang等[39]、李向宾等[71]引入水和水蒸汽混合密度函数对RANS模型进行了修正,提高了模型预测精度。黄彪等[72-73]基于对非定常空化的流动特性的认识,针对非定常空化流动的湍流多尺度和多相局部可压缩特性,提出了一种基于混合密度分域的混合湍流模型(FBDCM),综合考虑了空化流动的湍流多尺度效应和多相流动特性,实现了对附着空穴生长过程等流动细节的准确预测。图 6给出了采用FBDCM数值计算获得非定常云状空泡形成、发展、脱落与溃灭过程及其与实验结果的对比。综合实验与数值计算结果表明,伴随着空泡团的脱落,在空穴尾部形成U型的空泡涡腔,随着时间的推移,空泡腔逐渐向下游移动,随后U型空泡涡腔从其头部断裂,形成两个较小的空泡腔结构,涡腔两侧逐渐溃灭、消逝。数值计算结果较好地描述了空穴尾部U型空泡涡腔的非定常变化过程,从流场的压力分布云图可以看出,空腔头部瞬时的高压是造成其断裂的主要原因。Huang等[74]基于上述结果进一步通过分析涡输运方程发现了空泡与涡结构之间的强相关性。通过分析涡输运方程,结合实验结果与数值结果,发现空泡与涡结构之间的强相关性。回射流与空泡之间的相互作用可以引起气液两相的变化,增加壁面附近的涡量。
|
图 6 实验与数值预测非定常云状空泡形成、发展、脱落与溃灭过程[18] Fig.6 Formation, development, shedding and collapse process of unsteady cloud cavitation[18] |
研究表明,非定常空化流动中存在多尺度旋涡结构,RANS模型过高预估的湍流黏性会抑制空泡旋涡的脱落[75],从而影响空泡流动预测的精确性。为了实现高雷诺数湍流流场旋涡结构的精细捕捉,大涡模拟方法[76]基于滤波概念尝试捕捉流场中大部分湍流尺度,即对大尺度湍流进行直接计算,对可视为同向且均一的亚网格尺度湍流进行模化(Sub-Grid Scale,SGS),从而能够较好地预测各种空化湍流涡的运动及其造成的不稳定性和周期性。LES方法也被认为是最有可能提高空化湍流流动工程计算精度,从而推动计算空化流体动力学向精确定量预测技术转变的方法[77]。Wang和Ostoja-Starzewski[48]采用大涡模拟方法计算了不同迎角下绕NACA0015翼型空化流动,研究结果表明,大涡模拟方法能够捕捉到云状空泡溃灭及相关的不稳定性特征。Ji[78]等通过研究表明与无空化流动相比,空化的发生和溃灭使数值计算变得更加复杂,采用大涡模拟方法能够较好地获得非定常空化发展过程中的空泡演变规律及其与湍流旋涡结构的相互作用,并与实验结果吻合较好。Gnanaskandan和Mahesh[77]采用大涡模拟LES方法研究了雷诺数分别为Re=200和Re=3900时绕圆柱空化流动。研究发现空化会对圆柱表面压力、边界层和载荷均产生影响。空化的产生有效地降低了尾迹区的雷诺数,抑制了湍流并推迟了三维旋涡结构的破碎。Wang等[30]采用LES方法计算了雷诺数Re=6.7×104,通气率Qv=0.0866时绕钝体模型的空化流场结构,如图 7所示。数值计算结果较好地模拟出展向卡门涡街结构。由于流体的黏性剪切作用,剪切层卷起形成旋涡,上、下剪切层形成的涡对相互卷吸和耦合,最终导致旋涡脱落,形成两列旋转方向相反、交叉排列且相对稳定的涡街。在文献[3]中也表明,在湍流剪切流中,空泡的初生阶段主要受单相流中的流动结构控制。
|
图 7 通气空化旋涡脱落形态(Qv=0.0866,Re =6.7×104)[30] Fig.7 Evolution of ventilated cavitating vortex structures (Qv=0.0866, Re =6.7×104)[30] |
近年来,随着计算机软硬件技术的发展,直接数值模拟(Direct Numerical Simulation,DNS)也在低雷诺数湍流的研究中发挥了作用。直接数值模拟(DNS)不需要建立湍流模型[79-80],直接求解Navier-Stokes方程,几乎能够捕捉到湍流场中包含的所有尺度旋涡结构,即从大尺度到Kolmogorov尺度的涡结构。由于湍流场中大尺度涡与小尺度涡之间的比值,随着雷诺数的增加而变大,在高雷诺数时,湍流尺度的谱域较宽,要捕捉湍流流场中所有尺度的旋涡结构,需要很高的时间和空间分辨率[81],网格数要达到Re9/4的量级,才能满足直接数值模拟的计算要求[82],从而限制了DNS方法在工程上的运用。目前关于直接数值模拟的应用仍局限于相对较低的雷诺数。Rogers和Moin[83]基于DNS分析了均匀剪切层湍流内部旋涡结构,表明展向涡的卷起是“发卡”涡结构形成的主要原因,与壁面湍流的非均匀效应关系不大。Rodriguez等[84]通过直接数值模拟对雷诺数Re=3700的绕球体尾迹区旋涡结构进行了精细地捕捉,并对一阶和二阶统计量进行了分析。直接数值模拟方法在低雷诺数下单相湍流的精细预测方面发挥了其它方法不能替代的作用。王志英等[85]采用DNS方法精确地分析了绕圆柱湍流尾迹区的通气空泡与湍流的相互作用。
数值模拟方法在解决空化与湍流相互作用这一问题中仍然面临许多困难与挑战。空化非定常过程包含了从微米尺度的单个空泡到与流动几何尺度相当的多物理尺度的复杂流动现象,其中微米尺度的单个空泡或单个空泡聚集而成的空泡团的溃灭过程是空化现象的核心问题。在空化模型方面,现有的空化模型大多数基于单泡动力学或是平衡态模型。如果能将空泡群动力学和宏观空化流动模型有效结合起来,建立多尺度空化模型,将有利于更准确地描述空化区内部结构及其对宏观流场的影响,为分析空泡团溃灭产生的冲击压力波的传播对流动的影响提供手段。
2 空化流激振动特性的研究现状随着水力机械、船舶与海洋工程等领域的不断发展,人们对水中结构安全性能的要求也不断提高,流激振动及水动弹性问题也逐渐引起人们的关注。对于流激振动现象的早期认识源于机翼及叶片的气动弹性问题。早期的学者基于线性势流理论,利用解析方法对绕二维弹性机翼流动的空气动力特性进行了分析研究。Theodorsen[86]建立的非定常气动力理论奠定了气动弹性不稳定研究的基础。Sear[87],Garrick[88]等基于线性势流理论对二维机翼均匀来流小幅简谐振动条件下的气动力进行了理论分析。Thomas等[89]基于单自由度模型研究了非线性气动力作用对机翼颤振、气弹稳定性等的影响。Edwardshe和Wieseman[90]应用有限元分析方法与偶极子网格法对机翼静发散与颤振不稳定性进行了分析。然而与经典气动弹性问题不同的是,在水动力学相关领域中,复杂水力环境下的流固耦合效应会导致系统动力特性明显改变,并与流速、压力、湍动能、涡湍黏性等流动参数的变化紧密关联,随流态变化而异,这显著加剧了流激振动问题研究的理论难度。因此,在当前的理论条件下,处理流激振动问题仍然是基于模型试验或是数值模拟进行。
2.1 空化流激振动的试验研究国内外学者对水中绕流物体的流激振动特性及其影响因素进行了大量的实验研究工作。张效慈等[91]采用颜料示踪法进行实验观测,发现水翼结构近壁区域流线呈雾状扩散,表明结构振动对流场影响显著。王文全等[92]基于粒子图像测速系统和加速度传感器研究了方柱绕流后弹性薄板的流激振动特性,揭示了弹性薄板周围流场时空演化与结构振动运动的强非线性耦合作用。
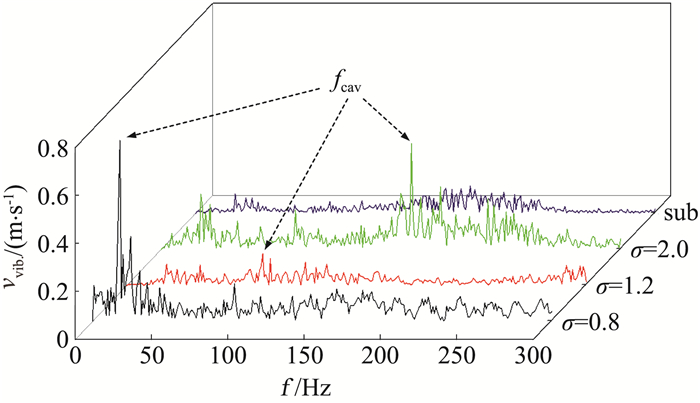
在空化载荷作用下,水中结构流激振动及水弹性问题更加复杂,尤其是大尺度云状空穴的溃灭导致的压力脉动会引起结构强烈振动、剧烈的噪声和结构空蚀等危害[93-95]。随着实验设备和技术手段的发展,流激振动问题的实验研究不断深入。Kubota等[51]测量了非定常空化流动时的速度和压力脉动,揭示了压力脉动和空化发展的联系。So等[96]采用激光多普勒测振仪和激光多普勒测速计对绕弹性圆柱体非定常流动的结构动力学特性及尾迹流动特征进行了研究,分别测得结构的弯曲变形量和尾迹区域的速度分布,结果表明由于圆柱体的振动,流场湍流强度显著增强。Glio等[97]基于高频压力传感器测量了叶轮流道内的压力脉动,分析了压力脉动作用下的叶轮振动特性。Ducoin等[98-99]采用微型压力传感器、激光多普勒测速计、激光多普勒测振仪等设备测量了水翼表面的压力、边界层速度分布以及水翼的振动速度,研究了流场层流向湍流转捩分离和非定常旋涡脱落引起的水翼结构振动响应,结果表明,振动特性与涡脱落频率及结构固有频率密切相关。De La Torre等[100]测量了水翼在空化条件下的固有频率,揭示了附加质量对流固耦合系统的影响。Lelong[101]测量了水翼的变形、振动、应力应变及空化特征,并发现了空化频率和弯曲频率的锁频现象。水翼结构在不同空化阶段呈现出不同的振动特点。水翼结构的流激振动频率随着空化数的降低而减小,最大振动速度在初生空化和片状空化阶段保持在较低水平,受云状空化阶段强烈的非定常特性影响,最大振动速度和位移大幅增加,在超空化阶段由于超空泡的包裹效应,最大振动速度和位移显著下降。如图 8所示,不同空化阶段下,随着空化数的减小,绕水翼空化流动诱导的主要流激振动频率分别为165 Hz、90 Hz和18 Hz。结合不同空化阶段下的空穴形态可知,流激振动频率与空泡脱落频率基本一致,且这一频率在无空化的单向流动中不存在。这说明,绕水翼非定常空化流动中,空泡的非定常脱落是导致水翼结构振动的主要因素,且随着空化数的减小,空化发展周期增大,从而导致空泡脱落频率和水翼结构的流激振动频率减小。
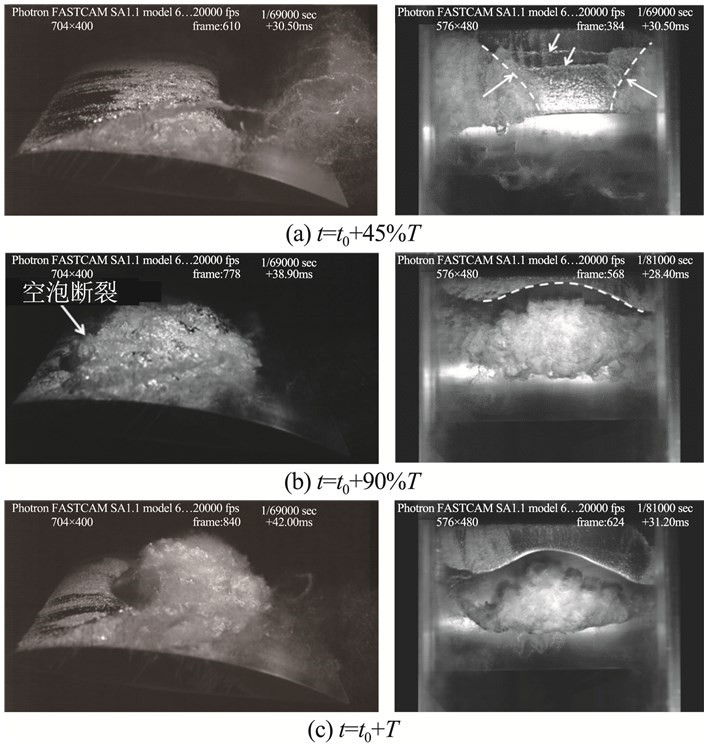
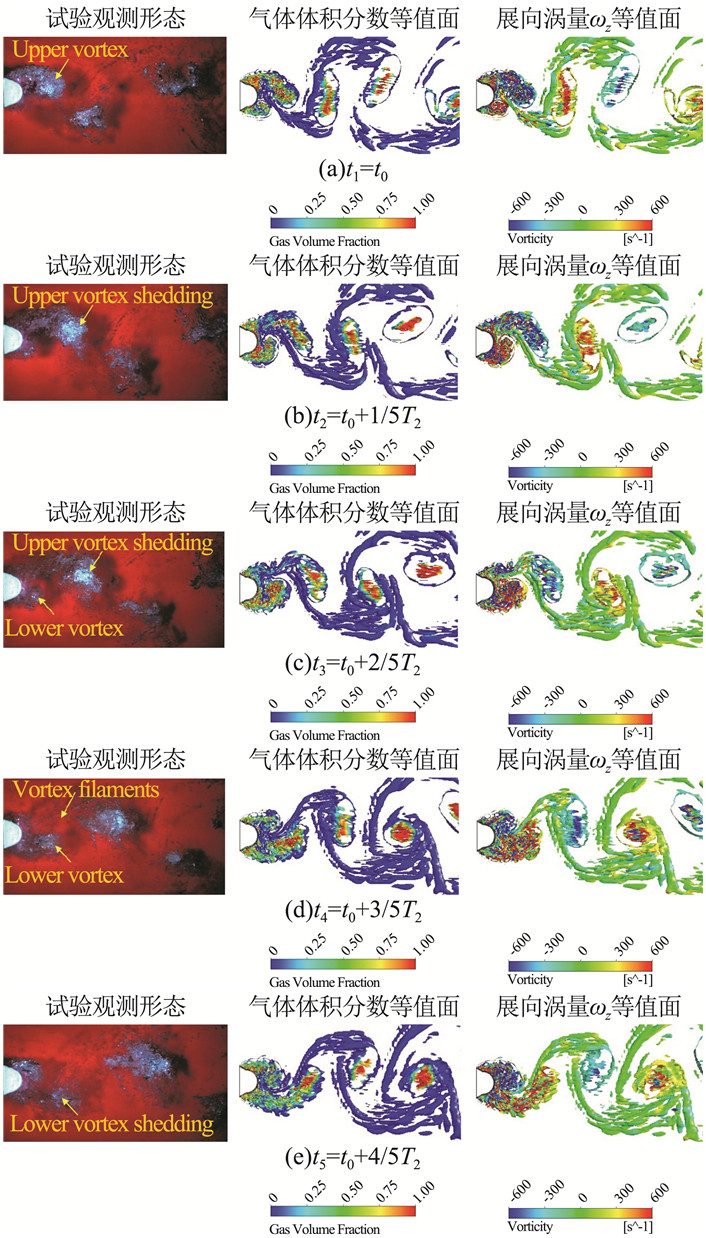
综合空化流动实验研究的现状与发展趋势,应用多场同步测量方法研究空化流动是实验技术的重要发展方向。Chen等[103]建立了一套基于空化水洞的空化流动多场同步测量系统,利用高速摄像机和动态压力传感器实现了收缩-扩张管内不同空化阶段的动态空穴形态和流道壁面压力脉动的同步采集,揭示了空穴形态演变规律与流体动力特性的相互关系,结果表明空化流场的压力波动幅度明显增大,研究进一步捕捉到了压力脉动的主导频率。Aktas等[104]进行高速摄像、压力脉动和振动噪声同步测量,由此发展了空化动力学分析方法,并进一步解释了空化诱导噪声机理。Ma等[105]通过同步观测不同碳纤维复合材料壁面附近空泡溃灭过程的流场形态演化过程,以及平板壁面变形特征,深入分析碳纤维复合材料壁面附近空泡发展过程的流动特性。对于空化流激振动,云状空化流场结构的瞬态演变是影响结构动态振动响应特性的主要因素。图 9给出了采用高速摄像机与激光多普勒测振系统同步观测获得的水翼空化非定常演变情况及其诱导振动速度。综合流场形态与结构振动的同步分析发现,空泡的非定常发展过程引起结构的振动,反向射流引起的云状空泡团断裂导致结构振动速度达到波动峰值,空泡的周期性脱落导致结构的振动速度发生大幅周期性变化。
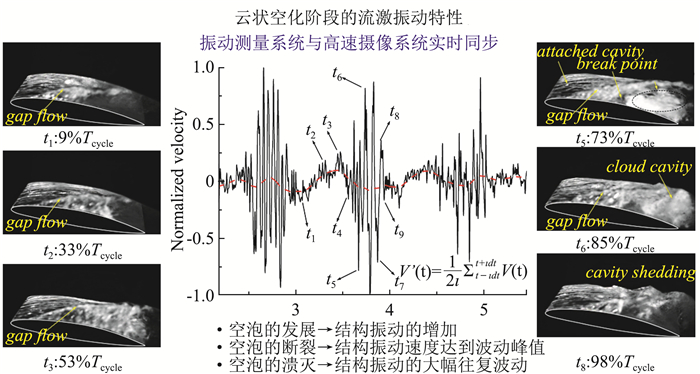
|
图 9 云状空化条件下瞬态空穴形态及其诱导振动速度随时间的演化规律[41] Fig.9 Evolution of cavity patterns and induced vibration velocity[41] |
由于其相关的实验测试对测量技术、成本的要求较高,同时往往会受到测试条件与环境的诸多干扰,针对流固耦合振动机理开展的实验研究具有一定的局限性。随着计算机技术的发展,数值计算方法逐渐成为研究流固耦合问题的主要手段。郑小波等[106]对轴流式叶片进行了振动特性分析,计算了叶片在空气中和水中的固有频率与振型。王福军等[107]应用耦合界面模型研究了国内某大型水电站安装的混流水轮机转轮在不稳定压力场与结构场耦合作用下的动态响应。Munch等[108]基于大量实验与数值计算结果提出了一种绕水翼非定常流动的水弹性响应预测模型,通过建立流体惯性、阻尼和刚度系数的经验表达式,准确预测了流固耦合作用下的水动力系数。
流固耦合问题的求解需要同时考虑流场和结构场的求解及其耦合。对于流固耦合场的求解算法,一般包括消除变量法、整体求解法和分步求解法。由于消除变量法只适用于线性问题中,且在数值方法计算时容易出现困难,因而应用较少。
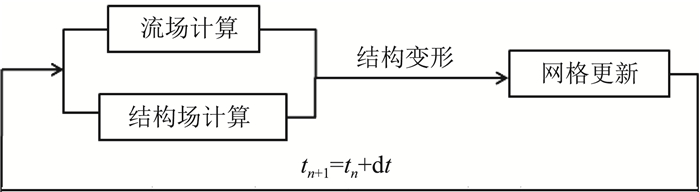
整体求解法(Monolithic Approach)也称完全耦合法(Fully Coupled,FC),对流体和结构建立统一的耦合方程,在一个时间步内对流体域和固体域中所有的未知量进行同时求解,如图 10所示。基于此建立的流场与结构场具有强烈的相关性,能精确求解出流体和结构的响应,完全消除求解过程中的时间延迟,且数值收敛性较好,计算精确度较高。Ryzhakov等[109]利用完全耦合法基于拉格朗日体系建立了流场和结构场控制方程,对水流冲击弹性平板和注水气球弹性变形等算例进行了分析研究,结果表明完全耦合法能精确求解流体与结构的动态响应,且数值收敛性较好。Michler[110]针对活塞与流体相互作用的一维模型问题,从算法稳定性、计算精度和计算效率等方面对比了不同流固耦合算法在流固耦合问题求解中的应用情况,结果表明完全耦合法无条件稳定且计算精确度相对较高。吴钦等[111]基于完全耦合算法对绕NACA009水翼流固耦合特性进行了数值模拟研究,揭示了流体与结构的惯性作用对水弹性响应有较大影响。然而对于复杂的流固耦合系统,流固耦合方程的理论推导过程相当复杂,求解难度较大,现有的流体和结构计算软件均无法实现,因此其在工程领域的适用性存在一定局限。
|
图 10 完全耦合算法示意图 Fig.10 Fully coupled algorithm schematic diagram |
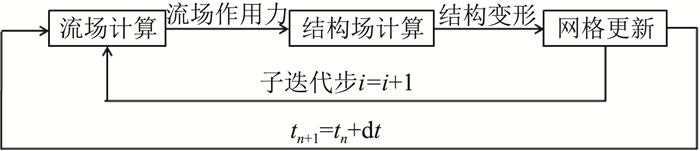
分步求解法(Partitioned Approach)分别对流场和结构场选择合适的数值算法进行独立求解,流固耦合界面数据通过反复迭代求解并传递直至获得收敛解。其中,分步求解法按照耦合的紧密程度,可分为松耦合算法(Loosely Coupled,LC)和紧耦合算法(Tightly Coupled,TC),如图 11和图 12所示。松耦合算法是在流体和固体各自的求解域内,用各自的求解器分别独立进行求解,在每个预定的计算时间步内进行流体域和固体域的数据交换。在松耦合算法的基础上,紧耦合算法在每一时间步中引入子迭代步,在每个子迭代步内交叉求解流动控制方程和结构动力学方程,并通过流固耦合界面进行数据传递。紧耦合算法相对于松耦合算法,较好地解决了流场与结构场求解时间延迟问题,子迭代过程中多次的数据交换保证了流场、结构场及流固耦合界面上合理的收敛精度,从而具有更高的计算精度。同时,紧耦合算法相对于完全耦合算法,在求解器、计算模型、网格尺度上都更加灵活。Ducoin等[112]利用松弛耦合分步求解算法研究了绕二维弹性水翼黏性流动的水弹性响应和结构稳定性,结果表明流场作用下,弹性水翼发生绕弹性轴顺时针方向的扭转变形,从而导致有效迎角增大,同时结构的变形加速了流场转捩和失速现象的发生,导致流场的非线性特性显著。Lee等[113]证实了紧耦合算法对研究弹性翼的涡激振动特性的可行性。

|
图 11 松耦合算法示意图 Fig.11 Loosely coupled algorithm schematic diagram |
|
图 12 紧耦合算法示意图 Fig.12 Tightly coupled algorithm schematic diagram |
表 1综合对比了上述流固耦合算法在水动力学研究中的应用情况。大量研究表明,分步求解法(LC算法、TC算法等)的优点是容易实施,通过交互程序即可实现结构求解器和流体求解器之间的数据交换,从而实现分步求解。其中,松耦合算法不能保证计算过程中流场与结构场的能量平衡,且计算稳定性受流固密度比等模型参数和计算时间步等计算参数的影响,通过在松耦合求解算法中引入子迭代过程,紧耦合算法能在一定程度上保证流场与结构场的能量平衡,并提高算法的收敛性和稳定性,但均没有考虑水的附加质量、阻尼等对水翼结构的运动和变形的影响,无法解决附加质量效应带来的数值收敛问题[114-115]。
| 表 1 流固耦合方法研究 Table 1 Fluid structure coupling algorithms |
|
|
为了进一步研究附加质量效应对结构流激振动特性的影响,Young等[118]、Wu等[119]发展了一种混合耦合算法,相比于其他分步耦合算法,混合耦合算法收敛性和数值稳定性更好。图 13给出了采用不同流固耦合算法对单自由度水翼结构动力学方程进行求解所得扭转变形角度随时间的演变情况。通过改变时间步长、激励频率等参数,对比不同耦合算法在求解过程中的数值稳定性发现,完全耦合算法(FC)在不同工况下的计算均无条件收敛,具有较好的数值稳定性。当dt=T/480时,松耦合(LC)、紧耦合(TC)和混合耦合算法(HC)均与完全耦合算法计算结果一致;当dt=T/120时,松耦合算法与最大迭代步数为1的混合耦合算法的计算结果均发散,随着迭代步数的增大,紧耦合算法和混合耦合算法均较好地获得收敛数值解,其中松耦合算法可看作最大迭代步数为1的紧耦合算法。这主要是因为,松耦合算法根据上一时间步流固界面位移计算得来的流体对结构的作用力与当前流场实际作用力存在一定误差,不能保证计算过程中流场与结构场的能量平衡,计算稳定性受计算时间步等计算参数的影响较大。同时,对于不同固体结构属性,在不同频率的激励条件,松耦合算法和紧耦合算法均发生明显的发散现象,这主要是因为松耦合和紧耦合算法均忽略了流体的附加质量效应,从而增大了数值计算误差。尤其对于流固相对密度较小的流固耦合问题,附加质量效应是造成数值不稳定性和降低计算精度的重要因素,数值计算稳定性受流固密度比等模型参数和计算时间步等计算参数的影响。混合耦合算法通过引入Theodorsen模型有效考虑了流体对结构的附加质量效应,可以减少对结构位移的过度预测,提高数值求解的稳定性和精确性。
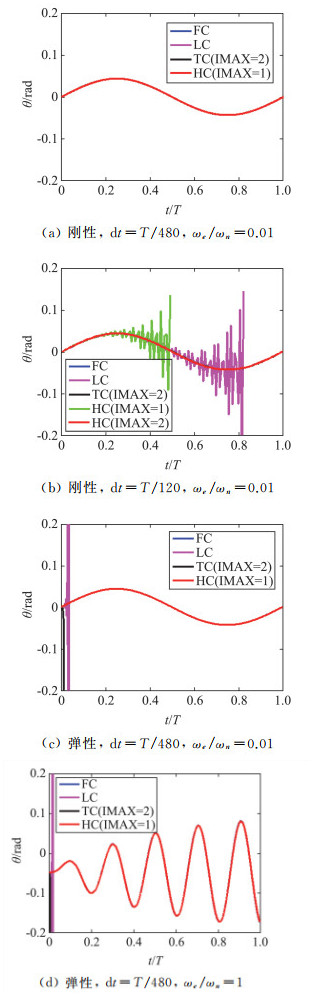
|
图 13 不同流固耦合算法稳定性对比 Fig.13 Comparison of stability of different fluid-structure interaction algorithm |
为了进一步研究不同材料水翼的非定常空化流激振动特性,Wu等[119-120]研究了绕弹性水翼非定常空化流动及其诱导振动特性。结合图 14和图 15所示,水动力随时间的变化主要分为三个阶段:伴随着附着空穴的发展,弯曲和扭转变形随着升力系数增大而增大;由于空穴的溃灭和与涡结构强烈的相互作用,水翼的弯曲和扭转变形产生大幅波动;随着空穴脱落和流场涡结构向水翼下游移动,水翼的弯曲、扭转变形与升力系数同步下降。
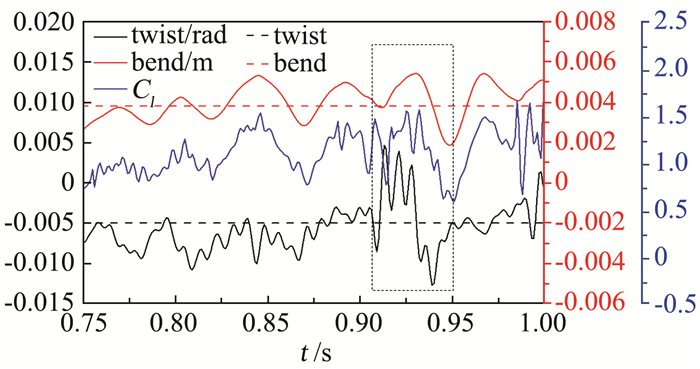
|
图 14 弹性水翼弯曲、扭转变形以及升力系数随时间的演变过程 Fig.14 The evolution of bending, torsional deformation and lift coefficient of flexible hydrofoil |
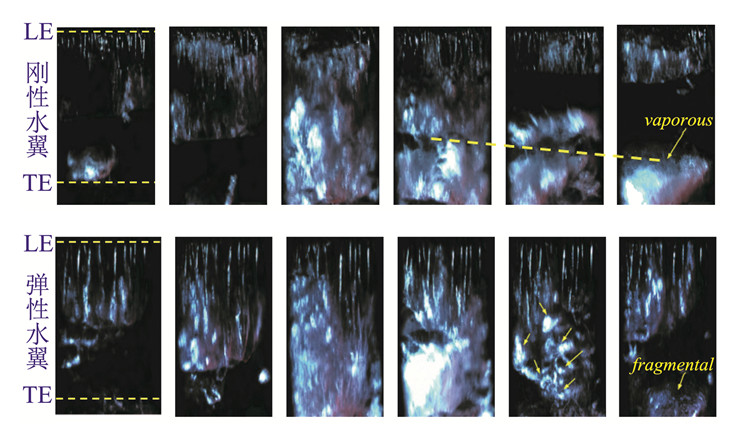
|
图 15 绕刚性和弹性水翼非定常空化形态随时间的演变过程 Fig.15 Evolution of unsteady cavitation around rigid and flexible hydrofoils |
通过对近年来国内外在非定常空化流动及其诱导振动特性的实验和数值计算方面研究工作的总结,认为在该领域仍有诸多工作值得进一步地探究:
1) 已有研究表明,非定常空化流动及其诱导振动特性涉及流场速度、压力、相变等与结构场振动位移、速度、加速度等的相互作用,现有的单一试验技术已经发展较为成熟,但单一试验测量结果不能较好地反映各瞬态物理场的相互作用。为了更好地研究空化流动及其诱导振动特性,针对空化流动的多场耦合特性,有必要建立集高速全流场显示技术、瞬态粒子测速技术、动态压力测试技术和结构瞬态振动速度、结构振动位移等为一体的多场同步测量试验平台,开发数据同步采集和后处理系统,解决瞬态空化形态观测、非接触速度测量、脉动压力测量、精确振动速度测量等问题,实现非定常空化特性与空化流激振动特性的同步观测与分析。
2) 随着互联网、大数据、云计算等技术的不断发展,机器学习与计算流体动力学(CFD)的结合已成为非定常空化流动和空化流激振动数值模拟方法发展的重要方向。Li等[121]结合深度学习理论,发展了一种基于长短时记忆神经网络的非定常气动力模型,该模型能够更好地体现气动力非定常特征引起的短时和长时时滞效应。Zhang等[122]采用卷积神经网络建立了一种基于DNS数值计算结果的RANS数值计算结果优化算法,结果大大提高了数值计算效率和精确度。尽管机器学习在非定常空化流动试验与数值计算领域的研究尚未起步,但已有研究充分表明,机器学习为试验数据分析与数值模拟方法的进一步发展提供了可能,也必将成为今后发展的重要方向。
3) 空化流动几乎包含了所有复杂的流动现象,尤其是云状空泡团发展过程的强烈不稳定行为是影响结构动态振动响应特性的主要因素。目前空化流激振动的研究主要关注流场空泡形态演变及其相应压力脉动和结构振动分析[123],对于流动与结构振动稳定性机制的研究尚不深入,尤其是针对压力波导致的空泡失稳机制。Arndt等[26]首先观察到NACA0015水翼的两种状态:当σ/2α>4时,回射流对空泡失稳起主要作用;当σ/2α < 4时,流动主要受激波影响。Leroux等[33]观察到了NACA66水翼的准稳定部分空泡和云状空化现象,并基于参数σ/2(α-α0)得到了类似的结论。吴钦等基于试验观察到了类似现象,并结合结构振动测量结果发现,与回射流导致的大尺度云状空泡团脱落诱导结构振动特性相比,大尺度云状空泡团的溃灭冲击波及其引起的附着空泡二次溃灭导致结构振动显著加剧。王畅畅等[124]进一步采用可压缩数值计算方法分析了上述不同云状空泡脱落机制。对于上述不同空泡脱落机制,国内外学者的说法尚未统一,通过X射线等技术深入分析空化区域内的回射流与冲击波演化特征,并结合结构精细化振动测试技术,对流动参数进行系统的归纳、分析,建立更完善的空化流激振动稳定性机制分析,是今后进一步研究空化流动机理、理解非定常空化流激振动特性的重要关注点。
| [1] |
BRENNEN C E. Cavitation and bubble dynamics[M]. Oxford Engineering & Sciences Series 44, Oxford University Press, 1995.
|
| [2] |
WANG G Y, SENOCAK I, SHYY W, et al. Dynamics of attached turbulent cavitating flows[J]. Progress in Aerospace Sciences, 2001, 37: 551-581. DOI:10.1016/S0376-0421(01)00014-8 |
| [3] |
FRANC J-P, MICHEL J-M. Fundamentals of cavitation[M]. Kluwer academic publishers, 2005.
|
| [4] |
黄彪, 吴钦, 王国玉. 非定常空化流动研究现状与进展[J]. 排灌机械工程学报, 2018, 36(01): 1-14. HUANG B, WU Q, WANG G Y. Progress and prospects of investigation into unsteadycavitating flows[J]. Journal of drainage and irrigation machinery engineering, 2018, 36(01): 1-14. (in Chinese) |
| [5] |
GEORGIOS M, NILLA K, GEORGE A, et al. Experimental analysis of cavitation in a centrifugal pump using acoustic emission, vibration measurements and flow visualization[J]. European Journal of Mechanics-B/Fluids, 2019, 75: 300-311. DOI:10.1016/j.euromechflu.2018.10.015 |
| [6] |
WU Q, WANG C C, HUANG B, et al. Measurement and prediction of cavitating flow-induced vibrations[J]. Journal of Hydrodynamics, 2018, 30(6): 1064-1071. DOI:10.1007/s42241-018-0115-5 |
| [7] |
CHENG H Y, BAI X R, LONG X P, et al. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence[J]. Applied Mathematical Modelling, 2020, 77: 788-809. DOI:10.1016/j.apm.2019.08.005 |
| [8] |
WU Q, HUANG B, WANG G Y, et al. Numerical modelling of unsteady cavitation and induced noise around a marine propeller[J]. Ocean Engineering, 2018, 160: 143-155. DOI:10.1016/j.oceaneng.2018.04.028 |
| [9] |
LIU T T, HUANG B, WANG G Y, et al. Experimental investigation of ventilated partial cavitating flows with special emphasis on flow pattern regime and unsteady shedding behavior around an axisymmetric body at different angles of attack[J]. Ocean Engineering, 2018, 147: 289-303. DOI:10.1016/j.oceaneng.2017.10.039 |
| [10] |
KIM D J, SUNG H J, CHOI C H, et al. Cavitation instabilities of an inducer in a cryogenic pump[J]. Acta Astronautica, 2017, 132: 19-24. DOI:10.1016/j.actaastro.2016.12.007 |
| [11] |
WANG Z Y, HUANG B, ZHANG M, et al. Experimental and numerical investigation of ventilated cavitating flow structures with special emphasis on vortex shedding dynamics[J]. International Journal of Multiphase Flow, 2018, 98: 79-95. DOI:10.1016/j.ijmultiphaseflow.2017.08.014 |
| [12] |
邬明, 孙善春. 基于SST湍流模型的二维操纵面空化流场研究[J]. 空气动力学学报, 2013, 31(01): 115-119. WU M, SUN S C. Research on cavitation flow field of two dimensions control surface based on SST turbulence model[J]. Acta Aerodynamica Sinica, 2013, 31(01): 115-119. (in Chinese) |
| [13] |
崔宗培. 中国水利百科全书[M]. 北京: 中国水利水电出版社, 2006. CUI Z P. Encyclopedia of Chinese water resources[M]. Beijing: China Water & Power Press, 2006. (in Chinese) |
| [14] |
KNAPP R T, DAILY J W, HAMMITT F G. Cavitation[M]. New York: McGraw Hill, 1970.
|
| [15] |
TULIN M P. Supercavitating propellers history, operating characteristics, mechanism of operation[M]. Hydronautics, 1964.
|
| [16] |
LI X B, WANG G Y, ZHANG M, et al. Structures of supercavitating multiphase flows[J]. International journal of thermal sciences, 2008, 47(10): 1263-1275. DOI:10.1016/j.ijthermalsci.2007.11.010 |
| [17] |
ZHANG M, CHEN H, WU Q, et al. Experimental and numerical investigation of cavitating vortical patterns around a Tulin hydrofoil[J]. Ocean Engineering, 2019, 173(1): 298-307. |
| [18] |
HUANG B, QIU S C, LI X B, et al. A review of transient flow structure and unsteady mechanism of cavitating flow[J]. Journal of Hydrodynamics, 2019, 31(3): 429-444. DOI:10.1007/s42241-019-0050-0 |
| [19] |
ARAKERI V H, ACOSTA A J. Viscous effects in the inception of cavitation on axisymmetric bodies[J]. Journal of Fluids Engineering, 1973, 519-527. |
| [20] |
KATZ J. Cavitation phenomena within regions of flow separation[J]. Journal of Fluid Mechanics, 1984, 140: 397-436. DOI:10.1017/S0022112084000665 |
| [21] |
GUENNOUN F, FARHAT M, BOUZIAD Y A, et al. Experimental investigation of a particular traveling bubble cavitation[C]//Fifth International Symposium on Cavitation, Osaka, Japan, 2003.
|
| [22] |
KUBOTA A., KATO H, YAMAGUCHI H, et al. Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling technique[J]. Journal of Fluids Engineering, 1989, 111: 204-210. DOI:10.1115/1.3243624 |
| [23] |
LIU S, HIGUCHI J, IKOHAGI T. Experimental study of cavity flow behavior on a 2-D hydrofoil[J]. Bulletin of the JSME, 1999, 42(4): 641-648. |
| [24] |
STUTZ B, REBOUD J. Measurements within unsteady cavitation[J]. Experiments in Fluids, 2000, 29(6): 545-552. DOI:10.1007/s003480000122 |
| [25] |
STUTZ B, REBOUD J. Two-phase flow structure of sheet cavitation[J]. Physics of Fluids, 1997, 9(12): 3678-3686. DOI:10.1063/1.869505 |
| [26] |
ARDNT R E A, WOSNIK M. Towards the control of cavitating flows[C]//The 12th International Symposium on Transport Phenomenon and Dynamics of Rotating Machinery, Honolulu, Hawaii, 2008.
|
| [27] |
张博, 王国玉, 黄彪, 等. 绕水翼空化非定常动力特性的时频分析[J]. 实验流体力学, 2009, 23(3): 44-49. ZHANG B, WANG G Y, HUANG B, et al. Unsteady dynamics of cavitating flows around a hydrofoil[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(3): 44-49. DOI:10.3969/j.issn.1672-9897.2009.03.010 (in Chinese) |
| [28] |
DREYER M, DECAIX J, MUNCH-ALLIGNE C, et al. Mind the gap:A new insight into the tip leakage vortex using stereo-PIV[J]. Experiments in Fluids, 2014, 55(11): 1-13. |
| [29] |
CHE B X, CAO LL, CHU N, et al. Dynamic behaviors of re-entrant jet and cavity shedding during transitional cavity oscillation on NACA0015 hydrofoil[J]. Journal of Fluids Engineering, 2019, 141(6): 061101. DOI:10.1115/1.4041716 |
| [30] |
WANG Z Y, ZHANG M D, KONG D C, et al. The influence of ventilated cavitation on vortex shedding behind a bluff body[J]. Experimental Thermal and Fluid Science, 2018, 98: 181-194. DOI:10.1016/j.expthermflusci.2018.05.029 |
| [31] |
GANESH H, MÄKIHARJU S A, CECCIO S L. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities[J]. Journal of Fluid Mechanics, 2016, 802: 37-78. |
| [32] |
LEROUX J B, ASTOLFI J A, BILLARD J Y. An experimental study of unsteady partial cavitation[J]. Journal of Fluids Engineering, 2004, 126: 94-101. DOI:10.1115/1.1627835 |
| [33] |
LEROUX J B, COUTIER-DELGOSHA O, ASTOLFI J A. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil[J]. Physics of Fluids, 2005, 17(5): 1-20. |
| [34] |
KJELDSEN M, ARNDT R E A, EFFERTZ M. Spectral characteristics of sheet/cloud cavitation[J]. Journal of Fluids Engineering, 2000, 122(3): 481-487. DOI:10.1115/1.1287854 |
| [35] |
张博.亚空化非定常流动机理及动力特性研究[D].北京理工大学, 2009. ZHANG B. Unsteady dynamic mechanism of sub-cavitating flows[D]. Beijing: Beijing Institute of Technology, 2009. |
| [36] |
KAWANAMI Y, KATO H, YAMAUCHI H, et al. Mechanism and control of cloud cavitation[J]. Journal of Fluids Engineering, 1997, 119(4): 788-794. DOI:10.1115/1.2819499 |
| [37] |
DE LANGE D F, DE BRUIN G J, VAN WIJNGAARDEN L. On the mechanism of cloud cavitation-experiment and modelling[C]//The second international symposium on Cavitation proceedings, Tokyo, Japan, 1994.
|
| [38] |
FRANC J P. Partial cavity instabilities and re-entrant jet[C]//Fourth International Symposium on Cavitation, Pasadena, California, USA, 2001.
|
| [39] |
YANG J, ZHOU L, WANG Z. Numerical simulation of three-dimensional cavitation around a hydrofoil[J]. Journal of Fluids Engineering, 2011, 133(8): 081301. DOI:10.1115/1.4004385 |
| [40] |
FOETH E J. The structure of three-dimensional sheet cavitation[D]. Delft, The Netherland: Delft University of Technology, 2008.
|
| [41] |
吴钦.非定常空化流动及其诱导振动特性研究[D].北京: 北京理工大学, 2016. WU Q. Physical and numerical investigation of cavitating flow-induced vibrations[D]. Beijing: Beijing Institute of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10007-1019828631.htm |
| [42] |
WU Y T. A wake model for free-streamline flow theory, part 1. fully and partially developed wake flows and cavity flows past an oblique flat plate[J]. Journal of Fluid Mechanics, 1962, 13(2): 161-181. DOI:10.1017/S0022112062000609 |
| [43] |
WU Y T. A wake model for free-streamline flow theory, part 2. cavity flows past obstacles of arbitrary profile[J]. Journal of Fluid Mechanics, 1964, 15: 65-93. |
| [44] |
KINNAS S A, FINE N E. A numerical nonlinear analysis of the flow around two and three dimensional partially cavitating hydrofoils[J]. Journal of Fluid Mechanics, 1993, 254: 151-181. |
| [45] |
YOUNG Y L, KINNAS S A. numerical modeling of supercavitating propeller flows[J]. Journal of Ship Research, 2003, 47(1): 48-62. |
| [46] |
DELANNOY Y, KUENY J L. Cavity flow predictions based on the Euler equations[C]//ASME Cavitation and Multiphase Flow Forum, 1990, Toronto, Canada.
|
| [47] |
OLIVER C D, ASTOLFI J A. Numerical prediction of the cavitation flow on a two-dimensional symmetrical hydrofoil with a single fluid model[C]//Fifth international symposium on cavitation, Osaka, Japan, Cav03-OS-1-013, 2003.
|
| [48] |
WANG G Y, OSTOJA-STARZEWSKI M. Large eddy simulation of a sheet/cloud cavitation on a NACA0015 hydrofoil[J]. Mathematical Modeling, 2006, 31(3): 417-447. |
| [49] |
RAYLEIGH B L. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine, 1917, 34(1): 94-98. |
| [50] |
PLESSET M S. The dynamics of cavitation bubbles[J]. Journal of Applied Mechanics, 1949, 16: 228-231. |
| [51] |
KUBOTA A, KATO H, YAMAGUCHI H. A new modeling of cavitating flows:a numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of Fluid Mechanics, 1992, 240(1): 59-96. |
| [52] |
ZWART P J, GERBER G, BELAMRI T. A two-phase flow model for prediction cavitation dynamics[C]//5th ICMF 2004 International Conference on Multiphase Flow, Yokohama, Japan, 2004.
|
| [53] |
SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]//4th International Conference on Multiphase Flow, New Orleans, USA, 2001.
|
| [54] |
SINGHAL A K, ATHAVALE M M, LI H, et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering, 2002, 124(3): 617-625. DOI:10.1115/1.1486223 |
| [55] |
GERBER A G. A CFD model for devices operating under extensive cavitation conditions[J]. International Mechanical Engineering Congress and Exhibit, 2002, 341-349. |
| [56] |
FROBENIUS M, SCHILLING R, BACHERT R, et al. Three dimensional unsteady cavitation effects on a single hydrofoil and in a radial pump-measurements and numerical simulations[C]//5th International Symposium on Cavitation, Osaka, Japan, 2003.
|
| [57] |
牟斌, 江雄, 王建涛. 空化流动隐式求解方法研究[J]. 空气动力学学报, 2017, 35(1): 27-32. MOU B, JIANG X, WANG J T. Investigation on implicit numerical method for cavitation flow[J]. Acta Aerodynamica Sinica, 2017, 35(1): 27-32. DOI:10.7638/kqdlxxb-2015.0027 (in Chinese) |
| [58] |
MERKLE C L, FENG J, BUELOW P E O. Computational modeling of the dynamics of sheet cavitation[C]//3rd International Symposium on Cavitation, Grenoble, France, 1998.
|
| [59] |
KUNZ R, BOGER D, STINEBRING D, et al. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]. Computers & Fluids, 2000, 29(8): 849-875. |
| [60] |
SENOCAK I, SHYY W. Interfacial dynamics-based modeling of turbulent cavitating flows Part-1:Model development and steady-state computations[J]. International Journal for Numerical Method in Fluid, 2004, 44(9): 975-995. DOI:10.1002/fld.692 |
| [61] |
SENOCAK I, SHYY W. Interfacial dynamics-based modeling of turbulent cavitating flows Part-2:Time-dependent computations[J]. International Journal for Numerical Method in Fluid, 2004, 44(9): 997-1016. DOI:10.1002/fld.693 |
| [62] |
黄彪.非定常空化流动机理及数值计算模型研究[D].北京: 北京理工大学, 2012. HUANG B. Physical and numerical investigation of unsteady cavitating flows[D]. Beijing: Beijing Institute of Technology, 2012. |
| [63] |
LAUNDER B E, SPALDING D B. The numerical computation of turbulent flows[J]. Computational Methods in Applied Mechanics and Engineering, 1974, 3(2): 269-289. DOI:10.1016/0045-7825(74)90029-2 |
| [64] |
KINZEL M P, LINDAU J W, PELTIER L J, et al. Detached-eddy simulations for cavitating flows[R]. AIAA 2007-4098, 2007.
|
| [65] |
JOHANSEN S T, WU J, SHYY W. Filter-based unsteady RANS computations[J]. International Journal of Heat & Fluid Flow, 2004, 25(1): 10-21. |
| [66] |
WU J, WANG G, SHYY W. Time-dependent turbulent cavitating flow computations with interfacial transport and filter based models[J]. International Journal for Numerical Methods in Fluids, 2005, 49(7): 739-761. DOI:10.1002/fld.1047 |
| [67] |
黄彪, 王国玉, 张博, 等. FBM湍流模型在云状空化流动数值计算中的应用于评价[J]. 机械工程学报, 2010, 46(8): 147-153. HUANG B, WANG G Y, ZHANG B, et al. Evaluation and application of filter based turbulence model for computations of cloud cavitating flows[J]. Journal of Mechanical Engineering, 2010, 46(8): 147-153. (in Chinese) |
| [68] |
YAKHOT V, ORSZAG S A, THANGHAM S, et al. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids, 1992, 4(7): 1510-1520. DOI:10.1063/1.858424 |
| [69] |
COUTIER-DELGOSHA O, FORTES-PATELLA R, REBOUD J. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J]. Journal of Fluids Engineering, 2003, 125(1): 38-45. |
| [70] |
ZHOU L J, WANG Z W. Numerical simulation of cavitation around a hydrofoil and evaluation of a RNG k-ε Model[J]. Journal of Fluids Engineering, 2008, 130: 1-7. |
| [71] |
李向宾, 王国玉, 张博, 等. RNG k-ε模型在超空化流动计算中的应用评价[J]. 水动力学研究与进展, 2008, 23(2): 181-188. LI X B, WANG G Y, ZHANG B, et al. Evaluation of the RNG k-ε model on the numerical simulations of supercavitating flows around a hydrofoil[J]. Chinese Journal of Hydrodynamics, 2008, 23(2): 181-188. (in Chinese) |
| [72] |
HUANG B, WANG G Y, ZHAO Y, et al. Physical and numerical investigation on transient cavitating flows[J]. Science China-Technological Sciences, 2013, 56(9): 2207-2218. DOI:10.1007/s11431-013-5315-1 |
| [73] |
HUANG B, YOUNG Y L, WANG G Y, et al. Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation[J]. Journal of Fluids Engineering, 2013, 135: 1-16. |
| [74] |
HUANG B, ZHAO Y, WANG G Y. Large eddy simulation of turbulent vortex-cavitation interactions in transient sheet/cloud cavitating flows[J]. Computers and Fluids, 2014, 92: 113-124. DOI:10.1016/j.compfluid.2013.12.024 |
| [75] |
胡常莉.绕回转体空化流动特性与机理研究[D].北京: 北京理工大学, 2015. HU C L. Study on the physical mechanism of cavitating flows around axisymmetric bodies[D]. Beijing: Beijing Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015029574.htm |
| [76] |
DEARDOFF J W. The use of subgrid transport equation in a three dimensional model of atmospheric turbulence[J]. ASME J Fluid Engineering, 1973, 95: 429. DOI:10.1115/1.3447047 |
| [77] |
GNANASKANDAN A, MAHESH K. Large eddy simulation of the transition from sheet to cloud cavitation over a wedge[J]. Int J Multiphase Flow, 2016, 83: 86-102. DOI:10.1016/j.ijmultiphaseflow.2016.03.015 |
| [78] |
JI B, LUO X W, ARNDT R E A, et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil[J]. International Journal of Multiphase Flow, 2015, 68: 121-134. DOI:10.1016/j.ijmultiphaseflow.2014.10.008 |
| [79] |
Steven A O. Numerical study of three-dimensional homogeneous, isotropic turbulence[J]. Physical Review Letter, 1972, 28: 76. DOI:10.1103/PhysRevLett.28.76 |
| [80] |
傅德薰, 马延文, 李新亮, 等. 可压缩湍流直接数值模拟[M]. 北京: 科学出版社, 2010. FU D X, MA Y W, LI X L, et al. Direct numerical simulation of compressible turbulence[M]. Beijing: Science Press, 2010. (in Chinese) |
| [81] |
许常悦.圆柱可压缩湍流及其流动控制的大涡模拟研究[D].合肥: 中国科学技术大学, 2009. XU C Y. Large eddy simulation of the compressible flow past a circular cylinder and its flow control[D]. Hefei: University of Science and Technology of China, 2009. http://d.wanfangdata.com.cn/Thesis/Y1498378 |
| [82] |
孙小波.可压缩剪切湍流的直接模拟和大涡模拟研究[D].合肥: 中国科学技术大学, 2007. SUN X B. Direct simulation and large eddy simulation of compressible shear turbulence[D]. Hefei: University of Science and Technology of China, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10358-2007098095.htm |
| [83] |
ROGERS M M, MOIN P. The structure of the vorticity field in homogeneous turbulent flows[J]. J Fluid Mech, 1987, 176: 33-66. DOI:10.1017/S0022112087000569 |
| [84] |
RODRIGUEZ I, BORELL R, LEHMKUHL O, et al. Direct numerical simulation of the flow over a sphere at Re=3700[J]. J Fluid Mech, 2011, 679: 263-287. DOI:10.1017/jfm.2011.136 |
| [85] |
王志英.通气空泡湍流旋涡特性与机理研究[D].北京理工大学, 2019. WANG Z Y. Study on the characteristics and mechanism of vortex shedding in the ventilated cavitating turbulence flow[D]. Beijing: Beijing Institute of Technology, 2019. |
| [86] |
THEODORSEN T. General theory of aerodynamic instability and the mechanism of flutter[R]. National Advisory Committee for Aeronautics, Technical Report 496, 1935.
|
| [87] |
SEARS W R. Some aspects of non-stationary airfoil theory and its practical application[J]. Journal of the Aeronautical Sciences, 1941, 8(3): 104-108. DOI:10.2514/8.10655 |
| [88] |
GARRICK I E. Bending-torsion flutter calculations modified by subsonic compressibility corrections[R]. National Advisory Committee for Aeronautics, Technical Report 836, 1946.
|
| [89] |
THOMAS J, DOWELL E, HALL K. Nonlinear inviscid aerodynamic effects on transonic divergence, flutter, and limit-cycle oscillations[J]. AIAA Journal, 2002, 40(4): 638-646. DOI:10.2514/2.1720 |
| [90] |
EDWARDS J, WIESEMA C. Flutter and divergence analysis using the generalized aeroelastic analysis method[J]. Journal of Aircraft, 2008, 45(3): 906-915. DOI:10.2514/1.30078 |
| [91] |
张效慈, 张军, 倪永良, 等. 两维翼水动力振动和流场显示的粒子图像测速实验[J]. 中国造船, 2000, 41(1): 26-30. ZHANG X C, ZHANG J, NI Y L, et al. PIV experiment of water-induced vibration and flow visualisation around a two-dimensional wing[J]. Shipbuilding of China, 2000, 41(1): 26-30. DOI:10.3969/j.issn.1000-4882.2000.01.005 (in Chinese) |
| [92] |
王文全, 张立翔, 闫妍, 等. 不同雷诺数下弹性薄板流激振动实验[J]. 北京工业大学学报, 2012, 38(1): 55-59. WANG W Q, ZHANG L X, YAN Y, et al. Fluid-induced vibrations of thin elastic plate for different inflow Reynolds numbers[J]. Journal of Beijing University of Technology, 2012, 38(1): 55-59. (in Chinese) |
| [93] |
WANG Y W, LIAO L J, DU T Z, et al. A study on the collapse of cavitation bubble surrounding the underwater-launched projectile and its fluid-structure coupling effects[J]. Ocean Engineering, 2014, 84: 228-236. DOI:10.1016/j.oceaneng.2014.04.014 |
| [94] |
CHAE E J. Dynamic response and stability of flexible hydrofoils in incompressible and viscous flow[J]. University of Michigan, 2015. |
| [95] |
ZOBEIRI A, AUSONI P, AVELLAN F, et al. How oblique trailing edge of a hydrofoil reduces the vortex-induced vibration[J]. Journal of Fluids and Structure, 2012, 32: 78-89. DOI:10.1016/j.jfluidstructs.2011.12.003 |
| [96] |
SO R M C, ZHOU Y, LIU M H. Free vibrations of an elastic cylinder in a cross flow and their effects on the near wake[J]. Experiments in Fluids, 2000, 29: 130-144. DOI:10.1007/s003489900065 |
| [97] |
GLIO S, MARUTA Y. Experimental investigations on pressure fluctuations and vibration of the impeller in a centrifugal pump with vaned diffusers[J]. JSME International Journal, 2005, 48(1): 136-143. DOI:10.1299/jsmeb.48.136 |
| [98] |
DUCOIN A, ASTOLFI J A, SIGRIST J F. An experimental analysis of fluid structure interaction on a flexible hydrofoil in various flow regimes including cavitating flow[J]. European Journal of Mechanics B/Fluids, 2012, 36: 63-74. DOI:10.1016/j.euromechflu.2012.03.009 |
| [99] |
DUCOIN A, ASTOLFI J A, GOBERT M L. An experimental study of boundary-layer transition induced vibrations on a hydrofoil[J]. Journal of Fluids and Structures, 2012, 32(3): 37-51. |
| [100] |
DE LA TORRE O, ESCALER X, EGUSQUIZA E, et al. Experimental investigation of added mass effects on a hydrofoil under cavitation conditions[J]. Fluids Struct, 2013, 39: 173-187. DOI:10.1016/j.jfluidstructs.2013.01.008 |
| [101] |
LELONG A, GUIFFANT P, ANDRE J. An experimental analysis of the structural response of flexible lightweight hydrofoils in various flow conditions[C]//Proceedings of the International Symp Transp Phenom Dyn Rotating Mach, Hawaii, Honolulu, 2016.
|
| [102] |
WU Q, WANG Y N, WANG G Y. Experimental investigation of cavitating flow-induced vibration of hydrofoils[J]. Ocean Engineering, 2017, 144(1): 50-60. |
| [103] |
CHEN G H, WANG G Y, HU C L, et al. Observations and measurements on unsteady cavitating flows using a simultaneous sampling approach[J]. Experiments in Fluids, 2015, 56(32): 1-11. |
| [104] |
AKTAS B, ATLAR M, FITZSIMMONS P, et al. An advanced joint time-frequency analysis procedure to study cavitation-induced noise by using standard series propeller data[J]. Ocean Engineering, 2018, 170: 329-350. DOI:10.1016/j.oceaneng.2018.10.026 |
| [105] |
MA X J, HUANG B, ZHAO X, et al. Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries[J]. Ultrasonics Sonochemistry, 2018, 43: 80-90. DOI:10.1016/j.ultsonch.2018.01.005 |
| [106] |
郑小波, 罗兴琦, 邬海军. 轴流式叶片的流固耦合振动特性分析[J]. 西安理工大学学报, 2005, 21(4): 342-346. ZHENG X B, LUO X Q, WU H J. Analysis of fluid-solid coupling dynamic characteristics for the axial flow blades[J]. Journal of Xi'an University of Technology, 2005, 21(4): 342-346. DOI:10.3969/j.issn.1006-4710.2005.04.002 (in Chinese) |
| [107] |
王福军, 赵薇, 杨敏, 等. 大型水轮机不稳定流体与结构耦合特性研究Ⅱ:结构动应力与疲劳可靠性分析[J]. 水利学报, 2012, 43(1): 15-21. WANG F J, ZHAO W, YANG M, et al. Analysis on unsteady fluid-structure interaction for a large scale hydraulic turbine Ⅱ. Structure dynamic stress and fatigue reliability[J]. Journal of Hydraulic Engineering, 2012, 43(1): 15-21. (in Chinese) |
| [108] |
MVNCH C, AUSONI P, BRAUN O, et al. Fluid-Structure Coupling for an Oscillating Hydrofoil[J]. Journal of Fluids and Structures, 2010, 26(6): 1018-1033. DOI:10.1016/j.jfluidstructs.2010.07.002 |
| [109] |
RYZHAKOV P B, ROSSI R, IDELSOHN S R, et al. A monolithic Lagrangian approach for fluid structure interaction problems[J]. Computational Mechanics, 2010, 46(6): 883-899. DOI:10.1007/s00466-010-0522-0 |
| [110] |
MICHLER C, HULSHOFF S J, VAN BRUMMELEN E H, et al. A monolithic approach to fluid structure interaction[J]. Computers & Fluids, 2004, 33(5): 839-848. |
| [111] |
吴钦, 黄彪, 王国玉, 等. 基于完全耦合算法的绕水翼流固耦合特性研究[J]. 船舶力学, 2017, 21(07): 804-813. WU Q, HUANG B, WANG G Y, et al. Fluid structure interaction analysis of a hydrofoil based on fully coupled algorithm[J]. Journal of Ship Mechanics, 2017, 21(07): 804-813. (in Chinese) |
| [112] |
DUCOIN A, YOUNG Y L. Hydroelastic response and stability of a hydrofoil in viscous flow[J]. Journal of Fluids and Structures, 2013, 38: 40-57. DOI:10.1016/j.jfluidstructs.2012.12.011 |
| [113] |
LEE A H, CAMPBELL R L, CRAVEN B A, et al. Fluid-structure interaction simulation of vortex-induced vibration of a flexible hydrofoil[J]. Journal of Vibration and Acoustics Transactions of the ASME, 2017, 139(4). |
| [114] |
CAUSIN P, GERBEAU J F, NOBILE F. Added-mass effect in the design of partitioned algorithms for fluid-structure problems[J]. Computer methods in applied mechanics and engineering, 2005, 194: 4506-4527. DOI:10.1016/j.cma.2004.12.005 |
| [115] |
LIU X, ZHOU L J, ESCALER X, et al. Numerical simulation of added mass effects on a hydrofoil incavitating flow using acoustic fluid-structure interaction[J]. Journal of Fluids Engineering, 2017, 139(4): 041301. DOI:10.1115/1.4035113 |
| [116] |
FARHAT C, VANDER ZEE K, GEUZAINE P H. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear aeroelasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(17): 1973-2001. |
| [117] |
CAMPBELL R L, PATERSON E G. Fluid-structure interaction analysis of flexible turbomachinery[J]. Journal of Fluids and Structure, 2011, 27: 1376-1391. DOI:10.1016/j.jfluidstructs.2011.08.010 |
| [118] |
YOUNG Y L, CHAE E J, AKCABAY D T. Hybrid algorithm for modeling of fluid-structure interaction in incompressible viscous flows[J]. Acta Mechanica Sinica, 2012, 28(4): 1030-1041. DOI:10.1007/s10409-012-0118-3 |
| [119] |
WU Q, HUANG B, WANG G Y, etc. Experimental and numerical investigation of hydroelastic response of a flexible hydrofoil in cavitating flow[J]. International Journal of Multiphase Flow, 2015, 74: 19-33. DOI:10.1016/j.ijmultiphaseflow.2015.03.023 |
| [120] |
WU Q, HUANG B, WANG G Y, et al. The transient characteristics of cloudcavitating flow over a flexible hydrofoil[J]. International Journal of Multiphase Flow, 2018, 99: 162-173. DOI:10.1016/j.ijmultiphaseflow.2017.10.006 |
| [121] |
LI K, KOU J, ZHANG W. Deep neural network for unsteady aerodynamic and aeroelastic modeling across multiple Mach numbers[J]. Nonline Dynamics, 2019, 1-21. |
| [122] |
ZHANG Z, SONG X, YE S, et al. Application of deep learning method to Reynolds stress models of channel flow based on reduced-order modeling of DNS data[J]. Journal of Hydrodynamics, 2019, 5(1): 58-65. |
| [123] |
王一伟, 黄晨光. 高速航行体水下发射水动力学研究进展[J]. 力学进展, 2018, 48: 259-298. WANG Y W, HUANG C G. Research progress on hydrodynamics of high speed vehicles in the underwater launching process[J]. Advances in Mechanics, 2018, 48: 259-298. (in Chinese) |
| [124] |
WANG C C, WU Q, HUANG B, et al. Numerical investigation of cavitation vortex dynamics in unsteady cavitating flow with shock wave propagation[J]. Ocean Engineering, 2018, 156: 424-434. DOI:10.1016/j.oceaneng.2018.03.011 |
 2020, Vol. 38
2020, Vol. 38