2. 湖南建工集团有限公司, 长沙 410004;
3. 湖南大学 土木工程学院, 长沙 410082
2. Hunan Construction Engineering Company Limited, Changsha 410004, China;
3. College of Civil Engineering, Hunan University, Changsha 410082, China
下击暴流是由强烈的下沉气流冲击地面并沿地面扩散的一种强风,具有非平稳性、突发性和强破坏性。早期由于下击暴流导致一些空难引起了学者的关注[1-2]。与常规大气边界层风场相比,下击暴流风场有显著不同[3-4];下击暴流破坏力很大,结构在下击暴流强风作用下会发生严重破坏,甚至垮塌[5]。因此下击暴流风荷载及工程结构在下击暴流作用下风致响应研究具有重要意义。
在下击暴流现场实测方面,Fujita[6-7]为研究下击暴流对飞机运营安全的影响,开展了Joint Airport Weather Studies(JAWS)和Northern Illinois Meteorological Research on Downburst(NIMROD)下击暴流实测项目,取得了下击暴流风样本。新加坡学者Choi[8]在离地高150 m观测塔上沿塔高布置了五个风观测点,得到了50多个下击暴流样本,研究了下击暴流风速随高度变化规律。Stengel[9]在输电线塔上布置13个风速仪进行现场观测,研究下击暴流作用下输电线塔破坏机理。由于下击暴流发生的尺度小、随机性强,现场实测获得下击暴流样本有限,目前关于下击暴流实测数据分析的文献较少[4]。
在下击暴流风荷载模拟及其对结构影响方面,Chen[10]提出混合随机模型模拟下击暴流,即平均风由Wood风剖面和Holmes时间函数得到,脉动风速由随时间变化的幅值调幅函数和服从标准正态分布高斯随机过程得到,并以一悬臂梁为实例计算了在下击暴流作用下的响应时程。Shehata[11]采用CFD方法,将下击暴流风速数据转换为作用于结构的风荷载进行下击暴流作用下结构响应研究。汤卓[12]为研究雷暴风场中建筑物所受风荷载,用大涡模拟方法获得雷暴冲击风荷载,并对雷暴冲击风场进行数值模拟,数值模拟结果与理论结果吻合较好。赵杨[13]利用“阶跃流法”在主动控制风洞中模拟了下击暴流突变风荷载。潘峰[14]以1000 kV钢管构架为工程背景,采用Chen提出的混合随机模型模拟下击暴流,计算了结构在下击暴流风作用下的风致振动响应。杨风利[15]采用下击暴流Vicroy经验风剖面模型模拟输电塔风荷载,研究了输电塔在下击暴流作用下的受力特性和破坏模式,但只考虑了下击暴流平均风部分。瞿伟廉[16]以Fujita记录华盛顿安德鲁空军基地一次下击暴流风速记录为模拟对象,考虑下击暴流风暴中心移动影响和出流强度演化影响模拟平均风速,采用快速傅里叶变换的谐波叠加法模拟下击暴流脉动风速。但文献[16]指出,由于缺乏下击暴流实测资料,下击暴流风速模拟尚应结合实测资料继续展开研究。黄国庆[17]对云南普立大桥桥位实测非平稳强风样本确定时变平均风并估计脉动风谱,分析了桥梁静风响应和抖振响应,研究结果表明非平稳强风采用传统分析方法会低估桥梁静风响应,采用规范风谱计算山区非平稳强风抖振响应偏于不安全。
综上所述,下击暴流风由于其具有瞬时突发性、风速大等特点,对工程结构的安全具有重要影响。由于下击暴流偶然性极强,现场实测和记录困难大。目前关于下击暴流对建筑结构和输电线塔的研究已取得一定的成果,关于桥梁结构在下击暴流作用下的响应特性则研究相对较少。
本文以湖南赤石大桥为工程背景,进行下击暴流风作用下桥梁结构风振响应研究。赤石大桥位于厦蓉高速湖南汝城至郴州段,主桥结构为四塔预应力混凝土斜拉桥,跨径布置为165 m+3×380 m+165 m。根据湖南郴州气象局提供气象资料和现场实测数据,桥址处多次突发雷暴大风[18-19]。以桥址实测下击暴流风为研究对象,采用小波变化法(WT)提取时变平均分量,得到随时间变化的调制函数,采用谐波叠加法模拟桥址区脉动风并加以调制,从而模拟得到桥址区下击暴流风时程。并对桥梁在下击暴流风场和大气边界层风场作用下的桥梁结构施工状态静风响应和非线性时域抖振响应进行了分析。本文旨在为下击暴流作用下大跨度桥梁风致响应研究提供参考。
1 下击暴流模型 1.1 下击暴流表达式下击暴流是一个非平稳随机过程,下击暴流风速U(z, t)表示为:
| $ U(z,t) = \bar U(z,t) + u(z,t) $ | (1) |
其中
按最不利情况考虑,假定不同高度处下击暴流平均风速在同一时刻达到最大值,则时变平均风速
| $ \bar U(z,t) = U(z) \times d(t) $ | (2) |
其中U(z)是沿高度变化的最大平均风速。d(t)为与时间有关的调制函数,其最大值等于1,用来描述竖向风剖面随时间变化的变化。受雷暴移动速度和径向风速影响。本文忽略下击暴流风暴中心移动引起的平均风速方向的改变,d(t)定义为[14-16]:
| $ d(t) = |{\mathit{\boldsymbol{V}}_c}(t)|/{\rm{max}}|{\mathit{\boldsymbol{V}}_c}(t)| $ | (3) |
式中Vc(t)任意时刻下击暴流平均风速。
1.3 脉动风下击暴流脉动风速可以表示为一个以时变平均风速为基准且随时间变化的幅值调制函数和一个给定功率谱的稳态高斯过程乘积:
| $ u(z,t) = \alpha (z,t)k(z,t) $ | (4) |
式中,随时间变化的幅值调制函数
| $ {S_{zz}}(z,t,\omega ) = |\alpha (z,t){|^2} \times \phi (z,\omega ) $ | (5) |
其中Szz为自谱密度,ω为频率参数,ϕ(ω)为功率谱密度函数。取两点相关系数为γ(z1, z2, ω),作用在结构上各点风速时程的功率谱密度函数矩阵S(t, ω)可表示为:
| $ S(t,\omega ) = A(t)\phi (\omega ){\bar A^{\rm{T}}}(t) $ | (6) |
式中,
对矩阵ϕ(ω)进行Cholesky分解:
| $ \phi (\omega ) = H(\omega ){\bar H^{\rm{T}}}(\omega ) $ | (7) |
H(ω)是下三角矩阵,
| $ \begin{array}{l} k({z_j},t) = \sum\limits_{m = 1}^j {\sum\limits_{l = 1}^N | } {H_{jm}}({\omega _{ml}})|\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {2\Delta \omega } {\rm{cos}}[{\omega _{ml}}t - {\theta _{jm}}({\omega _{ml}}) + {\psi _{ml}}] \end{array} $ | (8) |
式中:
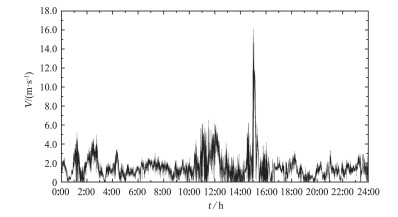
赤石大桥施工期桥位处曾出现了多次瞬时突发大风,如2013年3月20日桥址突发11级大风,距离地面10 m高度处瞬时最大风速为32.0 m/s。大风引起工棚和临时设施破坏,为此进行桥位风特性现场实测以获得桥位风特性参数,对大桥施工期的风振控制提供依据。刘志文等结合赤石大桥施工进度对桥位风特性进行了为期两年多的现场实测,获得了部分桥位风特性实测数据[18-19]。实测表明2013年~2014年桥位处共出现了17次下击暴流天气。限于篇幅,选取典型下击暴流风时程进行分析,选取的是2014年5月21日7#桥塔桥面高度处三维超声风速仪实测风速时程。按照矢量分解法处理得到顺风向风速时程,如图 1所示。风速仪距离地面184.90 m,采样频率为10.0 Hz。由图 1可知,在15:00时刻附近风速有明显的突变,为山区典型雷暴风天气。
|
图 1 2014年5月21日桥面顺风向风速时程 Fig.1 Windspeed time history of along the wind on the bridge deck on May 21, 2014 |
为便于比较,将实测风速样本进行了下击暴流风场模型与大气边界层风场(ABL)模型对比计算,本文定义下击暴流风场计算模型和大气边界层风场计算模型见表 1。
| 表 1 下击暴流风场与大气边界层风场计算模型 Table 1 Calculation models of downburst wind field and ABL wind field |
|
|
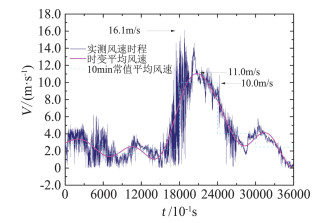
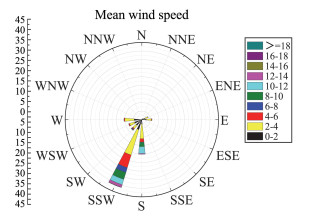
选取该天大风时段14:30-15:30进行分析(以下简称20140521风速记录)。分别提取20140521风速记录时变平均风和10 min常值平均风。采用小波变换法提取时变平均风,选取提取精度较好的Daubechies(DB10)小波函数[20-21],最佳分解层数取12层[22-23];10 min常值平均风则以10 min为时距对实测风速数据进行分段平均,图 2为20140521风速记录时变平均风速与常值平均风速时程曲线。由图 2可知,最大实测风速为16.1 m/s,最大时变平均风速为11.0 m/s,最大10 min常值平均风速为10.0 m/s。图 3为20140521风速记录顺风向风速对应风向玫瑰图。由图 3可以看出20140521风速记录主导风向为西南偏南(SSW)、南(S)。
|
图 2 时变平均风速与10 min常值平均风速 Fig.2 Time-varying mean wind speed and 10 min constant mean wind speed |
|
图 3 顺风向风速对应风向玫瑰图 Fig.3 Rosette of wind direction corresponds to wind speed along the wind |
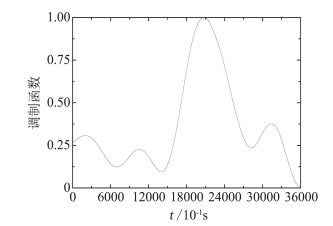
按式(3)计算出调制函数d(t),如图 4所示。
|
图 4 调制函数 Fig.4 Time function |
采用Wood风剖面模型描述下击暴流风剖面,沿高度变化最大平均风速U(z)可表示为:
| $ U(z) = 1.55{\left( {\frac{z}{\delta }} \right)^{\frac{1}{6}}} \times \left( {1 - {\rm{erf}} (0.7\frac{z}{\delta })} \right) \times {U_{{\rm{max}}}} $ | (9) |
式中,δ为高度参数,取δ=450;erf为误差函数,
| $ {U_z} = {U_{10}}{\left( {\frac{z}{{10}}} \right)^\alpha } $ | (10) |
其中:Uz为高度处z的平均风速;U10为10 m高度处的平均风速22.7 m/s,取C类地表地面粗糙度指数α=0.22。
根据桥位处离地高度184.89 m处实测风速时程,对下击暴流经验风剖面和大气边界层经验风剖面进行调制。表 2给出了下击暴流风场与大气边界层风场风剖面调制系数。其中U1为按经验风剖面计算的平均风速:在下击暴流风场下按经验风剖面计算的平均风速按式(9)计算;在大气边界层风场下按经验风剖面计算的平均风速按式(10)计算。U2为按实测风速计算最大平均风速:在下击暴流风场U2为最大时变平均风速;在大气边界层风场下U2为最大10 min平均风速。风剖面调制系数可表示为:
| $ {\rm{风剖面调制系数}} = \frac{{{\rm{按实测风速计算平均风速}}}}{{{\rm{按经验风剖面计算平均风速}}}} $ | (11) |
| 表 2 下击暴流与大气边界层风场风剖面调制系数 Table 2 Modulation coefficients of wind profiles between downburst wind field and ABL wind field |
|
|
图 5为调制后下击暴流和大气边界层风剖面。由图 5可知,下击暴流风剖面风速开始随高度的增加而增加,达到一定值后,随高度的增加而减小,与大气边界层风剖面存在显著区别。
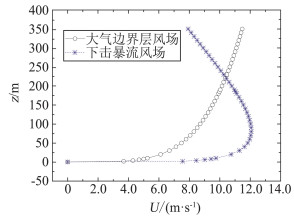
|
图 5 调制后风剖面 Fig.5 Modulated wind profiles |
根据规范[24]推荐Kaimal谱,高度z处平均风速U(z)时的水平及竖向脉动风功率谱密度函数分别为:
| $ {\frac{{n{S_u}(n)}}{{u_*^2}} = \frac{{200f}}{{{{(1 + 50f)}^{5/3}}}}} $ | (12) |
| $ {\frac{{n{S_w}(n)}}{{u_*^2}} = \frac{{6f}}{{{{(1 + 4f)}^2}}}} $ | (13) |
其中,Su(n)、Sw(n)分别为水平和竖向脉动风功率谱密度函数;n为风速频率;f=nZ/U(z); u*为摩阻速度,按风速沿高度分布对数率,可表示为u*=KU(z)/ln(z/z0), K为无量纲常数,取0.4,参考高度z取值为184.89 m,参考高度对应的平均风速U(z)=11.0 m/s。地面粗糙高度z取值为0.3。
采用谐波叠加法分别模拟了桥址下击暴流风场和大气边界层风场脉动风速,以规范谱(Kaimal谱)为目标谱,其中下击暴流脉动风速按式(4)调制得到。图 6为桥梁7号塔风场模拟位置示意图。模拟点数为18个,其中主梁共模拟11点脉动风速,桥塔模拟7点脉动风速。风场模拟主要参数为:截止频率ωu=4π rad/s,频率分段数N=2048,采样频率f=10 Hz,模拟时间Tu=3600 s。采用Matlab编写了脉动风场模拟程序,可以模拟上述18个点的脉动风速时程。限于篇幅,只给出实测点位处下击暴流风场模拟结果。图 7为模拟下击暴流脉动风功率谱与目标功率谱对比,由图 7可以得到模拟脉动风功率谱密度与采用Kaimal谱功率谱密度比较接近,从而保证了模拟方法的正确。
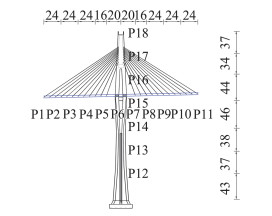
|
图 6 7号塔施工期风场模拟位置示意图(单位:m) Fig.6 Wind field simulation points of the No.7 pylon of the bridge (Unit: m) |
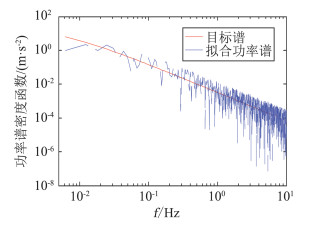
|
图 7 拟合脉动风功率谱和目标功率谱 Fig.7 Fitting fluctuating wind power spectrum and target power spectrum |
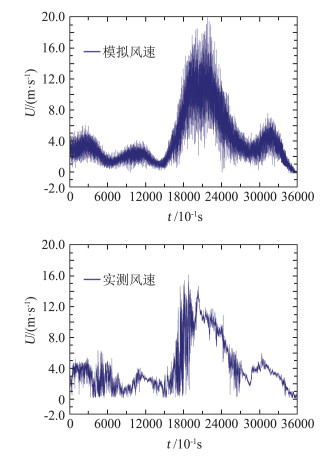
按式(4)对下击暴流风场模拟脉动风速幅值进行调制,参数η按最不利情况考虑,取η=0.11。将实测时变平均风速(图 2中实测时变平均风速)与模拟脉动风速合成为模拟下击暴流风速时程,图 8为下击暴流风速时程模拟结果。图 9为模拟下击暴流风速时程(含时变平均风速)与实测风速时程对比。由图 9可知,所模拟的下击暴流风速时程与实测风速时程总体吻合较好,模拟下击暴流风速时程较好地反映了下击暴流风速时程走势。应该指出的是,由于桥址地形等因素对实测风速的影响不在本文研究范围内,模拟下击暴流风速时程与实测风速时程存在一定偏差。
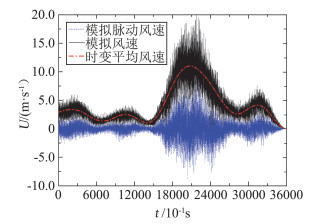
|
图 8 下击暴流风速时程模拟结果 Fig.8 Result of simulation for the downburst wind time |
|
图 9 模拟风速时程与实测风速时程对比 Fig.9 Comparison between the simulated wind time and the measured wind time |
采用小波包变换方法分别计算了下击暴流风场、大气边界层风场模拟脉动风时变功率谱密度。利用Matlab编写了计算程序,图 10为下击暴流风场、大气边界层风场模拟脉动风时变功率谱密度计算结果。由图 10可以得到,下击暴流风场模拟脉动风时变功率谱的幅值明显大于大气边界层B类风场模拟脉动风时变功率谱幅值。

|
图 10 下击暴流风场和大气边界层风场模拟脉动风时变功率谱密度 Fig.10 Time-varying power spectral density of fluctuating wind simulated under downburst wind field and atmospheric boundary layer wind field |
考虑平均风时变,作用在主梁单位长度上的抖振力为[25]:
| $ \begin{array}{*{20}{l}} {{F_{yb}}(t) = \rho \bar U(t)D{C_D}u(t) + \frac{1}{2}\rho \bar U(t)B\left( {\frac{D}{B}C_D^\prime - {C_L}} \right)w(t)}\\ {{F_{zb}}(t) = \rho \bar U(t)B{C_L}u(t) + \frac{1}{2}\rho \bar U(t)B\left( {\frac{D}{B}{C_D} + C_L^\prime } \right)w(t)}\\ {{M_x}(t) = - \rho \bar U(t){B^2}{C_M}u(t) + \frac{1}{2}\rho \bar U(t){B^2}C_M^\prime w(t)} \end{array} $ | (14) |
式中:Fyb(t)、Fzb(t)、Mx(t)分别为作用于主梁上的竖向、横向、扭转抖振力;ρ为空气密度,ρ=1.225 kg/m3;
作用在主梁单位长度上的自激力Fae(t)为:
| $ {F_{ae}}(t) = - {C^0}\delta (t) - {K^0}\delta (t) $ | (15) |
其中,C0为气动阻尼矩阵,K0为气动刚度矩阵,δ为主梁单元位移向量。
主梁单元气动阻尼矩阵为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C^0} = \frac{1}{2}\rho \bar U(t)B \times \\ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 0&{2\frac{{{A_n}}}{B}{C_D}}&{\left( {\frac{{{A_n}}}{B}C_D^\prime - {C_L}} \right)}&{ - {m_l}\left( {\frac{{{A_n}}}{B}C_D^\prime - {C_L}} \right)}&0&0\\ 0&{2{C_L}}&{\left( {\frac{{{A_n}}}{B}{C_D} + C_L^\prime } \right)}&{ - {m_l}\left( {\frac{{{A_n}}}{B}{C_D} + C_L^\prime } \right)}&0&0\\ 0&{ - 2B{C_M}}&{ - BC_M^\prime }&{{m_l}BC_M^\prime }&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{array}} \right] \end{array} $ | (16) |
主梁单元气动刚度矩阵为:
| $ {K^0} = \frac{1}{2}\rho \bar U{(t)^2}B\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 0&0&0&{\frac{{{A_n}}}{B}C_D^\prime }&0&0\\ 0&0&0&{C_L^\prime }&0&0\\ 0&0&0&{ - BC_M^\prime }&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{array}} \right] $ | (17) |
将主梁单元单位长度自激力转化为单元两端节点力,则单元节点集中力可表达为:
| $ \begin{array}{*{20}{l}} {{F_{iae}} \cdot \frac{L}{2} = - {C^0}{{\dot \delta }_i}(t)\frac{L}{2} - {K_0}{\delta _i}(t)\frac{L}{2}}\\ {{F_{jae}} \cdot \frac{L}{2} = - {C^0}{{\dot \delta }_j}(t)\frac{L}{2} - {K_0}{\delta _j}(t)\frac{L}{2}} \end{array} $ | (18) |
其中,Fiae、Fjae分别为单元i、j两端节点自激力;L为单元长度。将上式写成矩阵形式,得到作用于单元节点的气动刚度Ce0和气动阻尼矩阵Ke0,表达式为:
| $ \begin{array}{l} C_e^0 = \left[ {\begin{array}{*{20}{c}} { - {C^0}\frac{L}{2}}&0\\ 0&{ - {C^0}\frac{L}{2}} \end{array}} \right],\\ K_e^0 = \left[ {\begin{array}{*{20}{c}} { - {K^0}\frac{L}{2}}&0\\ 0&{ - {K^0}\frac{L}{2}} \end{array}} \right] \end{array} $ | (19) |
不考虑桥塔自激力作用,则桥塔单位长度截面所受风荷载为:
| $ {F_t}(t) = \left[ {\frac{1}{2}\rho u{{(t)}^2} + \rho U(t)u(t)} \right]{C_{D2}}B $ | (20) |
式中:Ft(t)作用于桥塔上的风荷载;CD2为桥塔塔柱截面阻力系数;B2为桥塔迎风面的宽度;u(t)为顺风向脉动风速;U(t)为桥塔处时变平均风速。
按照规范[24],斜拉索所受风荷载为:
| $ {F_c}(t) = \frac{1}{2}\rho U{(t)^2}{D_3}L{C_{D3}} $ | (21) |
式中:Fc(t)作用于斜拉索风荷载;CD3为斜拉索截面阻力系数;D3为斜拉索直径;L为斜拉索长度;U(t)为时变平均风速。
基于ANSYS软件对赤石大桥施工期静风响应和非线性抖振响应分析,采用Matrix27单元模拟主梁结构的气动自激力。赤石大桥主梁标准断面见图 11,主梁为单箱四室混凝土箱梁,桥宽为28.0 m,梁高为3.2 m。根据主梁节段模型风洞试验结果可知:主梁断面施工状态零度风迎角下三分力系数及其导数分别为:CD=0.6381,CL=-0.1624,CM=0.0257,C′D=0.8422,C′L=4.0917,C′M=0.8881。

|
图 11 赤石大桥主梁标准断面图(单位:cm) Fig.11 Standard cross section of main girder of the Chishi bridge (unit: cm) |
根据冲击射流模型[15]和部分实测下击暴流风特性可知,下击暴流对桥梁结构的作用主要表现为下击暴流冲击地面后所产生的水平风速对桥梁结构的影响。鉴于下击暴流风实测数据较少,且受地形影响较为复杂,目前桥梁结构在下击暴流作用下的研究相对较少。为了便于研究,本文重点考虑下击暴流水平风速对桥梁结构振动响应的影响,暂不考虑地形和风迎角效应的影响[4, 17],下击暴流风向改变对桥梁结构影响将在下击暴流风洞模拟试验中进行详细研究。
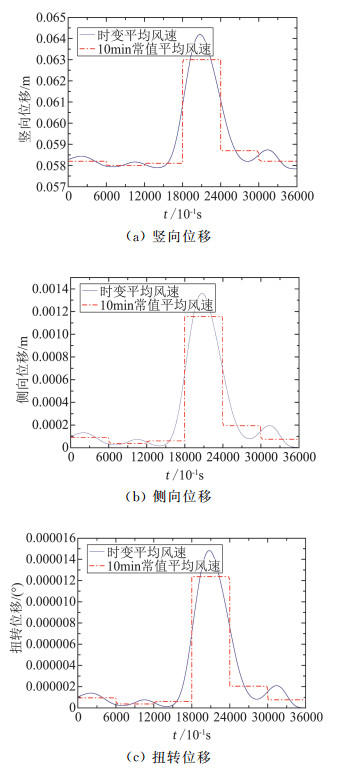
分别计算桥梁在时变平均风和10 min常值平均风下静风响应,计算时考虑静风荷载和几何非线性。图 12为主梁梁端静风响应计算结果。由图 12可知:
|
图 12 主梁梁端静风位移响应对比 Fig.12 Comparison of static wind displacements at the bridge girder end |
在静风荷载作用下的位移响应与平均风时程变化趋势一致;采用时变平均风计算的位移响应与采用10 min常值平均风计算位移存在较大差别。表 3列出主梁梁端静风响应最大值。由表 3可以看出,采用时变平均风所计算的桥梁梁端静风响应最大值均大于采用10 min常值平均风所计算的桥梁梁端静风响应最大值,且侧向和扭转位移最为明显,最大比值达到1.20倍。
| 表 3 主梁梁端静风响应最大位移值对比 Table 3 Comparison of maximum static wind displacements at the bridge girder end |
|
|
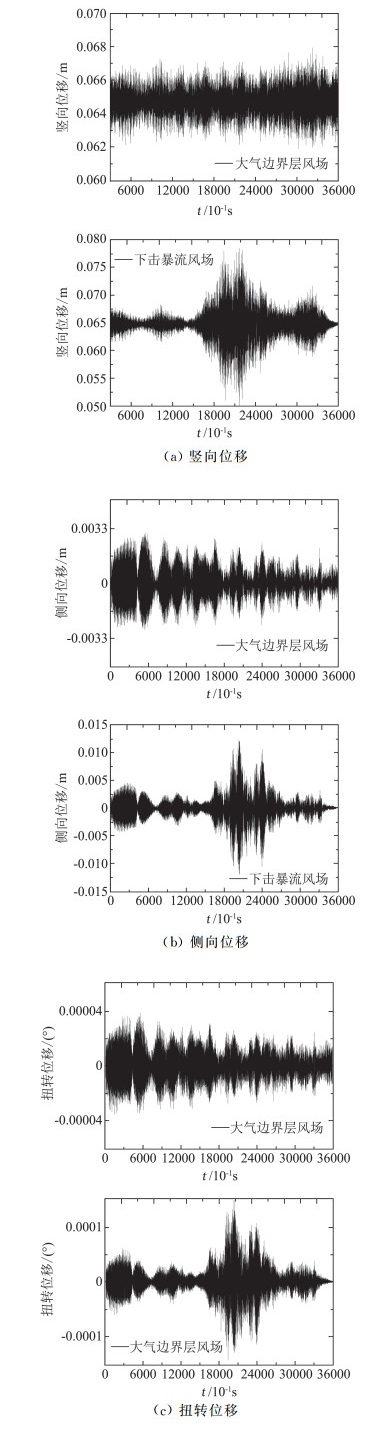
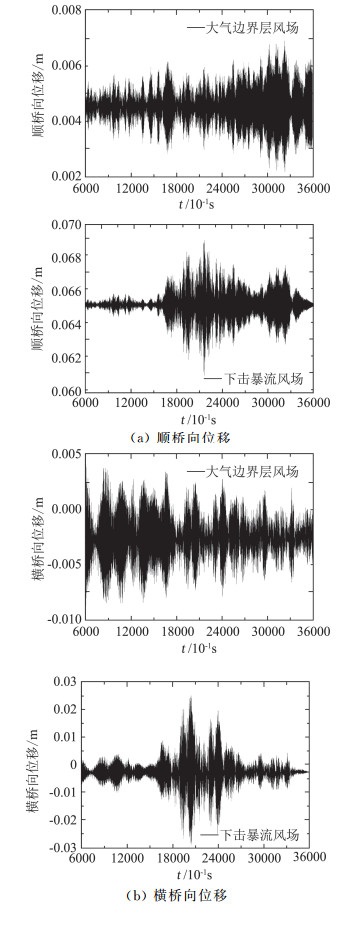
分别计算了下击暴流风场和大气边界层风场下桥梁抖振位移响应,并提取主梁梁端节点和桥塔塔顶位移时程。图 13为由两种风场计算主梁梁端竖向、侧向和扭转抖振位移响应时程对比,图 14为由两种风场计算桥塔塔顶抖振响应时程对比。由图 13、图 14可知,采用下击暴流风场计算得到的梁端抖振位移曲线与采用大气边界层风场计算得到的梁端抖振位移曲线存在较大差别。表 4给出了由两种风场计算梁端竖向、侧向和扭转抖振位移RMS计算结果。由表 4可知,采用下击暴流风场计算的主梁梁端竖向、侧向和扭转抖振位移RMS值均比采用大气边界层风场所计算的梁端竖向、侧向和扭转抖振位移RMS值大,最大比值为2.75。表 5给出了塔顶顺桥向和横桥向抖振位移RMS值的计算结果。由表 5可知,采用下击暴流风场计算的塔顶顺桥向、横桥向抖振位移RMS值也比采用大气边界层风场计算的塔顶顺桥向、横桥向抖振位移RMS值偏大,最大比值为2.78。
|
图 13 两种风场下主梁梁端抖振位移时程曲线对比 Fig.13 Comparison of curves of buffeting displacements at the main deck end under the two kinds of wind fields |
|
图 14 两种风场下桥塔塔顶抖振位移时程曲线对比 Fig.14 Comparison of curves of buffeting displacements at the pylon top under the two kinds of wind fields |
| 表 4 两种风场下主梁梁端抖振位移的RMS值对比 Table 4 Comparison of RMS values of displacements of buffeting responses at the main deck end under two kinds of wind fields |
|
|
| 表 5 两种风场下塔顶抖振位移的RMS值对比 Table 5 Comparison of RMS values of displacements of buffeting responses at the pylon top under two kinds of wind fields |
|
|
以赤石大桥现场实测下击暴流风速时程数据为基础,进行了下击暴流风场模拟方法及其对桥梁结构风致抖振响应特性研究,得到如下主要结论:
1) 桥址处实测下击暴流风速呈突变性。通过对实测风速记录模拟结果表明,模拟下击暴流风速时程与实测风速时程吻合较好。下击暴流风场模拟脉动风时变功率谱的幅值明显大于大气边界层B类风场模拟脉动风时变功率谱幅值。
2) 当桥面高度处下击暴流风与大气边界层风速相同时,采用时变平均风计算的主梁梁端静风响应最大值均大于采用10 min常值平均风计算的主梁梁端静风响应最大值,最大比值为1.20。对于下击暴流作用下桥梁静风响应,采用传统10 min常值平均计算可能会低估桥梁静风响应最大值。
3) 当桥面高度处下击暴流风与大气边界层风速相同时,采用下击暴流风场计算的主梁梁端竖向、侧向和扭转抖振位移RMS值分别比采用大气边界层风场计算的主梁梁端竖向、侧向和扭转抖振位移RMS值大,最大比值为2.75。采用下击暴流风场计算的塔顶顺桥向、横桥向抖振位移RMS值分别比采用大气边界层风场计算的塔顶顺桥向、横桥向抖振位移RMS值大,最大比值为2.78。
本文以桥址处典型实测下击暴流强风记录为例,采用经典Wood风剖面对桥梁结构进行了下击暴流作用下的风振响应进行了研究,为大跨度桥梁在下击暴流风作用下风致响应研究提供了参考。但是,山区地形桥位下击暴流风速沿高度实际分布情况和风向改变对桥梁结构影响则尚需进一步研究。
| [1] |
WILSON J W, ROBERTS R D, KESSINGER C, et al. Microburst wind structure and evaluation of doppler radar for airport wind shear detection[J]. Journal of Applied Meteorology, 1984, 23(6): 898-915. DOI:10.1175/1520-0450(1984)023 |
| [2] |
LETCHFORD C W, MANS C, CHAY M T. Thunderstorms-their importance in wind engineering (a case for the next generation wind tunnel)[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 1415-1433. doi: http://ecite.utas.edu.au/47831
|
| [3] |
EL-SAYED ABD-ELAAL, JULIE E M, XING M. Empirical models for predicting unsteady-state downburst wind speeds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 129: 49-63. DOI:10.1016/j.jweia.2014.03.011 |
| [4] |
瞿伟廉, 吉柏锋. 下击暴流的形成与扩散及其对电线塔的灾害作用[M]. 北京: 科学出版社, 2012. QU W L, JI B F. Formation and diffusion of downburst and effect on transmission tower[M]. Beijing: Science Press, 2012. (in Chinese) |
| [5] |
杜牧云, 肖艳娇, 吴涛. 多普勒天气雷达下击暴流图像识别[J]. 气象科技, 2015, 43(3): 368-372. DU M Y, XIAO Y J, WU T. Identification of downbursts based on W SR-88D doppler weather radar images[J]. Meteorological Science and Technology, 2015, 43(3): 368-372. DOI:10.3969/j.issn.1671-6345.2015.03.004 (in Chinese) |
| [6] |
FUJITA T T. Tornadoes and downbursts in the context of generalized planetary scales[J]. Journal of Atmospheric Sciences, 1981, 38: 1511-1534. DOI:10.1175/1520-0469(1981)038 |
| [7] |
FUJITA T T. The downburst: microburst and microburst[R]. SMRP Research Paper 210, University of Chicago, 1985.
|
| [8] |
EDMUND C C Choi. Field measurement and experimental study of wind speed profile during thunderstorms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92: 275-290. DOI:10.1016/j.jweia.2003.12.001 |
| [9] |
STENGEL D, THIELE K. Measurements of downburst wind loading acting on an overhead transmission line in northern Germany[J]. Procedia Engineering, 2017, 199: 3152-3157. DOI:10.1016/j.proeng.2017.09.578 |
| [10] |
CHEN L, LETCHFORD C W. A deterministic-stochastic hybrid model of downbursts and its impact on a cantilevered structure[J]. Engineering Structures, 2004, 26(5): 619-629. DOI:10.1016/j.engstruct.2003.12.009 |
| [11] |
SHEHATA A Y, EI DAMATTY A A, SAVORY E. Finite element modeling of transmission line under downburst wind loading[J]. Finite Elements in Analysis and Design, 2005, 42: 71-89. DOI:10.1016/j.finel.2005.05.005 |
| [12] |
汤卓, 吕令毅. 雷暴冲击风荷载的大涡模拟[J]. 空气动力学学报, 2011, 29(1): 47-51. TANG Z, LU L Y. Large eddy simulation of downburst wind load[J]. Acta Aerodynamica Sinica, 2011, 29(1): 47-51. DOI:10.3969/j.issn.0258-1825.2011.01.008 (in Chinese) |
| [13] |
赵杨, 曹曙阳, Yukio Tamura, 等. 雷暴冲击风模拟及其荷载的风洞试验研究[J]. 振动与冲击, 2009, 28(4): 1-9. ZHAO Y, CAO S Y, TAMURA Y, et al. Simulation and wind tunnel test on wind load of downburst[J]. Journal of Vibration and Shock, 2009, 28(4): 1-9. DOI:10.3969/j.issn.1000-3835.2009.04.001 (in Chinese) |
| [14] |
潘峰, 谢芳, 邢月龙, 等. 1000 kV特高压钢管构架雷暴冲击风致振动响应研究[J]. 空气动力学学报, 2012, 30(4): 502-507. PAN F, XIE F, XING Y L, et al. Wing-induced dynamic response of large steel tube frame for 1000 kV UHV transmission lines to thunderstorm downbursts[J]. ActaAerodynamica Sinica, 2012, 30(4): 502-507. DOI:10.3969/j.issn.0258-1825.2012.04.012 (in Chinese) |
| [15] |
杨风利, 张宏杰, 杨靖波, 等. 下击暴流作用下输电铁塔荷载取值及承载性能分析[J]. 中国电机工程学报, 2014, 34(24): 4179-4186. YANG F L, ZHANG H J, YANG J B, et al. Bearing capacity analysis and load values of transmission towers under thunderstorm downburst[J]. Proceedings of the CSEE, 2014, 34(24): 4179-4186. DOI:10.13334/j.0258-8013.pcsee.2014.24.023 (in Chinese) |
| [16] |
瞿伟廉, 吉柏锋, 王锦文. 基于改进的OBV模型的下击暴流风荷载模拟[J]. 地震工程与工程振动, 2009, 29(1): 146-152. QU W L, JI B F, WANG J B. Numerical simulation of downburst wind loads based on modified OBV model[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(1): 146-152. (in Chinese) |
| [17] |
黄国庆, 苏延文, 彭留留, 等. 山区风作用下大跨悬索桥响应分析[J]. 西南交通大学学报, 2015, 50(4): 610-616. HUANG G Q, SU Y W, PENG LL, et al. Response analysis of long-span suspension bridge under mountainous winds[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 610-616. DOI:10.3969/j.issn.0258-2724.2015.04.006 (in Chinese) |
| [18] |
刘志文, 丁冬, 贾亚光, 等. 山区大跨斜拉桥悬臂施工期风振响应实测[J]. 湖南大学学报:自然科学版, 2017, 44(1): 16-22. LIU Z W, DING D, JIA Y G, et al. Field measurement of wind-induced vibration responses of a large cable-stayed bridge during construction stages in mountainous terrain[J]. Journal of Hunan University:Natural Sciences, 2017, 44(1): 16-22. DOI:10.16339/j.cnki.hdxbzkb.2017.01.003 (in Chinese) |
| [19] |
辛亚兵, 邵旭东, 刘志文, 等. 高墩多塔斜拉桥沿桥轴向风特性实测分析[J]. 湖南大学学报:自然科学版, 2016, 43(11): 103-111. XIN Y B, SHAO X D, LIU Z W, et al. Wind characteristics along the bridge axis measured at multi-pylon cable-stayed bridge site with high piers[J]. Journal of Hunan University:Natural Sciences, 2016, 43(11): 103-111. DOI:10.16339/j.cnki.hdxbzkb.2016.11.015 (in Chinese) |
| [20] |
何旭辉, 陈政清, 李春光. 斜拉索风雨振非平稳风场特性分析[J]. 振动与冲击, 2011, 30(10): 54-60. HE X H, CHEN Z Q, LI C G, et al. Nonstationary wind characteristics analysis for wind-rain induced vibration of stay cables[J]. Journal of Vibration and Shock, 2011, 30(10): 54-60. DOI:10.3969/j.issn.1000-3835.2011.10.012 (in Chinese) |
| [21] |
申建红, 李春祥, 李锦华. 基于小波变换和EMD提取非平稳风速中的时变均值[J]. 振动与冲击, 2008, 27(112): 126-130. SHEN J H, LI C X, LI J H. Extracting time-varying mean of the non-stationary wind speeds based on wavelet transform and EMD[J]. Journal of Vibration and Shock, 2008, 27(112): 126-130. DOI:10.3969/j.issn.1000-3835.2008.12.028 (in Chinese) |
| [22] |
方俊.基于小波分析的斜拉桥拉索风雨振非平稳性研究[D].长沙: 中南大学土木工程学院, 2010. FANG J. Study on non-stationary characteristics of wind-rain-induced vibration of stay cables based on wavelet analysis[D]. Changsha: School of Civil Engineering Central South University, 2010. (in Chinese) |
| [23] |
辛亚兵, 刘志文, 邵旭东, 等. 山区地形实测风非平稳性和非高斯性分析[J]. 振动与冲击, 2018, 37(21): 247-252. XIN Y B, LIU Z W, SHAO X D, et al. Analysis of non-stationary and non-Gaussian feature of wind measured in mountainous terrain[J]. Journal of Vibration and Shock, 2018, 37(21): 247-252. DOI:10.13465/j.cnki.jvs.2018.21.035 (in Chinese) |
| [24] |
JTG/T 3360-01-2018.公路桥梁抗风设计规范[S]. 2018-11-19. JTG/T 3360-01-2018. Wind-resistant design specifications for highway bridges[S]. 2018-11-19. (in Chinese) |
| [25] |
AAS-JAKOBSENA K, STROMMEN E. Time domain buffeting response values of slender structures[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 89(5): 341-364. |
 2020, Vol. 38
2020, Vol. 38


