2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
表面热流辨识是通过材料边界或内部的温度测量值来反演表面热流,是一类典型的热传导逆问题,在航空航天、冶金制造等领域有广泛的应用。表面热流辨识是数学上的不适定问题,不满足解的稳定性,也就是说即使测点温度存在较小测量白噪声也可能导致解的“爆破”;具体来说,在频域,表面热流的辨识误差在白噪声的影响下随着频率的升高逼近无界。这给辨识精度估计带来了难度,而在工程实际的测热系统设计时,希望能够在对热环境有大致预测的情况下对其辨识结果误差给出较为准确的估计,进而根据辨识结果精度要求来确定传感器的测量位置和测量精度。文献[1]针对这一问题进行了探讨,结果显示,辨识结果误差不仅与防热材料物性参数、测量点位置、测量噪声形式、测量噪声大小有关,而且还与表面热流本身的频域特性有关。将傅立叶数作为相似参数,可以对辨识结果误差进行初步的分析。但是这一结果给出的主要还是定性分析的结论,在定量评估上还存在不足。因此,本文工作是文献[1]的进一步深入探索,首先对给定单一频率的热流辨识误差进行定量分析,然后结合频域分析方法[2-3]对两个和多个给定频率组合情况下的误差规律进行分析,初步建立热流辨识误差的定量分析方法。
1 热流辨识方法及辨识结果误差定义对典型的一维热传导问题,采用文献[1]中的无量纲方法后,传热方程可写为:
| $ \frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k\frac{{\partial T}}{{\partial x}}} \right) $ | (1) |
边界条件:
初始条件:t=0:T=0
观测方程:
其中,xi(i=1, P)为温度测点位置;P为测点数目;
表面热流辨识方法主要有顺序函数法和共轭梯度法[4-5],本文采用共轭梯度法来对式(1)进行表面热流辨识,共轭梯度法将辨识问题转化为求合适的Q(t)使如下目标函数达极小的优化问题:
| $ \begin{array}{l} J = \sum\limits_i {\int_0^{{t_f}} {{{\left[ {T\left( {{x_i}, t} \right) - \tilde T\left( {{x_i}, t} \right)} \right]}^2}} } {\rm{d}}t + \\ \int_0^{{t_f}} {\int_0^1 {\left[ {\frac{\partial }{{\partial x}}\left( {k\frac{{\partial T}}{{\partial x}}} \right) - \frac{{\partial T}}{{\partial t}}} \right]} } \lambda (x, t){\rm{d}}x{\rm{d}}t \end{array} $ |
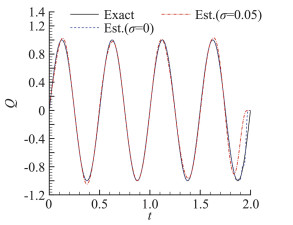
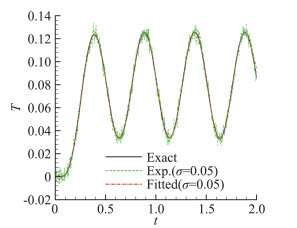
对上式做变分后可以得到伴随变量满足的伴随方程,同时可以得到目标函数对Q的梯度,然后代入具有“停止准则”的共轭梯度法进行优化计算;“停止准则”是一种迭代正则化方法,可以有效抑制辨识结果的高频非物理振荡。具体算法和有效性验证参见文献[5, 6]。图 1给出了典型算例的辨识结果,此时的表面热流真值取为频率f=2 Hz的正弦函数,即图 1中的“Exact”,测点位于绝热端x=1,算例中相应的无量纲量k为1。“Est.(σ=0)”表示不考虑测点温度测量误差情况下的热流辨识结果,“Est.(σ=0.05)”表示在测点温度叠加标准差σ=0.05Tmean白噪声情况下(图 2中的“Exp.(σ=0.05)”)的热流辨识结果,Tmean为测点温度变化平均值。从图中可以看到,在不考虑测量噪声和测量噪声标准差σ=0.05的情况下,热流辨识结果和真值都符合;在考虑测量噪声情况下,根据热流辨识结果计算出的测点温度(图 2中“Fitted(σ=0.05)”)也与测量值符合,表明辨识算法是有效的。
|
图 1 热流真值与辨识结果对比 Fig.1 Comparison of exact and estimated value of heat flux |
|
图 2 测点温度测量值与辨识拟合值对比 Fig.2 Comparison of measurement temperature |
定义辨识结果与真值之间的相对误差E为:
| $ {\rm{E = }}\sqrt {\int_{t1}^{t2} {{{\left[ {Q\left( t \right) - \hat Q\left( t \right)} \right]}^2}{\rm{d}}t} } /\sqrt {\int_{t1}^{t2} {{{\left[ {Q\left( t \right)} \right]}^2}{\rm{d}}t} } $ | (2) |
从图 1可以看到,由于传热的延迟特性,测点温度信息对表面热流尾段值不敏感,导致热流尾段值与真值存在一定误差,因而在式(2)计算时只取中间一段来进行分析,即t1=0.25,t2=1.25。此外,由文献[1]分析知,在白噪声的影响下辨识结果误差同样具有一定的随机性。为克服这一影响,采用如下方法:首先给定相同均值、相同标准差的N组白噪声;对叠加这些噪声后的测量结果分别辨识得出相对误差值Ei(i=1, N);然后对这些相对误差值取平均,将该平均值作为对应这一噪声标准差水平的平均相对误差值,记为Em,即
| $ {E_m} = \frac{1}{N}\sum\limits_{i = 1}^N {{E_i}} ;N = 64 $ | (3) |
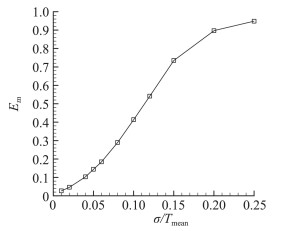
采用上节方法,首先针对五组不同频率(f=1, 2, 5, 8, 10 Hz)正弦形式热流在不同测量噪声方差σ=0.01Tmean、0.02Tmean、0.05Tmean、0.1Tmean情况下的辨识结果平均相对误差进行分析,计算结果如表 1所示,图 3中给出了频率10 Hz情况下不同噪声水平对应的热流辨识结果误差。
|
图 3 频率10 Hz不同噪声水平对应的热流辨识结果误差 Fig.3 Estimation error for 10 Hz heat flux with reapect to noise standard devition |
| 表 1 不同频率下对应不同噪声水平的热流辨识结果与给定值平均误差Em Table 1 Mean error of estimated heat flux with different frequencies for different noise standard devition levels |
|
|
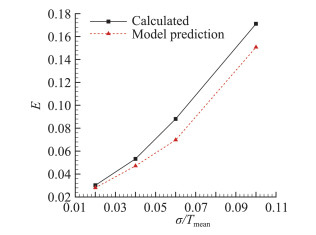
接下来以表 1中的f和σ/Tmean为输入,以Em为输出,采用Kriging响应面模型[7]进行建模,然后利用该模型对频率7 Hz热流在测量噪声水平σ=0.02Tmean、0.04Tmean、0.06Tmean、0.1Tmean情况下的辨识结果平均相对误差值进行预测,并与实际计算结果进行对比。如图 4所示,图中“Model prediction”为Kriging模型预测结果,“Calculated”为实际计算结果。从图中可以看到,模型预测结果与实际计算结果符合较好,数值略偏低。
|
图 4 频率7 Hz热流的辨识结果误差预测结果对比 Fig.4 Comparison of calculated and predicted estimation error for 7 Hz heat flux |
对于频率组合热流,选取如下几组热流进行分析:
| $ \begin{array}{*{20}{l}} {{\rm{a}}.Q(t) = 0.5\sin \left( {2\pi {f_1}t} \right) + 0.5\sin \left( {2\pi {f_2}t} \right);}\\ {{\rm{b}}.Q(t) = 0.8\sin \left( {2\pi {f_1}t} \right) + 0.2\sin \left( {2\pi {f_2}t} \right);}\\ {{\rm{c}}.Q(t) = 0.2\sin \left( {2\pi {f_1}t} \right) + 0.8\sin \left( {2\pi {f_2}t} \right);}\\ {{\rm{d}}.Q(t) = \frac{1}{3}\left[ {\sin \left( {2\pi {f_1}t} \right) + \sin \left( {2\pi {f_2}t} \right) + \sin \left( {2\pi {f_3}t} \right)} \right];} \end{array} $ | (4) |
其中f1=2 Hz,f2=10 Hz,f3=5Hz。
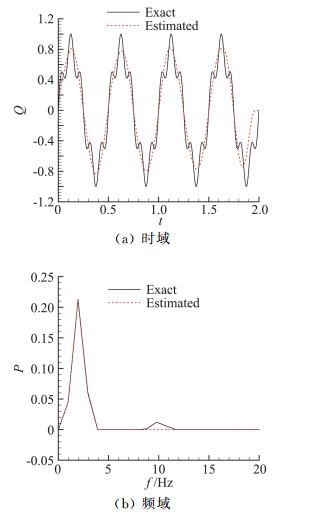
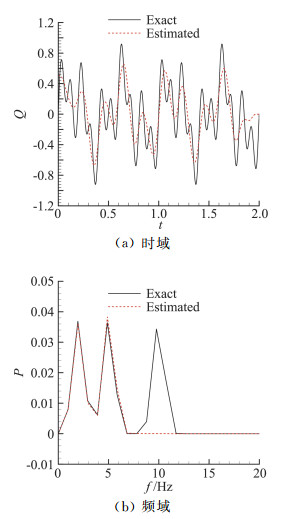
采用与上一小节相同的方法来计算不同噪声水平σ=0.01Tmean、0.02Tmean、0.05Tmean情况下的辨识结果平均相对误差值。图 5、图 6给出了σ=0.05Tmean情况下热流b和热流d的理论值、时域辨识值结果对比和频域的功率谱对比。从频域分析结果可以看到,在低频段,辨识结果与真值较为一致,差异主要体现在高频分量上。由此可知,对于频率组合的热流,低频分量能在辨识结果得到较好地复现,高频分量是导致辨识结果与理论值出现差异的主要原因,因此,辨识结果精度可以通过最高频率热流分量与测量噪声之间的对应关系来进行大致估计。
|
图 5 热流b理论值、时域辨识值结果和频域功率谱对比 Fig.5 Comparison of exact and estimated value in time and frequency domain for heat flux b |
|
图 6 热流d理论值、时域辨识值结果和频域功率谱对比 Fig.6 Comparison of exact and estimated value in time and frequency domain for heat flux d |
选取两种频率组合的情况进行分析,以热流b为例,将其重写为:
| $ \begin{array}{*{20}{l}} {Q(t) = {Q_1}(t) + {Q_2}(t)}\\ {{Q_1}(t) = 0.8\sin \left( {2\pi {f_1}t} \right), {Q_2}(t) = 0.2\sin \left( {2\pi {f_2}t} \right)} \end{array} $ |
并记Q1和Q2的辨识值为
| $ \begin{array}{*{20}{l}} {{E^2} = \frac{{\int_{t1}^{t2} {{{\left( {{Q_1} - {{\hat Q}_1}} \right)}^2}} {\rm{d}}t + \int_{t1}^{t2} {{{\left( {{Q_2} - {{\hat Q}_2}} \right)}^2}} {\rm{d}}t}}{{\int_{t1}^{t2} {Q_1^2} {\rm{d}}t + \int_{t1}^{t2} {Q_2^2} {\rm{d}}t}}}\\ { = \frac{{E_1^2\int_{t1}^{t2} {Q_1^2} {\rm{d}}t + E_2^2\int_{t1}^{t2} {Q_2^2} {\rm{d}}t}}{{\int_{t1}^{t2} {Q_1^2} {\rm{d}}t + \int_{t1}^{t2} {Q_2^2} {\rm{d}}t}}} \end{array} $ | (5) |
式中E1、E2表示Q1和Q2的辨识结果误差,由前面分析知,E1≈0,所以上式简化为:
| $ E = \frac{{{E_2}}}{{\sqrt {1 + C} }};\;\;\;C = \frac{{\int_{t1}^{t2} {Q_1^2} {\rm{d}}t}}{{\int_{t1}^{t2} {Q_2^2} {\rm{d}}t}} $ | (6) |
对于Q1和Q2,在时域无法分开,但在频域可分开,因此,由Parseval(帕塞瓦尔)定理[8]及图 5、图 6可知:
| $ \begin{array}{*{20}{l}} {\int_{t1}^{t2} {Q_1^2} {\rm{d}}t = \int_{{f_1} - \Delta }^{{f_1} + \Delta } P (f){\rm{d}}f}\\ {\int_{t1}^{t2} {Q_2^2} {\rm{d}}t = \int_{{f_2} - \Delta }^{{f_2} + \Delta } P (f){\rm{d}}f} \end{array} $ | (7) |
式中Δ为离散变换引起的频率变化量。则式(6)可另写为:
| $ E = \frac{{{E_2}}}{{\sqrt {1 + C} }};\;\;\;{\kern 1pt} C = \frac{{\int_{{f_1} - \Delta }^{{f_1} + \Delta } P (f){\rm{d}}f}}{{\int_{{f_2} - \Delta }^{{f_2} + \Delta } P (f){\rm{d}}f}} $ | (8) |
其中C的物理含义为频域中高频分量与低频分量的能量值对比。
对于N种频率组合(N≥3)的情况,设f1 < f2 < … < fN,由图 6知,与两种频率组合时类似,N种频率组合情况下的辨识结果与真值差异主要集中在最高频分量上,此时的误差值为:
| $ \begin{array}{l} E = \frac{{{E_N}}}{{\sqrt {1 + \sum\limits_{i = 1}^{N - 1} {{C_i}} } }};\;\;\;{\kern 1pt} {C_i} = \frac{{\int_{{f_i} - \Delta }^{{f_i} + \Delta } P (f){\rm{d}}f}}{{\int_{{f_N} - \Delta }^{{f_N} + \Delta } P (f){\rm{d}}f}}\\ \;\;\;\;\;\;\;\;\;\;\left( {i = 1, N - 1} \right) \end{array} $ | (9) |
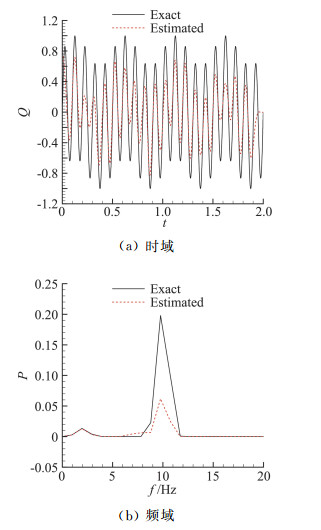
对于式(4)中的四种热流,由各自频谱曲线进行简单的积分运算可计算出C值,对热流a,C≈1.0;热流b,C≈16.0;热流c,C≈0.062;热流d,C1≈C2≈1.0;而对于式(9)中测量误差引起的最高频分量辨识结果误差EN的计算则略为复杂,首先需要计算测量误差与最高频热流分量振幅之间的比值,然后再基于这一比值从最高频热流分量的“测量噪声~辨识结果误差”曲线(类似图 3)中得出EN值。以热流c(图 7)为例,此时最高频热流分量的频率为10 Hz,振幅为0.8,C≈0.062,可计算出测点平均温升Tmean=0.0266;当测量误差σ=0.01Tmean时,由前面分析知,该误差将全部作用到10 Hz分量上,相当于10 Hz分量对应s=0.01Tmean/(0.8Tm10 Hz)=0.0228情况,其中Tm10 Hz为单独10 Hz热流振幅为1时对应的测点平均温升,本算例中计算值为0.01457;最后由s值在图 3中插值得出E2=0.0546;代入式(8)可估算出此时对组合热流的误差为E=0.0530,与采用式(3)和叠加64组同分布白噪声的热流辨识统计平均值0.0501接近。
|
图 7 热流c理论值、时域辨识值结果和频域功率谱对比 Fig.7 Comparison of exact and estimated value in time and frequency domain for heat flux c |
表 2也给出了对其余几组频率组合情况下采用上述方法的估计结果(表中“估算值”),并与采用式(3)和叠加64组同分布白噪声的热流辨识统计平均结果(表中“计算值”)进行了比较,可以看到,两组结果符合较好。
| 表 2 典型频率组合热流的辨识结果平均误差计算结果与分析预测结果对比 Table 2 Comparison of calculated and predicted mean error for estimated multiple-frequency combined heat flux |
|
|
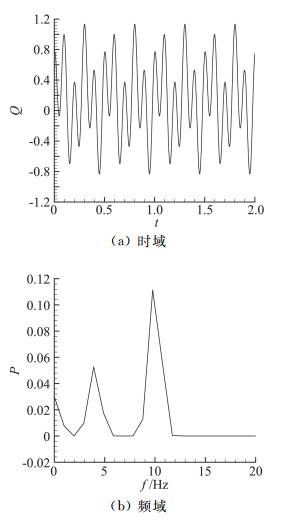
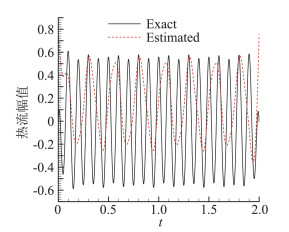
下面考虑更一般的情况,前面的分析中事先已知了热流中各分量的频率、幅值、相位等信息,且热流均值为0。而在工程实际应用中,这些信息,尤其是热流的幅值和相位信息不是十分明确,此时的估算方法需更多地借助频域分析技术。考虑图 8(a)的热流,对其进行频谱分析,得出功率谱如图 8(b),由功率谱知该热流的最大频率为10 Hz;由于热流均值不为0,频谱中包含低频分量;同时热流中还包含有频率为4 Hz的分量。由图中频谱曲线积分可知,低频分量对应的C1≈0.125,4 Hz分量对应的C2≈0.445。接下来还需要确定10 Hz热流分量的幅值,采用的方法是先滤掉热流中最大频率f=10 Hz的成分,再用原始热流值减去滤波后的热流,即得对应频率10 Hz的热流分量幅值,如图 9中的“Exact”示,可知,其幅值近似等于0.55。因此,当测量误差σ=0.005Tmean时,由前面分析知,该误差将全部作用到10 Hz分量上,相当于10 Hz分量对应s= 0.005Tmean/(0.55Tm10 Hz)情况,Tm10 Hz值在之前已计算出Tm10 Hz=0.01457,测点平均温升Tmean的值由式(1)计算出为Tmean=0.1414。于是,当σ=0.005Tmean时,s=0.0880,在图 3中插值得出E3=0.3396;代入式(9)可估算出此时对组合热流的误差为:
| $ E = \frac{{0.3396}}{{\sqrt {1 + 0.125 + 0.445} }} \approx 0.2710 $ | (10) |
|
图 8 待分析热流及其功率谱 Fig.8 Exemplified heat flux and its power spectrum |
|
图 9 高频热流分量的幅值计算 Fig.9 Amplitude calculation of high frequency component of heat flux |
该值与采用式(3)和叠加64组同分布白噪声的热流辨识统计平均值0.2576符合较好。进一步考虑测量误差σ=0.01Tmean的情况,可采用类似方法计算出s=0.176,E3=0.8196,E=0.6541,与采用式(3)和叠加64组同分布白噪声的热流辨识统计平均值0.6176也符合较好,进一步验证了估计方法的有效性。
综上所述,对于一多频率组合热流,快速分析其辨识结果误差的具体步骤为:
1) 对待分析的热流进行频谱分析,获知最大频率以及其余频率的能量占比;
2) 通过滤波计算获得对应最大频率热流分量的振幅AmaxHz;
3) 针对最大频率的周期热流,计算其测点平均温升TmaxHz及如图 3所示的“辨识结果误差~测量误差”对应关系曲线;
4) 由式(1)计算待分析热流对应的Tmean;
5) 根据测量误差及TmaxHz、Tmean、AmaxHz计算s;
6) 由s值在步骤(3)得出的“辨识结果误差~测量误差”关系曲线中插值得EN值;
7) 由式(9)估算出待分析热流的辨识结果误差E。
4 结论本文对表面热流的辨识误差进行了深入分析,首先对单一频率的热流辨识误差建立了其与热流频率和测量精度之间的响应面模型。然后重点对多个频率组合情况下的辨识结果误差进行了定量分析。结果显示,频率组合热流中的低频分量在辨识结果中能较好地复现,辨识结果误差可只考虑高频分量的辨识结果误差。于是,由辨识误差定义出发,通过频谱分析方法可计算出组合热流中高频分量的振幅及能量占比,进而建立了组合热流的辨识误差的估算方法,并通过多个算例进行了验证。这一结果一方面有较强的理论意义,揭示了频率组合热流与单一频率热流辨识误差之间的内在关联,深化了对辨识结果时域、频域特性的认识,并且不仅对传热逆问题适用,对其余领域的逆问题误差分析也有一定的参考价值。另一方面,这一结果在工程上也有实用价值,可减少“暴力”的仿真辨识计算,尤其是形成一些数据库后甚至可不进行数值计算,直接查表即可对辨识结果误差进行大致估算。
下一步,方法还需要在以下三个方面进行完善和推广,一是目前分析中热流的组合频率值较为稀疏,在频域中表现为离散谱,便于开展分析,而对于频谱范围较宽、频谱特性为连续谱的情况,需进一步挖掘辨识计算的“停止准则”与热流功率谱之间的内在关联,开展深入研究。二是温度的采样频率对辨识误差的影响。采样频率提高有利于热流辨识精度的提高,但是采样频率与热流辨识精度的定量关系还需进一步分析。三是目前分析中噪声形式只考虑了白噪声形式,对于有色噪声的情况还需要分析拓展。
| [1] |
钱炜祺, 周宇, 邵元培, 等. 表面热流可辨识性初步分析[J]. 实验流体力学, 2013, 27(4): 17-22. QIAN W Q, ZHOU Y, SHAO Y P, et al. A preliminary analysis of identifiability of surface heat flux[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(4): 17-22. DOI:10.3969/j.issn.1672-9897.2013.04.004 (in Chinese) |
| [2] |
BLUM J, MARQUARDT W. An optimal solution to inverse heat conduction problems based on frequency-domain interpretation and observers[J]. Numerical Heat Transfer, Part B, 1997, 453-478. |
| [3] |
PRUD'HOMME M, NGUYEN T H. Fourier analysis of conjugate gradient method applied to inverse heat conduction problems[J]. International Journal of Heat and Mass Transfer, 1999, 4447-4460. |
| [4] |
ALIFANOV O M. Inverse heat transfer problems[M]. Berlin: Springer-Verlag, 1994.
|
| [5] |
钱炜祺, 何开锋, 桂业伟, 等. 非稳态表面热流反演算法研究[J]. 空气动力学学报, 2010(2): 155-161. QIAN W Q, HE K F, GUI Y W, et al. Inverse estimation of surface heat flux for three-dimensional transient heat conduction problem[J]. Acta Aerodynamica Sinica, 2010(2): 155-161. DOI:10.3969/j.issn.0258-1825.2010.02.006 (in Chinese) |
| [6] |
钱炜祺, 周宇, 何开锋, 等. 非线性热传导逆问题的表面热流辨识方法[J]. 空气动力学学报, 2012(2): 145-150. QIAN W Q, ZHOU Y, HE K F, et al. Estimation of surface heat flux for nonlinear inverse heat conduction problem[J]. Acta Aerodynamica Sinica, 2012(2): 145-150. DOI:10.3969/j.issn.0258-1825.2012.02.002 (in Chinese) |
| [7] |
SIMPSON T W, et al. Kriging models for global approximation in simulation-based multidisciplinary design optimization[J]. AIAA Journal, 2001(12): 2233-2241. |
| [8] |
王里生, 罗永光. 信号与系统分析[M]. 长沙: 国防科技大学出版社, 1989. WANG L S, LUO Y G. Signals and system analysis[M]. Changsha: National University of Defense Technology Press, 1989. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38


