物面变形或运动下的非定常流动数值模拟、气动外形优化设计、静/动气动弹性计算中外形随时间发生变化,需要对流场计算网格进行更新以获取新外形下的流场,动态网格生成技术是解决这一问题的有效途径[1]。动态网格生成主要有两种实现方式:网格变形与网格重构。相比网格重构,网格变形具有算法简单、计算量小、自动化程度高和不改变网格拓扑及不引入新的离散误差等优点,能够减小网格变化对数值模拟结果的影响,在气动优化和流/固耦合模拟中被广泛采用[2]。但网格变形技术也存在一个明显的缺点,即在变形后网格质量会降低,尤其是大变形情况下,可能会出现网格单元交叉或负体积单元的现象,导致流场模拟失败。另一方面,在非定常计算中,网格变形方法会被反复调用,网格更新的时间消耗是影响流动模拟效率的关键因素。因此,发展高效/鲁棒/高质量的网格变形算法一直是动态网格生成领域的研究热点[3]。
近十年,一些优秀的网格变形算法相继被提出,如Delaunay背景映射[4]、径向基插值(Radial Basis Functions, RBF)[5-9]、反向距离加权(Inverse Distance Weight, IDW)[10]等代数方法,逐步取代早期采用基于偏微分方程求解的方法,成为目前网格变形采用的主要思路。而一些综合两种或多种方法的复合型网格变形策略也展现出更好的网格变形能力和更新效率,例如RBF-Delaunay[11]、RBFs-MSA[12]、RBF-TFI[13]等,其中RBF-TFI方法因其优异网格变形能力在多种问题中得到应用[14]。
尽管网格变形方法逐步趋向成熟和多样化,已经能够解决十分复杂的工程问题[15],但目前的算法实现主要以研究型代码为主,尚未有高效/鲁棒/易用的模块化网格变形程序供学术研究和工程问题模拟使用。
国家数值风洞(National Numerical Windtunnel, NNW)项目是中国政府在2018年底启动的大型自主软件研发项目,致力于发展以计算流体动力学(Computational Fluid Dynamics, CFD)为核心的流体数值模拟软件群,构建CFD产业应用生态圈,通过以点带面,推动中国计算机辅助设计行业的发展,助力未来中国制造业向着智能化、数字化方向升级。作为NNW项目共性基础库的重要组成部分,网格变形技术模块在吸收前期课题组研究代码的基础上,通过逻辑梳理、代码重构、接口规范、功能扩展和算例测试,首先实现了多块结构网格变形程序(Structured Grid Deformation Program, SGDP)V1.0版本的开发。目前,SGDP V1.0正在NNW项目内部开展测试,待成熟完善后,将在全国范围内推广使用,作为学术研究或工程问题模拟的有力工具逐步应用于气动外形优化、流/固耦合模拟等领域。
本文的目的是通过对SGDP V1.0程序的理论方法、组成架构、主要功能、运行方法、运行性能和工程应用等进行简要介绍,让使用者对SGDP程序有更深入的认识,促进用户之间进行交流和发现问题,推动SGDP的持续良性发展,为整个CFD行业提供性能更加优异的基础程序库。
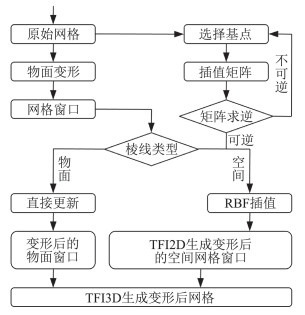
1 SGDP V1.0简介 1.1 理论方法结构网格变形程序SGDP V1.0采用了径向基函数(Radial Basis Functions, RBF)与超限插值(Transfinite Interpolation, TFI)结合的复合型动态网格变形方法来对物面变形后的网格进行更新。RBF方法能够获得高质量的变形网格,但标准形式的RBF为了保证物面的精确变形,需要将所有物面网格点选做径向基基点,导致插值矩阵庞大、计算效率低和鲁棒性差等问题。TFI方法基于棱线的网格点分布特性即可重构出新的面和体网格,具有良好的计算效率和网格质量,但TFI无法对物面变形后的网格棱线进行更新。复合方法RBF-TFI利用RBF对物面变形后的空间棱线坐标进行更新,然后利用TFI方法重构得到变形后的空间面网格和体网格。RBF-TFI方法中,变形后的物面网格直接利用物面网格点位移进行更新得到,物面的精准变形得到保证,从而RBF可以选择少量的径向基基点,能够极大改善网格变形的效率和鲁棒性。RBF-TFI方法具体的网格更新流程如图 1所示,其中为了保证物面和空间棱线交叉位置的一致性,选择基点时需要将空间棱线与物面连接的点选做径向基基点。基点选择算法首先选择所有物面网格窗口的角点,然后调用重复点查找模块去除重复的角点,并通过“贪婪”算法选择其他物面网格点作为剩余的径向基基点。
|
图 1 RBF-TFI方法网格更新流程 Fig.1 Grid updating procedure of RBF-TFI method |
SGDP V1.0中采用了不带多项式的RBF,可实现远场网格保持静止,并对网格块的棱线进行坐标更新。
径向基函数插值可以表示为:
| $ d(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^N {{\alpha _i}} \varphi \left( {\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right\|} \right) $ | (1) |
式中:d为网格点的位移,x为网格点的坐标矢量,N为径向基插值基点的数量,αi(i=1, 2, …, N)为插值系数,φ为基函数,‖x-xi‖为两点之间的距离。
两点之间距离‖x-xi‖可以表示为:
| $ \left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right\| = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} $ | (2) |
已知N个插值基点位置xi(i=1, 2, …, N)的位移di,利用式(1)可以构建关于N个关于插值系数ai的线性方程组
| $ \left[ {\begin{array}{*{20}{c}} {{\varphi _{x1x1}}}&{{\varphi _{x1x2}}}& \cdots &{{\varphi _{x1xN}}}\\ {{\varphi _{x2x1}}}&{{\varphi _{x2x2}}}& \cdots &{{\varphi _{x2xN}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{\varphi _{xNx1}}}&{{\varphi _{xNx2}}}& \cdots &{{\varphi _{xNxN}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\alpha _2}}\\ \vdots \\ {{\alpha _N}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_N}} \end{array}} \right] $ | (3) |
式中
| $ {\varphi _{xixj}} = \varphi \left( {\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|} \right) $ | (4) |
求解方程组(3)得到插值系数ai,然后利用式(1)可以插值得到任意位置x的位移d(x)。
变形网格质量与基函数的类型有关,根据大量网格算例测试结果,本文选择网格质量调控能力较好的Wendland’s C2函数,具体表示为:
| $ \varphi (\eta ) = \left\{ {\begin{array}{*{20}{l}} 0&{, \eta > 1}\\ {{{(1 - \eta )}^4}(4\eta + 1)}&{, \eta \le 1} \end{array}} \right. $ | (5) |
式中,η=‖x-xi‖/R,其中R为基函数的影响半径,更多有关RBF的理论可以参考文献[5]。
SGDP V1.0中采用了Soni等发展的标准形式TFI[16],能够更好地处理复杂外形和极端分布下的网格构造,有关TFI方法的详细可以参考文献[16]。
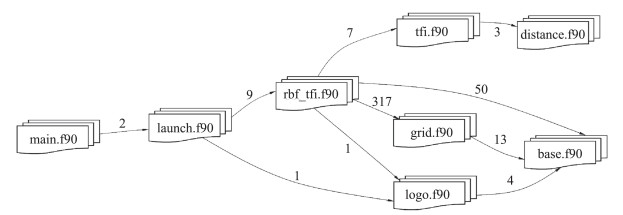
1.2 组成架构图 2给出了SGDP V1.0程序的文件架构,整个程序采用Fortran95语言编写,其中main.f90定义了程序的主入口,然后通过launch.f90文件可以选择调用不同的网格变形方法,目前仅定义了RBF-TFI方法,通过launch.f90可以快速扩展其他网格变形方法。文件rbf_tfi.f90定义了网格变形的流程和具体实现,包括物面网格提取、物面网格位移计算、径向基基点选择、插值与系数矩阵计算、面/体网格更新等,grid.f90定义了网格数据结构、网格数据、网格质量分析和网格输入/输出等模块,tfi.f90定义了二维/三维TFI的实现函数,logo.f90定义了一些程序的logo和版权信息,distance.f90定义了不同距离计算的函数,base.f90定义了矩阵运算、字符串处理、Tecplot文件IO和重复点查找等基础模块。
|
图 2 SGDP V1.0程序文件架构 Fig.2 File architecture of SGDP V1.0 |
SGDP V1.0程序的功能架构主要由网格文件输入/输出、网格变形、变形结果输出三个大模块组成。网格文件输入/输出模块用于读入和写出结构网格数据与边界信息定义文件,目前能够处理2种常用结构网格格式:Plot3d和Gridgen,3种文件存储格式:Binary、Unformatted、Ascii,2种数据精度:Single Precision和Double Precision,组合共计12种不同的结构网格数据文件格式,边界信息文件格式采用Gridgen中Generic Solver定义的方式,使用Ascii格式进行存储。网格变形模块根据不同的变形类型,计算物面网格点的位移运动,然后插值得到空间棱线网格点的位移,并利用TFI算法对空间网格数据进行构造更新。变形结果输出模块将变形前后网格质量分布、径向基基点选点结果、基点插值误差分布、变形外形等写出到指定的文件,便于程序运行后对网格变形效果进行分析。
1.3 主要功能SGDP V1.0程序目前支持4种类型的网格变形:平动、转动、弯曲和用户自定义。平动通过输入参数文件中X、Y、Z方向的位移进行定义;转动为绕固定轴转动,目前仅支持绕X、Y、Z三个轴转动,通过输入参数文件中的转动轴、转动中心和转动角度定义;弯曲主要用于描述沿特定方向的弯曲变形,通过输入参数文件中的最大弯曲变形、弯曲变形起始位置、弯曲变形最大位置进行定义;用户自定义通过读入文件的方式定义物面网格点的位移,可以描述任意种类的变形,输入文件的路径、文件名在参数文件中指定。
在实际工程应用中,单一的运动或变形方式非常少见,因此平动、转动、弯曲3种变形方式主要用来对程序进行测试和演示算例制作,用户自定义方式用来实现复杂变形或运动的输入。例如,气动弹性计算或气动外形优化设计中,流场物面网格点的位移文件可以通过结构变形插值或者几何参数化模块输出获得,然后调用SGDP V1.0,即可得到物面变形后的流场计算网格。
此外,SGDP V1.0通过对更新前后的网格单元数据进行分析,可以获得每个网格块的所有网格单元质量,并统计得到每个网格块的最差单元质量(worst)、最优单元质量(best)和平均单元质量(average),然后输出变形前后网格单元质量在不同块中的分布特性。
1.4 运行流程SGDP V1.0程序目前可以在Windows和Linux平台下运行,均采用命令行和配置文件的方式启动。
在Window下启动CMD或在Linux下启动Terminal,定位至工作目录后,SGDP V1.0可以通过下面3种方式运行:
1) SGDP
2) SGDP project_config
3) SGDP method project_config
其中,第1种运行方式,默认采用RBF-TFI作为网格变形方法,config.txt文件作为默认参数配置文件;第2中运行方式,RBF-TFI作为默认网格变形方法,配置参数文件的名称project_config可以用户自己定义,例如SGDP naca0012.txt;第3种运行方式,网格变形方法method和配置参数文件名称project_config均可以用户自己定义,例如SGDP RBF_TFI naca0012.txt。
SGDP V1.0程序运行前,需要准备好原始网格和边界信息文件,并配置好输入参数文件。SGDP V1.0借鉴了斯坦福非结构流场解算软件SU2的参数输入模式,采用扁平化参数组织结构,参数读入没有先后顺序,从而可以方便地添加或删除任意的参数,参数文件中没有定义的参数将使用程序中的默认定义值。图 3给出了某个网格变形算例的输入参数文件示例,这里采用了用户自定义的变形输入方式,只对相关的参数进行了定义。

|
图 3 SGDP V1.0输入参数文件定义示例 Fig.3 Input parameter file example of SGDP V1.0 |
SGDP V1.0程序启动后,会对读入的部分特定参数进行解析,并进行参数安全检查,然后将全部的参数信息输出到屏幕,方便用户了解程序运行情况,及时发现参数输入错误的情况并进行相应修正。图 4给出了SGDP V1.0的全部运行参数打印信息。有关每个参数的具体含义,可以参考SGDP V1.0的使用手册。

|
图 4 SGDP V1.0全部运行参数输出信息 Fig.4 Printing information of all running parameters of SGDP V1.0 |
计算时间消耗是网格变形程序的关键性能指标,在重复调用程序的仿真工程作业中,对整个仿真的时间和计算成本有着重要的影响。本节利用DLR-F6翼身组合体构型[17],采用不同规模的多块结构网格,对SGDP V1.0的运行时间性能进行测试。
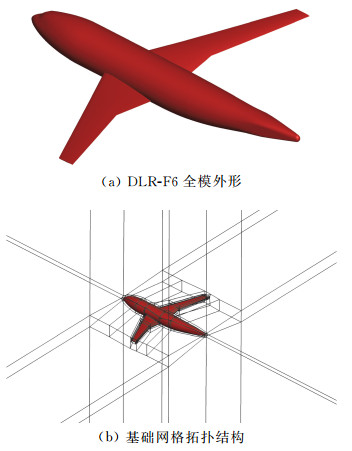
测试中采用的不同规模网格,基于1套基础网格数据,利用课题组自主开发的多块结构网格自适应稀疏/加密程序,成比例的加密得到,不同规模网格的拓扑结构和网格块数量是不变的。基础网格数据含有72个网格块,有3 868 996个网格点、3 566 336个六面体单元,图 5给出了DLR-F6翼身组合体外形和基础网格的拓扑结构。
|
图 5 DLR-F6翼身组合体外形及基础网格拓扑结构 Fig.5 Shape and basis grid topology of DLR-F6 wing-body configuration |
本次测试,网格加密系数在0.5~4.0之间变化,网格点数量从50万增长到2.3亿,选择DLR-F6模型绕质心旋转20°的算例,径向基插值最大基点数目为300。程序在Windows 7系统上运行,计算机硬件采用Intel i7-8700 CPU处理器,含有12个处理器单元,主频为3.2GHz,内存为32Gb。SGDP V1.0目前只有串行版本,采用单CPU方式运行。
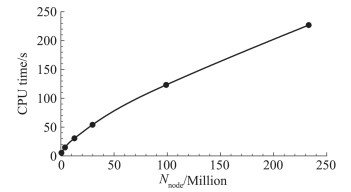
图 6给出了SGDP V1.0程序总的CPU运行时间随网格点数目Nnode的变化规律。随着Nnode的增加,网格变形消耗的CPU时间在逐步增大,但增加的速率是减小的,即每百万网格点消耗的时间随着网格点数的增加逐渐减小。
|
图 6 SGDP V1.0总运行时间随网格节点数目的变化 Fig.6 Total CPU time cost of SGDP V1.0 with different grid nodes |
SGDP V1.0程序总的运行时间主要包括4个部分:网格文件读取、径向基基点选择、体网格更新和网格文件写出。图 7给出了SGDP V1.0程序运行时间分布随网格节点数目的变化图,基于“贪婪”法的径向基基点选择占据程序全部运行时间的绝大部分,比例随着网格点数据的增加逐步减小。这是由于贪婪选点算法是将物面网格点位移误差最大的点逐步选择出来,算法的计算量正比于物面网格点数量。而随着网格规模增加,物面网格点数量是按照加密比例平方增加,而体网格点数量是按照加密比例立方增加,所以物面网格点数量的增加速度要远小于体网格点的增加速度。网格更新时间、网格数据读入/写出时间占总运行时间的比例随着网格点数目逐步增加的,但网格读入/写出时间占总运行时间的比例非常小,基本在1.0%以下。
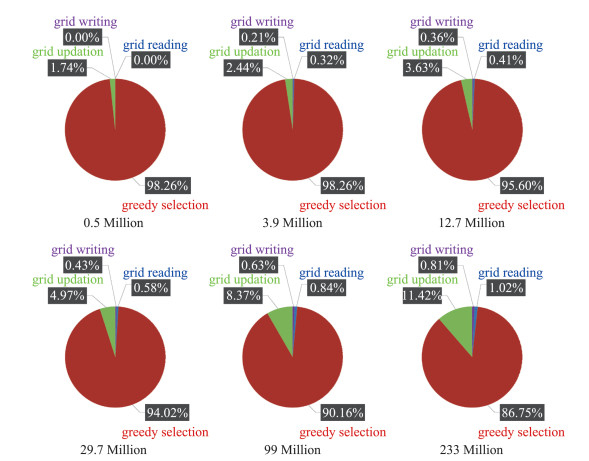
|
图 7 不同网格节点数目下SGDP V1.0运行时间分布 Fig.7 CPU time cost percent of SGDP V1.0 with different grid nodes |
对于网格变形程序多次调用的算例,由于物面精确变形不是通过径向基函数插值RBF来保证,所以基点贪婪选择算法可以利用最大变形只执行一次,然后将基点在物面网格点上的索引编号通过数组或文件记录下来,下一次程序调用直接使用此编号去获取径向基基点的坐标,然后更新系数和插值矩阵,将极大地改善程序的运行效率。对于这类情况,例如气动弹性多次迭代或优化中不同参数下气动外形变化,SGDP V1.0程序的运行时间主要依赖于网格读写时间和体网格更新时间。而对于利用内存进行网格数据传递的例子,网格读取时间也将是一次性的。
图 8给出了网格读写时间、网格变形更新时间随总的网格点数目的变化规律。可以看出,网格读写时间、网格更新时间随网格点数目基本是线性变化的趋势,每百万网格点的读取时间约为0.01 s,每百万网格点的写出时间约为0.008 s,每百万网格点的更新时间约为0.1 s。因此,对于千万量级的网格,SGDP V1.0程序可以在数秒内完成一次变形网格生成,综合来说是十分高效的。
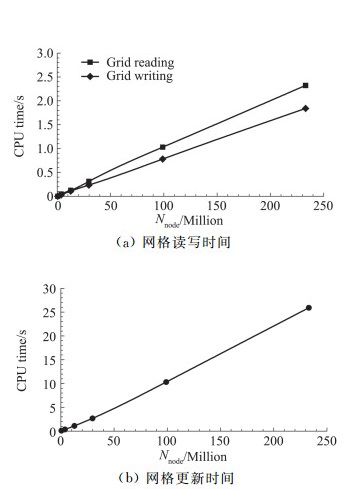
|
图 8 网格读写时间、更新时间随网格节点数目的变化 Fig.8 CPU time cost of grid reading, writing and updating with different grid nodes |
本节提供一些典型情况下的网格变形算例,用来验证SGDP V1.0网格变形能力和网格质量维持特性。
图 9给出了NACA0012翼型绕轴旋转90°前后的变形网格,其中旋转中心位于弦线1/4位置。旋转情况下,变形向远场的衰减过程会使网格单元产生明显的剪切变形,对网格单元质量有着显著的影响,如图 9(b)。
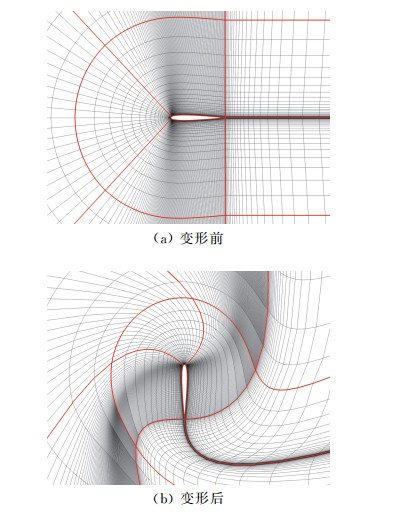
|
图 9 NACA0012旋转90°的变形网格 Fig.9 Deformed grid of NACA0012 airfoil with 90° rotation |
变形前,NACA0012网格最差单元质量为0.800,变形后,NACA0012网格最差单元质量为0.597。90°旋转后,尽管网格单元质量有了显著的降低,但依然维持较高的水平(>0.30),说明SGDP V1.0在显著旋转变形下仍然具有很好的网格质量维持能力。从图 9(b)还可以看出,物面附近网格随物面一起运动,能够保证物面附近黏性流场计算区域网格单元保持良好的连续性和正交性。
图 10为某大展弦比柔性机翼模型在气动载荷作用下变形前后的流场计算网格。该大展弦比机翼半展长为1542,翼梢最大弯曲变形达到402,约为半展长的26%。在如此大幅度变形下,机翼附近网格单元仍然能够随着机翼一起运动,保证了变形后的网格质量,说明SGDP V1.0具有处理大变形情况的能力。
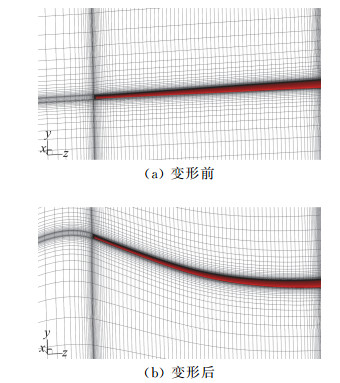
|
图 10 大展弦比柔性机翼模型变形前后网格剖面 Fig.10 Grid section of high aspect-ratio flexible wing model before and after deformation |
图 11为NASA共同研究模型翼/身/挂架/短舱组合体构型CRM-WBPN弯曲变形前后的流场计算网格。CRM-WBPN模型计算网格有153个网格块和约1200万网格点(半模),网格拓扑在机翼/挂架/短舱连接位置十分复杂。从图 11可以看出,SGDP V1.0能够很好地处理大弯曲变形下CRM的网格变形,表明SGDP V1.0具有非常好的复杂外形网格变形处理能力。
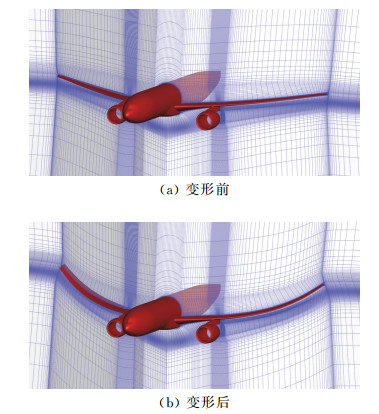
|
图 11 NASA CRM-WBPN模型变形前后网格剖面 Fig.11 Grid section of NASA CRM-WBPN model before and after deformation |
图 12为NASA CRM-WBPN大弯曲变形前后单个网格块最差和最优单元质量随网格块的分布。变形前后,最差、最优单元质量基本没有变化,依然具有较高的网格质量,甚至某些块变形后最差单元质量还有所改善(第88块),说明SGDP V1.0在大变形情况具有十分优异的网格质量维持能力。
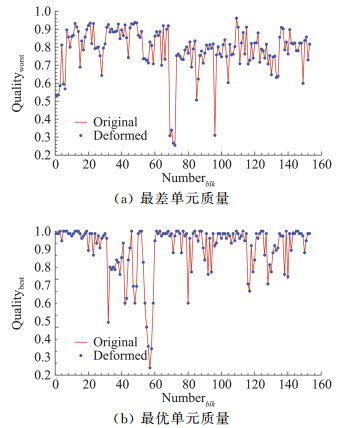
|
图 12 NASA CRM-WBPN模型变形前后最差、最优网格单元质量分布 Fig.12 Worst and best grid cell quality distribution of NASA CRM-WBPN model before and after deformation |
目前,结构网格变形程序SGDP V1.0已经被完整地集成到了亚跨超流场模拟平台(Trisonic Platform, TRIP)中,用于开展不同类型的静/动气动弹性耦合数值模拟,如机翼载荷分配、副翼效率、风洞模型结构静变形影响修正[18-19]、战斗机垂尾抖振、机翼颤振[15]、空调管道流/固耦合振动等。
图 13给出了HIRENASD机翼静气动弹性计算的变形结果。HIRENASD机翼是由德国亚琛工业大学设计,用于研究跨声速飞行雷诺数条件下气动弹性现象与机理的风洞试验模型,曾被选为第一届气动弹性预测研讨会(AePW1)的标准算例,详细信息见文献[20]。本文算例的计算条件取自文献[21],用于验证气动弹性计算程序的精准度,具体计算参数为马赫数Ma=0.80、雷诺数Rec=1.4×107、载荷因子q/E=4.7×10-7、迎角α=3°,其中载荷因子q/E为风洞来流速压q与风洞模型材料弹性模量E的比值。图 13中LE、TE分别表示机翼前后缘,TRIP表示采用SGDP V1.0的气动弹性计算模块,TAU为德国宇航院的CFD计算软件,EXP表示风洞试验得到的结果。可以看出,采用SGDP V1.0的TRIP获得和TAU、EXP比较一致的弯曲和扭转变形结果,在靠近翼梢位置TRIP与TAU计算的扭转变形存在略微的差异,可能是TAU仅采用了前4阶模态导致扭转变形计算截断误差增大引起的。
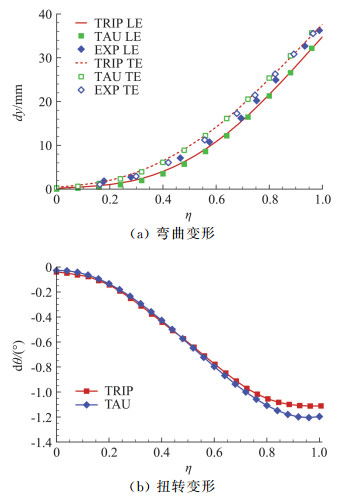
|
图 13 HIRENASD机翼变形计算结果 Fig.13 Deformation calculation results of HIRENASD wing |
图 14给出了HIRENASD机翼3个展向剖面位置的压力系数计算结果,图中Rigid表示机翼刚性条件下获得的压力分布,Elastic表示采用SGDP V1.0计算的弹性状态下的压力分布。可以看出,弹性状态下的压力分布与试验值十分吻合,在靠近翼梢位置与刚性结果差异明显,侧面验证了SGDP V1.0程序的可靠性,能够提供高质量的变形网格。
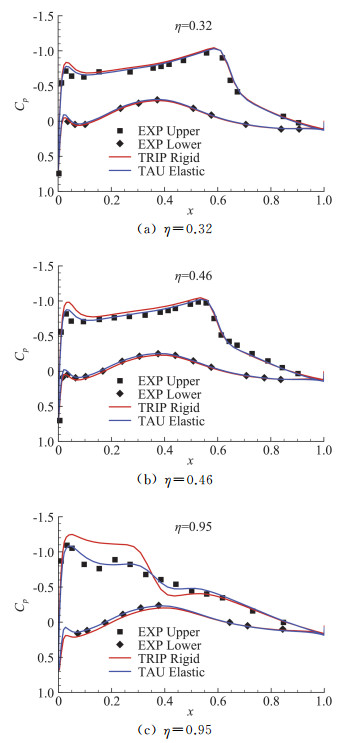
|
图 14 HIRENASD机翼压力系数计算结果 Fig.14 Pressure coefficients calculation results of HIRENASD wing |
对国家数值风洞工程NNW标准共性基础库的第1款结构网格变形程序SGDP V1.0的特性进行了简要的概述,并通过DLR-F6不同规模网格对SGDP V1.0的性能进行了测试,以及开展了SGDP V1.0网格变形能力和网格质量维持特性验证、静气动弹性数值模拟等工作。从测试与计算结果可以得到:
1) SGDP V1.0拥有非常高的网格变形效率,可以在数秒内完成千万量级结构网格更新,能够满足目前绝大多数工程实际中的网格变形需求。
2) 针对不同类型结构网格变形问题,SGDP V1.0均能获得较高质量的变形网格,具有良好的网格变形处理和质量维持能力,程序展示了优良的鲁棒性。
3) SGDP V1.0采用了扁平化和模块化的参数输入方式,可以通过少量几个输入参数的修改应用于不同类型的网格变形算例,展示了良好的通用性。
下一步SGDP V1.0将结合使用经验和反馈意见,对程序不断地进行迭代完善,并结合未来超大规模网格使用需求,开展并行版本的开发。SGDP V1.0将根据单位下一步的知识产权政策,在逐步完善后确定是否开源,如有使用需求,可以通过邮箱y.sun@cardc.cn与作者联系,研究团队将提供执行程序版本。
致谢: 感谢中国空气动力研究与发展中心洪俊武研究员在多块网格自适应稀疏/加密方面提供的建议和帮助。
| [1] |
张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4): 424-447. ZHANG L P, DENG X G, ZHANG H X. Reviews of moving grid generation techniques and numerical mehods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4): 424-447. (in Chinese) |
| [2] |
BYUN C, GURUSWAMY G P. A parallel, multi-block, moving grid method for aeroelastic applications on full aircraft: AIAA-98-4782[R]. Louis: AIAA, 1998.
|
| [3] |
周璇, 李水乡, 孙树立, 等. 非结构网格变形方法研究进展[J]. 力学进展, 2011, 41(5): 547-561. ZHOU X, LI S X, SUN S L, et al. Advances in the research on unstructured mesh deformation[J]. Advances in Mechanics, 2011, 41(5): 547-561. (in Chinese) |
| [4] |
LIU X Q, QIN N, XIA H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423. |
| [5] |
RENDALL T C, ALLEN C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics, 2010, 229(8): 2810-2820. DOI:10.1016/j.jcp.2009.12.006 |
| [6] |
RENDALL T C, ALLEN C B. Unified fluid-structure interpolation and mesh motion using radial basis functions[J]. International Journal for Numerical Methods in Engineering, 2008, 74(10): 1519-1559. DOI:10.1002/nme.2219 |
| [7] |
ALLEN C B, RENDALL T C. Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions: AIAA-2007-3804[R]. Miami: AIAA, 2007.
|
| [8] |
RENDALL T C, ALLEN C B. Efficient mesh motion using radial basis functions with data reduction algorithms[J]. Journal of Computational Physics, 2009, 228(17): 6231-6249. DOI:10.1016/j.jcp.2009.05.013 |
| [9] |
KEDWARD L, ALLEN C B, RENDALL T C S. Efficient and exact mesh deformation using multiscale RBF interpolation[J]. Journal of Computational Physics, 2017, 345: 732-751. DOI:10.1016/j.jcp.2017.05.042 |
| [10] |
WITTEVEEN J A, BIJL H. Explicit mesh deformation using inverse distance weighting interpolation: AIAA-2009-3996[R]. San Antonio: AIAA, 2009.
|
| [11] |
孙岩, 邓小刚, 王光学, 等. 基于径向基函数改进的Delaunay图映射动网格方法[J]. 航空学报, 2014, 35(3): 727-735. SUN Y, DENG X G, WANG G X, et al. An improvement on Delaunay graph mapping dynamic grid method based on radial basis functions[J]. Aeronautica et Astronautica Sinica, 2014, 35(3): 727-735. (in Chinese) |
| [12] |
LIU Y, GUO Z, LIU J. RBFs-MSA hybrid method for mesh deformation[J]. Chinese Journal of Aeronautics, 2012, 25(4): 500-507. DOI:10.1016/S1000-9361(11)60413-5 |
| [13] |
SPREKREIJSE S P, PRANANTA B B, KOK J C. A simple, robust and fast algorithm to compute deformations of multiblock structured grids: NLR-TP-2002-105[R]. Amsterdam: NLR, 2002.
|
| [14] |
孙岩, 邓小刚, 王运涛, 等. RBF_TFI结构动网格技术在风洞静气动弹性修正中的应用[J]. 工程力学, 2014, 31(10): 228-233. SUN Y, DENG X G, WANG Y T, et al. Application of structural dynamic grid method based on RBF_TFI on wind tunnel static aero-elastic modification[J]. Engineering Mechanics, 2014, 31(10): 228-233. (in Chinese) |
| [15] |
王运涛, 孟德虹, 孙岩, 等. 超大规模气动弹性数值模拟软件研制(2017)[J]. 空气动力学学报, 2018, 36(6): 1019-1026. WANG Y T, MENG D H, SUN Y, et al. Software development of ultra-scale numerical simulation for aero-elastic problem(2017)[J]. Acta Aerodynamica Sinica, 2018, 36(6): 1019-1026. DOI:10.7638/kqdlxxb-2018.0030 (in Chinese) |
| [16] |
SONI B K. Two-and three-dimensional grid generation for internal flow applications of computational fluid dynamics[R]. AIAA-85-1526, 1985.
|
| [17] |
LAFLIN K R, VASSBERG J C, WAHLS R A, et al. Summary of data from the second AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178. DOI:10.2514/1.10771 |
| [18] |
孟德虹, 李伟, 王运涛, 等. CRM-WBPN风洞试验模型数值模拟[J]. 航空学报, 2019, 40(2): 522402. MENG D H, LI W, WANG Y T, et al. Numerical simulation of CRM-WBPN wind tunnel model[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(2): 522402. (in Chinese) |
| [19] |
王运涛, 孟德虹, 孙岩, 等. 带支撑装置的CRM-WBH模型流固耦合数值模拟[J]. 气体物理, 2019, 4(1): 16-22. WANG Y T, MENG D H, SUN Y, et al. Fluid-structure-coupling simulation of CRM-WBH model with support system[J]. Physics of Gases, 2019, 4(1): 16-22. (in Chinese) |
| [20] |
BALLMANN J, DAFNIS A, KORSCH H, et al. Experimental analysis of high Reynolds number aero-structural dynamics in ETW[R]. AIAA-2008-841, 2008.
|
| [21] |
NEUMANN J, RITTER M. Steady and unsteady aeroelastic simulations of the HIRENASD wind tunnel experiment[R]. IFASD-2009-132, 2009.
|
 2020, Vol. 38
2020, Vol. 38


