2. 北京大学 工程科学与新兴技术高精尖创新中心, 北京 100871;
3. 北京大学 工学院 应用物理与技术研究中心, 北京 100871
2. BIC-ESAT, Peking University, Beijing 100871, China;
3. CAPT, College of Engineering, Peking University, Beijing 100871, China
湍流预混燃烧广泛存在于先进航空发动机、燃气轮机及内燃机内的能量转化过程,其中湍流与火焰相互作用是当今燃烧研究难点和关键所在[1-3]。对于两者之间的耦合作用,之前的研究主要集中在湍流对火焰的影响上,如湍流改变火焰燃烧速度[1]、火焰锋面结构[2]和标量输运等[3]。反之关于火焰如何影响湍流的研究相对比较缺乏[4]。
在湍流预混燃烧中,燃烧释热造成火焰附近的密度和黏性发生突变,从而影响流场统计性质;同时流场中的火焰又为湍流问题引入了新的长度和速度特征尺度。因此湍流理论和建模中常用的统计局部各向同性假设[5]在湍流预混燃烧中的适用性值得深入探究。由于实验测量困难、定量刻画各向同性程度难度较大等原因,三维湍流预混火焰中速度场非各向同性统计研究仍十分欠缺。
在已有相关研究中,Hamlington等人[6-7]、Poludnenko[8]和Lipatnikov等人[9]对湍流预混火焰中速度场小尺度各向同性统计进行了研究。在低Karlovitz数(Ka)湍流预混火焰直接数值模拟(direct numerical simulation, DNS)研究中,Lipatnikov等人发现涡量的非各向同性主要是由斜压项引起。Poludnenko利用隐式大涡模拟对氢气/空气湍流预混火焰进行了数值研究,发现在低Ka条件下,由于胀压和斜压项的作用,涡量总生成项表现为非各向同性;而在更高Ka时,涡量总生成项基本能保持各向同性。Hamlington等人对不同湍流度下的氢气/空气火焰开展了DNS计算,发现提高湍流度会降低局部非各向同性程度。最近Bobbitt和Blanquart[10]利用DNS研究了高Ka的正庚烷/空气湍流预混火焰。通过分析涡矢量发现增大Ka会降低局部非各向同性程度。而且Ka越大,涡拉伸项和涡量的动力学行为越接近均匀各向同性湍流(homogeneous isotropic turbulence, HIT)。此外,Kolla等人[11]利用湍流预混火焰三维DNS数据分析了湍动能和标量的谱函数,发现可能需要引入Kolmogorov尺度、层流火焰厚度、Damköhler数(Da)和Ka等多个参数才能建立完整的谱函数尺度关系。
为了表征湍流预混火焰中湍流场的小尺度行为,需要可识别完整涡结构的方法。目前常用的识别方法大多是基于局部欧拉速度梯度张量[12-13]。这些已被广泛应用的涡判据主要缺陷为:不同时刻识别出的涡结构不具备严格的时间相干性,以及结构识别结果可能依赖于等值面阈值选取等。特别是预混火焰中未燃侧和已燃侧的涡量强度可能相差几个量级,当等值面取某一阈值时,此类方法无法识别出火焰锋面前后完整的涡结构。
为了描述涡结构的连续演化过程,Yang和Pullin[14]提出了基于拉格朗日观点的涡面场(vortex-surface field, VSF)方法,可描述涡面的连续演化。目前VSF方法已经成功应用于高对称性黏性流动[15]、槽道流转捩[16-17]、激波与涡面相互作用[18]、磁流体[19]以及各向同性湍流[20]等。最近,Zhou等人[21]应用VSF方法研究了构型较简单的Taylor-Green流中预混火焰与三维涡结构的相互作用,一定程度上解决了预混燃烧流场中三维涡面识别的难题。
综上所述,目前关于化学反应释热如何影响小尺度湍流的研究十分有限,而且主要以基于局部欧拉观点的统计分析为主。因此本文研究目的是将VSF方法推广应用于流动结构复杂的湍流预混燃烧,从而表征火焰如何造成湍流场出现非各向同性的三维整体涡结构,并进行相关的涡量与速度结构函数统计分析。
1 直接数值模拟 1.1 数值模拟方法采用燃烧DNS计算湍流预混火焰。求解低马赫数、变密度的质量、动量、组分和温度输运方程,
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \boldsymbol{u})=0 $ | (1) |
| $ \frac{\partial(\rho \boldsymbol{u})}{\partial t}+\nabla \cdot(\rho \boldsymbol{u} \boldsymbol{u})=-\nabla p+\nabla \cdot \boldsymbol{\sigma}+\boldsymbol{f} $ | (2) |
| $ \frac{\partial\left(\rho Y_{k}\right)}{\partial t}+\nabla \cdot\left(\rho \boldsymbol{u} Y_{k}\right)=\nabla \cdot \boldsymbol{j}_{k}+w_{k} $ | (3) |
| $ \begin{array}{l} \frac{\partial(\rho T)}{\partial t}+\nabla \cdot(\rho \boldsymbol{u} T)=\nabla \cdot(\rho \alpha \nabla T)+w_{T}- \\ \frac{1}{c_{p}} \sum\limits_{k} c_{p, k} \boldsymbol{j} \cdot \nabla T+\frac{\rho \alpha}{c_{p}} \nabla c_{p} \cdot \nabla T \end{array} $ | (4) |
其中,ρ为密度,u为速度,p代表压强,f代表体积力,Yk为k组分质量分数,wk代表k组分化学反应源项,T为温度,wT为温度化学反应源项,为混合物热扩散系数,cp, k表示组分k的定压比热,cp表示混合物定压比热。另外,方程中黏性应力张量σ为:
| $ \boldsymbol{\sigma}=\mu\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{\mathrm{T}}\right)-\frac{2}{3}(\nabla \cdot \boldsymbol{u}) \boldsymbol{I} $ | (5) |
其中,μ为动力学黏性,I代表单位张量。组分扩散的质量通量项jk为:
| $ \boldsymbol{j}_{k}=-\rho D_{k} \frac{Y_{k}}{X_{k}} \nabla X_{k}-\rho Y_{k} \boldsymbol{V}_c $ | (6) |
这里,Dk表示组分k的扩散系数,修正速度为Vc=-∑kDkYk/Xk∇Xk,Xk表示组分k的摩尔分数。
为了隔除平均剪切效应而独立地研究火焰对湍流的影响,本DNS考虑统计稳态HIT中沿流向自由传播的平面甲烷/空气预混火焰。如图 1所示,计算域为长方体区域,边长分别为Lx×Ly×Lz=6L×L×L,其中L=2 mm。左右边界分别设置为入流和出流条件,侧面y和z方向设置为周期边界条件。计算域采用均匀网格离散,网格规模为Nx×Ny×Nz=6N×N×N。所有算例中解析度均满足通用的湍流燃烧DNS网格选取准则[22]。

|
图 1 直接数值模拟计算设置示意图 Fig.1 A schematic plot of DNS configuration |
本DNS中使用NGA程序[23]在交错网格上求解控制方程(1)~(4)。动量方程中的空间导数项采用具有动能守恒特性的二阶中心差分格式进行离散,而组分质量分数和温度输运方程中的对流项采用三阶有界QUICK格式[24]离散。时间推进采用二阶半隐式Crank-Nicolson格式[25]。化学反应计算采用13组分甲烷/空气骨架化学反应机理[26],并通过调用CHEMKIN软件库[27]获得化学反应速率、热物性等物理量。计算中采用常值Lewis数(Le)设定:先计算相同工况下的层流预混火焰,然后根据混合物平均的物性参数计算得到不同组分的Le用于燃烧DNS计算。化学反应源项的时间积分采用隐式ODE求解器DVODE[28]进行处理。所有DNS算例至少预先运行10Te时间以使流场达到统计稳态,然后在接下来的20Te时间段内进行数据统计分析,这里Te为湍流大涡翻转时间。
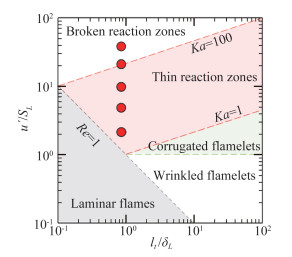
1.2 算例设置本DNS算例设置中的未燃预混气体为常压下Tu=300 K、当量比为0.9的贫燃甲烷/空气混合气。层流火焰速度SL=0.362 m/s,火焰厚度SL= 0.432 mm,火焰时间尺度τf=δL/SL=1.193 ms。在初始时刻利用层流火焰解在计算域流向中心对称面附近设置火焰。为了研究湍流预混火焰特征和速度场统计性质,设置了不同湍流度或Ka工况下的五组DNS算例(u′/SL=2~40)。算例参数汇总见表 1。从燃烧模式分区图 2可以看到,所有算例均处于薄反应区或破碎反应区。
| 表 1 直接数值模拟计算参数 Table 1 Parameters of combustion DNS cases |
|
|
|
图 2 湍流预混火焰分区图(红点标识本DNS算例参数) Fig.2 Regime diagram for turbulent premixed flames(with red dots for parameters in present DNS cases) |
为表征火焰预热区和反应区的演化过程,定义如下反应进度变量[29]:
| $ Y_{\mathrm{prog}}=Y_{\mathrm{H}_{2}}+Y_{\mathrm{H}_{2} \mathrm{O}}+Y_{\mathrm{CO}}+Y_{\mathrm{CO}_{2}} $ | (7) |
并对反应进度变量进行归一化:
| $ C=\frac{Y_{\mathrm{prog}}-Y_{\mathrm{prog}, \min }}{Y_{\mathrm{prog}, \max }-Y_{\mathrm{prog}, \min }} $ | (8) |
这样,C=0代表未燃侧,C=1代表已燃侧。在下文中,进行统计分析的区域为x=0.5L~5L。
1.3 湍流加力为了维持火焰前后的湍流强度,动量方程式(2)右端体积力项采用如下线性加力格式[10, 30],
| $ \boldsymbol{f}=A \frac{k_{0} \rho}{k(x, t)}(\boldsymbol{u}-\widetilde{\boldsymbol{u}}) $ | (9) |
式中A=1/(2Te)为加力参数, k0=27A2lt2/2为目标湍动能,具体参数取值见表 1, k(x, t)为Favre面平均的瞬时湍动能。对于给定物理场ψ,平面Favre平均定义为:
| $ \widetilde{\varPsi}=\frac{\overline{\rho \psi}}{\bar{\rho}} $ | (10) |
公式(10)中的面平均定义为:
| $ \bar{\psi}(x, t)=\frac{1}{L_{y} L_{z}} \int_{0}^{L_{y}} \int_{0}^{L_z} \psi(x, y, z, t) \mathrm{d} y \mathrm{d} z $ | (11) |
此加力格式不会改变湍流小尺度的动力学特性[10],因此不会干扰速度场非各向同性统计研究。
2 涡面场构造 2.1 VSF方法涡面指三维流场中每点均与当地涡量矢量ω相切的曲面,因此VSF约束为:
| $ \boldsymbol{\varOmega} \cdot \nabla \phi_{v}=0 $ | (12) |
则满足式(12)的三维标量场ϕv为VSF,其等值面为由涡线组成的涡面[14]。亥姆霍兹定理指出无黏、正压流体、外力有势下的理想流体中具有涡面跟随流体运动的性质,即在某一时刻组成涡面的流体质点在任意时刻均组成涡面[31-32]。
尽管黏性流体中亥姆霍兹定理失效,但Yang和Pullin[14]发展了数值正则化方法使得VSF仍可近似描述黏性流动中的涡面演化。如对于燃烧中的变密度、黏性流动,VSF数值解可能存在一定误差,并可通过以下ω和∇ϕv夹角的余弦值衡量:
| $ \lambda_{\varOmega} \equiv \frac{\boldsymbol{\varOmega} \cdot \nabla \phi_{v}}{|\boldsymbol{\varOmega}|\left|\nabla \phi_{v}\right|} $ | (13) |
全局平均VSF偏差〈|λω|〉可以通过计算域内的体积平均计算〈·〉得到。在VSF构造中,我们将从任意标量场出发,通过最小化平均VSF偏差,构造VSF数值解。
2.2 伪时间演化与局部优化方法对于任一物理时间t中的瞬时速度场,VSF可以由冻结涡量ω (x, t)场中的伪时间τ演化求解:
| $ \begin{array}{c} \frac{\partial \phi_{v}(x, t ; \tau)}{\partial \tau}+\boldsymbol{\varOmega}(x, t) \cdot \nabla \phi_{v}(x, t ; \tau)=0 , \\ 0<\tau \leqslant T_{\tau} \end{array} $ | (14) |
计算中可以根据涡面场偏差来自适应调整伪时间步的迭代时间Tτ。式(14)的数值求解采用二阶半隐Crank-Nicolson格式[25],而方程中的对流项采用五阶WENO格式求解[33]。
虽然式(14)中VSF偏差会在Tτ取值较大时逐渐收敛,但是湍流中的冻结涡量场对ϕv的拉伸作用往往使得收敛解中出现标量梯度很大的类奇异结构[34],这将会影响复杂流场的VSF可视化效果与定量分析,故我们应用局部优化方法[20]来进一步优化湍流预混火焰中的VSF数值解。
Xiong和Yang[20]提出如下混合约束条件来平衡VSF偏差和VSF解的光滑性:
| $ C_{h}=(1-\zeta)\left|\boldsymbol{\varOmega} \cdot \nabla \phi_{v}\right|^{2}+\zeta\left|\nabla \phi_{v}\right|^{2} $ | (15) |
其中的权重因子取为:
| $ \zeta(T)=\left(1-\frac{\tau}{T_{\tau}}\right)^{2} $ | (16) |
构造VSF解等价于求解如下优化问题:
| $ \min C_{h}, \mathrm{s .t.} \left\langle\phi_{v}\right\rangle=0 \text { and } \operatorname{var}\left(\phi_{v}\right)=1 $ | (17) |
其中,var(f)≡〈f2〉-〈f〉2, 表示任意函数f的方差。这样每个计算时间步构造VSF可分为两个子步:
(1) 求解伪时间输运方程式(14):根据式(14)在伪时间迭代求解临时ϕv;
(2) 求解局部优化问题式(17):利用变分法求解Ch最小化问题从而获得局部最优解。
2.3 湍流预混燃烧中的VSF构造由于火焰处于计算域中部且进出口未加力,湍流强度在进出口附近会有所衰减。为了简化VSF边界处理,在构造VSF时将涡量场乘以窗口衰减函数,
| $ \begin{aligned} f_{d}(x)=& \frac{1}{2}\left[\tanh \left(\frac{x-L_{x} / 2+l_{0}}{2 \delta_{d}}\right)-\right.\\ &\left.\tanh \left(\frac{x-L_{x} / 2-l_{0}}{2 \delta_{d}}\right)\right] \end{aligned} $ | (18) |
其中,l0=2.5L,δd=0.05L。该窗口衰减函数使涡量场在计算中心区域保持不变,而在进出口0.5L左右范围内光滑过渡衰减为零。该处理后全流场均可设置为周期性边界条件。具体计算某物理时刻的VSF时,伪时间初始涡面场设定为无量纲涡量强度,
| $ \phi_{v, 0}=\frac{L}{2 \pi u^{\prime}} | \boldsymbol{\varOmega}| $ | (19) |
然后利用伪时间演化式(14)和局部优化方法求得VSF数值解。
对于算例C中已到达湍流统计稳态的瞬时流场,图 3中给出了其平均VSF偏差随伪时间演化的衰减曲线。可看出初始VSF即涡量强度的VSF偏差很大,约为30%。随着伪时间迭代的进行,涡面场偏差迅速降低到10%以下,最终可降低至5%左右。该偏差远小于使用欧拉涡识别方法(涡量强度等值面)时的偏差。因此,伪时间修正和局部优化方法能有效降低VSF偏差,获得较准确的VSF数值解。该收敛时的平均VSF偏差大小依赖于流场中的涡线复杂度与VSF网格数[20]。本算例中VSF网格与DNS网格一致。通常当湍流强度增大时,需要进一步提高VSF网格数来获得相当大小的平均VSF偏差。

|
图 3 算例C中t=1.5×10-2 s时刻涡面场偏差随伪时间演化曲线 Fig.3 Pseudo-evolution of 〈|λω|〉 for case C at t=1.5×10-2 s |
我们采用VSF方法对涡面结构进行可视化,这样可直观地表征三维速度场的非各向同性特征。图 4中比较了两种不同结构识别方法——VSF等值面和传统的涡量强度识别法。图 4(a)中的VSF等值面上画出了一些代表性涡线,并由涡量强度染色。可以看出,涡线很好地附着在VSF等值面上,说明VSF等值面可准确地表示真实涡面,这与图 3中平均VSF偏差很小的结果吻合。相比之下,对于图 4(b)中的涡量强度等值面,其与涡量场偏差高达30% (见图 3中Tτ= 0时刻),无法显示真正的管状涡面。

|
图 4 算例C中不同涡识别方法对比 Fig.4 Comparison of different vortex-identification methods in case C |
更重要的是,VSF能够展示经过火焰前后涡结构的连续变化过程。从VSF等值面可以看出,在未燃侧小尺度扭曲涡管缠绕在一起,与无反应HIT中的涡面结构相似[20]。而这些涡面在计算区中央的火焰附近,由于热膨胀作用涡线被流向拉伸。进而在已燃侧这些小尺度涡管融合为大尺度块状结构。相比之下,由于经过火焰后温度升高、黏性增大,导致涡量强度迅速衰减,故图 4(b)中涡量强度等值面会有很大一部分在已燃区突然消失。因此,采用传统的欧拉涡判据识别方法无法显示完整涡面结构[21],用于表征湍流预混火焰中的涡动力学连续演化具有一定缺陷。
3 速度非各向同性统计分析 3.1 涡量输运方程分析图 4中的VSF可视化发现未燃侧近似于统计各向的纠缠小尺度涡管在受到火焰锋面处的热膨胀作用后,会融合为沿流向拉伸的大尺度结构。这一类宏观的结构特征与涨落速度的局部非各向同性统计高度相关。
以下我们定量考察火焰对涡量场的影响。由动量方程公式(2)可得拟涡能
| $ \begin{array}{c} \frac{1}{2} \frac{\mathrm{D} \Omega}{\mathrm{D} t}=\boldsymbol{\varOmega} \cdot S \cdot \boldsymbol{\varOmega}-\Omega(\nabla \cdot \boldsymbol{u})+\frac{\boldsymbol{\varOmega}}{\rho^{2}} \cdot(\nabla \rho \times \nabla p)+ \\ \boldsymbol{\varOmega} \cdot \nabla \times\left(\frac{1}{\rho} \nabla \cdot \boldsymbol{\sigma}\right)+\boldsymbol{\varOmega} \cdot \nabla \times \frac{\boldsymbol{f}}{\rho} \end{array} $ | (20) |
其中,D/Dt表示物质导数。式(20)右边的五项分别对应相关涡量动力学过程:涡拉伸、胀压、斜压、黏性耗散和外力作用。其中在常密度流动中涡拉伸、黏性耗散与外力项起主要作用,而在预混火焰中燃烧放热会造成流体性质改变,从而胀压和斜压项也可能会起到重要作用。
图 5中给出了式(20)右边五项时均值沿流向位置的分布曲线,用于分析不同未燃侧、火焰区和已燃区中造成拟涡能发生改变的主导物理过程。可看出x=0处入流湍流较弱。由于加力作用,湍流强度增加,涡拉伸、黏性耗散逐渐增加并占主导作用,它们大约在x=L处达到峰值。在火焰区上游(x < 3L)位置,涡拉伸、黏性耗散项均远大于其他三项,沿着下游它们逐渐减小。火焰锋面大约在x=3.5L处,此位置处密度梯度达到峰值,而且由于燃烧放热,由密度涨落引发的胀压项和斜压项也达到峰值。

|
图 5 算例C与E中拟涡能输运方程右边各项沿流向位置分布 Fig.5 Transport budget analysis of enstrophy along x-direction for cases C and E |
算例C中湍流度较低,燃烧放热引起的热膨胀作用较为显著,斜压项与未燃区中涡拉伸两项峰值相当。相对而言,算例E中湍流度有所提高,斜压项逐渐减弱,导致在整个火焰区中涡拉伸项和黏性耗散项占主导。总之,在低湍流条件下涡拉伸、黏性耗散、胀压和斜压项均起作用;而在高湍流条件下主要是涡拉伸项、黏性耗散项使得拟涡能发生改变。此外,加力项虽能维持加力区域的湍流度,但其量级比其他的主导项小得多。
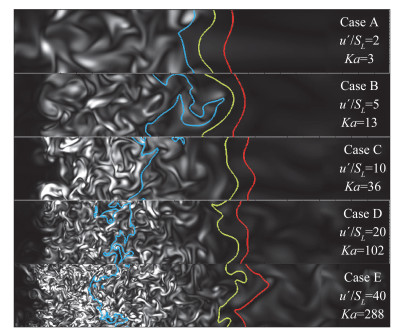
接下来进一步定性观察涡量经过火焰前后的转变过程。图 6中画出了不同算例展向对称平面上瞬时涡量的分布云图。可以看到,涡量强度在经过湍流火焰刷后迅速衰减,导致在已燃侧仅利用涡量强度无法看到明显的涡结构。从涡结构几何特征来看,算例D和E的未燃区接近于HIT[10]。其中小尺度涡管结构扭曲缠绕在一起,速度场近似为各向同性。而在预热区中,小尺度涡管结构沿流向拉伸,速度场非各向同性程度增加。最后,涡结构经过湍流火焰刷到达已燃区时被进一步拉伸,此时速度场主导方向为流向。由于涡量强度在火焰前后发生剧烈变化,如果采用涡量强度等值面则所显示的结构经过火焰后仿佛突然消失,因此欧拉涡识别方法通常不足以表征湍流燃烧中的三维涡结构及其演化过程。这些与图 4中的三维可视化结果相符。
|
图 6 沿流向涡量|ω|分布云图 Fig.6 Contours of |ω| along the streamwise direction 从上往下涡量取值范围分别为[0, 2.5×104 s-1]、[0, 1×105 s-1]、[0, 2×105 s-1]、[0, 5×105 s-1]和[0, 1×106 s-1]。蓝色、绿色和红色等值线分别对应C=0.05, 0.8, 0.95。 |
进一步通过雷诺应力定量表征速度场非各向同性程度及其经过火焰的变化规律。Lumley[35-36]提出利用无量纲雷诺偏应力的不变量表示雷诺应力局部几何特性,这里无量纲雷诺偏应力定义为:
| $ b_{i j}=\frac{\widetilde{u_{i}^{\prime \prime} u_{j}^{\prime \prime}}}{2 k}-\frac{1}{3} \delta_{i j} $ | (21) |
其中,u″i表示瞬时Favre涨落速度,δij表示克罗内克函数。雷诺应力张量bij为二阶对称张量,存在两个独立不变量Ⅱb和Ⅲb。为方便起见定义另一组独立变量ηb和ξb,它们满足
| $ -3 \eta_{b}^{2}=\mathrm{II}_{b}=-\frac{b_{i i}^{2}}{2}=-\frac{b_{i j} b_{j i}}{2} $ | (22) |
| $ 2 \xi_{b}^{3}=\mathrm{III}_{b}=\frac{b_{i i}^{3}}{3}=\frac{b_{i j} b_{j i} b_{k i}}{3} $ | (23) |
图 7中选用独立变量ηb和ξb绘制Lumley曲边三角形[35-36]表征涨落速度场的各向同性程度。该三角形内每一点都对应一种雷诺偏应力各向同性程度状态——下顶点对应各向同性状态,而上边曲线对应各向同性程度最低的二分量湍流状态。
图 7中不同湍流状态点(ξb, ηb)用反应进度变量染色以表征反应进程。可以看到,所有算例的未燃侧中涨落速度场均接近各向同性(ξb, ηb)=(0, 0),这与图 4中的定性结果相符。

|
图 7 算例C和E中ηb和ξb在Lumley三角中的分布,颜色代表C Fig.7 ηb and ξb with the Lumley triangle for cases C and E, colored by the value of C |
通过湍流火焰刷(C增大)时,算例C中湍流状态点向非各向同性最高的准二维湍流状态移动,近似球形的雷诺应力几何状态逐渐变形成椭球,同时涨落速度场非各向同性程度逐渐增加,ηb和ξb的最大值达到0.2左右。而在湍流度最高的算例E中,ηb和ξb的最大值仅为0.1左右,说明在整个湍流火焰刷中速度场各向同性程度一直较高。此外,由于燃烧DNS计算中y和z方向采用周期边界条件,火焰具有一维统计特性,因此湍流状态点在Lumley三角形中的演化路径始终靠近轴对称状态。可以推测在较低湍流度(或Re)条件下,燃烧模型中的统计各向同性假设可能不再成立;而在高湍流度条件下,整个湍流火焰刷中湍流的各向同性程度一直较高,此时引入统计各向同性假设来简化湍流预混燃烧的分析和建模似乎可行。
4 结论本研究将VSF方法推广于湍流预混燃烧,表征了湍流速度场的非各向同性性质。研究中采用DNS得到了不同湍流度下的甲烷/空气预混火焰的高精度数据,随后应用伪时间演化和局部优化算法求解VSF数值解。
相较于涡量等值面等传统的欧拉涡识别方法,VSF能够展示经过火焰前后涡结构的连续变化过程。我们发现在未燃侧小尺度扭曲涡管缠绕在一起,在火焰区涡管受到火焰锋面附近热膨胀的拉伸作用,在已燃侧这些小尺度涡管融合为大尺度块状结构。这些三维涡面几何结构的变化与速度场局部非各向同性高度相关。
通过对拟涡能输运方程各项进行定量分析,发现在未燃区涡拉伸项和黏性耗散项占主导,而在火焰区胀压项和斜压项占主导,说明火焰会增加局部速度场涨落。进一步利用雷诺应力Lumley曲边三角形定量表征了涨落速度场经过火焰前后的非各向同性程度变化规律。发现从未燃侧到已燃侧速度场统计非各向同性程度整体上逐步变大,且低湍流度下已燃侧的非各向同性程度显著高于高湍流度下的统计结果。
在成功构造VSF的基础上,未来工作中将进一步利用VSF研究湍流预混火焰中涡面结构的时间演化动力学。
致谢: 感谢加州理工学院、科罗拉多大学博德分校和斯坦福大学授权使用NGA程序。
| [1] |
LIPATNIKOV A N. Fundamentals of premixed turbulent combustion[M]. Boca Raton, FL, USA: CRC Press, 2012. DOI:10.1201/b12973
|
| [2] |
DRISCOLL J F. Turbulent premixed combustion:Flamelet structure and its effect on turbulent burning velocities[J]. Progress in Energy and Combustion Science, 2008, 34(1): 91-134. DOI:10.1016/j.pecs.2007.04.002 |
| [3] |
LIPATNIKOV A N, CHOMIAK J. Molecular transport effects on turbulent flame propagation and structure[J]. Progress in Energy and Combustion Science, 2005, 31(1): 1-73. DOI:10.1016/j.pecs.2004.07.001 |
| [4] |
SABELNIKOV V A, LIPATNIKOV A N. Recent advances in understanding of thermal expansion effects in premixed turbulent flames[J]. Annual Review of Fluid Mechanics, 2017, 49: 91-117. DOI:10.1146/annurev-fluid-010816-060104 |
| [5] |
POPE S B. Turbulent flows[M]. Cambridge: Cambridge University Press, 2000. DOI:10.1017/CBO9780511840531
|
| [6] |
HAMLINGTON P E, POLUDNENKO A Y, ORAN E S. Interactions between turbulence and flames in premixed reacting flows[J]. Physics of Fluids, 2011, 23(12): 125111. DOI:10.1063/1.3671736 |
| [7] |
HAMLINGTON P E, POLUDNENKO A Y, ORAN E S. Intermittency in premixed turbulent reacting flows[J]. Physics of Fluids, 2012, 24(7): 075111. DOI:10.1063/1.4729615 |
| [8] |
POLUDNENKO A Y. Pulsating instability and self-acceleration of fast turbulent flames[J]. Physics of Fluids, 2015, 27(1): 014106. DOI:10.1063/1.4905298 |
| [9] |
LIPATNIKOV A N, NISHIKI S, HASEGAWA T. A direct numerical simulation study of vorticity transformation in weakly turbulent premixed flames[J]. Physics of Fluids, 2014, 26(10): 105104. DOI:10.1063/1.4898640 |
| [10] |
BOBBITT B, LAPOINTE S, BLANQUART G. Vorticity transformation in high Karlovitz number premixed flames[J]. Physics of Fluids, 2016, 28(1): 015101. DOI:10.1063/1.4937947 |
| [11] |
KOLLA H, HAWKES E R, KERSTEIN A R, et al. On velocity and reactive scalar spectra in turbulent premixed flames[J]. Journal of Fluid Mechanics, 2014, 754: 456-487. DOI:10.1017/jfm.2014.392 |
| [12] |
HUNT J C R, WRAY A A, MOIN P. Eddies, streams, and convergence zones in turbulent flows[C]//Center for Turbulence Research. Studying Turbulence Using Numerical Simulation Databases, 2: Proceedings of the 1988 Summer Program, 1988: 193-208(SEE N89-2453818-34).
|
| [13] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285: 69-94. DOI:10.1017/S0022112095000462 |
| [14] |
YANG Y, PULLIN D I. OnLagrangian and vortex-surface fields for flows with Taylor-Green and Kida-Pelz initial conditions[J]. Journal of Fluid Mechanics, 2010, 661: 446-481. DOI:10.1017/s0022112010003125 |
| [15] |
YANG Y, PULLIN D I. Evolution of vortex-surface fields in viscous Taylor-Green and Kida-Pelz flows[J]. Journal of Fluid Mechanics, 2011, 685: 146-164. DOI:10.1017/jfm.2011.287 |
| [16] |
ZHAO Y M, YANG Y, CHEN S Y. Vortex reconnection in the late transition in channel flow[J]. Journal of Fluid Mechanics, 2016, 802: R4. DOI:10.1017/jfm.2016.492 |
| [17] |
XIONG S Y, YANG Y. The boundary-constraint method for constructing vortex-surface fields[J]. Journal of Computational Physics, 2017, 339: 31-45. DOI:10.1016/j.jcp.2017.03.013 |
| [18] |
PENG N F, YANG Y. Effects of the Mach number on the evolution of vortex-surface fields in compressible Taylor-Green flows[J]. Physical Review Fluids, 2018, 3(1): 013401. DOI:10.1103/PhysRevFluids.3.013401 |
| [19] |
HAO J H, XIONG S Y, YANG Y. Tracking vortex surfaces frozen in the virtual velocity in non-ideal flows[J]. Journal of Fluid Mechanics, 2019, 863: 513-544. DOI:10.1017/jfm.2018.1014 |
| [20] |
XIONG S Y, YANG Y. Identifying the tangle of vortex tubes in homogeneous isotropic turbulence[J]. Journal of Fluid Mechanics, 2019, 874: 952-978. DOI:10.1017/jfm.2019.487 |
| [21] |
ZHOU H, YOU J P, XIONG S Y, et al. Interactions between the premixed flame front and the three-dimensional Taylor-Green vortex[J]. Proceedings of the Combustion Institute, 2019, 37(2): 2461-2468. DOI:10.1016/j.proci.2018.08.015 |
| [22] |
YOU J P, YANG Y. Modelling of the turbulent burning velocity based on Lagrangian statistics of propagating surfaces[J]. Journal of Fluid Mechanics, 2020, 887: A11. DOI:10.1017/jfm.2019.1081 |
| [23] |
DESJARDINS O, BLANQUART G, BALARAC G, et al. High order conservative finite difference scheme for variable density low Mach number turbulent flows[J]. Journal of Computational Physics, 2008, 227(15): 7125-7159. DOI:10.1016/j.jcp.2008.03.027 |
| [24] |
HERRMANN M, BLANQUART G, RAMAN V. Flux corrected finite volume scheme for preserving scalar boundedness in reacting large-eddy simulations[J]. AIAA Journal, 2006, 44(12): 2879-2886. DOI:10.2514/1.18235 |
| [25] |
PIERCE C D. Progress-variable approach for large-eddy simulation of turbulent combustion[D]. Stanford, California: Standford University, 2001. https://www.researchgate.net/publication/23832769_Progress-Variable_Approach_for_Large_Eddy_Simulation_of_Turbulent_Combustion
|
| [26] |
SANKARAN R, HAWKES E R, CHEN J H, et al. Structure of a spatially developing turbulent lean methane-air Bunsen flame[J]. Proceedings of the Combustion Institute, 2007, 31(1): 1291-1298. DOI:10.1016/j.proci.2006.08.025 |
| [27] |
KEE R J, RUPLEY F M, MEEKS E, et al. CHEMKIN-III: A FORTRAN chemicalkinetics package for the analysis of gas-phase chemical and plasma kinetics[R]. Office of Scientific and Technical Information (OSTI), 1996. https: //doi.org/10.2172/481621
|
| [28] |
BROWN P N, BYRNE G D, HINDMARSH A C. VODE:a variable-coefficient ODE solver[J]. SIAM Journal on Scientific and Statistical Computing, 1989, 10(5): 1038-1051. DOI:10.1137/0910062 |
| [29] |
PITSCH H. Large-eddy simulation of turbulent combustion[J]. Annual Review of Fluid Mechanics, 2006, 38: 453-482. DOI:10.1146/annurev.fluid.38.050304.092133 |
| [30] |
CARROLL P L, BLANQUART G. A proposed modification to Lundgren's physical space velocity forcing method for isotropic turbulence[J]. Physics of Fluids, 2013, 25(10): 105114. DOI:10.1063/1.4826315 |
| [31] |
吴望一. 流体力学[M]. 北京: 北京大学出版社, 2004.
|
| [32] |
庄礼贤, 尹协远, 马晖扬. 流体力学(第2版)[M]. 合肥: 中国科学技术大学出版社, 2009.
|
| [33] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [34] |
PULLIN D I, YANG Y. Whither vortex tubes?[J]. Fluid Dynamics Research, 2014, 46(6): 061418. DOI:10.1088/0169-5983/46/6/061418 |
| [35] |
LUMLEY J L, NEWMAN G R. The return to isotropy of homogeneous turbulence[J]. Journal of Fluid Mechanics, 1977, 82(1): 161-178. DOI:10.1017/s0022112077000585 |
| [36] |
LUMLEY J L. Computational modeling of turbulent flows[J]. Advances in Applied Mechanics, 1979, 18: 123-176. DOI:10.1016/s0065-2156(08)70266-7 |
 2020, Vol. 38
2020, Vol. 38


