超燃冲压发动机被认为是未来高超声速吸气式飞行器的理想推进系统,因而超燃冲压发动机的研究受到了世界的广泛关注[1]。超燃冲压发动机实用化的一个技术难点是实现高推阻比,目前的研究主要集中于提高超声速燃烧效率而增加推力,而降低阻力的研究则相对较少[2]。在超燃冲压发动机内部摩擦阻力的构成中,由于近壁区流动的高剪切率致使燃烧室摩阻可占发动机内总摩阻的一半左右[3],因此超燃冲压发动机燃烧室的减阻设计是整个高超声速飞行器减阻设计的重要部分。
边界层减阻研究起始于20世纪60年代[4]。在20世纪90年代,Coustols[5]和Bushnell、Hefner[6]分别对边界层减阻进行了综述。减阻手段可分为被动、主动和混合方法[5]。Walsh和Weinstein[7-9]提出的壁面修正方法是一种典型的被动方法。壁面吸气法[10-13]以及壁面吹气法[14-17]是典型的主动控制方法。以上方法在飞行器外流的减阻控制中应用较多。
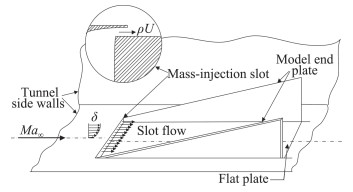
薄膜冷却方法[18]适用于发动机内流动控制。薄膜冷却方法是作为发动机内高温环境下的一种主动冷却技术提出的,该方法通过在边界层内注入低温气体来降低壁面热流。低温气体可通过多孔平板垂直吹入边界层内,或者通过狭缝平行射入边界层内。有研究[19]发现向边界层内平行射入流体的方式[18]较垂直吹入流体的方式可实现更大程度的减阻。而进一步研究发现[20],薄膜冷却方法在减少热流的同时还可以降低壁面摩阻。图 1给出了文献[20]中薄膜冷却减阻的实验装置示意图,通过狭缝射入边界层的低温、低速气体将增加边界层厚度、降低近壁区流动温度和速度,从而减小壁面热流和摩阻。由于薄膜冷却方法在高速流动中可有效进行壁面减阻和热流控制,在高超声速飞行器快速发展的背景下,该方法得到了持续的研究[21-25]。Richards和Stollery[21]发现采用薄膜冷却进行减阻控制时,注入气体为氢气时的减阻效果比氦气、氟利昂、氩气和空气时更好。在该实验中,主流气体为惰性气体,因此所注入的氢气不燃烧。然而真实情况下,超声速飞行将导致壁面气动热骤增从而点燃注入氢气。
2000年,Goyne等[26]开展了边界层燃烧减阻实验,他们发现相较于无燃烧的薄膜冷却,在边界层内平行射入氢气并随之燃烧可进一步使得壁面摩擦阻力降低,因此边界层燃烧作为一种降低摩擦阻力的技术开始被重视。实际应用该减阻技术时,可将超燃冲压发动机的少量燃料由近壁区狭缝平行射入边界层内并随之燃烧,在降低燃烧室摩阻的同时可提供部分推力[27]。平行燃料射流对主流流动干扰较小,所造成的发动机总压损失也较小[28]。
自Goyne等[26]于2000年首次以实验验证了边界层燃烧减阻的有效性后,经各国研究人员近20年的不懈努力,边界层燃烧减阻技术的研究已取得显著进展。本文将回顾国内外在可压缩边界层燃烧减阻方面的研究进展,主要从实验、理论和数值模拟三个方面进行综述,内容主要限制在以超燃冲压发动机为背景的超声速流动范围内。
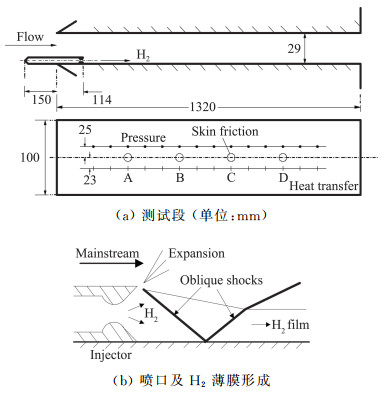
1 实验研究 1.1 Goyne实验(2000)2000年,Goyne等[26]在澳大利亚Queensland大学的反射激波风洞中开展了超声速边界层燃烧减阻实验研究,其装置如图 2所示。来流马赫数为4.5,在图 2(a)中的A、B、C、D四个站位处分别测量了压强、摩阻和热流。H2喷口结构如图 2(b)所示。实验共开展了4组,每组的来流条件一致,而氢气燃料的入射质量流量不同,分别为0.015、0.029、0.043和0.057 kg/s。基于板长的雷诺数约为9×106。
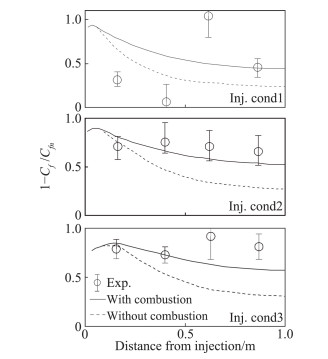
研究表明,相较于无燃烧的薄膜冷却(采用氮气替代空气以避免燃烧),边界层燃烧并未使得壁面加热恶化;且更有意义的是,边界层燃烧比薄膜冷却起到了更好的减阻效果。实验的边界层燃烧和薄膜冷却的减阻结果如图 3所示。其中,cfn表示无射流情况下的壁面摩阻,而cond1,cond2和cond3分别表示氢气射流质量流量为0.015、0.029和0.043 kg/s的情况。由图 3可见,在平板出口处,相较于薄膜冷却,边界层燃烧使得摩阻减小幅度增加一倍;而相较于无氢气射入流动,边界层燃烧最多使得壁面摩阻减小70%~80%。Goyne等[26]同时采用雷诺平均(RANS)数值方法验证了该实验结果的可靠性。该实验首次验证了边界层燃烧减阻的有效性,从此边界层燃烧作为一种降低摩擦阻力的技术开始被重视。
|
图 3 Goyne实验边界层燃烧和薄膜冷却减阻效率[26] Fig.3 Effectiveness of boundary layer combustion and film cooling for Goyne's experiment[26] |
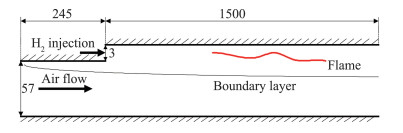
同样来自澳大利亚Queensland大学的Suraweera等[29-30]进一步研究了不同来流条件对边界层燃烧减阻的影响。所采用的实验装置如图 4所示。空气来流马赫数变化范围为4.0到4.5,驻点焓从4.8 MJ/kg到9.5 MJ/kg,单位雷诺数从1.0×107到1.9×107。实验测量了上壁面流向不同站位处的压强、摩阻和热流。
|
图 4 Suraweera实验装置示意图(单位:mm) Fig.4 Schematic of Suraweera's experiment (unit: mm) |
研究发现,不同来流条件均实现了不同程度、可观的壁面减阻量:当来流驻点焓为7.6 MJ/kg时,壁面摩阻最多减小了77%;而当驻点焓降低至5.6 MJ/kg时,壁面摩阻最多减小了60%。同样,相较于薄膜冷却,边界层燃烧并没有使得壁面加热恶化。Suraweera等[29]同时采用RANS验证了其实验结果的可靠性。然而,该研究并未得出不同来流条件对边界层燃烧减阻影响的规律性结果。
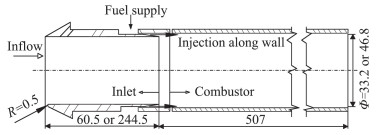
1.3 Kirchhartz实验(2012)澳大利亚Queensland大学的Kirchhartz等[31]研究了来流压力梯度对边界层燃烧减阻效率的影响。实验装置如图 5所示。实验分别采用尖前缘进气道(如图 5上半图所示)和钝前缘进气道(如图 5下半图所示),而钝前缘半径为0.5 mm。当采用钝前缘进气道时,来流经钝前缘压缩,形成强度较大的激波,激波与进气道壁面相互作用,使得流经进气道而进入燃烧室的流动存在较强压力梯度。而尖前缘进气道内流动的压力梯度相对较小。实验中来流马赫数为4.5,驻点焓从3.6 MJ/kg到7.8 MJ/kg。进气道长度可调为60.5 mm和244.5 mm,通过调整进气道长度可改变燃烧室入口边界层厚度。此外,该实验还研究了燃烧室入口边界层厚度对边界层燃烧减阻效率的影响。
研究发现,来流压力梯度并不影响边界层燃烧减阻效率,反而可能使其增加。如来流驻点焓为5.1 MJ/kg时,钝前缘进气道下的边界层燃烧使得摩阻减少量高达77%,高于尖前缘进气道下的摩阻减少量。增加进气道长度将使得燃烧室入口边界层厚度增加,湍流边界层发展更充分,从而有利于燃料和空气混合以及边界层燃烧发生,增加边界层燃烧减阻量。
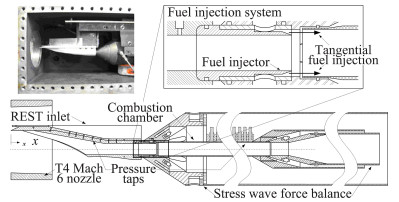
1.4 Chan实验(2015)为简化实验研究,Goyne[26]、Suraweera[29]和Kirchhartz等[31]采用了等截面进气道,进入燃烧室内流动的不均匀性较弱。然而,真实高超声速飞行器通常采用变截面进气道,飞行器做机动飞行使得来流条件复杂化。此来流经前体压缩后进入进气道产生复杂激波、膨胀波以及旋涡流动,进而进入燃烧室内流动具有较强不均匀性。2015年,澳大利亚Queensland大学Chan等[32]研究了来流不均匀性对边界层燃烧减阻效率的影响。Chan采用矩形-椭圆型变截面进气道(Rectangular-to-Elliptical-Shape-Transition inlet, REST)增强来流不均匀性(如图 6所示)。该实验装置为在Kirchhartz等[31]的实验装置前加装REST变截面进气道而成。实验分别研究了设计和非设计状态下来流不均匀性对边界层燃烧减阻效果的影响。
研究发现,尽管加装了REST变截面进气道而导致来流不均匀,然而燃烧室的总黏性阻力仍然由于边界层燃烧而减小了61%,与不采用REST进气道的实验[31, 33-34]取得了一致的减阻效果。当来流从设计状态(驻点焓4.8 MJ/kg,马赫数6.2)变为非设计状态(驻点焓分别为3.7~ 8.0 MJ/kg,马赫数为5.7~7.4)时,来流不均匀性同样没有降低边界层燃烧减阻的效率。因此,无论对设计或非设计状态而言,加装REST变截面进气道而产生的来流不均匀性并不影响边界层燃烧减阻效率。
综上所述,以往实验研究验证了边界层燃烧减阻的有效性[26],探究了不同因素(如来流驻点焓值、雷诺数、流动压力梯度等)对边界层燃烧减阻效果的影响[29-31],以及将该技术应用于真实高超声速飞行器时来流不均匀性的影响[32],已初步形成将该减阻技术应用于高超声速飞行器的能力。不过,上述研究只得到部分因素对边界层燃烧减阻效率影响的一般规律,如增加来流驻点焓有利于边界层燃烧发生,增加燃料射流质量流量可提高边界层燃烧减阻效率。其他因素(如主流马赫数、驻点焓、燃料射流马赫数和温度等)对边界层燃烧减阻影响的一般规律仍有待研究。考虑到实验研究耗费较大,未来可结合数值模拟共同开展研究。此外,以往边界层燃烧减阻实验缺少对减阻机理的研究,为了研究边界层燃烧减阻的物理机理,需要开展湍流脉动和输运的相关测量。澳大利亚Queensland大学在该方面研究较为系统,未见欧洲、美国、俄罗斯、日本等在该方面公开发表相关研究成果,而中国学者的研究重点在理论和数值模拟方面,实验研究的公开报道极为少见。
2 理论研究热载荷和摩擦阻力是超声速和高超声速飞行器结构和气动外形设计时的主要考量因素。摩阻、热流的理论、半经验模型可协助高速飞行器设计,尤其是在初步设计阶段。20世纪70年代,Hopins和Inouye[35]、Bradshaw[36]的综述对当前摩阻、热流理论模型研究仍有指导意义。van Driest理论模型[37-38](通常指van Driest Ⅱ模型[38])通常被认为是最准确的摩阻、热流计算模型。此外,Stollery理论模型[39]、Spalding和Chi半经验公式[40]也较常用。Stollery理论模型可考虑压力梯度,而Spalding和Chi半经验公式尤其适用于高冷壁的摩阻计算[41]。上述模型并不适用于有质量注入边界层的流动情况,而根据文献调研,仅澳大利亚Queensland大学的Stalker[42]对该问题进行了研究。通过对van Driest Ⅱ理论[38]进行推广,Stalker提出了考虑边界层氢气注入和燃烧的壁面摩阻、热流理论模型,下面对其进行简要介绍。
Stalker理论模型采用氢气和氧气的单步不可逆反应:
2H2+O2→2H2O+2 ΔQ
其中ΔQ为化学反应的生成热。
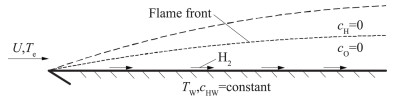
Stalker针对边界层燃烧提出了一种流动简化模型,如图 7所示。在该模型中,Stalker假设壁面的氢气质量分数为常数。这样的假设有利于简化推导,但显然与实际不符,实际上壁面氢气质量分数将由于氢气燃烧消耗而逐渐降低。因此在将该模型用到实际问题中时,Stalker采用了局部相似假设,即在真实流动中,氢气质量分数沿流向变化很小,因此流向所历经的各截面流场对应于一系列的流动简化模型。
|
图 7 Stalker氢气边界层燃烧简化流动模型[42] Fig.7 Stalker's simplified flow model for hydrogen boundary layer combustion[42] |
Stalker假设流动的Lewis数和Prandtl数为1,从而组分、动量和能量输运的控制方程有相同的数学形式。再通过Shvab-Zeldovich耦合方法引入类似混合分数的变量z可统一上述三个方程。各组分的质量定压比热容Cpi为被设为常数,流向压力梯度假设为零。在上述一系列假设前提下,得到考虑边界层燃烧的Crocco-Busemann密度ρ与Shvab-Zeldovich变量z的关系式:
| $ \left\{\begin{array}{l} \rho / \rho_{\mathrm{w}}=1+b_{1} z-a^{2} z^{2}, 0<z<g \\ \rho / \rho_{\mathrm{w}}=1+\alpha+b_{2} z-a^{2} z^{2}, g<z<1 \end{array}\right. $ | (1) |
式中,密度由火焰前锋位置g分为两段0 < z < g和g < z < 1。此外,
| $ \left\{\begin{array}{l} a^{2}=U^{2} /\left(2 H_{\mathrm{w}}\right) \\ \alpha=c_{\mathrm{HW}} \Delta Q / H_{\mathrm{w}} \\ b_{1}=\left(H_{\mathrm{e}}-H_{\mathrm{w}}+f c_{\mathrm{O} \mathrm{e}} \Delta Q\right) / H_{\mathrm{w}} \\ b_{2}=\left(H_{\mathrm{e}}-H_{\mathrm{w}}+c_{\mathrm{HW}} \Delta Q\right) / H_{\mathrm{w}} \\ H_{\mathrm{w}}=C_{p s, \mathrm{w}} T_{\mathrm{w}} \end{array}\right. $ | (2) |
U、H、c分别表示来流速度、驻点焓值以及质量分数。下标H和O分别表示氢气和氧气,而e和w分别表示边界层外和壁面。f表示氢气和氧气燃烧的质量当量比,即f=0.125;fcOeΔQ表示氢气燃烧所释放的热量,为3.45 MJ/kg。Cps表示混合物的比热容。van Driest模型通过动量与能量输运方程的一致性得到密度和速度的Crocco-Busemann关系式。Stalker理论模型与van Driest模型最大不同之一即为式(1)的密度关系式。
以下推导与van Driest Ⅱ理论的思路基本一致。首先采用混合长度理论模化雷诺应力:
| $ \tau=\rho \kappa^{2}\left(\frac{\mathrm{d} u}{\mathrm{d} y}\right)^{4} /\left(\frac{\mathrm{d}^{2} u}{\mathrm{d} y^{2}}\right)^{2} $ | (3) |
式中τ和κ分别为剪切应力和冯卡门常数,κ=0.41。将式(3)式沿壁面法向积分再引入表征密度分布的式(1),得到Shvab-Zeldovich变量z沿法向的梯度表达式dy/dz。将之引入动量损失厚度θ,
| $ \theta=\int_{0}^{z=1}\left(\rho / \rho_{\mathrm{e}}\right)(1-z) z \mathrm{d} y $ | (4) |
可以得动量损失厚度θ的表达式。而边界层内氢气质量流量
| $ \dot{m}=\frac{c_{\mathrm{HW}}+f c_{\mathrm{Oe}}}{1+f c_{\mathrm{Oe}}} \rho_{\mathrm{e}} U \theta $ | (5) |
通过动量守恒易建立考虑氢气注入的卡门动量积分关系式:
| $ \tau_{\mathrm{w}}=\rho_{\mathrm{e}} U^{2} \frac{\mathrm{d} \theta}{\mathrm{d} x}+\left(u_{\mathrm{j}}-U\right) \frac{\mathrm{d} \dot{m}}{\mathrm{d} x} $ | (6) |
其中,uj表示氢气射入速度。将上述推导中的动量厚度θ关系式和边界层内氢气质量流量
| $ \begin{array}{l} 4.17 \lg \left(c_{f} {Re}_{x} \mu_{\mathrm{e}} / \mu_{\mathrm{w}}\right)+1.7 \\ \qquad \begin{array}{l} =F_{1} / \sqrt{c_{f}\left(T_{\mathrm{aw}}-T_{\mathrm{e}}\right) / T_{\mathrm{e}}}+ \\ \qquad \begin{array}{l} 3.97 \mathrm{lg}\left[\frac{1-c_{\mathrm{HW}}+\left(c_{\mathrm{HW}}+f c_{\mathrm{Oe}}\right) u_{\mathrm{j}} / U}{1+f c_{\mathrm{Oe}}}\right]+ \\ 3.97 \lg \left[1+G \exp \left(\frac{K\left(F_{2}-F_{1}\right) \sqrt{2}}{\sqrt{c_{f}\left(T_{\mathrm{aw}}-T_{\mathrm{e}}\right) / T_{\mathrm{e}}}}\right)\right] \end{array} \end{array} \end{array} $ | (7) |
其中,Rex为基于板长x的雷诺数,即Rex=ρeUx/μe。下标aw表示绝热壁。此外,
| $ \left\{\begin{array}{l} Q_{1}=\sqrt{b_{1}^{2}+4 a^{2}} \\ Q_{2}=\sqrt{b_{1}^{2}+4 a^{2}(1+\alpha)} \\ G=0.5\left(b_{1}-b_{2}\right) g(1-g) /\left(1+b_{1} g-a^{2} g^{2}\right) \\ F_{1}=\arcsin \left(b_{1} / Q_{1}\right)+\arcsin \left[\left(2 a^{2}-b_{2}\right) / Q_{2}\right]+ \\ \quad \arcsin \left[\left(2 a^{2} g-b_{1}\right) / Q_{1}\right]- \\ \quad \arcsin \left[\left(2 a^{2} g-b_{2}\right) / Q_{2}\right] \\ F_{2}=\arcsin \left(b_{1} / Q_{1}\right)+\arcsin \left[\left(2 a^{2} g-b_{1}\right) / Q_{1}\right] \end{array}\right. $ |
对氢气的浓度在边界层内积分,可得到氢气注入量的表达式:
| $ \begin{array}{c} \dot{m}=0.187 \mu_{\mathrm{w}} \frac{c_{\mathrm{HW}}+fc_{{\rm Oe}}}{1+fc_{{\rm Oe}}} \exp \left\{\frac{\sqrt{2} F_{1} K}{\sqrt{\frac{c_{f}\left(T_{\mathrm{aw}}-T_{\mathrm{e}}\right)}{T_{\mathrm{e}}}}}\right\}\cdot \\ \left\{1+G \exp \left[\frac{\sqrt{2}\left(F_{2}-F_{1}\right) K}{\sqrt{\frac{c_{f}\left(T_{\mathrm{aw}}-T_{\mathrm{e}}\right)}{T_{\mathrm{e}}}}}\right]\right\} \end{array} $ | (8) |
采用雷诺比拟可确定Stanton数ch(ch=
| $ c_{h}=\frac{c_{f}}{2 P r} \frac{H_{\mathrm{e}}+f c_{\mathrm{Oe} } \Delta Q-0.90 C_{p, \mathrm{a}} T_{\mathrm{w}}}{H_{\mathrm{e}}-C_{p, \mathrm{a}} T_{\mathrm{w}}} $ | (9) |
式中,Pr表示普朗特数,取值为1;Cp, a表示空气的定压比热容。
以上是Stalker所建立的考虑边界层燃烧的壁面摩阻、热流理论模型的主要内容。其中,式(7)、(8)、(9)分别是预测摩阻系数cf、氢气质量流量以及Stanton数ch的公式,通过牛顿迭代算法可求解该隐式方程。
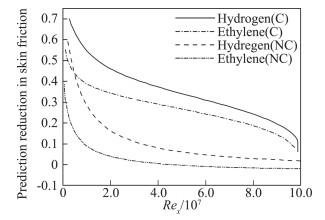
Stalker采用上述理论模型对上节Goyne等[26]的实验开展了计算,计算与实验结果吻合。Stalker的模型只适用于氢气燃料,而Barth等[43]将其进行了推广,使其适用于任意燃料。Barth对比研究了以氢气和乙烯为燃料的边界层燃烧减阻效果,结果如图 8所示。由图 8可见,乙烯的边界层燃烧减阻效率略低于氢气,但仍然可带来可观的减阻量。然而,乙烯在无燃烧的薄膜冷却状态下,雷诺数较高时会造成摩阻的轻微升高。Barth对边界层燃烧减阻机理进行了理论分析,发现边界层燃烧放热导致密度下降,且速度脉动下降,从而降低动量的法向输运,边界层外层的高速流体输运到近壁区的能力下降,最终导致摩阻降低。乙烯的边界层燃烧减阻结果还未得到实验或数值研究的验证。
|
图 8 氢气和乙烯燃料的边界层燃烧减阻(C:燃烧;NC:无燃烧)[43]Reduction of cf for hydrogen and ethylene injection (C: combustion; NC: non-combustion)[43] |
Stalker在建立模型时采用了Pr为常数1和局部相似假设,国内刘宏鹏、高振勋等[44]对其进行了改进,Pr采用分子动力学理论公式计算,此外不采用局部相似假设而直接建立卡门动量积分关系式。经验证,改进后的模型取得了更准确的计算结果。
综上所述,考虑边界层燃烧的壁面摩阻、热流理论计算模型得以建立,且计算精度得到了实验和数值模拟的验证。Barth等人[43]采用理论模型分析了边界层燃烧减阻的物理机理。不过,该理论模型只适用于零压力梯度,未来可进一步建立考虑压力梯度的理论计算模型。另一方面,采用实验和数值模拟研究验证Barth等[43]的以乙烯为燃料的边界层燃烧减阻的理论结论也有待开展。
3 数值模拟研究与边界层燃烧减阻相关的数值模拟按研究目的主要分为三部分:一部分复现实验结果以验证数值模拟程序[45],一部分验证边界层燃烧减阻的有效性及研究其影响因素[26, 29, 45-46],一部分开展与边界层燃烧减阻相关的物理机理研究[2, 45, 47-56]。下文将主要介绍与物理机理相关的数值模拟研究。此外,边界层燃烧的机理研究本质上是研究燃烧对湍流特性的影响,由于燃烧对壁湍流特性影响的研究[2, 45, 56]相对较少,且燃烧对自由剪切湍流特性影响的研究[47-55]与其有共通之处,因此,本文在主要介绍燃烧对壁湍流特性影响研究之前,首先简要介绍燃烧对自由剪切湍流特性影响的相关研究。
3.1 燃烧对自由剪切湍流特性的影响自由剪切流动主要以超声速湍流燃烧混合层流动为研究对象。Luo[47]采用时间发展直接数值模拟(DNS)详细考察了雷诺应力输运的支配项,分析了燃烧放热效应对湍流能量输运机制的影响,发现燃烧放热效应会增强流向湍流脉动向法向和展向脉动的传递,使得湍流各项异性减弱;压力-应变项将促进燃烧化学能向湍动能的转化,从而引发“燃烧诱导湍流生成”现象;此外,随着燃烧放热量增加,湍流耗散也将随之增加。Mahle等[48]的时间发展DNS研究发现燃烧放热效应将使超声速湍流混合层的增长率、湍动能和雷诺剪切应力减小,而湍动能和雷诺剪切应力的减小主要是平均密度效应。Knaus等[49]的时间发展DNS研究发现燃烧放热效应对湍流动能能谱几乎无影响但对温度谱影响明显。以上研究为减少计算量,均采用了时间发展DNS模式和简化化学反应机理,然而时间发展DNS无法模拟激波、膨胀波等空间结构。此外,这些DNS采用了无限快化学反应假设,难以模拟如点火/熄火等有限速率化学反应效应。为解决上述简化带来的模拟困境,Ferrer等[50-51]基于详细化学反应机理对超声速湍流燃烧混合层流动开展了空间发展DNS研究。该研究进一步验证Mahle等[48]的燃烧放热效应将使得混合层增长率降低的结论。然而,Menon和Fernando的二维DNS研究[52]发现对流马赫数为0.15和0.75时,燃烧放热效应使得混合层增长率减小,而对流马赫数为1.42时,燃烧放热效应却使得混合层增长率增大。Calhoon等的三维大涡模拟(LES)研究[53]发现对流马赫数为1.3时,燃烧放热效应也使得混合层增长率增大。Menon、Fernando[52]和Calhoon[53]的研究结论类似,因此关于高对流马赫数下燃烧放热效应对超声速湍流混合层发展的影响还有待进一步研究。国内苗文博等的二维DNS研究[54]支持燃烧放热效应使得混合层增长率减小的结论。刘宏鹏、高振勋等[55]基于详细化学反应机理并采用空间发展的LES研究发现点火将导致混合层厚度突增,而下游的燃烧放热效应将导致平均密度和湍流脉动减弱,进一步导致混合层增长率减小。该结论与Mahle等[48]、Ferrer等[50-51]的结论一致。
3.2 燃烧对壁湍流特性的影响壁湍流与自由剪切湍流的特性之间有明显不同,通常壁湍流尺度范围跨度更大(Kolmogorov耗散小尺度1×10-5 m~积分尺度1 m),因此数值模拟的网格分辨率要求更高。此外,壁面需要给定合适的边界条件,且进行高精度模拟时需要设计与内点高阶格式相匹配的边界格式。简言之,壁湍流的精确模拟难度相对更大。下面介绍燃烧对壁湍流特性影响的相关研究。
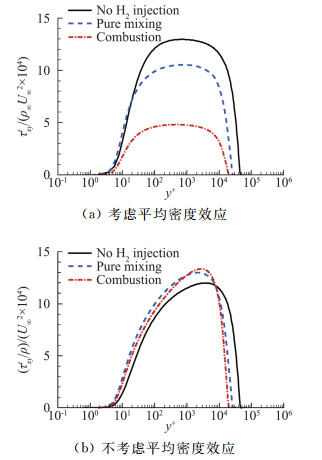
2015年,国内高振勋、李椿萱等[45]基于RANS对边界层燃烧减阻机理开展了研究。研究表明,边界层燃烧通过降低近壁区流体平均密度而降低近壁区雷诺应力,进一步降低壁面摩阻。结果如图 9所示。由图 9(a)可见,边界层燃烧下的考虑平均密度的雷诺剪切应力远小于无射流和薄膜冷却下的值。图 9(b)表明去掉平均密度后三个雷诺剪切应力分布相差不大。该结果与Barth等人[43]的理论结果略有差别——Barth的研究表明边界层燃烧同时通过降低平均密度和湍流脉动来降低壁面摩阻,但平均密度的降低是主要机制,而高振勋的研究中边界层燃烧对湍流脉动几乎无影响。
|
图 9 边界层燃烧减阻及薄膜冷却状态下的雷诺剪切应力[45] Fig.9 Reynolds shear stress for boundary layer combustion and film cooling[45] |
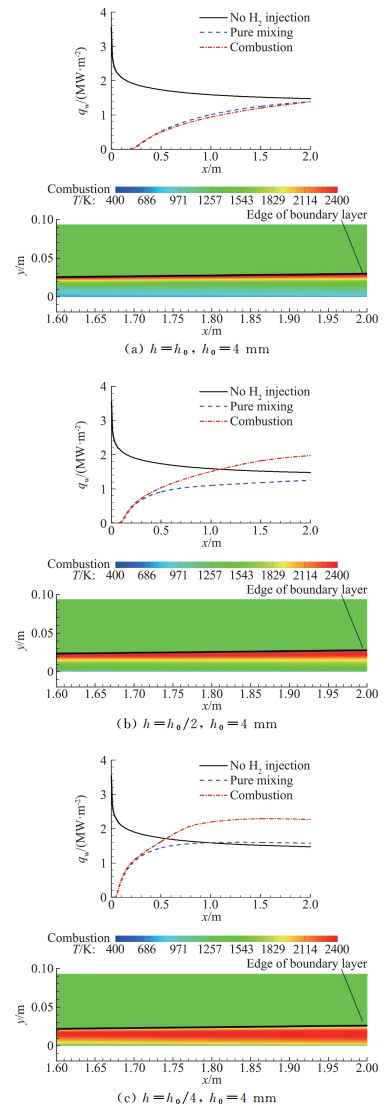
此外,高振勋、李椿萱等[45]进一步研究了边界层燃烧时壁面热流的变化规律。图 10给出了边界层燃烧时不同燃料射流高度对壁面热流的影响。由图 10(a)可见,当燃料射流高度较高(燃料喷口高度h=h0=4 mm)、火焰距壁面较远时,近壁区化学反应速率极低,因而壁面温度梯度变化小、湍流涡黏性低。因此,燃烧放热效应并未使得壁面热流增加,反而使其减小。当火焰逐渐靠近壁面,近壁区化学反应速率逐渐增加导致温度梯度增加,壁面热流将显著增加,如图 10(b)、10(c)所示。作者提出一种优化的射流方案——在氢气射流流量一定时,较高的喷口高度结合较低的入射速度的射流方案将有助于在不使得壁面加热恶化的同时实现较优的壁面减阻效果。高振勋等[45]的研究取得了一系列有意义的结论,然而,RANS方法难以预测湍流脉动和捕捉湍流结构,因而本研究未能探索更深层次的边界层燃烧减阻物理机理。
|
图 10 边界层燃烧时不同燃料射流高度对壁面热流的影响[45] Fig.10 Effects of different fuel injection heights on wall heat fluxes with boundary layer combustion[45] |
澳大利亚Queensland大学的Andrew Denman等人[2, 56]采用LES进一步研究了边界层燃烧减阻的物理机理。研究表明,边界层燃烧将使得近壁区雷诺应力降低,进一步使得壁面摩阻降低。而近壁区密度和脉动速度相关量的同时降低致使近壁区雷诺应力降低。此外,Andrew Denman进一步剖析了雷诺应力降低的物理机理——边界层燃烧放热,使得压力应变导致的脉动速度分配力减弱,从而使得流向脉动动能向法向脉动动能的分配量减少,导致法向脉动速度降低,从而使雷诺应力降低。研究还发现,边界层燃烧放热导致流向和展向速度条带尺度增大。从湍流结构角度看,速度条带尺度的变化将改变近壁区湍流的上冲、下扫等流体微团的运动机制,从而改变近壁区雷诺应力。边界层燃烧问题是包含燃烧和湍流相互作用的复杂流动问题,近壁区湍流尺度范围很宽,使得数值求解的刚性问题很严重。为简化计算,Andrew Denman等人[2, 56]采用了向流场中加入热量源项的方法代替对真实化学反应过程的模拟,然而该简化忽略了燃料和氧化剂的混合以及有限速率化学反应过程。随着计算能力的提升以及数值模拟方法的发展,基于高精度数值模拟开展考虑真实化学反应过程的边界层燃烧减阻机理的研究也具有可行性。
综上所述,考察边界层燃烧减阻物理机理的数值模拟研究取得了一定进展。燃烧效应对自由剪切湍流和对壁湍流特性的影响具有共通之处:燃烧放热效应降低平均密度和湍流脉动强度,减弱湍流动量输运,导致混合层厚度增长率降低(自由剪切湍流)或壁面摩阻减小(壁湍流)。然而,边界层燃烧减阻机理的数值模拟研究极少,而其中的LES研究采用了简化的向流场中加入热量源项的方法,难以考虑燃料和空气的混合以及有限速率化学反应等真实物理过程。因此,边界层燃烧减阻物理机理的数值模拟研究仍有待进一步开展,尤其是考虑真实化学反应过程的高精度LES或DNS研究。
4 结论减阻设计对于提高超燃冲压发动机推阻比具有重要意义,而边界层燃烧是一种有效的降低摩阻的方法。自2000年Goyne等人首次通过实验验证其有效性后,经过各国研究人员近20年不懈努力,边界层燃烧减阻在实验、理论和数值模拟研究方面已取得显著进展:
1) 在实验研究方面,验证了边界层燃烧减阻的有效性,研究了来流驻点焓、马赫数和压力梯度等因素对减阻效率的影响,并探究了将该技术应用于真实超燃冲压发动机时来流不均匀性的影响,已初步形成将该减阻技术应用于高超声速飞行器的能力。
2) 在理论研究方面,建立了以氢气为燃料的边界层燃烧壁面摩阻、热流理论计算模型,该模型的精度得到了实验和数值模拟验证。而后该模型被推广至适用于任意燃料。另一方面,通过改进Pr数计算方法和摒弃局部相似假设,该模型的精度得到了进一步提高。
3) 在数值模拟研究方面,边界层燃烧减阻的有效性、影响因素,尤其是内在物理机理,分别得到了研究。机理研究发现,边界层燃烧放热导致平均密度下降,且湍流脉动强度减弱,从而造成动量的法向输运降低,边界层外层的高速流体输运到近壁区的能力下降,最终导致摩阻降低。
笔者认为,后续研究可重点关注以下问题。在实验研究方面,一方面可结合数值模拟,进一步得到不同因素对边界层燃烧减阻影响的一般性规律;另一方面,可通过测量边界层内密度、速度和湍流脉动分布等研究边界层燃烧减阻的物理机理。在理论研究方面,可进一步考虑有压力梯度下的边界层燃烧摩阻、热流计算模型。在数值模拟研究方面,边界层燃烧减阻机理的数值模拟研究相对较少,仍有待进一步开展,尤其是考虑真实化学反应过程的高精度LES和DNS研究。此外,在将边界层燃烧方法实际应用于超燃冲压发动机减阻设计时,可进行优化设计。在不使得壁面热流增加的同时,优化喷口高度、减阻燃料质量流量等,以实现最优减阻效果。
| [1] |
FRY R S. A century of ramjet propulsion technology evolution[J]. Journal of Propulsion and Power, 2004, 20(1): 27-58. DOI:10.2514/1.9178 |
| [2] |
DENMAN A. Large eddy simulation of compressible turbulent boundary layers with heat addition[D]. Australia: University of Queensland, 2007.
|
| [3] |
KIRCHHARTZ R M, MEE D J, STALKER R J. Supersonic skin-friction drag with tangential wall slot fuel injection and combustion[J]. AIAA Journal, 2012, 50(2): 313-324. DOI:10.2514/1.j051073 |
| [4] |
李克文, 连淇祥. 边界层减阻研究综述[J]. 北京航空航天大学学报, 1991, 17(4): 68-76. LI K W, LIAN Q X. A review on drag reduction of boundary layer[J]. Journal of Beijing University of Aeronautics and Astronautics, 1991, 17(4): 68-76. (in Chinese) |
| [5] |
COUSTOLS E. Control of turbulent flows for skin friction drag reduction[M]. Vienna: Springer Vienna, 1996: 155-202. DOI:10.1007/978-3-7091-2688-2_4
|
| [6] |
BUSHNELL D, HEFNER J. Viscous drag reduction in boundary layers[M]//SEEBASS A R.Progress in Astronautics and Aeronautics. Washington DC: AIAA, 1990. https://doi.org/10.2514/4.865978
|
| [7] |
WALSH M J, WEINSTEIN L M. Drag and heat transfer on surfaces with small longitudinal fins[C]//11th Fluid and Plasma Dynamics Conference, Seattle, WA, USA. Reston, Virigina: AIAA, 1978: https://doi.org/10.2514/6.1978-1161
|
| [8] |
WALSH M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486. DOI:10.2514/3.60126 |
| [9] |
SAREEN A, DETERS R, HENRY S, et al. Drag reduction using riblet film applied to airfoils for wind turbines[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA. AIAA 2011-558. https://doi.org/10.2514/6.2011-558
|
| [10] |
ANTONIA R A, ZHU Y, SOKOLOV M. Effect of concentrated wall suction on a turbulent boundary layer[J]. Physics of Fluids, 1995, 7(10): 2465-2474. DOI:10.1063/1.868690 |
| [11] |
PARK J, CHOI H. Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow[J]. Physics of Fluids, 1999, 11(10): 3095-3105. DOI:10.1063/1.870167 |
| [12] |
CHUNG Y M, SUNG H J, KROGSTAD P A. Modulation of near-wall turbulence structure with wall blowing and suction[J]. AIAA Journal, 2002, 40(8): 1529-1535. DOI:10.2514/2.1849 |
| [13] |
OYEWOLA O M. Streamwise variations of higher-order turbulence statistics in a turbulent boundary layer subjected to localise wall suction[J]. International Journal of Mechanical Sciences, 2006, 48(10): 1163-1171. DOI:10.1016/j.ijmecsci.2006.04.001 |
| [14] |
SIMPSON R L. Characteristics of turbulent boundary layers at low Reynolds numbers with and without transpiration[J]. Journal of Fluid Mechanics, 1970, 42(4): 769-802. DOI:10.1017/s002211207000160x |
| [15] |
WILKINSON S P.. Influence of wall permeability on turbulent boundary-layer properties[C]//21st Aerospace Sciences Meeting, Reno, NV, USA. Reston, Virigina: AIAA, 1983. https://doi.org/10.2514/6.1983-294
|
| [16] |
DERSHIN H, LEONARD C A, GALLAHER W H. Direct measurement of skin friction on a porous flat plate with mass injection[J]. AIAA Journal, 1967, 5(11): 1934-1939. DOI:10.2514/3.4343 |
| [17] |
HWANG D. Review of research into the concept of the microblowing technique for turbulent skin friction reduction[J]. Progress in Aerospace Sciences, 2004, 40(8): 559-575. DOI:10.1016/j.paerosci.2005.01.002 |
| [18] |
PARTHASARATHY K, ZAKKAY V. An experimental investigation of turbulent slot injection at Mach 6[J]. AIAA Journal, 1970, 8(7): 1302-1307. DOI:10.2514/3.5889 |
| [19] |
SCHETZ J A, VANOVEREEM J. Skin friction reduction by injection through combinations of slots and porous sections[J]. AIAA Journal, 1975, 13(8): 971-972. DOI:10.2514/3.60492 |
| [20] |
CARY A M, HEFNER J N. Film-cooling effectiveness and skin friction in hypersonic turbulent flow[J]. AIAA Journal, 1972, 10(9): 1188-1193. DOI:10.2514/3.50348 |
| [21] |
RICHARDS B E, STOLLERY J L. Laminar film cooling experiments in hypersonic flow[J]. Journal of Aircraft, 1979, 16(3): 177-181. DOI:10.2514/3.58502 |
| [22] |
O'ONNOR J P, HAJI-SHEIKH A. Numerical study of film cooling in supersonic flow[J]. AIAA Journal, 1992, 30(10): 2426-2433. DOI:10.2514/3.11243 |
| [23] |
JUHANY K A, HUNT M L, SIVO J M. Influence of injectant Mach number and temperature on supersonic film cooling[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1): 59-67. DOI:10.2514/3.501 |
| [24] |
AUPOIX B, MIGNOSI A, VIALA S, et al. Experimental and numerical study of supersonic film cooling[J]. AIAA Journal, 1998, 36: 915-923. DOI:10.2514/3.13913 |
| [25] |
DELLIMORE K H, MARSHALL A W, CADOU C P. Influence of compressibility on film-cooling performance[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(3): 506-515. DOI:10.2514/1.45092 |
| [26] |
GOYNE C P, STALKER R J, PAULL A, et al. Hypervelocity skin-friction reduction by boundary-layer combustion of hydrogen[J]. Journal of Spacecraft and Rockets, 2000, 37(6): 740-746. DOI:10.2514/2.3645 |
| [27] |
SWITHENBANK J, EAMES I, CHIN S, et al. Turbulent mixing in supersonic combustion systems[C]//27th Aerospace Sciences Meeting, Reno, NV, USA. Reston, Virigina: AIAA. AIAA 89-0260. https://doi.org/10.2514/6.1989-260
|
| [28] |
BILLIG F S. Research on supersonic combustion[J]. Journal of Propulsion and Power, 1993, 9(4): 499-514. DOI:10.2514/3.23652 |
| [29] |
SURAWEERA M, MEE D, STALKER R. Skin friction reduction in hypersonic turbulent flow by boundary layer combustion[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA. AIAA-2005-0613. https: //doi.org/10.2514/6.2005-613
|
| [30] |
SURAWEERA M, et al. Reduction of skin friction drag in hypersonic flow by boundary layer combustion[D]. University of Queensland, 2006.
|
| [31] |
KIRCHHARTZ R M, MEE D J, STALKER R J. Supersonic skin-friction drag with tangential wall slot fuel injection and combustion[J]. AIAA Journal, 2012, 50(2): 313-324. DOI:10.2514/1.j051073 |
| [32] |
CHAN W Y K, MEE D J, SMART M K, et al. Drag reduction by boundary-layer combustion:effects of flow disturbances from rectangular-to-elliptical-shape-transition inlets[J]. Journal of Propulsion and Power, 2015, 31(5): 1256-1267. DOI:10.2514/1.b35335 |
| [33] |
KIRCHHARTZ R M, MEE D J, STALKER R J, et al. Supersonic boundary-layer combustion:effects of upstream entropy and shear-layer thickness[J]. Journal of Propulsion and Power, 2010, 26(1): 57-66. DOI:10.2514/1.44485 |
| [34] |
KIRCHHARTZ R M. Upstream wall layer effects on drag reduction with boundary layer combustion[D]. University of Queensland, 2010.
|
| [35] |
HOPKINS E J, INOUYE M. An evaluation of theories for predicting turbulent skin friction and heat transfer on flat plates at supersonic and hypersonic Mach numbers[J]. AIAA Journal, 1971, 9(6): 993-1003. DOI:10.2514/3.6323 |
| [36] |
BRADSHAW P. Compressible turbulent shear layers[J]. Annual Review of Fluid Mechanics, 1977, 9(1): 33-52. DOI:10.1146/annurev.fl.09.010177.000341 |
| [37] |
VAN DRIEST E R. Turbulent boundary layer in compressible fluids[J]. Journal of the Aeronautical Sciences, 1951, 18(3): 145-160. DOI:10.2514/8.1895 |
| [38] |
Van DRIEST E R. The problem of aerodynamic heating[J]. Aeronautical Engineering Review, 1956, 15(10): 26-41. |
| [39] |
STOLLERY J L. Supersonic turbulent boundary layers:some comparisons between experiment and a simple theory[J]. Aeronautical Quarterly, 1976, 27(2): 87-98. DOI:10.1017/s0001925900007599 |
| [40] |
SPALDING D B, CHI S W. The drag of a compressible turbulent boundary layer on a smooth flat plate with and without heat transfer[J]. Journal of Fluid Mechanics, 1964, 18(1): 117-143. DOI:10.1017/s0022112064000088 |
| [41] |
GOYNE C P, STALKER R J, PAULL A. Skin-friction measurements in high-enthalpy hypersonic boundary layers[J]. Journal of Fluid Mechanics, 2003, 485: 1-32. DOI:10.1017/s0022112003003975 |
| [42] |
STALKER R J. Control of hypersonic turbulent skin friction by boundary- layer combustion of hydrogen[J]. Journal of Spacecraft and Rockets, 2005, 42(4): 577-587. DOI:10.2514/1.8699 |
| [43] |
BARTH J E, WHEATLEY V, SMART M K. Hypersonic turbulent boundary-layer fuel injection and combustion:skin-friction reduction mechanisms[J]. AIAA Journal, 2013, 51(9): 2147-2157. DOI:10.2514/1.j052041 |
| [44] |
LIU H P, GAO Z X, TANG Y H, et al. Improvement of skin friction and heat transfer prediction theory of turbulent boundary-layer combustion of hydrogen[J]. International Journal of Hydrogen Energy, 2017, 42(41): 26123-26131. DOI:10.1016/j.ijhydene.2017.08.144 |
| [45] |
GAO Z X, JIANG C W, PAN S W, et al. Combustion heat-release effects on supersonic compressible turbulent boundary layers[J]. AIAA Journal, 2015, 53(7): 1949-1968. DOI:10.2514/1.j053585 |
| [46] |
CLARK R J, BADE SHRESTHA S O. Boundary layer combustion for skin friction drag reduction in scramjet combustors[C]//50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH. Reston, Virginia: AIAA. AIAA-2014-3667. https://doi.org/10.2514/6.2014-3667
|
| [47] |
LUO K H. Combustion effects on turbulence in a partially premixed supersonic diffusion flame[J]. Combustion and Flame, 1999, 119(4): 417-435. DOI:10.1016/S0010-2180(99)00074-7 |
| [48] |
MAHLE I, FOYSI H, SARKAR S, et al. On the turbulence structure in inert and reacting compressible mixing layers[J]. Journal of Fluid Mechanics, 2007, 593: 171-180. DOI:10.1017/s0022112007008919 |
| [49] |
KNAUS R, PANTANO C. On the effect of heat release in turbulence spectra of non-premixed reacting shear layers[J]. Journal of Fluid Mechanics, 2009, 626: 67-109. DOI:10.1017/s0022112008005636 |
| [50] |
FERRER P J M, LEHNASCH G, MURA A. Compressibility and heat release effects in high-speed reactive mixing layers Ⅰ.:Growth rates and turbulence characteristics[J]. Combustion and Flame, 2017, 180: 284-303. DOI:10.1016/j.combustflame.2016.09.008 |
| [51] |
FERRER P J M, LEHNASCH G, MURA A. Compressibility and heat release effects in high-speed reactive mixing layers Ⅱ. Structure of the stabilization zone and modeling issues relevant to turbulent combustion in supersonic flows[J]. Combustion and Flame, 2017, 180: 304-320. DOI:10.1016/j.combustflame.2016.09.009 |
| [52] |
MENON S, FERNANDO E. A numerical study of mixing and chemical heat release in supersonic mixing layers[C]//28th Aerospace Sciences Meeting, Reno, NV, USA. Reston, Virigina: AIAA. AIAA 1990-0152. https: //doi.org/10.2514/6.1990-152
|
| [53] |
JR CALHOON W H ARUNAJATESAN S, DASH S M. Heat release and compressibility effects on planar shear layer development[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2003. AIAA 2003-1273. https: //doi.org/10.2514/6.2003-1273.
|
| [54] |
苗文博, 程晓丽, 王强. 超声速空间发展燃烧反应剪切层放热效应分析[J]. 空气动力学学报, 2008, 26(3): 339-343. MIAO W B, CHENG X L, WANG Q. Analysis of the energy release effects in supersonic reacting flows[J]. Acta Aerodynamica Sinica, 2008, 26(3): 339-343. DOI:10.3969/j.issn.0258-1825.2008.03.012 (in Chinese) |
| [55] |
LIU H P, GAO Z X, JIANG C W, et al. Numerical study of combustion effects on the development of supersonic turbulent mixing layer flows with WENO schemes[J]. Computers & Fluids, 2019, 189: 82-93. DOI:10.1016/j.compfluid.2019.05.019 |
| [56] |
DENMAN A W, JACOBS P A, MEE D J. Compressible, turbulent flow with boundary-layer heat addition[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2005. AIAA 2005-1097. https: //doi.org/10.2514/6.2005-1097
|
 2020, Vol. 38
2020, Vol. 38