2. 清华大学 航天航空学院, 北京 100084
2. School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
湍流燃烧,特别是贫燃预混燃烧是当前能源和动力装置实现高效清洁燃烧的一个重要途径。如通用电气新一代燃气轮机和航空发动机,普遍采用局部预混或完全预混燃烧,通过控制火焰温度实现低NOx排放。燃烧室内流动、混合、燃烧等复杂过程可能引起局部熄火/再燃、燃烧不稳定和贫燃吹熄等现象。迄今为止,国内外已开展大量针对燃料/空气混合过程、混合物当量比、压力以及旋流等因素对火焰结构、稳定运行边界及污染物生成的影响机制的研究[1-8]。高精度数值模拟能揭示湍流预混燃烧中内在的复杂物理化学过程,对优化燃烧组织和减少污染物排放起到关键作用。当前,基于概率密度函数(PDF)方法的数值模拟是研究实际燃烧过程的最先进的手段之一。相比于小火焰面类模型[9],PDF方法[10-11]能不带任何假设地精确求解有限反应速率。这一特性对准确预测湍流火焰中的局部熄火/再燃现象和污染物生成非常重要。因此PDF方法在研究强湍流-化学反应相互作用方面有着独到的优势。
自美国康奈尔大学Pope教授课题组20世纪80年代初一系列创造性的工作以来,雷诺平均/概率密度函数(RANS/PDF)方法在过去的三十年中,已经从局限于典型简单算例问题和实验室尺度燃烧火焰的研究工具,发展成为一种可以应用到实际燃烧装置上的湍流燃烧模拟方法。PDF方法已成功地用于研究非预混湍流燃烧中局部熄火/再燃和污染物生成等复杂物理过程,同时已被用于模拟燃气轮机燃烧室和往复式活塞内燃机等发动机中的复杂燃烧过程[10-11]。近年来,随着计算机和数值方法的发展,将PDF方法用作大涡模拟(LES)亚网格模型的大涡模拟/概率密度函数(LES/PDF)相结合的方法有了显著的发展[12-14]。PDF方法为亚格子过滤尺度下的组分提供了完整的描述。LES/PDF相结合的方法能同时准确地描述湍流及湍流-化学反应相互作用。Sheikhi等人[12]用LES/PDF结合简单的化学反应机理来模拟Sandia火焰D。Lu等人[13]通过将动态自适应建表(ISAT)方法结合到LES/PDF中,实现了对湍流混合层的包含详细化学反应机理的LES/PDF模拟。近期Yang和Pope[14]用含有详细化学反应动力学的LES/PDF研究了随时间发展的非预混CO/H2湍流平面射流火焰,揭示了强烈的湍流-化学反应相互作用会导致局部熄火及再燃等物理现象。Han等人[15]用LES/PDF方法研究了燃烧模型对代夫特-阿德莱德天然气射流火焰中碳烟生成的影响,发现相较火焰面类燃烧模型,PDF方法所得结果与实验值更为接近。Ansari等人[16]用LES/PDF方法模拟了旋流燃烧室PRECCINSTA,计算结果与实验相符,这是首次尝试将LES/PDF方法应用于实际气体透平燃烧室。Han等人[17]用LES/PDF研究了热伴流条件下的氢气抬举火焰,发现解析尺度上的分子扩散是影响火焰稳定区域的重要因素。Zhou等人[18]在LES/PDF中同时考虑解析尺度上和亚网格内的差异扩散效应,并以此研究了热伴流条件下甲烷-氢气射流火焰中差异扩散的影响。Kim和Pope[19]通过结合降维与化学建表技术来加速对湍流贫燃预混丙烷-空气火焰的LES/PDF模拟。
然而,到目前为止基于PDF方法的数值模拟在湍流预混火焰中的研究还十分有限[20-24]。Lindstedt和Vaos[21]发现现有混合模型在预测湍流火焰燃烧速度方面有着明显的缺陷。最近,Rowinski和Pope采用速度-湍流频率-组分联合概率密度函数方法研究了甲烷预混值班火焰[23],发现运用现有混合模型,反应进度被不同程度地高估了。研究得出了和文献[22, 24]一致的结论:湍流预混燃烧中反应标量的小尺度混合过程同时受到湍流和化学反应的影响,现有标量混合模型将湍流混合与标量混合的时间尺度比设为常数而与燃烧状态无关是不合理的。Ren等人[25]从贫燃预混氢气-空气狭缝射流非稳态火焰的包含详细机理的千万亿次三维直接数值模拟数据[26]出发,研究了湍流对火焰结构、反应标量耗散率的影响机理,发展出一个适用于各个预混燃烧状态的标量小尺度混合模型,该模型考虑了预混燃烧中标量小尺度混合、湍流混合和化学反应这三个强耦合物理过程的内在联系,提升了PDF方法对预混燃烧预测精度。
本综述介绍当前湍流预混燃烧中混合模型研究的一些最新进展。第一章从混合形式和混合时间尺度两个方面简介了标量小尺度混合模型,并介绍了标量小尺度混合模型在预混燃烧中的表现。第二章介绍了从湍流燃烧直接数值模拟数据出发对湍流预混火焰中反应标量耗散率规律的研究,并重点介绍了新发展的反应标量线性混合时间尺度模型。第三章首先介绍了近极限条件下湍流预混燃烧LES/PDF模拟的最新进展,重点介绍了一个针对大涡/输运概率密度函数模拟的反应标量混合时间尺度模型及其在近极限湍流预混燃烧LES/PDF模拟中的应用,以及网格解析度对标量混合和燃烧特性预测影响的最新研究进展。
1 标量小尺度混合模型在PDF方法中,非线性化学源项是精确求解的,但小尺度上分子扩散引起的流体颗粒组分变化则需要通过标量小尺度混合模型来模拟。
在RANS(或LES)框架下,单点单时刻的组分联合概率密度函数f的输运方程为:
| $ \begin{array}{*{20}{l}} {\frac{{\partial \rho f}}{{\partial {\kern 1pt} t}} + \frac{{\partial ({{\tilde U}_i}\rho f)}}{{\partial {\kern 1pt} {x_i}}} + \frac{\partial }{{\partial {\kern 1pt} {\psi _k}}}({S_k}\rho f) = }\\ {\frac{\partial }{{\partial {\psi _k}}}\left( {\left\langle {\left. {\frac{{\partial {J_{i,k}}}}{{\partial {x_i}}}} \right|\mathit{\boldsymbol{\psi }}} \right\rangle f} \right) - \frac{\partial }{{\partial {\kern 1pt} {x_i}}}( < {u^{\prime \prime }}_i|\mathit{\boldsymbol{\psi }} > \rho f)} \end{array} $ | (1) |
式中重复指标约定求和。其中
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial {\psi _k}}}\left[ {\left\langle {\left. {\frac{{\partial {J_{i,k}}}}{{\partial {\kern 1pt} x{{\kern 1pt} _i}}}} \right|\mathit{\boldsymbol{\psi }}} \right\rangle f} \right] = \frac{\partial }{{\partial {\psi _k}}}\left[ {\frac{{\partial < {J_{i,k}} > }}{{\partial {\kern 1pt} x{{\kern 1pt} _i}}}f} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial {\psi _k}}}\left[ {\left\langle {\left. {\frac{{\partial J_{i,k}^\prime }}{{\partial {\kern 1pt} x{{\kern 1pt} _i}}}} \right|\mathit{\boldsymbol{\psi }}} \right\rangle f} \right]} \end{array} $ | (2) |
式(2)右侧第一项为质量流率的平均值导致的发生在物理空间的输运,在LES框架下需要被考虑而在RANS框架下一般被忽略。式(2)右侧第二项为由质量流率的脉动导致的发生在组分空间的混合,在RANS和LES框架下均需使用混合模型对该项进行建模。
蒙特卡洛计算颗粒/流场双向耦合方法是PDF方法的一种常用实现方式,每个计算网格内均包含多个计算颗粒,用以体现该空间位置处的组分联合概率密度信息。计算颗粒n携带有位置信息x(n)、权重信息w(n)及组分标量信息
在RANS框架下,前述欧拉观点下组分标量联合概率密度函数f输运方程(1)与拉格朗日观点下的计算颗粒随机微分方程组等价,
| $ {{\rm{d}}x_i^{(n)} = \tilde U_i^{(n)}{\rm{d}}t + {\rm{d}}x_{i,{\rm{ turb }}}^{(n)}} $ | (3) |
| $ {{\rm{d}}\phi _k^{(n)} = {S_k}({\mathit{\boldsymbol{\phi }} ^{(n)}}){\rm{d}}t + [M]/{\tau _\phi } \cdot {\rm{d}}t} $ | (4) |
其中
如前所述,分子扩散项所导致的组分空间的混合由混合模型刻画,混合模型分为混合形式
在对混合形式
| $ {\omega ^{(p)}}{\left. {\frac{{{\rm{d}}Y_\beta ^{(p)}}}{{{\rm{d}}t}}} \right|_q} = - {a^{(pq)}}(Y_\beta ^{(p)} - Y_\beta ^{(q)}) $ | (5) |
其中a(pq)为混合因子,表征颗粒之间相互作用的速率,记号
经典的常数湍流-标量时间尺度模型假设混合时间尺度正比于湍流时间尺度,即
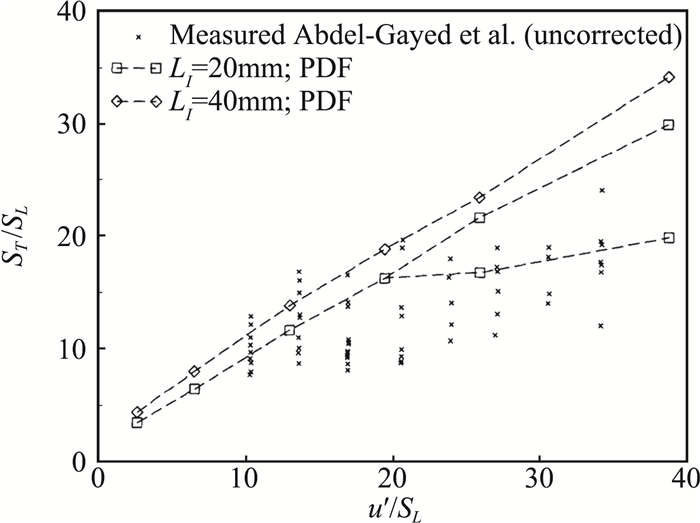
近些年,关于湍流预混火焰PDF数值模拟中混合模型表现的研究有一些最新进展[20, 23, 44-45]。举例来说Hulek和Lindstedt[20]用二项朗之万模型来封闭标量混合,对当量比为1的湍流甲烷-空气预混火焰传播进行了单点单时刻联合速度-组分PDF模拟。Hulek和Lindstedt采用类似于Anand和Pope[46]的模拟方法,进行了湍流预混火焰的稳态计算,火焰可以自由移动,计算域跟随火焰进行动态调整。利用多组不同的上游湍流条件(由湍流脉动速度u′和积分长度尺度LI定义)的模拟结果,Hulek和Lindstedt研究了湍流火焰传播速度的标度率。如图 1所示,模拟得到的湍流火焰传播速度与实验数据[47]相符。
|
图 1 两个积分长度尺度下的模拟结果与Abdel-Gayed等人的实验数据在湍流火焰传播速度随湍流强度变化关系上的对比(图来自文献[20]) Fig.1 Values of the turbulent burning velocity plotted against turbulence intensity. The experimental results of Abdel-Gayed et al. are compared with the calculations for two values of the integral length-scale of turbulence. (Reproduced from Ref.[20]) |
Sundaram和Klimenko[45]讨论了MMC模型在湍流预混燃烧模拟中的应用。在预混燃烧的PDF模拟中采用MMC的主要目的是通过避免已燃和未燃气体的直接混合来使PDF模拟与层流火焰结构之间的一致性更佳,但是具体实现起来并不容易。Sundaram和Klimenko重点关注湍流预混燃烧中参考变量的一般性选取原则,考虑了基于level set或影子位置来构建参考变量。
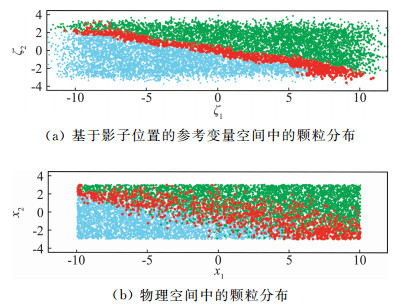
从物理观点出发,因为距瞬时火焰位置的距离比物理空间位置更具有物理意义,使用level set作为参考变量很有优势。然而,由于缺乏对惯性子区湍流预混火焰标度率的充分认识,基于level set的参考变量不适用于实际模拟中。Sundaram和Klimenko对高泽尔多维奇数下预混火焰的随机模拟表明,在实际模拟中影子位置可以用于方便地确定火焰位置,是参考变量的最佳选择。如图 2所示,在基于影子位置的参考变量空间中火焰的局部特性更佳,而在物理空间中反应区颗粒则十分分散。这表明在湍流预混火焰中选取影子位置作为MMC的参考变量是十分合理的。
|
图 2 10000个颗粒的二维湍流预混火焰随机模拟:蓝色表示未燃(ϕ < 0.05);红色代表反应中(0.05 < ϕ < 0.95);绿色代表已燃(ϕ>0.95) (图来自文献[45]) Fig.2 Simulation of a two-dimensional turbulent premixed flame in a channel with 10000 particles: blue markesr are unburned (ϕ < 0.05) red markers are burning (0.05 < ϕ < 0.95) and green markers are burned (ϕ>0.95). (Reproduced from Ref.[45]) |
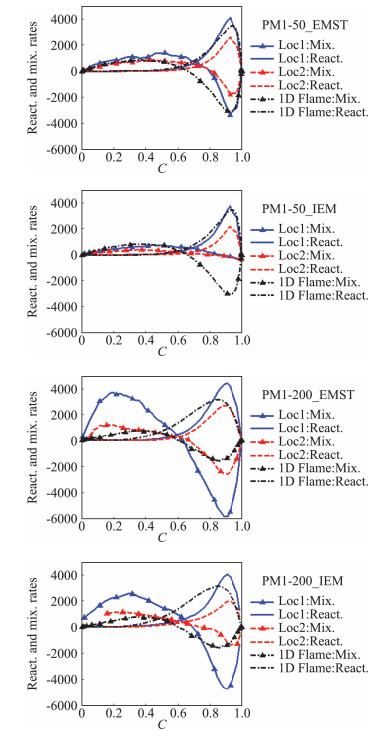
PPJB火焰[48-49]是近期提出的一种湍流预混火焰,用于研究贫燃、高湍流度条件下的湍流-化学反应相互作用。Rowinski和Pope[23]采用速度-湍流频率-组分联合概率密度函数方法研究甲烷预混值班PPJB火焰发现,运用现有混合模型,反应进度被不同程度地高估了。Zhou等人[50]对PPJB进行了RANS-PDF模拟,进一步研究了已有小尺度混合模型在PPJB火焰中的表现。通过分析IEM与EMST这两种小尺度混合模型对应的反应/混合速率在反应进度标量空间中的分布,揭示了在火焰面燃烧模式与破碎反应区燃烧模式下,两种混合模型预测的标量混合规律存在差异。如图 3所示,通过比较在反应区混合速率和反应速率的相对大小,可以发现对于中心射流速度为50 m/s的PPJB火焰(PM1-50,接近褶皱火焰面燃烧模式),尽管IEM模型能够正确地预测组分平均值的空间分布,但却错误地预测燃烧过程为自着火,EMST模型则能够正确的预测燃烧过程为火焰传播。对于中心射流速度为200 m/s的PPJB火焰(PM1-200,接近破碎反应区燃烧模式),IEM与EMST两种模型预测出的燃烧过程均为火焰传播。研究表明在火焰面燃烧模式下,保持组分空间临近非常重要,EMST模型优于IEM模型;在破碎反应区燃烧模式下,组分空间保持临近的重要性有所减弱,两种模型的性能相近。
|
图 3 PM1-50与PM1-200火焰,分别采用IEM与EMST模型得到的混合速率、反应速率在反应进度标量空间的条件平均值(图来自文献[50]) Fig.3 Conditional averaged reaction and mixing rates in the selected high-shear locations of PM1-50 and PM1-200. Lines with triangles: mixing/diffusion rates; Lines: reaction rates. (Reproduced from Ref.[50]) |
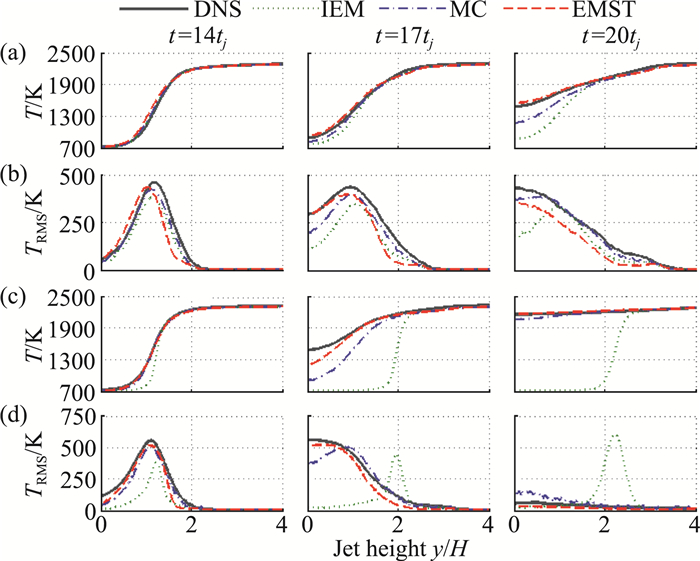
最近Kuron等人[44]利用贫燃预混氢气-空气火焰直接数值模拟(DNS)数据[26]评估了三种广泛使用的混合模型IEM、MC、EMST对PDF方法模拟湍流火焰传播过程的适用性。所采用的DNS是Sandia实验室用详细机理对贫燃预混氢气-空气狭缝射流非稳态火焰进行的千万亿次三维直接数值模拟[26],其中湍流雷诺数Ret高达1000,并固定Ret而改变邓克尔数Da,该DNS采用随时间演化的剪切层的配置在火焰结构中产生强烈湍流混合。DNS模拟为TPDF模拟提供了初始条件和随时间变化的输入参数,包括平均速度、湍流扩散系数以及标量混合时间尺度。研究发现三者之中EMST模型提供了对火焰结构和火焰传播速度的最佳预测。如图 4所示,IEM模型对条件平均和均方根扩散速率的预测值在定量上不准确;MC模型能够捕捉到条件平均扩散速率,但是过度预测均方根扩散速率;只有EMST模型能够同时准确地预测条件平均和均方根扩散速率,这是因为EMST模型可以强制混合发生在组分空间的相邻位置上。研究还开展了针对湍流-标量混合时间尺度比的参数研究。如图 5所示,结果表明尽管两个案例有相同的配置,然而两个案例中时间尺度比例常数的最优值相差两倍。因此,假定湍流-标量混合时间尺度比为常数这一方法对于湍流预混火焰并不可行,混合模型时间尺度模型的构建值得更多关注。
|
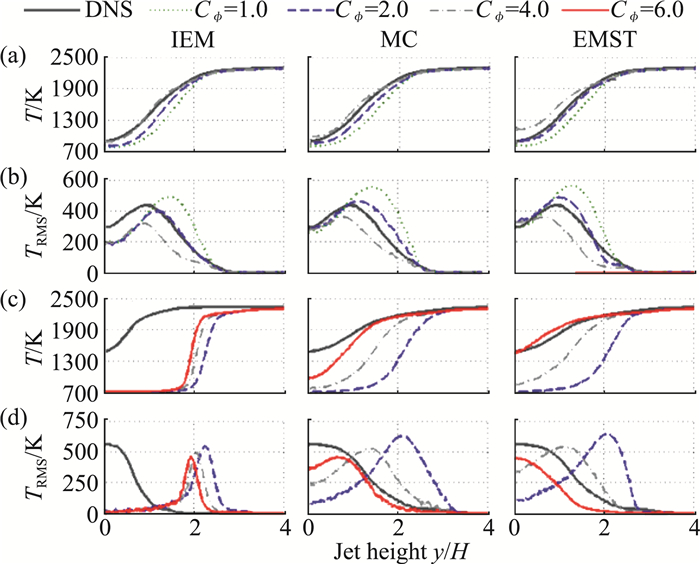
图 4 三个代表性时刻,分别采用IEM、MC、EMST模型预测出的温度沿射流高度方向的分布,(a)与(b): Case Da-,(c)与(d): Da+ (图来自文献[44]) Fig.4 Comparison of mixing model performance at different times using the progress variable defined on H2 mass fraction. Rows (a) and (b): Case Da-. Rows (c) and (d): Case Da+. (Reproduced from Ref.[44]) |
|
图 5 在t=17tj时刻,采用常数 |
在湍流预混火焰中,在较高邓克尔数(Da)情况下,小尺度分子输运和化学反应是强烈耦合的。在反应区,化学反应导致反应标量梯度变大,从而促进小尺度上的反应标量混合。因此,反应标量的小尺度混合过程同时受湍流和化学反应的影响,假设标量小尺度混合仅由湍流控制是不合理的。到目前为止,对湍流预混火焰,Lindstedt和Vaos[21]及Stollinger和Heinz[24]试图通过改进标量耗散率模型来考虑化学反应对湍流预混火焰中标量小尺度混合的影响。为了深入研究反应标量小尺度混合规律,反应标量(条件)耗散率是重要的研究对象。它是构建小尺度混合模型的重要基础量。然而实验测量湍流预混火焰中的反应标量耗散率十分困难。与之相比,DNS[26, 51]能够提供完整的流场、标量场和化学反应的信息,为研究小尺度混合过程提供了宝贵资源。从DNS数据出发,揭示小尺度湍流对火焰结构、反应标量耗散率的影响机理,发展适用于各个预混燃烧状态的标量小尺度混合模型,对于提升PDF方法对预混燃烧的预测精度有重要意义。
在研究湍流预混火焰中反应标量耗散率的规律方面,Ren等人[25]运用氢气贫预混湍流火焰的DNS数据[26]研究了处于薄反应区燃烧模式下的火焰结构对于标量耗散率的影响规律。该DNS[26]采用平面剪切层的配置产生湍流,通过调节流动的特征速度与特征长度,改变邓克尔数。在Da-的配置下,全场的邓克尔数保持始终小于1;在Da+的配置下,全场的邓克尔数保持始终大于1。Ren等人进一步将“化学爆炸模式分析(CEMA)”方法[52-53]应用于DNS数据,用以分辨不同的燃烧模式,从而分析不同燃烧模式下标量耗散率的特性。CEMA基于对化学反应源项雅克比矩阵
| $ D{a_e} = {\lambda _e}/\chi $ | (6) |
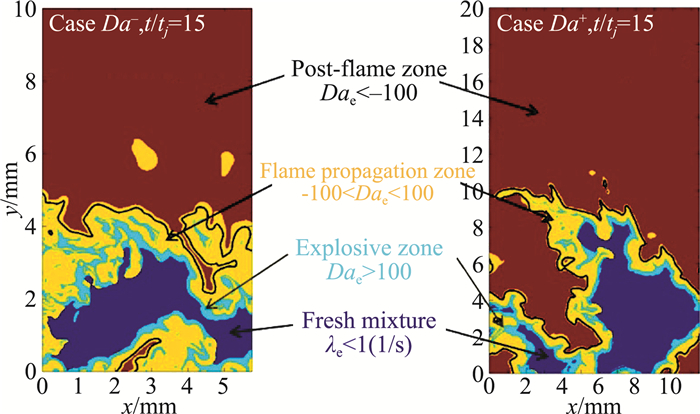
其中χ为进度变量的标量耗散率。根据λe和Dae可将该DNS流场分为4个区域,如图 6所示。
|
图 6 基于化学爆炸模拟分析的燃烧模式分区.黑线代表λe=0的等值线(图来自文献[25]) Fig.6 Flame zones segmented based on CEMA. The black isoline indicates λe =0(Reproduced from Ref.[25]) |
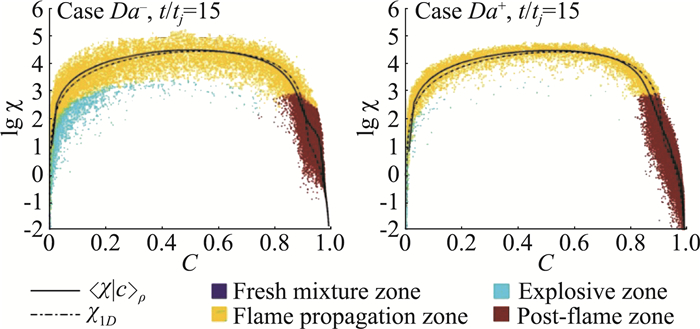
CEMA方法的结果表明该火焰中存在两种燃烧模式:火焰传播模式、火焰协助着火模式。如图 7所示,处于火焰传播模式下的标量耗散率在全局条件平均值附近的一个量级内变化;处于火焰协助着火模式下的标量耗散率比全局条件平均值小一个量级。对于火焰协助着火模式的进一步研究发现:火焰的瞬态过程,如自着火以及火焰之间相互作用,对于标量耗散率具有显著影响。与一维层流火焰模拟结果的对比发现:自着火转变为火焰传播以及火焰之间相互作用等瞬态过程都会造成标量耗散率的分布发生显著变化,这可能是造成DNS数据中标量耗散率分布非常分散的主要原因。对于DNS数据的统计分析表明,大涡模拟中的亚网格标量耗散率模型仍有待完善。
|
图 7 瞬态标量耗散率在反应进度标量空间中的分布.颜色代表不同的燃烧模式分区;实线代表条件平均的标量耗散率;点划线代表一维层流火焰中的标量耗散率(图来自文献[25]) Fig.7 Instantaneous conditional scalar dissipation rate colored by flame zone. Conditional mean SDR (solid black line) and conditional laminar 1D flame (dash-dot black line) are overlaid (Reproduced from Ref.[25]) |
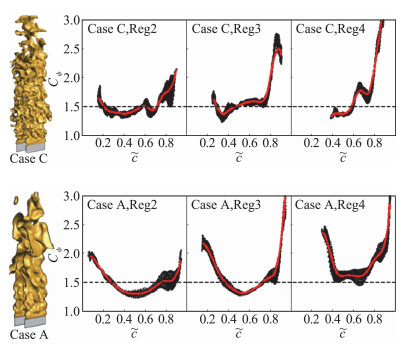
接着Zhou等人利用贫燃预混甲烷-空气射流火焰的DNS数据[54],分析了在不同湍流预混燃烧模式下反应进度变量混合时间尺度的演化规律。该DNS[54]是使用详细机理对空间演化的贫燃预混甲烷-空气湍流狭缝射流本生火焰进行的高分辨率三维直接数值模拟。保持邓克尔数Da不变,对不同的卡洛维兹数Ka进行模拟,Case A中Ka=3.0,Case C中Ka=7.2。如图 8所示,研究发现对于靠近破碎反应区模式的湍流火焰(Case C),反应进度变量的湍流-标量混合时间尺度比(
|
图 8 Case A(接近火焰面燃烧模式)与Case C (接近破碎反应区燃烧模式)中湍流-标量混合时间尺度比 |
基于上述研究发现,Kuron[55]等人发展了一种适用于所有湍流预混燃烧模式的混合时间尺度模型(hybrid timescale model)。该模型依据线性混合的思路来同时考虑湍流和火焰结构化学反应引入的小尺度混合,
| $ \varOmega = (1 - \eta )\frac{{{C_\phi }}}{{{\tau _{{\rm{ turb }}}}}} + \eta \frac{{\int_0^1 {\langle {\chi _c}|\zeta \rangle {f_c}(\zeta )} {\rm{d}}\zeta }}{{\widetilde {{c^{''}}^2}}} $ | (7) |
其中,
接下来,Kuron等人以贫燃预混氢气-空气平面火焰为目标火焰,利用DNS模拟数据为PDF模拟提供初始条件和随时间变化的输入参数(平均速度、湍流扩散系数以及标量混合时间尺度),对发展的hybrid timescale model进行了先验验证,并与另外两种混合时间尺度模型进行了对比[55]。研究发现,广泛使用的常数湍流-标量时间尺度模型,由于忽略了化学反应对标量混合的作用,低估了反应标量的标量耗散率。基于层流火焰特征时间的Kolla模型为:
| $ \varOmega = \frac{{{C_3}}}{{{\beta ^\prime }{\tau _{{\rm{ turb }}}}}} + \frac{1}{{{\beta ^\prime }}}(\frac{{2K_c^*}}{{{\tau _L}}} - {C_4}\theta \frac{{{\tau _{{\rm{ turb }}}}}}{{{\tau _L}}}) $ | (8) |
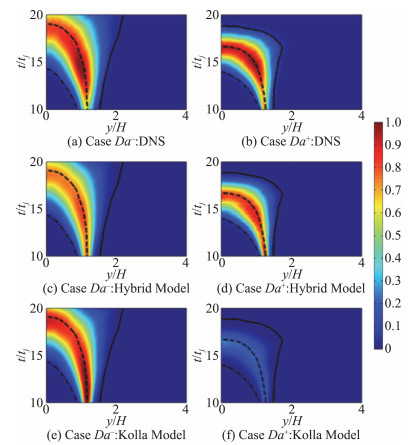
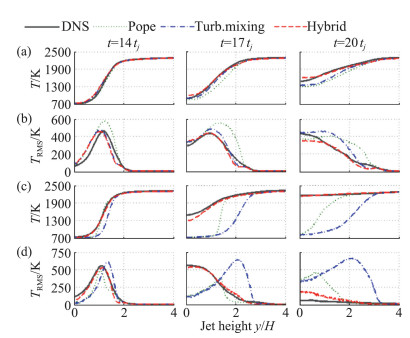
其中,C3、C4、β′为模型参数,τturb代表湍流特征时间尺度,τL代表基于层流火焰速度、厚度定义的火焰特征时间。如图 9所示,Kolla模型虽然在Da-的配置下预测性能较好,但由于无法恢复火焰面燃烧模式下标量耗散率的正确表达形式,在Da+配置下显著低估了火焰结构引起的标量耗散率。与之相比,新提出的hybrid timescale model则能够同时较好地预测Da+与Da-配置下反应标量的标量耗散率。如图 10所示,在不同时刻的温度展向分布也表明:采用常数湍流-标量时间尺度模型,会导致温度演化严重偏离准确值,尤其是在Da+的配置下;而采用新模型则能够准确地预测Da+与Da-两种配置下的温度随时间的演化。这证明了新模型由于考虑了湍流与化学反应的协同作用而具备优势。
|
图 9 贫燃预混氢气-空气平面火焰,不同时刻的标量耗散率沿展向的分布(图来自文献[55]) Fig.9 Scalar dissipation rate normalized by the maximum DNS value for DNS, new hybrid model, and Kolla model (Reproduced from Ref.[55]) |
|
图 10 贫燃预混氢气-空气平面火焰,三个代表时刻的温度平均值与脉动值的展向分布(图来自文献[55]) Fig.10 Predicted mean and RMS spatial temperature profiles from the DNS and TPDF solutions. Rows (a) and (b): Case Da-. Rows (c) and (d): Case Da+(Reproduced from Ref.[55]) |
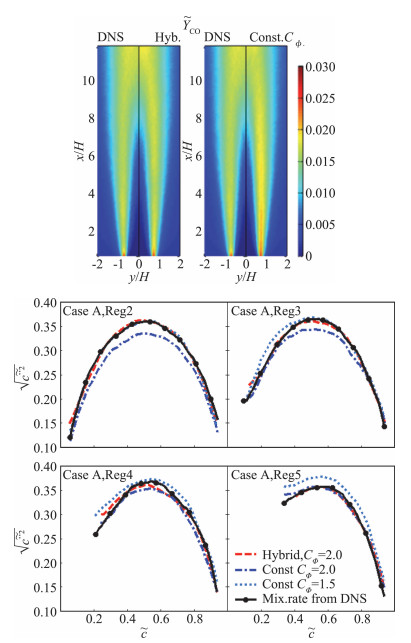
对贫燃预混甲烷-空气射流火焰的后验验证,同样证明了新提出的反应标量混合时间尺度模型能够改善不同湍流预混燃烧模式下输运概率密度函数方法的预测性能。图 11上部的CO质量分数空间分布云图直观地表明,采用常数湍流-标量时间尺度模型会显著高估上游位置处的CO质量分数,而采用新模型则可改善这一问题。分别采用常数湍流混合时间尺度模型与新模型,预测反应进度变量方差的条件平均值,从图 11下部发现:采用模型参数
|
图 11 上:分别采用常数湍流-标量时间尺度模型与新模型,预测的CO的空间分布云图.下:分别采用常数湍流-标量时间尺度模型与新模型,预测的反应进度变量方差的条件平均值 Fig.11 Top: Mean mass fraction of CO predicted by new hybrid timescale model and the constant mechanical-to-scalar mixing timescale ratio model. Bottom: Conditional RMS of progress variable predicted by new hybrid timescale model and the constant mechanical-to-scalar mixing timescale ratio model |
所发展的标量混合时间尺度模型公式(7)量化了预混燃烧中湍流混合和化学反应过程对反应标量混合的影响。同时,该模型具有适用于任何预混湍流燃烧模式的潜力,从建模层面提升了PDF方法对湍流预混燃烧的模拟精度。
3 近极限湍流预混燃烧的大涡/输运概率密度函数模拟由于强烈的湍流-化学反应相互作用,在近极限湍流预混燃烧中会有局部熄火及再燃等物理现象。近些年,值班预混射流燃烧室(PPJB)火焰[48-49]、高雷诺数甲烷-空气射流湍流预混火焰F1/F2/F3[56]、耶鲁湍流对冲预混火焰(TCF)[57]被广泛用于研究贫燃、高湍流度条件下的湍流-化学反应相互作用及局部熄火/再燃现象。
Wang等人[58]对于高雷诺数甲烷-空气射流湍流预混火焰F1/F2/F3[56]开展了LES/PDF模拟,主要关注混合频率模型对模拟结果的影响。传统的常数混合参数(CMP)模型基于局部平衡假设来给出混合频率:
| $ \varOmega = \frac{{C(\varGamma + {\varGamma _t})}}{{2{\varDelta ^2}}} $ | (9) |
该模型在非预混燃烧中表现良好,这是因为非预混燃烧特性是由混合分数这一被动标量表征的,混合分数仅由被解析的大尺度湍流确定,而不受化学反应影响。然而,在湍流预混火焰中,亚网格尺度下湍流与化学反应的耦合作用使得火焰面发生皱褶,进而强化了混合过程,因此在火焰锋面没有被完全解析(火焰厚度δth小于LES过滤尺度Δ)时传统的CMP模型会低估混合频率,从而无法准确捕捉火焰特性。在对标量耗散率的已有研究的基础上,Wang等人提出反应局部强化(LER)模型:
| $ \varOmega = \frac{{C(\varGamma + {\varGamma _t})}}{{2{\varDelta ^2}}}F\left( {\frac{\varDelta }{{{\delta _{{\rm{th}}}}}}} \right) $ | (10) |
其中
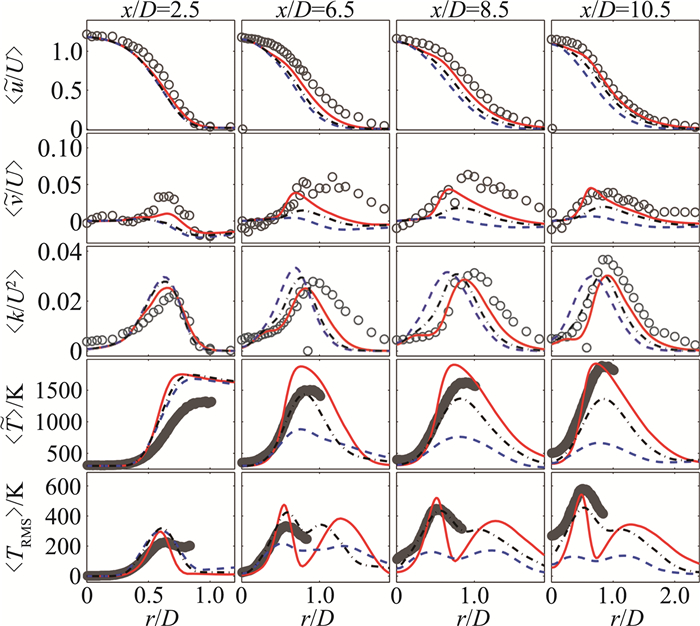
研究发现,在高雷诺数甲烷-空气射流湍流预混火焰F1[56]中,模拟结果对于混合频率模型的选取十分敏感。如图 12所示,传统的CMP模型无法准确捕捉预混火焰,会显著高估火焰锋面厚度。与之相比,新提出的LER模型对火焰的预测结果与实验值十分相符,这表明LER模型构建的依据是合理的。
|
图 12 F1火焰中不同轴向位置处时间平均的轴向速度、径向速度、湍动能、温度、温度均方根的径向分布(图来自文献[58]) Fig.12 Radial profiles of the time-averaged resolved axial velocity, radial velocity, turbulent kinetic energy, temperature, and resolved rms temperature at the different axial locations in flame F1 (Reproduced from Ref.[58]) 符号:实验数据;实线:LER模型;虚线:CMP模型,C=2;点划线:CMP模型,C=12 |
相类似地,Zhou等人对Kuron [55]提出的标量混合时间尺度模型在LES框架下加以拓展,发展了一个针对大涡/输运概率密度函数模拟的反应标量混合时间尺度模型。通过引入一个关于大涡模拟过滤尺度与湍流Kolmogorov尺度的削弱因子(ηa),使得该模型能够正确逼近流场的DNS极限:
| $ \begin{array}{*{20}{l}} {\varOmega = {\eta _a}(1 - \eta ){C_M}/\tau _{{\rm{ turb }}}^{{\rm{sgs}}} + [1 - {\eta _a}(1 - \eta )] \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^1 {\langle {\chi _c}|\zeta \rangle {f_c}(\zeta )} {\rm{d}}\zeta /\widetilde {{c^{''}}^2}} \end{array} $ | (11) |
其中
|
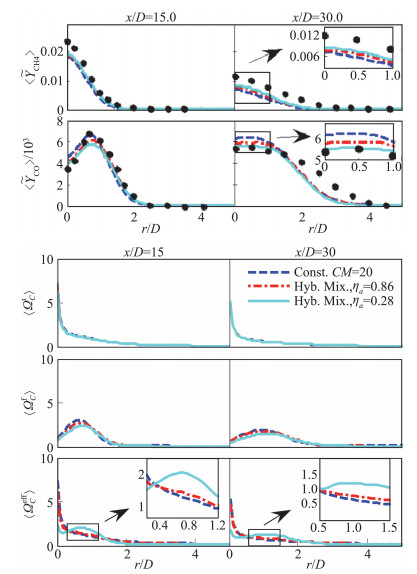
图 13 上图:高速甲烷-空气预混射流火焰PM1-150,不同标量混合模型预测的标量径向分布和实验值的比较.下图:不同轴向位置,由湍流、火焰结构引起的标量混合频率与有效标量混合频率的径向分布 Fig.13 Top: Comparison of scalar radial profile for high speed premixed methane-air jet flame PM1-150 between different mixing timescale models and experimental measurements. Bottom: Radial profile of scalar mixing frequency induced by turbulence and flame structure respectively and the effective scalar mixing frequency at different axial locations |
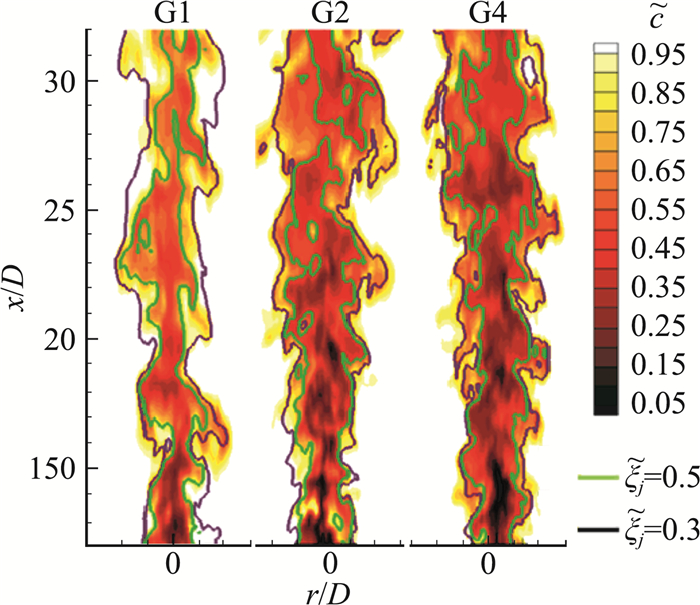
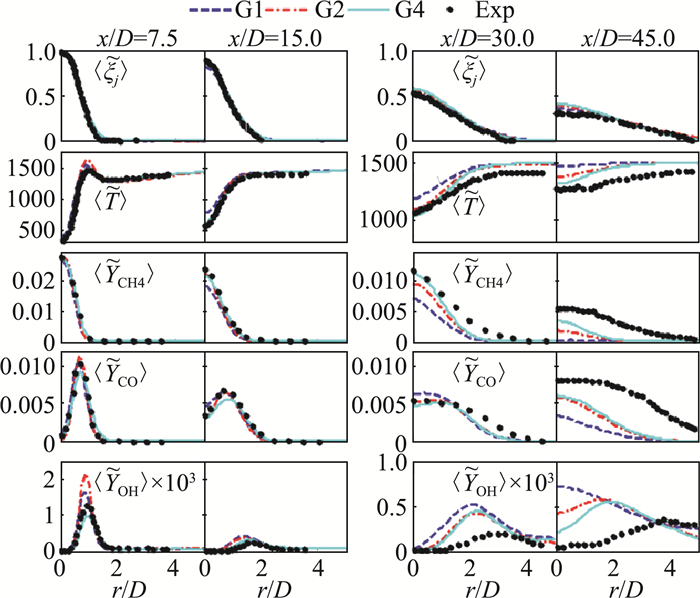
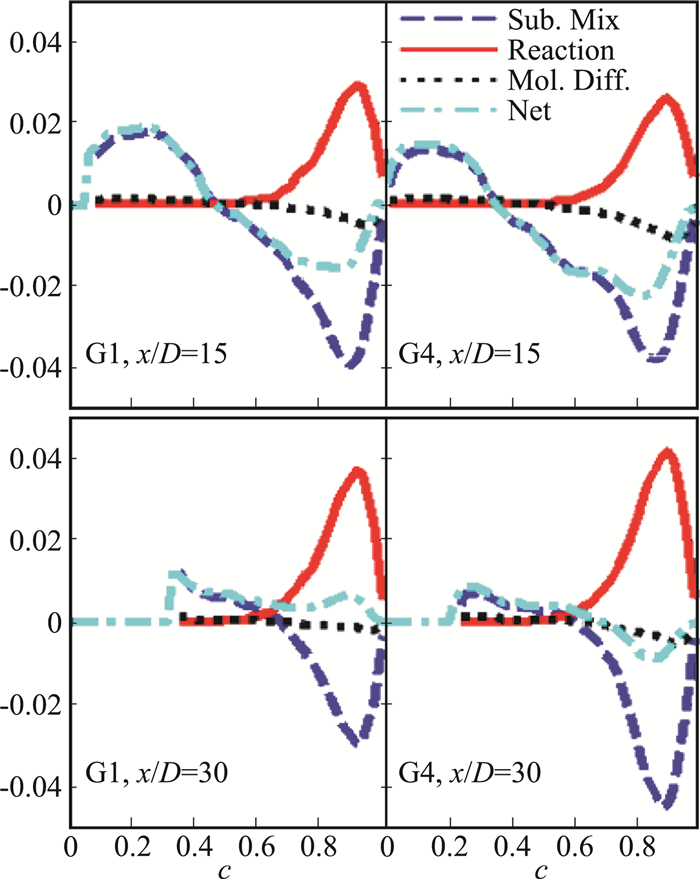
在网格解析度对于LES/PDF模拟预测湍流预混燃烧准确度的影响方面,Zhou等人[59]研究了网格解析度对于标量混合和燃烧特性预测的影响规律,采用解析度由低到高的三套网格:G1、G2、G4,对接近极限燃烧条件下的高速甲烷-空气预混射流火焰(PM1-150)进行了LES/PDF模拟。图 14展示分别采用三种网格解析度预测得到的瞬时火焰结构。研究发现,仅仅将单位火焰热厚度内的网格数量由1个增加至2个(G1→G4),就能显著提升对于局部熄火-再燃区域的预测精度。通过分析组分的空间分布、瞬态火焰结构、混合-反应速率,揭示了网格解析度对于湍流预混火焰的LES/PDF模拟具有显著影响。图 15中组分的空间分布表明,增大网格解析度对于大尺度混合的预测影响不大,但是能够显著提升对于组分径向分布的预测准确度。如图 16所示,通过分析亚网格内计算颗粒的反应、扩散、小尺度混合速率的条件平均值,发现增大网格解析度对于反应、扩散速率的影响较小,但是会显著增大亚网格混合速率,造成反应进度变量的净生成率为负,从而抑制了燃烧进程,进而改善了预测结果。因此,增大网格解析度改善模拟结果的本质原因可能在于:随着网格解析度的增大,亚网格颗粒在组分空间的局部性增强,这减轻了模拟结果对小尺度混合模型的依赖。因此,研究表明了网格解析度对于近极限湍流预混燃烧问题的大涡模拟预测结果有显著影响。
|
图 14 高速甲烷-空气预混射流火焰PM1-150,分别采用G1、G2、G4三种网格解析度,预测的瞬时火焰结构(图来自文献[59]) Fig.14 Contours of the instantaneous flame structure predicted with G1、G2、G4 grid resolutions for high speed premixed methane-air jet flame PM1-150 (Reproduced from Ref.[59]) |
|
图 15 高速甲烷-空气预混射流火焰PM1-150,分别采用G1、G2、G4三种网格解析度,得到的标量径向分布预测值与实验的对比(图来自文献[59]) Fig.15 Radial profiles of the time-averaged mean of scalars predicted with G1、G2、G4 grid resolutions for high speed premixed methane-air jet flame PM1-150 (Reproduced from Ref.[59]) |
|
图 16 x/D=15, 30两个代表性位置,分别采用G1、G4两种网格解析度,得到的反应进度标量的反应、扩散、小尺度混合速率的条件平均值(图来自文献[59]) Fig.16 Conditional averaged reaction, diffusion, and mixing rates with G1 and G4 grid resolutions at x/D=15 and 30 (Reproduced from Ref.[59]) |
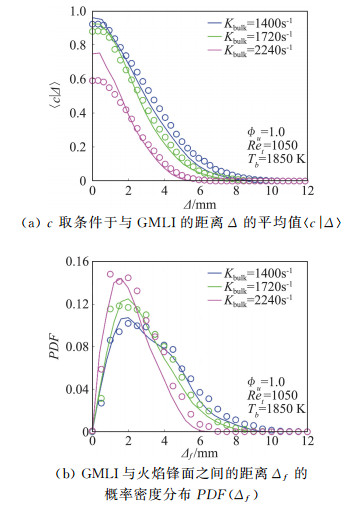
相比于射流火焰,耶鲁TCF燃烧室具有火焰稳定、不需值班火焰即可达到高雷诺数条件、燃烧区域更为紧凑等优势。Coriton等人[57]已经开展了湍流对冲预混火焰的一系列实验,确定了影响火焰特性的四个关键参数:整体拉伸率Kbulk、预混反应物当量比
|
图 17 在 |
概率密度函数方法能精确地求解有限反应速率,在预测近极限燃烧现象及强湍流-化学反应相互作用方面有着独到的优势,但小尺度上分子扩散引起的组分变化则需要通过标量小尺度混合模型来模拟。本综述介绍了当前湍流预混燃烧中混合模型研究的一些最新进展。现有标量混合模型与混合时间尺度模型在不同湍流预混燃烧模式下的性能研究表明:对于火焰面燃烧模式,保持组分空间的临近性对于标量混合模型非常重要,标量混合频率受火焰结构影响显著;对于破碎反应区模式,保持组分空间临近性的重要性有所减弱,标量混合频率由湍流主导。
基于湍流燃烧直接数值模拟数据的小尺度混合模型建模研究对提升PDF方法对湍流预混燃烧预测精度有重要意义。基于氢气预混火焰的直接数值模拟数据的研究表明处于薄反应区燃烧模式下的火焰结构对于标量耗散率的影响显著。另外,火焰的瞬态过程,如自着火以及火焰之间相互作用,对于标量耗散率有着显著影响。基于贫燃预混甲烷-空气射流火焰直接数值模拟数据的研究表明,对于靠近破碎反应区模式的湍流火焰,反应进度变量的湍流-标量混合时间尺度比
依据线性混合的思路构建的混合时间尺度模型,同时考虑了湍流和化学反应导致的小尺度混合。模型中包含一个区分因子(η),当η=0时,对应分布式燃烧类型的标量混合规律;当η=1时,对应理想火焰面燃烧类型的标量混合规律;当0 < η < 0时,燃烧类型介于分布式与理想火焰面两种模式之间,标量混合频率是上述两种情况对应混合频率的线性组合。新的标量混合时间尺度模型可以适用于任何预混湍流燃烧模式。针对不同湍流预混燃烧模式的模型验证表明:相比于已有的湍流混合时间尺度模型,新模型显著提升了对湍流预混火焰中的标量耗散率、燃烧特性的预测精度。
对近极限燃烧的研究表明,LES/PDF能准确地预测近极限湍流预混火焰中的局部熄火和再燃现象。另外,网格解析度对近极限湍流预混燃烧问题的LES/PDF模拟预测结果有着显著影响。随着网格解析度的增大,亚网格颗粒在组分空间的局部性增强,这减轻了模拟结果对小尺度混合模型的依赖程度,因此增大网格解析度能显著改善模拟结果。
| [1] |
BHARGAVA A, KENDRICK D, COLKET M, et al. Pressure effect on NOx and CO emissions in industrial gas turbines[C]//Proceedings of ASME Conference on ASME Turbo Expo 2000: Power for Land, Sea, and Air, Volume 2: Coal, Biomass and Alternative Fuels; Combustion and Fuels; Oil and Gas Applications; Cycle Innovations. Munich, Germany, 2000. http://dx.doi.org/10.1115/2000-GT-0097
|
| [2] |
CORREA S M. A review of NOx Formation under gas-turbine combustion conditions[J]. Combustion Science and Technology, 1993, 87(1-6): 329-362. DOI:10.1080/00102209208947221 |
| [3] |
ELKADY A M, HERBON J, KALITAN D M, et al. Gas turbine emission characteristics in perfectly premixed combustion[J]. Journal of Engineering for Gas Turbines and Power, 2012, 134(6): 061501. DOI:10.1115/1.4006058 |
| [4] |
VANOVERBERGHE K. Flow, turbulence and combustion of premixed swirling jet flames[D]. Katholieke Universiteit Leuven, 2004. ISBN 90-5682-465-1.
|
| [5] |
YEGIAN D T, CHENG R K. Development of a lean premixed low-swirl burner for lowNOx Practical applications[J]. Combustion Science and Technology, 1998, 139(1): 207-227. DOI:10.1080/00102209808952088 |
| [6] |
罗坤, 王海鸥, 樊建人, 等. 旋流燃烧器复合小火焰模型的大涡模拟[J]. 工程热物理学报, 2012, 33(1): 146-150. LUO K, WANG H O, FAN J R, et al. Large eddy simulation of a swirl combustor with a combined flamelet model[J]. Journal of Engineering Thermophysics, 2012, 33(1): 146-150. (in Chinese) |
| [7] |
张引弟, 周怀春, 谢明亮. 湍流扩散火焰的大涡模拟及验证[J]. 动力工程, 2009, 29(5): 451-455. ZHANG Y D, ZHOU H C, XIE M L. Large eddy simulation and verification for turbulent diffusion flame[J]. Journal of Power Engineering, 2009, 29(5): 451-455. (in Chinese) |
| [8] |
郑韫哲, 朱民, 姜羲. 旋流预混燃烧室流动混合的大涡模拟[J]. 航空动力学报, 2012, 27(1): 33-40. ZHENG Y Z, ZHU M, JIANG X. Flow and air-fuel mixing processes in a premixed swirl combustor with LES[J]. Journal of Aerospace Power, 2012, 27(1): 33-40. (in Chinese) |
| [9] |
IHME M, PITSCH H. Prediction of extinction and reignition in nonpremixed turbulent flames using a flamelet/progress variable model 1. A priori study and presumed PDF closure[J]. Combustion and Flame, 2008, 155(1/2): 70-89. DOI:10.1016/j.combustflame.2008.04.001 |
| [10] |
HAWORTH D C. Progress in probability density functionmethods for turbulent reacting flows[J]. Progress in Energy and Combustion Science, 2010, 36(2): 168-259. DOI:10.1016/j.pecs.2009.09.003 |
| [11] |
POPE S B. PDF methods for turbulent reactive flows[J]. Progress in Energy and Combustion Science, 1985, 11(2): 119-192. DOI:10.1016/0360-1285(85)90002-4 |
| [12] |
SHEIKHI M R H, DROZDA T G, GIVI P, et al. Large eddy simulation of a turbulent nonpremixed piloted methane jet flame (Sandia Flame D)[J]. Proceedings of the Combustion Institute, 2005, 30(1): 549-556. DOI:10.1016/j.proci.2004.08.028 |
| [13] |
LU L Y, REN Z Y, RAMAN K, et al. LES/FDF/ISAT computations of turbulent flames[C]//Proceedings of the CTR Summer Program, 2004: 283-294.
|
| [14] |
YANG Y, WANG H F, POPE S B, et al. Large-eddy simulation/probability density function modeling of a non-premixed CO/H2 temporally evolving jet flame[J]. Proceedings of the Combustion Institute, 2013, 34(1): 1241-1249. DOI:10.1016/j.proci.2012.08.015 |
| [15] |
HAN W, RAMAN V, MUELLER M E, et al. Effects of combustion models on soot formation and evolution in turbulent nonpremixed flames[J]. Proceedings of the Combustion Institute, 2019, 37(1): 985-992. DOI:10.1016/j.proci.2018.06.096 |
| [16] |
ANSARI N, STRAKEY P A, GOLDIN G M, et al. Filtered density function simulation of a realistic swirled combustor[J]. Proceedings of the Combustion Institute, 2015, 35(2): 1433-1442. DOI:10.1016/j.proci.2014.05.042 |
| [17] |
HAN W, RAMAN V, CHEN Z. LES/PDF modeling of autoignition in a lifted turbulent flame:Analysis of flame sensitivity to differential diffusion and scalar mixing time-scale[J]. Combustion and Flame, 2016, 171(1): 69-86. DOI:10.1016/j.combustflame.2016.05.027 |
| [18] |
ZHOU H, YANG T W, REN Z Y. Differential diffusion modeling in LES/FDF simulations of turbulent flames[J]. AIAA Journal, 2019, 57(8): 3206-3212. DOI:10.2514/1.j058524 |
| [19] |
KIM J, POPE S B. Effects of combined dimension reduction and tabulation on the simulations of a turbulent premixed flame using a large-eddy simulation/probability density function method[J]. Combustion Theory and Modelling, 2014, 18(3): 388-413. DOI:10.1080/13647830.2014.919411 |
| [20] |
HLEK T, LINDSTEDT R P. Computations of steady-state and transient premixed turbulent flames using pdf methods[J]. Combustion and Flame, 1996, 104(4): 481-504. DOI:10.1016/0010-2180(96)82294-2 |
| [21] |
LINDSTEDT R P, VAOS E M. Modeling of mixing processes in non-isothermal and combusting flows[C]//8th European Turbulence Conference, Advances in Turbulence VⅢ, Barcelona, 2000: 493-496.
|
| [22] |
LINDSTEDT R P, VAOS E M. Transported PDF modeling of high-Reynolds-number premixed turbulent flames[J]. Combustion and Flame, 2006, 145(3): 495-511. DOI:10.1016/j.combustflame.2005.12.015 |
| [23] |
ROWINSKI D H, POPE S B. PDF calculations of piloted premixed jet flames[J]. Combustion Theory and Modelling, 2011, 15(2): 245-266. DOI:10.1080/13647830.2010.535568 |
| [24] |
STÖLLINGER M, HEINZ S. Evaluation of scalar mixing and time scale models in PDF simulations of a turbulent premixed flame[J]. Combustion and Flame, 2010, 157(9): 1671-1685. DOI:10.1016/j.combustflame.2010.01.015 |
| [25] |
REN Z Y, KURON M, ZHAO X Y, et al. Micromixing models for PDF simulations of turbulent premixed flames[J]. Combustion Science and Technology, 2019, 191(8): 1430-1455. DOI:10.1080/00102202.2018.1530667 |
| [26] |
HAWKES E R, CHATAKONDA O, KOLLA H, et al. A petascale direct numerical simulation study of the modelling of flame wrinkling for large-eddy simulations in intense turbulence[J]. Combustion and Flame, 2012, 159(8): 2690-2703. DOI:10.1016/j.combustflame.2011.11.020 |
| [27] |
VILLERMAUX J, DEVILLON J C. Représentation de la coalescence et de la redispersion des domaines de ségrégation dans un fluide par un modèle d'interaction phénoménologique[C]//Proceedings of the Second International Symposium on Chemical Reaction Engineering, Elsevier, NY, 1972: 1-13.
|
| [28] |
DOPAZO C, O'BRIEN E E. An approach to the autoignition of a turbulent mixture[J]. Acta Astronautica, 1974, 1(9/10): 1239-1266. DOI:10.1016/0094-5765(74)90050-2 |
| [29] |
CURL R L. Dispersed phase mixing:I. Theory and effects in simple reactors[J]. AIChE Journal, 1963, 9(2): 175-181. DOI:10.1002/aic.690090207 |
| [30] |
DOPAZO C. Relaxation of initial probability density functions in the turbulent convection of scalar fields[J]. Physics of Fluids, 1979, 22(1): 20-30. DOI:10.1063/1.862431 |
| [31] |
JANICKA J, KOLBE W, KOLLMANN W. Closure of the transport equation for the probability density funcfion of turbulent scalar fields[J]. Journal of Non-Equilibrium Thermodynamics, 1979, 4(1): 47-66. DOI:10.1515/jnet.1979.4.1.47 |
| [32] |
REN Z Y, SUBRAMANIAM S, POPE S B. Implementation of the EMST mixing model[CP]. 2002.
|
| [33] |
SUBRAMANIAM S, POPE S B. A mixing model for turbulent reactive flows based on Euclidean minimum spanning trees[J]. Combustion and Flame, 1998, 115(4): 487-514. DOI:10.1016/S0010-2180(98)00023-6 |
| [34] |
VALIÑO L, DOPAZO C. A binomial Langevin model for turbulent mixing[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(12): 3034-3037. DOI:10.1063/1.857847 |
| [35] |
CHEN H D, CHEN S Y, KRAICHNAN R H. Probability distribution of a stochastically advected scalar field[J]. Physical Review Letters, 1989, 63(24): 2657-2660. DOI:10.1103/physrevlett.63.2657 |
| [36] |
POPE S B. Mapping closures for turbulent mixing and reaction[J]. Theoretical and Computational Fluid Dynamics, 1991, 2(5/6): 255-270. DOI:10.1007/bf00271466 |
| [37] |
SUBRAMANIAM S, POPE S B. Comparison of mixing model performance for nonpremixed turbulent reactive flow[J]. Combustion and Flame, 1999, 117(4): 732-754. DOI:10.1016/S0010-2180(98)00135-7 |
| [38] |
KLIMENKO A Y, POPE S B. The modeling of turbulent reactive flows based on multiple mapping conditioning[J]. Physics of Fluids, 2003, 15(7): 1907-1925. DOI:10.1063/1.1575754 |
| [39] |
FOX R O, CHA C M, TROUILLET P. Lagrangian PDF mixing models for reacting flows[R]. Center for Turbulence Research, Proceedings of the Summer Program, 2002: 369-380. http://web.stanford.edu/group/ctr/ctrsp02/fox.pdf
|
| [40] |
POPE S B. A model for turbulent mixing based on shadow-position conditioning[J]. Physics of Fluids, 2013, 25(11): 110803. DOI:10.1063/1.4818981 |
| [41] |
ZHAO X Y, BHAGATWALA A, CHEN J H, et al. An a priori DNS study of the shadow-position mixing model[J]. Combustion and Flame, 2016, 165(3): 223-245. DOI:10.1016/j.combustflame.2015.12.009 |
| [42] |
PIERCE C D. Progress-variable approach for large-eddy simulation of turbulent combustion[D]. Stanford University, 2001.
|
| [43] |
RAMAN V, PITSCH H. A consistent LES/filtered-density function formulation for the simulation of turbulent flames with detailed chemistry[J]. Proceedings of the Combustion Institute, 2007, 31(2): 1711-1719. DOI:10.1016/j.proci.2006.07.152 |
| [44] |
KURON M, HAWKES E R, REN Z Y, et al. Performance of transported PDF mixing models in a turbulent premixed flame[J]. Proceedings of the Combustion Institute, 2017, 36(2): 1987-1995. DOI:10.1016/j.proci.2016.05.019 |
| [45] |
SUNDARAM B, KLIMENKO A Y. A PDF approach to thin premixed flamelets using multiple mapping conditioning[J]. Proceedings of the Combustion Institute, 2017, 36(2): 1937-1945. DOI:10.1016/j.proci.2016.07.116 |
| [46] |
ANAND M S, POPE S B. Calculations of premixed turbulent flames by PDF methods[J]. Combustion and Flame, 1987, 67(2): 127-142. DOI:10.1016/0010-2180(87)90146-5 |
| [47] |
Abdel-Gayed R G, Al-Khishali K J, Bradley D. Turbulent burning velocities and flame straining in explosions[J]. Proceedings of the Royal Society of London A:Mathematical and Physical Sciences, 1984, 391(1801): 393-414. DOI:10.1098/rspa.1984.0019 |
| [48] |
DUNN M J, MASRI A R, BILGER R W. A new piloted premixed jet burner to study strong finite-rate chemistry effects[J]. Combustion and Flame, 2007, 151(1-2): 46-60. DOI:10.1016/j.combustflame.2007.05.010 |
| [49] |
DUNN M J, MASRI A R, BILGER R W, et al. The compositional structure of highly turbulent piloted premixed flames issuing into a hot coflow[J]. Proceedings of the Combustion Institute, 2009, 32(2): 1779-1786. DOI:10.1016/j.proci.2008.08.007 |
| [50] |
ZHOU H, LI S, REN Z Y, et al. Investigation of mixing model performance in transported PDF calculations of turbulent lean premixed jet flames through Lagrangian statistics and sensitivity analysis[J]. Combustion and Flame, 2017, 181: 136-148. DOI:10.1016/j.combustflame.2017.03.011 |
| [51] |
易富兴, 李德波, 卢树强, 等. H2/N2湍射流抬升火焰的直接数值模拟[J]. 工程热物理学报, 2011, 32(7): 1231-1235. YI F X, LI D B, LU S Q, et al. Direct numerical simulation of H2/N2 turbulent lifted-off jet flame[J]. Journal of Engineering Thermophysics, 2011, 32(7): 1231-1235. (in Chinese) |
| [52] |
LU T F, YOO C S, CHEN J H, et al. Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow:a chemical explosive mode analysis[J]. Journal of Fluid Mechanics, 2010, 652: 45-64. DOI:10.1017/S002211201000039X |
| [53] |
LUO Z Y, YOO C S, RICHARDSON E S, et al. Chemical explosive mode analysis for a turbulent lifted ethylene jet flame in highly-heated coflow[J]. Combustion and Flame, 2012, 159(1): 265-274. DOI:10.1016/j.combustflame.2011.05.023 |
| [54] |
SANKARAN R, HAWKES E R, CHEN J H, et al. Structure of a spatially developing turbulent lean methane-air Bunsen flame[J]. Proceedings of the Combustion Institute, 2007, 31(1): 1291-1298. DOI:10.1016/j.proci.2006.08.025 |
| [55] |
KURON M, REN Z Y, HAWKES E R, et al. A mixing timescale model for TPDF simulations of turbulent premixed flames[J]. Combustion and Flame, 2017, 177(3): 171-183. DOI:10.1016/j.combustflame.2016.12.011 |
| [56] |
YUNG C C, PETERS N, SCHNEEMANN G A, et al. The detailed flame structure of highly stretched turbulent premixed methane-air flames[J]. Combustion and Flame, 1996, 107(3): 223-244. DOI:10.1016/S0010-2180(96)00070-3 |
| [57] |
CORITON B, FRANK J H, GOMEZ A. Effects of strain rate, turbulence, reactant stoichiometry and heat losses on the interaction of turbulent premixed flames with stoichiometric counterflowing combustion products[J]. Combustion and Flame, 2013, 160(11): 2442-2456. DOI:10.1016/j.combustflame.2013.05.009 |
| [58] |
WANG H F, PANT T, ZHANG P. LES/PDF modeling of turbulent premixed flames with locally enhanced mixing by reaction[J]. Flow, Turbulence and Combustion, 2018, 100(1): 147-175. DOI:10.1007/s10494-017-9831-0 |
| [59] |
ZHOU H, REN Z Y, ROWINSKI D H, et al. Filtered density function simulations of a near-limit turbulent lean premixed flame[J]. Journal of Propulsion and Power, 2020.(Articles in Advance) https://doi.org/10.2514/1.b37707
|
| [60] |
TIRUNAGARI R R, POPE S B. An investigation of turbulent premixed counterflow flames using large-eddy simulations and probability density function methods[J]. Combustion and Flame, 2016, 166: 229-242. DOI:10.1016/j.combustflame.2016.01.024 |
 2019, Vol. 38
2019, Vol. 38

