在高超声速飞行条件下,流场中的高温导致气体各个内能模式激发并且发生化学反应,而高空条件气体密度低又使流场处于热力和化学非平衡状态。当温度足够高时,气体进一步发生辐射跃迁。各类微观反应和跃迁机制影响到飞行器的宏观气动热和气动物理特性。更深入地理解和更精确地模拟热化学非平衡和辐射现象在学术上和工程应用上都具有重要意义。
有两类描述流动中振动非平衡和振动-化学耦合的方法。一类是多温度模型法,以Park在1985年提出的双温度模型[1]为代表,引入不同于平动温度的振动温度Tvib表征非平衡振动能,在化学反应控制温度中引入振动温度反映热力-化学耦合。另一类是态-态模型法[2-3],直接描述各振动能级间的分子跃迁过程和各能级分子的化学反应,求解各能级粒子数变化率方程。
双温度模型及后来拓展的多温度模型,计算消耗小,且一定程度上反映了振动非平衡与振动-化学耦合,获得了广泛应用。许多气动热力学程序采用了该模型,包括Gnoff等发展的LAURA (Langely Aerothermodynamic Upwind Relaxation Algorithm)程序[4-5]和GASP(General Aerodynamic Simulation Program)程序[6-7]。采用该模型的数值模拟工作还有很多,例如:Tissera[8]等进行的高超声速绕钝锥-柱-裙的流动模拟,Sorensen等[9]进行的有限催化壁条件下的高超声速圆柱绕流模拟,美国和欧洲研究者们独立进行的为评估CFD方法预测高超声速条件下激波相互作用能力的一系列数值计算[10],汪球[11]、周凯[12]等进行的高焓风洞喷管非平衡流场计算,等。双温度模型在许多条件下获得了良好的数值结果,但也存在局限[13]。在温度很高条件下以及降温复合反应过程中,可能会产生较大误差,甚至出现模型失真[14]。双温度模型隐含着振动能级分布满足振动温度下玻尔兹曼(Boltzmann)分布的假设[15],而态-态模型方法的结果表明该假设在许多条件下并不成立。
态-态模型法将粒子在能级间的跃迁与化学反应视为同一性质的过程研究,描述振动非平衡及其与化学反应耦合的方法则更为精细和直接[16]。它直接研究各能级上粒子的化学反应,避免了多温度模型中经验性的热力-化学耦合方法。随着分子动力学的研究和计算机计算能力的发展,态-态模型作为一种高保真度模型逐渐进入人们的视野并在近十年来快速发展起来。采用态-态模型的研究由不涉及流动的零维问题[17],逐步发展到正激波后、边界层[18-21]和准一维喷管[22]非平衡流动问题。徐丹对N2/N系统采用态-态模型开展了零维问题研究[23],还数值求解了耦合态-态模型的N2/N准一维喷管非平衡流方程[16]。Druguet[24]采用态-态模型(考虑N2基态电子能级上68个振动能级)求解了N2/N的球头非平衡流场,考察态-态模型与流动耦合的可行性。应用CFD程序PINENS(并行隐式非平衡N-S方程求解程序)求解了包含69个组元连续方程的轴对称非平衡流N-S方程,结果表明仅在边界层外振动能级分布满足振动温度下的玻尔兹曼分布。
依赖于精确的双原子光谱常数[25-26]和辐射跃迁几率数据[27],态-态模型被越来越多地用于辐射特性的研究。Kustova[28]采用态-态模型,在合适的温度范围(6000 K~8000 K以下)忽略了电子能级的跃迁和电离,考虑了N2分子基态电子能级上振动能级跃迁伴随的束缚-束缚辐射跃迁,将辐射跃迁与振动松弛和离解过程耦合求解,计算红外辐射特性。Aliat[29]考虑了在更高的温度条件下(10 000 K以上)N2分子各电子能级之间跃迁,在文献[28]方法的基础上进而实现了振动-电子能相互转化,计算N2的第一正谱带系(B3Πg→A3∑u+)。Annaloro和Bultel[30]采用态-态模型对辐射特性进行了较系统的研究,发展出CR(collisional-radiative)模型。包含N2、O2、NO、N、O、Ar、N2+、O2+、NO+、N+、O+、Ar+和自由电子等组元,考虑基态电子能级上的共169个振动能级和所有组元的共829个电子能级之间的跃迁,耦合考虑电子能级跃迁、振动能级跃迁和辐射,涉及到几乎700 000个基元反应。他们还对N2、N、N2+、N+、e-系统,计算了正激波后的非平衡流动[31],综合考虑了振动能级跃迁、离解反应、电子能级激发、电子能相互转化、电离置换等过程。Bultel等人[32]还将该模型用于扩张喷管流动计算,研究分子正离子与电子结合所导致离解的过程对激波后离解占优区域和喷管中复合占优区的影响。
本文对封闭静止的O2/O气体系统,采用态-态模型研究热化学非平衡和辐射过程。考察不同初始条件和设定温度条件下(温度由初始值瞬时改变为设定值后保持系统等温等容)不同振动能级粒子分布随时间的演化特点,分析比较各类跃迁或化学反应过程以及辐射跃迁过程对系统化学组成和分子振动能级分布变化的贡献。为更好地理解O2/O和高温空气热化学反应机理提供新的思路,也为今后采用态-态模型研究高温空气的非平衡过程并进一步与流动耦合奠定基础。
1 态-态模型基本方程对O2/O混合物系统,本文不考虑O2分子和O原子的电离,涉及的微观非平衡过程包括:O2的振动能级跃迁、各振动能级上O2分子的离解反应、O原子的复合反应、O2分子的辐射。在设定的等温等容条件下,粒子的平动与转动能级分布迅速达到平动/转动温度下的平衡分布,但振动能级的分布需要经历一个非平衡变化过程。采用47(0~46)个能级的O2振动能级模型,振动能级分布的变化由有限速率的能级间的跃迁和各振动能级上分子的化学反应决定,当温度足够高发生辐射后,辐射跃迁也将影响分子振动能级的分布。不考虑O原子的辐射,只研究O2分子Schumann-Runge的束缚-束缚辐射谱带,涉及O2分子的基态电子能级(X3∑g-)和激发态电子能级(B3∑u-)。
为简单起见,态-态模型重点用于研究基态电子能级的各振动能级粒子分布的非平衡演化过程。分子在各电子能级上的分布视为电子温度下的玻尔兹曼分布,激发态电子能级(B3∑u-)上分子在各振动能级上的分布设为振动温度下的玻尔兹曼分布。O2/O系统的振动温度根据O2分子基态电子能级上的非平衡振动能级分布采用一定规则导出,而系统的电子温度设为等于振动温度。
1.1 采用态-态模型的粒子数密度变化率方程将位于基态电子能级上不同振动能级i的O2分子视为不同组元O2(X3∑g-, i),其数密度记为ni,它的变化起因于振动能级跃迁(振动-平动能量交换过程VT和振动-振动能量交换过程VV)、离解-复合化学反应(DR)以及辐射跃迁(rad)。VT过程又可细分为VTm、VTa,DR过程又可细分为DRm和DRa,其中m和a分别代表碰撞参与者是分子或是原子。
组元O2(X3∑g-, i)的数密度ni的变化率方程为:
| $ \frac{{{\rm{d}}{n_i}}}{{{\rm{d}}t}} = R_i^{{\rm{VTm}}} + R_i^{{\rm{VTa}}} + R_i^{{\rm{VV}}} + R_i^{{\rm{DRm}}} + R_i^{{\rm{DRa}}} + R_i^{{\rm{rad}}} $ | (1) |
式中i=0~46。式(1)右端分别为振动-平动跃迁、振动-振动跃迁、离解-复合化学反应和辐射几类微观过程对基态电子能级的i振动能级上O2分子数密度变化的贡献。热化学反应过程将在1.2节详细描述,辐射跃迁过程在1.3节详细描述。
O原子数密度nO的变化仅起因于离解-复合化学反应:
| $ \frac{{{\rm{d}}{n_{\rm{O}}}}}{{{\rm{d}}t}} = R_{\rm{O}}^{{\rm{DRm}}} + R_{\rm{O}}^{{\rm{DRa}}} $ | (2) |
在基态电子能级上振动能级分布确定后,可导出O2/O系统的振动温度Tvib,进一步设电子温度近似等于振动温度,从而确定激发态电子能级(B3∑u-)上的分布。根据电子能级分布满足电子温度下的玻尔兹曼分布假设,(B3∑u-)电子能级上的分子数密度nO2B可采用下式确定:
| $ \frac{{n_{{\rm{O2}}}^{\rm{B}}}}{{n_{{\rm{O2}}}^{\rm{X}}}} = \frac{{{g_{\rm{B}}}{\kern 1pt} {\rm{exp}}\left( { - \frac{{{\varepsilon _{{\rm{el,B}}}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right)}}{{{g_{\rm{X}}}{\kern 1pt} {\rm{exp}}\left( { - \frac{{{\varepsilon _{{\rm{el,X}}}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right)}} $ | (3) |
则,
| $ n_{{\rm{O2}}}^{\rm{B}} = \left( {\sum\limits_i {{n_i}} } \right)\frac{{{g_{\rm{B}}}}}{{{g_{\rm{X}}}}}{\rm{exp}}\left( { - \frac{{{\varepsilon _{{\rm{el,B}}}} - {\varepsilon _{{\rm{el,X}}}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right) $ | (4) |
其中nO2X为位于基态电子能级上的O2分子数密度,
| $ n_{{\rm{O2}}}^{\rm{X}} = \sum\limits_i {{n_i}} $ | (5) |
gX和gB分别为基态和激发态电子能级的简并度,εel, X和εel, 分别为基态和激发态电子能级的能值,kB为玻尔兹曼常数。激发态电子能级上各振动能级的分布则根据振动温度Tvib下的玻尔兹曼分布确定。系统中总的O2分子数密度为:
| $ {n_{{\rm{O2}}}} = n_{{\rm{O2}}}^{\rm{X}} + n_{{\rm{O2}}}^{\rm{B}} = \sum\limits_i {{n_i}} \left[ {1 + \frac{{{g_{\rm{B}}}}}{{{g_{\rm{X}}}}}\exp \left( { - \frac{{{\varepsilon _{{\rm{el,B}}}} - {\varepsilon _{{\rm{el,X}}}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right)} \right] $ | (6) |
不涉及辐射的微观过程包括:分子间的振动-平动能量交换过程VTm,分子与原子间的振动-平动能量交换过程VTa,振动-振动能量交换过程VV,原子作为碰撞参与者的离解-复合反应DRa,分子作为碰撞参与者的过程DRm。具体如下:
| $ \text{VTm}:{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i})+{{\text{O}}_{2}}\rightleftharpoons {{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i-1})+{{\text{O}}_{2}} $ | (7) |
| $ \text{VTa}:{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i})+\text{O}\rightleftharpoons {{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i}-\Delta v)+\text{O} $ | (8) |
| $ \text{VV}:\begin{array}{*{35}{l}} {{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i})+{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,j-1})\rightleftharpoons \\ {{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i}-1)+{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,j}) \\ \end{array} $ | (9) |
| $ \text{DRa}:{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i})+\text{O}\rightleftharpoons 2\text{O}+\text{O} $ | (10) |
| $ \text{DRm}:{{\text{O}}_{2}}({{\text{X}}^{3}}\sum\nolimits_{\text{g}}^{-}{,i})+{{\text{O}}_{2}}\rightleftharpoons 2\text{O}+{{\text{O}}_{2}} $ | (11) |
对VTm过程只考虑单量子数跃迁,对VTa过程考虑多量子数跃迁,Δv为跃迁量子数。VV过程中,i和j代表O2基态电子能级上的不同振动能级。
O2(X3∑g-, i)的数密度变化率方程式(1)右端各类过程的生成项为:
| $ \begin{array}{*{20}{l}} {R_i^{{\rm{VTm}}} = K_{i + 1,i}^{{\rm{VTm}}}{n_{i + 1}}{n_{{\rm{O2}}}} + K_{i - 1,i}^{{\rm{VTm}}}{n_{i - 1}}{n_{{\rm{O2}}}} - }\\ \ \ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K_{i,i + 1}^{{\rm{VTm}}}{n_i}{n_{{\rm{O2}}}} - K_{i,i - 1}^{{\rm{VTm}}}{n_i}{n_{{\rm{O2}}}}} \end{array} $ | (12) |
式(12)右端当i=0时仅含第1和第3项,i=46时仅含第2和第4项。
| $ \begin{align} & R_{i}^{\text{VTa}}=\sum\limits_{\begin{smallmatrix} 0<\Delta v\le 46-i \\ (i<0) \end{smallmatrix}}{K_{i+\Delta v,i}^{\text{VTa}}}{{n}_{i+\Delta v}}{{n}_{\text{O}}}+\sum\limits_{\begin{matrix} 0<\Delta v\le i \\ (i>0) \\ \end{matrix}}{K_{i-\Delta v,i}^{\text{VTa}}}{{n}_{i-\Delta v}}{{n}_{\text{O}}}- \\ & \sum\limits_{\begin{smallmatrix} 0<\Delta v\le 46-i \\ (i<0) \end{smallmatrix}}{K_{i,i+\Delta v}^{\text{VTa}}}{{n}_{i}}{{n}_{\text{O}}}-\sum\limits_{\begin{matrix} 0<\Delta v\le i \\ (i>0) \\ \end{matrix}}{K_{i,i-\Delta v}^{\text{VTa}}{{n}_{i}}{{n}_{\text{O}}}} \\ \end{align} $ | (13) |
| $ \begin{align} & R_{i}^{VV}=\sum\limits_{\begin{matrix} 0<j<i \\ (i>0) \\ \end{matrix}}{K_{i-1,j}^{\begin{smallmatrix} VV \\ i,j-1 \end{smallmatrix}}}{{n}_{i-1}}{{n}_{j}}+\sum\limits_{\begin{matrix} 0<j<i-2 \\ (i<46) \\ \end{matrix}}{K_{i+1,j-1}^{\begin{smallmatrix} VV \\ i,j \end{smallmatrix}}{{n}_{i+1}}{{n}_{j-1}}}- \\ & \sum\limits_{\begin{matrix} 0<j<i \\ (i>0) \\ \end{matrix}}{K_{i,j-1}^{\begin{smallmatrix} VV \\ i-1,j \end{smallmatrix}}}{{n}_{i}}{{n}_{j-1}}+\sum\limits_{\begin{matrix} 0<j<i-2 \\ (i<46) \\ \end{matrix}}{K_{i,j}^{\begin{smallmatrix} VV \\ i+1,j-1 \end{smallmatrix}}{{n}_{i}}{{n}_{j}}} \\ \end{align} $ | (14) |
| $ {R_i^{{\rm{DRm}}} = K_{{\rm{O}},i}^{{\rm{DRm}}}n_{\rm{O}}^2{n_{{\rm{O2}}}} - K_{i,{\rm{O}}}^{{\rm{DRm}}}{n_i}{n_{{\rm{O2}}}}} $ | (15) |
| $ {R_i^{{\rm{DRa}}} = K_{{\rm{O}},i}^{{\rm{DRa}}}n_{\rm{O}}^3 - K_{i,{\rm{O}}}^{{\rm{DRa}}}{n_i}{n_{\rm{O}}}} $ | (16) |
O原子数密度变化方程式(2)右端的两项生成项为:
| $ {R_{\rm{O}}^{{\rm{DRm}}} = 2K_{i,{\rm{O}}}^{{\rm{DRm}}}{n_i}{n_{{\rm{O2}}}} - 2K_{{\rm{O}},i}^{{\rm{DRm}}}n_{\rm{O}}^2{n_{\rm{O}}}} $ | (17) |
| $ {R_{\rm{O}}^{{\rm{DRa}}} = 2K_{i,{\rm{O}}}^{{\rm{DRa}}}{n_i}{n_{\rm{O}}} - 2K_{{\rm{O}},i}^{{\rm{DRa}}}n_{\rm{O}}^3} $ | (18) |
上述VT过程、VV过程的速率系数Ki+1, iVTm、Ki+Δv, iVTa、$K_{i - 1, j}^{_{i, j - 1}^{{\text{VV}}}}$等采用强迫谐振子模型(FHO)[33]计算,而DR过程的速率系数Ki, ODRm、Ki, ODRa等采用准经典轨道理论(QCT)[34]计算,具体的计算公式和相关数据见文献[33-35]。
1.3 辐射跃迁过程粒子的辐射跃迁可以分为自发发射、诱导发射和辐射吸收。分子辐射光谱一般包含若干谱带系,不同的谱带系对应不同的电子能级跃迁;一个谱带系中含有若干谱带,不同的谱带对应不同振动能级间的跃迁;同一谱带中又包含不同的谱线,每一条谱线对应于转动能级的跃迁[36]。本文只研究O2的Schumann-Runge辐射谱带系,即O2分子基态电子能级(X3∑g-)和激发态电子能级(B3∑u-)之间的束缚-束缚辐射跃迁,采用文献[29]的方法计算。假设转动能级按照平动/转动温度下的玻尔兹曼分布,对同一振动能级下所有的转动能级对辐射跃迁的贡献求和,仅细分到电子和振动能级的跃迁,即按照辐射谱带计算辐射。
辐射跃迁包括三类——自发发射、诱导发射、辐射吸收。具体表示如下:
| $ {{\rm{O}}_2}({{\rm{B}}^3}{\sum\nolimits_{\rm{u}}^ - {,i} ^\prime }) \to {{\rm{O}}_2}({{\rm{X}}^3}\sum\nolimits_{\rm{g}}^ - {,i} ) + h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}} $ | (19) |
| $ {{\rm{O}}_2}({{\rm{B}}^3}{\sum\nolimits_{\rm{u}}^ - {,i} ^\prime }) + h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}} \to {{\rm{O}}_2}({{\rm{X}}^3}\sum\nolimits_{\rm{g}}^ - {,i} ) + 2h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}} $ | (20) |
| $ {{\rm{O}}_2}({{\rm{X}}^3}\sum\nolimits_{\rm{g}}^ - {,i} ) + h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}} \to {{\rm{O}}_2}({{\rm{B}}^3}{\sum\nolimits_{\rm{u}}^ - {,i} ^\prime }) $ | (21) |
上面采用α代表O2基态电子能级(X3∑g-),α′代表激发态电子能级(B3∑u-),i和i′分别代表基态电子能级和激发态电子能级上的振动能级,h为普朗克常数。να′i′, αi表示由α′i′→αi的跃迁辐射光子的中心频率。则单位时间内由特定的α′i′→αi跃迁对辐射谱强度Iνα′i′, αi随时间变化率的贡献为:
| $ \begin{array}{l} \frac{{{\rm{d}}I_\nu ^{{\alpha ^\prime }{i^\prime },\alpha i}}}{{{\rm{d}}t}} = ch{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}{\varphi _\nu }(\nu - {\nu _{{\alpha ^\prime }{i^\prime },\alpha i}})[{A_{{\alpha ^\prime }{i^\prime },\alpha i}}{n_{{\alpha ^\prime }{i^\prime }}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({B_{{\alpha ^\prime }{i^\prime },\alpha i}}{n_{{\alpha ^\prime }{i^\prime }}} - {B_{\alpha i,{\alpha ^\prime }{i^\prime }}}{n_{\alpha i}})I_\nu ^{{\alpha ^\prime }{i^\prime },\alpha i}] \end{array} $ | (22) |
式(22)中c为光速。Aα′i′, αi、Bα′i′, αi、Bαi, α′i′分别为自发发射、诱导发射和辐射吸收的爱因斯坦系数。根据细致平衡原理,它们之间满足如下关系:
| $ {g_{{\alpha ^\prime }{i^\prime }}}{A_{{\alpha ^\prime }{i^\prime },\alpha i}} = {g_{\alpha i}}\frac{{2h\nu _{{\alpha ^\prime }{i^\prime },\alpha i}^3}}{{{c^2}}}{B_{\alpha i,{\alpha ^\prime }{i^\prime }}} $ | (23) |
| $ {g_{{\alpha ^\prime }{i^\prime }}}{B_{{\alpha ^\prime }{i^\prime },\alpha i}} = {g_{\alpha i}}{B_{\alpha i,{\alpha ^\prime }{i^\prime }}} $ | (24) |
| $ {A_{{\alpha ^\prime }{i^\prime },\alpha i}} = \frac{{2h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{c^2}}}{B_{{\alpha ^\prime }{i^\prime },\alpha i}} $ | (25) |
式中gα′i′是激发态电子能级的i′振动能级的简并度,gαi是基态电子能级的i振动能级的简并度。由于双原子分子的振动能级简并度为1,这里考虑O2的电子能级仅有基态O2(X3∑g-)和激发态O2(B3∑u-),所以gα′i′=gB, gαi=gX。辐射跃迁的爱因斯坦系数见文献[27]。
式(22)中nα′i′为位于激发态电子能级、振动能级i′上的O2分子数密度,这里根据激发态电子能级上的分子数密度nO2B再按照振动温度下的玻尔兹曼分布确定。nαi为位于基态电子能级、振动能级i上的O2分子数密度,本文中即为ni。式(22)中φν(ν-να′i′, αi)为以να′i′, αi为中心的辐射谱线线型分布,
| $ \int_0^\infty {{\varphi _\nu }} (\nu - {\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}){\rm{d}}\nu = 1 $ | (26) |
本文对三种辐射跃迁机制的谱线均采用多普勒增宽的线型分布,谱线互不重叠。将式(22)对频率积分后得:
| $ \begin{array}{l} \frac{{{\rm{d}}{I^{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{\rm{d}}t}} = ch{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}{B_{{\alpha ^\prime }{i^\prime },\alpha i}}{n_{{\alpha ^\prime }{i^\prime }}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\frac{{2h\nu _{{\alpha ^\prime }{i^\prime },\alpha i}^3}}{{{c^2}}} + \sqrt {\frac{{{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}}{{2\pi }}} \frac{{{I^{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{\gamma _{{\alpha ^\prime }{i^\prime },\alpha i}^D}}\left( {1 - \frac{{{g_{\rm{B}}}}}{{{g_{\rm{X}}}}}\frac{{{n_{\alpha i}}}}{{{n_{{\alpha ^\prime }{i^\prime }}}}}} \right)} \right] \end{array} $ | (27) |
式(27)中γα′i′, αiD为多普勒线型半峰值对应的宽度。式(27)即单位时间内特定的α′i′→αi辐射跃迁产生的辐射强度(单位时间、单位立体角、单位面积上辐射的能量)对时间的变化率。将它对立体角积分,然后除以光速、除以1个该跃迁对应频率的光子的能量hνα′i′, αi后,就得到了单位时间单位体积内发生的α′i′→αi辐射跃迁数目。这也就是单位时间内由α′i′→αi辐射跃迁而引起的基态电子能级上振动能级i的分子数密度ni的变化率,对激发态电子能级上所有振动能级i′求和,即得式(1)中的辐射生成项Rirad。采用辐射各向同性假设后,有:
| $ R_i^{{\rm{rad}}} \approx \frac{{4\pi }}{{hc}}\sum\limits_{{i^\prime }} {\frac{1}{{{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}}}} \frac{{{\rm{d}}{I^{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{\rm{d}}t}} $ | (28) |
本文仅对基态电子能级上各振动能级的粒子分布通过求解非平衡变化率方程式(1)得到详细的非平衡分布随时间演化过程。各电子能级上的分子分布视为电子温度下的玻尔兹曼分布,激发态电子能级(B3∑u-)上分子在各振动能级的分布也设为振动温度下的玻尔兹曼分布。这需要确定系统的振动温度。该振动温度基于态-态模型方法求得的基态电子能级的非平衡分布确定。态-态模型方法中常用的确定系统振动温度的方法有两种,简述如下。
1.4.1 根据非平衡振动能级分布确定振动温度一种方法是通过假设非平衡的各振动能级分布尽可能接近振动温度下的玻尔兹曼分布导出一个统一的振动温度。需要采用线性回归的方法。
振动温度Tvib下的玻尔兹曼分布为:
| $ n_i^{{T_{{\rm{vib}}}}} = \frac{{n_{{\rm{O2}}}^{\rm{X}}}}{{{Q_{{\rm{vib}}}}}}{\rm{exp}}\left( { - \frac{{{\varepsilon _{{\rm{vib}},i}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right) $ | (29) |
式(29)中εvib, i为位于振动能级i的一个分子具有的振动能。Qvib为振动配分函数,
| $ {Q_{{\rm{vib}}}} = \sum\limits_i {{\rm{exp}}} \left( { - \frac{{{\varepsilon _{{\rm{vib}},i}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}}} \right) $ | (30) |
对式(29)两边取对数,得:
| $ {\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n_i^{{T_{{\rm{vib}}}}} = ({\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n_{{\rm{O2}}}^{\rm{X}} - {\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_{{\rm{vib}}}}) - \frac{{{\varepsilon _{{\rm{vib}},i}}}}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}} $ | (31) |
近似将上式中的振动配分函数Qvib视为常数,则i能级粒子数密度的对数便为该能级能值的线性函数,记作:
| $ {\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n_i^{{T_{{\rm{vib}}}}} = {K_0} + {K_1}{\varepsilon _{{\rm{vib}},i}} $ | (32) |
其中K1为该线性函数的斜率,
| $ {K_1} = - \frac{1}{{{k_{\rm{B}}}{T_{{\rm{vib}}}}}} $ | (33) |
根据已知求得的各振动能级非平衡粒子数密度,采用线性回归方法确定式(32)的斜率,即得到对应的振动温度Tvib。
| $ {K_1} = \frac{{\sum\limits_i {{w_i}} {\varepsilon _{{\rm{vib}},i}}{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {n_i} - \overline {{\varepsilon _{{\rm{vib}},i}}} \cdot \overline {{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {n_i}} }}{{\sum\limits_i {{w_i}} \varepsilon _{{\rm{vib}},i}^2 - {{(\overline {{\varepsilon _{{\rm{vib}},i}}} )}^2}}} $ | (34) |
式(34)中wi为权重因子,根据该能级的粒子占比确定:
| $ {\omega _i} = \frac{{{n_i}}}{{n_{{\rm{O2}}}^{\rm{X}}}} $ | (35) |
$\overline {{\varepsilon _{{\text{vib}}}}{, _i}} $为加权平均的振动能:
| $ \overline {{\varepsilon _{{\rm{vib}},i}}} = \sum\limits_i {{w_i}} {\varepsilon _{{\rm{vib}},i}} $ | (36) |
$\overline {\ln\; {n_i}} $为加权平均的粒子数密度对数
| $ \overline {{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {n_i}} = \sum\limits_i {{w_i}{\kern 1pt} } {\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {n_i} $ | (37) |
另一种方法是根据系统的非平衡振动能导出振动温度,即令一个分子的平均非平衡振动能和振动温度Tvib对应的平衡振动能相等,反推出振动温度Tvib。一个分子的平均非平衡振动能即式(36)定义的$\overline {{\varepsilon _{{\text{vib}}}}{, _i}} $,而振动温度下的平衡振动能,就是当分子满足式(29)给出的振动温度下的玻尔兹曼分布时的平均振动能,从而有:
| $ {{\bar \varepsilon }_{{\rm{vib}},i}} = \frac{{\sum\limits_i {n_i^{{T_{{\rm{vib}}}}}} {\varepsilon _{{\rm{vib}},i}}}}{{\sum\limits_i {n_i^{{T_{{\rm{vib}}}}}} }} = \frac{{\sum\limits_i {{\rm{exp}}} \left( { - \frac{{{\varepsilon _{{\rm{vib}},i}}}}{{{k_B}{T_{{\rm{vib}}}}}}} \right){\varepsilon _{{\rm{vib}},i}}}}{{{Q_{{\rm{vib}}}}}} $ | (38) |
式(38)为根据$\overline {{\varepsilon _{{\text{vib}}}}{, _i}} $确定振动温度Tvib方法的隐函数形式公式,需要迭代求解。
2 计算方法对包含振动能级跃迁、化学反应和辐射的O2/O混合物系统,求解热化学非平衡与辐射特性随时间的演化,归结为求解由组元O(X3∑g-, i)的数密度变化率方程式(1)、O的数密度的变化率方程式(2)和辐射强度变化率方程式(27)组成的常微分方程组。其中式(1)包含47个方程。对辐射跃迁,激发态电子能级对应的振动能级范围取为i′=0~14,基态电子能级对应的振动能级范围为取为i=0~21,因此式(27)对应330个方程。式(1)、式(2)的生成项由式(12)~式(18)、式(28)给出,各生成项为与温度相关的速率常数和组元数密度(或辐射强度)的幂次积;辐射强度变化率方程式(27)的生成项涉及爱因斯坦系数、组元数密度和辐射强度本身。数值求解由式(1)、式(2)、式(27)共378个方程构成的常微分方程组后,就可得到O、O2各能级粒子数密度和各辐射谱带强度随时间的变化。
由于各类跃迁机制的速率差别大,导致常微分方程组的数值求解存在严重刚性问题,可以采用Euler隐式方法求解。另外,VODE(变系数的常微分方程求解器)[37]是变系数的BDF(向后分化公式)方法,可以高效地解决具有刚性的问题。α-QSS(拟稳态逼近方法)[38]是具有二阶精度的预测-校验方法,常用于反应速率系数随时间缓变的多组元化学反应模拟。考虑到Euler隐式算法形式简单、应用方便,对本文算例从计算精度和计算消耗上可以接受,本文采用了Euler隐式算法。
将待求解的378个方程对应变量记为φj,则采用迭代的方法由t时刻的φjt推进得到t+Δt时刻的φjt+Δt的步骤如下:首先令φj(1)=φjt,采用下式得到φj(m+1),
| $ \varphi _j^{(m + 1)} = \frac{1}{2}\left[ {\varphi _j^{(m)} + \varphi _j^t + \Delta t{{\left( {\frac{{{\rm{d}}{\varphi _j}}}{{{\rm{d}}t}}} \right)}^{(m)}}} \right] $ | (39) |
其中,
| $ {\left( {\frac{{{\rm{d}}{\varphi _j}}}{{{\rm{d}}t}}} \right)^{(m)}} = f(\varphi _1^{(m)},\varphi _2^{(m)}, \cdots ,\varphi _j^{(m)}, \cdots ) $ | (40) |
当φj(m+1)和φj(m)的相对差值达到收敛要求时,令φjt+Δt=φj(m+1)。
初始条件给定温度T0,O2与O的数密度nO2, 0、nO, 0,O2在各能级的分布设为T0下的平衡值,辐射强度初值采用T0下的黑体辐射谱带强度I0, eq, Bα′i′, αi(令式(27)为0、且粒子分布为平衡分布得到):
| $ \begin{array}{l} I_{{\rm{0,eq,B}}}^{{\alpha ^\prime }{i^\prime },\alpha i} = \frac{{2h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{c^2}}}\gamma _{{\alpha ^\prime }{i^\prime },\alpha i}^D\sqrt {\frac{{2\pi }}{{{\rm{ln}}2}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\frac{{Q_\alpha ^{{\rm{vib}}}({T_0})}}{{Q_{{\alpha ^\prime }}^{{\rm{vib}}}({T_0})}}{\rm{exp}}\left( {\frac{{h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{k_{\rm{B}}}{T_0}}}} \right) - 1} \right]^{ - 1}} \end{array} $ | (41) |
由于系统在初始瞬间改变温度后保持等温等容,各生成项中的速率常数在起始时刻根据系统设定温度计算一次即可。时间推进的步长视具体温度和压力条件,可在10-11~10-8 s之间取值。本文涉及的不耦合辐射的算例条件(设定温度分别为3000 K、10 000 K、20 000 K)下,时间步长均取为10-10 s。包含辐射机制时,由于辐射强度随时间变化率较大,时间推进步长需进一步减小至10-14~10-13 s,本文含辐射的算例条件(设定温度20 000 K)时间步长均取为10-13 s。
3 算例及计算结果分析 3.1 态-态模型热化学非平衡程序校验首先根据文献[35]计算结果对本文编制的O2/O态-态模型热化学非平衡程序进行校验。文献[35]给出了两组算例,初始的O2/O数密度均为nO2, 0=1×1017/cm3、nO, 0=9×1017/cm3,设定的系统温度分别为T=3000 K和T=10 000 K。两组算例分别设定不同的初始温度:T=3000 K组的初始温度分别为T0=100 K和T0=10 000 K; T=10 000 K组的初始温度分别为T0=100 K和T0=20 000 K。模拟了两组系统在起始时刻突然升温或降温并保持等温等容条件下的热化学非平衡过渡过程。
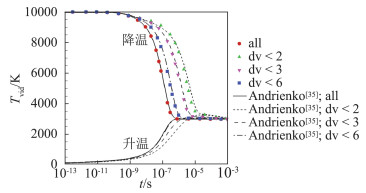
图 1、图 2分别给出了两组算例系统的振动温度随时间的变化,振动温度为应用式(38)根据基态电子能级上振动能级分布导出的Tvib。图中“dv”代表VTa过程中的振动跃迁量子数Δv,all代表允许Δv取任意可能值。可见本文计算结果与文献[35]的计算结果一致性良好,验证了本文方法和程序的正确性。
|
图 1 由T0=100 K或T0=10 000 K升温或降温至T=3000 K后振动温度随时间变化 Fig.1 Time evolution of vibrational temperature (T0=100 K or T0=10 000 K, T=3000 K) |
|
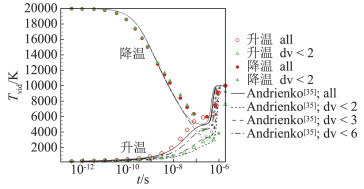
图 2 由T0=100 K或T0=20 000 K升温或降温至T=10 000 K后振动温度随时间变化 Fig.2 Time evolution of vibrational temperature (T0=100 K or T0=20 000 K, T=10 000 K) |
从图 1和图 2均可发现限制跃迁量子数Δv的影响,可见VTa过程中的多量子数跃迁的重要性。不过Δv < 6与不限制Δv的结果差异就不大了。无论是升温还是降温至T=3000 K条件,随着时间推进,振动温度都是近似以指数方式趋近于平动温度,约在10-6s时与平动温度相等,基于振动温度的定义,可以说振动能和平动/转动能此时基本达到了平衡。但设定温度T=10 000 K条件的情况中振动温度随时间的变化特点不同,见图 2。初始T0=100 K条件下,振动温度在10-7s升至6000 K附近后有一段平台区,到10-6s后又开始迅速爬升,达到10 000 K,整体呈现了台阶形状。初始T0=20 000 K条件下,振动温度在10-7s前一直下降,达到6000 K左右,之后和T0=100 K条件的变化曲线几乎重合,经历平台区后再迅速爬升至T=10 000 K。振动温度在10-7~10-6s期间的平台区与此时开始的化学反应有关,后面再进一步分析。
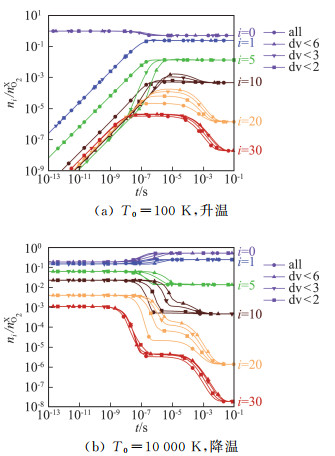
3.2 O2/O系统的热化学非平衡过程分析图 3分别给出了由T0=100 K或T0=10 000 K升温或降温至T=3000 K的两个算例O2分子归一化振动能级分布随时间的变化曲线,图中不同能级采用了不同颜色的曲线,符号标识对VTa过程中振动跃迁量子数Δv的限制。这里和后面的振动能级分布均指基态电子能级上的振动能级分布。初始时刻振动能级分布为初始温度下的平衡分布,因此由T0=100 K升温的算例(见图 3a)中,随着时间推进,低能级分子数减小,高能级分子数增大;低能级(i < 10)分布在10-7s时就接近平衡,但i>20能级上的O2分子,在10-6~10-4s区间存在一个粒子数密度基本不变的平台区,到10-2s后才接近平衡。由T0=10 000 K降温的算例,随时间推进,高、低能级分子数变化的趋势与由T0=100 K升温的算例相反,但分布达到平衡的时间和过渡过程出现的平台区与初始温度为T0=100 K的情况类似。这是因为振动跃迁和化学反应速率均取决于设定的系统温度(T=3000 K)。两个算例中都体现了限制跃迁量子数的影响,特别是对高振动能级,多量子数的跃迁更加重要。与图 1给出的振动温度随时间变化曲线比较,可知高振动能级分布达到平衡的松弛时间比振动温度的长得多,这正是高振动能级粒子分布不满足振动温度下的玻尔兹曼分布的体现。不过,由于高能级分子占比很小,其对总体振动能的影响也很小。
|
图 3 由T0=100 K或T0=10 000 K升温或降温至T=3000 K后O2振动能级分布随时间变化 Fig.3 Time evolution of O2 vibrational population distribution (T0=100 K or T0=20 000 K, T=10 000 K) |
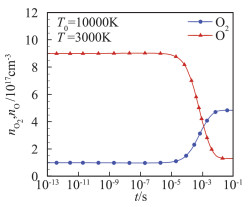
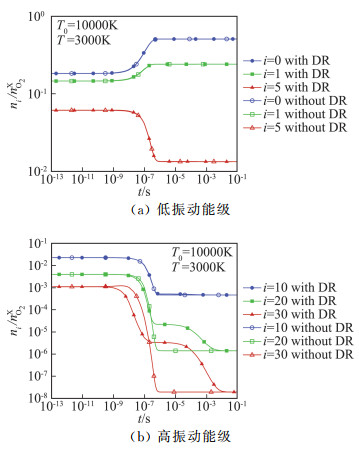
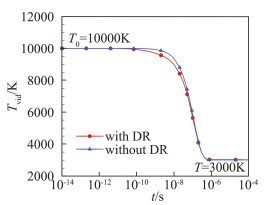
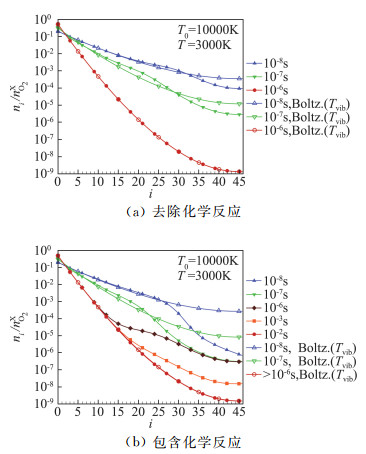
振动能级分布在非平衡过渡过程中的变化与化学反应相关。这里首先以初始T0=10 000 K降温至T=3000 K的算例为代表进行分析。图 4给出了O2与O粒子数密度随时间的变化,图 5对比了包含所有振动跃迁、化学反应过程(VTm、VTa、VV、DRa、DRm)和去除化学反应计算得到的振动能级分布随时间的变化,图中含所有振动跃迁和化学反应过程的用实心符号,去除化学反应的则用空心符号。图 6对比了包含或去除化学反应计算得到的振动温度变化曲线。图 7则分别给出了包含或去除化学反应时振动能级分布与对应振动温度下的玻尔兹曼分布的对比。
|
图 4 由T0=10 000 K降温至T=3000 K后O2和O数密度变化 Fig.4 Time evolution of number densities of O2 and O (T0=10 000 K, T=3000 K) |
|
图 5 由T0=10 000 K降温至T=3000 K后O2振动能级分布随时间变化(含或不含化学反应) Fig.5 Time evolution of O2 vibrational population distribution (with or without DR processes, T0=10 000 K, T=3000 K) |
|
图 6 由T0=10 000 K降温至T=3000 K后振动温度随时间变化(含或不含化学反应的对比) Fig.6 Time evolution of vibrational temperature(with or without DR processes, T0=10 000 K, T=3000 K) |
|
图 7 由T0=10 000 K降温至T=3000 K后的O2振动能级分布和振动温度下玻尔兹曼分布对比(含或不含化学反应) Fig.7 Comparison of vibrational population distribution with Boltzmann distribution(with or without chemical reactions, T0=10 000 K, T=3000 K) |
相对于算例设定的温度T=3000 K下的平衡化学组成,初始时刻的nO, 0/nO2, 0偏大,非平衡过渡过程中将发生O原子的复合反应。化学反应有一定的“孵化”时间,由图 4可见该设定温度T=3000 K条件下大约10-6s复合反应才起步,到10-5s后才有明显的反应,大约10-2s反应达到平衡。结合图 5给出的有无化学反应的振动能级分布对比,可以看到二者的高振动能级分布的明显差异正是化学反应开始的时间。可以分析得出这里的复合反应生成的O2分子主要是在高振动能级。高振动能级的分子分布受到化学反应的明显影响,而低能级分布几乎不受影响。10-6s~10-4s之间出现的高振动能级分子数密度的平台区,是该区间复合生成高能级O2和高能级O2通过振动松弛向低能级跃迁互相平衡的结果。
由图 6可知算例条件下,是否包含化学反应对振动温度没有明显影响,这和高能级分子占比小因而对振动能贡献小的特点是一致的。另外可看出以振动温度衡量的振动松弛时间大约为10-6s,远小于以高振动能级分布衡量的松弛时间和离解-复合反应达到平衡所需要的时间(约10-2s)。
从图 7可见,包含或去除化学反应时振动能级分布均偏离了对应振动温度下的玻尔兹曼分布,包含化学反应时偏离程度更大,特别是高振动能级的分布。从随时间的变化来看,由图 7(b)可见t < 10-7s时,化学反应尚未发生,振动松弛占主导地位,位于高能级的O2分子数低于振动温度下的玻尔兹曼分布。而t>10-6s后,复合反应开始,生成大量的高能级O2分子,使得位于高能级的O2分子数密度高于此时振动温度下的玻尔兹曼分布。
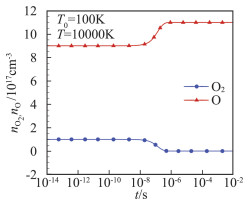
接下来对初始T0=100 K升温至T=10 000 K的算例,分析化学组成随时间的变化(见图 8),振动能级分布和振动温度的演化特点及其受化学反应的影响(见图 9、图 10),不同时刻振动能级分布与振动温度下玻尔兹曼分布的差异(见图 11)。相对于算例设定的温度T=10 000 K下的平衡化学组成,初始时刻的nO, 0/nO2, 0偏小,非平衡过渡过程中将发生O2分子的离解反应。在设定温度下,振动跃迁和化学反应的速率都较T=3000 K算例条件下更快,松弛时间也大大减小。
|
图 8 由T0=100 K升温至T=10 000 K后O2和O数密度变化 Fig.8 Time evolution of number densities of O2 and O(T0=100 K, T=10 000 K) |
|
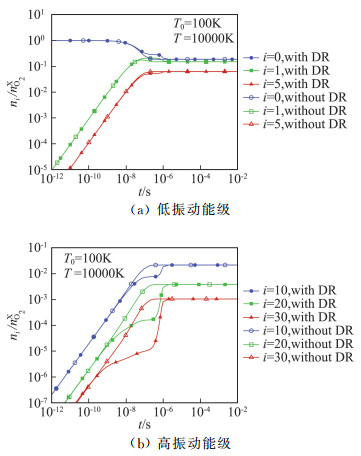
图 9 由T0=100 K升温至T=10 000 K后振动能级分布随时间变化(含或不含化学反应的对比) Fig.9 Time evolution of O2 vibrational population distribution(with or without DR processes, T0=100 K, T=10 000 K) |
|
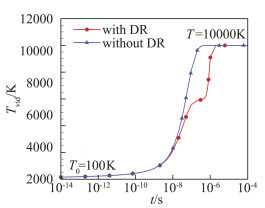
图 10 由T0=100 K升温至T=10 000 K后振动温度随时间变化(含或不含化学反应的对比) Fig.10 Time evolution of vibrational temperature(with or without DR processes, T0=100 K, T=10 000 K) |
|
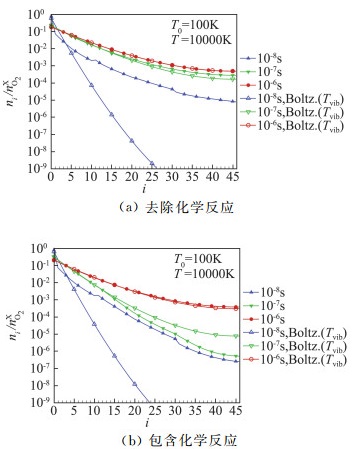
图 11 由T0=100 K升温至T=10 000 K后的振动能级分布和振动温度下玻尔兹曼分布的对比(含或不含化学反应) Fig.11 Comparison of vibrational population distribution with Boltzmann distribution(with or without chemical reactions, T0=100 K, T=10 000 K) |
由图 8~图 10可知,化学反应达到平衡的特征时间、以振动温度或高振动能级分布表征的松弛时间,都在10-7s~10-6s之间。化学反应对振动能级分布的影响,比T=3000 K算例条件下更大。离解反应主要发生在10-8s~10-6s时间段内,且存在高振动能级优先离解的特点。由图 11(a)可见,不包含化学反应时,高振动能级的O2分子数密度高于振动温度下的玻尔兹曼分布。而包含化学反应后,较高能级的分子优先离解,导致高能级分子数低于振动温度下的玻尔兹曼分布值,见图 11(b)。
对比分析T=3000 K和T=10 000 K算例可知,较低的设定温度下,化学反应所需时间比振动松弛时间大得多,两个过程相对独立,化学反应对振动松弛产生的影响较小。而高设定温度下,化学反应特征时间和振动松弛时间可以相比拟,彼此耦合程度更高,互相影响更大。
3.3 O2/O系统的热化学非平衡与辐射过程分析选取设定温度为T=20 000 K,初始的O2和O数密度均为nO2, 0=1×1017/cm3、nO, 0=9×1017/cm3,初始温度分别为T0=10 000 K和T0=30 000 K的两个算例条件,对O2/O系统研究高温下耦合辐射的热化学非平衡过渡过程,考察辐射生成项对粒子能级分布的贡献。
首先研究总的辐射强度。将式(27)给出的针对跃迁α′i′→αi的辐射带强度对所有的跃迁求和,即得到总的辐射强度随时间的变化率方程。本文考虑的辐射跃迁包括由激发态电子能级上振动能级i′=0~14至基态电子能级上振动能级i=0~21的共计330个辐射谱带跃迁。总的辐射强度记为I。
令式(27)为0,得到平衡辐射谱带强度:
| $ I_{{\rm{eq}}}^{{\alpha ^\prime }{i^\prime },\alpha i} = \frac{{2h{\nu _{{\alpha ^\prime }{i^\prime },\alpha i}}}}{{{c^2}}}\gamma _{{\alpha ^\prime }{i^\prime },\alpha i}^D\sqrt {\frac{{2\pi }}{{{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}}} {\left( {\frac{{{g_{\rm{B}}}}}{{{g_{\rm{X}}}}}\frac{{{n_{\alpha i}}}}{{{n_{{\alpha ^\prime }{i^\prime }}}}} - 1} \right)^{ - 1}} $ | (42) |
其中的各能级分子数密度为热化学非平衡过渡过程中的值。对比式(27)和式(42)可知非平衡辐射谱带强度Iα′i′, αi和平衡辐射谱带强度Ieqα′i′, αi的差异体现了辐射本身的非平衡特点,Iα′i′, αi不能像Ieqα′i′, αi这样直接由分子的能级分布确定,而是取决于有限速率的辐射跃迁。而当各能级分子数密度达到平衡玻尔兹曼分布后,辐射谱带强度即为黑体平衡辐射谱带强度Ieq, Bα′i′, αi,将式(41)中的初始温度改为设定温度即得Ieq, Bα′i′, αi。将Ieqα′i′, αi和Ieq, Bα′i′, αi对所有跃迁谱带求和,分别得到总的平衡辐射强度Ieq和总的黑体平衡辐射强度Ieq, B。
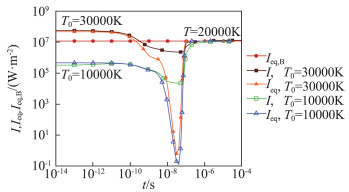
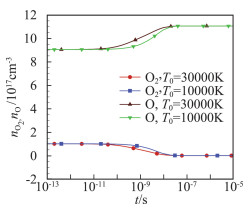
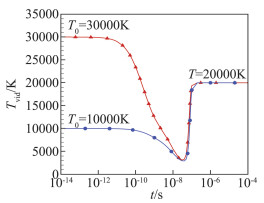
图 12给出了由T0=30 000 K或T0=10 000 K降温或升温至T=20 000 K后三个总辐射强度I、Ieq、Ieq, B辐射强度随时间的变化。为分析辐射与热化学非平衡过程的相互影响特点,图 13、图 14还给出了相应的O2、O数密度和振动温度的时间演化曲线。由图 12可见随着时间的推进,辐射强度I和平衡辐射强度Ieq最终将达到设定温度下的黑体平衡辐射强度Ieq, B。可将辐射强度I达到黑体平衡辐射强度Ieq, B的时间定义为非平衡辐射特征时间,则由T0=10 000 K升温至设定T=20 000 K的算例中,非平衡辐射特征时间在10-5s量级,而振动松弛时间(参见图 14)在10-7~10-6s量级。由T0=30 000 K降温至T=20 000 K的条件下振动松弛时间与升温条件接近,但非平衡辐射特征时间在10-6s量级,明显低于升温条件。
|
图 12 由T0=10 000 K或T0=30 000 K升温或降温至T=20 000 K后辐射总强度随时间变化 Fig.12 Time evolution of total radiative intensity(T0=10 000 K or T0=30 000 K, T=20 000 K) |
|
图 13 由T0=10 000 K或T0=30 000 K升温或降温至T=20 000 K后O2和O数密度随时间变化 Fig.13 Time evolution of number densities of O2 and O(T0=10 000 K or T0=30 000 K, T=20 000 K) |
|
图 14 由T0=10 000 K或T0=30 000 K升温或降温至T=20 000 K后振动温度随时间变化 Fig.14 Time evolution of vibrational temperature(T0=10 000 K or T0=30 000 K, T=20 000 K) |
从图 12看出,无论升温条件还是降温条件,I和Ieq都不是单调趋近Ieq, B的。以T0=30 000 K的降温条件为例,在10-9s~10-7s区间,I降至低于Ieq, B,之后迅速回升,再渐近趋近Ieq, B。这反映出在该时间段内大量基态电子能级上的分子吸收光子向激发态电子能级跃迁,超越了设定温度对应的平衡辐射跃迁数,导致激发态电子能级的粒子数开始超过设定温度下的平衡分布粒子数、之后再回迁的特点。Ieq在10-9s~10-7s区间的下降程度更大,这与图 14体现出的该时间段内振动温度(由非平衡的振动能级分布确定)的大幅变化是一致的。I和Ieq的差异体现了辐射本身的非平衡特点(I不能像Ieq那样直接由分子的能级分布确定),Ieq与Ieq, B的差异则体现了真实的非平衡分子能级分布与设定温度下玻尔兹曼分布的差异。I与Ieq在10-9s~10-7s时间段内的明显差异说明真实的辐射跃迁数远低于根据能级分布确定的辐射跃迁数,辐射的非平衡程度很强。
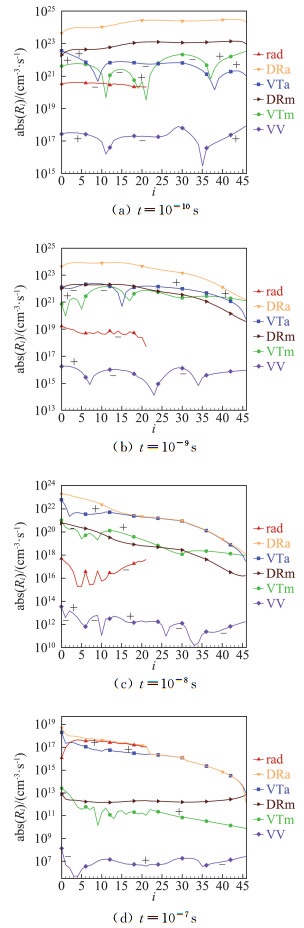
图 15展示了由T0=30 000 K降温至T=20 000 K条件下,在不同时刻各个跃迁或反应机制以及辐射对各振动能级数密度变化的贡献,即式(1)右端的各生成项。图中给出各项的绝对值,其中DRa和DRm的贡献为负(算例条件下是发生离解反应,参见图 13),其他各项采用“+”、“-”表示正负。由于初始辐射强度设定为T0=30 000 K下的黑体平衡辐射强度,所以降温条件下系统是吸收辐射,基态电子能级各振动能级上的粒子数是减小的,rad过程的贡献也为负,到10-7s后rad过程贡献变为正。由图 15可见在t < 10-9s时,离解反应尤其是DRa过程起主导作用。到了10-8s时,DR反应的生成项减小,VT过程生成项的贡献逐渐凸显。图 14中t =10-8s~10-7s时间段内振动温度的迅速回升就主要是VT过程贡献。到10-7s时VT和DR过程的生成项迅速下降,比10-8s时低4个数量级,由图 14也可知此时振动温度基本达到设定温度。rad过程生成项在10-10s时比VT过程低一个量级,而到10-9~10-8s时则比VT过程低了2~3个数量级,但其后rad生成项量级变化不大,达到了与DRa、VTa项相同的数量级。该算例条件下,VV过程的生成项一直远低于其他机制。
|
图 15 由T0=30 000 K降温至T=20 000 K后各机制对粒子能级分布变化率贡献的绝对值 Fig.15 The absolute values of source terms in Eq.(1)from each mechanism(T0=30 000 K, T=20 000 K) |
这里对本文算例在Intel(R) Core(TM) i7-7700处理器上单机计算的耗时做一统计,见表 1。表中算例1~6不包含辐射的计算,算例7和8包含辐射计算,τeq代表算例条件下O2/O系统达到平衡的时间。对不含辐射的算例1~6,τeq是系统达到化学平衡且振动能级分布亦达到平衡分布的时间,对包含辐射的算例7和算例8,除达到上述热化学平衡外,还要求辐射强度达到黑体平衡辐射强度,τeq为非平衡辐射特征时间。不含辐射算例的时间推进步长均取为Δt=10-10s,含辐射的取为Δt=10-13s。T=3000 K算例起始时间步长取为Δt=10-10s,在10-2 s后增大时间推进步长至Δt=10-9 s。Tstepcal为平均一个时间步的计算耗时,Teqcal则为算例推进到平衡的大约总计算耗时。
| 表 1 各算例计算耗时统计 Table 1 Calculation time cost of each case |
|
|
由于反应速率随设定温度升高而升高,高温下系统较快达到平衡,而温度降低后达到平衡所需时间明显变长。本文含辐射算例(T=20 000 K)的τeq在10-6 s~10-5 s量级,不含辐射的算例中,T=20 000 K的τeq在10-6 s量级,而T=3000 K的τeq则达到了10-1 s量级。可能由于Euler隐式方法解决数值计算刚性问题的效果不够好,即使对T=3000 K算例,起始的时间步长也只能取为Δt=10-10 s,在推进至10-2 s后再增大时间步长以减小计算消耗。后续研究应尝试更有效的VODE方法等。
不包含辐射时,T=3000 K和T=10 000 K算例一个时间步的计算时间约0.5 ms,但T=20 000 K算例的计算时间仅0.2 ms左右,这与不同温度下刚性问题程度不同因而需要的Euler隐式内迭代次数不同有关。T=20 000 K条件包含辐射后,由于求解方程增多,每个时间步的计算时间增大至0.6 ms左右。可见态-态模型的计算消耗确实很大,但未来随着计算机性能的进一步提高和发展更先进的计算技术,将态-态模型用到二维非平衡流动模拟(如文献[24]),或者是三维流场中非平衡程度特别强的局部区域采用态-态模型,也是具有工程可行性的。
4 结论本文对封闭静止的O2/O系统采用态-态模型模拟包含辐射的热化学非平衡过渡过程,得到以下结论:
1) 根据非平衡振动能级分布导出的振动温度随时间变化情况与双温度模型所描述的按指数律逼近平衡值的特点不同,有些条件下还出现了振动温度随时间并非单调变化的现象。各算例条件下的非平衡振动能级分布均不满足当时振动温度下的玻尔兹曼分布。
2) 当温度较低时,化学反应特征时间远大于振动松弛时间,振动非平衡过程对化学反应的影响不强。而当温度较高(T >10 000 K)时,化学反应和振动松弛过程同时发生,同时对振动能级分布演化产生影响。这时双温度模型不能很好反映粒子的非平衡振动能级分布,也就不能很好处理化学反应和振动松弛过程的耦合。
3) 本文算例显示出O2/O系统在高温条件下的非平衡辐射特征,不过辐射跃迁对热化学非平衡过程的影响不明显。非平衡过程初期,粒子能级分布变化率中辐射生成项的贡献远低于平动-振动跃迁。非平衡辐射的特征时间也远大于振动松弛时间,非平衡辐射特征时间在由T0=10 000 K升温至设定T= 20 000 K的算例中为10-5s量级,由T0=30 000 K降温至T=20 000 K的条件下为10-6s量级;而振动松弛时间在升温和降温条件下均在10-7~10-6s量级。
4) 包含各类跃迁机制的非平衡过程数值计算中刚性问题严重,本文采用Euler隐式算法求解时要求极小的时间推进步长,限制了计算效率。未来研究中需选用对刚性问题更加高效的VODE方法或α-QSS方法。
| [1] |
PARK C. Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles[C]//Thermal Design of Aeroassisted Orbital Transfer Vehicles. AIAA 19th Thermophysics Coference, Snowmass, clorrado, 1984. New York: AIAA, 1985: 511-537. https://doi.org/10.2514/5.9781600865718.0511.0537
|
| [2] |
CAPITELLI M, ARMENISE I, GORSE C. State-to-state approach in the kinetics of air components under re-entry conditions[J]. Journal of Thermophysics and Heat Transfer, 1997, 11(4): 570-578. DOI:10.2514/2.6281 |
| [3] |
DA SILVA M L, GUERRA V, LOUREIRO J. State-resolved dissociation rates for extremely nonequilibrium atmospheric entries[J]. Journal of Thermophysics and Heat Transfer, 2007, 21(1): 40-49. |
| [4] |
GNOFFO P. Upwind-biased, point-implicit relaxation strategies for viscous, hypersonic flows[C]//9th Computational Fluid Dynamics Conference, Buffalo, NY, USA. Reston, Virgina: AIAA, 1989.89-1972-CP https://doi.org/10.2514/6.1989-1972
|
| [5] |
CHEATWOOD F M, GNOFFO P A. User's manual for the Langely Aerothermodynamic Upwind Relaxation Algorithm (LAURA)[R]. NASA TM-4674, 1996.
|
| [6] |
MCGRORY W, HUEBNER L, SLACK D, et al. Development and application of GASP 2.0[C]//Fourth International Aerospace Planes Conference, Orlando, FL, USA. Reston, Virgina: AIAA, 1992. AIAA 92-5067. https://doi.org/10.2514/6.1992-5067
|
| [7] |
OLYNICK D, TAM T. Trajectory based validation of the Shuttle heating environment[C]//31st Thermophysics Conference, New Orleans, LA, USA. Reston, Virginia: AIAA, 1996. AIAA 96-1891. https://doi.org/10.2514/6.1996-1891
|
| [8] |
TISSERA S, DRIKAKIS D, BIRCH T. Computational fluid dynamics methods for hypersonic flow around blunted-cone-cylinder-flare[J]. Journal of Spacecraft and Rockets, 2010, 47(4): 563-570. DOI:10.2514/1.46722 |
| [9] |
SORENSEN C, VALENTINI P, SCHWARTZENTRUBER T E. Uncertainty analysis of reaction rates in a finite-rate surface-catalysis model[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(3): 407-416. DOI:10.2514/1.T3823 |
| [10] |
KNIGHT D, LONGO J, DRIKAKIS D, et al. Assessment of CFD capability for prediction of hypersonic shock interactions[J]. Progress in Aerospace Sciences, 2012, 48. DOI:10.1016/j.paerosci.2011.10.001 |
| [11] |
汪球, 赵伟, 滕宏辉, 等. 高焓激波风洞喷管流场非平衡特性研究[J]. 空气动力学学报, 2015, 33(1): 66-71. WANG Q, ZHAO W, TENG H H, et al. Numerical simulation of nonequilibrium characteristics of high enthalpy shock tunnel nozzle flow[J]. Acta Aerodynamica Sinica, 2015, 33(1): 66-71. DOI:10.7638/kqdlxxb-2013.0001 (in Chinese) |
| [12] |
周凯.膨胀风洞与超高速流动实验研究[D].北京: 中国科学院力学研究所, 2017. ZHOU K. Experimental study on hypervelocity flow in expansion tunnel[D]. Beijing: Institute of Mechanics, Chinese Academy of Sciences, 2017. (in Chinese) |
| [13] |
PARK C. The limits of two-temperature model[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, 2010. AIAA 2010-911. https://doi.org/10.2514/6.2010-911
|
| [14] |
NEITZEL K, ANDRIENKO D, BOYD I D. Aerothermochemical nonequilibrium modeling for oxygen flows[J]. Journal of Thermophysics and Heat Transfer, 2017, 31(3): 634-645. DOI:10.2514/1.T4962 |
| [15] |
徐丹.高温热化学非平衡模型研究[D].长沙: 国防科学技术大学, 2012. XU D. Study of thermo-chemical models for non-equilibrium flow in high-temperature conditions[D]. Changsha: National University of Defense Technology, 2012. (in Chinese) |
| [16] |
徐丹, 曾明, 张威, 等. 采用态-态模型的热化学非平衡喷管流数值研究[J]. 计算物理, 2014, 31(5): 531-538. XU D, ZENG M, ZHANG W, et al. Numerical study of thermochemical non-equilibrium nozzle flow in state-to-state model[J]. Chinese Journal of Computational Physics, 2014, 31(5): 531-538. DOI:10.3969/j.issn.1001-246X.2014.05.004 (in Chinese) |
| [17] |
COLONNA G, ARMENISE I, BRUNO D, et al. Reduction of state-to-state kinetics to macroscopic models in hypersonic flows[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(3): 477-486. |
| [18] |
ARMENISE I, CAPITELLI M, COLONNA G, et al. Non-equilibrium vibrational kinetics during hypersonic flow of a solid body in nitrogen and its influence on the surface heat flux[J]. Plasma Chemistry and Plasma Processing, 1995, 15(3): 501-528. |
| [19] |
ARMENISE I, CAPITELLI M, GORSE C. Nitrogen nonequilibrium vibrational distributions and non-Arrhenius dissociation constants in hypersonic boundary layers[J]. Journal of Thermophysics and Heat Transfer, 1998, 12(1): 45-51. DOI:10.2514/2.6300 |
| [20] |
ARMENISE I, BARBATO M, CAPITELLI M, et al. State-to-state catalytic models, kinetics, and transport in hypersonic boundary layers[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(3): 465-476. DOI:10.2514/1.18218 |
| [21] |
BELOUAGGADIA N, ARMENISE I, CAPITELLI M, et al. Computation of vibration-dissociation nonequilibrium boundary layers:comparison of various models[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(4): 684-693. DOI:10.2514/1.46520 |
| [22] |
COLONNA G, TUTTAFESTA M, CAPITELLI M, et al. Non-Arrhenius NO formation rate in one-dimensional nozzle airflow[J]. Journal of Thermophysics and Heat Transfer, 1999, 13(3): 372-375. DOI:10.2514/2.6448 |
| [23] |
徐丹, 曾明, 张威, 等. 态-态模型下N2/N混合物的热化学非平衡过程研究[J]. 空气动力学学报, 2014, 32(3): 280-288. XU D, ZENG M, ZHANG W, et al. Thermo-chemical nonequilibrium process in N2/N mixture with state-to-state model[J]. Acta Aerodynamica Sinica, 2014, 32(3): 280-288. DOI:10.7638/kqdlxxb-2012.0139 (in Chinese) |
| [24] |
DRUGUET M C, BULTEL A, MOREL V, et al. Non-equilibrium nitrogen re-entry flow computed with a vibrational-specific kinetics model[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. AIAA 2019-2283. https://doi.org/10.2514/6.2019-2283
|
| [25] |
BABOU Y, RIVIÈRE P, PERRIN M Y, et al. High-temperature and nonequilibrium partition function and thermodynamic data of diatomic molecules[J]. International Journal of Thermophysics, 2009, 30: 416-438. DOI:10.1007/s10765-007-0288-6 |
| [26] |
QIN Z, ZHAO J M, LIU L H. High-temperature partition functions, specific heats and spectral radiative properties of diatomic molecules with an improved calculation of energy levels[J]. Journal of Quantitative Spectroscopyand Radiative Transfer, 2018, 210: 1-18. DOI:10.1016/j.jqsrt.2018.02.004 |
| [27] |
LAUX C O, KRUGER C H. Arrays of radiative transition probabilities for the N2 first and second positive, NO beta and gamma, N2+ first negative, and O2 Schumann-Runge band systems[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1992, 48(1): 9-24. DOI:10.1016/0022-4073(92)90003-M |
| [28] |
KUSTOVA E V, CHIKHAOUI A. Kinetic modelling of radiative reacting gas flow under strong nonequilibrium conditions[J]. Chemical Physics, 2000, 255(1): 59-71. |
| [29] |
ALIAT A, VEDULA P, JOSYULA E. State-to-state modeling of radiation coupled to vibration-translation relaxation and dissociation in non-equilibrium gas flows[J]. Physical Review E, 2011, 83(6): 067302. DOI:10.1103/PhysRevE.83.067302 |
| [30] |
ANNALORO J, BULTEL A. Vibrational and electronic collisional-radiative model in air for Earth entry problems[J]. Physics of Plasmas, 2014, 21(12): 123512. DOI:10.1063/1.4904817 |
| [31] |
ANNALORO J, BULTEL A, OMALY P. Collisional-radiative modeling behind shock waves in nitrogen[J]. Journal of Thermophysics and Heat Transfer, 2014, 28(4): 608-622. DOI:10.2514/1.T4263 |
| [32] |
BULTEL A, ANNALORO J, DRUGUET M C. Dissociative recombination in reactive flows related to planetary atmospheric entries[C]//Ninth International Conference on Dissociative Recombination: Theory, Experiment, and Applications. EPJ Web of Conferences, 2015, 84: 06005. https://doi.org/10.1051/epjconf/20158406005
|
| [33] |
Adamovich I V, Macheret S O, RICH JW, et al. Vibrational relaxation and dissociation behind shock waves, part 1: kinetic rate models[R]. AIAA Journal, 1995, 33(6): 1064-1069. https://doi.org/10.2514/3.12528
|
| [34] |
ESPOSITO F, ARMENISE I, CAPITTA G, et al. O-O2 state-to-state vibrational relaxation and dissociation rates based on quasiclassical calculations[J]. Chemical Physics, 2008, 351(1-3): 91-98. DOI:10.1016/j.chemphys.2008.04.004 |
| [35] |
ANDRIENKO D A, BOYD I D. High fidelity modeling of thermal relaxation and dissociation of oxygen[J]. Physics of Fluids, 2015, 27(11): 116101. DOI:10.1063/1.4935241 |
| [36] |
曾明, 黄华, 柳军, 等. 高超声速风洞热化学非平衡流场辐射谱的数值计算[J]. 国防科技大学学报, 2002, 24(4): 1-4. ZENG M, HUANG H, LIU J, et al. Numerical computation of radiation spectrum in hypersonic tunnel thermochemical nonequilibrium flowfield[J]. Journal of National University of Defense Technology, 2002, 24(4): 1-4. DOI:10.3969/j.issn.1001-2486.2002.04.001 (in Chinese) |
| [37] |
BROWN P N, BYRNE G D, HINDMARSH A C. VODE:a variable-coefficient ODE solver[J]. SIAM Journal on Scientific and Statistical Computing, 1989, 10(5): 1038-1051. DOI:10.1137/0910062 |
| [38] |
MOTT D R, ORAN E S, VAN LEER B. A quasi-steady-state solver for the stiff ordinary differential equations of reaction kinetics[J]. Journal of Computational Physics, 2000, 164(2): 407-428. |
 2020, Vol. 38
2020, Vol. 38


