自普朗特1904年首先提出边界层理论以来以来,边界层问题始终是流体力学研究的核心问题之一。一百多年来,针对边界层开展的研究极大地丰富了我们的物理认知,显著地推动了航空工业的发展。在实际应用中,飞行器表面通常是弯曲的,弯曲壁面的边界层与平面边界层有明显差异,对航空飞行器部件性能有很大影响。近年来国际上高超声速飞行器成为关注的焦点,其气动布局以及吸气式推进系统设计中采用了包括流向形式在内的各种曲率,如图 1所示。流向曲率影响下超声速边界层流动行为成为高超声速飞行器设计关注的重要内容之一。

|
图 1 典型高超声速飞行器方案:飞行器表面存在包括流向形式在内的各种曲率(图片来自互联网) Fig.1 Two Typical hypersonic plans, showing streamwise curvature existence for both external and internal flows (Pictures are from the internet) |
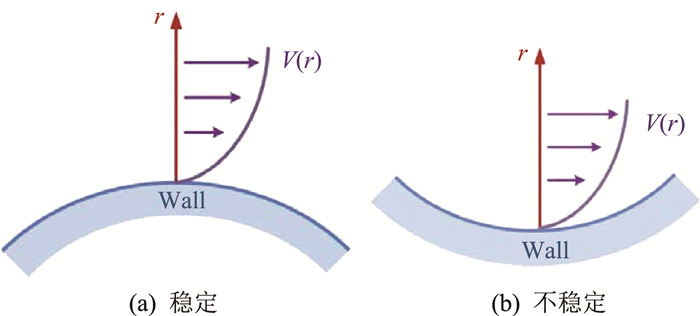
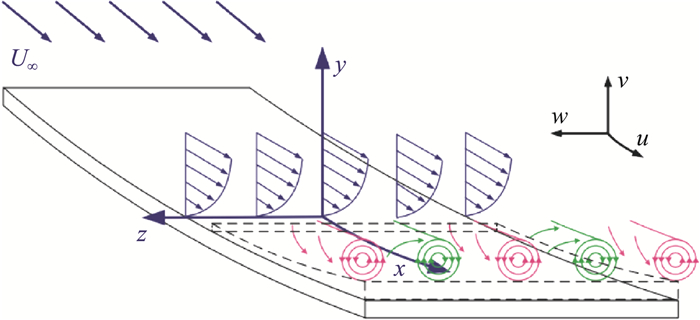
弯曲边界层流动的稳定性不同于平板边界层。基于无黏分析,Reyleigh最早给出了不同型面弯曲形式下速度剖面与流动稳定性之间的关系[1],指出弯曲流动产生离心不稳定的主要原因是d(Γ2)/dr < 0,其中Γ=rU为旋度,U=U(r)为流向速度,r是到圆心的距离。考虑到边界层内的速度分布,凸曲壁对边界层具有稳定效果,而凹曲壁则会促进边界层失稳,如图 2所示。Görtler[2]通过线性稳定性分析,指出凹曲壁会在边界层中产生沿流向对转的Görtler涡[3-9],如图 3所示。Görtler涡的形成与二次失稳破碎主导凹边界层的失稳和转捩过程[10-11]。在流向曲率的影响下,边界层内流体摩阻系数、速度型、湍流度、形状因子、对流换热系数以及雷诺应力均会受到影响,凹曲壁和凸曲壁对时均参数具有相反的作用效果[12-17]。
|
图 2 边界层的速度型对应于不同曲壁下的稳定性分析 Fig.2 Stability of boundary layer under the impact of different curvatures |
|
图 3 凹曲壁边界层中的Görtler涡示意图[10] Fig.3 A schematic of Görtler vortices generated in the concave boundary layer[10] |
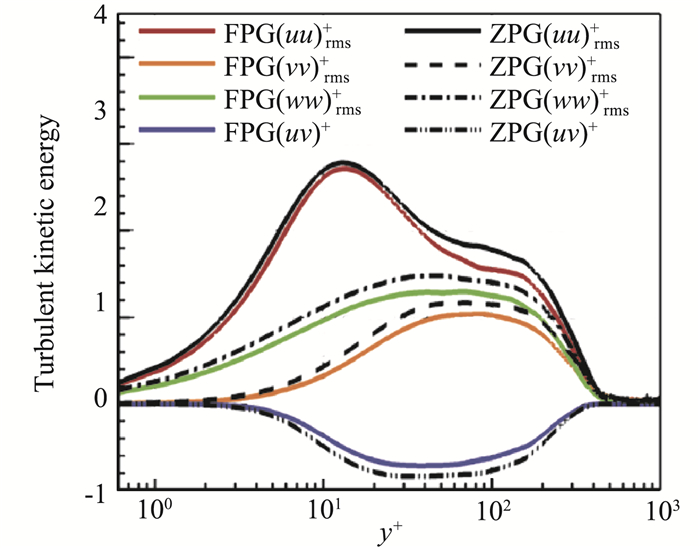
亚声速条件下的研究显示,凹曲壁能够增强湍流边界层的湍流度和壁面摩阻,而凸曲壁则具有抑制湍流脉动并减小壁面摩阻的效果。相较于亚声速流动边界层,超声速条件下曲壁边界层的影响因素更为复杂,边界层除受主应变率∂U/∂y的影响外,还受到流线弯曲∂V/∂x、法向压力梯度∂p/∂y、流向压力梯度∂p/∂x和体积膨胀▽·U等“额外应变率”的综合影响,这些因素在超声速条件下都会有所不同[18]。由于影响因素较多,为深入分析超声速曲壁边界层,需要分别探究压力梯度、曲率本身和可压缩性对边界层的影响规律,这也使得现有在低速条件下得到的研究结论难以直接用于超声速流动。此外,超声速条件下流动各向异性特点相较于亚声速流动更加显著,使得研究单一因素对超声速湍流的影响效果变得更为困难[19-20]。激波的存在更会使湍流流动与激波本身产生相互作用,从而导致激波非定常运动甚至激波面扭曲,穿过激波的湍流由于熵变也会发生相应的变化,特别是不同尺度湍流结构对于激波的响应也存在差异。当激波强度足够高时,流动还会发生分离,进一步增加了流动的非线性特性。在超声速条件下,受扰动超声速湍流中不同尺度湍流结构在压力梯度、额外应变率作用下的演化规律依然不十分清晰,而这些尺度的演化规律与流动的宏观力学、热力学特性紧密相关,直接影响着湍流建模的准确性。
Floryan[21]和Saric[1]曾就弯曲边界层的稳定性和转捩问题进行过综述,但关于充分发展的湍流边界层受流向弯曲影响的问题未有提及。早期Spina等[22]在关于超声速湍流边界层结构的综述中,简要叙述了压力梯度、流向曲率等额外应变率的对边界层时均和统计特性的影响。本文在这些经典综述文章的基础上,针对超声速湍流边界层对弯曲壁的响应特性进行梳理,总结凸曲壁和凹曲壁两种流向曲率形式下的超声速湍流边界层的时均和统计特性,并重点对近年来弯曲壁超声速湍流边界层的结构演化特征和湍流受扰机制方面进行综述,提炼发展趋势,为后续研究及其应用提供参考。
1 凸曲壁超声速湍流边界层超声速条件下,边界层受流向凸曲壁的影响,其湍流统计和结构特性均会发生变化。本节首先将对凸曲壁超声速边界层的典型特征进行综述,然后将对诱导凸曲壁边界层湍流衰减的成因——体积膨胀和流向顺压梯度等因素的影响——进行总结。
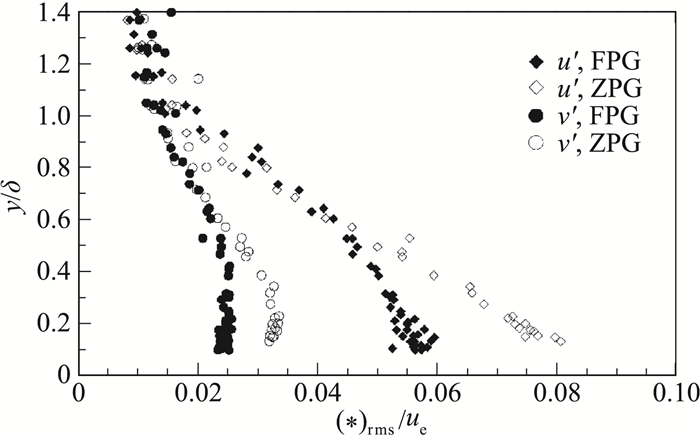
1.1 凸曲壁的影响机制与平板边界层相比,凸曲壁具有衰减超声速湍流的效果[13, 23-24]。在凸曲率对超声速湍流边界层各类湍流参数影响的研究中,Bowersox和Buter[25]通过马赫数2.9条件下的实验发现,凸曲壁对雷诺剪应力的大小和分布均有较大的影响。整个边界层内,剪切应力存在幅度达50%~100%的降低,类似的实验[26]也报告了边界层剪应力的大幅下降。Arnette等[27]使用流动可视化和激光多普勒测速(LDV)相结合的方法,在马赫数3的条件下对比测试了4个构型的流场特性。Luker等[28]使用LDV对马赫数2.9的凸曲壁边界层的平均和湍流特性进行了详细的实验测量,并留意到了湍流逆转捩现象。Ekoto等[29]通过平面粒子图像测速技术(PIV)研究了马赫数为2.9时的两个不同曲率的曲面,同时考虑了表面粗糙度的影响。这些研究表明,受凸曲壁影响的超声速湍流边界层的轴向湍流强度可以降低到70%~90%,且减弱程度取决于流向曲率的大小。Luker等[28]观察到近壁区域中雷诺切应力与平板边界层相比减小了约25%(如图 4所示),然而整个边界层内雷诺切应力对壁面弯曲响应却是不同的。在外部区域(如y/δ>0.5,其中δ是边界层厚度),雷诺剪应力通常为负,而主应变率则保持为正。Arnette[27]和Tichenor等[30]观察到了类似的趋势。Luker等[28]的应变率和相关的额外量测量表明在边界层的外侧(y/δ>0.5)的总湍流产生是负的,这意味着部分能量从波动的流场反馈回了平均流。
|
图 4 凸曲率和零压力梯度下湍流特性对比曲线[28] Fig.4 Comparison of turbulence fluctuations between the convex and zero-pressure-gradient boundary layers[28] |
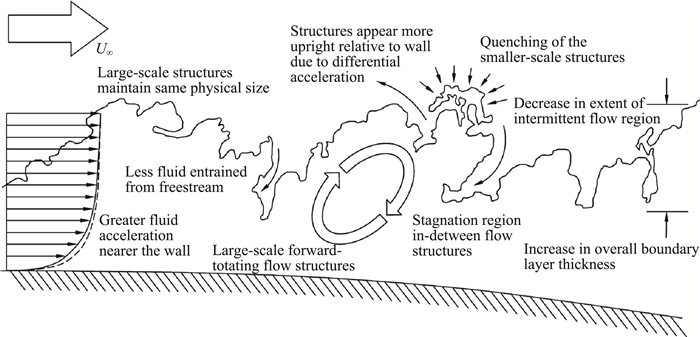
在超声速凸曲壁边界层结构特征的研究方面,Humble等[31]通过实验研究了马赫数为4.9的湍流边界层对凸曲率壁面的响应规律,发现边界层外无旋流动进入边界层的频率明显降低,湍流/非湍流界面的不规则性随曲率的增大而减小,如图 5所示。Luker[28]等观察了凸曲率影响下湍流间歇性的增加,同时间歇流开始朝向边界层的边缘移动,引起负湍流生成。Wang等[32]则通过激光平面纳米粒子散射技术发现超声速湍流边界层在进入凸曲壁段后,湍流结构的尺度明显放大(如图 6所示),同时湍流结构与壁面之间的倾角沿流向增加。Gillis等[33]和Goldfeld等[34]则指出,超声速湍流在受凸曲壁影响的膨胀和恢复过程中,边界层外层的大尺度结构对顺压梯度的响应较为缓慢,而靠近壁面处的流动结构尺寸在顺压梯度的作用下明显减小,上游大尺度结构的保留被认为是湍流生成主要局限于具有较大平均梯度的近壁区的结果。
|
图 5 流向凸曲率对超声速湍流边界层的影响[31] Fig.5 Impact of the convex wall on the supersonic turbulent boundary layer[31] |

|
图 6 流向凸曲率影响的超声速湍流边界层观测[32] Fig.6 Visualization of the supersonic convex turbulent boundary layer[32] |
关于引起凸曲壁超声速边界层湍流统计特性和结构特征变化的原因一直是研究人员最为关注的问题之一。由于超声速条件下,弯曲边界层问题的影响因素复杂,除显而易见的流向曲率本身的影响之外,压力梯度、体积膨胀效应等均是影响边界层特性的重要因素[23],近年来的研究也揭示了体积膨胀和流向顺压梯度对于超声速凸曲壁边界层湍流衰减的贡献[19, 35]。
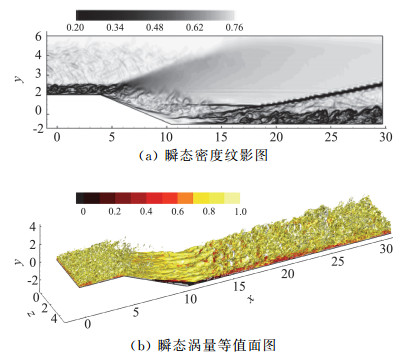
1.2 体积膨胀和顺压梯度的影响在以往的许多研究中,研究人员发现凸曲壁与膨胀拐角表面形成的边界层存在诸多相似之处,如对衰减湍流、扩展速度剖面中的对数区、较于零压梯度边界层对数律上移、尾迹区强度降低等[22, 26, 36-37]。体积膨胀和流向顺压梯度在诱导边界层湍流特性发生以上变化的过程中发挥了重要作用。这两种效应在对于边界层外层湍流具有相似的衰减效果。但在近壁区,二者对边界层的影响则存在较为显著的区别:其中体积膨胀主要在膨胀斜坡的拐角处对近壁湍流存在显著的衰减作用,而在随后的发展中,近壁湍流特征则逐渐恢复[35];而与体积膨胀的影响不同,流向顺压梯度对湍流的衰减作用则主要表现在外层,其在整个压力梯度影响区域内对近壁湍流的衰减则较为微弱[19]。
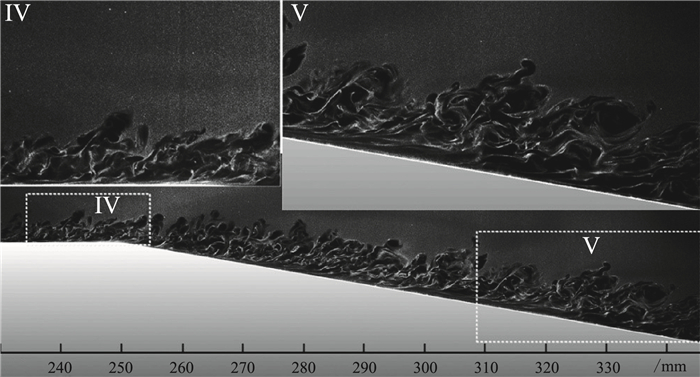
Knight等[38]指出,湍流衰减是超声速气流通过膨胀拐角的一个重要特征。Arnette等[39]发现,在膨胀过程中,湍流水平显著降低,在靠近壁面处会更加显著。在强膨胀作用下,甚至会出现逆转捩现象,表现为湍动能水平的急剧下降和负雷诺应力值的出现。Wang等[32]利用基于纳米粒子的平面激光散射方法,在膨胀拐角后的湍流边界层近壁区域同样观察到这种再层流化的现象,如图 7所示。Bradshaw[18]指出,体积膨胀是影响湍流剪切层的主要因素,尤其是在降低雷诺应力方面。Humble等[31]证实,在膨胀过程中,小尺度结构因体积膨胀而湮灭。Wang等[32]也通过实验指出,体积膨胀对边界层湍流衰减的贡献要强于离心力效应。Dussauge和Gaviglio[40]用解析和实验方法研究了体积膨胀对超声速湍流边界层湍流脉动的影响。他们得出结论,体积膨胀是导致雷诺应力变化的主要原因。Teramoto等[35]通过大涡模拟发现了湍流边界层的再层流化(如图 8所示,x=0到5之间涡结构明显减小),同样指出由体积膨胀所引入的负湍流生成项导致了该现象的发生。
|
图 7 膨胀拐角表面的超声速湍流边界层结构[32] Fig.7 Visualizations of the instantaneous supersonic turbulent boundary layer after expansions |
近期,Fang等[41]利用直接数值模拟研究了超声速湍流边界层在串联膨胀-压缩拐角中的响应规律。超声速湍流边界层经过膨胀拐角后出现了明显的双层化特点,外层湍流结构被明显抑制(如图 9所示)。Tong等[42]利用直接数值模拟研究了马赫数2.9条件下膨胀拐角对激波边界层干扰问题的影响。研究发现,膨胀拐角能够明显减小激波所致流动分离区的大小及由流动分离带来的三维效应,同时有利于湍流恢复。该研究同样观察到膨胀拐角下游的流场中,边界层外层湍流水平被明显抑制,而内层湍流仍持续生成的现象。Sun等[43]通过DNS(直接数值模拟)研究了湍流边界层通过膨胀拐角后的恢复机制,研究表明:与平板边界层相比,膨胀拐角增加了近壁面区条带结构间距,在边界层内部湍动能分布和生成呈现出典型的双层结构,近壁区域内湍流在内层比在外层拥有更快的恢复速度。
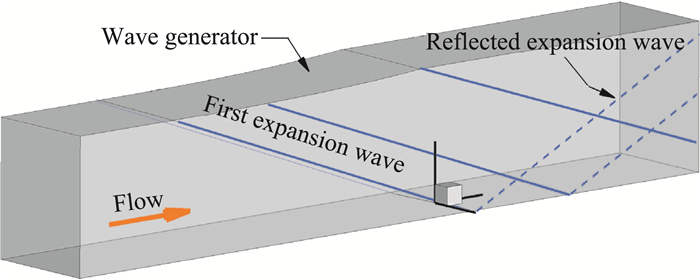
在受顺压梯度效应的影响的超声速湍流边界层中也存在分层现象。揭示流向顺压梯度影响的前提是解耦流向曲率的影响,并避免早期研究中采用弯曲壁面引入压力梯度的方法,因此需要将曲率效应与压力梯度及体积膨胀效应解耦开来。Wang等[15, 20]采用的通过外源反射膨胀波调节壁面附近压力分布的等效压力梯度方法为此提供了一个可靠的解决方案(如图 10)。在此基础上Wang等[19]通过对顺压梯度作用下的平板超声速湍流边界层进行直接数值模拟研究发现,与膨胀拐角流动中内层湍流受到快速抑制不同,当湍流边界层只受到顺压梯度影响时,内层湍流衰减的速度要明显慢于外层,如图 11所示,同为分层,但体积膨胀和流向顺压梯度所诱导形成的分层方式截然不同。
|
图 10 等效压力梯度方法产生顺压梯度示意图[19] Fig.10 A schematic of the method used to generate streamwise favorable pressure gradient for a supersonic flat-plate boundary layer[19] |
|
图 11 顺压梯度边界层对外层湍流的衰减作用[19] Fig.11 The supression of turbulence in the outer layer of a supersonic turbulent boundary layer subjected to favorable pressure gradient[19] |
最近,Wu等[44]在比较充分发展湍流边界层与转捩边界层的时空湍流结构时,发现在零压梯度充分发展湍流边界层中可能存在湍流型湍流涡斑(turbulent-turbulent spots, TUTs)。Wang等[19]在零压力梯度的平板边界层中同样观察到类似的TUTs结构,并且TUTs结构在顺压梯度作用下,会受到明显抑制,如图 12所示。从结构特征上来看,TUTs结构的减弱也是超声速凸曲壁边界层湍流特性减弱的直观体现。
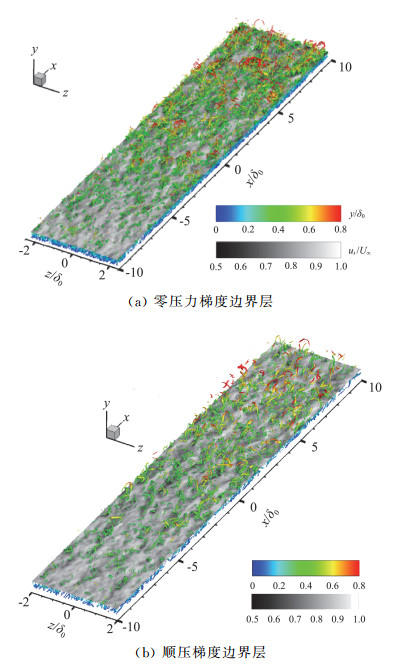
|
图 12 顺压梯度下湍流边界层中的TUTs示意图[19] Fig.12 TUTs in a supersonic flat-plate turbulent boundary layer with streamwise zero and favorable pressure gradients[19] |
流向凸曲壁能够诱导边界层厚度增加、湍流度降低、摩阻系数减小、对流换热系数减小等。体积膨胀和流向顺压梯度是诱导超声速湍流边界层的时均和统计特性变化的重要因素。在这两个因素的影响下,湍流边界层的分层响应机制依然是目前研究人员关心的问题,也是进一步深入研究超声速凸曲壁边界层中湍流结构和流动特性的变化规律的突破点之一。
2 凹曲壁超声速湍流边界层和流向凸曲壁边界层类似,超声速条件下的流向凹曲壁边界层中也存在流向逆压梯度、流向曲率等多重因素影响的问题。近年来的研究逐步揭示了超声速湍流边界层对流向弯曲的响应机制,流向压力梯度对湍流结构和统计特性改变的贡献也逐渐清晰。本节将首先对流向逆压梯度的影响及其作用机制进行梳理,然后就超声速湍流边界层对凹曲壁的响应进行总结。
2.1 逆压梯度对超声速湍流边界层的影响在早期的研究中,流向压力梯度主要由凹曲率壁面及压缩拐角等具有收缩特性的几何构型产生,湍流特性的变化受到流线弯曲的耦合作用。Smith和Smits[45]以及Fernando[46]等首先尝试分离相互间的干扰,来对比研究流向逆压力梯度和流向弯曲的影响,结果显示压力梯度和纯流向曲率对边界层时均和湍流特性的影响均非常显著,但凹曲率导致的湍流脉动则比单纯的流向逆压梯度增强近50%,如图 13所示。
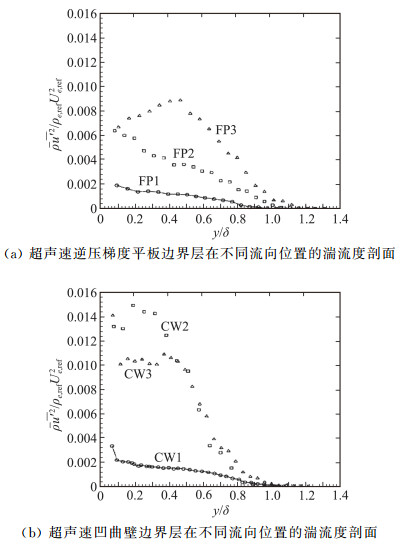
|
图 13 逆压梯度和凹曲壁条件下超声速边界层的在不同流向位置湍流度分布对比[45] Fig.13 A comparison of the turbulence intensity between the adverse-pressure-gradient and concave boundary layers[45] |
压力梯度通常用Clauser压力梯度参数β=(dp/dx)(τw/δ*)(其中δ*是位移厚度;τw是壁面剪应力;dp/dx是流向压力梯度)表征[47]。正值β表示逆压梯度,负值表示顺压提速。当β=0时,表示零压梯度。由于角动量守恒,体积压缩-▽·U和横向扩散都可以减小流体单元的展向截面面积,从而增加展向涡量。前者由“额外应变率”引起,会减小边界层的厚度;后者即使在很小的水平上也可能对边界层流动产生较大的影响[18, 48-49]。与零压梯度湍流边界层相比,逆压梯度作用下的不可压缩壁面流动沿流动方向具有呈降低趋势的表面摩擦系数[47, 50-53],而超声速条件下,表面摩擦系数则会沿流动方向不断增大[54-55]。除了表面摩擦系数会在逆压梯度作用下发生显著的改变,平均速度沿边界层厚度方向的分布相较于零压梯度边界层通常也会发生显著的改变。然而由于现有数据多来源于实验研究,受限于速度测量的精度,不同实验得到的速度剖面数据往往具有一定出入。根据文献[51, 56-57]的报道,逆压梯度可能导致不可压缩流动速度剖面的对数律区低于经典的对数律分布,而文献[58]则得出即使存在逆压梯度,经典对数律依然存在的结论。对于超声速边界层,文献[59]观测到van-Driest变换速度剖面在逆压梯度的作用下会发生相对于零压梯度对数律区的上移。文献[46]则表示对数律区基本维持不变。
Wang等[15, 20]通过采用等效压力梯度方法来分离流向压力梯度和流向曲率的影响,并开展的实验(如图 14所示)[20]和直接数值模拟研究[60],得出了相似的结论。除了对数律区的可能偏移外,文献[46, 61]还发现受逆压梯度的影响,对数律区的斜率也会发生变化,这可能是由于边界层内湍流运动的长度尺度增加导致的。在逆压梯度的影响下,速度剖面的尾迹区相较于零压梯度边界层明显上移。逆压梯度能显著地促进不稳定性的增长并加速流动转捩,当逆压梯度效应足够强时,边界层还可能发生流动分离[36, 62-63]。与零压梯度边界层流动相比,逆压梯度作用下的高阶统计特征和流动结构会发生明显变化。湍动能和雷诺应力通常会被显著放大,特别是在外层,当用壁面单位无量纲化湍流脉动时,边界层外层区域可以观察到第二峰值[50-51, 64]。
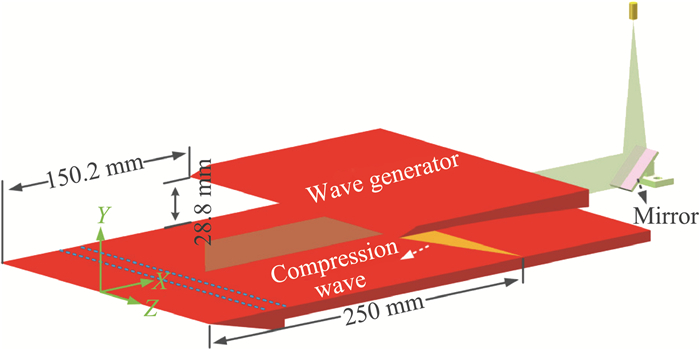
|
图 14 等效逆压梯度超声速湍流边界层实验设计示意图[20] Fig.14 A schematic of experimental setup to generate streamwise adverse pressure gradient for a supersonic flat- plate boundary layer[20] |
湍流结构特征在逆压梯度的作用下也与零压梯度边界层不同。具体表现为大尺度结构(large-scale motions)在边界层内更为活跃,涡结构能量增益显著[52, 53, 65-68]。由大尺度涡结构产生的上喷、下扫和展向事件被认为是导致平均流动特性和湍流统计量改变的主要诱因。Bobke等[69]研究了在恒定和可变逆压梯度下,不同摩擦雷诺数湍流边界层的历史效应。结果表明,平均速度和雷诺应力分布依赖于边界层流动的下游发展。由于存在历史效应,逆压梯度对湍流边界层有累积效应。此外,针对凹曲壁超声速湍流边界层和逆压梯度作用下的平板超声速湍流边界层的数值模拟[14, 60, 70]均发现了类似于湍流型湍流涡斑的流场结构(如图 15所示),这种结构在逆压梯度的作用下呈现出增强的趋势,其与边界层外层大尺度结构的增强之间的关联仍有待进一步研究。
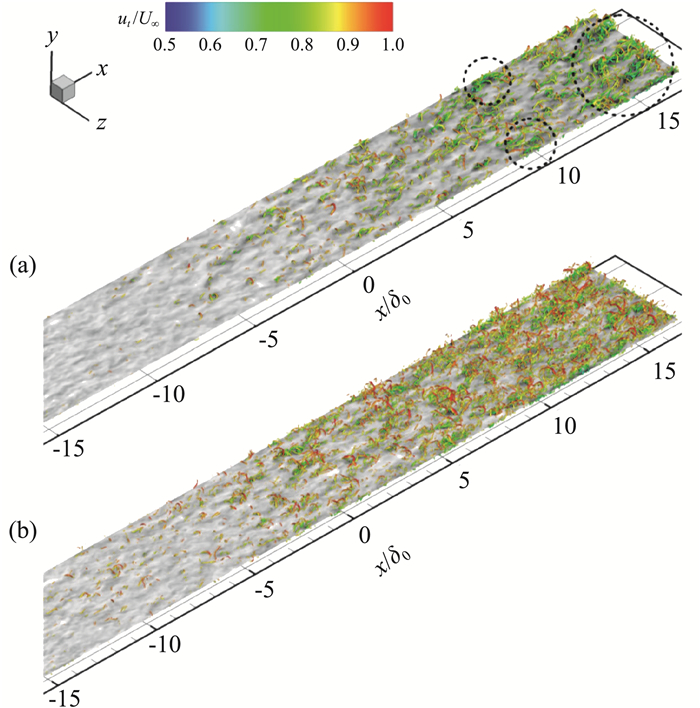
|
图 15 (a) 逆压梯度作用下湍流边界层中的类湍流型湍流涡斑(TUTs)结构; (b)零压梯度作用下湍流边界层中的类湍流型湍流涡斑结构[60] Fig.15 (a) TUTs in a supersonic adverse-pressure-gradient boundary layer; (b) TUTs in a supersonic zero-pressure- gradient boundary layer[60] |
流向逆压梯度对边界层时均和湍流特性的显著影响源于其对边界层中法向输运的增强。在凹曲壁超声速边界层流动中,边界层除受到压力梯度的影响外,由流向弯曲带来的离心不稳定的作用会进一步加强边界层的法向输运,并改变边界层特性。
2.2 凹曲壁超声速湍流边界层近些年来,随着实验测试和数值仿真手段的改善,关于凹曲壁超声速湍流边界层的认识在湍流统计特性和湍流结构的演化机制方面均逐步深入。
实验研究方面,Jayaram等[61]在自由来流马赫数为2.87的条件下测试了流向凹曲壁和压缩拐角上形成的边界层,他们发现这两种构型均能够显著增强边界层的湍流特性,致使其流向速度型在对数律层存在一个凹陷,低于正常的平板边界层的对数律层,他们将其归因为凹曲壁边界层中湍流运动的长度和时间尺度的增加所诱导的速度分布的变化。此外,Hoffmann等[71]也在实验中发现了类似的现象。Donovan等[55]在马赫数2.86条件下发现,与平板边界层相比,凹曲壁边界层壁面切应力增长了约125%。不同的是,他们在实验的弯曲段并没有发现边界层速度剖面中存在的凹陷现象,但却在弯曲段下游的恢复段中发现了速度剖面中的凹陷。Wang等[16]在实验中发现超声速平板边界层进入弯曲段后,原本的较大尺度结构迅速转变为大量小尺度结构,如图 16所示。

|
图 16 实验观测到的超声速凹曲壁边界层中的瞬时流场结构[16] Fig.16 Instantaneous turbulent structures visualized in experiment[16] |
近期,Flaherty和Austin[72]对最高马赫数达到7.45的高超声速曲壁边界层开展了研究。纹影结果显示,相较于平板边界层,凹曲壁段的边界层厚度可以看到明显变薄的现象,如图 17所示。此外,他们还对不同曲率弯曲壁面的近壁热流进行了详细测量,结果表面,相较于平板边界层,凹曲壁能够显著提高壁面的换热系数。并且他们发现,对于不同曲率的边界层,当以流向偏转角为横坐标时,不同曲壁边界层的壁面热流数据分布具有自相似性,如图 18所示,这对于工程设计具有重要意义,意味着工程中可以基于壁面偏转角来对弯曲壁面的表面热流进行估算。

|
图 17 平板边界层和凹曲壁边界层的纹影图[72] Fig.17 Schlieren of flat-plate boundary layer and concave boundary layer[72] |
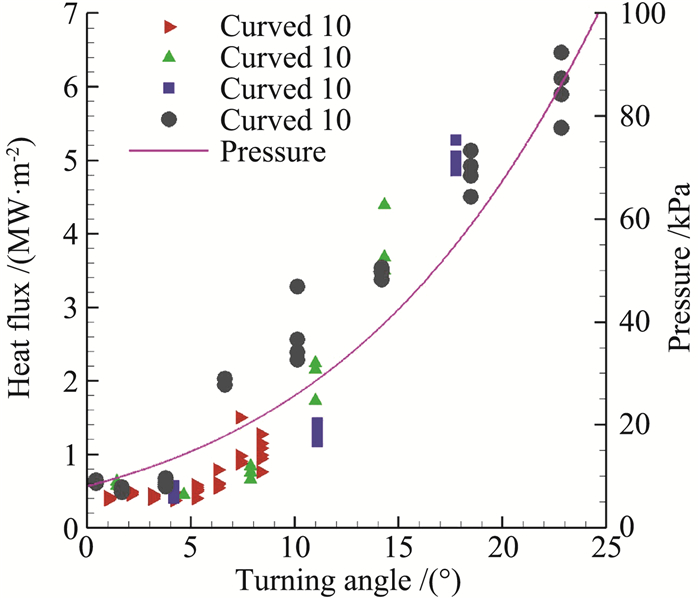
|
图 18 不同流向曲率边界层的近壁热流随壁面偏转角的变化[72] Fig.18 Variation of the near-wall heat flux with wall turning for boundary layers subjected to different curvatures[72] |
边界层时均和湍流特性的变化主要来源于流场结构的变化。对于凹曲壁超声速层流边界层,Görtler涡的形成及其二次失稳是边界层转捩的重要因素,符松课题组[6-7, 10]采用稳定性分析研究了超声速层流边界层在曲率影响下其中Görtler涡的非线性增长过程,如图 19所示,揭示了不同模态波的影响和作用机制。
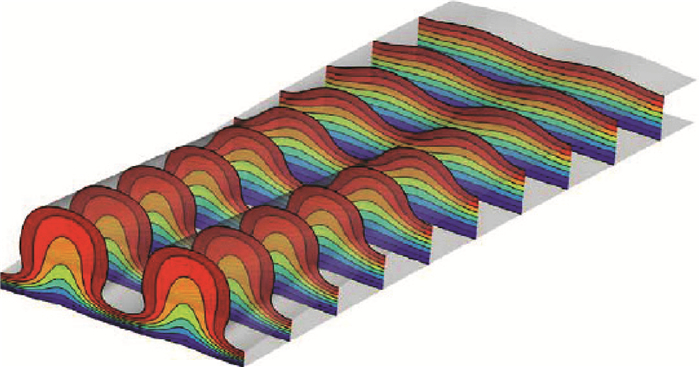
|
图 19 马赫数4.5边界层中Görtler涡及低速与高度条带的形成过程[10] Fig.19 Formation of Görtler vortices and the streaks within a Mach 4.5 boundary layer[10] |
对于湍流边界层,由于流场结构的复杂性,其中的Görtler不稳定难以直接辨识,但是边界层在进入弯曲段后,其中低速和高速流动沿展向的交错与周期性分布表明,即使在湍流边界层中, Görtler不稳定对流场结构的影响依然显著,如图 20所示。Hoffmann等[71]以及Barlow和Johnston[73-74]均通过实验中发现Görtler不稳定能够在边界层中引入大尺度的流向涡旋结构,很多研究中也称其为类Görtler涡,这些结构能够诱导边界层中形成明显强于一般平板边界层的内外层之间的法向对流与动量交换运动。但是不同于层流边界层中产生的Görtler涡,湍流边界层中这些流向涡旋结构并没有对应的涡核和集中涡量。
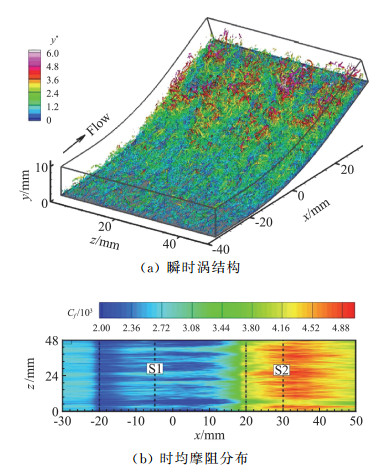
|
图 20 凹曲壁边界层中瞬时涡结构和时均摩阻分布云图[75] Fig.20 Instantaneous vortices and time-averaged wall friction for a supersonic concave boundary layer[75] |
Tong等[75]在马赫数2.9条件下的直接数值模拟研究也发现了平板边界层在进入到弯曲段之后,边界层中会形成明显大尺度的类Görtler涡结构,同时这种大尺度结构会诱导边界层的时均摩阻分布形成展向周期性分布(如图 20所示),这也表明类Görtler涡结构的展向位置是总体稳定的。但是,需要强调的是,从涡的任何定义来看,这些大尺度的类Görtler涡结构都难以称之为单一的涡。此外,Tong等[75]模拟结果还显示流向曲率对边界层对数率层的影响较小,这也表明,在关于流向曲率对边界层对数率层的影响方面依然存在争论。此外,他们的数值模拟结果同样显示了边界层中湍流脉动的显著增强,其中在边界层外层的增长尤为明显。
近年来,Wang等[14, 16-17]和Sun等[70]通过系统的实验和直接数值模拟研究,揭示了Görtler不稳定诱导边界层中形成大尺度运动的机制。
Wang等[14]指出,边界层中大尺度结构的变化是导致其湍流统计特性变化的直接原因。湍流边界层超级结构(VLSM)中存在丰富的发卡涡结构,这些结构在Görtler不稳定的作用下其强度会明显增强,并同时诱导形成更多的流向结构。这些结构的综合作用显著增强了边界层中的动量交换,放大平板边界层中VLSM结构并导致了展向不均匀,形成了Barlow和Johnston[73-74]在凹曲壁边界层中观测到的大尺度的类Görtler涡结构。凹曲壁边界层中大尺度法向运动的形成,进一步促使边界层中上喷(Q2)和下洗(Q4)事件明显增强,由于Q2和Q4事件是边界层中湍流生成的最主要贡献者,边界层的湍流脉动也随之增强,并在边界层外层形成了湍流脉动的第二峰值[14],如图 21所示。
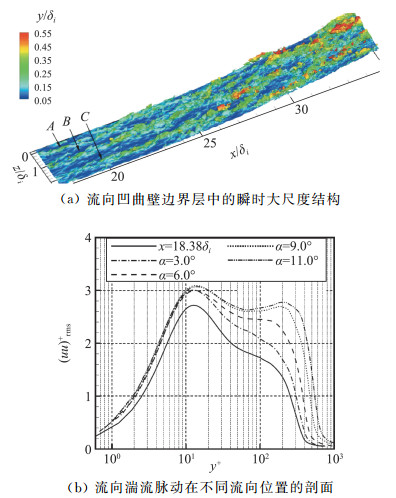
|
图 21 流向凹曲壁边界层中的瞬时大尺度结构及其诱导形成的外层湍流脉动第二峰值[14] Fig.21 Instantaneous structures of a supersonic concave boundary layer and the secondary bump induced by the large scale motions[14] |
Sun等[70]指出,凹曲壁上超声速湍流边界层内部存在的大尺度类Görtler结构会扭曲当地密度梯度,与密度和压力梯度有关的斜压涡量生成项相比逆压力梯度边界层会显著增强,该项对小尺度涡的形成具有显著的贡献,这一机制同样诱导了流向逆压梯度边界层中大量小尺度湍流结构的形成,如图 22所示。关于Görtler不稳定在超声速凹曲壁边界层中增强并诱导形成更多流向结构的发现也进一步解释了Wang等[16]在实验中发现的超声速平板边界层进入弯曲段后出现大量小尺度结构(如图 22所示)的原因。
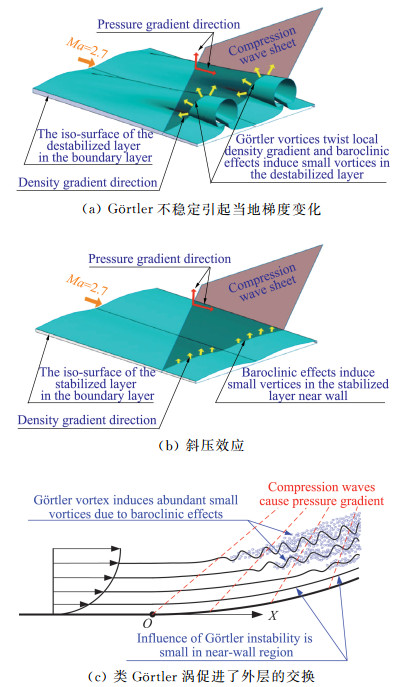
|
图 22 超声速凹曲壁边界层中的Görtler不稳定及由斜压涡量生成项诱导形成类Görtler涡结构的原理简图[70] Fig.22 Schematic of Görtler instabilities and the small vortices formed by the large baroclinic production[70] |
总的来看,流向凹曲壁作用于超声速湍流边界层会增大摩阻系数、减小形状因子、增强对流换热系数等[45, 54-55, 71-72, 76-78]。由于凹曲壁诱导的湍流结构特性的改变,尤其是大尺度类Görtler结构的形成是导致时均和湍流统计特性改变和关键,这方面的研究目前正获得越来越多的关注。
3 结束语多年来国内外研究人员关于超声速边界层中流向曲率和压力梯度影响方面的研究取得了丰硕的成果。在早期发现的流向凸曲壁对湍流衰减作用和流向凹曲壁对湍流增强作用的基础上,近年来的研究在流向弯曲壁影响超声速湍流边界层的物理机制方面取得了显著进展:揭示了体积膨胀效应在超声速湍流衰减中的重要作用,其在凸曲壁边界层中的影响强于离心效应和流向顺压梯度;发现了在凹曲壁边界层中导致湍流特性增强的多重影响因素,包括Görtler不稳定对流向结构的放大效应、斜压涡量生成以及流向逆压梯度作用等,揭示了超声速湍流边界层对流向凹曲壁的响应机制。这些研究成果对于湍流模化和发展基于型面优化的流动控制技术具有指导意义。
但是总体来看,目前不论是从理论认识还是从指际工程实践方面来看,依然存在诸多问题需要进一步深入研究:
1) 近壁湍流对流向曲率和压力梯度响应规律。目前的研究多关注于外层湍流结构演化特性,但考虑到湍流边界层的维持依赖于近壁湍流的自持循环,揭示近壁湍流在流向曲率和压力梯度影响下的响应规律,对于深刻认识流向弯曲壁超声速湍流边界层并对其演化进行预测具有重要意义。
2) 高马赫数、高雷诺数、不同壁面温度条件下流向弯曲壁对超声速湍流边界层的影响。目前研究结论主要源于马赫数3以下的实验和仿真,不论是从理论研究还是从指导工程实践角度来看,关于边界层湍流特性、壁面热流、壁面摩阻等随马赫数、雷诺数、壁面温度等参数变化规律的研究都亟待开展。
3) 超声速三维流场中流向弯曲壁的影响机制。在工程问题中,流向弯曲的影响往往同激波/边界层干扰、展向弯曲等共同存在,三维性强,相互作用机制复杂。进一步需要针对激波与弯曲边界层相互作用、多弯曲扰动条件下的超声速湍流边界层发展特性等问题开展研究,这对于高超声速飞行器内外流道的设计具有重要意义。
致谢: 感谢清华大学符松教授、中科院力学所李新亮研究员以及国防科技大学赵玉新教授在撰写本文过程中的探讨以及提供的资料。
| [1] |
SARIC W S. Görtler vortices[J]. Annual Review of Fluid Mechanics, 1994, 26(1): 379-409. |
| [2] |
GÖRTLER H. On the three dimensional instability of laminar boundary layers on concave walls[R]. 1954, NACA TM 1375.
|
| [3] |
WORTMANN F X. Visualization of transition[J]. Journal of Fluid Mechanics, 1969, 38(3): 473-480. |
| [4] |
BIPPES H, GöRTLER H. Three-dimensional disturbances in the boundary layer along a concave wall[J]. Acta Mechanica, 1972, 14: 251-267. DOI:10.1007/BF01387373 |
| [5] |
TANI I, AIHARA Y. Görtler vortices and boundary-layer transition[J]. Zeitschrift Für Angewandte Mathematik Und Physik ZAMP, 1969, 20(5): 609-618. |
| [6] |
REN J, FU S. Study of the discrete spectrum in a Mach 4.5 görtler flow[J]. Flow, Turbulence and Combustion, 2015, 94(2): 339-357. DOI:10.1007/s10494-014-9575-z |
| [7] |
REN J, FU S. Competition of the multiple Görtler modes in hypersonic boundary layer flows[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(6): 1178-1193. |
| [8] |
WANG J S, FENG L H, WANG J J, et al. Görtler vortices in low-Reynolds-number flow over multi-element airfoil[J]. Journal of Fluid Mechanics, 2018, 835: 898-935. DOI:10.1017/jfm.2017.781 |
| [9] |
CHEN X, HUANG G L, LEE C B. Hypersonic boundary layer transition on a concave wall:stationary Görtler vortices[J]. Journal of Fluid Mechanics, 2019, 865: 1-40. DOI:10.1017/jfm.2019.24 |
| [10] |
REN J, FU S. Secondary instabilities of Görtler vortices in high-speed boundary layer flows[J]. Journal of Fluid Mechanics, 2015, 781: 388-421. DOI:10.1017/jfm.2015.490 |
| [11] |
XU D D, ZHANG Y M, WU X S. Nonlinear evolution and secondary instability of steady and unsteady Görtler vortices induced by free-stream vortical disturbances[J]. Journal of Fluid Mechanics, 2017, 829: 681-730. DOI:10.1017/jfm.2017.572 |
| [12] |
BRADSHAW P. The analogy between streamline curvature and buoyancy in turbulent shear flow[J]. Journal of Fluid Mechanics, 1969, 36(1): 177-191. |
| [13] |
MUCK K C, HOFFMANN P H, BRADSHAW P. The effect of convex surface curvature on turbulent boundary layers[J]. Journal of Fluid Mechanics, 1985, 161: 347. DOI:10.1017/S002211208500297X |
| [14] |
WANG Q C, WANG Z G, SUN M B, et al. The amplification of large-scale motion in a supersonic concave turbulent boundary layer and its impact on the mean and statistical properties[J]. Journal of Fluid Mechanics, 2019, 863: 454-493. DOI:10.1017/jfm.2018.1004 |
| [15] |
WANG Q C, WANG Z G, ZHAO Y X. The impact of streamwise convex curvature on the supersonic turbulent boundary layer[J]. Physics of Fluids, 2017, 29(11): 116106. DOI:10.1063/1.4994928 |
| [16] |
WANG Q C, WANG Z G. Structural characteristics of the supersonic turbulent boundary layer subjected to concave curvature[J]. Applied Physics Letters, 2016, 108(11): 114102. DOI:10.1063/1.4944536 |
| [17] |
WANG Q C, WANG Z G, ZHAO Y X. An experimental investigation of the supersonic turbulent boundary layer subjected to concave curvature[J]. Physics of Fluids, 2016, 28(9): 096104. DOI:10.1063/1.4962563 |
| [18] |
BRADSHAW P. The effect of mean compression or dilatation on the turbulence structure of supersonic boundary layers[J]. Journal of Fluid Mechanics, 1974, 63(3): 449-464. |
| [19] |
WANG X, WANG Z G, SUN M B, et al. Effects of favorable pressure gradient on turbulence structures and statistics of a flat-plate supersonic turbulent boundary layer[J]. Physics of Fluids, 2020, 32(2): 025107. DOI:10.1063/1.5143433 |
| [20] |
WANG Q C, WANG Z G, ZHAO Y X. On the impact of adverse pressure gradient on the supersonic turbulent boundary layer[J]. Physics of Fluids, 2016, 28(11): 116101. DOI:10.1063/1.4968527 |
| [21] |
FLORYAN J M. On the görtler instability of boundary layers[J]. Progress in Aerospace Sciences, 1991, 28(3): 235-271. |
| [22] |
SPINA E F, SMITS A J, ROBINSON S K. The physics of supersonic turbulent boundary layers[J]. Annual Review of Fluid Mechanics, 1994, 26(1): 287-319. |
| [23] |
GIBSON M M, VERRIOPOULOS C A, NAGANO Y. Measurements in the heated turbulent boundary layer on a mildly curved convex surface[M]//Turbulent Shear Flows 3. Berlin, Heidelberg:Springer Berlin Heidelberg, 1982:80-89.
|
| [24] |
GIBSON M M, VERRIOPOULOS C A, VLACHOS N S. Turbulent boundary layer on a mildly curved convex surface[J]. Experiments in Fluids, 1984, 2(1): 17-24. DOI:10.1007/BF00266314 |
| [25] |
BOWERSOX R D W, BUTER T A. Turbulence measurements in a Mach 2.9 boundary layer including mild pressure gradients[J]. AIAA Journal, 1996, 34(12): 2479-2483. DOI:10.2514/3.13427 |
| [26] |
LUKER J J, HALE C S, BOWERSOX R D W. Experimental analysis of the turbulent shear stresses for distorted supersonic boundary layers[J]. Journal of Propulsion and Power, 1998, 14(1): 110-118. DOI:10.2514/2.5256 |
| [27] |
ARNETTE S A, SAMIMY M O, ELLIOTT G S. The effects of expansion on the turbulence structure of compressible boundary layers[J]. Journal of Fluid Mechanics, 1998, 367: 67-105. DOI:10.1017/S0022112098001475 |
| [28] |
LUKER J J, BOWERSOX R D W, BUTER T A. Influence of curvature-driven favorable pressure gradient on supersonic turbulent boundary layer[J]. AIAA Journal, 2000, 38: 1351-1359. DOI:10.2514/2.1134 |
| [29] |
EKOTO I W, BOWERSOX R D W, BEUTNER T, et al. Response of supersonic turbulent boundary layers to local and global mechanical distortions[J]. Journal of Fluid Mechanics, 2009, 630: 225-265. DOI:10.1017/S0022112009006752 |
| [30] |
TICHENOR N R, HUMBLE R A, BOWERSOX R D W. Response of a hypersonic turbulent boundary layer to favourable pressure gradients[J]. Journal of Fluid Mechanics, 2013, 722: 187-213. DOI:10.1017/jfm.2013.89 |
| [31] |
HUMBLE R A, PELTIER S J, BOWERSOX R D W. Visualization of the structural response of a hypersonic turbulent boundary layer to convex curvature[J]. Physics of Fluids, 2012, 24(10): 106103. DOI:10.1063/1.4761833 |
| [32] |
WANG Q C, WANG Z G, ZHAO Y X. Structural responses of the supersonic turbulent boundary layer to expansions[J]. Applied Physics Letters, 2016, 109(12): 124104. DOI:10.1063/1.4963382 |
| [33] |
GILLIS J C, JOHNSTON J P. Turbulent boundary-layer flow and structure on a convex wall and its redevelopment on a flat wall[J]. Journal of Fluid Mechanics, 1983, 135: 123-153. DOI:10.1017/S0022112083002992 |
| [34] |
GOLDFELD M A, NESTOULIA R V, SHIPLYUK A N. Relaminarization of a turbulent boundary layer with a mach number M∞=4[J]. Journal of Applied Mechanics and Technical Physics, 2002, 43: 76-82. DOI:10.1023/A:1013914212127 |
| [35] |
TERAMOTO S, SANADA H, OKAMOTO K. Dilatation effect in relaminarization of an accelerating supersonic turbulent boundary layer[J]. AIAA Journal, 2017, 55(4): 1469-1474. DOI:10.2514/1.J055368 |
| [36] |
SMITS A J, WOOD D H. The response of turbulent boundary layers to sudden perturbations[J]. Annual Review of Fluid Mechanics, 1985, 17(1): 321-358. |
| [37] |
LEWIS J E, GRAN R L, KUBOTA T. An experiment on the adiabatic compressible turbulent boundary layer in adverse and favourable pressure gradients[J]. Journal of Fluid Mechanics, 1972, 51(4): 657-672. |
| [38] |
KNIGHT D, YAN H, PANARAS A G, et al. Advances in CFD prediction of shock wave turbulent boundary layer interactions[J]. Progress in Aerospace Sciences, 2003, 39(2/3): 121-184. |
| [39] |
ARNETTE S A, SAMIMY M, ELLIOTT G S. Structure of supersonic turbulent boundary layer after expansion regions[J]. AIAA Journal, 1995, 33(3): 430-438. DOI:10.2514/3.60007 |
| [40] |
DUSSAUGE J P, GAVIGLIO J. The rapid expansion of a supersonic turbulent flow:role of bulk dilatation[J]. Journal of Fluid Mechanics, 1987, 174: 81-112. DOI:10.1017/S0022112087000053 |
| [41] |
FANG J, YAO Y F, ZHELTOVODOV A A, et al. Direct numerical simulation of supersonic turbulent flows around a tandem expansion-compression corner[J]. Physics of Fluids, 2015, 27(12): 125104. DOI:10.1063/1.4936576 |
| [42] |
TONG F L, LI X L, YUAN X X, et al. Incident shock wave and supersonic turbulent boundarylayer interactions near an expansion corner[J]. Computers & Fluids, 2020, 198: 104385. |
| [43] |
SUN M B, HU Z W, SANDHAM N D. Recovery of a supersonic turbulent boundary layer after an expansion corner[J]. Physics of Fluids, 2017, 29(7): 076103. DOI:10.1063/1.4995293 |
| [44] |
WU X H, MOIN P, WALLACE J M, et al. Transitional-turbulent spots and turbulent-turbulent spots in boundary layers[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(27): E5292-E5299. DOI:10.1073/pnas.1704671114 |
| [45] |
SMITH D R, SMITS A J. A study of the effects of curvature and compression on the behavior of a supersonic turbulent boundary layer[J]. Experiments in Fluids, 1995, 18(5): 363-369. DOI:10.1007/BF00211393 |
| [46] |
FERNANDO E M, SMITS A J. A supersonic turbulent boundary layer in an adverse pressure gradient[J]. Journal of Fluid Mechanics, 1990, 211: 285-307. DOI:10.1017/S0022112090001574 |
| [47] |
CLAUSER F H. Turbulent boundary layers in adverse pressure gradients[J]. Journal of the Aeronautical Sciences, 1954, 21(2): 91-108. DOI:10.2514/8.2938 |
| [48] |
KIM J H, SAMIMY M, LEE S. Effects of compression and expansion on turbulence intensity in supersonic boundary layers[J]. AIAA Journal, 2001, 39: 1071-1077. DOI:10.2514/2.1419 |
| [49] |
SMITS A J, EATON J A, BRADSHAW P. The response of a turbulent boundary layer to lateral divergence[J]. Journal of Fluid Mechanics, 1979, 94(2): 243-268. |
| [50] |
LEE J H, SUNG H J. Effects of an adverse pressure gradient on a turbulent boundary layer[J]. International Journal of Heat and Fluid Flow, 2008, 29(3): 568-578. DOI:10.1016/j.ijheatfluidflow.2008.01.016 |
| [51] |
MONTY J P, HARUN Z, MARUSIC I. A parametric study of adverse pressure gradient turbulent boundary layers[J]. International Journal of Heat and Fluid Flow, 2011, 32(3): 575-585. DOI:10.1016/j.ijheatfluidflow.2011.03.004 |
| [52] |
VINUESA R, NEGI P S, ATZORI M, et al. Turbulent boundary layers around wing sections up to Rec=1, 000, 000[J]. International Journal of Heat and Fluid Flow, 2018, 72: 86-99. DOI:10.1016/j.ijheatfluidflow.2018.04.017 |
| [53] |
VINUESA R, ÖRLÜ R, SANMIGUEL VILA C, et al. Revisiting history effects in adverse-pressure-gradient turbulent boundary layers[J]. Flow, Turbulence and Combustion, 2017, 99(3/4): 565-587. |
| [54] |
STUREK W B, DANBERG J E. Supersonic turbulent boundary layer in adverse pressure gradient. Part 11:data analysis[J]. AIAA Journal, 1972, 10(5): 630-635. DOI:10.2514/3.50167 |
| [55] |
DONOVAN J F, SPINA E F, SMITS A J. The structure of a supersonic turbulent boundary layer subjected to concave surface curvature[J]. Journal of Fluid Mechanics, 1994, 259: 1-24. DOI:10.1017/S0022112094000017 |
| [56] |
NAGANO Y, TSUJI T, HOURA T. Structure of turbulent boundary layer subjected to adverse pressure gradient[J]. International Journal of Heat and Fluid Flow, 1998, 19(5): 563-572. DOI:10.1016/S0142-727X(98)10013-9 |
| [57] |
SPALART P R, WATMUFF J H. Experimental and numerical study of a turbulent boundary layer with pressure gradients[J]. Journal of Fluid Mechanics, 1993, 249: 337. DOI:10.1017/S002211209300120X |
| [58] |
AUBERTINE C D, EATON J K. Turbulence development in a non-equilibrium turbulent boundary layer with mild adverse pressure gradient[J]. Journal of Fluid Mechanics, 2005, 532: 345-364. DOI:10.1017/S0022112005004143 |
| [59] |
FRANKO K J, LELE S. Effect of adverse pressure gradient on high speed boundary layer transition[J]. Physics of Fluids, 2014, 26(2): 024106. |
| [60] |
WANG X, WANG Z G, SUN M B, et al. Direct numerical simulation of a supersonic turbulent boundary layer subject to adverse pressure gradient induced by external successive compression waves[J]. AIP Advances, 2019, 9(8): 085215. DOI:10.1063/1.5112040 |
| [61] |
JAYARAM M, TAYLOR M W, SMITS A J. The response of a compressible turbulent boundary layer to short regions of concave surface curvature[J]. Journal of Fluid Mechanics, 1987, 175: 343. DOI:10.1017/S0022112087000429 |
| [62] |
SIMPSON R L. Turbulent boundary-layer separation[J]. Annual Review of Fluid Mechanics, 1989, 21(1): 205-232. |
| [63] |
LÖGDBERG O, ANGELE K, ALFREDSSON P H. On the scaling of turbulent separating boundary layers[J]. Physics of Fluids, 2008, 20(7): 075104. DOI:10.1063/1.2958317 |
| [64] |
KITSIOS V, ATKINSON C, SILLERO J A, et al. Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer[J]. International Journal of Heat and Fluid Flow, 2016, 61: 129-136. DOI:10.1016/j.ijheatfluidflow.2016.04.008 |
| [65] |
MACIEL Y, GUNGOR A G, SIMENS M. Structural differences between small and large momentum-defect turbulent boundary layers[J]. International Journal of Heat and Fluid Flow, 2017, 67: 95-110. DOI:10.1016/j.ijheatfluidflow.2017.07.011 |
| [66] |
HARUN Z, MONTY J P, MATHIS R, et al. Pressure gradient effects on the large-scale structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2013, 715: 477-498. DOI:10.1017/jfm.2012.531 |
| [67] |
LEE J, LEE J H, LEE J H, et al. Coherent structures in turbulent boundary layers with adverse pressure gradients[J]. Journal of Turbulence, 2010, 11: N28. DOI:10.1080/14685248.2010.496786 |
| [68] |
LEE J H. Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients[J]. Journal of Fluid Mechanics, 2017, 810: 323-361. DOI:10.1017/jfm.2016.715 |
| [69] |
BOBKE A, VINUESA R, ÖRLÜ R, et al. History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers[J]. Journal of Fluid Mechanics, 2017, 820: 667-692. DOI:10.1017/jfm.2017.236 |
| [70] |
SUN M B, SANDHAM N D, HU Z W. Turbulence structures and statistics of a supersonic turbulent boundary layer subjected to concave surface curvature[J]. Journal of Fluid Mechanics, 2019, 865: 60-99. DOI:10.1017/jfm.2019.19 |
| [71] |
HOFFMANN P H, MUCK K C, BRADSHAW P. The effect of concave surface curvature on turbulent boundary layers[J]. Journal of Fluid Mechanics, 1985, 161: 371. DOI:10.1017/S0022112085002981 |
| [72] |
FLAHERTY W, AUSTIN J M. Scaling of heat transfer augmentation due to mechanical distortions in hypervelocity boundary layers[J]. Physics of Fluids, 2013, 25(10): 106106. DOI:10.1063/1.4826476 |
| [73] |
BARLOW R S, JOHNSTON J P. Structure of a turbulent boundary layer on a concave surface[J]. Journal of Fluid Mechanics, 1988, 191: 137. DOI:10.1017/S0022112088001545 |
| [74] |
BARLOW R S, JOHNSTON J P. Local effects of large-scale eddies on bursting in a concave boundary layer[J]. Journal of Fluid Mechanics, 1988, 191: 177. DOI:10.1017/S0022112088001557 |
| [75] |
TONG F L, LI X L, DUAN Y H, et al. Direct numerical simulation of supersonic turbulent boundary layer subjected to a curved compression ramp[J]. Physics of Fluids, 2017, 29(12): 125101. DOI:10.1063/1.4996762 |
| [76] |
STUREK W B, DANBERG J E. Supersonic turbulent boundary layer in adverse pressure gradient. Part Ⅰ:the experiment[J]. AIAA Journal, 1972, 10(4): 475-480. DOI:10.2514/3.50122 |
| [77] |
LADERMAN A J. Adverse pressure gradient effects on supersonic boundary-layer turbulence[J]. AIAA Journal, 1980, 18(10): 1186-1195. DOI:10.2514/3.50870 |
| [78] |
OZALP A A, UMUR H. An experimental investigation of the combined effects of surface curvature and streamwise pressure gradients both in laminar and turbulent flows[J]. Heat and Mass Transfer, 2003, 39(10): 869-876. DOI:10.1007/s00231-003-0413-4 |
 2020, Vol. 38
2020, Vol. 38