层流-湍流转捩是流动从有序到无序的演化过程,与湍流问题一道,构成流体力学乃至经典物理学中尚未解决的重大基本科学问题。在高超声速条件下,湍流状态下的壁面摩阻和热流比层流状态下大得多,需要准确地预测转捩发生的位置,才能准确计算气动力和合理设计热防护系统。因此,对于长时间在大气层中飞行的高超声速飞行器,边界层的转捩预测是飞行器设计中必须考虑的问题[1-2]。
早在20世纪50年代,由于大型民用客机的发展,转捩问题便受到了航空技术界的重视。当时有人提出基于线性稳定性理论(LST)的转捩预测方法,即eN方法,在当时对转捩问题研究的不够深入的条件下,结合实验和经验提出的转捩判据,进行转捩预测。迄今为止,该方法仍然在航空界广泛应用。然而,对于临近空间高超声速飞行器,由于实验很难做,即使要用半经验的方法,也很难取得足够的实验数据用以确定相关参数。而且,在新的飞行参数条件下,原有的方法常常不能给出合理的结果。直到2006年,Bertin和Cummings[3]在Annual Review of fluids发表的综述文章中仍引用NASA首席科学家Bushnell在1997年的话:“历史上人类在预测所有高超声速(甚至超声速)飞行器的转捩时几乎从来没有成功过”[4]。
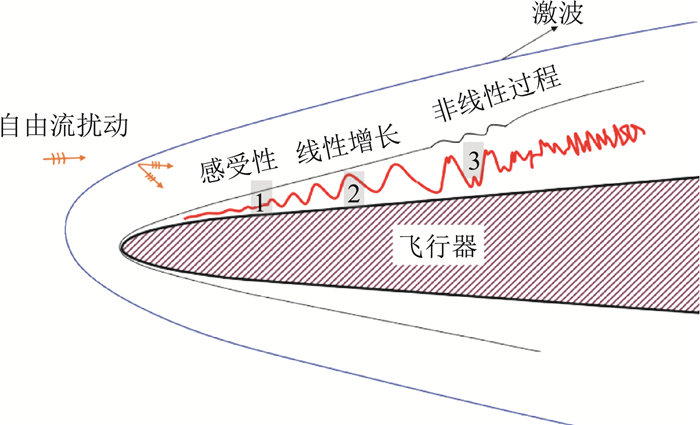
想要对转捩位置进行可靠预测,最合理的方法是从科学上弄清楚转捩所包含的关键物理过程中的规律。目前一般认为,转捩发生的本质是,飞行器的边界层在外界扰动的激励下产生了以不稳定波形式出现的扰动,扰动的演化结果会使得流动状态发生改变,即从层流转为湍流。高空中背景湍流度较低,飞行器表面边界层发生的转捩是由小扰动引起的自然转捩。如图 1所示,其过程包含以下三个具有不同特征的阶段:(1)感受性; (2)扰动波的线性增长; (3)非线性演化和breakdown至湍流。其中,感受性指的是外界扰动如何激发边界层中的不稳定波;激发出的扰动波在阶段(2)中经历较长的线性增长过程,小幅值扰动波的持续增长是转捩能够发生的内在机理;在阶段(3),扰动波的演化不再是线性的,非线性演化最终使流动突变为湍流。因此,想要完全从理论上预测转捩,需要回答以下三个方面的问题:(1)外界扰动是如何激发边界层中不稳定波的?更具体地,在何处激发,幅值为何?(2)边界层中的不稳定波是如何发展和演化的?(3)扰动波演化到何种程度转捩发生,即转捩的机理如何?可用于转捩预测的判据是什么?
|
图 1 飞行器表面边界层的转捩过程示意图 Fig.1 Sketch of transition process of a boundary layer on a flight vehicle |
以上三个方面的问题就是转捩预测中需要解决的基本问题,即感受性、扰动演化、转捩机理和判据。其中第二个问题是研究得最早和最充分的,有成熟的线性稳定性理论[5]可以用于描述小扰动的线性演化。对于二维低速流动,已无原则上的困难。但是,在高超声速边界层的实际应用中还存在一些新的挑战。2015年,罗纪生[6]从边界层转捩的基本过程出发,对高超声速边界层转捩研究中涉及的几个关键科学问题做了很好的综述。与高超声速飞行器转捩有关的综述可见文献[7, 8]。
本文以发展基于物理机理的转捩预测方法所包含的科学问题为主线,重点介绍了在感受性、转捩机理及判据方面的最新研究进展及主要面临的挑战,最后讨论了eN方法在高超声速边界层计算扰动演化时遇到的问题。
1 基于科学问题的转捩预测方法基于科学问题的转捩预测需要研究引言中提到的三个方面的问题。目前熟知的eN方法,是基于线性稳定性理论,通过描述扰动的线性演化,并结合一定的转捩判据来预测转捩。以二维问题为例,根据线性稳定性理论,小扰动可写为
| $ q^{\prime}=\widehat{q}(y) \mathrm{e}^{\mathrm{i}(\alpha x-\omega t)} $ | (1) |
其中,q′代表任一扰动物理量,
| $ A=A_{0} \mathrm{e}^{-\int \alpha_{i} \mathrm{d} x} $ | (2) |
若不考虑非线性作用,假设转捩发生的阈值是Ac,则可确定该扰动幅值达到Ac时对应的流向位置。基于模态竞争的思想,在所有被激发的扰动中,最先达到Ac的扰动是触发转捩的关键扰动,而其对应的位置即是转捩发生的位置。显然,A0与扰动频率有关,由于A0和Ac并不清楚,在传统的eN方法中,定义Nc=Ac/A0,Nc即为由实验和经验给出的转捩判据。研究结果表明,对于马赫数不超过3.5的流动,Nc多取为9~11[9-11]。
不难发现,传统的eN方法所隐含的对感受性的考虑是,所有频率的扰动波在其中性点处具有相同的初始幅值。这显然是不合理的。由于高超声速边界层中存在多种模态,流动复杂,用于确定Nc的值的实验和经验也远不如低速流中的多,很难找到普遍适用的Nc值。因此,假设线性稳定性理论对小扰动演化的描述是准确的,即边界层非平行性的影响可以忽略(事实证明,大部分大雷诺数的情况确实如此),转捩预测方法的不确定性主要来自于转捩过程的一“头”和一“尾”,即如何确定不稳定波的初始幅值A0和转捩阈值Ac。
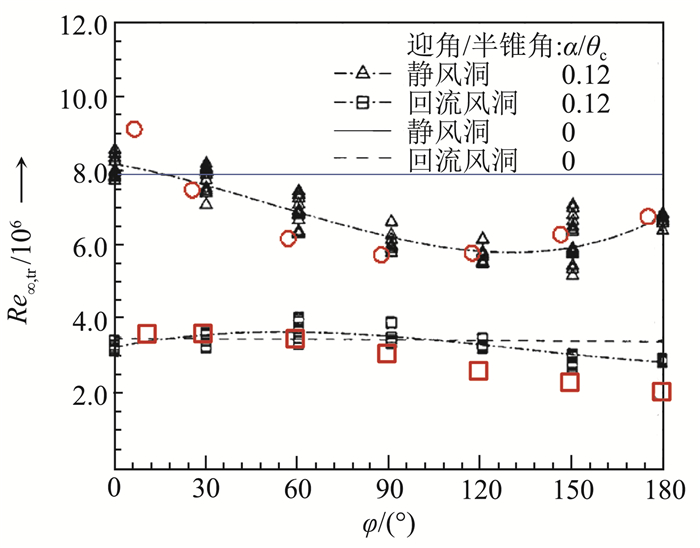
Su和Zhou[12-14]在对小迎角圆锥边界层进行转捩预测时,曾对传统的eN方法做了改进。在改进的eN方法中,包含两种对感受性的考虑:(1)对于静风洞或高空飞行的情况,假设所有频率的扰动都在头部附近激发,且具有相同的幅值[12-13],其大小与自由流扰动幅值相当;(2)对于回流风洞的情况,背景扰动主要是实验段上游的风洞壁面湍流边界层发射的声波,需要考虑慢声波的感受性[14]。还提出一个转捩判据,即当边界层内速度扰动的幅值达到自由流速度的1%~2%,转捩便发生[12]。King[15]曾对同一实验模型,分别在静风洞和回流风洞中做转捩实验,所得结果如图 2所示。模型为马赫数3.5的尖锥,迎角为0.6°。横坐标为圆锥周向角度,纵坐标为转捩雷诺数。显然,静风洞中的转捩位置比回流风洞中的显著靠后,并且,转捩线的形状显著不同。静风洞的转捩线是下凹的,而回流风洞中的转捩线略微上凸。分别采用改进eN方法对两种情况进行转捩预测,可以得到与实验吻合很好的转捩结果。需要说明的是,调整转捩判据的阈值,只能整体调整转捩的位置,并不能改变转捩线的形状。这样的比较结果是令人鼓舞的,这表明能否正确考虑感受性,关系到转捩预测的成败。
|
图 2 小迎角圆锥边界层转捩预测与实验结果[15]的比较 Fig.2 Transition prediction of a cone boundary layer with small AOA in comparison of experimental results (○为文献[13]中的结果,□为文献[14]中的结果) (○ is from Ref.[13] and □ is from Ref.[14]) |
在改进的eN方法中,对于扰动初始幅值A0和转捩阈值Ac的考虑是非常粗略的。为了建立基于科学问题和物理机理的转捩预测方法,需要系统、细致地研究边界层的感受性,尽可能准确地给出在边界层中激发的扰动的初始幅值,而是否能够采用扰动线性增长的幅值Ac作为转捩判据,且应取何值,则与转捩机理有关。
2 高超声速边界层的感受性研究对于三维边界层中横流转捩的情况,低背景扰动环境下起主导作用的是横流定常涡,主要由壁面粗糙度激发,机理相对简单。本节仅讨论二维或轴对称边界层中激发Mack模态的情况。
2.1 感受性研究概述转捩是一个初值问题,其结果严重依赖于外界扰动。目前,高空中背景扰动的具体情况很难获得,然而,均匀来流中的小扰动总能表达成三种基本扰动形式,即涡波、熵波和声波(包括快声波和慢声波)的线性组合[16]。因此,感受性研究需要给出这些基本自由流扰动与边界层内激发的不稳定波之间幅值的定量关系,即确定感受性系数Λ。Λ=A0/Ae,其中,Ae为自由流扰动的幅值。感受性系数与流动条件有关,还与具体的感受机理和扰动频率有关。然而,目前对感受性的研究仍然集中在机理的理解上,研究成果还远未达到能在转捩预测中实用的程度[17]。
在感受性机理方面的研究从20世纪80年代就开始了。对于低速流动,由于自由流扰动的尺度通常大于边界层内T-S波的尺度,不稳定波通过“尺度转换”机制[18-19]被激发。该机制的实现可以是声波与前缘作用[20-21],或声(涡)波与壁面粗糙元[22]或波纹壁作用[23]。虽然涡波不能直接进入边界层,但可以与局部粗糙元引起的边界层外缘的定常扰动相互作用从而激发不稳定波。低速流感受性方面的理论和实验工作可参考Saric等[24]的综述文章。而高速流中的感受性机理则显著不同。由于自由流扰动的时间和空间尺度与边界层不稳定波的是相当的,Fedorov和Khokhlov[25-26]最先发现,自由流中的快声波和慢声波可以在前缘处通过“同步机制”分别激发边界层中的快模态和慢模态。快、慢模态在下游的演化过程中可以与Mack第二模态“同步”,将后者激发。这里的“同步”并非真正意义上的同步,因为对于某个固定的频率而言,在所谓的“同步点”处,只能保证外界扰动和边界层模态的相速度的实部相同,而虚部相差一个小量。
高超声速感受性实验难度很大,实验结果并不多,如文献[27]。大量的关于感受性的结果是基于直接数值模拟的,研究模型包括平板[28-31]、楔[32-34]和圆锥[35-40]等,内容包括自由流扰动和壁面扰动的感受性,以及不同因素如钝度、壁面温度的影响规律。相关的综述可参考文献[41-43],以及吴雪松在周恒等人专著[44]中撰写的第四章关于感受性的综述。
目前为止,被理解和接受的高速流动感受性机理和过程基本上就是所谓的“同步机制”。但是,这些理论工作并没有考虑高超声速流动的主要特征——激波的存在。而事实上,激波在感受性问题中扮演了至关重要的角色[17, 45]。因为,直接通过感受性机制激发边界层模态的扰动是激波后的扰动。任意一种自由流中的基本扰动和激波相互作用,在激波后都会产生包含三种基本扰动的组合[16-17]。对于钝头体而言,问题变得更加复杂。脱体激波的激波角从头部开始沿下游逐渐减小,随着激波角的改变,激波后产生的扰动类型也不同。考虑到扰动波的波长显著小于激波的曲率半径,可将激波当成局部平面激波处理,采用扰动形式的Rankine-Hugoniot方程求解自由流扰动和激波作用在激波后产生的扰动情况[45]。图 3给出了平面慢声波以零度入射圆锥头激波时激波后的扰动情况示意图[40]。可见,激波后不同区域内激发的扰动显著不同。因此,要理解感受性,需要回答究竟是哪一区域内的何种扰动通过何种机制最终激发了不稳定波。
|
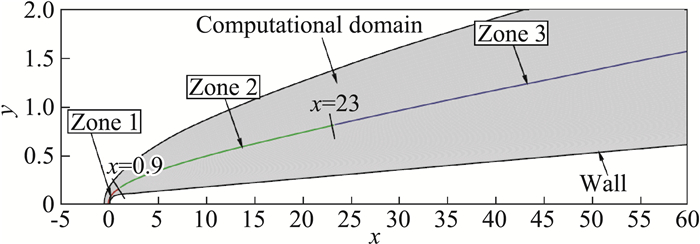
图 3 激波后扰动情况示意图 Fig.3 Three zones behind the shock (Zone 1:快声波,熵、涡波;Zone 2:熵、涡波;Zone 3:慢声波,熵、涡波)[40] (Zone 1: fast acoustic wave, entropy and vorticity wave; Zone 2: entropy and vorticity wave; Zone 3: slow acoustic wave, entropy and vorticity wave)[40] |
采用直接数值模拟方法可以考虑激波的影响,但是对于大部分数值模拟研究而言,例如文献[28-39],都是以激波前的外界扰动为输入,边界层内的不稳定波为输出,尽管能够得到感受性系数的具体数值,但实际上,在激波后产生的声波、涡波和熵波中,究竟是哪一种扰动最终引发边界层中的扰动波是不清楚的。因此,整个感受过程就好像被关在一个“黑箱子”里,无法了解具体的感受路径。近年来,为了使感受性计算尽可能地贴近真实的情况,Balakumar等在感受性的数值模拟中,采用实验测得的外界扰动频谱构造来流扰动[38],或以波纹壁散射的声波作为初始扰动,用来模拟实际中风洞壁面辐射的背景扰动[39]。这样并不能对理解真正的感受过程有所帮助,也无法回答究竟是激波后的何种扰动通过何种路径激发了可能触发转捩的不稳定波。因此,需要打开感受性的“黑箱子”,理解真正的感受过程。
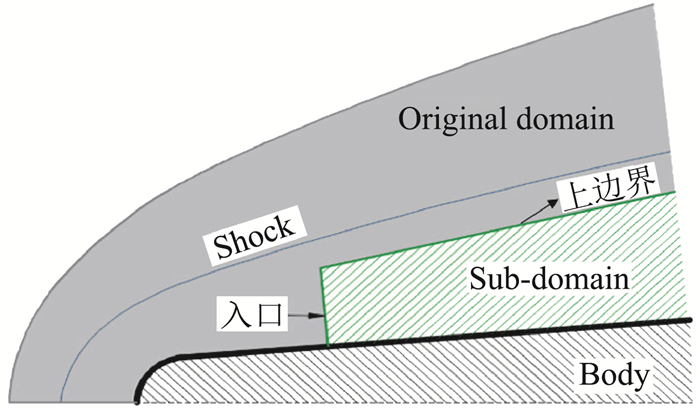
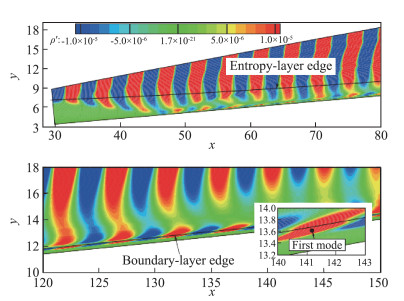
2.2 打开感受性的“黑箱子”我们设想出一种打开“黑箱子”的方法[40, 46],在激波后选择一个计算域(以下简称为“子计算域”),分别以激波后的某一种扰动波作为输入扰动,进行数值模拟,以分析其具体的感受过程。以钝头圆锥的感受性问题为例,子计算域如图 4所示,激波后的某一种扰动可以在其入口或上边界引入,将所得结果与基准算例进行比较。基准算例是指采用类似文献[30-39]的方法,在激波前引入自由流扰动,对整个感受性过程进行的直接数值模拟。仍以慢声波入射的情况为例,子计算域的上边界取在图 3所示的Zone 3中,则包含的主要扰动为从激波传过来的慢声波。入口则一般包含了边界层内激发的快模态(由头部激波后的快声波激发),以及边界层外熵层中的扰动。两者可以借助线性稳定性理论分析进一步区别,具体方法可参考文献[46]。研究发现[40],对于频率较低的第一模态波的激发,激波后的慢声波起主导作用。图 5给出的脉动密度的等值线图显示了激波后慢声波激发边界层内不稳定波的过程。由于慢声波的相速度与第一模态接近,感受性激发的机制是所谓的“同步”机制。
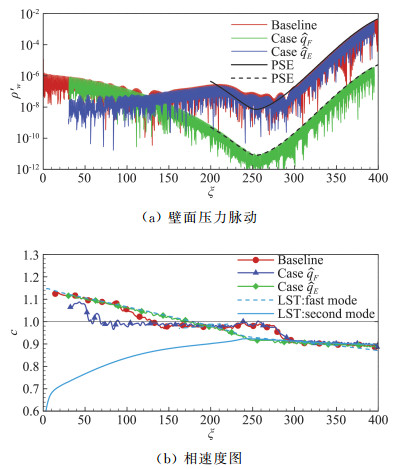
采用类似的方法研究第二模态的感受性[46],发现激波后的慢声波几乎没有作用,起主导作用的是熵层中的扰动。如图 6(a)和(b)所示,Baseline为基准算例,Case
前面曾提到,在改进的eN方法[12-13]中,转捩判据取为速度扰动幅值达到自由流速度的1%~2%。提出这个判据的依据是,大量的关于T-S波/Mack模态导致转捩的直接数值模拟结果显示,当扰动增长到一定程度,非线性作用会激发更多的高阶波,转捩便发生。另一方面,不少数值模拟结果表明,非线性作用在基本扰动波幅值达到1%~2%时开始变得明显起来[47]。事实上,1%~2%的数值并不是绝对的,与扰动具体的演化情况有关。问题的关键是,以扰动线性演化的幅值作为转捩判据是否是合理的,即eN方法忽略非线性作用是否会成为该方法的重要缺陷。
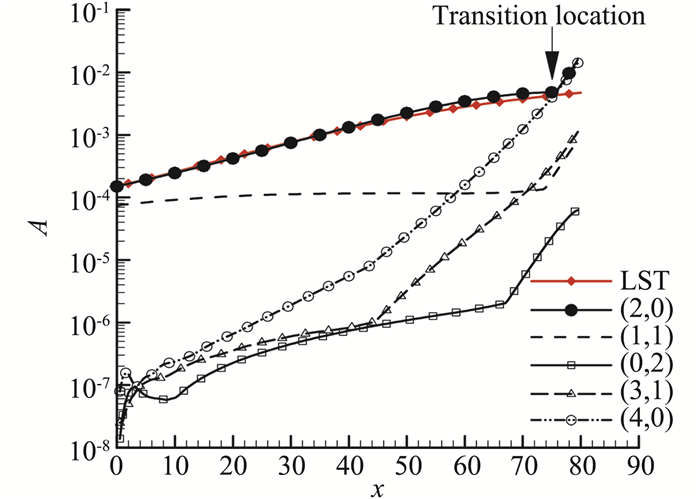
对于高超声速边界层,二维的Mack第二模态是最不稳定的。但是,它本身并不导致转捩,而是通过非线性作用促使三维扰动快速增长。有关非线性作用的理论研究表明[48],存在亚谐共振、基本波共振和锁相位模态作用三种。2019年Wu[49]在对非线性理论的综述文章中指出,理论分析揭示了一种所谓的“催化效应”,即线性增长最强的模态,在其幅值达到一定阈值时,三维波快速增长,而它本身仍然保持线性特征。数值计算也证明了这一点[47]。例如,图 7给出了由非线性PSE方法(该方法的验证可参考文献[50])计算的马赫数为6的平板边界层中扰动演化的情况(算例来自于文献[47])。入口扰动为一个二维的第二模态波(2,0)和一对等幅值的三维斜波(1,1)和(1,-1)。图中标出的转捩位置对应于壁面摩擦系数曲线抬升的位置。可见,在转捩前,非线性作用促使高次谐波快速增长,而(2,0)的幅值演化曲线与LST的结果始终是相近的。
|
图 7 非线性PSE计算的扰动增长情况 Fig.7 Evolutions of disturbances computed by nonlinear PSE |
判据的合理性还与转捩机理有关。T-S波/Mack模态导致的转捩有个显著的特点,即非线性作用开始之后的转捩过程具有突变的性质。其内在机理最早在2005年由Luo等[51]在平面槽道流中进行了研究,后来扩展到不可压平板边界层[52]、超声速平板[53-54]、圆锥边界层[55]。读者也可参考罗纪生的综述文章[6]和周恒等的专著[44]。对于高速边界层,研究发现[53-55],在壁面摩擦曲线抬升的过程中,非线性作用对平均流剖面进行修正,修正后的平均流使得边界层中高频扰动的不稳定区缩小,而与此同时,低频扰动的不稳定区迅速放大,进一步修正平均流,促进更多低频扰动的增长,形成一种正反馈机制。这种机制使扰动呈现爆发式的增长,快速促发转捩。Zhu等在实验[56]中也观察到了类似的现象。
此外,由北约科学技术组织NATO STO AVT-240开展的国际联合研究项目——“高超边界层转捩预测”,涉及到4个国家的11座高超声速风洞,以细长锥第二模态转捩为主要研究对象,马赫数从5到14,单元雷诺数从1.5×106到1.6×107。实验结果表明[57-58],对于第二模态主导的高超声速圆锥边界层的转捩,以第二模态扰动幅值为基础的转捩判据在很大的参数范围内是适用的。文章认为[58],转捩预测方法的改进更有可能通过联系风洞设备中的背景噪声得到。这与Wu[49]的观点一致,认为感受性的考虑对转捩预测方法结果影响更大。因此,综合来看,尽管eN方法长期以来被诟病没有考虑扰动波之间的非线性作用,但是,其带来的影响远不如忽略感受性的大。换句话说,以扰动线性增长的幅值作为转捩判据是具有一定的物理依据的。
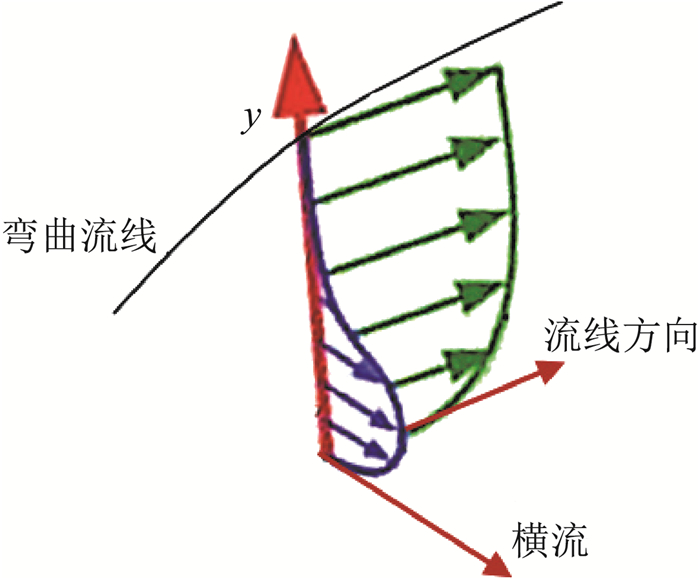
3.2 横流转捩的机理相比T-S波/Mack模态主导的转捩,横流的转捩预测面临的挑战更大。对于一般的三维边界层,外缘流线弯曲,压力在与流线垂直的方向上存在梯度,引起边界层内的相应流动,即横流。图 8给出了横流速度剖面的示意图。由于横流速度剖面存在拐点,具有很强的无黏不稳定性,存在定常横流涡和横流行进波两种不稳定的横流涡。前者对壁面粗糙度非常敏感,很容易被激发,被证实在低背景环境下起主导作用[59]。横流转捩预测最大的困难是,目前并没有可用的基于物理的转捩判据。很多横流的转捩预测采用的仍是基于RANS框架下的转捩模式的方法,例如文献[60-61],也有的直接借用eN方法中的N判据[62-63],但是,后面会说明,这样的判据是值得怀疑的。
|
图 8 横流速度剖面示意图 Fig.8 Sketch of velocity profiles of cross flow |
与T-S波/Mack模态主导的转捩过程的显著区别是,横流转捩有着非常长的非线性过程。横流定常涡或行进波经历线性放大后,会发生非线性饱和。非线性饱和过程很长,在此过程中,扰动幅值变化非常缓慢。非线性作用修正平均流,使之发生二次失稳,最终二次失稳波的快速增长促使转捩发生。通常,转捩位置与开始发生非线性饱和的位置有相当长的距离。因此,直接借用eN方法的判据,采用首次失稳波线性演化幅值作为转捩判据是不可行的[64-68]。
由于二次模态出现“爆发式”增长,其激发预示着转捩将快速发生,有人认为可以用二次模态开始激发的位置作为转捩位置[64, 66]。Malik等[67]发现,可以将二次失稳波的线性演化幅值与转捩位置联系起来作为转捩判据。Li等[69]在后掠翼的转捩预测上使用了该方法。然而,这样带来的困难是,在转捩预测时,除了需要给出首次失稳波的幅值外,还需要对二次模态进行计算,且多个二次模态的出现会为转捩预测带来额外的不确定性。更重要的是,这样的转捩判据无法给出转捩区壁面摩擦系数抬升及对阻力的影响等信息[70-71]。
以上都是基于低速流得到的研究结果。尽管不少研究表明[72],高速流与低速流中的横流转捩存在着本质上的相似之处,但是也有显著的差别。最近,Kocian等[72]在对NATO STO AVT-240项目中的高超声速横流不稳定性的工作做总结时提到,实验发现[73-74],在高超声速流中,在横流涡开始饱和时,便测量到了类型Ⅰ(Z模态)的二次模态,且并不像低速流中那样表现出“爆发式”的增长。具体原因还不清楚。
高超声速横流问题具有代表性的模型是椭圆锥和有迎角圆锥。在转捩过程中,Mack模态和横流失稳同时存在且相互影响,转捩机制非常复杂。目前,尽管在实验方面已经有了不少有价值的结果[73-76],然而,直接数值模拟计算转捩过程计算量非常大,因此大部分的工作仍主要集中在首次失稳和二次模态的稳定性和演化上[77-78]。最近,中国空气动力研究与发展中心的陈坚强团队对有迎角圆锥的转捩问题开展了15亿网格的超大规模的直接数值模拟(私人通讯)。总的来说,对高超声速横流边界层实现基于物理机理的转捩预测,还有相当长的距离。理解横流转捩过程的机理是迫切需要解决的问题。
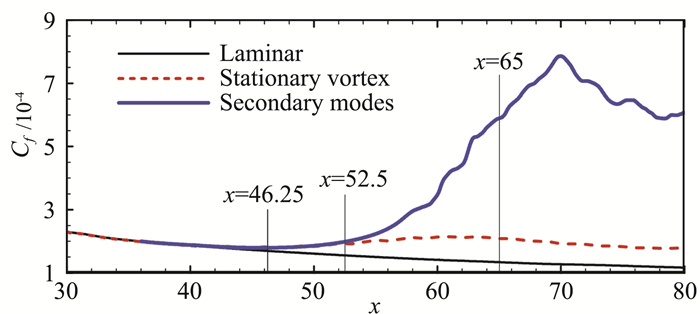
为此,可先针对一个构型相对简单的情况,研究其内在机理,弄清楚其与Mack模态转捩机理的区别和联系。韩宇峰等[79-80]以马赫数为6的后掠钝板为研究对象,研究了横流的转捩机理。他们采用直接数值模拟方法计算了从定常涡开始到非线性饱和,以及引入二次模态后,扰动放大促发转捩的整个过程。图 9给出了引入二次模态后转捩的过程。可见,二次模态的增长破坏了横流涡的展向周期性,最终促使流动转捩为湍流。转捩发生的位置与二次模态的初始幅值和引入的位置有关。如果不引入二次模态,定常涡本身并不会导致转捩发生,但会使壁面摩擦系数Cf曲线略有抬升。在图 10所示的Cf曲线中,若不引入二次模态(stationary vortex的情况),Cf曲线在x=46.25处偏离层流值,但最终会保持在某一数值上。而对于引入二次模态的情况(用secondary modes表示),Cf曲线在x=52.5处偏离饱和横流涡对应的值,继续抬升,流动最终转捩为湍流。
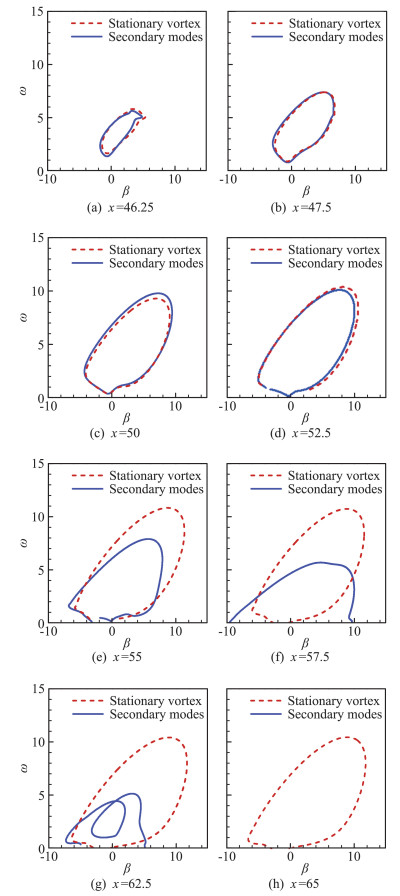
借鉴研究Mack模态转捩机理的方法,采用线性稳定性理论分析Cf曲线抬升过程中平均流的不稳定区,如图 11所示。图 11(a~d)对应于从x=46.25到x=52.5的Cf曲线首次抬升过程,图 11(e~h)对应于从x=52.5开始Cf曲线继续抬升直至最终促发湍流的过程。在首次抬升过程中,不稳定区显著扩大,意味更多频率范围的扰动会被放大。这是因为,此时二次模态幅值还比较小,横流涡起主导作用。定常涡对平均流的修正产生了新的拐点,且拐点逐渐增强,不稳定区明显扩大。但从x=52.5开始,引入二次模态的情况(图中secondary modes的情况)不稳定区逐渐下移,同时低频的不稳定区显著扩大,如图 11(f)所示,意味着高频扰动受到抑制,更多的低频扰动被放大。在x=62.5处还发现了不止一种模态,这些扰动快速修正平均流,使之变为湍流剖面。在x=65处,剖面已经接近于湍流,找不到不稳定区,说明转捩已经完成。
|
图 11 横流转捩过程中平均流的不稳定区[80] Fig.11 Unstable region of distorted mean flow in transition induced by cross flow[80] |
以上结果表明,横流的转捩过程比Mack模态的转捩更加复杂。但是,两者之间有着一种内在的联系。即在转捩发生的关键阶段(图 10和图 11中从x=52.5到x=65),都会发生高频扰动受到抑制、低频扰动迅速放大的现象。放大的低频扰动快速修正平均流,最终促使转捩发生。上述机理还有待于在更多的算例中进行验证。同时,需要通过大量参数研究,探寻Cf曲线首次抬升和二次抬升与扰动波幅值之间的联系,探索可能的转捩判据。
4 高超声速边界层中扰动波的演化边界层不稳定性及不稳定波在超及高超声速边界层中的演化在过去很多年已经进行过充分的研究,此处只讨论两个在实际中应用eN方法计算扰动波演化时遇到的问题。
4.1 eN方法在三维边界层中的应用对于三维不稳定波,O-S方程增加了两个未知数,βr和βi,分别表示展向波数和展向增长率。因此,需要补充条件才能唯一地确定α和β。此外,不像二维情况那样,可以简单地向下游积分,在三维边界层中,还需明确扰动传播的方向,即积分的路径。
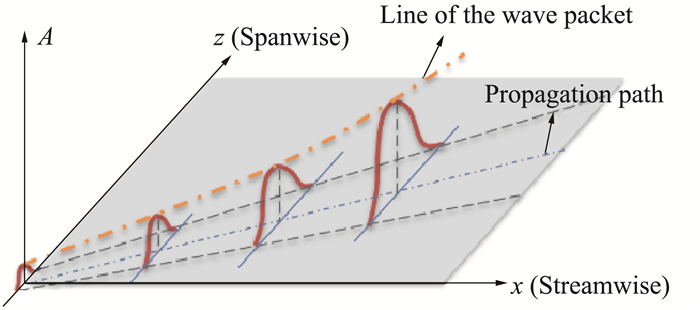
Malik[81]曾采用时间模式的思想,将α和β用波角ϕ=tan-1(β/α)联系起来,利用群速度将增长率转换为空间模式。为了提高效率,计算时对波角迭代,得到最大的增长率进行积分。由于很多问题中扰动增长方向主要在流向上,Mack[82]建议,假设扰动波沿展向不增长,即β为实数,在积分过程中保持β为常数。事实上,若对每一个频率所有可能的β都进行计算,计算量很大,在实际中应用时很不方便。Cebeci和Stewartson[83]从复变函数的角度,研究一个波包的演化,提出鞍点法,即用(∂α/∂β)i=0确定展向波数,沿着扰动传播的群速度方向,即ϕ=atan(-∂α/∂β)r进行积分。结合β为实数的假设,即转变为迭代β,寻找αi的极小值(代表最不稳定波的波),计算大大简化,被广泛采用[12-14, 84-85]。Su[86]采用数值模拟方法证明了该方法所代表的物理内涵。如图 12所示,鞍点法实际上跟随的扰动传播方向是波包波峰的演化方向,积分得到的幅值是波包锋值。于高通等[87]证明了扰动波波数α和β并不是相互独立的,推导出了它们满足的相容关系,从而给出了β为实数的理论根据。Zhao等[88]在此基础上提出了射线跟踪法,Song等[89]推导了在三维边界层中沿着扰动波群速度方向的广义增长率的守恒关系,从理论上进一步完善了eN方法在三维边界层中的应用。
|
图 12 采用鞍点法的积分策略的物理含义 Fig.12 Physical meaning of using saddle point method as integral strategy |
从准确预测扰动演化的角度来讲,好的积分策略应尽可能接近真实的情况(例如DNS结果),但同时还受到计算量的限制。若计算量太大则无法在工程中使用。此外,由于LST本身的局限性,其对小扰动在三维边界层中演化的描述是近似的,这种近似带来的不确定性有时可以和转捩判据带来的不确定性一并处理。
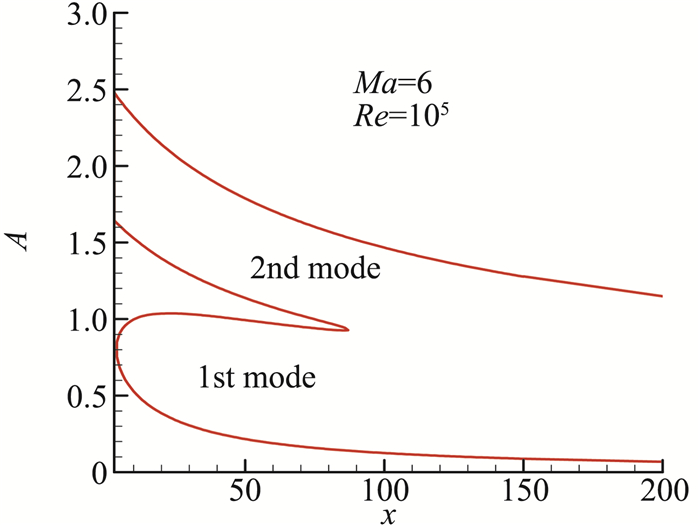
4.2 第一模态与第二模态的模态转换在高超声速边界层中,常常同时存在不稳定的第一模态和第二模态。第一模态即本文在感受性部分提到的慢模态。若在可能发生转捩的区域内,两个模态不稳定波的频率范围始终是分开的,前面提到的方法可以分别应用于两个模态,寻找最先达到转捩阈值的扰动预测转捩。但是,如图 13那样的情况,低频的第一模态会在下游通过模态转换激发第二模态。此时,应用eN方法会遇到困难。
|
图 13 平板边界层第一、第二模态的中性曲线 Fig.13 Neutral curves of 1st and 2nd modes in a flat plate boundary layer |
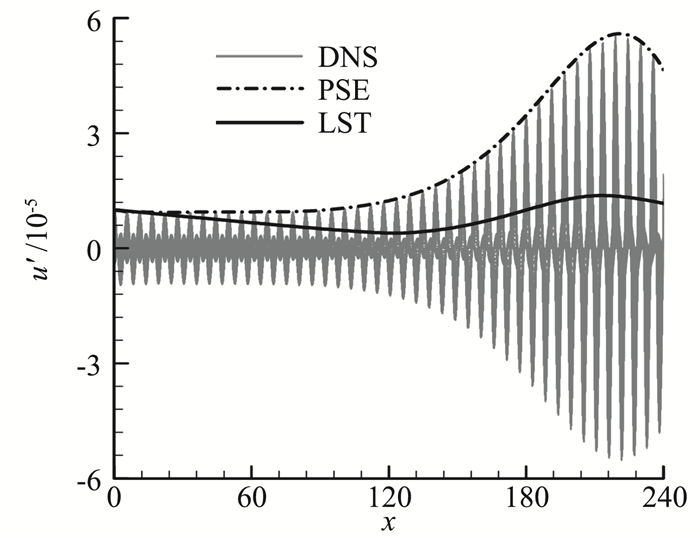
前面曾提到,边界层中的慢声波在向下游的传播过程中,会与第二模态“同步”而将后者激发。由于模态转换与第二模态的生成有关,通常在感受性的研究中受到关注[6, 43]。但这实质上并不是边界层扰动对外界扰动的响应问题,而是扰动在边界层内的演化问题。根据Fedorov等[26]的研究,在“同步”点附近,边界层的非平行性扮演了非常重要的角色。因此,忽略非平行性的线性稳定性理论无法正确描述从第一模态发展到第二模态的幅值演化过程。图 14给出了一个第一模态波在平板边界层中演化为第二模态波的例子。在x=0处引入的是第一模态波,在下游激发了不稳定的第二模态波。可见,LST明显地低估了第二模态波的幅值,而考虑非平行性的PSE可以给出和DNS吻合很好的结果。
|
图 14 不同方法给出的扰动演化结果 Fig.14 Results of evolutions of disturbance obtained by different methods |
|
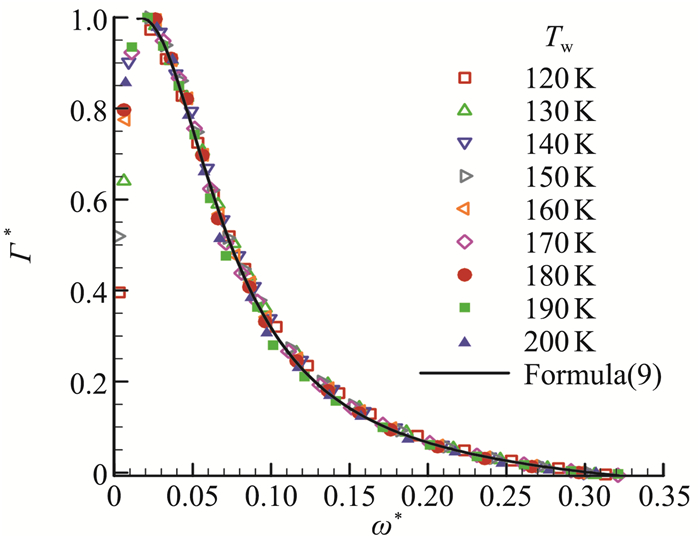
图 15 不同壁面温度条件下的Γ*~ω*曲线[96] Fig.15 The relation between Γ* and ω* in different wall temperature conditions[96] |
采用PSE代替LST进行转捩预测似乎可以解决上述问题。事实上,有不少采用PSE预测转捩的工作[50, 90-91]。例如,在无限翼展后掠翼边界层的转捩预测中,Cebeci等[91]曾建议由LST给出初值,用PSE进行扰动演化的计算。但是,由于PSE不是特征值问题,除了求解时需要给出上游条件外,确定扰动波的演化方向也是一个非常困难的事情,特别在三维复杂边界层中。有人提出PSE-3D[92-93],可沿流向推进,但需要在展向和法向求解二阶偏微分方程,这样计算量太大,难以用于实际的转捩预测中。于高通等[94]提出EPSE方法,将问题转变为局部特征值问题,能够考虑形状函数沿流向变化。韩宇峰等[95]对该方法进行了进一步的改进,提高了其计算精度。但是,大量的测试表明,EPSE的鲁棒性不如LST,并不能全面取代LST。
目前,对于实际的转捩预测问题,并没有好的办法来解决模态转换的问题。苏彩虹等[96]曾研究了超声速平板边界层中快模态到第二模态的模态转换,或许提供了一种考虑模态转换的可能思路。定义模态转换系数Γ=A0/AF和模态转换区间Δx,其中,AF为中性点上游某处快模态的幅值,A0为在第二模态下支界处激发的等效幅值。通过DNS或PSE方法,可确定Γ和Δx。研究表明,经过适当的变换[96],模态转换系数随频率的变化曲线对于不同壁面温度的边界层可以重合在一起,可采用公式进行拟合。因此,考虑到模态转换,扰动的幅值演化可以修正为:
| $ A=A_{F} \mathit{\Gamma} \mathrm{e}^{-\int_{x_{N}}^{x-\Delta x} \alpha_{i} \mathrm{d} x} $ | (3) |
由于快模态总是衰减的,慢模态有可能是增长的,显然后者到第二模态的模态转换更加复杂。目前在这方面的研究还有待于进一步深入。
5 总结和讨论随着临近空间高超声速飞行技术的发展,预测高超声速边界层转捩位置的需求越来越迫切。由于高超声速实验很难做,不可能像低速飞行器那样,有足够的实验数据支撑半经验的预测方法。为此,需要理解转捩所包含的关键物理机理,发展基于物理机理的转捩预测方法。本文介绍了高超声速边界层转捩预测中的关键科学问题,即感受性、扰动演化及转捩判据近年来的研究进展,由于问题本身的复杂程度,基于物理机理的转捩预测仍面临着很多挑战。
(1) 对于高超声速边界层中Mack模态主导的转捩,以线性稳定性理论为基础的预测方法,即所谓的eN方法正在从两个方面向更加理性化的方向发展和完善。一是,充分地考虑感受性,二是,基于物理的转捩判据。尽管eN方法忽略了扰动波的非线性作用,以不稳定波线性演化的幅值为转捩判据,这样带来的误差要远比忽略感受性小得多。感受性的考虑对高超声速边界层的转捩预测至关重要。
(2) 在高超声速边界层中,被理解和接受的经典的感受性理论是所谓的“同步机制”。然而,该理论并没有考虑激波——这一高超声速流动关键特征的存在。而实际上,激波在感受性中扮演着非常重要的作用,因为激波后产生的扰动是真正进入边界激发不稳定波的扰动。从理论研究的角度,有待于探索和理解考虑激波影响的新的感受性机制。此外,过去大部分感受性的数值模拟工作将边界层看作一个系统,以外界扰动波作为输入,边界层的不稳定波为输出,真正的感受性过程被关在一个“黑箱子”里。近期的研究表明,打开“黑箱子”可以更深层次的揭示和理解感受性的内在机理。然而,另一个值得注意的问题是,过去研究得最多的是对声波的感受性,但高空中并没有发声的声源,因此今后需多关注对涡波或熵波的感受性。而尽管之前有柱状涡的感受性研究[33],但这是极特殊的情况,并不符合实际情况。因此,对于更一般的情况,例如平面涡波的感受性问题(这并非单纯的二维问题),还有待于研究。目前已经知道打开感受性“黑箱子”的方法,理解了自由流扰动激发不稳定波的具体路径,涡波的感受性研究可以在此基础上进行,不必从头开始。
需要说明的是,即使完全理解了感受机理,在不清楚背景扰动的情况,也无法做出准确的转捩预测。因此,还需要尽可能理解飞行环境中背景扰动的情况。但是,周恒和张涵信在2017年发表的文章中指出,这是非常困难的事情[97]。首先,不可能做足够多的飞行实验,特别是,不可能把未来所有可能飞行的空域全部事先测量。其次,所有接触式传感器都要受在其前段产生的激波的影响,如何从激波后的信息还原激波前的信息也是问题。传感器即使在实验室条件下,也只能测得非常有限的信息。目前已有工作将数值模拟和实验测量相结合,旨在全面、深入地理解风洞中的背景噪声情况[98]。
(3) 与T-S波/Mack模态主导的转捩相比,三维边界层中横流主导的转捩问题还没有被充分的理解。对于横流不稳定性和转捩的认识主要来自于低速流动,尽管不少研究表明,高速流与低速流中的横流转捩存在着本质上的相似之处,但也发现一些显著的差别。近年来,从实验、理论和数值模拟方面,在以有迎角圆锥为典型模型的横流转捩问题上取得很多前所未有的认识[72],但仍主要集中在首次失稳、二次失稳方面。对于后掠平板的转捩机理有了初步的认识,但是,转捩判据的建立仍面临着很大的挑战,基于物理机制的横流转捩预测还有相当长的距离。
(4) 不稳定波在边界层中的演化似乎是转捩涉及的三个科学问题中挑战性最小的。在实际复杂外形的转捩预测中,流动往往是三维的,在二维边界层中的eN积分并不能简单地推广至三维边界层。近年来,eN方法在三维边界层的应用得到不断地发展和完善。本文提到的第一模态到第二模态的模态转换问题,是高超声速边界层的转捩预测中常常遇到的问题。由于线性稳定性理论本身的局限性,原有的eN方法不再适用,目前并没有很好的解决方法。更多细致的研究有待于开展。
转捩是包含众多影响因素的强非线性问题。对于高超声速飞行器,还存在表面凸起物、缝隙、粗糙度等影响,高温真实气体效应、激波边界层干扰等复杂物理现象。本文没有讨论这些干扰因素,这方面的研究和理解无疑会有助于修正转捩预测方法。总之,高超声速边界层的转捩预测未来还有长期艰苦的工作开展。
致谢: 感谢天津大学周恒教授指引作者进入高超声速转捩预测这一研究领域,并多年来给予作者极大的支持和鼓励;感谢吴雪松教授长期以来与作者在相关科学问题上的有益的讨论。
| [1] |
BERTIN J J, CUMMINGS R M. Fifty years of hypersonics:where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39(6/7): 511-536. |
| [2] |
叶友达, 张涵信, 蒋勤学, 等. 近空间高超声速飞行器气动特性研究的若干关键问题[J]. 力学学报, 2018, 50(6): 1292-1310. YE Y D, ZHANG H X, JIANG Q X, et al. Some key problems in the study of aerodynamic characteristics of near-space hypersonicvehicles[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(6): 1292-1310. (in Chinese) |
| [3] |
BERTIN J J, CUMMINGS R M. Critical hypersonic aerothermodynamic phenomena[J]. Annual Review of Fluid Mechanics, 2006, 38(1): 129-157. |
| [4] |
BUSHNELL D M. Hypersonic flight experimentation: status and shortfalls: AGARD CP-600[R]//Future Aerospace Technology in the Service of the Alliance. France: Advisory Group for Aerospace Research & Development. 1997.
|
| [5] |
MACK L M. Special course on stability and transition of laminar flow[R]. AGARD report, 1984, 709: 1-81
|
| [6] |
罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357-372. LUO J S. Transition and prediction for hypersonic boundarylayers[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357-372. (in Chinese) |
| [7] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. DOI:10.7638/kqdlxxb-2017.0030 (in Chinese) |
| [8] |
杨武兵, 沈清, 朱德华, 等. 高超声速边界层转捩研究现状与趋势[J]. 空气动力学学报, 2018, 36(2): 183-195. YANG W B, SHEN Q, ZHU D H, et al. Tendency and current status of hypersonic boundary layertransition[J]. Acta Aerodynamica Sinica, 2018, 36(2): 183-195. DOI:10.7638/kqdlxxb-2018.0011 (in Chinese) |
| [9] |
JAFFE N A, OKAMURA T T, SMITH A M O. Determination of spatial amplification factors and their application to predicting transition[J]. AIAA Journal, 1970, 8(2): 301-308. DOI:10.2514/3.5660 |
| [10] |
MALIK M R. Prediction and control of transition in hypersonic boundary layers[C]//19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference, Honolulu, HI, USA. Reston, Virigina: AIAA, 1987: 1987-1414.
|
| [11] |
CHEN F J, MALIK M R, BECKWITH I E. Boundary-layer transition on a cone and flat plate at Mach 3.5[J]. AIAA Journal, 1989, 27(6): 687-693. DOI:10.2514/3.10166 |
| [12] |
SU C H, ZHOU H. Transition prediction of a hypersonic boundary layer over a cone at small angle of attack:with the improvement of e N method[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(1): 115-123. DOI:10.1007/s11433-009-0006-4 |
| [13] |
SU C H, ZHOU H. Transition prediction for supersonic and hypersonic boundary layers on a cone with angle of attack[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(8): 1223-1232. DOI:10.1007/s11433-009-0162-6 |
| [14] |
SU C H, ZHOU H. Transition prediction of the supersonic boundary layer on a cone under the consideration of receptivity to slow acoustic waves[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(10): 1875-1882. DOI:10.1007/s11433-011-4472-0 |
| [15] |
KING R A. Three-dimensional boundary-layer transition on a cone at Mach 3.5[J]. Experiments in Fluids, 1992, 13(5): 305-314. DOI:10.1007/BF00209502 |
| [16] |
MCKENZIE J F. Interaction of linear waves with oblique shock waves[J]. Physics of Fluids, 1968, 11(11): 2350. DOI:10.1063/1.1691825 |
| [17] |
QIN F F, WU X S. Response and receptivity of the hypersonic boundary layer past a wedge to free-stream acoustic, vortical and entropy disturbances[J]. Journal of Fluid Mechanics, 2016, 797: 874-915. DOI:10.1017/jfm.2016.287 |
| [18] |
GOLDSTEIN M E. Scattering of acoustic waves into Tollmien-Schlichting waves by small streamwise variations in surface geometry[J]. Journal of Fluid Mechanics, 1985, 154: 509-529. DOI:10.1017/S0022112085001641 |
| [19] |
RUBAN A I. On tollmien-schlichting wave generation by sound[M]//Laminar-Turbulent Transition. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 313-320.
|
| [20] |
HAMMERTON P W, KERSCHEN E J. Boundary-layer receptivity for a parabolic leading edge[J]. Journal of Fluid Mechanics, 1996, 310: 243-267. DOI:10.1017/S0022112096001796 |
| [21] |
WANDERLEY J B V, CORKE T C. Boundary layer receptivity to free-stream sound on elliptic leading edges of flat plates[J]. Journal of Fluid Mechanics, 2001, 429: 1-21. DOI:10.1017/S0022112000002548 |
| [22] |
WU X S. Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances:a second-order asymptotic theory and comparison with experiments[J]. Journal of Fluid Mechanics, 2001, 431: 91-133. DOI:10.1017/S0022112000002962 |
| [23] |
CHOUDHARI M M. Boundary-layer receptivity due to distributed surface imperfections of a deterministic or random nature[J]. Theoretical and Computational Fluid Dynamics, 1993, 4(3): 101-117. |
| [24] |
SARIC W S, REED H L, KERSCHEN E J. Boundary-layer receptivity to free stream disturbances[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 291-319. |
| [25] |
FEDOROV A V, KHOKHLOV A P. Excitation of unstable modes in a supersonic boundary layer by acoustic waves[J]. Fluid Dynamics, 1992, 26(4): 531-537. DOI:10.1007/BF01050314 |
| [26] |
FEDOROV A V, KHOKHLOV A P. Prehistory of instability in a hypersonic boundary layer[J]. Theoretical and Computational Fluid Dynamics, 2001, 14(6): 359-375. DOI:10.1007/s001620100038 |
| [27] |
MASLOV A A, SHIPLYUK A N, SIDORENKO A A, et al. Leading-edge receptivity of a hypersonic boundary layer on a flat plate[J]. Journal of Fluid Mechanics, 2001, 426: 73-94. DOI:10.1017/S0022112000002147 |
| [28] |
MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions[J]. Journal of Fluid Mechanics, 2003, 488: 31-78. DOI:10.1017/S0022112003004786 |
| [29] |
MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 2. Receptivity to free-stream sound[J]. Journal of Fluid Mechanics, 2003, 488: 79-121. DOI:10.1017/S0022112003004798 |
| [30] |
BALAKUMAR P. Transition in a supersonic boundary layer due to acoustic disturbances[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2005: 96.
|
| [31] |
EGOROV I V, FEDOROV A V, SOUDAKOV V G. Direct numerical simulations of supersonic boundary layer receptivity to acoustic disturbances[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2005: 97.
|
| [32] |
BALAKUMAR P. Stability of supersonic boundary layers over blunt wedges[C]//36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, California. Reston, Virigina: AIAA, 2006: 3053.
|
| [33] |
BALAKUMAR P. Receptivity of hypersonic boundary layers to acoustic and vortical disturbances[C]//45th AIAA Fluid Dynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 2015: 2473.
|
| [34] |
CERMINARA A, SANDHAM N D. Acoustic leading-edge receptivity for supersonic/hypersonic flows over a blunt wedge[J]. AIAA Journal, 2017, 55(12): 4234-4244. DOI:10.2514/1.J055749 |
| [35] |
ZHONG X L, MA Y B. Boundary-layer receptivity of Mach 7.99 flow over a blunt cone to free-stream acoustic waves[J]. Journal of Fluid Mechanics, 2006, 556: 55. DOI:10.1017/S0022112006009293 |
| [36] |
KARA K, BALAKUMAR P, KANDIL O A. Effects of nose bluntness on hypersonic boundary-layer receptivity and stability over cones[J]. AIAA Journal, 2011, 49(12): 2593-2606. DOI:10.2514/1.J050032 |
| [37] |
LEI J, ZHONG X L. Numerical simulation of freestream waves receptivity and breakdown over Mach 6 flared cone[C]//43rd Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013.
|
| [38] |
BALAKUMAR P, CHOU A. Transition prediction in hypersonic boundary layers using receptivity and freestream spectra[J]. AIAA Journal, 2018, 56(1): 193-208. DOI:10.2514/1.J056040 |
| [39] |
BALAKUMAR P, KING R A, CHOU A, et al. Receptivity and forced response to acoustic disturbances in high-speed boundary layers[J]. AIAA Journal, 2018, 56(2): 510-523. DOI:10.2514/1.J056145 |
| [40] |
WAN B B, LUO J S, SU C H. Response of a hypersonic blunt cone boundary layer to slow acoustic waves with assessment of various routes of receptivity[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1643-1660. DOI:10.1007/s10483-018-2391-6 |
| [41] |
FEDOROV A V. Transition and stability of high-speed boundary layers[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 79-95. |
| [42] |
ZHONG X L, WANG X W. Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers[J]. Annual Review of Fluid Mechanics, 2012, 44(1): 527-561. |
| [43] |
江贤洋, 李存标. 高超声速边界层感受性研究综述[J]. 实验流体力学, 2017, 31(2): 1-11. JIANG X Y, LI C B. Review of research on the receptivity of hypersonic boundarylayer[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(2): 1-11. (in Chinese) |
| [44] |
周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M]. 北京: 科学出版社, 2015.
|
| [45] |
SU C H, GENG J L. Interaction of weak free-stream disturbance with an oblique shock:validation of the shock-capturing method[J]. Applied Mathematics and Mechanics, 2017, 38(11): 1601-1612. DOI:10.1007/s10483-017-2279-9 |
| [46] |
WAN B B, SU C H, CHEN J Q. Receptivity of a hypersonic blunt cone: role of disturbances in entropy layer[J/OL]. 2020-04-27[2020-04-28]. AIAA Journal. https: //doi.org/10.2514/1.J058816
|
| [47] |
SU C H. The reliability of the improved e-N method for the transition prediction of boundary layers on a flat plate[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(5): 837-843. DOI:10.1007/s11433-012-4692-y |
| [48] |
WU X, STEWART P A, COWLEY S J. On the catalytic role of the phase-locked interaction of Tollmien-Schlichting waves in boundary-layer transition[J]. Journal of Fluid Mechanics, 2007, 590: 265-294. DOI:10.1017/S002211200700804X |
| [49] |
WU X. Nonlinear theories for shear flow instabilities:physical insights and practical implications[J]. Annual Review of Fluid Mechanics, 2019, 51(1): 451-485. |
| [50] |
张永明, 周恒. PSE在可压缩边界层转捩问题中的应用[J]. 应用数学和力学, 2008, 29(7): 757-763. ZHANG Y M, ZHOU H. PSE as applied to problems of transition in compressible boundarylayers[J]. Applied Mathematics and Mechanics, 2008, 29(7): 757-763. DOI:10.3879/j.issn.1000-0887.2008.07.001 (in Chinese) |
| [51] |
LUO J S. Inherent mechanism of breakdown in laminar-turbulent transition of plane channel flows[J]. Science in China Series G, 2005, 48(2): 228. DOI:10.1360/04yw0168 |
| [52] |
TANG H, LUO J, ZHOU H. Mechanism of breakdown in laminar-turbulent transition of incompressible boundary layer on a flat plate[J]. Transaction of Tianjin University, 2007, 13(2): 79-87. |
| [53] |
HUANG Z F. The mechanism of breakdown in laminar-turbulent transition of a supersonic boundary layer on a flat plate-temporal mode[J]. Science in China Series G, 2005, 48(5): 614. DOI:10.1360/142005-19 |
| [54] |
CAO W, HUANG Z F, ZHOU H. Study of mechanism of breakdown in laminar-turbulent transition of supersonic boundary layer on flat plate[J]. Applied Mathematics and Mechanics, 2006, 27(4): 425-434. DOI:10.1007/s10483-006-0401-1 |
| [55] |
DONG M, ZHOU H. A simulation on bypass transition and its key mechanism[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(4): 775-784. DOI:10.1007/s11433-013-5036-2 |
| [56] |
ZHU Y D, ZHANG C H, CHEN X, et al. Transition in hypersonic boundary layers:role of dilatational waves[J]. AIAA Journal, 2016, 54(10): 3039-3049. DOI:10.2514/1.J054702 |
| [57] |
MARINEAU E C. Prediction methodology for second-mode-dominated boundary-layer transition in wind tunnels[J]. AIAA Journal, 2017, 55(2): 484-499. DOI:10.2514/1.J055061 |
| [58] |
MARINEAU E C, GROSSIR G, WAGNER A, et al. Analysis of second-mode amplitudes on sharp cones in hypersonic wind tunnels[J]. Journal of Spacecraft and Rockets, 2019, 56(2): 307-318. DOI:10.2514/1.A34286 |
| [59] |
SARIC W S, REED H L, WHITE E B. Stability and transition of three-dimensional boundary layers[J]. Annual Review of Fluid Mechanics, 2003, 35(1): 413-440. |
| [60] |
徐家宽, 白俊强, 乔磊, 等. 横流不稳定性转捩预测模型[J]. 航空学报, 2015, 36(6): 1814-1822. XU J K, BAI J Q, QIAO L, et al. Transition model for predictingcrossflow instabilities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1814-1822. (in Chinese) |
| [61] |
WANG L, XIAO L H, FU S. A modular RANS approach for modeling hypersonic flow transition on a scramjet-forebody configuration[J]. Aerospace Science and Technology, 2016, 56: 112-124. DOI:10.1016/j.ast.2016.07.004 |
| [62] |
黄章峰, 逯学志, 于高通. 机翼边界层的横流稳定性分析和转捩预测[J]. 空气动力学学报, 2014, 32(1): 14-20. HUANG Z F, LU X Z, YU G T. Cross-flow instability analysis and transition prediction of airfoil boundarylayer[J]. Acta Aerodynamica Sinica, 2014, 32(1): 14-20. (in Chinese) |
| [63] |
朱震, 宋文萍, 韩忠华. 基于双eN方法的翼身组合体流动转捩自动判断[J]. 航空学报, 2018, 39(2): 128-139. ZHU Z, SONG W P, HAN Z H. Automatic transition prediction for wing-body configurations using dual eN method[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 128-139. (in Chinese) |
| [64] |
MALIK M R, LI F, CHANG C L. Crossflow disturbances in three-dimensional boundary layers:nonlinear development, wave interaction and secondary instability[J]. Journal of Fluid Mechanics, 1994, 268: 1-36. DOI:10.1017/S0022112094001242 |
| [65] |
REIBERT M, SARIC W, REIBERT M, et al. Review of swept-wing transition[C]//28th Fluid Dynamics Conference, Snowmass Village, CO, USA. Reston, Virigina: AIAA, 1997: 1816.
|
| [66] |
DEYHLE H, BIPPES H. Disturbance growth in an unstable three-dimensional boundary layer and its dependence on environmental conditions[J]. Journal of Fluid Mechanics, 1996, 316: 73-113. DOI:10.1017/S0022112096000456 |
| [67] |
MALIK M R, LI F, CHOUDHARI M M, et al. Secondary instability of crossflow vortices and swept-wing boundary-layer transition[J]. Journal of Fluid Mechanics, 1999, 399: 85-115. DOI:10.1017/S0022112099006291 |
| [68] |
WHITE E B, SARIC W S. Secondary instability of crossflow vortices[J]. Journal of Fluid Mechanics, 2005, 525: 275-308. DOI:10.1017/S002211200400268X |
| [69] |
LI F, CHOUDHARI M M, CHANG C L, et al. Computational modeling of roughness-based laminar flow control on a subsonic swept wing[J]. AIAA Journal, 2011, 49(3): 520-529. DOI:10.2514/1.J050503 |
| [70] |
LI F, CHOUDHARI M M, DUAN L. Stationary crossflow breakdown due to mixed mode spectra of secondary instabilities[C]//46th AIAA Fluid Dynamics Conference, Washington, D. C.. Reston, Virginia: AIAA, 2016: 3789.
|
| [71] |
LI F, CHOUDHARI M M, DUAN L. Stationary crossflow breakdown due to interaction between secondary instabilities[C]//47th AIAA Fluid Dynamics Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017: 4302.
|
| [72] |
KOCIAN T S, MOYES A J, REED H L, et al. Hypersonic crossflow instability[J]. Journal of Spacecraft and Rockets, 2019, 56(2): 432-446. DOI:10.2514/1.A34289 |
| [73] |
CRAIG S A, SARIC W S. Crossflow instability in a hypersonic boundary layer[J]. Journal of Fluid Mechanics, 2016, 808: 224-244. DOI:10.1017/jfm.2016.643 |
| [74] |
EDELMAN J B, SCHNEIDER S P. Secondary instabilities of hypersonic stationary crossflow waves[J]. AIAA Journal, 2018, 56(1): 182-192. DOI:10.2514/1.J056028 |
| [75] |
MUÑOZ F, HEITMANN D, RADESPIEL R. Instability modes in boundary layers of an inclined cone at Mach 6[J]. Journal of Spacecraft and Rockets, 2014, 51(2): 442-454. DOI:10.2514/1.A32564 |
| [76] |
NIU H B, YI S H, LIU X L, et al. Experimental study of crossflow instability over a delta flat plate at Mach 6[J]. AIAA Journal, 2019, 57(12): 5566-5574. DOI:10.2514/1.J058576 |
| [77] |
MOYES A J, PAREDES P, KOCIAN T S, et al. Secondary instability analysis of crossflow on a hypersonic yawed straight circular cone[J]. Journal of Fluid Mechanics, 2017, 812: 370-397. DOI:10.1017/jfm.2016.793 |
| [78] |
XU G L, CHEN J Q, LIU G, et al. The secondary instabilities of stationary cross-flow vortices in a Mach 6 swept wing flow[J]. Journal of Fluid Mechanics, 2019, 873: 914-941. DOI:10.1017/jfm.2019.397 |
| [79] |
韩宇峰, 马绍贤, 苏彩虹. 高超声速三维边界层横流转捩的数值研究[J]. 空气动力学学报, 2019, 37(4): 522-529. HAN Y F, MA S X, SU C H. Numerical study on cross-flow transition in three-dimensional hypersonic boundary layers[J]. Acta Aerodynamica Sinica, 2019, 37(4): 522-529. DOI:10.7638/kqdlxxb-2019.0015 (in Chinese) |
| [80] |
HAN Y F, SU C H. Numerical Research on Mechanism of Cross-Flow Induced Transition in a Hypersonic Boundary Layer. IUTAM-Transition, 2019, London, 2019.9. 2-6.
|
| [81] |
MALIK M R. 'COSAL' A black box compressible stability analysis code for transition prediction in three-dimensional boundary layers[R]. NASA CR-165925, 1982.
|
| [82] |
MACK L M. Stability of three-dimensional boundary layers on swept wings at transonic speeds[M]//Symposium Transsonicum Ⅲ. Berlin, Heidelberg: Springer Berlin Heidelberg, 1989: 209-223.
|
| [83] |
CEBECI T, STEWARTSON K. On stability and transition in three-dimensional flows[J]. AIAA Journal, 1980, 18(4): 398-405. DOI:10.2514/3.50772 |
| [84] |
SU C H, ZHOU H. Stability analysis and transition prediction of hypersonic boundary layer over a blunt cone with small nose bluntness at zero angle of attack[J]. Applied Mathematics and Mechanics, 2007, 28(5): 563-572. DOI:10.1007/s10483-007-0501-1 |
| [85] |
于高通, 罗纪生. 三维高超声速边界层中e-N方法的应用[J]. 航空动力学报, 2014, 29(9): 2047-2054. YU G T, LUO J S. Application of e N method in three-dimensional hypersonic boundary layers[J]. Journal of Aerospace Power, 2014, 29(9): 2047-2054. (in Chinese) |
| [86] |
SU C H. Physical implication of two problems in transition prediction of boundary layers based on linear stability theory[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(5): 950-962. |
| [87] |
于高通.高超声速三维边界层e-N方法的应用及扰动演化的预测[D].天津: 天津大学, 2015. YU G T. Application of e-N method and prediction of disturbances propagation in three-dimensional hypersonic boundarylayers[D]. Tianjin: Tianjin University, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10056-1017134281.htm |
| [88] |
ZHAO L, YU G T, LUO J S. Extension of e N method to general three-dimensional boundary layers[J]. Applied Mathematics and Mechanics, 2017, 38(7): 1007-1018. DOI:10.1007/s10483-017-2215-6 |
| [89] |
SONG R J, ZHAO L, HUANG Z F. Conservation relation of generalized growth rate in boundary layers[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1755-1768. DOI:10.1007/s10483-018-2394-9 |
| [90] |
LI J, LUO J S. Applications of parabolized stability equation for predicting transition position in boundary layers[J]. Applied Mathematics and Mechanics, 2012, 33(6): 679-686. DOI:10.1007/s10483-012-1579-7 |
| [91] |
CEBECI T, SHAO J, CHEN H, et al. On the calculation of initial conditions for parabolized stability equations for predicting transition[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2004: 98.
|
| [92] |
CHANG C L. LASTRAC. 3d: transition prediction in 3D boundary layers[C]//34th AIAA Fluid Dynamics Conference and Exhibit, Portland, Oregon. Reston, Virigina: AIAA, 2004: 2542.
|
| [93] |
PAREDES P, THEOFILIS V, RODRIGUEZ D, et al. The PSE-3D instability analysis methodology for flows depending strongly on two and weakly on the third spatial dimension[C]//6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii. Reston, Virigina: AIAA, 2011: 3752.
|
| [94] |
YU G T, GAO J, LUO J S. Stability analysis method considering non-parallelism:EPSE method and its application[J]. Applied Mathematics and Mechanics, 2016, 37(1): 27-36. DOI:10.1007/s10483-016-2013-9 |
| [95] |
HAN Y F, LIU J X, LUO J S. Improvement for expansion of parabolized stability equation method in boundary layer stability analysis[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1737-1754. DOI:10.1007/s10483-019-2401-9 |
| [96] |
苏彩虹, 宋明真.超声速边界层中的模态转换及壁温影响效应[J/OL]. 2019-10-10[2020-03-05].空气动力学学报. http://journal16.magtechjournal.com/Jweb_aas/CN/abstract/abstract12424.shtml SU C H, SONG M Z. Intermodal exchange and wall temperature effect in a supersonic boundary layer[J/OL]. 2019-10-10[2020-03-05]. Acta Aerodynamica Sinica. http://journal16.magtechjournal.com/Jweb_aas/CN/abstract/abstract12424.shtml. (in Chinese) doi: 10.7638/kqdlxxb-2019.0048 |
| [97] |
周恒, 张涵信. 有关近空间高超声速飞行器边界层转捩和湍流的两个问题[J]. 空气动力学学报, 2017, 35(2): 151-155. ZHOU H, ZHANG H X. Two problems in the transition and turbulence for near space hypersonic flying vehicles[J]. Acta Aerodynamica Sinica, 2017, 35(2): 151-155. DOI:10.7638/kqdlxxb-2017.0016 (in Chinese) |
| [98] |
DUAN L, CHOUDHARI M M, CHOU A, et al. Characterization of freestream disturbances in conventional hypersonic wind tunnels[J]. Journal of Spacecraft and Rockets, 2019, 56(2): 357-368. DOI:10.2514/1.A34290 |
 2020, Vol. 38
2020, Vol. 38