2. 国网浙江省电力有限公司, 杭州 310007
2. State Grid Zhejiang Electric Power Company Limited, Hangzhou 310007, China
山区地形比平地更为复杂,特别是双山风场,风经过山地时会引起风场的较大变化。现有关于山地风场的规范中,均采用在平地风场基础上考虑修正因子来表达山地风场。但目前关于山地风场的规范公式只针对二维或三维的单个山体,对于双山风场没有规定。
现场实测[1-3]、数值模拟计算[4-6]和风洞试验[7-13]是研究山地风场常用的研究方法。现场实测能获得风流经山体时的实际情况,数据可用做其他研究方法的基准,但代价十分昂贵,更常规的是采用CFD模拟和风洞试验进行山地风场的研究。De Bray[5]和Jackson等[6]提出了上下游的风速模型和平面对称山体的风速剖面模型;Kim等[7]和Breuer等[8]给出了二维山体的风场分布;肖仪清等[9]利用CFD对复杂地形进行模拟计算,并与实测结果进行对比;李朝[10]、孙毅等[11]、沈国辉等[12]和姚旦等[13]利用风洞试验方法研究了不同形状山体的风场,给出了水平风速的加速比。以上研究成果主要体现了单山的风场特征,而双山的风场特征有待进一步研究;各国规范没有给出双山风场的规定。
基于以上背景,本文采取CFD数值模拟方法研究双山地形的风场特性,分析双山左右排列、前后排列和斜列三种情况下水平风的加速效应,给出加速比等值线图以探讨双山的风场特征,对比了CFD模拟和风洞试验结果,最后将研究结果与各国规范规定进行对比,研究成果供相关工程设计人员参考。
1 各国规范关于山体风场的规定(1) 中国规范GB 50009-2012[14]采用风压高度变化系数的地形修正系数来考虑山地地形的影响,其中山顶处修正系数ηB的表达式为:
| $ {\eta _B} = {\left[ {1 + \kappa \cdot {\rm{tan}}\alpha \cdot \left( {1 - \frac{z}{{2.5H}}} \right)} \right]^2} $ | (1) |
式中:tanα为迎风面坡度(山峰或山坡);当坡度大于0.3时,tanα取0.3;κ对于山峰和山坡分别为2.2和1.4;H为山顶或山坡的高度;z为离山体表面的高度。
(2) 美国规范ASCE 7-10[15]采用基于风压的修正因素Kzt来考虑山地风场:
| $ {K_{zt}} = {(1 + {K_1}{K_2}{K_3})^2} $ | (2) |
式中:K1为增速因子,K2为水平距离换算因子,K3为垂直距离的换算因子。
(3) 欧洲规范EN 2004-1-4[16]采用基于风速的修正因素来考虑山地风场:
| $ {C_0} = 1 + ks\phi $ | (3) |
式中:k为常数;s为地形系数;ϕ为迎风面的坡度。
(4) 澳大利亚/新西兰规范AS/NZS 1170.2: 2011[17]采用基于风速的修正因素Mh来考虑山地风场。当0.05≤H/2L < 0.45时:
| $ {M_h} = 1 + \frac{H}{{3.5(z + {L_1})}}\left( {1 - \frac{{\left| x \right|}}{{{L_2}}}} \right) $ | (4) |
式中:L1=max(0.36L,0.4H);L为山顶至迎风坡上高度为山顶1/2处的水平距离;对山坡而言,L2在迎风面取4L1,在背风面取10L1,对山脊而言,L2在迎风面和背风面都取4L1。
(5) 日本规范AIJ 2004[18]采用修正系数Eg来考虑山地风场:
| $ \begin{array}{l} {E_g} = \left( {{C_1} - 1} \right)\left[ {{C_2}\left( {\frac{Z}{{{H_s}}} - {C_3}} \right) + 1} \right] \cdot \\ \;\;\;\;\;\;\;{\rm{exp}}\left[ { - {C_2}\left( {\frac{Z}{{{H_s}}} - {C_3}} \right)} \right] + 1 \end{array} $ | (5) |
式中:Hs为山坡高度,计算参数C1、C2、C3采用相关图表给出。
2 双山工况的CFD数值模拟计算双山工况山体采用常见的余弦形三维山体,底部直径D为300 m,高度H为100 m,平均坡度为33.69°。余弦形三维山体的轮廓方程满足:
| $ z\left( {x, y} \right) = H\;{\rm{co}}{{\rm{s}}^2}\left[ {\frac{{\pi {{({x^2} + {y^2})}^{\frac{1}{2}}}}}{D}} \right] $ | (6) |
式中:z为高度方向,x、y为水平方向。
采用FLUENT软件计算双山情况的平均风速,网格划分如图 1所示,计算域划分为:长度方向上双山中心与入流面距离为3D,双山中心与出流面距离为4.5D;高度方向为8H;宽度方向随双山位置的改变而改变。流场内采用结构化六面体单元网格进行划分,所有工况下山体的阻塞率均小于3%。

|
图 1 双山的网格划分 Fig.1 Grid meshing of two adjacent hills |
湍流采用Realizable k-ε模型,依据荷载规范[14]定义来流风剖面及湍流度,地貌类型为B类,地貌粗糙度指数α为0.15,基本风速为30 m/s。风剖面、湍流度、湍流动能k和湍流耗散率ε均通过UDF(User-defined function)输入,各物理量表达如下:
| $ u = {u_{10}}{\left( {z/10} \right)^{0.15}} $ | (7) |
| $ {{I}_{u}}=0.14{{\left( z/10 \right)}^{-0.15}} $ | (8) |
| $ k=3{{(u{{I}_{u}})}^{2}}/2 $ | (9) |
| $ \varepsilon =C_{\mu }^{3/4}{{k}^{3/2}}/l $ | (10) |
式中:Cμ=0.09;l为湍流积分尺度。入流面和出流面分别设定速度入口和压力出口,流场侧面、顶面设定为对称面,山体表面和流场底面设为壁面,计算时近壁面的流动采用非平衡壁面函数进行模拟,数值离散格式采用二阶格式。山体表面的粗糙高度设为1 m,地面的粗糙高度设为0 m。
为定量表征双山地形风速对于平地地形的加速效应,定义水平风的加速比s为:
| $ s\left( z \right)=u\left( z \right)/{{u}_{0}}\left( z \right) $ | (11) |
式中:u(z)为离山表面z高度的风速,u0(z)为无干扰来流情况离平地z高度处的风速。
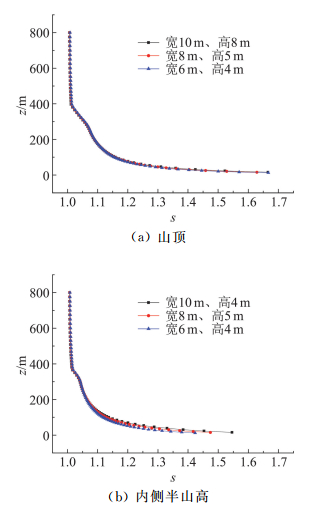
针对双山左右排列且间距为0的情况进行网格独立性验证,分别计算了:①宽10 m、高8 m,②宽8 m、高5 m,③宽6 m、高4 m的网格结果,网格数分别为101万、113万和130万,计算结果的收敛性均较好,其中山顶和内侧半山高的加速比如图 2所示,可见宽8 m、高5 m网格划分的计算结果已非常接近宽6 m、高4 m网格划分的结果。考虑到大规模计算的需要,本文后续采用宽8 m、高5 m的网格划分。
|
图 2 网格独立性验证 Fig.2 Grid independence verification |
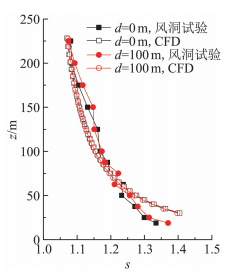
为验证CFD模拟的准确性,针对典型工况进行风洞试验,几何缩尺比为1:500,山体形状为余弦形,左右排列山体间距分别为d=0 m和100 m。试验在B类地貌下进行,如图 3所示,采用五孔风速探针进行风速测试。CFD模拟与风洞试验在两山间距d=0 m、100 m时山顶位置的加速比如图 4所示,可知:1) CFD和风洞试验结果总体上比较接近;2) CFD结果比较光滑,风洞试验结果较离散;3)当z>60 m时风洞试验结果略大,当z < 50 m时CFD结果略大;4)两者差异主要由湍流模型、表面粗糙度处理、数值计算误差和风洞试验误差等原因引起。

|
图 3 左右排列双山的风洞试验 Fig.3 Testing of two adjacent hills in parallel arrangement |
|
图 4 山顶位置的加速比对比 Fig.4 Comparison of acceleration ratios on hill top |
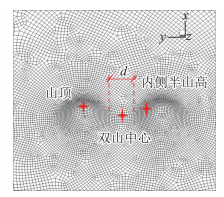
左右排列双山的网格划分如图 5所示,其中双山间距d分别取0 m、50 m、100 m、200 m和300 m。
|
图 5 左右排列双山的网格划分 Fig.5 Grid meshing of two hills in parallel arrangement |
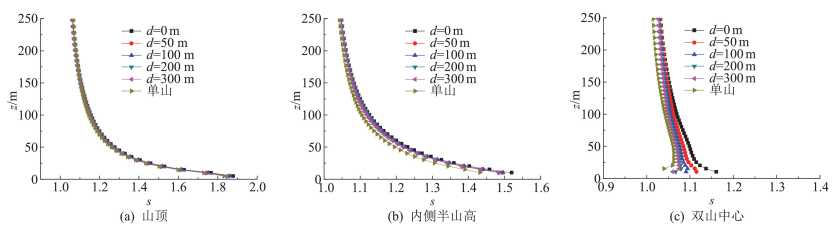
山体间距d为0~300 m时山顶、内侧半山高和双山中心的加速比如图 6所示,由图可知:1)山顶加速比最大,双山中心加速比最小,各加速比均随着高度的增加而减小;2)山顶加速比与山体间距的关系很小,且与单山结果非常接近;3)内侧半山高位置的加速比随着山体间距增大略有减小趋势,但均大于单山结果;4)双山中心的加速比随着山体间距增大呈减小趋势,单山的山体侧风面的山脚处的加速比最小,单山相当于双山间距无穷远情况。
|
图 6 左右排列双山的加速比 Fig.6 Speed-up ratios of two hills in parallel arrangement |
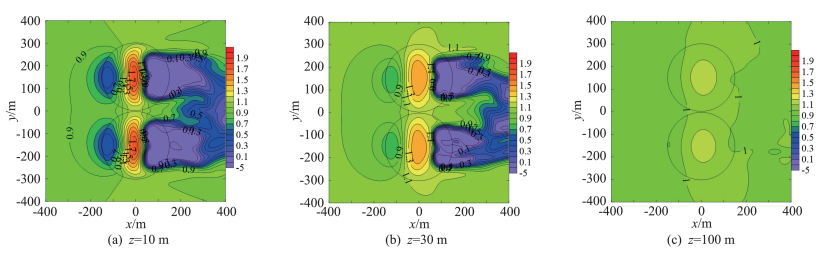
图 7给出了双山d=0 m时距离山体(平地)表面z=10 m、30 m和100 m的加速比等值线,由图可知:1)山前存在减速区,加速区出现在山顶及横风方向的山坡,最大加速比出现在山顶,山后为尾流区;2) z=10 m高度的加速比较大,而z=100 m高度的加速比较小,且开始趋向均匀,可以预见,离表面高度更大时加速比会趋向于1;3)不同高度情况下双山中心的加速比不大,不如山顶显著。
|
图 7 不同高度的加速比等值线 Fig.7 Contour of speed-up ratios on different heights |
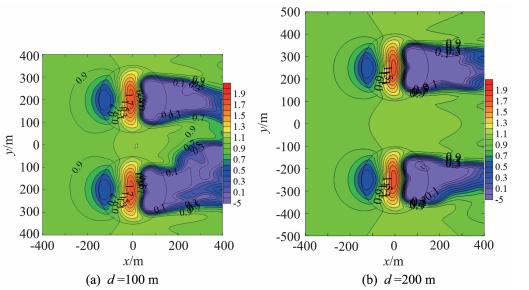
图 8给出了z=10 m高度d=100 m和200 m时加速比等值线,d=0 m时加速比见图 7(a),由图可知:1)山顶和山体上的加速比非常接近,山体间距的影响较小;2)双山尾流区在d=0 m时连在一起,随着山间距的增大尾流区慢慢分离,成为两个独立的尾流区;3)双山中心在d=0 m时加速比在1.1~1.2之间,随着山间距的增大,减小至1。
|
图 8 不同山间距的加速比等值线图 Fig.8 Contour of speed-up ratios on different hill distances |
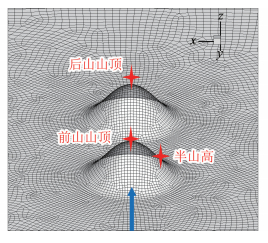
前后紧密排列双山工况的网格划分如图 9所示,前后双山距离d=0 m。
|
图 9 前后排列双山的网格划分 Fig.9 Grid meshing of two hills in tandem arrangement |
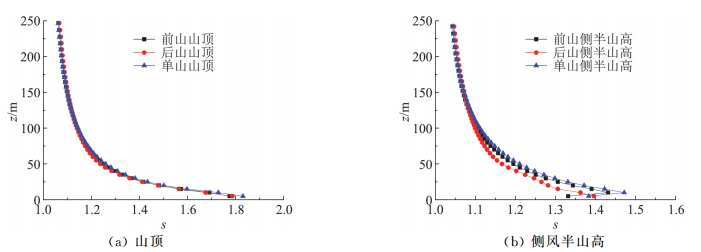
前后紧密排列双山工况加速比如图 10所示,可知:1)山顶的加速比较大,加速比随着高度的增加而减小;2)山顶处,前山、后山和单山的加速比非常接近,后山山顶的加速比略小,主要是受前山的遮挡;3)半山高处,存在单山>前山>后山的规律,主要是前山对后山有一定的遮挡效应,而后山的存在使得前山流速略有降低,单山情况的加速比最大。
|
图 10 前后排列双山的加速比 Fig.10 Speed-up ratios of two hills in tandem arrangement |
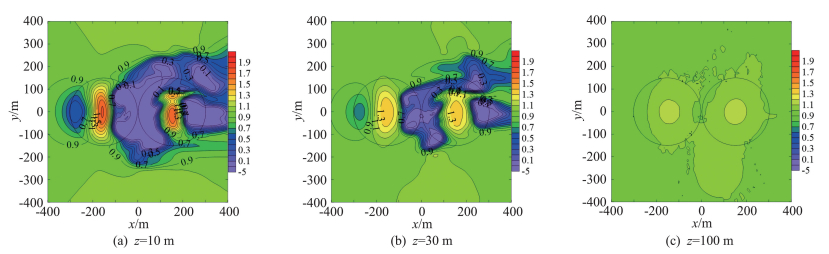
图 11给出了前后紧密排列双山z=10 m、30 m和100 m的加速比,可知:1)总体上后山处于前山的尾流区,后山的加速比小于前山,加速比呈单山>前山>后山的规律;2) z=10 m高度的加速比变化较大,z=100 m高度的加速比变化较小,且开始趋向均匀,可以预见,离表面高度更大时加速比均会趋向1。
|
图 11 不同高度的加速比等值线图 Fig.11 Contour of speed-up ratios on different heights |
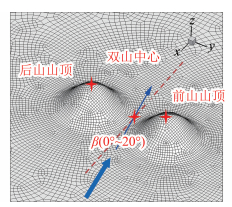
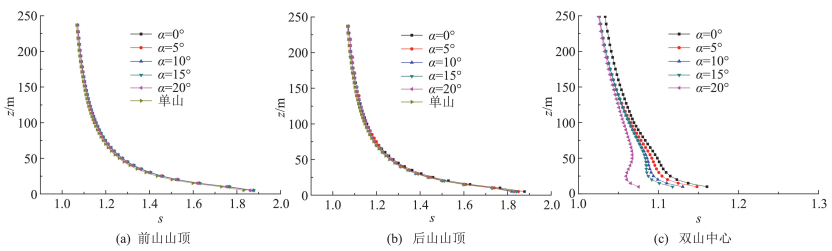
由于斜列工况较多,限于篇幅,本文只给出干扰效应最显著的紧密排列工况,即d=0 m。同时风向角β取狭道风效应最显著的几个角度,即0°、5°、10°、15°和20°。斜列情况下双山的网格划分和风向角定义如图 12所示,风向角取0°~20°,两山间距d取0 m。斜列情况下前山山顶、后山山顶和双山中心的加速比如图 13所示,可知:1)斜列情况下前山和后山山顶的加速比差别不大,均与单山山顶结果非常接近;2)双山中心的加速比随着风向角的增大而减小,说明风向角增大后双山中间的流速降低。
|
图 12 斜列情况下双山的网格划分 Fig.12 Grid meshing of two hills in staggered arrangement |
|
图 13 斜列情况双山的加速比 Fig.13 Speed-up ratio of two hills in staggered arrangement |
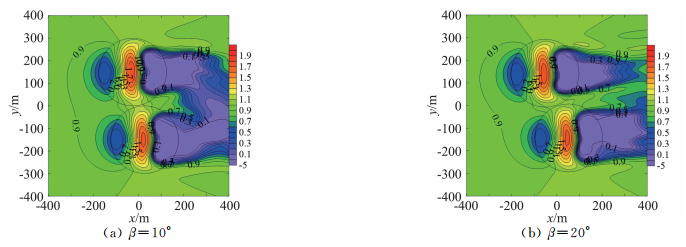
图 14给出了双山在风向角β=10°和20°时z= 10 m高度加速比的等值线,β=0°情况见图 7(a),由图可知:1)总体上不同角度风情况下山体上的加速比分布比较相似,即山前是减速区,山顶是加速区,山后是尾流区;2)山顶和山体上的加速比比较接近,山间距的影响较小;3)双山尾流区在β=0°时连在一起,随着风向角的增大,双山的尾流区慢慢分离,成为两个独立的尾流区。
|
图 14 斜列情况加速比的等值线 Fig.14 Contour of speed-up ratios in staggered arrangement |
对于山地风场,各国规范只对于孤立单山进行了详细的相关规定,没有对双山风场进行说明。而山区建筑物或者构筑物高度一般不会太高,取z为20 m~150 m时的加速比进行比较。
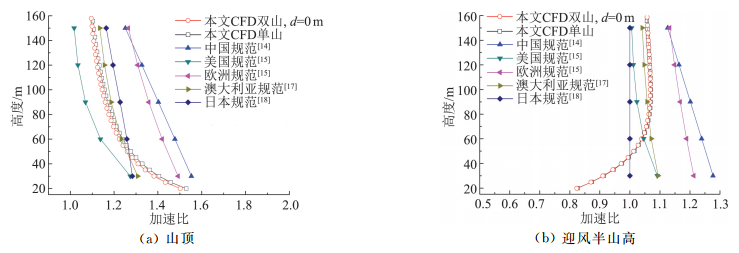
图 15给出了单山和左右排列双山典型位置加速比及与规范的比较,由图可知:1)本文单山和双山在两个典型位置处加速比几乎一样;2)山顶加速比最大的是中国规范,其次为欧洲规范,美国规范最小,当z>60 m时本文CFD结果与澳大利亚、日本规范比较接近,当z < 60 m时本文CFD结果与澳大利亚、欧洲规范比较接近;3)在迎风半山高处,加速比最大为中国规范,欧洲规范次之,日本规范最小,在z>80 m时与澳大利亚规范非常接近,在50 m以下本文CFD结果的加速比小于1,而规范的值都大于等于1;4)总体而言本文CFD结果与澳大利亚规范比较接近,中国规范比较保守。
|
图 15 典型位置加速比与规范数据的比较 Fig.15 Comparison of speed-up ratios of typical positions with those calculated by Codes |
本文对双山地形风场进行研究,有以下结论:
1) 左右排列双山情况下,双山加速比的分布与单山基本相同;随着山体间距的减少,双山的加速比呈稍微增加的趋势,双山间距为0 m时加速比最大,单山加速比最小,单山相当于双山间距无穷远的情况;典型工况下本文CFD结果与风洞试验结果比较接近,验证了本文CFD方法的可靠性。
2) 前后紧密排列双山情况下,前山对后山有一定的遮挡效应,而后山的存在使得前山的流速略有降低,单山情况的加速比最大;加速比总体上呈单山>前山>后山的趋势,但差别较小。
3) 斜列情况下,角度风对前山和后山山顶的加速比影响很小;双山中心位置的加速比随着风向角的增大而减小,说明风向角增大后双山中间的流速降低了;双山尾流区在风向角0°时连在一起,随着风向角的增大,双山的尾流区慢慢分离成为两个独立的尾流区。
4) 各国规范中,中国和欧洲规范的数据较大;与本文CFD结果最接近的为澳大利亚规范,中国规范对山地风场的规定相对比较保守;规范只给出了单山迎风剖面上的风速加速比,本文给出了各种工况下双山的风速加速比。
| [1] |
MICKLE R E, SALMON J R, TAYLOR P A. Kettles Hill 1984: velocity profile measurements over a low hill[R]. Atmospheric Environment Service, Downsview, Canada, 1984.
|
| [2] |
MASON P J. Diurnal variations in flow overa succession of ridges and valleys[J]. Quarterly Journal of the Royal Meteorological Society, 2007, 113(478): 1117-1140. |
| [3] |
WALMSLEY J L, TAYLOR P A. Boundary-layer flow over topography:Impacts of the Askervein study[J]. Boundary-Layer Meteorology, 1996, 78(3/4): 291-320. |
| [4] |
吉柏锋, 柳广义, 尹旭, 等. 地面粗糙度对下击暴流风剖面特征影响[J]. 空气动力学学报, 2019, 37(3): 393-399. JI B F, LIU G Y, YIN X, et al. Effects of terrain roughness on downburst wind profile characteristics[J]. Acta Aerodynamica Sinica, 2019, 37(3): 393-399. (in Chinese) |
| [5] |
DE BRAY B G. Atmospheric shear flows over ramps and escarpments[J]. Industrial Aerodynamics Abstracts, 1973, 9(1-4). |
| [6] |
JACKSON P S, HUNT J C R. Turbulent wind flow over a low hill[J]. Quarterly Journal of the Royal Meteorological Society, 1975, 101(430): 929-955. |
| [7] |
KIM H G, LEE C M, LIM H C, et al. An experimental and numerical study on the flow over two-dimensional hills[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 66(1): 17-33. |
| [8] |
BREUER M, PELLER N, RAPP C, et al. Flow over periodic hills-Numerical and experimental study in a wide range of Reynolds numbers[J]. Computers & Fluids, 2009, 38(2): 433-457. |
| [9] |
肖仪清, 李朝, 欧进萍, 等. 复杂地形风能评估的CFD方法[J]. 华南理工大学学报(自然科学版), 2009, 37(9): 30-35. XIAO Y Q, LI C, OU J P, et al. CFD approach to evaluation of wind energy in complex terrain[J]. Journal of South China University of Technology (Natural Science Edition), 2009, 37(9): 30-35. (in Chinese) |
| [10] |
李朝.近地湍流风场的CFD模拟研究[D].哈尔滨: 哈尔滨工业大学, 2010. LI C. Study on CFD simulation of turbulence wind field near ground[D]. Harbin: Harbin Institute of Technology, 2010. (in Chinese) |
| [11] |
孙毅, 李正良, 黄汉杰, 等. 山地风场平均及脉动风速特性试验研究[J]. 空气动力学学报, 2011, 29(5): 593-599. SUN Y, LI Z L, HUANG H J, et al. Experimental research on mean and fluctuating wind velocity in hilly terrain wind field[J]. Acta Aerodynamica Sinica, 2011, 29(5): 593-599. (in Chinese) |
| [12] |
沈国辉, 姚旦, 余世策, 等. 单山和双山风场特性的风洞试验[J]. 浙江大学学报(工学版), 2016, 50(5): 805-812. SHEN G H, YAO D, YU S C, et al. Wind tunnel test of wind field characteristics on isolated hill and two adjacent hills[J]. Journal of Zhejiang University(Engineering Science), 2016, 50(5): 805-812. (in Chinese) |
| [13] |
姚旦.山丘地形风场特性及对输电塔的风荷载作用研究[D].杭州: 浙江大学, 2014. YAO D. Research on characteristics of wind field on hillv terrain and its wind load effect on lattice transmission towers[D]. Hangzhou: Zhejiang University, 2014. (in Chinese) |
| [14] |
建筑结构荷载规范: GB50009-2012[S].北京: 中国建筑工业出版, 2012. Load code for the design of building structures: GB50009-2012[S]. Beijing: China Architecture and Building Press, 2012. (in Chinese) |
| [15] |
AS CE. Minimum design loads for buildings and other structures[M]. Reston, VA: American Society of Civil Engineers, 2003.
|
| [16] |
European standard EN1991-1-4. Actions on structures[S]. Brussels: European Committee for Standardization, 2004.
|
| [17] |
Australian/New Zealand standard: AS/NZS 1170.0[S]. Sydney: AS/NZS, 2002.
|
| [18] |
AIJ recommendations for loads on buildings[S]. Tokyo: Architectural Institute of Japan, 2004.
|
 2020, Vol. 38
2020, Vol. 38

