再入飞行器再入过程中由于气动烧蚀和侵蚀的作用,气动外形呈现小不对称特征,从而产生较小量级的滚转力矩。在此小量级滚转力矩作用下,当飞行器滚转速率与俯仰速率接近时易发生滚转共振现象,极大降低飞行性能[1-2];当飞行器滚转速率接近零时, 将导致落点精度下降[3];同时也可能由于配平迎角过大而产生过大的横向过载,带来结构强度方面的问题。如何准确地测定此小量级滚转力矩, 为再入飞行器的滚控设计提供依据显得尤为重要。
但是,由于烧蚀产生的外形小不对称所引起的滚转力矩非常小,平均滚转力矩系数低至10-6~10-5量级,波动量低至10-3~10-4量级,所以测量难度非常大,传统静态天平测量方法难以满足要求。针对小滚转力矩试验测量的这一难点,国内外作出了一定的研究工作[3-14]。在研究早期,Williams[4]以圆锥模型等作为研究对象,试验给出了烧蚀的产生和变化结果,并采用直接测量方式确认了烧蚀产生的滚转力矩作用。随着测量技术的不断发展,为了对小滚转力矩进行精确测量,其中一种思路是固定天平测量法,对测量天平进行结构优化,提高滚转力矩量的测量精度。如蒋忠东等[5]、王树民等[6]采用气浮轴承与固定天平相结合的方式,天平仅受到滚转力矩量的作用,避免了天平强度和灵敏度间的矛盾,实现了固定姿态模型的小滚转静力矩系数测量。刘明霞等[7]、于卫青等[8, 9]、秦永明等[10]利用滚珠轴承、简支梁等机构对测量天平进行结构改进,抑制其他五个测量单元干扰的同时减小摩擦阻尼对滚转力矩单元的影响,从而达到提高滚转力矩测量灵敏度的目的。Wang等[11]采用复合式结构,在提高滚转力矩量测量的同时兼顾了其他分量的测量。另一种思路是自由滚转测量法,如白葵等[12]利用基于气浮轴承的自由滚转试验方法,实现了平均小滚转气动力矩系数和滚转阻尼力矩系数测量。赵俊波等[13-14]在基于气浮轴承系统试验技术的基础上,进一步获取了滚转静力矩的周期性动态波动量。
由于设备条件所限,上述针对再入飞行器小量级滚转力矩系数测量试验研究工作均在Φ0.5 m量级高超声速风洞中展开,且各自具有一定的局限性:固定天平测量方式测量精度较低,且不能兼顾滚转阻尼力矩系数的测量;传统气浮轴承自由滚转测量方式试验迎角范围较小,最大迎角约6°。随着对再入战略武器有效突防要求的不断提高,再入飞行器型号的不断创新发展,研制过程中出现了大口径风洞、大迎角范围试验测量的迫切需求,随之出现气动载荷增加、模型转动惯量增大等问题以及一系列衍生技术难题。
本文在近年来Φ0.5 m量级风洞以气浮轴承为核心建立的低阻尼自由滚转测量试验技术的研究工作[13-14]基础上,针对大口径风洞进行了试验系统的优化改进和创新,发展了Φ1 m高超声速风洞再入飞行器小滚转气动力矩测量试验技术,并完成试验模型高马赫数、大迎角条件下多个状态点的小滚转力矩精细化测量试验研究。
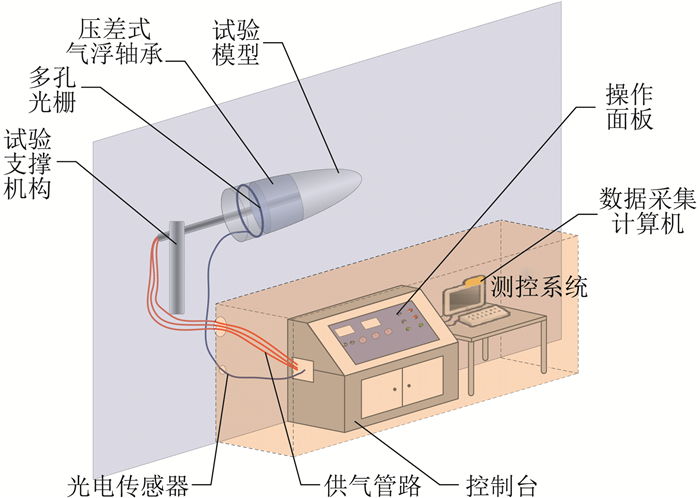
1 试验系统Φ1 m高超声速风洞再入飞行器小滚转气动力测量试验系统如图 1所示,主要由风洞、气浮轴承、测控系统和模型构成,其中气浮轴承和测控系统是试验系统的主要组成部分。
|
图 1 再入飞行器小滚转力矩测量试验系统 Fig.1 Measurement system for micro rolling moments of re-entry vehicle |
风洞试验前,首先对气浮轴承供气使其正常工作,同时利用轴承中的涡轮将轴承转子和与转子固连的模型驱动至试验所需转速,然后开始进行风洞试验。在试验吹风过程中测量系统采集模型转速变化过程数据,最后通过试验数据辨识获得模型滚转力矩和滚转阻尼力矩系数。
1.1 风洞本文研究工作在中国空气动力研究与发展中心超高速空气动力研究所的Φ1 m高超声速风洞(FD-30)中进行。风洞喷管出口直径1m,采用高压下吹-真空抽吸的运行方式,试验马赫数范围为4~10,具有运行参数范围宽、运行时间长、口径大等优点,利于特种试验的开展[15-16]。
1.2 压差式气浮轴承气浮轴承作为试验系统的核心设备,优点在于摩擦阻尼极小,能够在小量级滚转力矩的测量中将摩擦阻尼的干扰最大程度降低,但抗载荷能力较弱。当风洞口径较大时,缩比模型尺寸增大使得风洞试验中有量纲气动载荷成倍增加,气浮轴承抗载荷能力不足造成旋转不畅、卡死等问题,甚至损坏气浮轴承,导致试验失败。因此在大口径风洞中进行试验,需要气浮轴承具有较好的抗载荷能力。本文在传统气浮轴承的基础上进行了优化改进,设计加工了适用于Φ1 m高超声速风洞、具有较好抗载荷能力的大尺寸压差式气浮轴承。
压差式气浮轴承实物在风洞中安装照片如图 2所示。基本原理如图 3所示,由于气浮轴承转子和定子之间缝隙约为0.05 mm,供气后形成一层合适的薄空气膜,因此轴承阻尼极低。轴承内部气膜面分为前后气膜面和周向气膜面,保证了转子的浮起和轴向、周向定位。

|
图 2 压差式气浮轴承 Fig.2 Photo of differential pressure gas bearing |
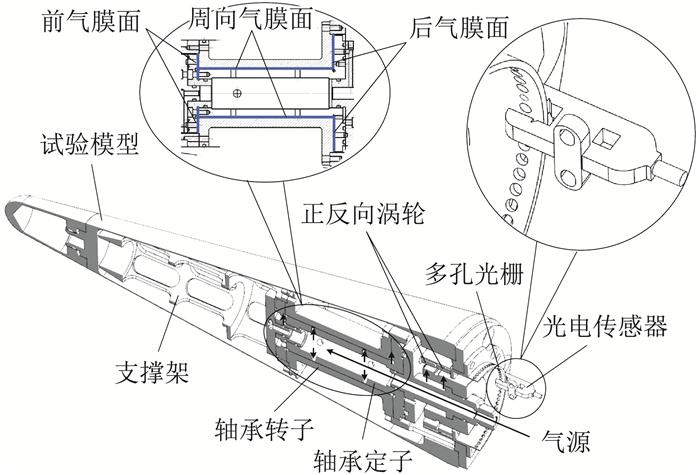
|
图 3 压差式气浮轴承原理 Fig.3 Principle of differential pressure gas bearing |
压差式气浮轴承充分利用模型内腔增大的空间,增加了轴承内部气膜总面积,提高气浮轴承的抗法向载荷能力。同时,将前后气膜面设计为前小后大,利用前后气膜面气浮面积差异带来的压差(图 3),进一步提高轴承的抗轴向载荷能力。表 1中给出了传统气浮轴承与大尺寸压差式气浮轴承的性能对比。表 1中可以看到,两种气浮轴承转速下降速率近似,阻尼性能无明显差别。压差式气浮轴承的承载能力远高于传统气浮轴承,特别是轴向承载能力优势明显。同时由于轴承整体和气膜面尺寸的增大,压差式气浮轴承的供压需求也相应增大,但可用供压压力范围较小。原因在于供压压力较小时不足以支持转子正常浮起工作,而供压压力较大时前后气膜面面积差异带来的压力差使得在无风测试状态下对转子产生较大的向前作用力,造成前气膜面变薄,超出理想工作范围。这里需要说明的是,由于气浮轴承为精密器件,超负荷运转、抱死、磕碰等行为极易造成内部气膜接触面损伤,导致性能下降甚至损坏。为保护气浮轴承,性能测试时未进行重复性测试,且未试探其临界工作状态,测试结果仅为单次近似结果。同时,无风测试状态和风洞试验状态下气浮轴承工况存在差别,性能测试仅具有对比定性和初步分析作用,并非风洞试验时的实际工作性能。但是,在风洞试验前进行气浮轴承无风状态性能测试非常关键,不仅能够估算气浮轴承承载、阻尼、供压范围等基本性能,为风洞试验提供重要参考;还能起到试验前的系统调试作用,及时发现和解决异常现象,确保风洞试验顺利开展。
| 表 1 传统式与大尺寸压差式气浮轴承性能对比 Table 1 Comparison of properties of different gas bearing |
|
|
另外,轴承后端安装了可以进行正、反向气流驱动的涡轮机构,通过对气路的控制能够方便的对模型转向和转速进行控制。同时,针对以往研究中出现的风洞低压或近似真空环境下气浮轴承承载能力下降的问题,在气浮轴承中新设计了阻气装置,尽量减弱外界环境对轴承性能的影响(图 2)。同时,由于整体尺寸的增大,对气浮轴承的加工精度提出了更高要求。
1.3 测控系统如图 1所示,测控系统硬件设备主要包括多孔光栅和光电传感器、供气管路、控制柜和数据采集计算机等。测控系统主要实现气路的控制和试验数据的采集功能,其工作原理与文献[13]类似,本文简述如下:中压气源经控制柜分三路分别实现气浮轴承内部气膜供气和正反向涡轮驱动。多孔光栅和试验模型均固连于轴承转子上,试验时多孔光栅和模型随转子旋转,而固定于定子上的光电传感器保持不动。光电传感器根据和光栅间相对运动生成电压信号,并由数据采集计算机采集(图 1)。其中,光栅孔对应低电压信号(约0 mV),反之为高电压信号(约5000 mV)。根据信号采集频率、光栅孔间隔角度等系统信息,可通过电压信号计算获得模型转动角速度随时间的变化(图 4)。
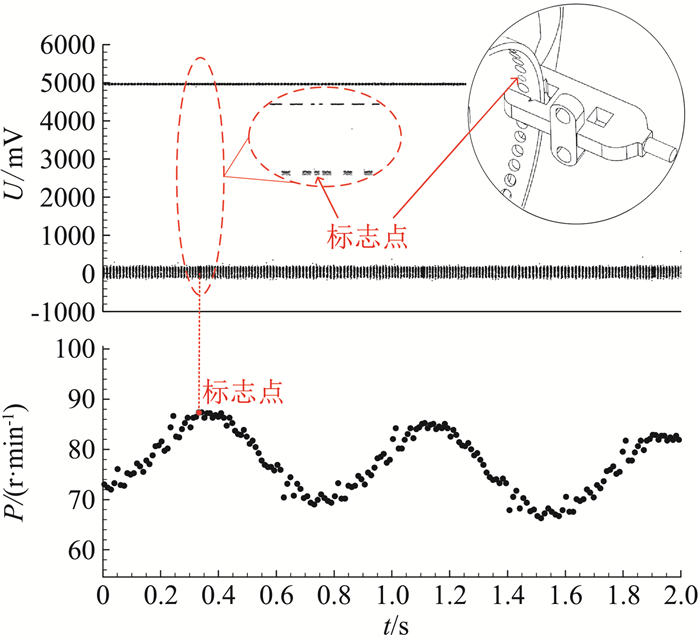
|
图 4 多孔光栅和原始电压信号 Fig.4 Grating and original voltage signals |
在前期Φ0.5 m风洞自由滚转测量试验技术的研究工作[13-14]中,完成了对模型转速变化曲线周期性波动规律的测量,但并未对模型滚转角位置进行精确定位和测量。为了满足再入飞行器日益增长的设计需求和试验技术发展需求,本文测控系统中光栅进行了改进,准确获取了试验中模型滚转角的位置变化信息。采用了1个较小的光栅孔作为模型滚转角度定位,起到标识作用。如图 4所示差异化多孔光栅机构,宽度较小的光栅孔与模型对称面之间相对位置已知。试验过程中通过追踪小光栅孔的位置实现模型对称面方位的辨识,从而实现气动力测量与模型滚转位置的精确匹配。标识孔的标识作用可在原始电压数据上轻易识别标志点位置,进而在模型转速变化曲线上对模型滚转角位置进行一一对应标识(图 4)。除标识孔外,光栅板共有72个孔,每孔角度间隔为5°。
1.4 试验模型根据风洞喷管堵塞比要求以及气浮轴承尺寸等限制,确定本文试验模型缩比和尺寸。本文中所采用的研究对象为自主设计的非轴对称再入飞行器模型,底部直径200 mm,模型示意图如图 5所示。为达到准确测量再入飞行器烧蚀作用造成的小滚转力矩的研究目的,试验模型分为无烧蚀外形和烧蚀外形。
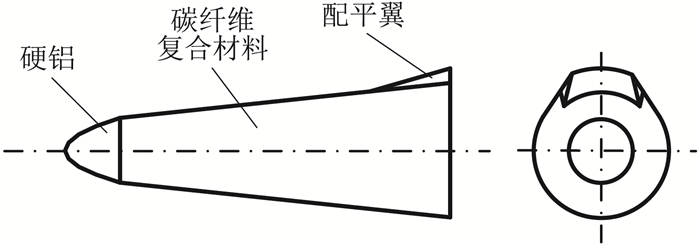
|
图 5 模型示意图 Fig.5 Sketch of model |
本文中,由于风洞口径和模型尺寸较大,若采用钢、铝等常用材料进行加工,模型滚转转动惯量大幅增大,将严重影响试验结果的气动参数辨识,无法保证预期试验效果(详细分析和结果见2.2节)。因此,为了避免高超声速风洞中高温等恶劣条件对模型造成的损伤,同时兼顾试验模型滚转转动惯量较小的设计要求,模型后部主体材料为碳纤维复合材料整体编织,头部材料为硬铝。
为计算无量纲滚转气动力参数,必须对模型滚转转动惯量进行测量。由于试验过程中模型与气浮轴承转子固连,实际滚转转动惯量为试验模型和气浮轴承转子转动惯量之和。本文采用附加质量法[3]对模型和气浮轴承转子的滚转转动惯量进行准确测量,测量结果如表 2所示。
| 表 2 滚转转动惯量测量结果 Table 2 Measurement results of rolling moment of inertia |
|
|
根据以往的研究结果[13],再入飞行器基本外形的不对称及再入烧蚀造成的小不对称导致滚转静力矩随滚转角变化而变化,传统将小滚转力矩系数视为常数的气动建模方法无法精细化描述小不对称滚转力矩的周期性变化情况,首先应建立能够合理描述滚转静力矩周期性变化的滚转运动控制方程模型:
| $ I \frac{\mathrm{d} P}{\mathrm{d} t}-C_{l P} q s D \frac{D}{v} P-\left(\bar{C}_{l 0}+A \sin \phi\right) q s D=0 $ | (1) |
其中:P为模型转速,I为模型滚转转动惯量,D为模型底部直径,v为来流速度,q为来流动压,s为模型底部面积,ClP为滚转阻尼力矩系数,Cl0为滚转静力矩系数,A为滚转静力矩周期性波动幅值,
在气动力建模的基础上,利用最小二乘法结合动力学仿真分析方法,采用打靶法不断迭代接近试验曲线,设立合理的判据,最终获得滚转气动力矩的平均量和动态变化量。详细的数据辨识方法和流程与文献[13]一致,本文不再赘述。该数据分析技术在进行数据辨识和分析的同时还能对试验结果进行有效验证,监测试验异常现象。模型转速随时间变化的结果中,体现了风洞试验曲线和数据分析仿真模拟曲线的一致性,将在后文试验结果与分析中给出。
2.2 试验系统性能预估在大口径风洞中进行试验时,随着风洞口径和模型尺寸增大,模型滚转转动惯量和有量纲气动载荷等参数与小口径风洞试验相比有明显区别,结合模型转速、来流动压等其他影响模型转动运动试验条件的综合作用下,模型转速变化曲线特征相应发生改变。风洞试验时,若各因素设计或选择不合理,将造成模型转速变化曲线可辨识度降低,直接影响试验的测量能力和精度。
为了在Φ1 m高超声速风洞中进行有效的试验,保证试验曲线的可辨识度,特别是精确测量和辨识滚转静力矩系数波动幅值和任意周向角位置的滚转静力矩系数,本文研究中在试验方案设计阶段创新引入了试验系统的性能预估,进一步指导完成系统优化设计。主要方法是通过动力学仿真手段在试验前期进行了仿真模拟试验。根据仿真结果综合分析了滚转转动惯量、模型转速、来流动压和气动载荷等多种因素与试验曲线可辨识度间关系,最终给出了综合性性能预估结果。
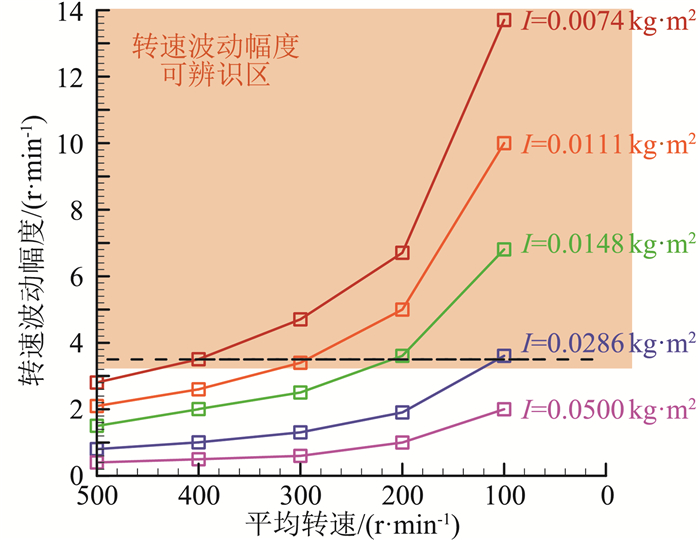
图 6中显示了以动压16.2 kPa时为例,仿真分析结果给出的模型-转子系统转动惯量、模型转速与转速波动幅度间关系。其中,转速波动幅度直接决定了试验模型转速变化曲线中滚转静力矩系数周期性变化量的可辨识度,根据以往的研究结果,设定转速波动幅度3.5 r/min为试验曲线可辨识区域下限。如图 6所示,模型-转子系统转动惯量和模型转速越低,越有利于试验曲线的辨识,即滚转静力矩系数周期性变化量的辨识和测量。其物理原因如下:转动惯量和转速较低时,滚转运动控制方程(1)中惯性项
|
图 6 试验性能预估结果 Fig.6 Prediction of test performance |
综合考虑上述分析结果,在大口径风洞中进行试验,选择合理的试验条件和方案尤其重要,试验系统的性能预估和优化设计是必不可少的关键环节。首先如1.4节所述,在选取合适的模型缩比基础上,采用轻质的碳纤维复合材料作为模型加工的主要材料,同时调整模型内部结构分布,在保证结构强度、模型实际滚转轴心与气浮轴承转心重合的前提下最大限度降低模型转动惯量(表 2)。同时,风洞试验时,对试验动压和转速测量范围进行了合理选择,大部分状态点分为高、低多个转速测量段分别进行试验,兼顾了滚转静力矩系数平均值、滚转阻尼力矩系数与滚转静力矩系数周期性变化量的有效辨识。
最终,风洞试验表明,试验现象和试验结果与前期性能预估结果完全一致,试验方案合理有效,试验中不仅保证了滚转静力矩系数平均值和滚转阻尼力矩系数的准确测量,还成功对任意周向角位置的滚转静力矩系数瞬时量进行了测量和辨识,对转速测量范围的合理分配也显著减少了风洞试验次数,提高了风洞试验效率。试验结果将在后文中详细列出和分析。
3 试验结果与分析本文研究中,试验马赫数Ma=6.0,试验迎角α=0°、2°、4°、6°、8°、10°,来流动压q=16.2 kPa,来流速度v=900 m/s。试验时模型角速度变化范围约为500~50 r/min(包括高、低转速车次)。
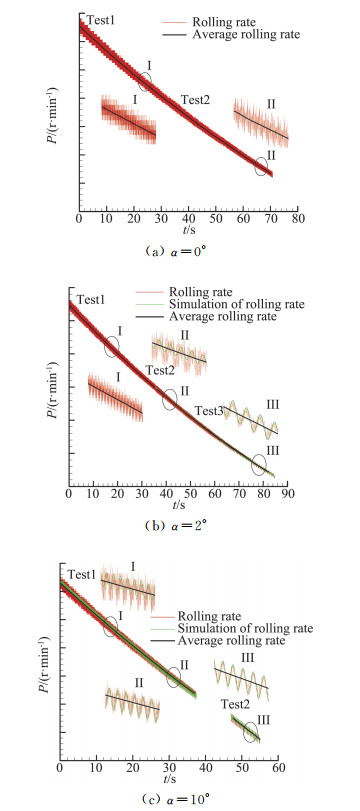
图 7以无烧蚀外形模型为例显示了典型试验状态下各车次的模型转速变化曲线、平均转速变化曲线和仿真转速变化曲线(便于对比,仿真曲线仅在转速波动明显时给出)。图中可见:同试验状态下不同转速段模型转速变化规律一致,试验具有良好的重复性和连续性。
|
图 7 无烧蚀外形模型转速变化曲线 Fig.7 Time courses of rolling rate of model of non-ablation shape |
图 7中结果可以看到,当迎角为零时(图 7(a)),因滚转静力矩系数无周期性变化,故转速变化曲线上无论高、低转速范围均未出现转速波动现象,此时数据辨识时认为滚转静力矩系数波动幅值A为零值。当迎角不为零时(图 7(b、c)),在模型转速较低的范围,均可在转速变化曲线上明显体现出滚转静力矩系数周期性变化所造成的转速波动现象,且迎角越大、转速越低,转速波动就越明显、越有利于滚转静力矩系数变化量的辨识,试验现象如前文2.2节所述,与前期试验性能预估一致。因此数据处理获取滚转静力矩系数波动幅值A时,采用较低转速范围的结果进行辨识。烧蚀外形模型的试验结果相似。
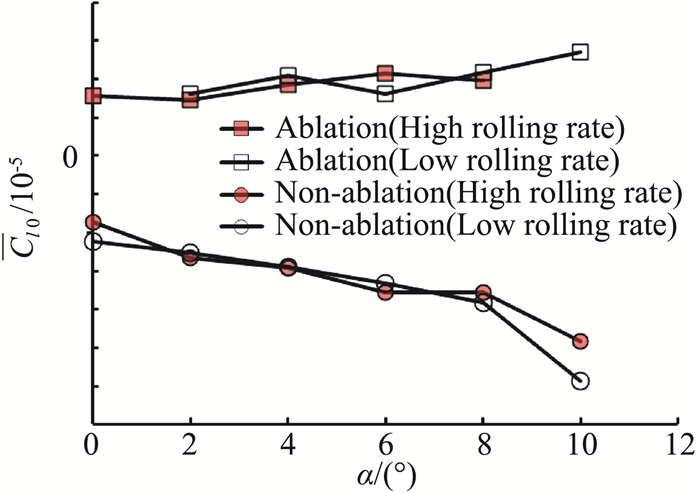
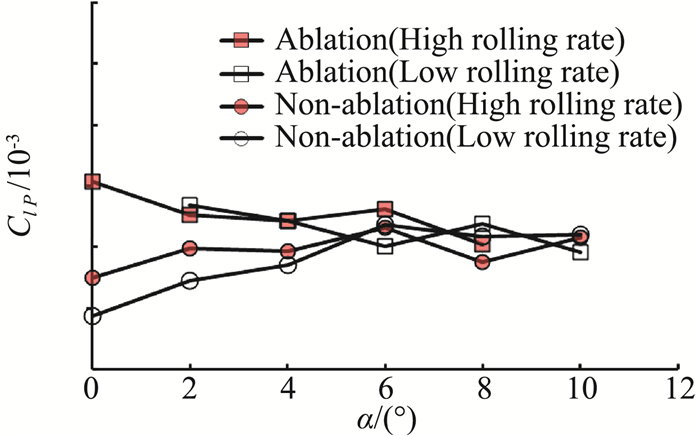
图 8至图 10中给出了无烧蚀外形和烧蚀外形模型各试验状态下平均滚转静力矩系数
|
图 8 平均滚转静力矩系数 |
|
图 9 滚转阻尼力矩系数 |
|
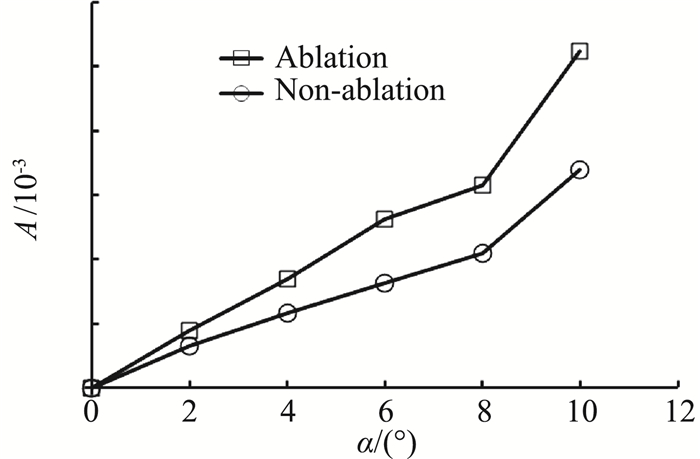
图 10 滚转静力矩系数波动幅值A变化曲线 Fig.10 Experimental results of rolling-moment coefficient amplitude A |
首先分析平均滚转静力矩系数
其次分析滚转阻尼力矩系数
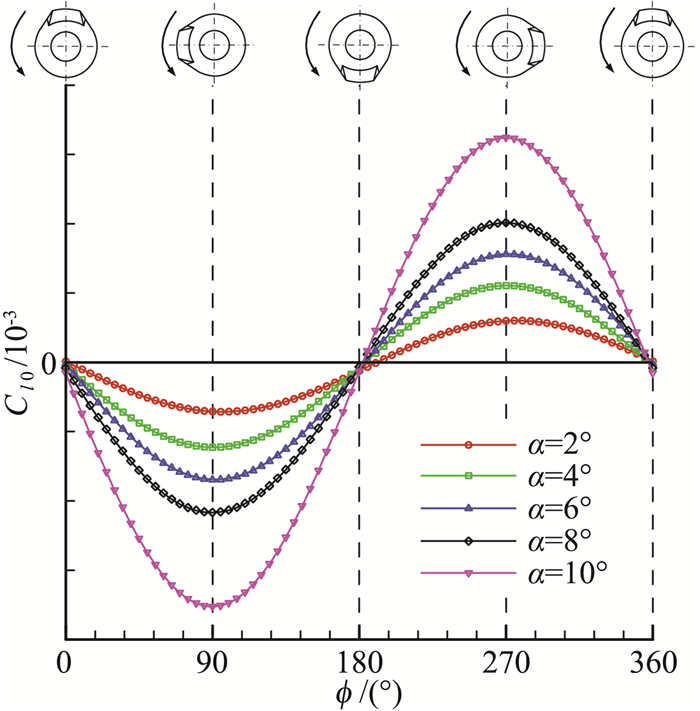
接下来分析滚转静力矩系数的周期性波动变化规律。滚转静力矩系数随滚转角以正弦函数变化,其波动幅值A可描述其波动特征。如图 10所示,无烧蚀外形和烧蚀外形滚转静力矩系数周期性波动幅值A随迎角增大而增大,结果合理、符合基本气动规律。烧蚀作用造成的滚转静力矩系数周期性波动更为明显,同一迎角下烧蚀外形的波动幅值A量值比无烧蚀外形稍大。在获得
|
图 11 无烧蚀外形Cl0随滚转角变化曲线 Fig.11 Experimental results of Cl0 of non-ablation shape |
在近年来Φ0.5 m量级高超声速风洞小滚转力矩测量试验技术研究工作基础上,本文针对大口径风洞进行了试验技术的优化改进和创新,最终研究结果表明:
(1) 本文中应用于Φ1 m高超声速风洞的小滚转气动力测量技术通过对模型和试验系统的优化改进,解决了风洞口径增大带来的气动载荷增加、模型转动惯量增大等问题以及一系列衍生技术难题。试验技术测量精度高,试验系统性能稳定可靠,最大试验迎角达到10°,实现了大迎角、高载荷的Φ1 m高超声速风洞试验能力。
(2) 作为大口径风洞中试验实施的关键环节,创新引入了试验系统的性能预估,为试验方案优化设计提供了重要依据,并最终得到了风洞试验的验证。试验现象和结果与预估结果完全一致,试验方案合理有效,极大提高了试验效果和效率。
(3) 试验结果符合基本气动特性规律,各滚转气动力矩系数均得到了准确测量和辨识。试验模型受烧蚀作用的气动影响在试验中也得到了有效测量:滚转静力矩系数周期性波动幅值随迎角增大而增大;迎角一致时烧蚀外形的滚转静力矩系数变化幅度比无烧蚀外形稍大。
致谢: 感谢李潜研究员、毕志献研究员、秦永明研究员以及中国航天空气动力技术研究院空气动力实验与工程应用研究所科技处在本文工作开展过程中给予的指导与帮助, 同时感谢中国空气动力研究与发展中心超高速空气动力研究所FD-30风洞运行组在试验过程中的配合与支持。
| [1] |
GLOVER L S, HAGEN J C. The motion of ballistic missiles[R]. AD731662, 1971.
|
| [2] |
蔡金狮, 董能力. 再入弹头滚转共振概率估算[J]. 宇航学报, 1995, 16(1): 1-7. CAT J S, DONG N L. Roll resonance probability prediction for re-entry vehicle[J]. Journal of Astronautics, 1995, 16(1): 1-7. (in Chinese) |
| [3] |
付光明, 冯明溪.小不对称弹头滚转气动阻尼试验[R].北京: 北京空气动力研究所, 1996. FU G M, FENG M X. Experiment for rolling aerodynamic damping of slight asymmetric re-entry body[R]. Beijing: Beijing Institute of Aerodynamics, 1996. (in Chinese) |
| [4] |
WILLIAMS E P. Experimental studies of ablation surface patterns and resulting roll torques[J]. AIAA Journal, 1971, 9(7): 1315-1321. DOI:10.2514/3.49941 |
| [5] |
蒋忠东, 赵忠良, 王树民, 等. 高超声速风洞小滚转力矩测量技术研究[J]. 航空学报, 2001, 22(6): 486-490. JIANG Z D, ZHAO Z L, WANG S M, et al. Research on the measurement techniques for micro-rolling-moment in a hypersonic wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(6): 486-490. DOI:10.3321/j.issn:1000-6893.2001.06.002 (in Chinese) |
| [6] |
王树民, 谢斌, 刘伟. 带气浮轴承的小滚转力矩气动天平的研制[J]. 流体力学实验与测量, 2002, 16(1): 94-98. WANG S M, XIE B, LIU W. The development of the wind tunnel balance measuring for tiny roll moment with gas bearing[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(1): 94-98. DOI:10.3969/j.issn.1672-9897.2002.01.015 (in Chinese) |
| [7] |
刘明霞, 田锋, 杨辉. 带五分量抑制机构的高精度滚转力矩测量技术[J]. 实验流体力学, 2013, 27(5): 71-74. LIU M X, TIAN F, YANG H. A high-precision rolling moment measuring technique of five components restraining system[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(5): 71-74. DOI:10.3969/j.issn.1672-9897.2013.05.013 (in Chinese) |
| [8] |
于卫青, 解亚军, 刘高计, 等. 小量程滚转力矩天平设计[J]. 弹箭与制导学报, 2013, 33(6): 125-128, 132. YU W Q, XIE Y J, LIU G J, et al. The design of a novel micro-scale roll moment balance[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(6): 125-128, 132. DOI:10.3969/j.issn.1673-9728.2013.06.035 (in Chinese) |
| [9] |
于卫青, 刘高计, 袁先士, 等. 微量滚转力矩天平测量技术研究[J]. 弹箭与制导学报, 2015, 35(1): 107-110, 117. YU W Q, LIU G J, YUAN X S, et al. The study of measurement technology of micro-scale roll moment balance[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(1): 107-110, 117. (in Chinese) |
| [10] |
秦永明, 田晓虎, 董金刚. 无翼/舵布局导弹小载荷滚转力矩测量研究[J]. 弹道学报, 2014, 26(2): 48-51. QIN Y M, TIAN X H, DONG J G. Measurement study of small rolling moment on missile without wing/rudder[J]. Journal of Ballistics, 2014, 26(2): 48-51. DOI:10.3969/j.issn.1004-499X.2014.02.010 (in Chinese) |
| [11] |
WANG Y, LIU W, XIE B, et al. Research on a micro-rolling-moment six-component strain gauge balance of composite structure[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(3): 76-79. |
| [12] |
白葵, 冯明溪, 付光明. 小不对称再入体滚转气动力测量技术[J]. 流体力学实验与测量, 2002, 16(3): 63-67, 72. BAI K, FENG M X, FU G M. Experimental technique for rolling aerodynamic of slight asymmetric re-entry body[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(3): 63-67, 72. DOI:10.3969/j.issn.1672-9897.2002.03.011 (in Chinese) |
| [13] |
赵俊波, 梁彬, 付增良, 等. 机动式再入弹头小滚转气动力风洞试验技术[J]. 空气动力学学报, 2016, 34(1): 53-58. ZHAO J B, LIANG B, FU Z L, et al. Experimental technique for micro rolling aerodynamics of a maneuvering reentry body[J]. Acta Aerodynamica Sinica, 2016, 34(1): 53-58. (in Chinese) |
| [14] |
张石玉, 赵俊波, 梁彬, 等. 参数辨识技术在再入弹头自由滚转风洞试验中的应用[J]. 弹箭与制导学报, 2016, 36(6): 113-117. ZHANG S Y, ZHAO J B, LIANG B, et al. Application of parameter identification technology in free-rolling wind tunnel tests of reentry body[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(6): 113-117. (in Chinese) |
| [15] |
唐志共, 许晓斌, 杨彦广, 等. 高超声速风洞气动力试验技术进展[J]. 航空学报, 2015, 36(1): 86-97. TANG Z G, XU X B, YANG Y G, et al. Research progress on hypersonic wind tunnel aerodynamic testing techniques[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97. (in Chinese) |
| [16] |
谢飞, 郭雷涛, 朱涛, 等. 高超声速风洞变雷诺数试验技术研究[J]. 空气动力学学报, 2016, 34(3): 398-403. XIE F, GUO L T, ZHU T, et al. Research on the test technique of Reynolds number variety in a hypersonic wind tunnel[J]. Acta Aerodynamica Sinica, 2016, 34(3): 398-403. DOI:10.7638/kqdlxxb-2015.0152 (in Chinese) |
 2019, Vol. 38
2019, Vol. 38


