圆柱绕流属于非定常分离流问题,该问题一直受到研究者的广泛关注,不仅因为它是流体力学领域的一个基本机理问题,更多的是它具有广泛的应用背景[1-7]。其主要应用领域有航天航空领域、机械设计领域、桥梁建筑领域、海洋装备领域等等。对圆柱绕流加以有效的控制,可以达到增升减阻、推迟或抑制分离的效果,因此控制圆柱绕流一直是流动控制领域的重要方向。
主动流动控制技术近几十年来呈多样化发展,目前研究较为广泛的有声激励[7-9]、电磁式激励[10]、微吹气或微射流[11-12]以及最新的合成射流激励[13]等方式。从20世纪90年代中期起,合成射流作为一种新发展的主动流动控制技术,正日益深入到各个领域。Glezer[14]首先成功研制了一种基于压电式的合成射流激励器,该激励器利用压电陶瓷片在周期性变化电压信号下的逆压电效应,将电能转化为压电陶瓷片的振动能,其工作原理如图 1所示。压电振动膜在电信号驱动下上下振动,使得腔体内的压强呈周期性变化。当膜片向下振动时,腔体内压强降低,外界出口附近的气流会被吸入腔体;当膜片向上振动时,腔体内的气体受到压缩会在出口形成射流。气体在这种周期性吹/吸过程中,形成一系列向下游发展的涡对,最终在出口形成一股稳定的射流。
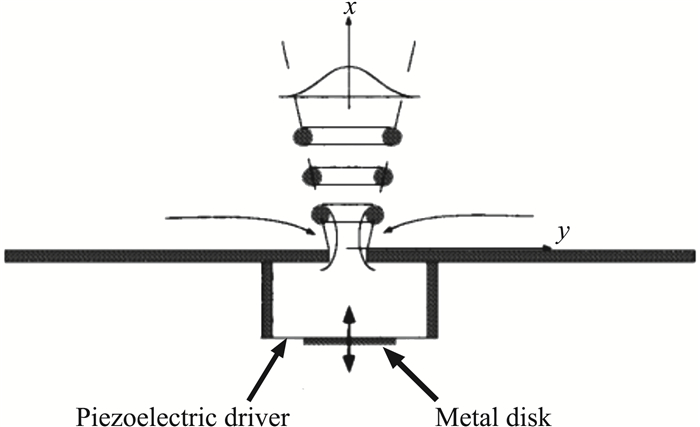
|
图 1 合成射流工作原理示意图 Fig.1 Schematic diagrams of synthetic jet |
Krieg[15-16]研制了一种活塞型合成射流激励器,证明了零质量射流也可以产生净推力,可用于水下推进和姿态控制。冯立好[17]在水槽中开展了合成射流对圆柱绕流的实验研究,结论表明将合成射流放置于圆柱前后驻点位置,均可以对流动分离起到较好的控制效果。
罗振兵[18-19]等研发的新型合成双射流激励器(DSJA)作为合成射流技术的最新发展成果,该型激励器采用单膜双腔的结构,相比普通单腔体激励器具有能量利用率高、结构紧凑、易于小型化、环境适应能力强等突出优点。该腔体由一个滑块、一片振动膜、两个腔体构成。其工作原理与图 1类似,如图 2所示:压电陶瓷振动膜在电信号驱动作用下来回振动,两腔体内流体在这种膨胀/压缩交替进行过程中,于激励器两侧出口分别形成一股非定常射流1和射流2,两股射流在向下游发展过程中相互作用并融合成一股新的合成射流。
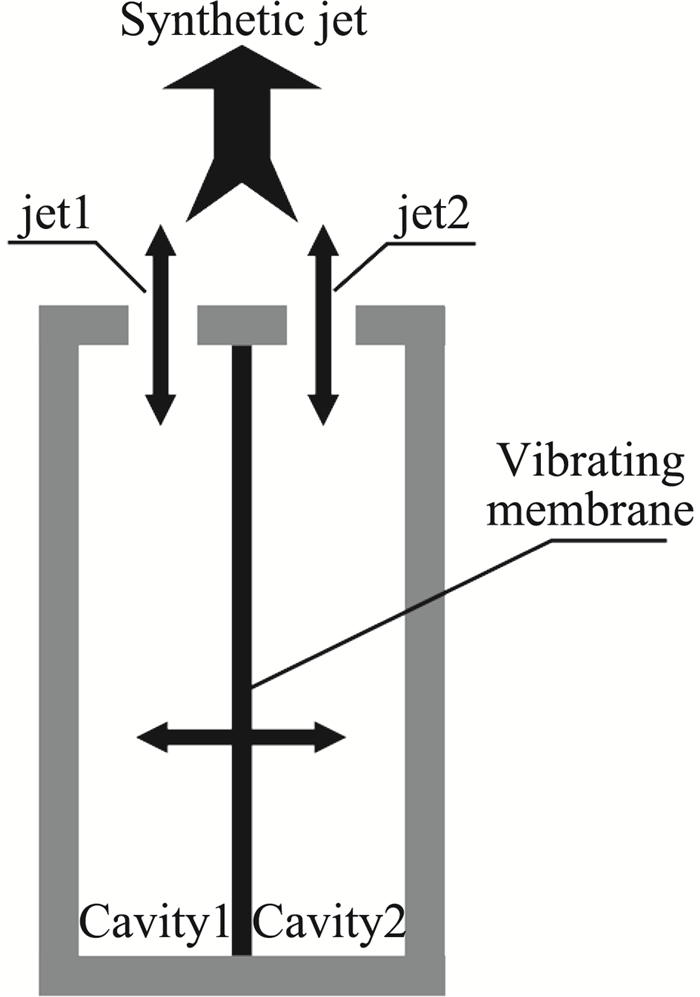
|
图 2 合成双射流激励器结构 Fig.2 DSJA structure |
从目前研究来看,利用合成双射流技术已经在流动分离控制、矢量控制、超声速/高超声速进气道流场控制、散热冷却、防除冰、水下仿生推进等[20]领域开展了研究,但还未见采用合成双射流技术控制水下圆柱绕流流动分离的文献资料。由于传统的合成射流激励器应用于水下流动控制时,压载会导致振动膜失效,而合成双射流激励器环境适应能力强,单膜双腔的结构设计能够有效克服压载失效问题。本文基于合成双射流激励器,数值仿真研究了激励器出口射流频率、出口射流振幅对水下圆柱绕流流动分离的影响,为进一步拓展合成双射流应用提供依据。
1 物理模型和数值方法 1.1 物理模型数值模拟环境为水槽内的二维圆柱绕流,其中设计实验段长0.9 m,高0.6 m,圆柱直径Dh为0.03 m,其前缘距来流入口0.3 m,高度为0.3 m,圆柱足够长以保证二维的可靠性。激励器射流出口宽度为0.001 m,来流速度为0.0345 m/s(Re≈1000),激励器射流出口位置分别位于圆柱前、后驻点。坐标系原点定义为圆柱截面的几何中心,采用直角正交坐标系,x轴沿来流方向向下,y轴垂直向上,如图 3所示。
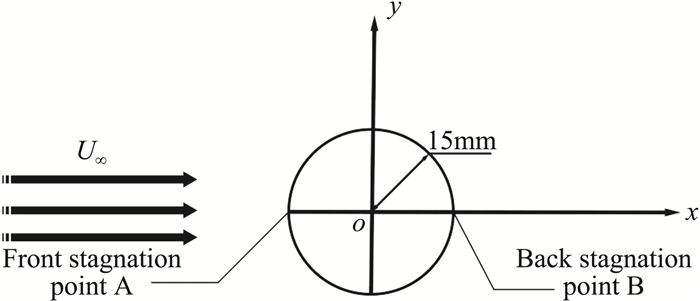
|
图 3 物理模型 Fig.3 Physical model |
考虑到DSJA出口处会存在较大的旋涡运动和速度梯度,在保证精度较高的情况下,选用带壁面函数的重整化群(RNG) k-ε湍流模型。相对于标准k-ε模型,该模型在对近壁面作适当处理后可有效模拟低Re的流动现象。
空间离散采用二阶迎风格式,压力-速度关联算法采用压力基的PISO算法,相比SIMPLE算法、SIMPLEC算法,PISO算法更加适用于非定常流计算,并且允许使用较大的时间步长,可以缩短计算时间。
1.3 网格生成与边界条件网格划分采用ICEM结构化网格方法,圆柱表面附近采用O-block进行划分以保证较好的正交性,边界层附近等流动变化剧烈处采用加密处理以提高计算精度,计算域尺寸相比圆柱特征尺寸均高一个数量级,计算域具体划分情况如图 4所示。
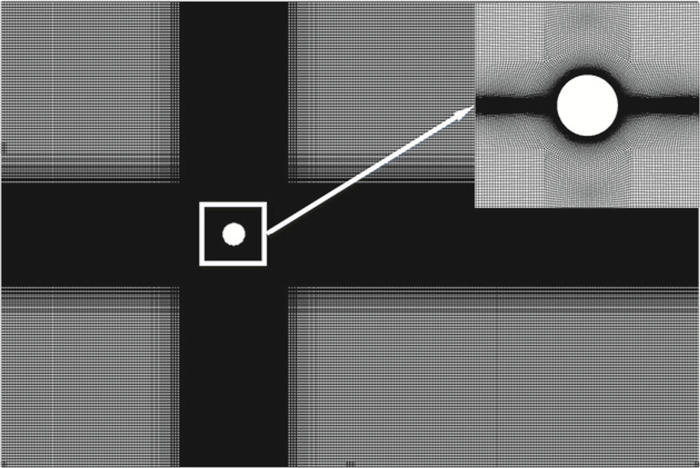
|
图 4 计算域 Fig.4 Computational domain |
计算中使用的边界条件类型有:速度入口条件(velocity inlet)、壁面条件(wall)、出流条件(outflow)。来流入口和激励器射流出口采用速度入口边界条件,设置来流入口速度为0.0345 m/s, 激励器射流出口速度采用自定义函数(见2.1节公式(2)),静温均为300 K; 圆柱表面采用无滑移壁面条件; 考虑到计算域速度较低且计算域比圆柱特征尺寸大一个数量级以上,故出口边界采用出流条件。
1.4 理论验证和试验确认为检验计算方法的可靠性,一方面利用冯立好等人的实验数据进行实验确认,仿真所用参数与实验条件完全一致;另一方面,从理论角度出发,根据所给模型参数利用涡脱落公式计算理论涡脱落频率,与仿真结果进行理论验证。
根据实验工况雷诺数为1000,此时应取斯特劳哈尔数St=0.21,则涡脱落特征频率为:
| $ f_{0}=S t \cdot \frac{v}{d}=0.2415 \mathrm{Hz} $ | (1) |
冯立好[17]等通过对圆柱绕流的实验结果进行频谱分析,得到实验中涡脱落的频率为0.24 Hz。
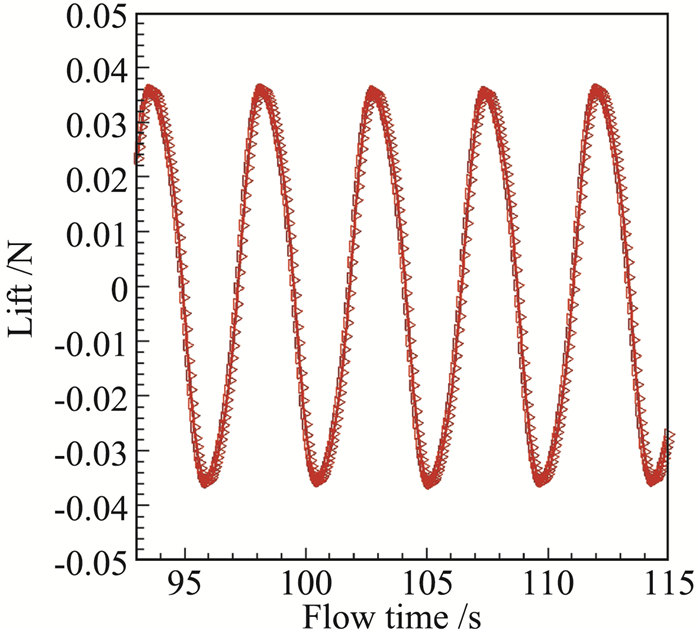
通过数值模拟,取10万网格量进行计算,经流场充分发展后,圆柱表面升力曲线变化如图 5所示。
|
图 5 圆柱表面所受升力随时间变化曲线 Fig.5 Time history of lift coefficient |
由图 5数据通过多周期平均的方式,得到数值仿真结果的涡脱落特征频率约为0.236 Hz,在容许误差范围内,数值模拟结果与实验、理论解对比都比较吻合,表明本计算方法具有一定的可信度。
2 计算结果讨论与分析 2.1 工况设置为了研究合成双射流激励器、射流频率、射流振幅对圆柱绕流流动分离的影响,采用控制变量的原则设置工况,如表 1所示。其中Case 0为无控状态;Case 1、Case 2、Case 3对射流频率影响进行了对比仿真;Case 1、Case 4、Case 5对射流振幅影响进行了对比仿真。射流出口速度边界条件采用自定义函数导入Fluent进行计算,速度表达式设置为如下形式:
| $ u(t)=A \sin \left(2 \pi f t+\phi_{0}\right) $ | (2) |
| 表 1 激励器工况设置 Table 1 DSJA parameter settings |
|
|
由于合成双射流激励器工作方式为单膜双腔, 两股射流速度相位必然相差180°,故ϕ0为0或者π。
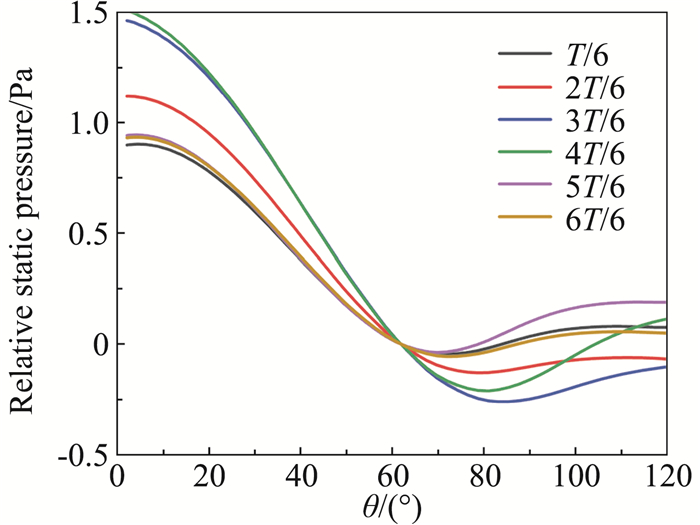
2.2 无控状态下圆柱绕流流动特性分析图 6为无控状态(Case 0)下一个周期不同时刻的圆柱上表面的相对静压分布(以原点深度处压强为基准)。可以看出:从圆柱前缘至圆柱后缘表面压力先降低后升高,圆柱前缘压力最高是因为来流在前驻点处速度滞止;随后来流沿圆柱表面流动但未发生分离,此时由于型面变化速度不断增快而导致压强逐渐降低;当压力曲线达到最小值(θ≈84°)时,此时发生了流动分离,分离后速度减小,压力曲线又开始爬升,而分离后流体在分离区内速度变化不大,因此压力上升阶段表现较为缓慢。从图 6可以看出,分离最早发生于θ≈84°附近, 即分离发生于圆柱前缘, 分离点未过圆柱上表面顶点。
|
图 6 圆柱上表面的相对静压分布 Fig.6 Relative static pressure distributions on the upper wall of the cylinder |
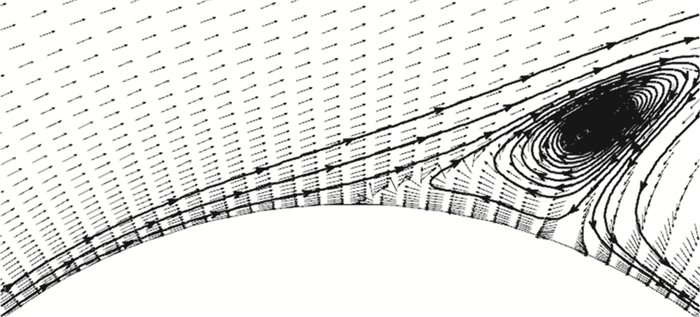
为了探究合成双射流对圆柱绕流流动分离控制的典型影响,这里取Case 1的仿真结果进行分析。流动分离是一个非定常的变化过程,分离点也会随着时间从前向后推移直至最终分离涡脱离,为了方便比较控制效果,图 7取自Case 1最靠近前缘分离时刻的速度矢量图。可以发现,加入合成射流进行主动控制后,分离发生于圆柱后缘, 相比无控状态分离点(θ≈84°)得到明显推迟, 不仅改善了圆柱前缘的流场结构,同时还进一步提前了分离涡的再附着,这是因为在后驻点布置射流,形成的低压区域提高了圆柱后缘抗逆压梯度的能力,使得那些即将要脱落的涡在低压的诱导下又重新附着在圆柱后表面。
|
图 7 圆柱分离区域的速度矢量图 Fig.7 Velocity vector of cylindrical separation domain |
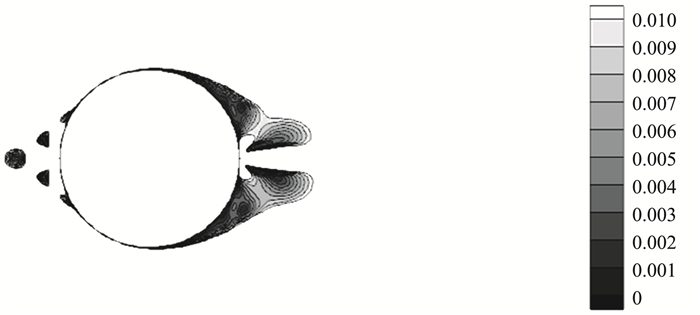
如果可以确定各工况分离区尺寸的相对大小,在同等来流情况下,阻力的相对大小也可以进行比较,这样就可以评判各类控制流动分离方法的效果优劣。这里主流速度为0.0345 m/s,首先对充分发展后多个周期的工况进行时间平均处理,之后提取流场中速度低于主流速度1/3(这里约取0.01 m/s)以下的区域,认定其与分离的低速区尺寸相当,显然低速的区域越大,分离区尺寸也会越大。图 8是Case 1的速度时间平均云图,为方便比较,速度大于0.01 m/s的区域统一处理为白色。
|
图 8 Case 1时间平均的速度云图 Fig.8 Time-averaged velocity contours of Case 1 |
从图 8看出前驻点射流的控制作用体现在圆柱前缘形成虚拟流动外形,改善绕流型面减阻;而后驻点的控制作用体现为在靠近分离涡的区域形成低压区加速分离涡的再附,减小前后压差阻力。
2.4 出口射流频率对控制效果的影响分析激励器出口射流频率是影响控制效果的重要参数。尾迹涡脱落的特征频率约为0.24 Hz,因此在数值模拟中设置了单倍频、半倍频、2倍频三种工况,分别对应Case 1、Case 2、Case 3。图 9是该三种工况的时间平均的速度云图。

|
图 9 Case 1、Case 2、Case 3时间平均的速度云图 Fig.9 Time-averaged velocity contours for Case 1, 2, and 3 |
从图 9可以看出,2倍频控制效果最差,单倍频控制效果最好。这说明在其他条件一致的情况下,并不是频率越高,动量掺混的能力就越强,对流场的控制效果就越好。结果表明,当出口射流频率等于尾迹涡脱落的特征频率时,控制效果最好。控制过程中存在激励器射流频率与尾迹涡脱落的耦合过程,如果频率一致,可以达到一种比较“理想和谐”的控制状态。频率过高会打破原流场,并且带来不利的扰动;而频率过低则吸附作用较弱,控制效果不强。
2.5 出口射流振幅对控制效果的影响分析激励器出口射流振幅也是影响控制效果的重要参数,其直接表现为射流动量的大小。研究中保持频率为最佳控制频率,即单倍频。振幅分别设置为0.16 m/s、0.25 m/s、0.5 m/s,对应Case 4、Case 1、Case 5三种工况,图 10为上述三种工况的时间平均的速度云图。

|
图 10 Case 4、Case 1、Case 5时间平均的速度云图 Fig.10 Time-averaged velocity contours for Case 4, 1, and 5 |
从图 10可以看出,保持激励器出口射流频率为尾迹涡脱落特征频率条件下,随着出口射流振幅的增大,射流动量掺混的能力增强,控制流动分离的效果越好,从而流场低速区域越小,分离区域也越小,起到了较好的控制效果。
2.6 合成双射流控制圆柱绕流流动分离的机理探讨表 2为圆柱表面所受压阻和摩阻的时间平均统计。从表中可以看出加入合成双射流控制后,圆柱表面所受压差阻力和摩擦阻力都有所减小。但是在该雷诺数下,圆柱所受阻力主要来自于压差阻力。从Case 1、Case 2、Case 3可以看出,随着频率接近卡门涡脱落特征频率,压差阻力减小较多,从而总阻力也得以减小。由Case 1、Case 4、Case 5可以看出,在给定频率的情况下,增大射流的振幅可以明显减小阻力,这是由于随着振幅增大,射流的动量掺混能力增强,从而抑制分离的能量更多。
| 表 2 圆柱表面的压差阻力和摩擦阻力 Table 2 Drag of pressure and friction on cylindrical surface |
|
|
图 11是合成双射流分别置于前后驻点控制圆柱绕流的示意图。射流出口位于前驻点,则可以通过出口射流对附近流体的卷吸作用形成一个涡对,不间断地在圆柱前缘形成虚拟气动外形改善型面,从而减小迎面来流流过圆柱表面的阻力。表 2的数据统计结果表明主要是减小了压差阻力。而射流出口位于后驻点,则会在靠近分离涡的区域形成一个低压区,加速分离涡的再附或抑制涡的分离,从而减小分离区尺寸,同样是通过降低前后压差阻力来达到控制效果。
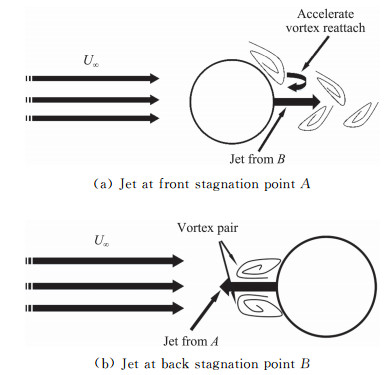
|
图 11 射流位于前后驻点控制过程示意图 Fig.11 Control process at the stagnation point A and B |
最佳频率主要的控制作用除了体现为增强动量掺混能力来抑制分离的作用之外[21-22],本文还发现了射流频率与涡脱落同频带来的减阻增益。该减阻效果主要体现在后驻点射流的控制过程。如果射流与尾迹涡脱落同频率,每当涡即将要脱落时,射流刚好这时形成一个低压区又把涡给吸附到圆柱表面,从而减小压差阻力;如果射流频率过大,则后驻点的出口射流不与尾迹涡脱落同频,会把原本即将要脱落的涡冲碎形成更大的分离区,还会加大阻力,起到不利的效果;如果射流频率低于涡脱落的特征频率,此时不会打破原本的分离涡,同时还会起到一定的吸附作用,只是吸附作用比同频的射流小一些,因为同频射流对每个分离涡都可以起到吸附作用,而半倍频只能对“一半”的分离涡起到吸附作用。
对于射流振幅的影响探究,把射流频率设置为最佳控制频率下研究,这样才能保证频率对绕流控制只会起到好的控制效果,否则后缘涡的破碎有可能是振幅过大或者频率不适应涡脱落导致的。当固定频率为最佳频率时,对振幅的影响因素探究才是单变量研究。随着振幅的增大,射流对流场的动量掺混能力增强,可以更加快速地形成更低压强的区域,增大对分离涡的吸附作用。数值模拟结果也表明,固定激励器工作频率为涡脱落特征频率时,在振幅变化一定范围内,随着振幅的增大,控制效果越强。
3 结论文章研究了合成双射流的流动控制特性以及激励器出口射流参数对圆柱绕流流动分离控制效果的影响,通过比较各工况分离区尺寸相对大小来评判流动分离的控制效果,得到以下结论:
(1) 相比无控状态下的圆柱绕流,加入合成双射流激励器进行主动流动控制可以改善前缘迎流型面和加速后缘分离涡的再附,同时减小摩擦阻力和压差阻力。
(2) 在保持激励器出口射流振幅不变的情况下,出口射流频率越接近尾迹涡的脱落频率,射流扰动与原绕流流场的耦合效应越好,控制流动分离的效果越好。
(3) 保持激励器出口射流频率为尾迹涡特征频率,出口射流振幅在一定变化范围内,随着振幅的增大,射流对流场的动量掺混能力增强,控制绕流流动分离的效果越好。
(4) 初步探究了合成双射流控制圆柱绕流流动分离的机理:前后驻点不论是通过形成虚拟气动外形还是增强回流区的动量掺混,都主要是通过减小前后压差阻力来达到控制效果。
| [1] |
REHMAN N M A, KUMAR A, SHUKLA R K. Influence of hydrodynamic slip on convective transport in flow past a circular cylinder[J]. Theoretical and Computational Fluid Dynamics, 2017, 31(3): 251-280. |
| [2] |
GAO D L, CHEN W L, LI H, et al. Flow around a circular cylinder with slit[J]. Experimental Thermal and Fluid Science, 2017, 82: 287-301. DOI:10.1016/j.expthermflusci.2016.11.025 |
| [3] |
JIANG H Y, CHENG L, AN H W. On numerical aspects of simulating flow past a circular cylinder[J]. International Journal for Numerical Methods in Fluids, 2017, 85(2): 113-132. DOI:10.1002/fld.4376 |
| [4] |
LIU Y G, FENG L H. Suppression of lift fluctuations on a circular cylinder by inducing the symmetric vortex shedding mode[J]. Journal of Fluids and Structures, 2015, 54: 743-759. DOI:10.1016/j.jfluidstructs.2015.01.011 |
| [5] |
PASIOK R, STILGER-SZYDŁO E. Sediment particles and turbulent flow simulation around bridge piers[J]. Archives of Civil and Mechanical Engineering, 2010, 10(2): 67-79. |
| [6] |
尹纪富, 尤云祥, 李巍, 等. 电磁力控制湍流边界层分离圆柱绕流场特性数值分析[J]. 物理学报, 2014, 63(4): 044701-15. YIN J F, YOU Y X, LI W, et al. Numerical analysis for the characteristics of flow control around a circular cylinder with a turbulent boundary layer separation using the electromagnetic force[J]. Acta Physica Sinica, 2014, 63(4): 044701-15. (in Chinese) |
| [7] |
程霄翔, 赵林, 葛耀君. 高超临界雷诺数区间内二维圆柱绕流的实测研究[J]. 物理学报, 2016, 65(21): 232-247. CHENG X X, ZHAO L, GE Y J. Field measurements on flow past a circular cylinder in transcritical Reynolds number regime[J]. Acta Physica Sinica, 2016, 65(21): 232-247. (in Chinese) |
| [8] |
董宇飞, 魏中磊, 徐诚, 等. 钝圆柱体分离流动声振控制的实验研究[J]. 空气动力学学报, 1999, 17(2): 130-140. DONG Y F, WEI Z L, XU C, et al. Experimental investigation of control of a separated shear layer of a blunt circular cylinder by means of an acoustic forcing[J]. Acta Aerodynamica Sinica, 1999, 17(2): 130-140. DOI:10.3969/j.issn.0258-1825.1999.02.002 (in Chinese) |
| [9] |
BLEVINS R D. The effect of sound on vortex shedding from cylinders[J]. Journal of Fluid Mechanics, 1985, 161: 217. DOI:10.1017/S0022112085002890 |
| [10] |
KALRA C, ZAIDI S, ALDERMAN B, et al. Magnetically driven surface discharges for shock-wave induced boundary-layer separation control[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2007.
|
| [11] |
叶楠, 程克明, 顾蕴松, 等. 微吹气前体非对称涡控制[J]. 航空学报, 2016, 37(6): 1763-1770. YE N, CHENG K M, GU Y S, et al. Forebody asymmetric vortex control with microblowing[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1763-1770. (in Chinese) |
| [12] |
BERNHARDT J E, WILLIAMS D R. Proportional control of asymmetric forebody vortices[J]. AIAA Journal, 1998, 36(11): 2087-2093. DOI:10.2514/2.310 |
| [13] |
罗振兵, 夏智勋. 合成射流技术及其在流动控制中应用的进展[J]. 力学进展, 2005, 35(2): 221-234. LUO Z B, XIA Z X. Advances in synthetic jet technology and applications in flow control[J]. Advances in Mechanics, 2005, 35(2): 221-234. DOI:10.3321/j.issn:1000-0992.2005.02.009 (in Chinese) |
| [14] |
SMITH B L, GLEZER A. The formation and evolution of synthetic jets[J]. Physics of Fluids, 1998, 10(9): 2281-2297. DOI:10.1063/1.869828 |
| [15] |
KRIEG M, MOHSENI K. Thrust characterization of a bioinspired vortex ring thruster for locomotion of underwater robots[J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 123-132. DOI:10.1109/JOE.2008.920171 |
| [16] |
KRIEG M, MOHSENI K. Dynamic modeling and control of biologically inspired vortex ring thrusters for underwater robot locomotion[J]. IEEE Transactions on Robotics, 2010, 26(3): 542-554. DOI:10.1109/TRO.2010.2046069 |
| [17] |
冯立好.合成射流控制圆柱绕流结构及其机理的实验研究[D].北京: 北京航空航天大学, 2012.(in Chinese) FENG L H. Experimental Investigation on Control of Flow Structure around a Circular Cylinder by a Synthetic Jet and its Mechanism[D]. Beihang University.2012. |
| [18] |
罗振兵, 夏智勋, 刘冰.单膜双腔双口合成射流激励器: CN1818399A[P]. 2006-08-16. |
| [19] |
LUO Z B, XIA Z X, LIU B. New generation of synthetic jet actuators[J]. AIAA Journal, 2006, 44(10): 2418-2420. DOI:10.2514/1.20747 |
| [20] |
罗振兵, 夏智勋, 邓雄, 等. 合成双射流及其流动控制技术研究进展[J]. 空气动力学学报, 2017, 35(2): 252-264, 251. LUO Z B, XIA Z X, DENG X, et al. Research progress of dual synthetic jets and its flow control technology[J]. Acta Aerodynamica Sinica, 2017, 35(2): 252-264, 251. DOI:10.7638/kqdlxxb-2017.0053 (in Chinese) |
| [21] |
FENG L H, WANG J J. The virtual aeroshaping enhancement by synthetic jets with variable suction and blowing cycles[J]. Physics of Fluids, 2014, 26(1): 014105. DOI:10.1063/1.4861367 |
| [22] |
FENG L H, WANG J J. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point[J]. Journal of Fluid Mechanics, 2010, 662: 232-259. DOI:10.1017/S0022112010003174 |
 2019, Vol. 38
2019, Vol. 38


