模拟激波一直是计算流体力学(Computational Fluid Dynamics,CFD)的重要研究内容,Godunov、MUSCL、TVD、ENO、WENO、WCNS等差分格式,Steger、Van Leer、Roe、AUSM、HLLC等通量格式,这些被当做里程碑事件写入CFD教科书的研究成果大多和激波有关。近些年本课题组提出了自适应间断装配求解器(Adaptive Discontinuity Fitting solver, ADFs)[1],应用成熟的非结构动网格技术[2]很好地解决了因激波运动引起的计算域空间几何变化的难题[3-5],通过把R-H(Rankine-Hugoniot)关系式当作一种新的通量分裂形式在程序中实现了捕捉法和装配法的自由转换[6],这种方法不仅编程方便,且应用简单的结构辨识算法就能在计算得到的流场基础上“逢山开路、遇水搭桥”很容易的完成复杂激波结构的自动装配。
在高精度格式方面,基于体积平均思想的有限体积法(此处特指使用高斯定理把体积分转换为面积分以后建立的算法)在构建高精度格式方面存在理论上的先天不足,国内外从事这方面算法和应用的研究者也较少[7-8],而有限差分方法因理论完善、操作简单而成为高精度格式发展的主要方向,这也是本文讨论的范围。搜索“高精度格式”文献很多,遗憾的是至今还没有哪种高精度格式能像当年TVD那样在学术界得到普遍认可、在工程领域被广泛使用,目前商业软件的主流格式依然是二阶精度。在本文中,作者针对有限差分的高精度格式在应用研究中所遇到的两个问题进行分析讨论,探索解决的途径。每个问题论述结构相似,先介绍研究背景、数值现象和文献综述,然后分析讨论和提出看法,最后是对解决问题的初步探索。
1 曲线坐标变换的误差问题装配了激波以后流场空间形成互不重叠的相邻区域,原则上可在多块分区拼接网格上应用高精度有限差分法求解,但是由于激波在收敛过程中存在运动,因此,需要解决变形网格引起的几何守恒律问题。
早期几何守恒律用来消除因网格变形给流场引入的新误差[9-10],后来人们发现均匀流场在坐标变换后即使网格不发生变形也会出现误差,为便于区分,把前者称为体积守恒律(Volume Conservation Law,VCL),后者称为面积守恒律(Surface Conservation Law,SCL)。从文献调研情况看,对体积守恒律的研究主要集中于有限体积法领域[2, 10];对有限差分法,日本的Abe、Nonomura[11-12]团队分别于2012年、2013年提出了对称守恒度量算法及非对称守恒度量算法,对任意线性的高阶有限差分格式具有很好的效果。近些年随着高精度格式进入应用,对面积守恒律的研究越来越受关注[13-16]。基于变形网格的激波装配法应用高精度格式,两种几何守恒律都需要注意,下面先讨论静止网格的面积守恒律。
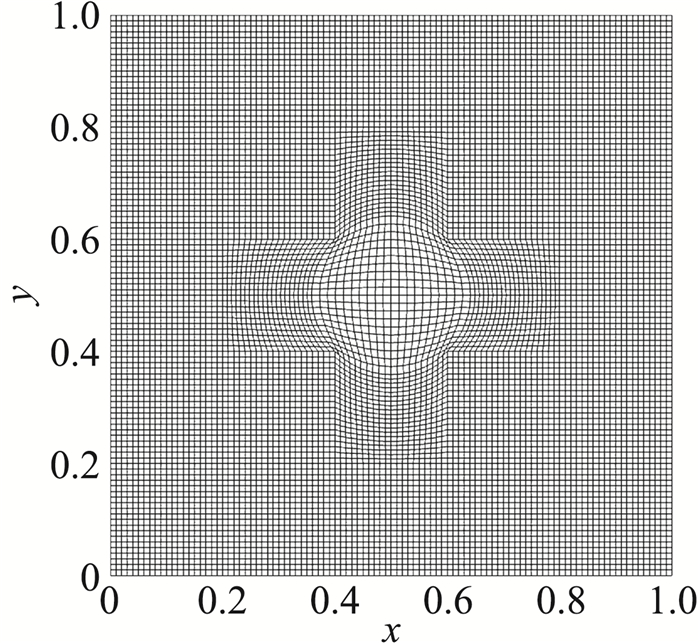
关于曲线坐标变换以后出现的问题,文献[17]在一阶迎风格式的基础上开展了研究,这里主要验证其结论对高精度格式的有效性,因此,取同样的算例进行对比,计算网格如图 1所示。
|
图 1 计算网格 Fig.1 Computational grids |
对任意坐标系下二维Euler方程:
| $\frac{\partial \hat{U}}{\partial \tau}+\frac{\partial \hat{F}}{\partial \xi}+\frac{\partial \hat{G}}{\partial \eta}=0 $ | (1) |
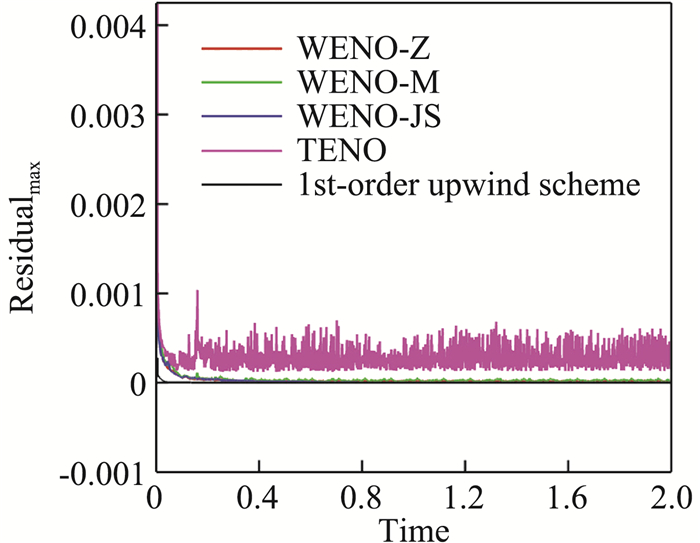
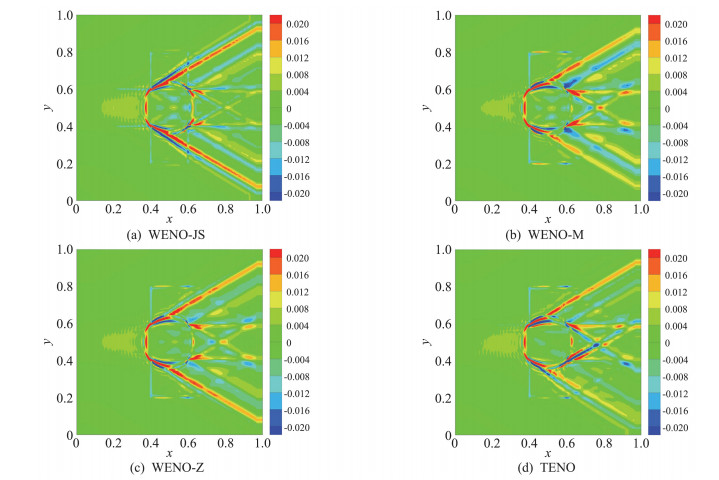
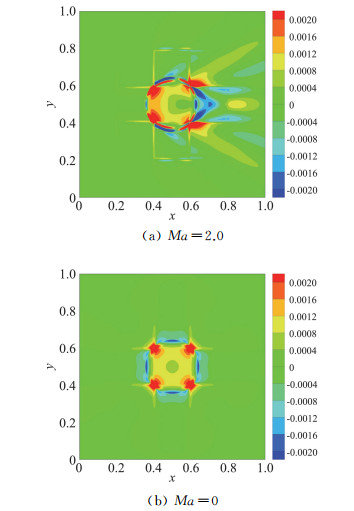
通量分裂采用VanLeer格式,时间推进采用3阶Runge-Kutta格式,按照CFL=0.9计算时间推进步长,计算时间t=2.0。通量导数计算分别选取五阶WENO-JS[18]、WENO-M[19]、WENO-Z[20]、TENO[21]格式,首先计算进出口边界条件确定的超声速均匀流场,流场初场参数(ρ, u, v, p)=(1.4, 2.0, 0.0, 1.0),四种格式的最大残差收敛曲线如图 2所示。图 3为采用不同格式计算得到的密度误差分布云图,从图中可以看出密度误差产生于网格非均匀区域,并沿着马赫锥向下游传播。图 4为流场参数(ρ, u, v, p)= (1.4, 0.0, 0.0, 1.0)时的静止流场的计算结果,可以看出,边界附近并没有更大的误差。
|
图 2 最大残差收敛曲线 Fig.2 Maximum residual convergence curves for the uniform flow with different schemes |
|
图 3 超声速流场密度误差云图 Fig.3 Contours of density error for the supersonic flow |
从几何诱导均匀流场产生数值误差的问题被发现开始,CFD研究者们对如何保持均匀流守恒性的研究便从未停止,其中发展较为成熟的是对几何守恒律的研究。几何守恒律认为原物理坐标系下的控制方程经坐标变换后在计算坐标系下的完整形式如式(2)所示,式(2)的右端项S=0在微分形式下自动成立,但经过有限差分离散之后一般不再成立;离散后的S不为0是导致均匀流不能保持守恒特性的主要原因。因此,几何守恒律的研究主要是通过构造合适的坐标变换系数及坐标变换雅克比的离散格式使得S在离散形式下仍然能保持为0,以式(1)作为控制方程进行数值模拟,如现今被广泛使用的由邓小刚等研究学者提出的几何守恒律的守恒计算方法(Conservative Metric Method, CMM)[13]及对称守恒计算方法(Symmetrical Conservative Metric Method, SCMM)[14]。此外,Cai和Ladeinde[22]、Sun等[16]以式(2)作为控制方程在WENO格式上做了一系列工作,取得了很好的成果。本文的工作便是以式(2)作为控制方程进行开展的。为便于区分及表达,本文将式(1)称为离散近似方程,将式(2)称为离散等价方程。
| $ \frac{\partial \hat{U}}{\partial \tau}+\frac{\partial \hat{F}}{\partial \xi}+\frac{\partial \hat{G}}{\partial \eta}=S $ | (2) |
式中:S=FIx+GIy。
作者在文献[17]中提出了只要源项和对流项的离散格式相等就能满足几何守恒律的构造准则,得到方程(2)对应的半离散形式为:
| $ \frac{\partial \hat{U}}{\partial \tau}=-\left(\frac{\tilde{F}_{i+1 / 2}-\tilde{F}_{i-1 / 2}}{\Delta \xi}\right)-\left(\frac{\tilde{G}_{j+1 / 2}-\tilde{G}_{j-1 / 2}}{\Delta \eta}\right) $ | (3) |
其中:
| $ \left\{\begin{array}{l} \hat{F}_{i \pm 1 / 2}=\hat{F}\left(U_{i \pm 1 / 2}, \xi_{x, i \pm 1 / 2}, \xi_{y, i \pm 1 / 2}, J_{i \pm 1 / 2}\right) \\ \widetilde{F}_{i \pm 1 / 2}=\widetilde{F}\left(U_{i \pm 1 / 2}, \xi_{x, i}, \xi_{y, i}, J_{i}\right) \end{array}\right. $ |
由于采用离散等价方程和相容性准则消除坐标变换引起的误差,和几何守恒律采用构造坐标变换系数使得源项离散后仍为0的算法思路不同,文章发表后同行提出异议,因此在后续论文[23]中不再提几何守恒律,而是采用“离散等价方程的相容性算法”来表述。文献[23]采用算子形式证明了提出的离散等价方程相容性准则适用于任意格式,本文采用以上五阶ENO类格式计算均匀流场,可以完全消除图 3和图 4中的误差,进一步验证了上述结论的正确性。

|
图 4 静止流场密度误差云图 Fig.4 Contours of density error for the stationary flow |
文献[17]中给出了亚跨超声速流场的算例,定性比较误差云图, 和本文的高精度格式结果非常相似,因此本文不再给出更多马赫数的计算结果,而是给出了采用一阶迎风格式时的数值模拟结果(如图 5所示)作为对比。
|
图 5 一阶迎风格式密度误差云图 Fig.5 Contours of density error for the uniform flow with the first-order upwind scheme |
对比图 3、图 4和图 5中相同来流条件下的计算结果,可发现在本文计算条件下,使用五阶ENO类格式计算得到的误差结果比使用一阶迎风格式计算得到的误差结果高一个量级,这是个还没有看到文献报道的新现象,下面进行初步分析。
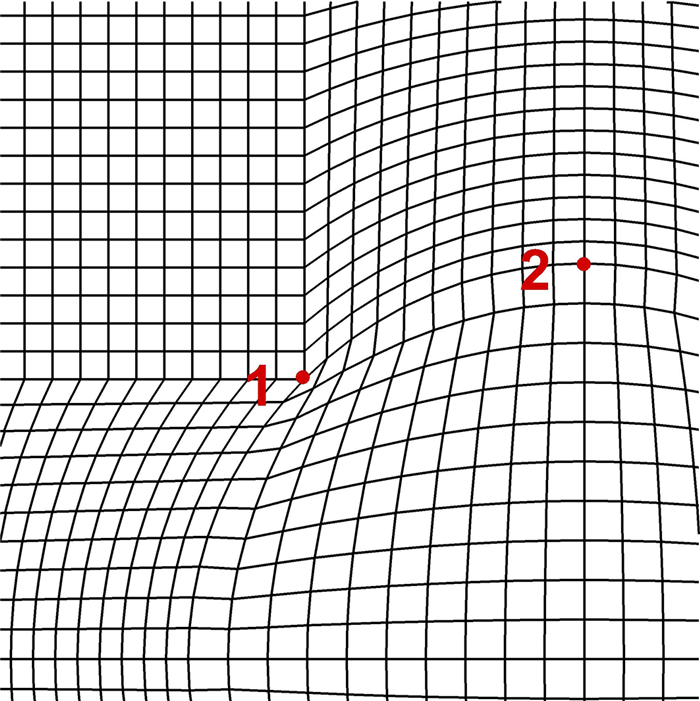
选取如图 6所示2个网格点,以ξ方向为例,对离散点xi的模板区域内各点的对流通量进行计算,一阶迎风格式的模板区域为(xi-1, xi+1),五阶ENO类格式的模板区域为(xi-3, xi+3)。计算模板区域内各个点上对应的ξ方向的正通量,将传统CFD方法计算的结果记为
|
图 6 通量计算选取计算点 Fig.6 Calculation points selected for flux calculation |
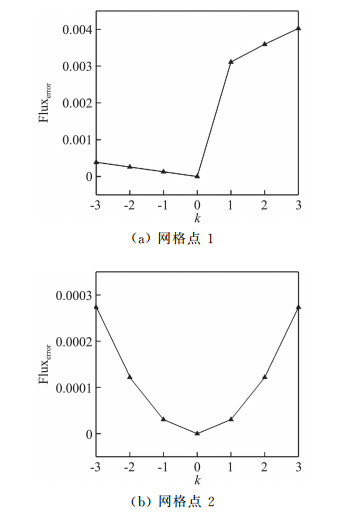
|
图 7 不同计算方法得到的对流通量差值 Fig.7 Errors of convex flux obtained by different methods |
对于存在激波的流动,由于模板选择与流动参数相关,给理论分析带来难度,只能通过数值算例进行研究。对图 1所示计算网格,在x=0.1处放置一道Ma=3.0的正激波,给定初始计算条件为:
| $ \begin{array}{ll} (\rho, u, v, p)= & \\ \left\{\begin{array}{ll} 5.4, 2.222, 0.0, 10.333), & x \leqslant 0.1 \\ (1.4, 0.0, 0.0, 1.0), & \text { else } \end{array}\right. \end{array} $ | (4) |
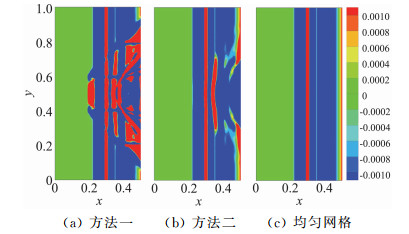
对流通量导数采用五阶WENO-Z格式计算,时间步长参数选取CFL=0.5,经过时间t=0.25,激波运动至x=0.85的位置。比较数值解和理论值的计算结果,发现在激波附近密度误差最大,因此,选择0≤x≤0.5区域进行结果分析,密度误差采用同样幅度显示,结果如图 8所示,其中图 8(a)是传统CFD方法的计算结果,8(b)是采用离散等价方程的相容性算法得到的计算结果,图 8(c)为选择同样网格数目的正方形均匀网格的计算结果。
|
图 8 x≤0.5区域的密度误差云图 Fig.8 Contours of density error in the area of x≤0.5 |
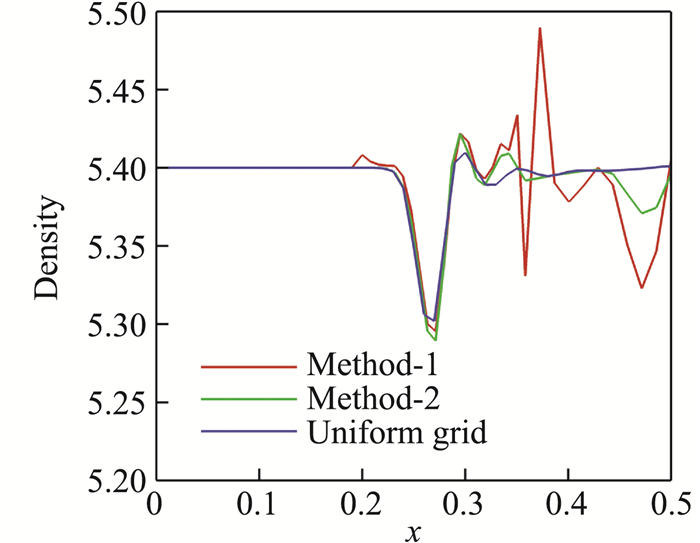
对应云图,图 9给出了t=0.25时刻沿着上下对称线y=0.5的密度分布曲线。三种结果在激波下游都存在明显的波动特性,从分布曲线及误差云图沿纵向的平行度来分析,采用离散等价方程的相容性算法后,误差特性更接近没有坐标变换的正方形均匀网格,表明这种算法对于存在激波的流场也是有效的。
|
图 9 y=0.5线上密度分布 Fig.9 Density distributions along line y=0.5 |
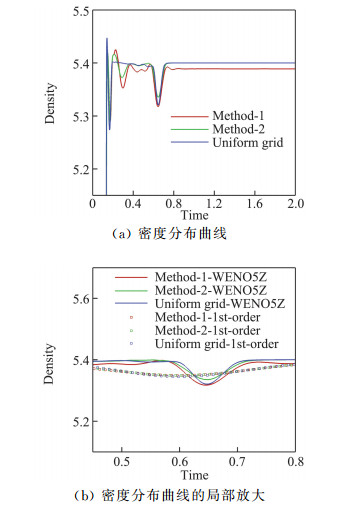
图 10为计算区域中心点(x, y)=(0.5, 0.5)处密度随时间变化曲线,为了更好地分辨及分析计算结果,在其局部放大图中给出一阶迎风格式的计算结果。从图中可以得到如下认识:
|
图 10 中心点处密度随时间变化曲线及其局部放大 Fig.10 Time-density curves at the central point and its partial enlarged drawing |
(1) 这种波动现象与坐标变换及格式精度无关,高精度格式的低耗散特性在维持波动向下游发展过程中比一阶格式的幅值更高、宽度更窄;
(2) 波动从下游边界离开后流场趋于稳定,收敛解存在可辨识的差异,齐次方程的高精度格式计算结果和一阶迎风接近,曲线坐标离散等价方程和正方形网格的高精度格式计算结果接近。
经过以上数值试验和理论分析,得出如下结论:对于采用模板扩展方式构造的高精度格式,在计算均匀流场时出现曲线坐标变换引起的误差比低精度格式更大的现象,这是造成高精度格式在复杂工程应用中效果不佳的主要原因。从离散等价方程出发, 采用相容性算法时使用高精度格式可以把曲线坐标变换引起的误差降低到直角坐标系量级,有效解决了高精度格式的工程应用难题。
2 激波捕捉法和Riemann分解的匹配问题很多高精度格式的应用,例如旋涡主导的流动、湍流模拟、气动声学等,大多采用正方形均匀网格,以下算例均采用笛卡尔直角坐标系下Euler方程的直接离散,大部分算例是正方形网格,少量算例是长方形网格。
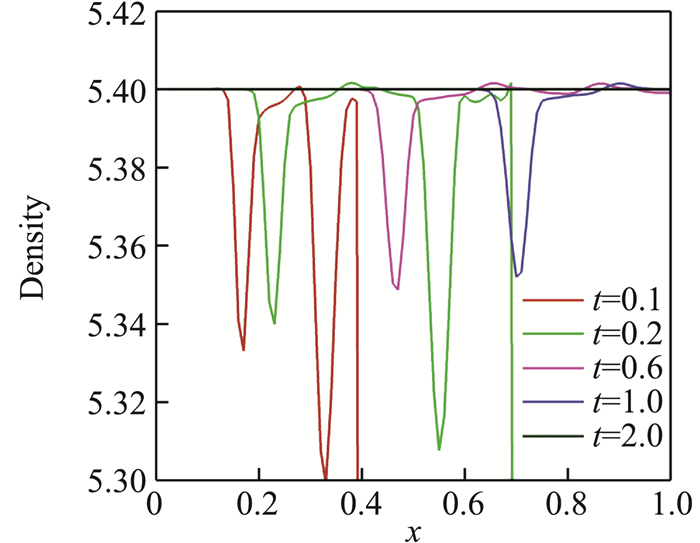
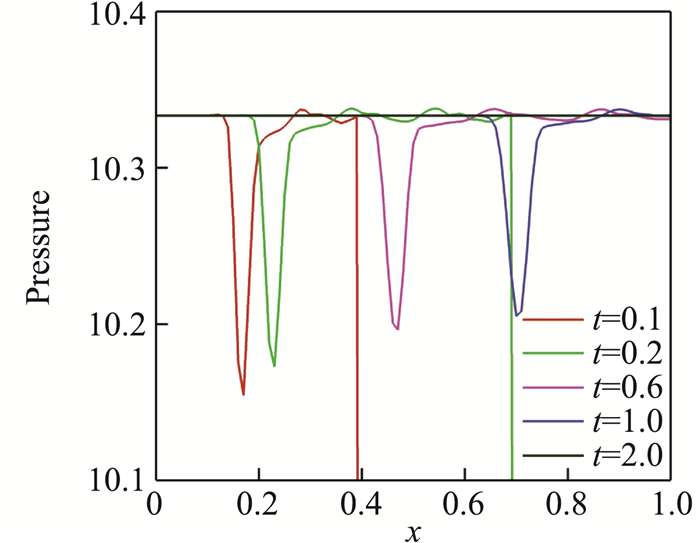
首先,采用正方形均匀网格考察式(4)所描述的流场,其对称线上不同时刻密度和压力的波动曲线如图 11和图 12所示。通过比较发现,密度曲线存在两个逐步拉开的波动,而压力曲线只有一个波动,且与密度曲线其中一个波动的位置相同。此外还给出一阶迎风格式的计算结果,峰值基本一致,影响区域较宽,为便于分辨未标出。
|
图 11 y=0.5线上密度随时间变化曲线 Fig.11 Time-varying densities along the line y=0.5 |
|
图 12 y=0.5线上压力随时间变化曲线 Fig.12 Time-varying pressures along the line y=0.5 |
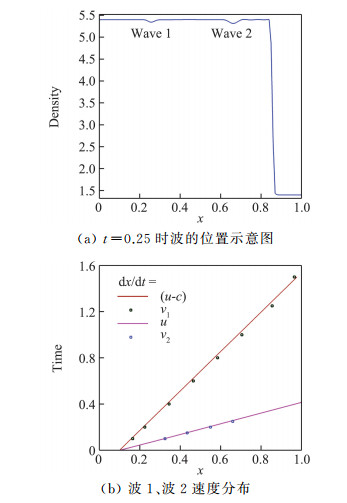
选取时间t=0.1, 0.2, 0.4, 0.6, 0.8, 1.0, 1.25, 1.5时的计算结果,画出波1、波2的极小值位置随时间变化曲线如图 13所示,其斜率正好是激波后流动的两个特征速度u2和u2-a2,这个规律的发现有助于解释波动现象的机理。
|
图 13 波后扰动的传播速度 Fig.13 Propagation velocities of these two disturbance waves after the shock |
计算网格采用正方形均匀网格时,由图 8(c)看出变量沿纵向没有变化,因此对以上结果下面按照一维Euler方程进行理论分析。Euler方程不考虑黏性,激波是上下游参数满足R-H关系式的数学间断。20世纪50年代,Lax等提出了双曲型守恒律方程的弱解理论,其中的Reimann分解理论能够给出Euler方程在任意初始流场参数下的解析式。对CFD建立在离散空间网格上的求解模型,将相邻网格之间物理量的差异当做间断处理可以很好地利用弱解理论来构建算法。精确Reimann分解存在多种结构,计算较为耗时,因此后续发展出Steger、Van Leer、Roe、HLLC等通量格式来近似Reimann分解以提高计算效率。
激波捕捉法最早是von Neumann提出的,他认为激波具有有限的厚度,在离散空间可以由若干网格构成的过渡区描述,因此整个流场可以采用统一的计算格式。由于激波在理论上不存在过渡区,无法评价数值解的精度,只能是定性比较,认为过渡区涉及网格点越少或者曲线斜率较大的格式精度越高。而根据CFD理论,即使包含激波的流场,差分格式离散后的数值解也需要满足如下修正方程:
| $ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} = \sum\limits_{n = 2}^\infty {{\gamma _n}} \frac{{{\partial ^n}U}}{{\partial {x^n}}} $ | (5) |
以上两个理论在激波处出现了矛盾:
(1) 由于每个网格点上只能存在一个数值解,利用捕捉法描述的间断存在过渡区,而过渡区在数学上是不存在的,依然要进行Reimann分解,从而产生更多的非物理结构。高精度格式采用限制器抑制过渡区内的虚假结构不发散,因此,不同格式的效果不一样(见图 3~图 5)。
(2) 初始时刻根据R-H关系式得到的激波本来是Reimann分解中的单一结构,由于不满足以上修正方程在计算过程中也会被Reimann分解成多个结构。把初始激波分解出来的虚假结构当做输入条件进行计算,不同格式精度的计算结果均会出现这种虚假波动现象(见图 10~图 12)。
很多时候网格和激波不能像以上算例保持完全匹配,为此,把以上正激波旋转一定角度,旋转后的激波与x轴的夹角记为α,计算初始条件为:
| $ \begin{array}{l} (\rho , u, v, p) = \\ \left\{ \begin{array}{l} (1.4, 0.0, 0.0, 1.0), \quad x \ge 0.07, y \le \tan \alpha + 0.07\\ (5.4, 2.222\sin \alpha , - 2.222\cos \alpha , 10.333), \quad {\rm{ else}} \end{array} \right. \end{array} $ | (6) |
对流通量导数仍然采用五阶WENO-Z格式计算,通量分裂采用VanLeer格式,时间步长参数CFL=0.5,计算时间t=0.1。
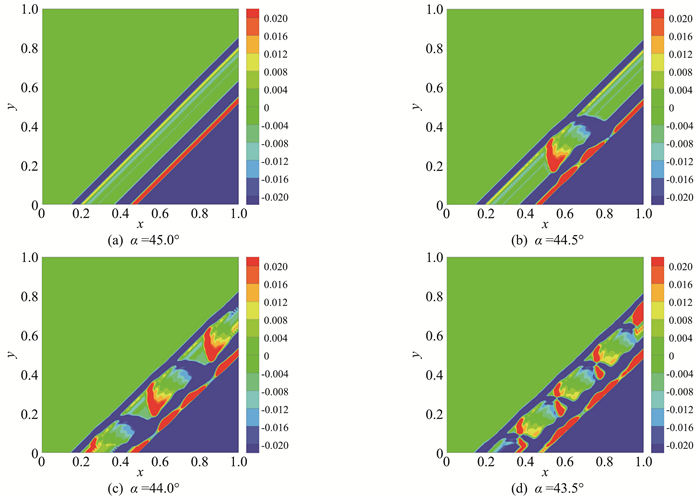
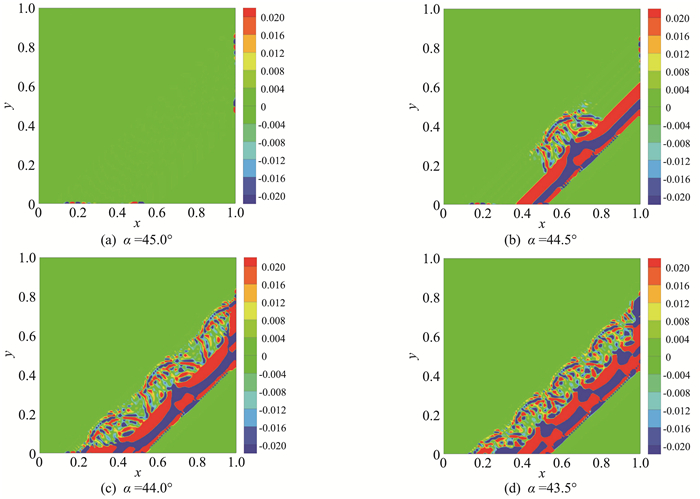
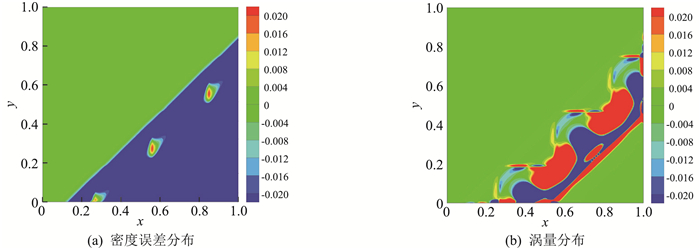
选取的旋转角度不同,计算结果也不相同,计算得到的密度误差云图和涡量云图分别如图 14、图 15所示,可以看出小的角度变化会引起非常大的流场差异。同样给出一阶迎风格式的计算结果(图 16)作为对比,除了验证以上分析结论,还发现高精度格式的高分辨率特性可以使这种虚假结构的结构更为清晰,在网格不匹配条件下相互干扰易出现虚假的“数值湍流”。
|
图 14 不同激波运动角度下的密度误差云图 Fig.14 Contours of density error for the shock moving problem with different inclined angles |
|
图 15 不同激波运动角度下的涡量分布云图 Fig.15 Contours of vorticity for the shock moving problem with different inclined angles |
|
图 16 一阶迎风格式α=44.0°下时的密度误差和涡量分布云图 Fig.16 Contours of density error and vorticity for the shock moving problem at α=44.0° with the first-order upwind scheme |
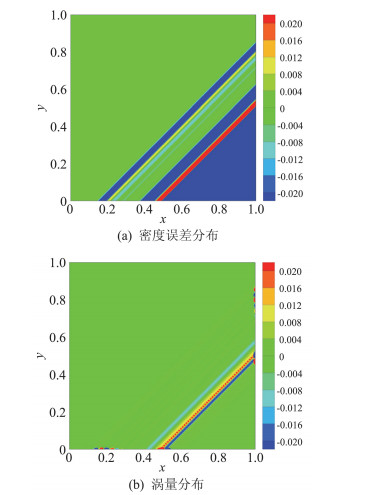
在激波捕捉法范围内只能采用网格匹配来消除这种“数值湍流”,图 17是采用Δx≠Δy的长方形网格保证初始激波全部落在对角线网格点上的密度误差云图。不管定常或非定常问题,计算过程中激波都是运动的,因此要想实现激波与网格完全匹配只能采用激波装配法。
|
图 17 网格匹配时计算得到的密度误差云图及涡量分布云图(α=44.0°) Fig.17 Contours of density error and vorticity for the shock matched grids (α=44.0°) |
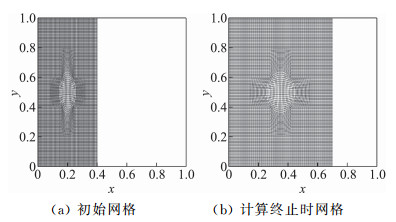
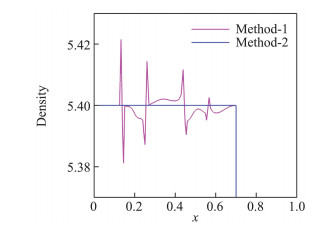
关于装配法的验证和演示算例可以参考文献[4-5],本文给出以上正激波算例的装配法计算结果来进行简单比较。给定初始正激波位于x=0.4,时间步长参数CFL=0.5,运动时间t=0.1时计算停止,计算过程中网格变化如图 18所示。图 19为分别采用传统CFD计算方法(方法1)和基于离散等价方程的相容性算法(方法2)得到的对称线y=0.5上的密度分布曲线,因为装配法直接采用R-H关系式计算激波,初始激波不会分解出虚假结构,激波后流动参数理论上为均匀流场的参数。图 19的计算结果也证明了这一观点,采用方法1计算时,激波波后有因网格变换而产生的误差,采用方法2后,误差消除,激波波后为均匀流场。
|
图 18 激波装配计算过程中的网格变化 Fig.18 Illustration diagrams of the grid changes during the shock-fitting process |
|
图 19 y=0.5线上密度分布的局部放大图 Fig.19 Partial enlarged drawing of the density distribution curves alone the line y=0.5 |
(1) 有限差分格式应用于贴体坐标系时会因为不满足几何守恒律而产生数值误差,本文通过数值实验发现在同一计算条件下,对均匀流场来说,高阶格式产生的误差比一阶迎风格式要大,经过初步分析认为因为高阶格式选用的模板比一阶格式的模板涉及到的网格点更多,每个网格点上的误差叠加导致引入了更多的误差。作者提出的基于离散等价方程的相容性算法在本文中被证明对高阶格式同样具有适用性,能够消除高精度格式应用于贴体坐标系时产生的数值误差。
(2) 本文在求解正方形均匀网格上的正激波运动问题时发现,在运动激波的波后会产生两个新的波的结构,经过初步分析认为这是通量分裂格式在激波处产生的随着特征线传播的非物理波动。在二维问题中,高精度格式的高分辨特性导致在激波与网格不能完全匹配情况下多维波动相互干扰出现虚假的“数值湍流”现象,激波装配法能够很好地解决这个难题。
| [1] |
常思源, 邹东阳, 刘君. 自适应间断装配法模拟弹道靶中超高速弹丸发射[J]. 实验流体力学, 2019, 33(2): 23-29. CHANG S Y, ZOU D Y, LIU J. Simulating hypersonic projectile launching process in the ballistic range by adaptive discontinuity fitting solver technique[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(2): 23-29. (in Chinese) |
| [2] |
刘君, 刘瑜, 陈泽栋. 非结构变形网格和离散几何守恒律[J]. 航空学报, 2016, 37(8): 2395-2407. LIU J, LIU Y, CHEN Z D. Unstructured deforming mesh and discrete geometric conservation law[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2395-2407. (in Chinese) |
| [3] |
ZOU D Y, XU C G, DONG H B, et al. A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes[J]. Journal of Computational Physics, 2017, 345: 866-882. |
| [4] |
刘君, 邹东阳, 董海波. 动态间断装配法模拟斜激波壁面反射[J]. 航空学报, 2016, 37(3): 836-846. LIU J, ZOU D Y, DONG H B. A moving discontinuity fitting technique to simulate shock waves impinged on a straight wall[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 836-846. (in Chinese) |
| [5] |
邹东阳, 刘君, 邹丽. 可压缩流动激波装配在格心型有限体积法中的应用[J]. 航空学报, 2017, 38(11): 139-149. ZOU D Y, LIU J, ZOU L. Applications of shock-fitting technique for compressible flow in cell-centered finite volume methods[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(11): 139-149. (in Chinese) |
| [6] |
MARCELLO O, RENATO P. Shock fitting: classical techniques, recent developments, and memoirs of gino moretti[M]. Springer, 2017: 131-149.
|
| [7] |
ZHANG L P, WANG Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33(7): 891-916. |
| [8] |
LI W N, REN Y X. The multi-dimensional limiters for solving hyperbolic conservation laws on unstructured grids Ⅱ:Extension to high order finite volume schemes[J]. Journal of Computational Physics, 2012, 231(11): 4053-4077. |
| [9] |
THOMAS P D, LOMBARD C K. The geometric conservation law-a link between finite-difference and finite-volume methods of flow computation on moving grids[C]//11th Fluid and PlasmaDynamics Conference, Seattle, WA, USA. Reston, Virigina: AIAA, 1978.
|
| [10] |
THOMAS P D, LOMBARD C K. Geometric conservation law and its application to flow computations on moving grids[J]. AIAA Journal, 1979, 17(10): 1030-1037. |
| [11] |
ABE Y, ⅡZUKA N, NONOMURA T, et al. Symmetric-conservative metric evaluations for higher-order finite difference scheme with the GCL identities on three-dimensional moving and deforming meshs[J]. Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, Hawaii, 2012. |
| [12] |
ABE Y, ⅡZUKA N, NONOMURA T, et al. Conservative metric evaluation for high-order finite difference schemes with the GCL identities on moving and deforming grids[J]. Journal of Computational Physics, 2013, 232(1): 14-21. |
| [13] |
DENG X G, MAO M L, TU G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2011, 230(4): 1100-1115. |
| [14] |
DENG X G, MIN Y B, MAO M L, et al. Further studies on geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2013, 239: 90-111. |
| [15] |
NONOMURA T, TERAKADO D, ABE Y, et al. A new technique for freestream preservation of finite-difference WENO on curvilinear grid[J]. Computers & Fluids, 2015, 107: 242-255. |
| [16] |
ZHU Y J, SUN Z S, REN Y X, et al. A numerical strategy for freestream preservation of the high order weighted essentially non-oscillatory schemes on stationary curvilinear grids[J]. Journal of Scientific Computing, 2017, 72(3): 1021-1048. |
| [17] |
刘君, 韩芳, 夏冰. 有限差分法中几何守恒律的机理及算法[J]. 空气动力学学报, 2018, 36(6): 917-926. LIU J, HAN F, XIA B. Mechanism and algorithm for geometric conservation law in finite difference method[J]. Acta Aerodynamica Sinica, 2018, 36(6): 917-926. (in Chinese) |
| [18] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. |
| [19] |
HENRICK A K, ASLAM T D, POWERS J M. Mapped weighted essentially non-oscillatory schemes:Achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207(2): 542-567. |
| [20] |
BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227(6): 3191-3211. |
| [21] |
FU L, HU X Y, ADAMS N A. A family of high-order targeted ENO schemes for compressible-fluid simulations[J]. Journal of Computational Physics, 2016, 305: 333-359. |
| [22] |
CAI X D, LADEINDE F. Performance of WENO scheme in generalized curvilinear coordinate systems[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2008: 36.
|
| [23] |
刘君, 韩芳. 有限差分法中的贴体坐标变换[J]. 气体物理, 2018, 3(5): 18-29. LIU J, HAN F. Body-fitted coordinate transformation for finite difference method[J]. Physics of Gases, 2018, 3(5): 18-29. (in Chinese) |
 2019, Vol. 38
2019, Vol. 38

