2. 陕西省先进飞行器服役环境与控制重点实验室, 西安 710049
2. Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, Xi'an 710049, China
近来在计算流体力学(Computational Fluid Dynamics, CFD)中,数值模拟宽范围努森数Kn的多尺度流动问题成为一个热点。随着Kn的变化,流动对应领域及流动特征尺度不尽相同,对传统CFD方法提出了挑战。通常根据Kn对气体流动领域进行了如下划分[1]:在Kn < 0.001时属于连续流动领域,传统基于连续介质假设的N-S方程和黏性壁面处的无滑移边界条件是适用的,流动对应宏观动力学特征尺度,如绕流物体特征长度,这正是传统CFD方法蓬勃发展并得到广泛应用的领域;当0.001 < Kn < 0.1,流动进入滑移区,N-S方程本身是适用的,但是壁面处速度滑移效应和温度跳跃现象将出现,需要对传统无滑移边界条件进行修正;进一步当Kn增加满足0.1 < Kn < 10,流动进入过渡流领域,具有明显非平衡效应,基于连续介质假设的N-S方程失效,壁面滑移效应也将进一步增强;当Kn>10时流动属于自由分子流领域,非平衡效应很强,流动对应微观动理学特征尺度,即分子平均自由程和平均碰撞松弛时间。上述对流动领域的划分属于比较粗线条的,一个全场定义的Kn不足以精确刻画流场当地每点的流动特征。最近陈杰等[2]提出一个反映气体局部稀薄效应判据的工作值得关注。
尽管对于Kn较大的过渡流及自由分子流,Bird[3]提出的Direct Simulation Monte Carlo(DSMC)方法是一种有效方法,但是对于连续流动,DSMC所消耗的计算时间及计算资源将异常巨大。因此发展适用于宽范围Kn数变化、跨流域的统一算法对解决实际工程当中的多尺度流动是一个关键问题。
另一方面,直接求解分布函数满足的Boltzmann方程是气体动理学方法的研究思路,近来一些气体动理学格式也应运而生。如格子Boltzmann方法(Lattice Boltzmann Method, LBM)[4-6]、气体动理学统一算法(Gas Kinetic Unified Algorithms, GKUA)[7-11]、气体动理学格式(Gas Kinetic Scheme, GKS)[12-16]、统一气体动理学格式(Unified Gas Kinetic Scheme, UGKS)[17-22]、离散统一气体动理学格式(Discrete Unified Gas Kinetic Scheme, DUGKS)[23-25]等。这些方法与传统基于N-S方程的CFD方法相比,可以获得更多的流动信息,且已有大量成功的应用[26-33]。
本文从DUGKS格式出发,指出DUGKS在处理碰撞项时,采用显式和隐式的简单算术平均并未充分考虑不同流动领域碰撞项对应物理过程的不同,尤其没有充分考虑两个时间尺度即计算时间步长和碰撞松弛时间之间的相对大小对粒子碰撞过程宏观表现的影响。为此,本文将对碰撞项的离散采用显式和隐式的加权平均,且权系数紧密依赖于计算时间步长和当地碰撞松弛时间之比,即当地努森数。进一步通过物理上的分析与数学上的推演,表明该权系数可以根据当地流动特征尺度进行自适应调节,从而将原始DUGKS格式进一步发展成为具有尺度自适应特性的离散统一气体动理学格式(Scale Adaptive Discrete Unified Gas Kinetic Scheme, SADUGKS)。
1 Boltzmann-Shakhov模型方程及其沿特征线离散的一般形式为了克服Boltzmann-BGK模型对应普朗特数Pr≡1与实际气体不相符,本文基于Boltzmann- Shakhov模型来构造计算格式。
在D维空间中,Boltzmann-Shakhov模型[24, 34]如下:
| $ \frac{\partial f}{\partial t}+u_{i} \frac{\partial f}{\partial x_{i}}=\mathit{\Omega}=\frac{1}{\tau}\left(f^{s}-f\right) $ | (1) |
其中,f=f(xi, t, uj, ηk, ξl)为D维空间中t时刻、位置x =(x1, ..., xD)处、速度为u =(u1, …, uD)的粒子分布函数,η =(η1, ..., η3-D)为宏观速度恒为零的方向上的粒子运动速度,ξ =(ξ1, …, ξK)为粒子内自由度,K为粒子内自由度的维度,与粒子种类相关;τ为碰撞松弛时间,与动力学黏性系数μ及压力p相关,τ=μ/p;fs为Shakhov平衡态分布函数,可表示为Maxwell平衡态分布函数及Pr数修正两部分。
为节约内存开销和计算量,将f对内自由度和宏观速度恒为零的速度方向上积分得到两个约化分布函数:
| $ g\left(x_{i}, t, u_{j}\right)=\int f\left(x_{i}, t, u_{j}, \eta_{k}, \xi_{l}\right) \mathrm{d} \boldsymbol{\eta} \mathrm{d} \boldsymbol{\xi} $ | (2) |
| $ h\left(x_{i}, t, u_{j}\right)=\int\left(|\boldsymbol{\eta}|^{2}+|\boldsymbol{\xi}|^{2}\right) f\left(x_{i}, t, u_{j}, \eta_{k}, \xi_{l}\right) \mathrm{d} \boldsymbol{\eta} \mathrm{d} \boldsymbol{\xi} $ | (3) |
宏观守恒量Q =(ρ, ρU, ρE)T、应力张量τ及热流q可由分布函数求矩得到:
| $ \begin{array}{l} \rho=\int g \mathrm{d} \boldsymbol{u}, \rho \boldsymbol{U}=\int \boldsymbol{u} g \mathrm{d} \boldsymbol{u} \\ \rho E=\frac{1}{2} \int\left(|\boldsymbol{u}|^{2} g+h\right) \mathrm{d} \boldsymbol{u} \end{array} $ | (4) |
| $ \boldsymbol{q}=\frac{1}{2} \int \boldsymbol{c}\left(|\boldsymbol{c}|^{2} g+h\right) \mathrm{d} \boldsymbol{u} $ | (5) |
| $ \boldsymbol{\tau}=\int \boldsymbol{c c}\left(g-g^{\mathrm{eq}}\right) \mathrm{d} \boldsymbol{u} $ | (6) |
其中c = u - U,geq为Maxwell平衡态分布:
| $ g^{\mathrm{eq}}=\frac{\rho}{(2 \pi R T)^{D / 2}} \exp \left[-|\boldsymbol{c}|^{2} /(2 R T)\right] $ | (7) |
对式(1)积分可得到约化分布函数g及h的控制方程:
| $ \frac{\partial g}{\partial t}+u_{i} \frac{\partial g}{\partial x_{i}}=\mathit{\Omega}_{g}=\frac{1}{\tau}\left(g^{s}-g\right) $ | (8) |
| $ \frac{{\partial h}}{{\partial t}} + {u_i}\frac{{\partial h}}{{\partial {x_i}}} = {\mathit{\Omega} _h} = \frac{1}{\tau }\left( {{h^s} - h} \right) $ | (9) |
其中,gs和hs分别为g和h的Shakhov平衡态分布函数,二者均可表示为Maxwell平衡态及Pr修正两部分:
| $ {g^s} = \int {{f^s}{\rm{d}}\mathit{\boldsymbol{\eta }}{\rm{d}}\mathit{\boldsymbol{\xi }} = {g^{{\rm{eq}}}} + {g_{{\rm{Pr}}}}} $ | (10) |
| $ {g_{Pr}} = \left( {1 - Pr} \right){\rm{ }}\frac{{{c_i}{q_i}}}{{5pRT}}\left( {\frac{{{{\left| \mathit{\boldsymbol{c}} \right|}^2}}}{{RT}}{\rm{ }} - D - 2} \right){g^{{\rm{eq}}}} $ | (11) |
| $ {h^s} = \smallint ({\left| \mathit{\boldsymbol{\eta }} \right|^2} + {\left| \mathit{\boldsymbol{\xi }} \right|^2}){f^s}{\rm{d}}\mathit{\boldsymbol{\eta }}{\rm{d}}\mathit{\boldsymbol{\xi }} = {h^{{\rm{eq}}}} + {h_{{\rm{Pr}}}} $ | (12) |
| $ {h^{{\rm{eq}}}} = \left( {K + 3 - D} \right)RT{g^{{\rm{eq}}}} $ | (13) |
| $ \begin{array}{l} {h_{Pr}} = \left( {1 - Pr} \right)\frac{{{c_i}{q_i}}}{{5p}}{g^{{\rm{eq}}}}\cdot\\ \;\;\;\;\;\;\;\;\;\left[ {\left( {\frac{{{{\left| \mathit{\boldsymbol{c }} \right|}^2}}}{{RT}} - D} \right)\left( {K + 3 - D} \right) - 2K} \right] \end{array} $ | (14) |
根据粒子碰撞过程满足质量、动量与能量守恒定律,约化分布函数g及h满足相应相容关系:
| $ \smallint {\mathit{\Omega} _g}\mathit{\boldsymbol{\psi }}{\rm{d}}\mathit{\boldsymbol{u}} + \smallint {\mathit{\Omega} _h}\mathit{\boldsymbol{\tilde \omega }}{\rm{d}}\mathit{\boldsymbol{u}} = 0 $ | (15) |
其中,
式(8)与式(9)形式上一致,可统一表示为:
| $ \frac{{\partial \phi }}{{\partial t}} + {u_i}\frac{{\partial \phi }}{{\partial {x_i}}} = {\mathit{\Omega} _\phi } = \frac{1}{\tau }({\phi ^s} - \phi ) $ | (16) |
其中ϕ=g或h。对于式(16),t+s时刻的分布函数可形式上表示为[12]:
| $ \begin{array}{l} \phi\left(x_{i}, t+s, u_{j}\right)= \\ \quad \frac{1}{\tau} \int_{0}^{s}\left[\phi^{s}\left(x_{i}^{\prime}, t+t^{\prime}, u_{j}\right) \cdot \mathrm{e}^{-\left(s-t^{\prime}\right) / \tau}\right] \mathrm{d} t^{\prime}+ \\ \quad \mathrm{e}^{-s / \tau} \phi^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right) \end{array} $ | (17) |
其中:t为初始时刻,s为时间发展长度,x′i=xi-ui(s-t′)为粒子运动轨迹;ϕini为初始t时刻的气体分布函数,即ϕini(xi, uj)=ϕ(xi, t, uj)。
尽管Boltzmann-Shakhov方程(16)基于微观观点建立,其所蕴含的流动尺度却不限于微观动理学尺度,这一点可以从式(17)清楚看出:式(17)右边第一项积分项反映粒子之间相互大量碰撞作用的积累效果,该项已被证明可以看作为宏观连续流动动力学模型[12, 35],对应尺度为宏观动力学尺度,如绕流物体特征长度;式(17)右边第二项反映粒子的迁移运动,对应尺度为微观动理学尺度,即分子平均自由程和平均碰撞松弛时间。式(17)将宏观动力学尺度和微观动理学尺度有机地结合到一起,可以很好反映多尺度流动特性。但是式(17)并不能直接使用,因为右边第一项积分项所涉及的ϕs是未知的,需要满足相容关系式(15)。因此从这个角度上来说式(17)只是式(16)形式上的解。
另一方面,认识到Boltzmann-Shakhov方程(16)自身已将宏观动力学尺度和微观动理学尺度有机地结合到一起,因此可以直接从Boltzmann-Shakhov方程(16)出发来构造多尺度计算格式。这里将式(16)沿特征线进行离散,可得到:
| $ \begin{array}{l} \frac{1}{s}\left[\phi\left(x_{i}, t+s, u_{j}\right)-\phi^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right)\right] \\ =\alpha {\mathit{\Omega}}_{\phi}\left(x_{i}, t+s, u_{j}\right)+(1-\alpha) {\mathit{\Omega}}_{\phi}^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right) \\ =\frac{\alpha}{\tau}\left[\phi^{s}\left(x_{i}, t+s, u_{j}\right)-\phi\left(x_{i}, t+s, u_{j}\right)\right]+ \\ \frac{1-\alpha}{\tau}\left[\phi^{s, \text { ini }}\left(x_{i}-u_{i} s, u_{j}\right)-\phi^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right)\right] \end{array} $ | (18) |
其中:
| $ \begin{array}{l} {\phi ^{s, {\rm{ini}}}}({x_i}, {u_j}) = {\phi ^s}({x_i}, t, {u_j})\\ \mathit{\Omega} _\phi ^{{\rm{ini}}}({x_i}, {u_j}) = {\mathit{\Omega} _\phi }({x_i}, t, {u_j}) \end{array} $ | (19) |
分别代表初始时刻t的平衡态分布函数和碰撞项。式(18)右端的碰撞项采用了显式和隐式加权平均处理。α为隐式部分对应的权系数,其为碰撞松弛时间τ和时间发展长度s的比值τ/s的函数,具体形式待定。式(18)可进一步整理为:
| $ \begin{array}{c} \phi\left(x_{i}, t+s, u_{j}\right)=\vartheta_{1} \phi^{s}\left(x_{i}, t+s, u_{j}\right)+ \\ \vartheta_{2} \phi^{s \cdot \text { ini }}\left(x_{i}-u_{i} s, u_{j}\right)+\vartheta_{3} \phi^{\text {ini }}\left(x_{i}-u_{i} s, u_{j}\right) \end{array} $ | (20) |
其中,系数
| $ \begin{array}{l} \vartheta_{1}(s)=\frac{\alpha s}{\tau+\alpha s} \\ \vartheta_{2}(s)=\frac{s-\alpha s}{\tau+\alpha s} \\ \vartheta_{3}(s)=1-\frac{s}{\tau+\alpha s} \end{array} $ | (21) |
式(20)为Boltzmann-Shakhov方程沿特征线离散的一般形式,其右端前两项和平衡态分布函数相关反映粒子之间的碰撞作用,将和式(17)右端第一项积分项对应;式(20)右端第三项和初始非平衡态分布函数相关反映粒子的迁移效应,将和式(17)右端第二项相对应。通过对比式(17)和式(20)中的非平衡态分布函数相关项,并令
| $ \alpha(s)=\frac{1}{1-\mathrm{e}^{-s / \tau}}-\frac{\tau}{s} $ | (22) |
式(22)表明权系数α数学上直接依赖于时间比值τ/s,物理上的讨论将在后面第3节给出。确定了α后将其带入到式(21),可得系数
| $ \left\{\begin{array}{l} \vartheta_{1}(s)=1-\frac{\tau}{s}\left(1-\mathrm{e}^{-s / \tau}\right) \\ \vartheta_{2}(s)=\frac{\tau}{s}\left(1-\mathrm{e}^{-s / \tau}\right)-\mathrm{e}^{-s / \tau} \\ \vartheta_{3}(s)=\mathrm{e}^{-s / \tau} \end{array}\right. $ | (23) |
为了进一步分析式(20)的数学物理特性,这里将从两种极限流动的角度来讨论,首先将式(20)整理为以下形式:
| $ \begin{array}{c} \phi\left(x_{i}, t+s, u_{j}\right)=\phi^{s}\left(x_{i}, t+s, u_{j}\right)+ \\ \beta_{1}\left[\phi^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right)-\phi^{s, \text { ini }}\left(x_{i}-u_{i} s, u_{j}\right)\right]+ \\ \beta_{2}\left[\phi^{s, \text { ini }}\left(x_{i}-u_{i} s, u_{j}\right)-\phi^{s}\left(x_{i}, t+s, u_{j}\right)\right] \end{array} $ | (24) |
其中:
| $ \beta_{1}=\mathrm{e}^{-s / \tau}, \quad \beta_{2}=\left(1-\mathrm{e}^{-s / \tau}\right) \tau / s $ | (25) |
对于Kn→0的宏观连续流动问题,物理上在一个时间步长内粒子经历的碰撞次数足够多,即τ
| $ \begin{array}{c} \phi\left(x_{i}, t+s, u_{j}\right) \approx \phi^{s}\left(x_{i}, t+s, u_{j}\right)+ \\ \frac{\tau}{s}\left[\phi^{s, \text { ini }}\left(x_{i}-u_{i} s, u_{j}\right)-\phi^{s}\left(x_{i}, t+s, u_{j}\right)\right] \\ \approx \phi^{s}\left(x_{i}, t+s, u_{j}\right)-\tau D_{t} \phi^{s}\left(x_{i}, t+s, u_{j}\right) \end{array} $ | (26) |
其中Dt=∂t+uj∂xj。对式(8)进行Chapman-Enskog展开至O(τ)(对应为宏观N-S方程)同样可以得到式(26)[12],因此说明在宏观连续流动区域式(20)与N-S方程一致, 此时流动尺度为宏观动力学尺度。
对于Kn
| $ \phi\left(x_{i}, t+s, u_{j}\right) \rightarrow \phi^{\mathrm{ini}}\left(x_{i}-u_{i} s, u_{j}\right) $ | (27) |
上式其实就是自由分子流运动的解,此时流动对应微观动理学尺度。
由上述分析可知,Boltzmann-Shakhov方程沿特征线离散的一般形式(20)将宏观动力学尺度和微观动理学尺度有机地结合到一起,其中引入的系数
尺度自适应的离散统一气体动理学格式(Scale Adaptive Discrete Unified Gas Kinetic Scheme, SADUGKS)可视为在原始DUGKS格式[24]的基础上进行改进,二者主要区别在于权系数α的形式不同。
基于有限体积法框架,将式(16)在网格单元Vj及时间步长(tn, tn+Δt)内积分,得:
| $ \left(\phi_{j}^{n+1}-\phi_{j}^{n}\right) V_{j}+\sum\limits_{m} \int_{t_{n}}^{t_{n+\Delta t}} F_{m} \mathrm{d} t=V_{j} \int_{t_{n}}^{t_{n}+\Delta t} \mathit{\Omega}_{\phi, j} \mathrm{d} t $ | (28) |
其中,ϕjn、Ωϕ, j分别为网格单元Vj内分布函数及碰撞项的平均值,Fm为单元第m个界面Sm处的通量:
| $ \begin{array}{l} \phi_{j}^{n}=\frac{1}{V_{j}} \int_{V_{j}} \phi^{n} \mathrm{d} V, \mathit{\Omega}_{\phi, j}=\frac{1}{V_{j}} \int_{V_{j}} \mathit{\Omega}_{\phi} \mathrm{d} V \\ F_{m}=\int_{S_{m}} u_{k} n_{k} \phi \mathrm{d} S \end{array} $ | (29) |
对式(28)中通量的时间积分项采用中点公式处理:
| $ \int_{t_{n}}^{t_{n}+\Delta t} F_{m} \mathrm{d} t \approx \Delta t F_{m}\left(t_{n}+\Delta t / 2\right)=\Delta t F_{m}^{n+\frac{1}{2}} $ | (30) |
对式(28)中碰撞项的时间积分采用加权梯形公式:
| $ \int_{t_{n}}^{t_{n}+\Delta t} \mathit{\Omega}_{\phi, j} \mathrm{d} t \approx \Delta t\left[\alpha(\Delta t) \mathit{\Omega}_{\phi, j}^{n+1}+(1-\alpha(\Delta t)) \mathit{\Omega}_{\phi, j}^{n}\right] $ | (31) |
其中α(Δt)为式(22)给出的权系数:
| $ \alpha(\Delta t)=\frac{1}{1-\mathrm{e}^{-\Delta t / \tau}}-\frac{\tau}{\Delta t} $ | (32) |
需要指出的是在原始DUGKS格式中[24],式(31)中的权系数取为αDUGKS≡0.5,即代表碰撞项的显式和隐式算术平均。
将式(30)和式(31)代入到式(28)中,可得:
| $ \begin{aligned} \phi_{j}^{n+1}=& \phi_{j}^{n}-\frac{\Delta t}{V_{j}} \sum\limits_{m} F_{m}^{n+\frac{1}{2}}+\\ & \Delta t\left[\alpha(\Delta t) \mathit{\Omega}_{\phi, j}^{n+1}+(1-\alpha(\Delta t)) \mathit{\Omega}_{\phi, j}^{n}\right] \end{aligned} $ | (33) |
从式(33)可以看出该式右端包含了通量和碰撞项的隐式部分,因此在使用该式进行迭代递推之前必须先解决通量和碰撞项的隐式离散问题,下面对其分别进行处理。
首先对隐式通量
| $ \begin{aligned} & \frac{1}{r}\left[\phi\left(x_{i, b}, t_{n}+r, u_{j}\right)-\phi^{\mathrm{ini}}\left(x_{i, b}-u_{i} r, u_{j}\right)\right] \\ =& \alpha(r) \mathit{\Omega}_{\phi}\left(x_{i, b}, t_{n}+r, u_{j}\right)+(1-\alpha(r)) \mathit{\Omega}_{\phi}^{\mathrm{ini}}\left(x_{i, b}-u_{i} r, u_{j}\right) \end{aligned} $ | (34) |
其中t=tn为初始时刻,时间发展长度为r=Δt/2,xi, b为第m个网格单元界面Sm的位置(一维情况下,xi, b=xi+1/2),
进一步引入辅助分布函数ϕ定义:
| $ \bar{\phi}\left(x_{i}, t, u_{j}\right)=\phi\left(x_{i}, t, u_{j}\right)-r \alpha(r) \mathit{\Omega}_{\phi}\left(x_{i}, t, u_{j}\right) $ | (35) |
上式也等价于:
| $ \phi=\varphi_{1} \phi^{s}+\varphi_{2} \bar{\phi} $ | (36) |
其中系数φ1和φ2为,
| $ \varphi_{1}=\frac{\alpha r}{\tau+\alpha r}, \quad \varphi_{2}=1-\varphi_{1} $ | (37) |
则式(34)可化为:
| $ \begin{aligned} & \bar{\phi}\left(x_{i, b}, t_{n}+r, u_{j}\right) \\ =& \phi^{\operatorname{ini}}\left(x_{i, b}-u_{i} r, u_{j}\right)+r(1-\alpha(r)) \mathit{\Omega}_{\phi}^{\text {ini }}\left(x_{i, b}-u_{i} r, u_{j}\right) \\ =& \bar{\phi}^{+}\left(x_{i, b}-u_{i} r, t_{n}, u_{j}\right) \\ =& \bar{\phi}^{+, \text {ini }}\left(x_{i, b}-u_{i} r, u_{j}\right) \end{aligned} $ | (38) |
式(38)中引入的中间分布函数ϕ+定义为:
| $ \bar{\phi}^{+}\left(x_{i}, t, u_{j}\right)=\phi\left(x_{i}, t, u_{j}\right)+r(1-\alpha(r)) \mathit{\Omega}_{\phi}\left(x_{i}, t, u_{j}\right) $ | (39) |
其中ϕ+, ini(xi, uj)=ϕ+(xi, t, uj)为初始时刻ϕ+的值。在有限体积法框架下,式(38)中ϕ+, ini(xi, b-uir, uj)可根据初始时刻控制体内ϕ+的平均值进行重构从而得到ϕ+在空间上的分布以及网格界面处的值。对于本文中的可压缩流动,流动伴有间断现象,如激波,在重构时为了抑制间断附近的振荡可采用MUSCL或WENO重构等。
将式(36)和式(38)代入到通量
| $ \begin{aligned} F_{m}^{n+\frac{1}{2}}=& \int_{S_{m}} u_{k} n_{k} \phi\left(x_{i, b}, t_{n}+r, u_{j}\right) \mathrm{d} S \\ =& \varphi_{1} \int_{S_{m}} u_{k} n_{k} \phi^{s}\left(x_{i, b}, t_{n}+r, u_{j}\right) \mathrm{d} S+\\ & \varphi_{2} \int_{S_{m}} u_{k} n_{k} \bar{\phi}^{+}, \text {ini }\left(x_{i, b}-u_{i} r, u_{j}\right) \mathrm{d} S \end{aligned} $ | (40) |
由式(4)、(15)和(35)可知:
| $ \boldsymbol{Q}=\int g \boldsymbol{\psi} \mathrm{d} \boldsymbol{u}+\int h \tilde{\boldsymbol{\omega}} \mathrm{d} \boldsymbol{u}=\int \bar{g} \boldsymbol{\psi} \mathrm{d} \boldsymbol{u}+\int \bar{h} \tilde{\boldsymbol{\omega}} \mathrm{d} \boldsymbol{u} $ | (41) |
结合式(38)位于界面xi, b处,tn + r时刻的宏观守恒量为:
| $ \begin{aligned} & {\boldsymbol{Q}}\left(x_{i, b}, t_{n}+r\right) \\ =& \int \bar{g}\left(x_{i, b}, t_{n}+r, u_{j}\right) \boldsymbol{\psi} \mathrm{d} \boldsymbol{u}+\int \bar{h}\left(x_{i, b}, t_{n}+r, u_{j}\right) \tilde{\boldsymbol{\omega}} \mathrm{d} \boldsymbol{u} \\ =& \int \bar{g}^{+}, \text {ini }\left(x_{i, b}-u_{i} r, u_{j}\right) \boldsymbol{\psi} \mathrm{d} \boldsymbol{u}+\int \bar{h}^{+, \text {ini }}\left(x_{i, b}-u_{i} r, u_{j}\right) \tilde{\boldsymbol{\omega}} \mathrm{d} \boldsymbol{u} \end{aligned} $ | (42) |
从而式(40)中的ϕs(xi, b, tn+r, uj)可根据式(10)、(12)和式(42)进行计算,至此隐式通量
接下来处理碰撞项中的隐式部分Ωϕn+1,引入新的辅助分布函数
| $ \tilde{\phi}\left(x_{i}, t, u_{j}\right)=\phi\left(x_{i}, t, u_{j}\right)-\Delta t \alpha(\Delta t) \mathit{\Omega}_{\phi}\left(x_{i}, t, u_{j}\right) $ | (43) |
由相容关系式(15)同时结合定义式(43)可知:
| $ \mathit{\boldsymbol{Q}} = \int g \mathit{\boldsymbol{\psi }}{\rm{d}}\mathit{\boldsymbol{u}} + \int h \mathit{\boldsymbol{\tilde \omega }}{\rm{d}}\mathit{\boldsymbol{u}} = \int {\tilde g} \mathit{\boldsymbol{\psi }}{\rm{d}}\mathit{\boldsymbol{u}} + \int {\tilde h} \mathit{\boldsymbol{\tilde \omega }}{\rm{d}}\mathit{\boldsymbol{u}} $ | (44) |
将式(43)代入到式(33),整理得:
| $ \tilde{\phi}_{j}^{n+1}=\phi_{j}^{n}-\frac{\Delta t}{V_{j}} \sum\limits_{m} F_{m}^{n+\frac{1}{2}}+\Delta t(1-\alpha(\Delta t)) \mathit{\Omega}_{\phi, j}^{n} $ | (45) |
可以看出将式(40)给出的界面通量
再次指出的是在原始DUGKS格式中,从式(34)至式(39),式(43)和式(45)中出现的所有权系数α恒取为αDUGKS≡0.5。
需要说明的是上述在推导SADUGKS中速度空间是连续的,实际在使用SADUGKS时还需将速度空间离散,其离散方法与现有DUGKS[23-24]格式相同。关于边界条件的处理分两类,针对宏观连续流动问题,SADUGKS格式在固体壁面处采用了无滑移边界条件;而对较大Kn流动问题,则采用了完全漫反射边界条件,具体实现与DUGKS格式[23-24]亦相同,不再赘述。
3 尺度自适应的离散统一气体动理学格式的性质首先,作为DUGKS格式的一种改进,SADUGKS格式同样具有渐近保持性[23-24],这一点可以清楚地从式(26)看出。
其次,SADUGKS格式具有尺度自适应特性,能够根据当地流动特征尺度的不同进行自适应调节。SADUGKS格式中,时间步长按照CFL条件确定:
| $ \Delta t=C F L \frac{\Delta}{|u|_{\max }+a} \sim \frac{\Delta}{a} $ | (46) |
其中,Δ为空间网格尺度,CFL为CFL数;|u|max为粒子最大离散速度,通常与声速a同量级。同时,碰撞松弛时间τ可近似为:
| $ \tau \sim l_{s} / \bar{u} \sim l_{s} / a $ | (47) |
式中ls为分子平均自由程,u为粒子平均运动速率与声速a同量级。因此可以得到:
| $ \tau / \Delta t \sim l_{s} / \Delta \sim K n_{\text {local }} $ | (48) |
其中Knlocal为当地努森数,反映当地的流动状态和流动尺度。在SADUGKS格式中,用来计算界面通量的式(40)和碰撞项加权离散的式(31)中皆出现权系数α,式(32)给出权系数α的定义式反映出α依赖于比值τ/Δt,即依赖于当地努森数,因此α取值的大小会随着当地流动状态和尺度的不同而进行自适应调节。
最后,从权系数的数学形式和物理意义上来讨论。权系数α定义式在式(32)给出,数学上α的取值范围为
| $ \begin{array}{lr} \alpha \rightarrow 1, & \tau \ll \Delta t \\ \alpha \rightarrow 1 / 2, & \tau \gg \Delta t \end{array} $ | (49) |
Shakhov模型将气体从当前非平衡状态向平衡态的过渡看做一个驰豫过程。对于Kn→0的宏观连续流动问题,从物理上分析,此时碰撞弛豫时间远小于时间步长,τ
| $ \begin{aligned} \frac{1}{\Delta t}\left[\phi\left(x_{i}, t+\Delta t, u_{j}\right)-\phi^{\mathrm{ini}}\left(x_{i}-u_{i} \Delta t, u_{j}\right)\right] \\ \approx \mathit{\Omega}_{\phi}\left(x_{i}, t+\Delta t, u_{j}\right) & \end{aligned} $ | (50) |
可见数学结果与上述物理分析一致。
对于Kn
| $ \begin{aligned} & \frac{1}{\Delta t}\left[\phi\left(x_{i}, t+\Delta t, u_{j}\right)-\phi^{\mathrm{ini}}\left(x_{i}-u_{i} \Delta t, u_{j}\right)\right] \\ \approx & \frac{1}{2}\left[\mathit{\Omega}_{\phi}\left(x_{i}, t+\Delta t, u_{j}\right)+\mathit{\Omega}_{\dot{\phi}}^{\mathrm{ini}}\left(x_{i}-u_{i} \Delta t, u_{j}\right)\right] \end{aligned} $ | (51) |
可见此时数学结果也与上述物理分析相一致。
在原始DUGKS格式中,本文所有出现权系数α的地方都取为常数αDUGKS≡1/2。通过上面的分析可以看出,这种常数取法主要是从数值离散的角度考虑,并未充分考虑在不同流动领域碰撞项对应物理过程的不同,尤其没有考虑两个时间尺度即计算时间步长和碰撞松弛时间之间的相对大小对粒子碰撞过程宏观表现的影响。
根据上述分析可知,式(32)给出的权系数α紧密依赖于时间比值τ/Δt,并可根据当地流动状态和流动尺度的不同进行自适应调节。当地努森数越小、越接近连续流动时α越接近于1;当地努森数越大、流动非平衡效应越强时α越接近于1/2。综合来说,SADUGKS是一种尺度自适应的格式,适用于从连续流动到滑移流动、过渡流动及自由分子流所有流动领域的问题,在第4节将通过若干典型算例对这一点进行检验。
4 尺度自适应的离散统一气体动理学格式在可压缩流动中的应用 4.1 一维激波结构问题本问题中将用SADUGKS格式研究一维激波结构问题,并将结果与文献[36, 37]的结果进行对比。气体为氩气,分子内自由度设置为K=0,普朗特数Pr=2/3,比热比γ=5/3,黏性系数与温度相关:μ∝Tw,其中w与分子模型相关。分子平均自由程λ与黏性系数直接相关[24]:
| $ \lambda=\frac{2 \mu(7-2 w)(5-2 w)}{15 \rho(2 \pi R T)^{0.5}} $ | (52) |
激波上下游的密度、速度和温度分别为ρ1、u1、T1与ρ2、u2、T2。计算时流动物理量均采用激波上游的物理量进行无量纲化,即特征密度为ρ1,特征长度为λ1,特征温度为T1,因此上游的入口边界条件为:ρ1=1.0,λ1=1.0,T1=1,u1则由来流马赫数Ma决定,
选取计算区域为-25λ1≤x≤25λ1,并采用100个均匀网格将其离散,每个网格单元大小Δx=0.5λ1,由于网格单元Δx和分子平均自由程λ1量级相当,计算将给出激波内部结构中物理量的变化。速度空间采用32×32半平面Gauss-Hermite积分离散[38]。初始时刻,x≤0处的流场采用激波上游条件及其Maxwell平衡态分布进行初始化,x>0处的流场采用激波下游条件及其Maxwell平衡态分布进行初始化。左右边界均采用外推边界条件, CFL数设置为0.5。
本文采用硬球模型w=0.5,图 1展示了Ma=1.2数值模拟结果,并与文献[36, 37]中的结果进行了对比。其中物理量的无量纲化方法如下:
| $ \rho^{*}=\frac{\rho}{\rho_{1}}, \quad T^{*}=\frac{T}{T_{1}}, \quad q_{x}^{*}=\frac{q_{x}}{p_{1} \sqrt{2 R T_{1}}}, \\ \tau _{xx}^* = \frac{{{\tau _{xx}}}}{{{p_1}}} $ | (53) |
|
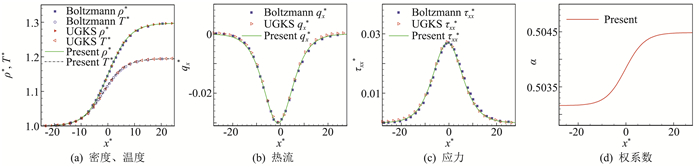
图 1 SADUGKS格式求解激波结构问题的密度、温度、热流、应力与权系数α分布(Ma=1.2) Fig.1 Distribution of density, temperature, heat flux, stress and α for shock structure problem (Ma=1.2) |
另外,参照文献[36]给出固定激波所在位置的方法,选取ρ(x0)=(ρ1+ρ2)/2处为坐标原点,将坐标进行无量纲化:
| $ {x^*} = (x - {x_0})/(0.5\sqrt {\rm{ \mathsf{ π} }} {\lambda _1}) $ | (54) |
从图 1中可以看出,SADUGKS的结果与UGKS[37]及完整Boltzmann方程[36]都能很好地吻合。由于本问题是分辨激波内部结构,流动对应尺度为分子平均自由程尺度,按照前面关于权系数α的讨论,此时α应接近0.5,从图 1中也可以清楚看出全场α范围在0.503至0.505之间。
4.2 从激波结构分辨格式到激波捕捉格式在4.1小节问题中,由于所用网格单元Δx和分子平均自由程λ1量级相当,因此计算结果可以分辨激波内部结构。接下来本节将重点讨论当网格单元大小变化时对数值结果的影响,以验证SADUGKS格式的尺度自适应特性。
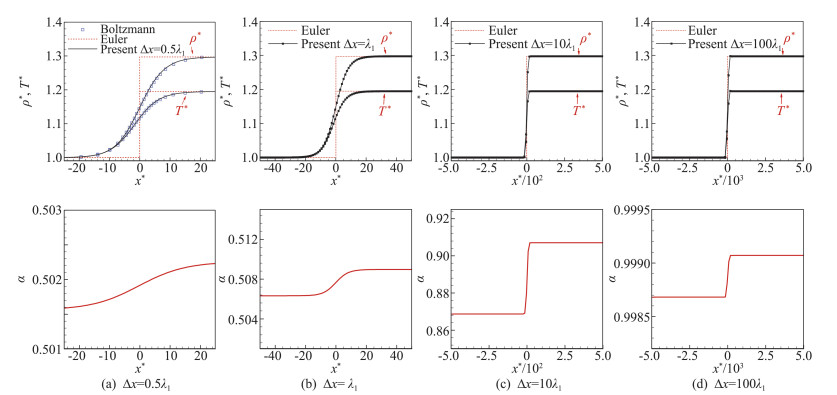
气体参数、激波上下游初值等参数与4.1小节一致,CFL数取为0.9。速度空间采用32×32半平面Gauss-Hermite积分离散[38]。选取计算区域为-50Δx≤x≤50Δx,区域总长为L=100Δx,采用100个均匀网格将其离散,网格单元Δx选取了四种不同大小,分别是Δx=0.5λ1,λ1,10λ1和100λ1。图 2给出了无量纲密度、温度以及权系数α在不同Δx时的空间分布曲线,其中横坐标x*为采用激波上游的分子平均自由程λ1进行无量纲化后的空间位置,x*具体形式见式(54),同时无黏Euler方程的精确解也画在图中作为对比。从图 2可以看出,当Δx较小,满足Δx~λ1时,真实激波内部结构可以被分辨出来,此时SADUGKS表现为激波结构分辨格式(shock structure resolving scheme);随着Δx增加,如当Δx≥10λ1时,SADUGKS给出的结果将逼近无黏Euler方程的精确解,说明对于网格单元远大于分子平均自由程时,激波被作为理想间断面来处理,SADUGKS通过自身格式黏性最后得到的是数值激波,此时SADUGKS表现为激波捕捉格式(shock capturing scheme)。
|
图 2 SADUGKS格式求解激波结构问题的密度、温度与权系数α随网格大小变化,CFL=0.9, Ma=1.2 Fig.2 Density, temperature and α profiles of the shock structure with different cell sizes, CFL=0.9, Ma=1.2 |
这个例子说明SADUGKS可以根据比值Δx/λ1的变化而在激波结构分辨格式和激波捕捉格式之间做出自适应调整,这对于实际复杂工程问题获得所用计算网格下的合理物理解是很有益的。因为一个问题在求解前进行网格划分时并不知道流场物理量的局部细节特性,所以划分的网格带有较强的人为因素,但是SADUGKS格式自身可以通过一套统一的算法自动获得流场在所用网格尺度下的合理物理解。
SADUGKS格式在激波结构分辨格式和激波捕捉格式之间的切换得益于权系数α的引入,从图 2权系数α的变化曲线可以清楚看出:当Δx
作为对比,对于传统在连续介质框架下基于N-S方程建立的CFD方法来说,N-S方程建立后被作为一个数学偏微分方程来处理,网格进行加密的主要目的是减小N-S方程离散误差,网格的作用未被充分发挥出来。另外,从物理上考虑,N-S方程是基于连续介质框架得到的,N-S方程蕴含的流动物理尺度是远大于分子平均自由程的,因此即便将网格加密到分子平均自由程的量级,也只是获得N-S方程作为一个数学偏微分方程更为精确的数值解,但所获得的结果不可能超过N-S方程物理上成立的范围,即无法给出在分子平均自由程尺度上的流动物理信息。
4.3 从自由分子流领域到连续流领域Sod问题为一维Riemann问题中的一个经典问题,其无黏解包含激波、膨胀波及接触间断多种波系结构。该问题被广泛用来检验数值格式捕捉间断的能力,其初始条件如下:
| $ \left\{ \begin{array}{l} ({\rho _1}, {u_1}, {p_1}) = \left( {1.0, 0.0, 1.0} \right), \;\;\;\;\;\;\;x \le 0\\ ({\rho _2}, {u_2}, {p_2}) = \left( {0.125, 0.0, 0.1} \right), \;\;\;x > 0 \end{array} \right. $ | (55) |
本文这里考虑在上述初值下,引入气体黏性后的流动。气体考虑为空气,分子内自由度设置为K=2,普朗特数Pr=0.72,比热比γ=1.4。气体黏性系数与温度满足μ=μ0(T/T0)w,其中w与分子模型相关,这里采用硬球模型w=0.5,μ0为参考黏性系数,T0为参考温度。参考分子平均自由程λ0与参考黏性系数直接相关:
| $ {\lambda _0} = \frac{{2{\mu _0}\left( {7 - 2w} \right)\left( {5 - 2w} \right)}}{{15{\rho _0}{{(2{\rm{ \mathsf{ π} }}R{T_0})}^{0.5}}}} $ | (56) |
其中ρ0为参考密度。本文中,选用左侧(x < 0)初值ρ1、p1、T1分别作为参考密度、压力和温度。
在前面4.2节中, μ0给定是通过改变计算网格单元大小考察格式的尺度自适应特性。这里与4.2节不同,本问题中计算区域固定为-0.5≤x≤0.5,并采用100个均匀网格将其离散,计算网格单元Δx=0.01大小固定。通过改变μ0,实现分子平均自由程λ0的变化,从而比值λ0/Δx将不同,因此本问题也能够很好地检验SADUGKS格式的尺度自适应特性。本节计算了5组不同μ0(=10, 1, 0.1, 10-3, 10-5)下的流动。计算μ0 < 0.1的流动时,速度空间采用32×32半平面Gauss-Hermite积分离散[38];计算μ0≥0.1的流动时,速度空间采用100×100的Newton-Cotes积分进行离散,积分区域选择
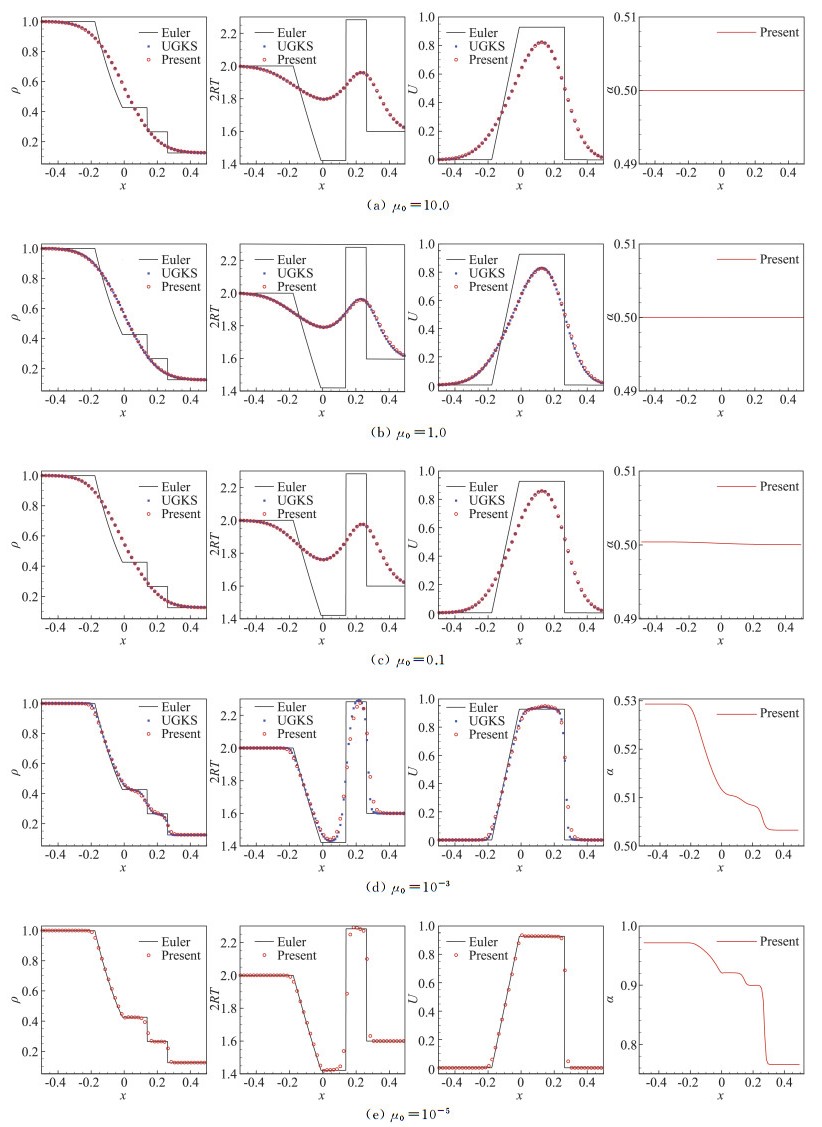
μ0=10时的密度、温度、速度以及此时流场中式(32)给出的权系数α随空间分布如图 3(a)所示。在此黏性系数下,左侧初值对应分子平均自由程λ0=12.77,比值λ0/Δx=1277,此时流动对应为自由分子流。从图 2中可以看出,SADUGKS结果与UGKS结果基本完全重合,且这种远偏离平衡态的流动与无黏Euler解有着明显的区别:一方面,由于流动更为稀薄,分子平均自由程远大于网格单元,因此空间网格可以分辨包括激波在内的各种波系内部结构;另一方面,流动黏性很大,耗散作用增强,各种波系被显著光滑抹平,物理量在整个空间上连续变化。图中给出的权系数α在整个空间几乎是一条平直线,值为0.5,这一点和前面第3节中提到的对于大Kn数的流动α→1/2结论一致。当黏性系数μ0减小到1时,左侧初值对应分子平均自由程λ0=1.277,比值λ0/Δx= 127.7,从图 3(b)可以看出,相比μ0=10时物理量分布变化不大,同样此时权系数α在整个空间都接近0.5。
|
图 3 SADUGKS格式求解Sod问题的密度、温度、速度和权系数α分布 Fig.3 Distribution of density, temperature, velocity and α for Sod problem by SADUGKS |
随着黏性系数μ0减小到0.1时,左侧初值对应分子平均自由程λ0=0.1277,比值λ0/Δx=12.77,相比前两个较大黏性系数的工况来说,图 3(c)给出的物理量分布已出现一些变化,尤其速度峰值已明显增加,并且权系数α在整个空间也出现起伏,不再是平直直线了。
当黏性系数μ0减小到10-3时,左侧初值对应分子平均自由程λ0=1.277×10-3,比值λ0/Δx=0.1277,在此时的网格下已不能分辨激波内部结构了,从图 3(d)中可见,SADUGKS结果逐渐接近无黏Euler解。权系数α在整个空间已出现显著变化,从最左侧的0.5293逐渐减小到右侧的0.5033。
当黏性系数μ0进一步减小到10-5时,左侧初值对应分子平均自由程λ0=1.277×10-5,比值λ0/Δx=1.277×10-3,此时流动属于连续流领域,并且由于黏性非常小,从图 3(e)可以看出,SADUGKS的结果几乎与无黏Euler解完全重合。当前空间网格尺度远大于分子平均自由程尺度,对应网格不再能分辨激波内部流动细节,激波表现为宏观物理量的间断。此时,SADUGKS表现为激波捕捉格式。从权系数α分布图中可以看到α随空间显著变化,从左侧的0.9716逐渐减小到右侧的0.7660,这反映当地努森数和当地特征尺度随空间的变化。
本算例计算网格单元大小不变,改变μ0实现分子平均自由程λ0的变化,验证了SADUGKS格式的尺度自适应特性。对于实际工程问题,使用一种能够根据当地流动尺度进行自适应调节的统一算法显得尤为重要,而SADUGKS格式正是这样一种尺度自适应的算法,能够反映出当地流动物理特性。且根据当地流动尺度不同,SADUGKS格式可在激波结构分辨格式和激波捕捉格式之间进行自适应切换。
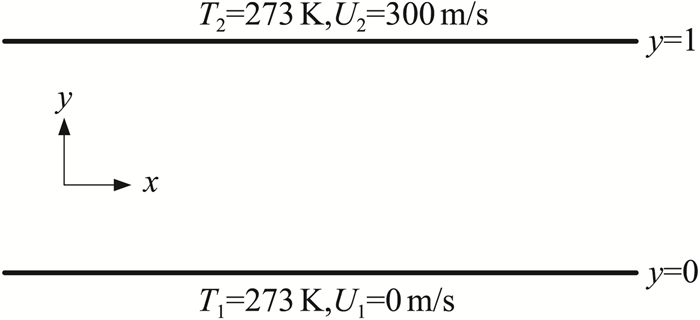
4.4 高速可压缩Couette流动问题最后将SADUGKS格式应用于高速可压缩Couette流动问题,流动参数与采用IP方法[39]进行计算的文献一致。流动示意图如图 4所示,两无限大平行平板之间距离为1,两板之间充满氩气,分子内自由度K=0,普朗特数Pr=2/3,比热比γ=5/3,黏性系数与温度相关μ=μ0(T/T0)w,采用变径硬球模型w=0.81。两板温度固定为273 K,下板静止,上板在自身平面内匀速运动,速度为U2=300 m/s,对应马赫数Ma约为0.97。流体与壁面之间存在剪切作用,同时黏性耗散作用会使得流场内部温度升高。通过改变初始氩气密度以改变流动努森数Kn,本文共选取五组Kn=0.01,0.1,1.0,10和100,涵盖了从连续流动到自由分子流的流动领域。不同Kn下流动将表现出不同的温度及速度分布。
|
图 4 高速可压缩Couette流动示意图 Fig.4 Schematic diagram for the compressible Couette flow |
两板间布置数目为31的均匀网格,速度空间采用28×28半平面Gauss-Hermite积分离散[38]。入口与出口采用周期性边界条件,上下壁面采用完全漫反射边界条件[19]。CFL数设置为0.5。
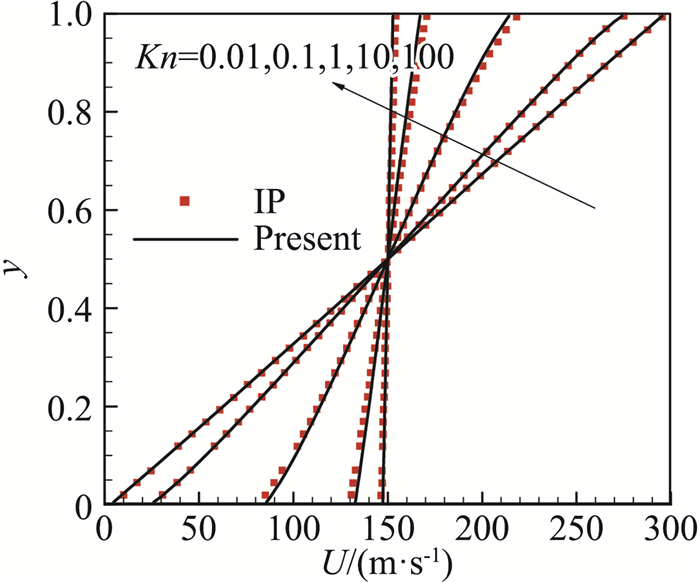
不同Kn下的速度剖面如图 5所示,从图中可以看出,当Kn=0.01时,流动可认为仍满足连续介质假设,但是上下壁面已出现轻微的速度滑移现象。随着Kn不断增加,非平衡效应变强,壁面处的滑移效应逐渐变得显著,尤其当Kn=100时,板间气体速度分布趋于均匀,约为150 m/s,和上、下板速度远不相同。
|
图 5 SADUGKS计算所得不同Kn下的速度剖面图 Fig.5 Velocity profiles for the compressible Couette flow at different Knudsen numbers |
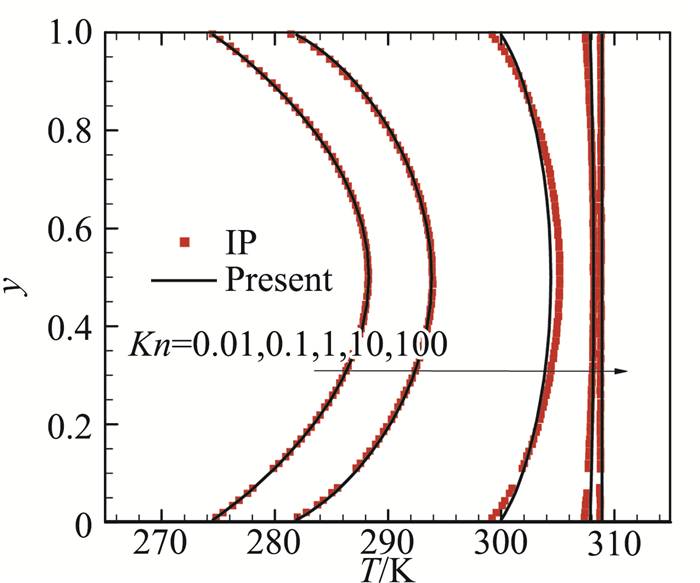
图 6所示为不同努森数下的温度剖面。当Kn=0.01时,流动在壁面已出现轻微温度跳跃现象。由于上板克服壁面黏性剪切做功最终转化为热能,并逐渐向流道中间集中,造成温度峰值出现在中心对称线上。随着Kn不断增加,非平衡效应变强,壁面处的温度跳跃现象更为明显,板间气体的温度梯度逐渐减小。尤其当Kn=100时,板间流动趋于自由分子流,板间气体温度几乎相同,约为308 K,和上、下板温度远不相同。
|
图 6 SADUGKS计算所得不同Kn下的温度剖面图 Fig.6 Temperature profiles for the compressible Couette flow at different Knudsen numbers |
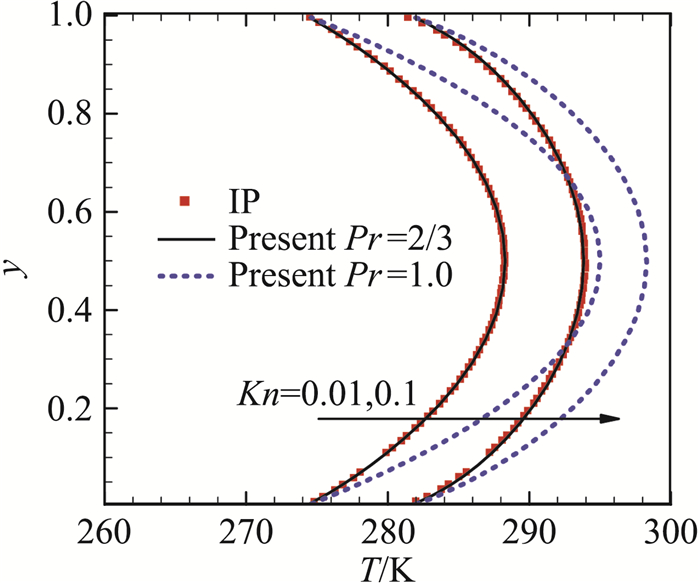
为了反映气体Pr数对结果的影响,这里考虑了Pr=1时Kn=0.01和Kn=0.1两种工况,并和前面Pr=2/3的对应结果进行了对比,见图 7给出的温度分布曲线,可以清楚看出Pr=1时的结果与Pr=2/3及文献IP方法[39]的结果出现了较大的偏差。从式(10~14)可以看出,Boltzmann-Shakhov模型中取Pr=1时退化为Boltzmann-BGK模型,这说明为了正确反映气体Pr数的影响从而获得准确温度场,基于Boltzmann-Shakhov模型构造计算格式是适当的。
|
图 7 Pr=1和Pr=2/3的结果对比(Kn=0.01和Kn=0.1) Fig.7 Temperature profiles for the compressible Couette flow at different Knudsen numbers with Pr=1 and Pr=2/3 |
无论对于速度还是温度,在所有Kn情况下,SADUGKS格式所得结果均能与文献IP方法[39]的结果很好地吻合,表明了SADUGKS格式对于宽Kn流动计算的有效性和尺度自适应特性。
5 结论文中提出了Boltzmann方程沿特征线离散的一般形式,式中碰撞项的离散采用显式和隐式加权平均的方法,权系数α依赖于当地碰撞松弛时间和计算时间步长的比值。通过权系数α的引入,对文献现有离散统一气体动理学格式(DUGKS)进行了改进,提出了具有尺度自适应特性的离散统一气体动理学格式(SADUGKS)。对SADUGKS进行分析,明确权系数α与反映当地流动尺度的当地努森数直接相关,表明SADUGKS格式能够根据当地流动尺度进行自适应调节。SADUGKS格式的自适应特性和有效性通过典型可压缩流动进行了检验,取得了较好的计算结果,表明SADUGKS格式适用于宽范围Kn变化、跨流域的多尺度流动问题的数值模拟。后续将选用更为复杂的流动问题对SADUGKS做进一步的检验和验证。
| [1] |
GUO Z L, SHU C. Lattice Boltzmann method and its applications in engineering[M]. Singapore: World Scientific, 2013.
|
| [2] |
陈杰, 赵磊. 高超声速流存在局部稀薄效应的一个判据及相应的流动特性[J]. 空气动力学学报, 2018, 36(1): 4-11. CHEN J, ZHAO L. A criterion for the existence of local rarefaction effect in a hypersonic flow field and the corresponding flow characteristics[J]. Acta Aerodynamica Sinica, 2018, 36(1): 4-11. DOI:10.7638/kqdlxxb-2017.0179 (in Chinese) |
| [3] |
BIRD G A. Recent advances and current challenges for DSMC[J]. Computers & Mathematics with Applications, 1998, 35(1/2): 1-14. |
| [4] |
MCNAMARA G R, ZANETTI G. Use of the Boltzmann equation to simulate lattice gas automata[J]. Physical Review Letters, 1988, 61(20): 2332. DOI:10.1103/PhysRevLett.61.2332 |
| [5] |
QIAN Y H, D'HUMIōRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters (EPL), 1992, 17(6): 479-484. DOI:10.1209/0295-5075/17/6/001 |
| [6] |
LIN Z F, FANG H P, TAO R B. Improved lattice Boltzmann model for incompressible two-dimensional steady flows[J]. Physical Review E, 1996, 54(6): 6323. |
| [7] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一算法研究[J]. 空气动力学学报, 2003, 21(3): 255-266. LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2003, 21(3): 255-266. DOI:10.3969/j.issn.0258-1825.2003.03.001 (in Chinese) |
| [8] |
LI Z H, ZHANG H X. Numerical investigation from rarefied flow to continuum by solving the Boltzmann model equation[J]. International Journal for Numerical Methods in Fluids, 2003, 42(4): 361-382. DOI:10.1002/fld.517 |
| [9] |
LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. |
| [10] |
LI Z H, PENG A P, ZHANG H X, et al. Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations[J]. Progress in Aerospace Sciences, 2015, 74: 81-113. DOI:10.1016/j.paerosci.2014.12.002 |
| [11] |
李志辉, 彭傲平, 方方, 等. 跨流域高超声速绕流环境Boltzmann模型方程统一算法研究[J]. 物理学报, 2015, 64(22): 224703. LI Z H, PENG A P, FANG F, et al. Gas-kinetic unified algorithm for hypersonic aerothermo dynamics covering various flow regimes solving Boltzmann model equation[J]. Acta Physica Sinica, 2015, 64(22): 224703. DOI:10.7498/aps.64.224703 (in Chinese) |
| [12] |
XU K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. |
| [13] |
LI Q B, FU S, XU K. Application of gas-kinetic scheme with kinetic boundary conditions in hypersonic flow[J]. AIAA Journal, 2005, 43(10): 2170-2176. DOI:10.2514/1.14130 |
| [14] |
XU K, MAO M L, TANG L. A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow[J]. Journal of Computational Physics, 2005, 203(2): 405-421. |
| [15] |
XU K, MAO M L. Gas-kinetic BGK scheme for hypersonic viscous flow[M]//GROTH C, ZINGG D W. Computational Fluid Dynamics 2004. Berlin Heidelberg: Springer. Proceedings of the Third International Conference on Computational Fluid Dynamics, ICCFD3, Toronto, 12-16 July 2004: 183-188.
|
| [16] |
李启兵, 徐昆. 气体动理学格式研究进展[J]. 力学进展, 2012, 42(5): 522-537. LI Q B, XU K. Progress in gas-kinetic scheme[J]. Advances in Mechanics, 2012, 42(5): 522-537. (in Chinese) |
| [17] |
XU K, HUANG J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764. DOI:10.1016/j.jcp.2010.06.032 |
| [18] |
HUANG J C, XU K, YU P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ:multi-dimensional cases[J]. Communications in Computational Physics, 2012, 12(3): 662-690. |
| [19] |
HUANG J C, XU K, YU P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅲ:microflow simulations[J]. Communications in Computational Physics, 2013, 14(5): 1147-1173. |
| [20] |
LIU C, XU K, SUN Q H, et al. A unified gas-kinetic scheme for continuum and rarefied flows Ⅳ:Full Boltzmann and model equations[J]. Journal of Computational Physics, 2016, 314: 305-340. DOI:10.1016/j.jcp.2016.03.014 |
| [21] |
LIU C, XU K. A unified gas kinetic scheme for continuum and rarefied flows Ⅴ:multiscale and multi-component plasma transport[J]. Communications in Computational Physics, 2017, 22(5): 1175-1223. |
| [22] |
XU K, LIU C. A paradigm for modeling and computation of gas dynamics[J]. Physics of Fluids, 2017, 29(2): 026101. |
| [23] |
GUO Z L, XU K, WANG R J. Discrete unified gas kinetic scheme for all Knudsen number flows:Low-speed isothermal case[J]. Physical Review E, 2013, 88(3): 033305. |
| [24] |
GUO Z L, WANG R J, XU K. Discrete unified gas kinetic scheme for all Knudsen number flows. Ⅱ. Thermal compressible case[J]. Physical Review E, 2015, 91(3): 033313. |
| [25] |
ZHU L H, GUO Z L, XU K. Discrete unified gas kinetic scheme on unstructured meshes[J]. Computers & Fluids, 2016, 127: 211-225. |
| [26] |
SWIFT M R, ORLANDINI E, OSBORN W R, et al. Lattice Boltzmann simulations of liquid-gas and binary fluid systems[J]. Physical Review E, 1996, 54(5): 5041. |
| [27] |
XU K, HE X, CAI C P. Multiple temperature kinetic model and gas-kinetic method for hypersonic non-equilibrium flow computations[J]. Journal of Computational Physics, 2008, 227(14): 6779-6794. DOI:10.1016/j.jcp.2008.03.035 |
| [28] |
XIONG S W, ZHONG C W, ZHUO C S, et al. Numerical simulation of compressible turbulent flow via improved gas-kinetic BGK scheme[J]. International Journal for Numerical Methods in Fluids, 2011, 67(12): 1833-1847. DOI:10.1002/fld.2449 |
| [29] |
WANG R J, XU K. The study of sound wave propagation in rarefied gases using unified gas-kinetic scheme[J]. Acta Mechanica Sinica, 2012, 28(4): 1022-1029. DOI:10.1007/s10409-012-0116-5 |
| [30] |
ZHU L H, GUO Z L. Numerical study of nonequilibrium gas flow in a microchannel with a ratchet surface[J]. Physical Review E, 2017, 95(2): 023113. |
| [31] |
ZHU L H, GUO Z L. Application of discrete unified gas kinetic scheme to thermally induced nonequilibrium flows[J]. Computers & Fluids, 2019, 193: 103613. |
| [32] |
LI Z H, ZHANG H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. |
| [33] |
李志辉, 蒋新宇, 吴俊林, 等. 求解Boltzmann模型方程高性能并行算法在航天跨流域空气动力学应用研究[J]. 计算机学报, 2016, 39(9): 1801-1811. LI Z H, JIANG X Y, WU J L, et al. Study on high performance parallel algorithm for spacecraft re-entry aerodynamics in the whole of flow regimes using Boltzmann model equation[J]. Chinese Journal of Computers, 2016, 39(9): 1801-1811. (in Chinese) |
| [34] |
SHAKHOV E M. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1972, 3(5): 95-96. DOI:10.1007/BF01029546 |
| [35] |
SU M D, XU K, GHIDAOUI M. Low-speed flow simulation by the gas-kinetic scheme[J]. Journal of Computational Physics, 1999, 150(1): 17-39. |
| [36] |
OHWADA T. Structure of normal shock waves:direct numerical analysis of the Boltzmann equation for hard-sphere molecules[J]. Physics of Fluids A:Fluid Dynamics, 1993, 5(1): 217-234. |
| [37] |
XU K, HUANG J C. An improved unified gas-kinetic scheme and the study of shock structures[J]. IMA Journal of Applied Mathematics, 2011, 76(5): 698-711. DOI:10.1093/imamat/hxr002 |
| [38] |
SHIZGAL B. A Gaussian quadrature procedure for use in the solution of the Boltzmann equation and related problems[J]. Journal of Computational Physics, 1981, 41(2): 309-328. |
| [39] |
SUN Q H, BOYD I D. A direct simulation method for subsonic, microscale gas flows[J]. Journal of Computational Physics, 2002, 179(2): 400-425. |
 2020, Vol. 38
2020, Vol. 38

