2. 香港科技大学 深圳研究院, 深圳 518057
2. Shenzhen Research Institute, The Hong Kong University of Science and Technology, Shenzhen 518057, China
历史上人们对于空气动力学的研究是从宏观、近平衡态规律开始,逐步认识到微观、介观及非平衡的气体动理论,进而建立起从微观动理学到宏观动力学的联系。对于宏观连续流域的气体,通常被认为是满足连续介质假设并满足质量、动量和能量守恒定律,在此基础上Bernoulli和Euler在18世纪中叶提出了描述无黏流体的欧拉方程。19世纪中叶,斯托克斯将黏性应力项加入动量方程中,发展了纳维-斯托克斯(N-S)方程,其中应力与应变率的本构关系采用了牛顿的线性本构假设。N-S方程是流体力学中最普遍使用的控制方程,但对于高超声速、非平衡气体流动描述不够准确。在其后两百年的研究中,人们不断尝试将宏观方程的应用范围推广,进而发展出一系列拓展的宏观方程。三大守恒定律方程仍是流体宏观方程中最为可靠的方程,统一气体动理学格式的宏观演化方程也是基于宏观守恒定律而建立起来的,而且这组方程适用于从自由分子流到连续流的整个流域。
微观、介观层面气体动理论的研究可以追溯到1738年,Bernoulli从分子迁移和碰撞的角度解释了恒温气体的压力与密度成正比,19世纪50年代到80年代,Clausius、Maxwell和Boltzmann的工作完成了分子动理论的奠基和全面发展。其中,Clausius提出了分子自由程这一重要概念,即连续两次分子碰撞间分子自由迁移的距离。Maxwell引入了气体分子速度分布函数的概念,并且得到了平衡态速度分布函数,求得了包含黏性系数、导热系数在内的气体输运系数的表达式,Boltzmann于1879年提出并证明了H定理,并给出了速度分布函数的积分微分方程,即气体动理学理论中奠基性的Boltzmann方程。由于Boltzmann方程碰撞项较为复杂,研究者们进一步提出了线性化Boltzmann方程[2],以及一系列的简化动理学模型方程,包括Bhatnagar、Gross和Krook三人提出的BGK模型[3],以及ES-BGK、Shakhov和Fokker-Planck等模型[4-6]。在动理学中,努森数是衡量气体稀薄程度的参数,也是联系宏观和微观的重要参数,通常努森数Kn定义为气体分子的平均自由程
| $ K n=\frac{\ell}{L} $ | (1) |
在20世纪初,Chapman和Enskog研究了Boltzmann方程在小努森数下的渐进性质,从介观层面恢复了欧拉和N-S方程,并得出了宏观输运系数与微观分子碰撞参数之间的关系,建立了宏观和微观间的联系[7]。Chapman和Enskog的理论是研究动理学方程在近连续流域性质的重要方法,也是从Boltzmann方程建立以来最为成功的动理学理论。
钱学森根据努森数将气体的流域分为连续流域、滑移流域、过渡流域和自由分子流域[8]。气体在不同的流域内的流动特性有显著区别,因而通常采用不同的控制方程和计算方法,而基于离散时空直接建模思想的UGKS、DUGKS、UGKWP等多尺度格式能够适用于从无碰撞流域到连续流域的流场流动物理的直接模拟,见图 1。在Kn≤10-3的连续流域内,N-S方程能够很好地描述流场的流动特性,连续流域内的计算流体力学的研究主要集中在发展高精度流体数值模拟方法和发展湍流模型两个方向。流体数值模拟方法包括基于数值求解流动控制方程的高阶计算流体力学方法和对流动物理过程进行直接模拟的基于格子气自动机的格子Boltzmann(LB)方法[9-10]。高阶计算流体力学方法的研究包括空间高阶重构和时间高阶演化两个方面,目前较为流行的空间高阶重构方法有加权基本无震荡(WENO)方法[11],间断伽辽金(DG)方法[12],spectral volume (SV)[13], spectral difference (SD)[14], 修正重构(CPR)[15], 通量重构(FR)[16]方法等;在时间精度的研究方面,数值常微分方程时间高精度格式的发展源于20世纪40年代,包括单步的Taylor型方法,和以龙格库塔方法为代表的多步法。而对于数值偏微分方程时间高精度格式的研究,李杰权等首先提出了基于多步多导数的两步四阶格式(two-stage fourth order scheme)[17-19],综合了单步Taylor型方法和多步法的优点,并强调了在高阶格式构造中时空耦合的重要性[20]。在近期发展中,基于气体动理学格式和两步四阶格式发展的高精度格式在精度和稳定性上都体现出了显著的优势[21-28],尤其是空间八阶紧致格式能够在捕捉间断的同时,解析声学量级扰动[10, 29-30],也说明了未来高阶格式的发展要将时间高精度演化和空间高阶重构相结合[20]。在10-3 < Kn≤10-2的滑移流域内,非平衡效应在边界处体现,出现速度滑移和温度跳跃现象,其表达式可以通过气体动理论推导。在滑移流域内,可以采用N-S方程加滑移边条件进行近似处理,或者更进一步推导高阶矩方程,例如Burnett根据Chapman-Enskog理论发展的Burnett方程[31-32],Grad基于Hermite展开发展的Grad-13矩方程[33], 以及Struchtrup结合Chapman-Enskog理论和Hermite展开发展的R13方法等[34]。

|
图 1 根据努森数对气体流域的划分,以及对应流域内的模型方程和数值方法 Fig.1 Classification of flow regime based on the Knudsen number, and the corresponding governing equations |
在10-2 < Kn≤10的过渡流域和Kn>10的自由分子流域,非平衡效应显著出现,基于宏观方程的数值方法如N-S方程、矩方法难以准确描述该流域内的非平衡物理,因而在过渡和稀薄流域,通常需要求解动理学方程。对稀薄气体动力学数值模拟主要有两类建模方法,其一为对流动物理过程进行直接模拟的方法,其二为数值离散求解动理学方程的方法。直接模拟的方法中最为流行的是Bird发展的直接数值模拟蒙特卡洛(Direct Simulation Monte Carlo, DSMC)方法[35]。DSMC方法通过模拟粒子来代替真实气体粒子,采用算子分裂方法解耦粒子的自由迁移和碰撞。其中粒子迁移过程可以准确跟踪,粒子的碰撞过程采用蒙特卡洛方法计算。DSMC方法对应的物理过程简单,因而容易应用到复杂外形、化学反应和辐射输运等领域[36]。DSMC对于高超声速问题的模拟具有很高的效率,但由于其解耦了迁移和碰撞,因而时间步长和网格尺寸都需要小于碰撞时间和平均自由程,这大大降低了DSMC方法对于近平衡流动的模拟效率。同时,粒子方法所带来的统计噪音也限制了DSMC方法对于微流动的模拟精度。为了提高DSMC方法在连续流域的计算效率,发展了渐进保持的DSMC方法(AP-DSMC)[37, 38]和矩方程引导DSMC方法[39]等。为了降低DSMC方法的噪音,发展了低噪音DSMC(LVDSMC)方法[40, 41]等。在众多统计学粒子方法中,Jenny发展的粒子Fokker-Planck方法[42]和费飞等人发展的多尺度粒子BGK方法[43]不仅适用于稀薄流域,在连续流域内也有较好的数值表现。
包括离散速度法、谱方法等在内的数值离散求解动理学方程的方法在近几十年也有长足的发展[44-55]。谱方法通过将Boltzmann碰撞项投影到谱空间,将卷积形碰撞项解耦从而提高计算效率,谱方法的计算精度很高,但由于Boltzmann碰撞项积分维度过高,受内存和计算量限制仍需要进一步发展加速算法才能适用于三维工程计算[51-53, 56]。为了降低碰撞项计算量,通常采用离散速度方法求解动理学模型方程,离散速度方法不受统计噪音影响,计算精度高,同时能够通过隐式迭代方法进行加速求解,对于微流动问题的计算有较大优势。近年来,基于离散速度的渐进保持(AP)格式[57-59]、高阶-低阶(High Order-Low Order, HO-LO)格式的发展拓展了传统离散速度格式的适用流域[60],并应用到多组分气体、辐射输运等领域。其包括AP格式在内的离散速度方法,其出发点都是从微分动理学方程出发,通过一定的离散方法得到数值格式,而微分动理学方程在粒子迁移和碰撞解耦的建模基础上得到的,其对应于建模尺度小于粒子碰撞时间和平均自由程。完全以离散动理学方程建立起来的数值格式通常求通量时只考虑粒子的自由输运。但对于这类数值格式,解耦了迁移和碰撞过程,为得到精确的物理解,格式需要网格尺度和时间步长小于粒子平均自由程和碰撞时间,对于连续流域的模拟效率和精度都较低[61]。
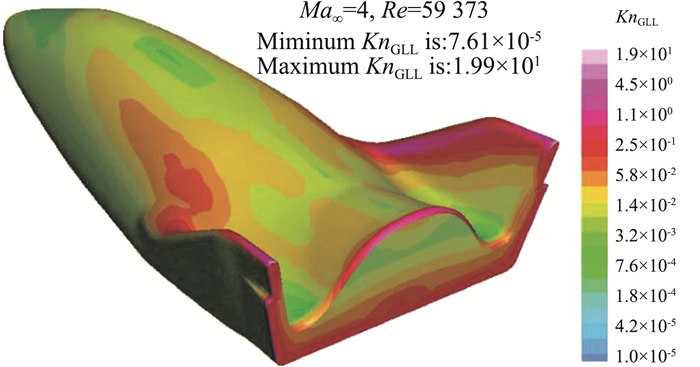
传统数值求解流动控制方程的方法通常是从微分方程出发,通过离散方法得到对应的数值格式。考虑到偏微分方程是在固定物理尺度上建模得到的,像Boltzmann方程的平均自由程和N-S方程的宏观流体力学尺度。用这种偏微分方程数值解的计算思想只能得到单尺度的计算格式,没有考虑到物理尺度变化对流动物理和方程本身描述的影响。对于复杂工程问题,如高超声速飞行的临近空间飞行器,其周围流场的局部努森数变化可以达到五个数量级(见图 2),传统的计算流体力学方法难以高效准确模拟。同样对于直接模拟方法,如DSMC方法,由于其在建模过程中解耦了迁移和碰撞,因而其适用的时空尺度被限制在平均自由程和碰撞时间量级,对于跨尺度和连续流域的模拟计算效率较低,比如DSMC方法很难适用于在80 km以下对飞行器的流场计算。徐昆提出的离散时空直接数值模拟的建模思想回归建模的出发点,在数值离散控制体上建立数值控制方程,从数值控制体上的守恒律出发,通过微分动理学方程的演化解得到网格界面局部的数值通量[62]。离散时空直接数值模拟的建模思想的核心在于将网格尺度加入建模过程中,耦合粒子迁移、碰撞、加速等过程,以及它们在一个时间步长内的累积效应,实现从稀薄到连续全流域内对流场的流动物理的准确求解。离散时空直接数值模拟的建模思想的关键在于采用了动理学方程的演化解构建数值通量,演化过程在形式上包含了粒子迁移和碰撞效应,在不同尺度上能够准确反映粒子的运动特性,例如在稀薄流域内的自由输运特性和在连续流域内由于碰撞而产生的流体力学波传播的物理特性。离散时空直接数值模拟的建模不仅能够在极限流域给出相应的流动控制方程的解,例如在稀薄流域内的动理学方程解和在连续流域内的N-S/Euler方程的解,更重要的是能够在过渡流域内能够准确地描述流动物理,填补了过渡流域内缺乏合理流动控制方程的空白。由于在网格尺度上直接建模,网格大小变成了影响气体运动模式的动力学量,决定了在不同流域上的气体演化过程。基于直接建模的思想,徐昆与他的合作者提出和发展了统一气体动理学格式(unified gas-kinetic scheme, UGKS)[24, 63-70]。统一气体动理学格式一方面耦合宏观守恒量和微观分布函数的更新,另一方面由网格界面处的演化解构建数值通量,实现了从动理学方程向流体力学方程的自然过渡,能够准确捕捉多尺度复杂流场的流动物理。通过采用隐式加速和多重网格技术[71-73],统一气体动理学格式能够高效准确应用于三维工程问题的模拟。如图 2、图 3所示,统一气体动理学格式能够准确模拟临近空间飞行器周围的多尺度流场[74]。统一气体动理学格式在构造数值格式的过程中,不仅考虑了流场的局部努森数,同时考虑了网格尺度上的流动物理,即网格努森数Knc [75-76]
| $K n_{c}=\frac{\tau}{\Delta t} $ | (2) |
|
图 2 江定武应用统一气体动理学格式对临近空间飞行器周围流场地模拟得到的流场局部努森数分布[74] (Ma∞=4,Re=59373) Fig.2 Local Knudsen number of flow around a near space aircraft simulated by Jang[74], with Mach number 4 and Reynolds number 59373 |
其中:τ为局部的碰撞时间,Δt为局部时间步长。统一气体动理学数值通量中的流体力学部分和自由输运部分的所占比例由网格努森数决定,实现了数值格式对网格尺度上的流动物理的自适应(见图 3)。基于直接建模思想,研究者们发展了一些统一气体动理学格式的变形格式,包括郭照立等人发展了离散统一气体动理学格式(DUGKS)[77-87],刘畅和朱亚军等发展了统一气体波粒方法(UGKWP)[88-90]等。在过去十年的研究中,统一气体动理学格式被应用到气体输运、等离子体输运[91]、离散两相流[92]、光子输运[93-96]、中子输运[97]等领域。统一气体动理学格式准确地连接了不同流域的物理过程,比如在光子输运中给出了从光学薄的光子自由传输到光学厚的光扩散过程的连续过渡,在计算精度和计算效率都体现出显著优势。
|
图 3 多尺度格式对于不同网格努森数的自适应 Fig.3 Adaptation of the multiscale scheme to local cell Knudsen number |
接下来,我们将在第1节中介绍离散时空直接建模的思想,并总结基于离散时空建模构建的多尺度数值格式:统一气体动理学格式、离散统一气体动理学格式、统一气体动理学波粒格式。在第2节中,我们将总结统一气体动理学格式在多尺度气体、等离子体、气固离散两相流、光子输运等领域的应用,以及其隐式加速机制。在第3节中,我们将给出总结和展望。
1 离散时空直接建模方法离散时空直接建模方法是在数值离散控制体上基于守恒律构建数值控制方程,构建数值控制方程的过程中需要考虑流域变化对控制体界面数值通量的影响。数值通量的构造依据在网格尺度上的演化过程,最为直接的是利用动理学微分方程在网格界面局部的积分解,即考虑了气体演化过程的时间累积效应,这是一种基于偏微分方程演化解的建模方法,而不是传统意义上对偏微分方程的直接离散。在某种意义上说,这种构造数值格式的思想很接近于Gounov方法,即把在网格界面上的演化解直接用于格式构造。而超出Godunov格式的地方包括演化解有时间精度和它的多尺度性质。我们将相空间划分为离散的物理空间
| $ \begin{array}{*{20}{c}} {f_{ij}^{n + 1} = f_{ij}^n - \frac{1}{{\left| {{\mathit{\Omega} _{ij}}} \right|}}\int_{{t^n}}^{tn + 1} {\oint_{\partial {\mathit{\Omega} _{{x_i}}}} {{\mathit{\boldsymbol{v}}_j}} } \cdot \mathit{\boldsymbol{n}}{f_{\partial {\mathit{\Omega} _{{x_i}}}}}\left( {t, {v_j}} \right){\rm{d}}s{\rm{d}}t + }\\ {\frac{{\Delta t}}{2}\left( {Q_{ij}^n + Q_{ij}^{n + 1}} \right)} \end{array} $ | (3) |
其中
| $ \begin{array}{l} f_{i j}^{n}=\frac{1}{\left|\mathit{\Omega}_{i j}\right|} \int_{\mathit{\Omega}_{i j}} f\left(x, t^{n}, v\right) \mathrm{d} x \\ Q_{i j}^{n}=\frac{1}{\left|\mathit{\Omega}_{i j}\right|} \int_{\mathit{\Omega}_{i j}} Q\left(x, t^{n}, v\right) \mathrm{d} x \end{array} $ |
为速度分布函数
| $ \boldsymbol{W}_{i}^{n+1}=\boldsymbol{W}_{i}^{n}-\frac{1}{\left|\mathit{\Omega}_{x_{i}}\right|} \int_{t^{n}}^{t n+1} \int \oint_{\partial \mathit{\Omega}_{x_{i}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\boldsymbol{v}} \cdot \boldsymbol{n} f_{\partial \mathit{\Omega}_{x_{i}}}(t, \boldsymbol{v}) \mathrm{d} s \mathrm{d} \mathit{\Xi} \mathrm{d} t $ | (4) |
其中
对应于网格尺度和时间步长,Knc决定了气体通过界面的物理过程。当
在离散空间直接建模给出的控制方程(3)和方程(4)框架下,基于构建网格界面处的演化解来求得数值通量,从而得到统一气体动理学格式。统一气体动理学格式的有限体积更新框架为
| $ \mathit{\boldsymbol{W}}_i^{n + 1} = \mathit{\boldsymbol{W}}_i^n - \sum\limits_s {\frac{{\Delta t}}{{\left| {{\mathit{\Omega} _{{x_i}}}} \right|}}} \left| {{l_s}} \right|{F_s} $ | (5) |
| $ \begin{array}{l} f_{ij}^{n + 1} = f_{ij}^n - \sum\limits_s {\frac{{\Delta t}}{{\left| {{\mathit{\Omega} _{ij}}} \right|}}} \left| {{l_s}} \right|{{\cal F}_{sj}} + \\ \frac{{\Delta t}}{2}\left( {\frac{{{g^n} - {f^n}}}{{{\tau ^n}}} - \frac{{{g^{n + 1}} - {f^{n + 1}}}}{{{\tau ^{n + 1}}}}} \right) \end{array} $ | (6) |
其中,
| $ \mathcal{F}_{s j}=\frac{1}{\Delta t} \int_{t_{m}}^{t^{n+1}} \boldsymbol{v} \cdot \boldsymbol{n}_{s} f\left(\boldsymbol{x}_{s}, t, \boldsymbol{v}\right) \mathrm{d} t $ | (7) |
宏观守恒量的界面通量Fs为
| $ {F_s} = \frac{1}{{\Delta t}}\int_{{t^n}}^{tn + 1} {\int \mathit{\boldsymbol{v}} } \cdot {\mathit{\boldsymbol{n}}_s}f\left( {{x_s}, t, v} \right)\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} {\rm{d}}t $ | (8) |
令tn=0,气体在界面x0处的演化是根据动理学方程的积分解给出
| $ f\left(\boldsymbol{x}_{0}, t, \boldsymbol{v}\right)=\frac{1}{\tau} \int_{0}^{t} \mathrm{e}^{-\frac{t-t^{\prime}}{\tau}} g\left(\boldsymbol{x}^{\prime}, t^{\prime}, \boldsymbol{v}\right) \mathrm{d} t^{\prime}-\mathrm{e}^{-\frac{t}{\tau}} f_{0}\left(\boldsymbol{x}_{0}, \boldsymbol{v}\right) $ | (9) |
这个演化解直接连接了自由分子流f0到平衡态g的演化过程,其权重e-t/τ对从动理学尺度到流体力学尺度的建模起了重要的作用。如果想得到在τ时间尺度上更精确的物理过程,两体碰撞的Boltzmann碰撞过程也可以融合在上面的演化解里面[64]。为了得到二阶时间精度的数值通量表达式,我们将初始t=0时刻的速度分布函数f0(x, v)和平衡态分布函数g(x, t, v)在时空展开为
| $ \begin{array}{l} f_{0}(\boldsymbol{x}, \boldsymbol{v})=f_{0}+\nabla_{x} f_{0} \cdot\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right) \\ g(\boldsymbol{x}, t, \boldsymbol{v})=g_{0}+\nabla_{x} g_{0} \cdot\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right)+\partial_{t} g_{0} t \end{array} $ | (10) |
其中
| $ \begin{array}{*{20}{l}} {\int {{\nabla _x}} g{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}\mathit{\Xi} = {\nabla _x}\mathit{\boldsymbol{W, }}}\\ {\int g \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} = \int_{\mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}} > 0} {{g^l}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} + \int_{\mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}} < 0} {{g^r}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} } \end{array} $ | (11) |
而平衡态分布函数的时间导数由相容性条件得到
| $ \int {{\partial _t}} g\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} = - \int \mathit{\boldsymbol{v}} \cdot {\nabla _x}g\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} $ | (12) |
其中
| $ \begin{array}{*{20}{c}} {{{\cal F}_s} = {\mathit{\boldsymbol{v}}_j} \cdot {\mathit{\boldsymbol{n}}_s}(\underbrace {{C_1}{g_{0, j}} + {C_2}{\mathit{\boldsymbol{v}}_j} \cdot {\nabla _x}{g_{0, j}} + {C_3}{\partial _t}{g_{0, j}}}_{平衡态通量} + }\\ {\left. {\qquad \underbrace {{C_4}{f_{0, j}} + {C_5}{\mathit{\boldsymbol{v}}_j} \cdot {\nabla _x}{f_{0, j}}}_{自由输运通量}} \right)} \end{array} $ | (13) |
可以看到,通量包含由平衡态分布贡献的平衡态通量和初始分布函数贡献的自由输运通量两部分构成。对微观分布函数求矩,我们得到宏观守恒量的数值通量表达式
| $ \begin{array}{l} {F_s} = \int \mathit{\boldsymbol{v}} \cdot {\mathit{\boldsymbol{n}}_s}\left( {{C_1}{g_0} + {C_2}{\bf{v}} \cdot {\nabla _x}{g_0} + {C_3}{\partial _t}{g_0}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{d}}}\mathit{\Xi} + \\ \sum\limits_j {{\mathit{\Omega} _{{v_j}}}} \left( {{C_4}{f_{0, j}} + {C_5}{\mathit{\boldsymbol{v}}_j} \cdot {\nabla _x}{f_{0, j}}} \right) \end{array} $ | (14) |
其中,时间积分系数C1-5为网格努森数Knc的函数
| $ \begin{array}{l} C_{1}=1-C_{4} \\ C_{2}=-\tau C_{1}-C_{5} \\ C_{3}=\Delta t / 2-\tau C_{1} \\ C_{4}=K n_{c}\left[1-\exp \left(-K n_{c}^{-1}\right)\right] \\ C_{5}=\tau \exp \left(-K n_{c}^{-1}\right)-\tau C_{4} \end{array} $ | (15) |
值得注意的是上述流量通过Knc直接取决于网格大小,即网格大小影响到气体通过界面的演化过程。在连续流域Knc→0,若分布函数初值满足N-S分布
| $ f_{0}(\boldsymbol{v}, \boldsymbol{x})=\left.\left[g-\tau\left(\partial_{t} g+\boldsymbol{v} \cdot \nabla_{x} g\right)\right]\right|_{t=0} $ | (16) |
数值通量将给出与N-S方程一致的通量, 例如分布函数通量收敛到
| $ \mathcal{F}_{s}=\boldsymbol{v}_{j} \cdot \boldsymbol{n}_{s}\left[g_{0, j}-\tau\left(\partial_{t} g_{0, j}+\boldsymbol{v}_{j} \cdot \nabla_{x} g_{0, j}\right)+\frac{\Delta t}{2} \partial_{t} g_{0, j}\right] $ | (17) |
对于统一气体动理学格式(UGKS),即使f0不是N-S分布,在连续流当
| $ \mathcal{F}_{s}=\boldsymbol{v}_{j} \cdot \boldsymbol{n}_{s}\left(f_{0, j}+\frac{\Delta t}{2} \boldsymbol{v}_{j} \cdot \nabla_{x} f_{0, j}\right) $ | (18) |
在上面两个极限的中间流域,f0和g共同起作用,它们的贡献由网格努森数决定。
1.2 离散统一气体动理学格式(DUGKS)与UGKS的框架一致,离散统一气体动理学格式(DUGKS)采用基于有限体积的分布函数演化方程(6),并通过求矩完成对宏观守恒量的更新。DUGKS与UGKS的主要区别在于数值通量的求解。DUGKS采用梯形积分公式对碰撞项的时间积分进行近似,在时间区间[tn, tn+1/2]内
| $ \begin{array}{l} f\left(\boldsymbol{x}_{s}, \boldsymbol{v}, t^{n+1 / 2}\right)-f\left(\boldsymbol{x}_{s}-\boldsymbol{v} \Delta t / 2, \boldsymbol{v}, t^{n}\right)= \\ \frac{\Delta t}{4}\left[Q\left(\boldsymbol{x}_{s}, \boldsymbol{v}, t^{n+1 / 2}\right)+Q\left(\boldsymbol{x}_{s}-\boldsymbol{v} \Delta t / 2, \boldsymbol{v}, t^{n}\right)\right] \end{array} $ | (19) |
引入新变量
| $ \begin{array}{c} \mathcal{F}_{s}=\left(1-\frac{\Delta t}{4 \tau+\Delta t}\right) \bar{f}_{0}\left(\boldsymbol{x}_{s}-\boldsymbol{v} \Delta t / 2, \boldsymbol{v}\right)+ \\ \frac{\Delta t}{4 \tau+\Delta t} g\left(\boldsymbol{x}_{s}, \boldsymbol{v}, t^{n+1 / 2}\right)\\ { = {\mathit{\boldsymbol{v}}_j} \cdot {\mathit{\boldsymbol{n}}_s}(\underbrace {{{\tilde C}_1}{g_{0, j}} + {{\tilde C}_2}{\mathit{\boldsymbol{v}}_j} \cdot {\nabla _x}{g_{0, j}} + {{\tilde C}_3}{\partial _t}{g_{0, j}}}_{平衡态通量} + }\\ {\left. {\qquad \begin{array}{*{20}{c}} {{\rm{ }}}\\ {\underbrace {{{\tilde C}_4}{f_{0, j}} + {{\tilde C}_5}{\mathit{\boldsymbol{v}}_j} \cdot {\nabla _x}{f_{0, j}}}_{自由输运通量}} \end{array}} \right)} \end{array} $ | (20) |
其中,时间积分系数
| $ \begin{array}{l} \tilde{C}_{1}=1-C_{4}, \quad \tilde{C}_{2}=\frac{-\Delta t}{8 K n_{c}+2}, \\ \tilde{C}_{3}=\frac{\Delta t}{8 K n_{c}+2}, \quad \tilde{C}_{4}=\frac{4 K n_{c}-1}{4 K n_{c}+1} ,\\ \widetilde{C}_{5}=-\Delta t \frac{\left(4 K n_{c}-1\right)}{8 K n_{c}+2} \end{array} $ | (21) |
与UGKS相同,在连续流域Knc→0,若分布函数初值满足N-S分布,DUGKS的数值通量将给出与N-S方程一致的通量(17),而在自由分子流域Knc→∞,数值通量(20)将给出与无碰撞动理学方程一致的通量(18)。
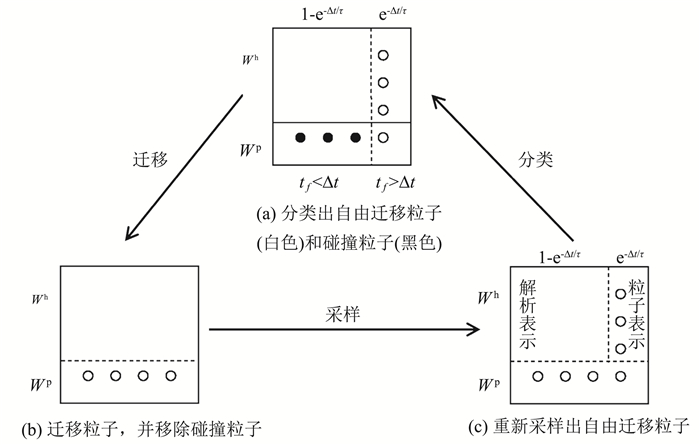
1.3 统一气体动理学波粒格式(UGKWP)UGKS和DUGKS都是基于离散坐标方法发展的确定性数值方法,在离散空间直接建模的框架下,我们采用统计学方法,用模拟粒子离散速度空间,发展了统一气体动理学波粒方法[88-90]。UGKWP方法的关键想法在于,将在流场演化过程中,所有粒子可分为自由输运粒子和碰撞粒子,对于发生碰撞的粒子不需要严格解析其碰撞过程,而可以直接由动理学方程的积分解给出其最终满足的速度分布,从而实现粗粒化多尺度建模。UGKWP的粒子演化方程为动理学方程积分解,宏观量演化是与UGKS相同的有限体积更新方程。演化过程可以由循环图 4表示。
|
图 4 统一气体波粒格式一个控制体内守恒量和粒子一个时间步内的演化循环示意图: (a)演化起始时刻,根据粒子的自由输运时间和时间步长的关系,将粒子分为碰撞粒子(Δt>tf),和自由输运粒子(Δt≤tf); (b)将所有粒子自由迁移其对应的自由输运时间,并保留自由输运粒子; (c)将下一时间步内自由迁移粒子从宏观量中依据分布g+采样出来 Fig.4 Sampling process of UGKWP in a numerical control volume: (a) Initially, the particles are categorized into collision-less (white) and collisional (black) particles according to their free stream time tf, (b) Stream all particles by tf and keep collision-less particles, (c) Re-sample collisional particles from g+. |
UGKWP的粒子演化方程为
| $ \begin{aligned} f(\boldsymbol{x}, t, \boldsymbol{v}) &=\frac{1}{\tau} \int_{0}^{t} \mathrm{e}^{-\left(t-t^{\prime}\right) / \tau} g\left(\boldsymbol{x}^{\prime}, t^{\prime}, \boldsymbol{v}\right) \mathrm{d} t^{\prime}+\mathrm{e}^{-t / \tau} f_{0}\left(\boldsymbol{x}_{0}, \boldsymbol{v}\right) \\ &=\underbrace{\left(1-\mathrm{e}^{-t / \tau}\right) g^{+}(\boldsymbol{x}, t, \boldsymbol{v})}_{\text {碰撞粒子分布 }}+\underbrace{\mathrm{e}^{-t / \tau} f_{0}\left(\boldsymbol{x}_{0}, \boldsymbol{v}\right)}_{\text {自由输运粒子分布 }} \end{aligned} $ | (22) |
其中碰撞粒子分布为
| $ \begin{array}{l} g^{+}(\boldsymbol{x}, t, \boldsymbol{v})=g(\boldsymbol{x}, t, \boldsymbol{v})+\left(\frac{t \mathrm{e}^{-t / \tau}}{1-\mathrm{e}^{-t / \tau}}-\tau\right) \cdot \\ {\left[\partial_{t} g(\boldsymbol{x}, t, \boldsymbol{v})+\boldsymbol{v} \cdot \nabla_{x} g(\boldsymbol{x}, t, \boldsymbol{v})\right]} \end{array} $ | (23) |
在UGKWP的粒子更新过程中,我们只追踪粒子的自由输运过程,并从更新的宏观量中依据碰撞粒子分布g+采样出下一时间步内自由输运的粒子。需要指出的是在UGKWP重采样过程中,我们只需要采样下一时间步自由输运的粒子,其余部分速度分布由解析的速度分布函数表示,因而UGKWP的速度分布由解析部分和粒子部分组成,见图 4(c)。UGKWP的宏观量演化是与UGKS相同的有限体积更新方程
| $ \boldsymbol{W}_{i}^{n+1}=\boldsymbol{W}_{i}^{n} \underbrace{-\sum\limits_{s} \frac{\Delta t}{\left|\mathit{\Omega}_{x_{i}}\right|}\left|l_{s}\right| F_{s}^{\mathrm{eq}}}_{\text {平衡态通量 }}\\ \frac{-\sum\limits_{s} \frac{\Delta t}{\left|\mathit{\Omega}_{x_{i}}\right|}\left|l_{s}\right| F_{s}^{f r, w}+\frac{\Delta t}{\left|\mathit{\Omega}_{x_{i}}\right|} \boldsymbol{W}_{i}^{f_{r}}}{\text { 自由输运通量 }} $ | (24) |
其中,平衡态通量求解与UGKS平衡态通量求解过程相同,即
| $ F_{s}^{\mathrm{eq}}=\int \boldsymbol{v} \cdot \boldsymbol{n}_{s}\left(C_{1} g_{0}+C_{2} \boldsymbol{v} \cdot \nabla_{x} g_{0}+C_{3} \partial_{t} g_{0}\right) \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \mathrm{d} \mathit{\Xi} $ | (25) |
而UGKWP的自由输运通量由解析自由输运通量
| $ \begin{array}{l} F_j^{fr, w} = \int \mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}}\left( {{C_4}g_j^ + + {C_5}v \cdot {\nabla _x}g_j^ + } \right)\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} - \\ \int \mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}}\left( {{C_6}g_j^h - {C_7}{\nabla _x}g_j^h} \right)\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\rm{d}}\mathit{\Xi} \end{array} $ | (26) |
和粒子自由输运通量
| $ \mathit{\boldsymbol{W}}_i^{fr} = \frac{1}{{\Delta t}}\left( {\sum\limits_{k \in {P_{\partial \mathit{\Omega} _{{x_i}}^ + }}} {{\mathit{\boldsymbol{W}}_{{P_k}}}} - \sum\limits_{k \in {P_{\partial \mathit{\Omega} _{{x_i}}^ - }}} {{\mathit{\boldsymbol{W}}_{{P_k}}}} } \right) $ | (27) |
两部分组成,其中
基于直接建模方法发展的三种数值方法,即UGKS、DUGKS和UGKWP都具有二阶一致渐进保持(unified preserving, UP)的性质,即格式不仅能够在连续和无碰撞的极限流域收敛到欧拉和无碰撞动理学方程的数值格式,同时在连续流域内,格式能够准确捕捉N-S方程的数值解[64, 98]。特别的,郭照立在最近的文章中给出了UP的数学定义,即在一定条件下,数值格式对应的修正方程能够保持动理学方程的二阶渐进展开。以一维为例,我们给出UGKS在
| $ \begin{array}{l} \partial_{t} f+v \partial_{x}\left[g-\tau\left(g_{t}+v g_{x}\right)\right] \\ +\frac{\Delta t}{2}\left\{\partial_{t}^{2} f+v \partial_{t} \partial_{x}\left[g-\tau\left(g_{t}+v g_{x}\right)\right]+\frac{1}{\tau}\left(\partial_{t} g-\partial_{t} f\right)\right\} \\ +\frac{\tau^{2}}{\Delta t}\left(2 u^{2} \partial_{x}^{2} g+u \partial_{t} \partial_{x} g-u^{2} \partial_{x}^{2} f\right) \\ -\frac{\tau}{\Delta t}\left(u \partial_{x} g-u \partial_{x} f\right)+\frac{\Delta x^{3}}{6} u \partial_{x}^{3} g \\ =\frac{1}{\tau}(g-f)+O\left(\Delta t^{2}\right) \end{array} $ | (28) |
对修正方程进行渐进分析,我们将分布函数f展开为
| $ f=f^{(0)}+\varepsilon f^{(1)}+\varepsilon^{2} f^{(2)}+O\left(\varepsilon^{3}\right) $ |
将时间导数展开为
| $ \partial_{t}=\partial_{t 0}+\varepsilon \partial_{t_{1}}+\varepsilon^{2} \partial_{t 2}+O\left(\varepsilon^{3}\right) $ |
其中,
| $ \begin{aligned} O\left(\varepsilon^{0}+\varepsilon^{1}\right) &: \sum\limits_{k=0}^{1} \partial_{t_{k}} g+D_{0}\left[g-\tau\left(g_{t}+v g_{x}\right)\right] \\ &=-\tau f^{(2)}+O\left(\Delta t^{2}, \Delta x^{3}\right) \end{aligned} $ | (29) |
即UGKS在连续流域给出时间二阶精度的N-S方程数值格式。需要特别指出的是,从UGKS的修正方程(28)可以看出,在小网格努森数(Knc)流域UGKS的误差主要来源于平衡态通量,这是由于在小网格努森数流域UGKS的平衡态通量占主导。关于DUGKS和UGKWP格式UP性质的论证,参见文献[90, 98]。
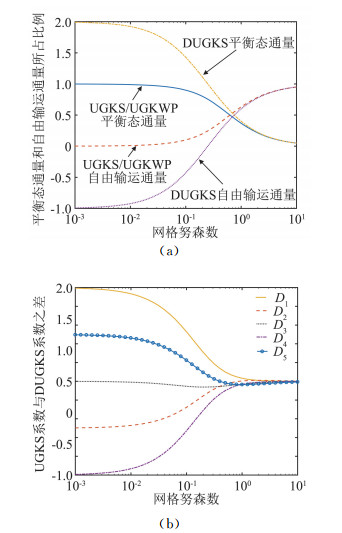
UGKS和DUGKS的主要区别在于数值通量系数的不同,尤其是在小网格努森数时差别较大。图 5为UGKS和DUGKS通量系数的差别
| $ D_{1.5}=C_{1.5}-\tilde{C}_{1.5}, D_{2, 3, 4}=\left(C_{2, 3 , 4}-\tilde{C}_{2, 3 , 4}\right) / \Delta t $ | (30) |
|
图 5 统一气体动理学格式和离散统一气体动理学格式平衡态通量和自由输运通量占比(a)、统一气体动理学格式和离散统一气体动理学格式通量系数差别(b)随网格努森数的变化 Fig.5 Proportion of equilibrium flux and free stream flux of UGKS and DUGKS (a)、Flux coefficients of UGKS and DUGKS (b) according to cell Knudsen number |
可以看到,在小网格努森数流域UGKS的平衡态通量占主导,而DUGKS的连续通量和自由输运通量之比为C1/C4=-2。因而要提高UGKS在小网格努森数流域的精度,即在连续流的精度,只需要提高平衡态对应的重构精度和时间演化精度,即格式完全有宏观量决定,这个性质使其回到连续流的GKS,虽然这时UGKS还保持着不必要的速度空间网格点。不同的是,要提高DUGKS在连续流域的精度,需要同时提高平衡态和分布函数的重构精度和时间精度,即它们的结合给出DUGKS在连续流时的数值通量。另一方面由于DUGKS的通量计算相对简洁,因此DUGKS相对于UGKS计算量有一定程度的降低。
基于离散速度的确定性格式UGKS和DUGKS,由于不受统计噪音的影响,因而对于微流动问题的模拟有很高的精度和计算效率。而基于统计学的UGKWP,采用模拟粒子能够高效地实现速度空间的自适应,因而对于高超声速和三维工程问题的计算由较高的计算效率。同时UGKWP只需要采样自由输运粒子,因而UGKWP计算所需粒子数随着网格努森数的降低而以指数减小,计算控制体
| $ N_{p, i}=\exp \left(-K n_{c}^{-1}\right) \rho_{i}\left|\mathit{\Omega}_{x_{i}}\right| / m_{p} $ | (31) |
其中,mp为模拟粒子的参考质量。另一方面,随着网格努森数的降低,UGKWP自由输运通量在总通量中所占比例以指数降低,因此统计噪音也以指数降低。在参考文献[90]中我们证明了UGKWP不仅是多尺度格式同时也是计算复杂度渐进降低和统计噪音渐进降低的格式。在连续流,由于自由粒子的消失,UGKWP完全回到以前计算N-S方程的气体动理学方法(GKS)[24]。和UGKS比较,UGKWP没有了速度空间,在连续流区内存也大大降低。
总体来讲,基于离散时空直接建模而发展起来的三种格式都具有多尺度性质,不仅对于气体输运,还能够很好地模拟等离子体输运、气固离散两相流、辐射输运、中子输运等等尺度输运问题。
2 统一气体动理学格式的应用 2.1 连续层流及高超声速问题统一气体动理学格式的首次提出是用于多尺度气体输运问题的计算[50]。在之后的十年中不断发展,在多尺度气体流动、微流动、高超声速气体输运问题的模拟以及三维工程问题的计算中,体现出精度、稳定性以及计算效率等方面的优势[50, 63-64, 71-74, 88-90]。在这一章节中,我们一方面将通过UGKS在连续层流问题的算例说明UGKS的准确性,另一方面通过UGKWP在高超声速问题的算例说明格式的计算效率。
首先,我们考察二维的Taylor涡,计算域为0 < x, y < 1,在连续流域
| $ \begin{array}{*{20}{l}} {{u_x} = - \frac{{{u_0}}}{A}\cos (Ax)\sin (By){{\rm{e}}^{ - \nu \alpha t}}}\\ {{u_y} = \frac{{{u_0}}}{B}\sin (Ax)\cos (By){{\rm{e}}^{ - \nu \alpha t}}} \end{array} $ |
| $ p(x, y, t)=p_{0}-\frac{\rho_{0} u_{0}^{2}}{4}\left[\frac{\cos (2 A x)}{A^{2}}+\frac{\cos (2 B x)}{B^{2}}\right] \mathrm{e}^{-\nu \alpha t} $ | (32) |
其中
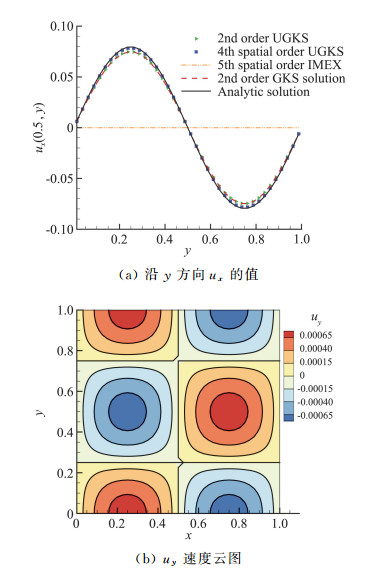
|
图 6 (a) 不同格式对Taylor涡的模拟结果,t=ln2/(μα),x=0.5;(b) UGKS(实线)和精确解(云图)的uy速度云图, t=ln2/(μα) Fig.6 (a) Velocity profile of the Taylor vertex at t=ln2/(μα), x=0.5; (b) Velocity contour of the Taylor vertex at t=ln2/(μα), The solid line is UGKS solution and flood is the analytic solution. |
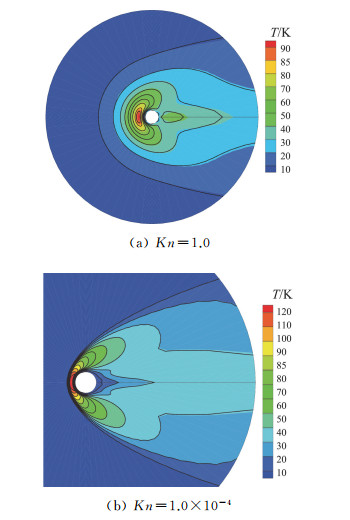
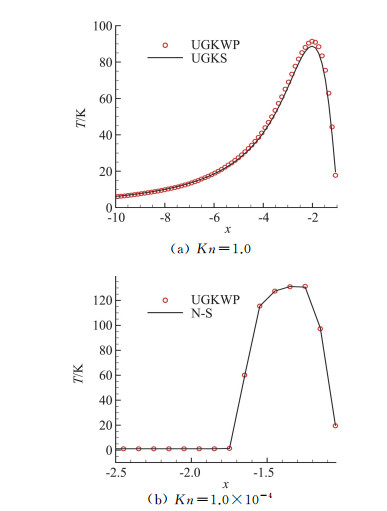
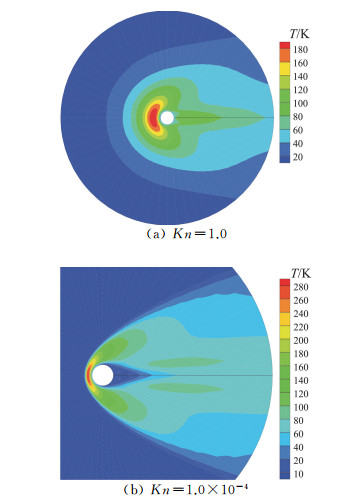
对于高超声速问题,我们给出UGKWP对经典的二维圆柱扰流问题的计算界结果[90]。分子模型采用氩气的VHS模型,来流马赫数为Ma=20、30,以圆柱半径为参考长度的来流努森数为Kn=1.0、1.0×10-4。图 7和图 8分别给出Ma=20不同努森数下流场温度云图和中轴线上的云图分布,可以看出UGKWP在不同流域都能与参考解吻合。图 9给出Ma=30不同努森数下流场温度云图。对于Ma=20, Kn=1.0的算例,UGKWP物理空间网格为径向110网格,周向64网格,粒子参考质量为mp=1.0×10-3,计算时间消耗为36 min,内存消耗为100 MB (i7-8700K CPU)比传统DSMC方法的计算量更低。而对于Ma=20, Kn=10-4的算例,UGKWP物理空间网格为径向150网格,周向100网格,粒子参考质量为mp=4.7×10-3,计算时间消耗为17.2 min,基本与连续流域N-S求解器的计算效率相当。
|
图 7 马赫数20的圆柱绕流问题的温度分布云图(UGKWP解为黑线,参考解为云图) Fig.7 Temperature contour of the cylinder flow with Mach 20 (solid line is UGKWP solution and flood is the reference solution) |
|
图 8 马赫数20的圆柱绕流问题的中轴线温度分布(符号为UGKWP解,实线为参考解) Fig.8 Temperature profile along the stagnation line with Mach 20 (symbols are UGKWP solution and solid ine is the reference solution) |
|
图 9 UGKWP马赫数30的圆柱绕流问题的温度分布云图 Fig.9 Temperature contour of cylinder flow with Mach 30 |
统一气体动理学格式还可以应用于多组分气体[99],以及在外力场作用下的流体[100]。这里我们以等离子体为例来介绍UGKS在多尺度等离子体输运中的应用[91]。等离子体的流域可以根据等离子体和电磁场的耦合强度参数,即归一化回旋半径rL,划分为双流体流域和磁流体流域,同时可以根据等离子体组分间的耦合强度参数,即努森数,划分为无碰撞等离子体流域和连续流域。我们提出了包含等离子体和电磁场以及等离子体间碰撞的动理学耦合电磁学方程组
| $ \begin{array}{l} \frac{\partial f_{a}}{\partial t}+\boldsymbol{v} \cdot \nabla_{x} f_{a}+\frac{\boldsymbol{F}_{a}}{m_{a}} \cdot \nabla_{v} f_{a}=\frac{f_{a}^{+}-f_{a}}{\tau_{a}} \\ \frac{\partial \boldsymbol{B}}{\partial t}=-\nabla_{x} \times \boldsymbol{E} \\ \frac{\partial \boldsymbol{E}}{\partial t}=c^{2} \nabla_{x} \times \boldsymbol{B}-\frac{1}{\varepsilon_{0}} \boldsymbol{J} \end{array} $ | (33) |
其中fα为组分α的分布函数,τα为松弛系数,Fα为洛伦兹力,E、B为电磁场,J为电流。在数值离散时空控制体上,根据直接建模方法,我们建立等离子体流场微观分布函数的有限体积格式
| $ \begin{array}{*{20}{l}} {\left( {{f_\alpha }} \right)_{ij}^{n + 1} = \left( {{f_\alpha }} \right)_{ij}^n - \frac{1}{{\left| {{\mathit{\Omega} _x}} \right|}}\sum\limits_{{s_i} \in {\partial _{{\mathit{\Omega} _x}}}} {\left| {{s_i}} \right|} \mathit{\boldsymbol{F}}_{f\alpha si}^x - }\\ {\frac{1}{{\left| {{\mathit{\Omega} _v}} \right|}}\sum\limits_{{s_j} \in {\partial _{{\mathit{\Omega} _v}}}} {\left| {{s_j}} \right|} \mathit{\boldsymbol{F}}_{f\alpha sj}^{{v_{{v_j}}}} + \int_{{t_n}}^{{t_{n + 1}}} {\frac{{f_{\alpha ij}^ + - {f_{{\alpha _{ij}}}}}}{{{\tau _\alpha }}}} {\rm{d}}t} \end{array} $ | (34) |
和流场宏观量的有限体积格式
| $ \begin{array}{*{20}{l}} {\left( {{\mathit{\boldsymbol{W}}_\alpha }} \right)_i^{n + 1} = \left( {{\mathit{\boldsymbol{W}}_\alpha }} \right)_i^n - \frac{1}{{\left| {{\mathit{\Omega} _x}} \right|}}\sum\limits_{{s_i} \in \partial {\mathit{\Omega} _x}} {\left| {{s_i}} \right|} {\mathit{\boldsymbol{F}}_{{\mathit{\boldsymbol{W}}_{\alpha si}}}} + }\\ {\quad \frac{{\Delta t}}{{{\tau _\alpha }}}\left( {(\mathit{\boldsymbol{\overline W}} )_i^n - \left( {{\mathit{\boldsymbol{W}}_\alpha }} \right)_i^n} \right) + \Delta t\mathit{\boldsymbol{S}}_{{\mathit{\boldsymbol{W}}_\alpha }i}^{n + 1}} \end{array} $ | (35) |
以及电磁场的有限体积格式
| $ \boldsymbol{Q}_{i}^{n+1}=\boldsymbol{Q}_{i}^{n}+\frac{\Delta t}{\left|\mathit{\Omega}_{x}\right|} \sum\limits_{s_{i} \in \partial \mathit{\Omega}_{x}}\left|s_{i}\right| \boldsymbol{F}_{Q s_{i}}+\Delta t \boldsymbol{S}_{Q_{i}}^{n+1} $ | (36) |
格式的核心在于采用网格界面动理学方程的积分解构建数值通量
| $ \begin{array}{l} f(\boldsymbol{x}, t, \boldsymbol{v})=\frac{1}{\tau} \int_{t^{n}}^{t} f^{+}\left(\boldsymbol{x}^{\prime}, t^{\prime}, \boldsymbol{v}^{\prime}\right) \mathrm{e}^{-\frac{t-t^{\prime}}{\tau}} \mathrm{d} t^{\prime}+ \\ \mathrm{e}^{-\frac{t-t^{n}}{\tau}} f_{0}\left(\boldsymbol{x}-\boldsymbol{v}\left(t-t^{n}\right)+\frac{\boldsymbol{F}_{l}}{2}\left(t-t^{n}\right)^{2}, \boldsymbol{v}-\boldsymbol{F}_{l}\left(t-t^{n}\right)\right) \end{array} $ | (37) |
需要指出的是,粒子的特征线
统一气体动理学格式能够捕捉从无碰撞等离子体到磁流体在不同流域的等离子体流动物理,这里我们给出UGKS对朗道阻尼,Orszag-Tang涡问题,和磁重联问题的模拟。朗道阻尼是一种由电磁场作用引发的无碰撞阻尼现象,由于流场扰动较小,需要格式具有较高的计算精度。电子的初始扰动为
| $ f_{0}(x, u)=\frac{1}{\sqrt{2 \pi}}(1+\alpha \cos (k x)) \mathrm{e}^{-\frac{u^{2}}{2}} $ | (38) |
其中k=0.5,扰动α=0.01对应线性朗道阻尼,较大扰动α=0.5则会产生非线性效应。我们采用UGKS模拟计算域L=2π/k内的线性和非线性朗道阻尼现象,采用速度空间128个离散点,物理空间128个离散点。如图 10所示,UGKS能够准确捕捉无碰撞等离子体的精细结构。
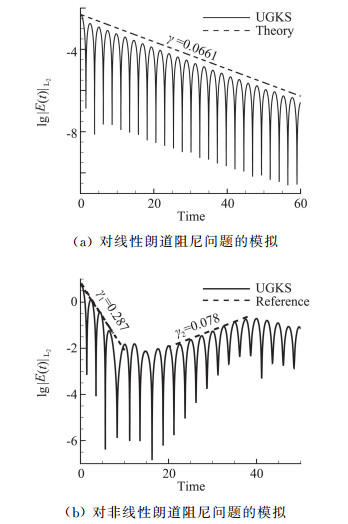
|
图 10 UGKS对线性和非线性朗道阻尼问题的模拟结果 Fig.10 The UGKS simulation of linear and nonlinear Landau damping comparing to the theoretical solution |
为了验证UGKS在磁流体流域的数值表现,我们计算了Kn=10-4, rLi=10-4的Orszag-Tang问题,计算的初始条件为
| $ \begin{array}{l} n_{i}=n_{e}=\gamma^{2}, P_{i}=P_{e}=\gamma, B_{y}=\sin (2 x) \\ u_{i, x}=u_{e, x}=-\sin y, u_{i, y}=u_{e, y}=\sin x \end{array} $ |
其中γ=5/3,物理空间离散为200×200个网格,速度空间采用28×28的Gauss积分。图 11给出t=3时刻的压力云图以及沿y=0.625π的x方向的压力分布。可以看出UGKS在连续流域能够准确捕捉磁流体方程的解。UGKS不仅能够捕捉极限流域的物理解,同时能够为过渡流域内较为复杂的物理问题提供有效的研究方法,例如对于磁场重联问题,UGKS能够在连续流域恢复双流体模型的结果,在无碰撞流域恢复Vlasov方程的结果,同时能够给出在适中努森数和无量纲回旋半径流域的重联结果,见图 12,UGKS为多尺度等离子体物理问题的研究提供有力的数值工具。
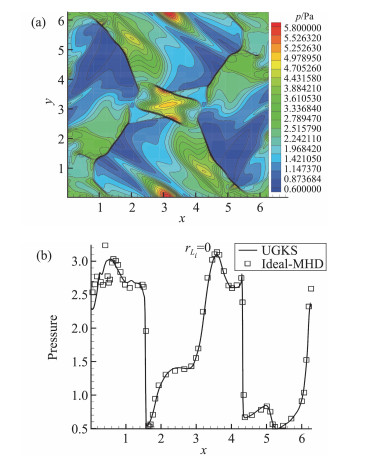
|
图 11 (a) Orszag-Tang问题在t=3时刻的压力云图;(b) Orszag-Tan问题在t=3时刻沿y=0.625π的x方向的压力分布(实线)与磁流体方程结果(符号)的比较 Fig.11 (a) Pressure contour of Orszag-Tang vertex problem at t=3; (b) Pressure profile along y=0.625π at t=3, solid line is UGKS solution and symbol is reference solution |
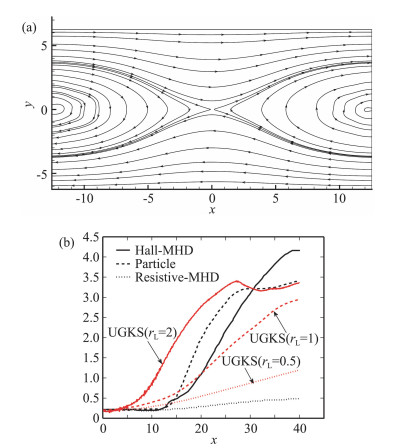
|
图 12 (a) Kn=10-4, rLi=1的磁重联问题在t=40的磁力线分布;(b) UGKS给出的不同无量纲回旋半径的磁场重连率以及参考解 Fig.12 (a) Magnetic lines of magnetic reconnection problem at t=40 with Kn=10-4, rLi=1; (b) Reconnection rate of UGKS with different Larmor radius comparing to reference results |
多尺度气固两相流也是一种典型的多尺度输运系统,可以由固体颗粒相的动理学方程和气相的流体力学N-S方程组成的方程组来描述,流域可以由颗粒碰撞频率的强弱划分为无碰撞气固两相流和双流体流域;根据颗粒跟随系数可以划分为颗粒流(granular flow)流域和尘埃流域(dusty flow)。气固离散两相流的控制方程为颗粒相的动理学方程
| $\begin{array}{l} \frac{\partial f_{s}}{\partial t}+\nabla_{x} \cdot\left(\boldsymbol{v} f_{s}\right)+\nabla_{v} \cdot\left[\left(\boldsymbol{g}-\frac{1}{\rho_{s}} \nabla_{x} p_{g}\right) f_{s}\right] \\ \quad+\nabla_{v} \cdot\left(\frac{\boldsymbol{D}}{m_{s}} f\right)=Q \end{array} $ | (39) |
| $\begin{array}{l} \frac{\partial C_{s} \rho_{s} \varepsilon_{s} T_{s}^{M}}{\partial t}+\nabla_{x} \cdot\left(C_{s} \rho_{s} \varepsilon_{s} T_{s}^{M} \boldsymbol{U}_{s}\right)= \\ r_{T_{m}}\left(1-r^{2}\right) \frac{3 \varepsilon_{s} \rho_{s} k_{B} T_{s}}{4 \tau_{s} m_{s}}+C_{s} \varepsilon_{s} \rho_{s} \frac{T_{g}-T_{s}^{M}}{\tau_{T}} \end{array} $ | (40) |
和气相的N-S方程组成
| $ \begin{array}{l} \frac{\partial \varepsilon_{g} \rho_{g}}{\partial t}+\nabla_{x} \cdot\left(\rho_{g} \boldsymbol{U}_{g}\right)=0 \\ \frac{\partial \varepsilon_{g} \rho_{g} \boldsymbol{U}_{g}}{\partial t}+\nabla_{x} \cdot\left(\rho_{g} \boldsymbol{U}_{g} \boldsymbol{U}_{g}+p_{g} \mathbb{I}-\mu_{g} \sigma\left(\boldsymbol{U}_{g}\right)\right)= \\ \quad-\frac{\varepsilon_{s} \rho_{s}\left(\boldsymbol{U}_{g}-\boldsymbol{U}_{s}\right)}{\tau_{s t}}+\varepsilon_{g} \rho_{g} \boldsymbol{g}+\varepsilon_{s} \nabla_{x} p_{g} \end{array} $ |
| $ \begin{array}{l} \frac{\partial \varepsilon_{g} \rho_{g} E_{g}}{\partial t}+\nabla_{x} \cdot\left[\boldsymbol{U}_{g}\left(\rho_{g} E_{g}+p_{g}\right)\right. \\ \left.-\mu_{g} \sigma\left(\boldsymbol{U}_{g}\right) \boldsymbol{U}+\kappa_{g} \nabla_{x} T_{g}\right]= \\ -\frac{\varepsilon_{s} \rho_{s} \boldsymbol{U}_{s}}{\tau_{s t}}\left(\boldsymbol{U}_{g}-\boldsymbol{U}_{s}\right)+\varepsilon_{s} \nabla_{x} p_{g} \cdot \boldsymbol{U}_{s}+ \\ \frac{3 p_{s}}{\tau_{s t}}+\varepsilon_{g} \rho_{g} \boldsymbol{U}_{g} \cdot \boldsymbol{g}-C_{s} \varepsilon_{s} \rho_{s} \frac{T_{g}-T_{s}^{M}}{\tau_{T}} \end{array} $ | (41) |
在方程(39)中, g为重力加速度,ρs为颗粒相的物质密度; pg为气相压力; ms为颗粒相单个颗粒的质量; 下表s表示颗粒相相关参数; 下表g表示气相相关参数。气相和颗粒相的相互作用通过组分间作用力实现
| $ \boldsymbol{F}_{\mathrm{hydro}}=-\frac{m_{s}}{\rho_{s}} \nabla_{x} p_{g}+\boldsymbol{D} $ | (42) |
其中
| $ Q=\frac{g_{s}-f_{s}}{\tau_{s}} $ | (43) |
其中平衡态满足
| $ {\int {\mathit{\boldsymbol{\psi }}g} _s}{\rm{d}}\mathit{\Xi} = \int {{\mathit{\boldsymbol{\psi }}^\prime }} {f_s}{\rm{d}}\mathit{\Xi} $ | (44) |
其中:
| $ {\mathit{\boldsymbol{\psi }}^\prime } = {\left( {1, v, \frac{1}{2}{\mathit{\boldsymbol{v}}^2} + \frac{{{r^2} - 1}}{2}{{\left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{U}}_s}} \right)}^2}} \right)^{\rm{T}}}, $ |
参数r描述非弹性碰撞的能量损失率。
基于离散空间直接建模方法,我们构建由微观和宏观演化方程耦合的颗粒相的UGKS格式[92]。其中微观分布函数的数值演化方程为
| $ \begin{array}{*{20}{l}} {{{\cal L}_{sf1}}:\quad f_{s, ij}^* = f_{s, ij}^n + }\\ {\qquad \begin{array}{*{20}{l}} {\frac{1}{{\left| {{\mathit{\Omega} _{{x_i}}}} \right|}}\int_{{t_n}}^{{t_{n + 1}}} {\oint_{\partial {\mathit{\Omega} _{{x_i}}}} {{f_{s, \partial {\mathit{\Omega} _{{x_i}}}}}} } \left( {t, {\mathit{\boldsymbol{v}}_j}} \right){\mathit{\boldsymbol{v}}_j} \cdot {\rm{d}}\mathit{\boldsymbol{s}}{\rm{d}}t + }\\ {\frac{1}{{\left| {{\mathit{\Omega} _{{v_j}}}} \right|}}\int_{{t_m}}^{{t_{n + 1}}} {\oint_{\partial {\mathit{\Omega} _{ij}}} {{f_{s, \partial {\mathit{\Omega} _{vj}}}}} } \left( {{\mathit{\boldsymbol{x}}_i}, t} \right){\mathit{\boldsymbol{\omega }}_1} \cdot {\rm{d}}\mathit{\boldsymbol{s}}{\rm{d}}t} \end{array}} \end{array} $ | (45) |
| $ \mathcal{L}_{s f 2}: \quad f_{s, i j}^{* *}=\frac{1}{\left|\mathit{\Omega}_{v j}\right|} \int_{P_{\omega 2}\left(\mathit{\Omega}_{v j}\right)} f_{s, i}^{*}(\mathit{\boldsymbol{v}}) \mathrm{d} \mathit{\boldsymbol{v}} $ | (46) |
| $ \mathcal{L}_{s f 3}: \quad f_{s, i j}^{n+1}=\left(f_{s, i j}^{* *}+\frac{\Delta t}{\tau_{s, i j}} g_{s, i j}^{n+1}\right) /\left(1+\frac{\Delta t}{\tau_{s, i j}}\right) $ | (47) |
对应的,颗粒相宏观量的演化方程为
| $ \begin{array}{l} \mathcal{L}_{s w 1}: \quad \boldsymbol{W}_{s, i}^{*}=\boldsymbol{W}_{s, i}^{n}+\frac{1}{\left|\mathit{\Omega}_{x_{i}}\right|} \cdot \\ \oint_{\partial \mathit{\Omega}_{x_{i}}} \int_{t_{n}}^{t n+1} \int \boldsymbol{\psi} f_{s, \partial \mathit{\Omega}_{x_{i}}}(\boldsymbol{v}, t) \boldsymbol{v} \cdot \boldsymbol{e}_{1} \mathrm{d} \mathit{\Xi} \mathrm{d} t \mathrm{d} s+\Delta t \boldsymbol{S}_{s, i}^{n} \end{array} $ | (48) |
| $ \begin{array}{*{20}{c}} {{C_s}{\rho _s}\varepsilon _{s, i}^{n + 1}T_{s, i}^* = {C_s}{\rho _s}\varepsilon _{s, i}^{n + 1}T_{s, i}^n + \frac{1}{{\left| {{\mathit{\Omega} _{{x_i}}}} \right|}} \cdot }\\ {\oint_{\partial {\mathit{\Omega} _{{x_i}}}} {\int_{{t_n}}^{{t_{n + 1}}} {\int {{f_{sT, \partial {\mathit{\Omega} _{{x_i}}}}}} } } (\mathit{\boldsymbol{v}}, t)\mathit{\boldsymbol{v}} \cdot {\mathit{\boldsymbol{e}}_1}{\rm{d}}\mathit{\Xi} {\rm{d}}t{\rm{d}}s} \end{array} $ | (49) |
| $ \begin{array}{ll} \mathcal{L}_{s w 2}: \boldsymbol{U}_{s , i}^{n+1}=\gamma_{U s 1} \boldsymbol{U}_{s, i}^{*}+\gamma_{U s 2} \boldsymbol{U}_{g , i}^{*} \end{array} $ | (50) |
| $ \mathcal{L}_{s w 3}: \boldsymbol{W}_{s, i}^{* *}=\int \boldsymbol{\psi} f_{s, i j}^{* *} \mathrm{d} \mathit{\Xi} $ | (51) |
| $ \mathcal{L}_{s w 4}: \quad e_{s, i}^{n+1}=e_{s, i}^{* *} /\left[1+\frac{\Delta t}{2 \tau_{s, i}}\left(1-r^{2}\right)\right] $ | (52) |
| $ \begin{array}{l} \mathcal{L}_{s w 5}: T_{s, i}^{M, n+1}= \\ \gamma_{T 1}\left[T_{s, i}^{M, *}+\frac{\Delta t\left(1-r^{2}\right) e_{s, i}^{* *}}{\left[2 \tau_{s, i}+\Delta t\left(1-r^{2}\right)\right] C_{s, i}}\right]- \\ \gamma_{T 2}\left[T_{g, i}^{*}+\frac{\varepsilon_{s . i}^{n+1} \rho_{s}\left(E_{s, i}^{* *}-E_{s, i}^{*}\right)}{\varepsilon_{g, i}^{n+1} \rho_{g, i}^{n+1} C_{v, i}}\right] \end{array} $ | (53) |
其中源项为
| $ \boldsymbol{S}_{i}^{n}=\left(0, \theta_{i} \rho_{s} \boldsymbol{g}-\theta_{i} \nabla_{x} p_{g, i}^{n}, \theta_{i} \rho_{s} \boldsymbol{U}_{s, i} \cdot \boldsymbol{g}-\theta_{i} \boldsymbol{U}_{s, i} \cdot \nabla_{x} p_{g, i}^{n}\right) $ |
速度和能量方程中的参数为
| $ {\gamma _{Us1}} = \frac{{\varepsilon _{s, i}^{n + 1}{\rho _s} + \varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}\exp \left[ { - \left( {1 + \frac{{\varepsilon _{s, i}^{n + 1}{\rho _s}}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}}}} \right)\frac{{\Delta t}}{{{\tau _{{\rm{st}}, i}}}}} \right]}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1} + \varepsilon _{s, i}^{n + 1}{\rho _s}}} $ |
| $ {\gamma _{Us2}} = \frac{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1} - \varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}\exp \left[ { - \left( {1 + \frac{{\varepsilon _{s, i}^{n + 1}{\rho _s}}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}}}} \right)\frac{{\Delta t}}{{{\tau _{{\rm{st}}, i}}}}} \right]}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1} + \varepsilon _{s, i}^{n + 1}{\rho _s}}} $ |
| $ \gamma_{T_{s 1}}=\frac{\varepsilon_{s, i}^{n+1} \rho_{s} C_{s}+\varepsilon_{g, i}^{n+1} \rho_{g, i}^{n+1} C_{v} \exp \left[-\left(1+\frac{\varepsilon_{s, i}^{n+1} \rho_{s} C_{s}}{\varepsilon_{g, i}^{n+1} \rho_{g, i}^{n+1} C_{v}}\right) \frac{\Delta t}{\tau_{T, i}}\right]}{\varepsilon_{g, i}^{n+1} \rho_{g, i}^{n+1} C_{v}+\varepsilon_{s, i}^{n+1} \rho_{s} C_{s}} $ |
| $ {\gamma _{Ts2}} = \frac{{ - \varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}{C_v} + \varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}{C_v}\exp \left[ { - \left( {1 + \frac{{\varepsilon _{s, i}^{n + 1}{\rho _s}{C_s}}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}{C_v}}}} \right)\frac{{\Delta t}}{{{\varepsilon _{T, i}}}}} \right]}}{{\varepsilon _{g, i}^{n + 1}\rho _{g, i}^{n + 1}{C_v} + \varepsilon _{s, i}^{n + 1}{\rho _s}}} $ |
颗粒相UGKS格式多尺度性质的核心在于其在微观分布函数演化方程(45)和宏观量的演化方程(48)中的数值通量由动理学方程(39)界面处积分解构建
| $ \begin{array}{l} f_{s}\left(\boldsymbol{x}_{0}, t, \boldsymbol{v}_{j}\right)=\frac{1}{\tau_{s}} \int_{0}^{t} g_{s}\left(\boldsymbol{x}^{\prime}, t^{\prime}, \boldsymbol{v}^{\prime}\right) \mathrm{e}^{-\left(t-t^{\prime}\right) / \tau} \mathrm{d} t^{\prime}+ \\ \mathrm{e}^{-t / \tau_{s}} f_{s, 0}\left(\boldsymbol{x}_{0}-\boldsymbol{u} t, \boldsymbol{v}_{j}-\boldsymbol{\omega}_{1} t\right) \end{array} $ | (54) |
因而可以在稀薄颗粒流和连续流域分别给出颗粒自由输运和双流体方程对应的通量。气相的演化方程为基于GKS的有限体积格式[24]
| $ \begin{array}{l} {{\cal L}_{gw1}}:\\ \mathit{\boldsymbol{W}}_{g, i}^{n + 1} = \mathit{\boldsymbol{W}}_{g, i}^n + \frac{1}{{\left| {{\mathit{\Omega} _{{x_i}}}} \right|}}\int_{{t_n}}^{{t^{n + 1}}} {\int {\oint_{\partial {\mathit{\Omega} _{{x_i}}}} \mathit{\boldsymbol{\psi }} } } {f_{g, \partial {\mathit{\Omega} _{{x_i}}}}}(\mathit{\boldsymbol{v}}, t)\mathit{\boldsymbol{u}} \cdot {\rm{d}}\mathit{\boldsymbol{s}}{\rm{d}}\mathit{\Xi} {\rm{d}}t\\ + \Delta t\mathit{\boldsymbol{S}}_{g, i}^n - \Delta t\mathit{\boldsymbol{S}}_{s, i}^n \end{array} $ | (55) |
| $ \mathcal{L}_{g w 2}: \quad \boldsymbol{U}_{g, i}^{n+1}=\gamma_{U g 1} \boldsymbol{U}_{s, i}^{n}+\gamma_{U g 2} \boldsymbol{U}_{g, i}^{n} $ | (56) |
| $ \begin{aligned} &\mathcal{L}_{g w 3}:\\ &\begin{aligned} \boldsymbol{T}_{g, i}^{n+1}=& \gamma_{T_{g 3}}\left[\boldsymbol{T}_{s, i}^{M, *}+\frac{\Delta t\left(1-r^{2}\right) e_{s, i}^{* *}}{\tau_{s}+\Delta t\left(1-r^{2}\right)} \rho_{s} C_{s, i}\right]+\\ & \gamma_{T_{g 4}}\left[\boldsymbol{T}_{g, i}^{*}+\frac{\varepsilon_{s}^{n+1} \rho_{s}\left(E_{s, i}^{* *}-E_{s, i}^{*}\right)}{\varepsilon_{g, i}^{n+1} \rho_{g, i}^{n+1} C_{v}}\right] \end{aligned} \end{aligned} $ | (57) |
其中源项为
| $ {\gamma _{Ug1}} = \frac{{\theta _i^{n + 1}{\rho _s} - \theta _i^{n + 1}{\rho _s}\exp \left[ { - \left( {1 + \frac{{\theta _i^{n + 1}{\rho _s}}}{{\varepsilon _g^{n + 1}\rho _{g, i}^{n + 1}}}} \right)\frac{{\Delta t}}{{{\tau _{st, i}}}}} \right]}}{{\varepsilon _g^{n + 1}\rho _{g, i}^{n + 1} + \theta _i^{n + 1}{\rho _s}}} $ |
| $ \gamma_{U g 2}=\frac{\theta_{i}^{n+1} \rho_{s}+\varepsilon_{g}^{n+1} \rho_{g, i}^{n+1} \exp \left[-\left(1+\frac{\theta_{i}^{n+1} \rho_{s}}{\varepsilon_{g}^{n+1} \rho_{g, i}^{n+1}}\right) \frac{\Delta t}{\tau_{s t, i}}\right]}{\varepsilon_{g}^{n+1} \rho_{g, i}^{n+1}+\theta_{i}^{n+1} \rho_{s}} $ |
| $ \begin{array}{*{20}{l}} {{\gamma _{Tg3}} = }\\ {\frac{{\theta _i^{n + 1}{\rho _s}{C_{s, i}} - \theta _i^{n + 1}{\rho _s}{C_s}\exp \left[ { - \left( {1 + \frac{{\theta _i^{n + 1}{\rho _s}{C_s}}}{{\varepsilon _g^{n + 1}\rho _{g, i}^{n + 1}{C_v}}}} \right)\frac{{\Delta t}}{{{\tau _{T, i}}}}} \right]}}{{\varepsilon _k^{n + 1}\rho _{g, i}^{n + 1}{C_v} + \theta _i^{n + 1}{\rho _s}{C_s}}}} \end{array} $ |
| $ \begin{array}{*{20}{l}} {{\gamma _{Tg4}} = }\\ {\qquad \begin{array}{*{20}{l}} {\theta _i^{n + 1}{\rho _s}{C_{s, i}} + \varepsilon _g^{n + 1}\rho _{g, i}^{n + 1}{C_v}\exp \left[ { - \left( {1 + \frac{{\theta _i^{n + 1}{\rho _s}{C_s}}}{{\varepsilon _g^{n + 1}\rho _{g, i}^{n + 1}{C_v}}}} \right)\frac{{\Delta t}}{{{\tau _{T, i}}}}} \right]}\\ {\frac{{\varepsilon _g^{n + 1}\rho _{g, i}^{n + 1}{C_v} + \theta _i^{n + 1}{\rho _s}{C_s}}}{{{\varepsilon _s}}}} \end{array}} \end{array} $ |
气相方程的数值通量由基于网格界面积分解的GKS通量给出,其中网格界面积分解为
| $ \begin{array}{l} f_{g}\left(\boldsymbol{x}_{0}, t, \boldsymbol{v}\right)=\frac{1}{\tau} \int_{0}^{t} g_{g}\left(\boldsymbol{x}^{\prime}, t^{\prime}, \boldsymbol{v}^{\prime}\right) \mathrm{e}^{-\left(t-t^{\prime}\right) / \tau} \mathrm{d} t^{\prime}+ \\ \mathrm{e}^{-t / \tau} f_{0 , \mathrm{NS}}\left(\boldsymbol{x}_{0}-\boldsymbol{v} t, \boldsymbol{v}-\boldsymbol{g} t\right) \end{array} $ | (58) |
与颗粒相不同,气相网格界面积分解的初值由N-S方程对应的一阶CE展开f0, NS给出[24]。颗粒相和气相的演化相耦合,构成描述气固离散两相流的多尺度数值格式UGKS-Multiphase[92]。
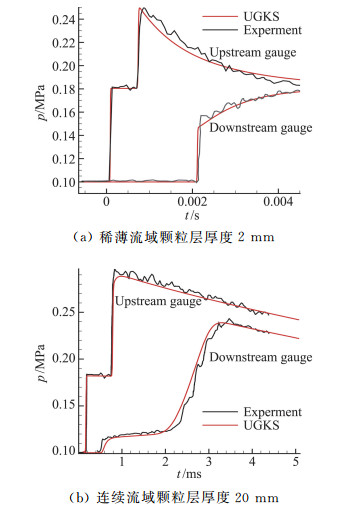
这里我们给出UGKS-Multiphase对激波驱动的颗粒层实验的数值模拟,实验装置设置如图 13所示,颗粒层初始位置为150 mm,在颗粒层下方110 mm,颗粒层上方43 mm和718 mm处有三个压力感应器。初始激波强度为Ma=1.3,气相密度1.2 kg/m3,颗粒相密度2500 kg/m3。计算数值分辨率为Δx=3.75×10-3,Δv=4.4375。我们分别计算了不同颗粒层流域的情形,包括稀薄流域颗粒层厚度2 mm和连续流域颗粒层厚度20 mm的情况,都能够和实验数据相吻合, 见图 14。
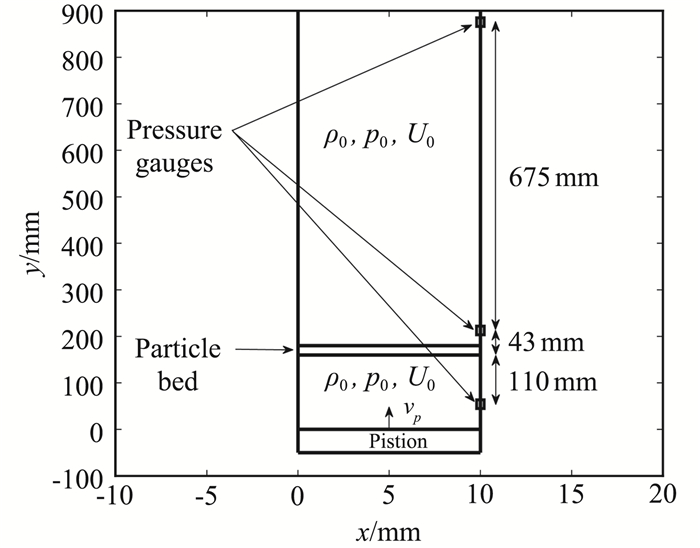
|
图 13 激波驱动的颗粒层实验装置设置 Fig.13 Set up of shock driven particle bed experiment |
|
图 14 激波驱动的颗粒层实验UGKS的数值模拟结果和实验数据的对比 Fig.14 Comparison the pressure profile of pressure driven particle bed |
根据介质的透光性,光子输运可以分为在光性薄介质的稀薄流域、过渡流域和在光性厚介质的扩散流域。传统的隐式蒙卡方法、离散速度方法和扩散方程等方法,都是单尺度数值方法,不能够在全流域适用。根据离散时空直接建模方法,我们发展了基于离散速度的UGKS格式[93-94, 96]和基于统计学粒子的UGKWP格式[89]。这里我们以纯散射介质内的UGKWP格式为例介绍多尺度光子输运数值方法的建模思想。纯散射介质光子输运的动理学方程为
| $ \frac{\varepsilon^{2}}{c} \frac{\partial I}{\partial t}+\varepsilon \mathit{\Omega} \cdot \nabla I=\sigma\left(\frac{1}{4 \pi} E-I\right) $ | (59) |
其中
| $ \begin{array}{l} I(t, x, \mathit{\Omega} ) = \int_0^t {{{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}}}(t - s)}}} \frac{{c\sigma }}{{{\varepsilon ^2}}}\frac{1}{{4\pi }}E\left( {s, x - \frac{c}{\varepsilon }\mathit{\Omega} (t - s), \mathit{\Omega} } \right){\rm{d}}s\\ + {{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}t}}}}{I_0}\left( {x - \frac{c}{\varepsilon }\mathit{\Omega} t} \right)\\ = \left( {1 - {{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}}}t}}} \right)\frac{1}{{4\pi }}{E^ + }(t, x, \mathit{\Omega} ) + {{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}}}t{I_0}}}\left( {x - \frac{c}{\varepsilon }\mathit{\Omega} t} \right) \end{array} $ | (60) |
其中
| $ \begin{array}{l} {E^ + }(t, x, \mathit{\Omega} ) = E(\mathit{\Omega} ) + \frac{{{{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}}}\left( {t + \frac{{{\varepsilon ^2}}}{{c\sigma }}} \right) - \frac{{c\sigma }}{{{\varepsilon ^2}}}}}}}{{1 - {{\rm{e}}^{ - \frac{{c\sigma }}{{{\varepsilon ^2}}}t}}}} \cdot \\ \left[ {{E_t}(\mathit{\Omega} ) + \frac{c}{\varepsilon }\mathit{\Omega} {E_x}(\mathit{\Omega} )} \right] \end{array} $ | (61) |
宏观守恒量的演化方程为
| $ E_m^{n + 1} = E_m^n + \sum\limits_{{\tau _j} \in \partial {D_m}} {\frac{{\Delta t}}{{{V_m}}}} \frac{c}{{\varepsilon \Delta t}}\int_{{t^n}}^{tn + 1} {\int_{{\tau _j}} {\left( {\mathit{\Omega} \cdot {n_j}} \right)} } \cdot I(t, x, \mathit{\Omega} ){\rm{d}}l{\rm{d}}t $ | (62) |
UGKWP的核心在于采用网格界面处动理学方程积分解构造数值通量,即
| $ \begin{array}{l} I(t, x, \mathit{\Omega})=\mathrm{e}^{-\frac{c \sigma\left(t-t^{n}\right)}{\varepsilon^{2}}} I\left(t^{n}, x-\frac{c}{\varepsilon} \mathit{\Omega}\left(t-t^{n}\right)\right)+ \\ \quad \int_{t^{n}}^{t} \mathrm{e}^{-\frac{c(t-s)}{\varepsilon^{2}}} \times \frac{c \sigma}{\varepsilon^{2}} \frac{1}{4 \pi} E\left(s, x-\frac{c}{\varepsilon} \mathit{\Omega}(t-s)\right) \mathrm{d} s \end{array} $ | (63) |
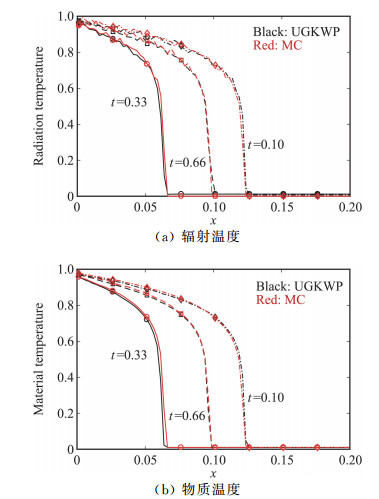
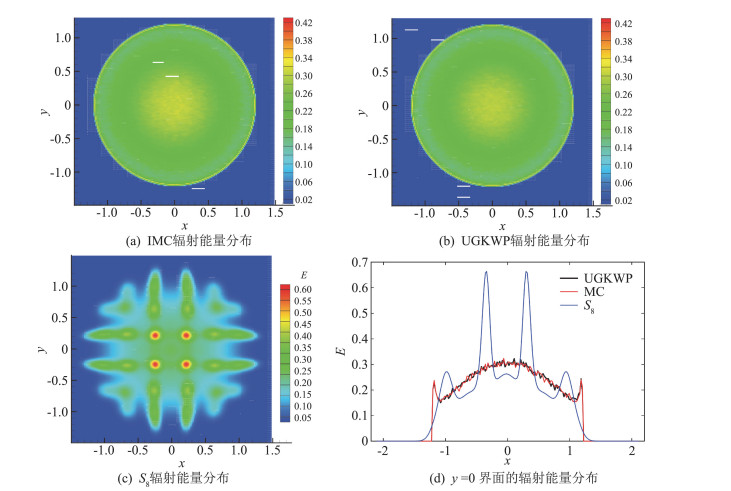
我们给出采用UGKWP计算的Marshak波和线光源传播问题。对于Marshak波问题,吸收系数设为σ=30/T3,光速c=29.98,物质比热容Cv=0.3。图 15给出时间t=0.33, 0.66, 1.0时刻的光子和物质能量分布。由于Marshak问题的吸收系数与温度相关,低温区为扩散流域,高温区为稀薄流域,UGKWP在不同流域都能够和参考解吻合,同时计算效率高于隐式蒙卡。对于线光源问题,计算参数为σ=1, ε=1, c=1。计算域为[-1.5, 1.5]×[-1.5, 1.5],物理空间网格量为201×201。图 16给出UGKWP、S8、隐式蒙卡的结果,可以看到UGKWP与参考解吻合,同时没有Sn方法的非物理射线效应。
|
图 15 Marshak问题t=0.33, 0.66, 1.0时刻UGKWP的计算结果与IMC方法的比较 Fig.15 UGKWP simulation of Marshak problem compared to IMC result at t=0.33, 0.66, 1.0 |
|
图 16 线光源问题t=1.2的解 Fig.16 Line source scattering problem at t=1.2 |
基于离散空间直接建模方法的UGKS格式还被应用中子输运[97]、双原子气体[101]、多组分气体[102]等领域,DUGKS格式被成功应用于微流动[103-104]、两相流及固液相变[105-107]、混合气体流动[108]、颗粒流动[107]、电渗流动[109]、热辐射[110]等领域,在计算精度和计算效率上相对于传统单尺度方法由体现出明显优势。DUGKS还被应用于多尺度声子输运的模拟,能够准确模拟从弹道输运流域(ballistic transport regime)到扩散流域(diffusive regime)的声子输运物理[111-112]。在体元尺度渗流和气固颗粒两项流等领域,DUGKS也有具有较高的准确性和计算效率[83, 86]。另一方面,GKS和DUGKS格式也在湍流的直接模拟和湍流建模方面提供了新的思路和手段,有望为湍流建模开辟一条更为有效的研究道路[68, 113-115]。
2.5 加速机制在近年的发展中,我们提出了一系列针对UGKS的加速机制,包括速度空间自适应[116]和隐式和多重网格加速方法[71-73]。这里我们简要介绍UGKS的隐式加速方法。隐式UGKS的宏观迭代控制方程为
| $ \frac{V_{i}}{\Delta t} \Delta \boldsymbol{W}_{i}^{n+1}+\sum\limits_{j \in N} S_{i j} \Delta \boldsymbol{F}_{i j}^{n+1}=\sum\limits_{j \in N} S_{i j} \boldsymbol{F}_{i j}^{n} $ | (64) |
微观迭代方程为
| $ \begin{array}{l} \left(\frac{V_{i}}{\Delta t}+\frac{V_{i}}{\tau_{i}^{n+1}}\right) \Delta f_{i, k}^{n+1}+\sum\limits_{j \in N} v_{k, n} S_{i j} \Delta f_{i j, k}^{n+1}= \\ -\sum\limits_{j \in N} S_{i j} v_{k, n} f_{i j, k}^{n}+V_{i} \frac{g_{i, k}^{n+1}-f_{i, k}^{n}}{\tau_{i}^{n+1}} \end{array} $ | (65) |
通过采用多重网格等迭代技术可以快速得到隐式控制方程的解,相对于显式推进的UGKS,计算时间可以提高至少两个数量级。隐式UGKS在不同流域都快速收敛的关键在于宏观和微观耦合迭代,在连续流域通过宏观迭代驱动微观分布函数快速达到收敛,近年来基于这种想法发展了一些高效的多尺度隐式算法[56, 117]。
3 多尺度建模方法的总结和展望传统的偏微分方程数值解往往是从偏微分方程出发,通过一定的离散方法得到相应的数值格式,但偏微分方程都是对固定物理尺度建模得到的方程,因而对其直接的离散不能改变其物理本质,因而只能发展出单尺度的方法,比如针对N-S方程的各种算法和直接离散Boltzmann方程的DVM方法。离散时空直接建模思想是回到有限控制体上,把有限大小的控制体当成物理尺度,建立对应于此尺度上的离散演化方程,以及通过界面的数值通量。此格式的构建完全根据物理守恒率,以及在不同网格尺度上的传输过程。格式直接给出了在离散空间上物理量的演化方程和它的演化解。根据网格尺度和分子平均自由程的随地方变化的不同比值,实现了对不同流域的物理描述和直接的数值自适应,即在连续流域收敛到N-S方程数值解,在稀薄流域收敛到动理学方程的解。在中间流域,由于多尺度建模中严格遵从物理守恒率和从非平衡态到平衡态满足熵增的演化规律,方法本身是可靠的。在所有算例中还没有发现过违背物理规律的数值解。基于这种思想,我们还发展了包含气体、等离子体、光子、中子、离散两相流在内的多种输运过程的数值多尺度控制方程,并且在计算精度和效率上相对于传统单尺度格式体现出明显优势。离散时空直接建模思想不仅为物理研究和工程应用提供了有力的数值方法,同时为包含湍流建模在内的建模难题提供了一个新的思路。直接建模思想有深刻的物理基础和独特的建模手段,跳出了传统数值计算的制约,把建立演化方程和得到数值解紧密地结合起来。直接建模为解决多尺度问题和刻画非平衡传输提供了一种重要的解决方案,在未来输运问题研究以及湍流建模的研究中必将发挥重要作用,成为多尺度建模的重要工具。
| [1] |
BOLTZMANN L. Lectures on gas theory[M]. Cambridge University Press, 1964.
|
| [2] |
CERCIGNANI C. The Boltzmann equation and its applications[M]. New York, NY: Springer New York, 1988.
|
| [3] |
BHATNAGAR P L, GROSS E P, KROOK M. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511. |
| [4] |
SHAKHOV E. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(5): 95-96. |
| [5] |
HOLWAY L H. New statistical models for kinetic theory:methods of construction[J]. Physics of Fluids, 1966, 9(9): 1658-1673. |
| [6] |
GORJI M H, TORRILHON M, JENNY P. Fokker-Planck model for computational studies of monatomic rarefied gas flows[J]. Journal of Fluid Mechanics, 2011, 680: 574-601. |
| [7] |
FERRARO V C A, CHAPMAN S, COWLING T G. The mathematical theory of non-uniform gases. An account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases[J]. The Mathematical Gazette, 1954, 38(323): 63. |
| [8] |
TSIEN H S. Superaerodynamics, mechanics of rarefied gases[J]. Journal of the Aeronautical Sciences, 1946, 13(12): 653-664. |
| [9] |
CHEN S Y, DOOLEN G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 329-364. |
| [10] |
GUO Z L, SHU C. Lattice Boltzmann method and its applications in engineering[M]//SHU C W, SHU C. Advances in Computational Fluid Dynamics: Volume 3. Singapore: World Scientific, 2013. doi.org/10.1142/8806
|
| [11] |
LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. |
| [12] |
COCKBURN B, LIN S Y, SHU C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅲ:One-dimensional systems[J]. Journal of Computational Physics, 1989, 84(1): 90-113. |
| [13] |
WANG Z J. Spectral (finite) volume method for conservation laws on unstructured grids. Basic formulation[J]. Journal of Computational Physics, 2002, 178(1): 210-251. |
| [14] |
LIU Y, VINOKUR M, WANG Z J. Spectral difference method for unstructured grids I:basic formulation[J]. Journal of Computational Physics, 2006. |
| [15] |
GAO H Y, WANG Z J. A high-order lifting collocation penalty formulation for the Navier-Stokes equations on 2-D mixed grids[C]//19th AIAA Computational Fluid Dynamics, San Antonio, Texas. Reston, Virigina: AIAA, 2009.
|
| [16] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[C]//18th AIAA Computational Fluid Dynamics Conference.
|
| [17] |
LI J Q, DU Z F. A two-stage fourth order time-accurate discretization for lax:wendroff type flow solvers I. hyperbolic conservation laws[J]. SIAM Journal on Scientific Computing, 2016, 38(5): A3046-A3069. |
| [18] |
DU Z F, LI J Q. A Hermite WENO reconstruction for fourth order temporal accurate schemes based on the GRP solver for hyperbolic conservation laws[J]. Journal of Computational Physics, 2018, 355: 385-396. |
| [19] |
DU Z F, LI J Q. A two-stage fourth order time-accurate discretization for Lax-Wendroff type flow solvers Ⅱ. High order numerical boundary conditions[J]. Journal of Computational Physics, 2018, 369: 125-147. |
| [20] |
LI J Q. Two-stage fourth order:temporal-spatial coupling in computational fluid dynamics (CFD)[J]. Advances in Aerodynamics, 2019, 1: 3. |
| [21] |
PAN L, XU K, LI Q B, et al. An efficient and accurate two-stage fourth-order gas-kinetic scheme for the Euler and Navier-Stokes equations[J]. Journal of Computational Physics, 2016, 326: 197-221. |
| [22] |
PAN L, CHENG J X, WANG S H, et al. A two-stage fourth-order gas-kinetic scheme for compressible multicomponent flows[J]. Communications in Computational Physics, 2017, 22(4): 1123-1149. |
| [23] |
PAN L, XU K. Two-stage fourth-order gas-kinetic scheme for three-dimensional Euler and Navier-Stokes solutions[J]. International Journal of Computational Fluid Dynamics, 2018, 32(10): 395-411. |
| [24] |
XU K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. |
| [25] |
JI X, ZHAO F X, SHYY W, et al. A family of high-order gas-kinetic schemes and its comparison with Riemann solver based high-order methods[J]. Journal of Computational Physics, 2018, 356: 150-173. |
| [26] |
毛枚良, 徐昆, 邓小刚. 动能BGK算法在近连续流模拟中的应用[J]. 空气动力学学报, 2005, 23(3): 317-321. MAO M L, XU K, DENG X G. Application of kinetic BGK algorithm in simulating near continuum flow[J]. Acta Aerodynamica Sinica, 2005, 23(3): 317-321. (in Chinese) |
| [27] |
李启兵, 徐昆. 气体动理学格式研究进展[J]. 力学进展, 2012, 42(5): 522-537. LI Q B, XU K. Progress in gas-kinetic scheme[J]. Advances in Mechanics, 2012, 42(5): 522-537. (in Chinese) |
| [28] |
邹兴, 陈松泽, 郭照立.精细平衡气体动理学格式[J/OL].计算物理: 1-16[2020-03-19].http://kns.cnki.net/kcms/detail/11.2011.o4.20200218.1711.006.html.
|
| [29] |
ZHAO F X, JI X, SHYY W, et al. An acoustic and shock wave capturing compact high-order gas-kinetic scheme with spectral-like resolution[J/OL]. Computational Physics, arXiv: 2001.01570.[2019-12-27]. https://arxiv.org/abs/2001.01570.
|
| [30] |
ZHAO F X, JI X, SHYY W, et al. Compact higher-order gas-kinetic schemes with spectral-like resolution for compressible flow simulations[J]. Advances in Aerodynamics, 2019, 1: 13. |
| [31] |
SHEN C. Rarefied gas dynamics: fundamentals, simulations and micro flows[M]. Springer Science & Business Media, 2006.
|
| [32] |
BURNETT D. The distribution of molecular velocities and the mean motion in a non-uniform gas[J]. Proceedings of the London Mathematical Society, 1936(1): 382-435. |
| [33] |
GRAD H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2(4): 331-407. |
| [34] |
STRUCHTRUP H. Macroscopic transport equations for rarefied gas flows[M]. Berlin, Heidelberg: Springer, 2005: 145-160.
|
| [35] |
BIRD G A. Approach to translational equilibrium in a rigid sphere gas[J]. Physics of Fluids, 1963, 6(10): 1518-1519. |
| [36] |
BIRD G A. Molecular gas dynamics and the direct simulation of Monte Carlo[M]. Clarendon Press Oxford Science, 1994.
|
| [37] |
PARESCHI L, RUSSO G. Asymptotic preserving Monte Carlo methods for the Boltzmann equation[J]. Transport Theory and Statistical Physics, 2000, 29(3/4/5): 415-430. |
| [38] |
REN W, LIU H, JIN S. An asymptotic-preserving Monte Carlo method for the Boltzmann equation[J]. Journal of Computational Physics, 2014, 276: 380-404. |
| [39] |
DEGOND P, DIMARCO G, PARESCHI L. The moment-guided Monte Carlo method[J]. International Journal for Numerical Methods in Fluids, 2011, 67(2): 189-213. |
| [40] |
BAKER L L, HADJICONSTANTINOU N G. Variance reduction for Monte Carlo solutions of the Boltzmann equation[J]. Physics of Fluids, 2005, 17(5): 051703. |
| [41] |
HOMOLLE T M M, HADJICONSTANTINOU N G. A low-variance deviational simulation Monte Carlo for the Boltzmann equation[J]. Journal of Computational Physics, 2007, 226(2): 2341-2358. |
| [42] |
JENNY P, TORRILHON M, HEINZ S. A solution algorithm for the fluid dynamic equations based on a stochastic model for molecular motion[J]. Journal of Computational Physics, 2010, 229(4): 1077-1098. |
| [43] |
F EI, ZHANG J, LI J, et al. A unified stochastic particle Bhatnagar-Gross-Krook method for multiscale gas flows[J]. Journal of Computational Physics, 2020, 400: 108972. |
| [44] |
CHU C K. Kinetic-theoretic description of the formation of a shock wave[J]. Physics of Fluids, 1965, 8(1): 12-22. |
| [45] |
YANG J Y, HUANG J C. Rarefied flow computations using nonlinear model Boltzmann equations[J]. Journal of Computational Physics, 1995, 120(2): 323-339. |
| [46] |
MIEUSSENS L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries[J]. Journal of Computational Physics, 2000, 162(2): 429-466. |
| [47] |
ARISTOV V V, CHEREMISSINE F G. Direct numerical solution of the kinetic Boltzmann equation[EB/OL]. 2005. https://www.researchgate.net/publication/265375118_Direct_numerical_solution_of_the_kinetic_Boltzmann_equation
|
| [48] |
KOLOBOV V I, ARSLANBEKOV R R, ARISTOV V V, et al. Unified solver for rarefied and continuum flows with adaptive mesh and algorithm refinement[J]. Journal of Computational Physics, 2007, 223(2): 589-608. |
| [49] |
LI Z H, ZHANG H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. |
| [50] |
XU K, HUANG J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764. |
| [51] |
WU L, WHITE C, SCANLON T J, et al. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method[J]. Journal of Computational Physics, 2013, 250: 27-52. |
| [52] |
WU L, REESE J M, ZHANG Y H. Solving the Boltzmann equation deterministically by the fast spectral method:application to gas microflows[J]. Journal of Fluid Mechanics, 2014, 746: 53-84. |
| [53] |
WU L, ZHANG J, REESE J M, et al. A fast spectral method for the Boltzmann equation for monatomic gas mixtures[J]. Journal of Computational Physics, 2015, 298: 602-621. |
| [54] |
ARISTOV V V. Direct methods for solving the Boltzmann equation and study of nonequilibrium flows[M]. Dordrecht: Springer Netherlands, 2001.
|
| [55] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一数值算法初步研究[J]. 空气动力学学报, 2000, 18(3): 255-263. LI Z H, ZHANG H X. Study on gas kinetic algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2000, 18(3): 255-263. (in Chinese) |
| [56] |
SU W, ZHU L H, WANG P, et al. Can we find steady-state solutions to multiscale rarefied gas flows within dozens of iterations?[J]. Journal of Computational Physics, 2020, 407: 109245. |
| [57] |
JIN S. Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations[J]. SIAM Journal on Scientific Computing, 1999, 21(2): 441-454. |
| [58] |
FILBET F, JIN S. A class of asymptotic-preserving schemes for kinetic equations and related problems with stiff sources[J]. Journal of Computational Physics, 2010, 229(20): 7625-7648. |
| [59] |
HU J W, JIN S. A stochastic Galerkin method for the Boltzmann equation with uncertainty[J]. Journal of Computational Physics, 2016, 315: 150-168. |
| [60] |
WOLLABER A B, PARK H, LOWRIE R B, et al. Multigroup radiation hydrodynamics with a high-order-low-order method[J]. Nuclear Science and Engineering, 2017, 185(1): 117-129. |
| [61] |
CHEN S Z, XU K. A comparative study of an asymptotic preserving scheme and unified gas-kinetic scheme in continuum flow limit[J]. Journal of Computational Physics, 2015, 288: 52-65. |
| [62] |
XU K. Construction and application of unified gas-kinetic scheme[M]//SHU C W, SHU C. Advances in Computational Fluid Dynamics: Volume 4. Singapore: World Scientific, 2015.
|
| [63] |
HUANG J C, XU K, YU P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ:multi-dimensional cases[J]. Communications in Computational Physics, 2012, 12(3): 662-690. |
| [64] |
LIU C, XU K, SUN Q H, et al. A unified gas-kinetic scheme for continuum and rarefied flows IV:Full Boltzmann and model equations[J]. Journal of Computational Physics, 2016, 314: 305-340. |
| [65] |
徐昆, 李启兵, 黎作武. 离散空间直接建模的计算流体力学方法[J]. 中国科学:物理学力学天文学, 2014, 44(5): 519-530. XU K, LI Q B, LI Z W. Direct modeling-based computational fluid dynamics[J]. Scientia Sinica(Physica, Mechanica & Astronomica), 2014, 44(5): 519-530. (in Chinese) |
| [66] |
毛枚良, 江定武, 李锦, 等. 气体动理学统一算法的隐式方法研究[J]. 力学学报, 2015, 47(5): 822-829. MAO M L, JIANG D W, LI J, et al. Study on implicit implementation of the unified gas kinetic scheme[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(5): 822-829. (in Chinese) |
| [67] |
江定武.基于模型方程解析解的气体动理学算法研究[D].绵阳: 中国空气动力研究与发展中心, 2016. JIANG D W. Study of the gas kinetic scheme based on the analytic solution of model equations[D]. Mianyang: China Aerodynamics Research and Development Center, 2016. (in Chinese) |
| [68] |
谭爽, 李诗一, 李启兵, 等. 气体动理学格式与多尺度流动模拟[J]. 计算力学学报, 2017, 34(1): 88-94. TAN S, LI S Y, LI Q B, et al. Gas kinetic scheme and numerical simulation of multiscale flows[J]. Chinese Journal of Computational Mechanics, 2017, 34(1): 88-94. (in Chinese) |
| [69] |
刘沙.统一气体动理论格式研究[D].西安: 西北工业大学, 2015. LIU S. Unified gas-kinetic scheme[D]. Xi'an: Northwestern Polytechnical University, 2015. (in Chinese) |
| [70] |
刘沙, 王勇, 袁瑞峰, 等. 统一气体动理学方法研究进展[J]. 气体物理, 2019, 4(4): 1-13. LIU S, WANG Y, YUAN R F, et al. Advance in unified methods based on gas-kinetic theory[J]. Physics of Gases, 2019, 4(4): 1-13. (in Chinese) |
| [71] |
ZHU Y J, ZHONG C W, XU K. Implicit unified gas-kinetic scheme for steady state solutions in all flow regimes[J]. Journal of Computational Physics, 2016, 315: 16-38. |
| [72] |
ZHU Y, ZHONG C, XU K. Unified gas-kinetic scheme with multigrid convergence for rarefied flow study[J]. Physics of Fluids, 2017, 29(9): 096102. |
| [73] |
ZHU Y J, ZHONG C W, XU K. An implicit unified gas-kinetic scheme for unsteady flow in all Knudsen regimes[J]. Journal of Computational Physics, 2019, 386: 190-217. |
| [74] |
JIANG D. Study of the gas-kinetic scheme based on the analytic solution of model equations[D]. Ph. D. Thesis, China Aerodynamics Research and Development Center, 2016.
|
| [75] |
XU K, LIU C. A paradigm for modeling and computation of gas dynamics[EB/OL]. 2016: arXiv: 1608.00303[physics. flu-dyn]. https: //arxiv.org/abs/1608.00303
|
| [76] |
LIU C, ZHOU G, SHYY W, et al. Limitation principle for computational fluid dynamics[J]. Shock Waves, 2019, 29(8): 1083-1102. |
| [77] |
GUO Z, XU K, WANG R. Discrete unified gas kinetic scheme for all Knudsen number flows:Low-speed isothermal case[J]. Physical Review E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2013, 88: 033305. |
| [78] |
GUO Z L, WANG R J, XU K. Discrete unified gas kinetic scheme for all Knudsen number flows. Ⅱ. Thermal compressible case[J]. Physical Review E, 2015, 91(3): 033313. |
| [79] |
WANG P, TAO S, GUO Z L. A coupled discrete unified gas-kinetic scheme for Boussinesq flows[J]. Computers & Fluids, 2015, 120: 70-81. |
| [80] |
GUO Z L, XU K. Discrete unified gas kinetic scheme for multiscale heat transfer based on the phonon Boltzmann transport equation[J]. International Journal of Heat and Mass Transfer, 2016, 102: 944-958. |
| [81] |
ZHU L H, GUO Z L, XU K. Discrete unified gas kinetic scheme on unstructured meshes[J]. Computers & Fluids, 2016, 127: 211-225. |
| [82] |
王朋.不可压流动的离散统一气体动理学方法及应用[D].武汉: 华中科技大学, 2016. WANG P. Discrete unified gas-kinetic scheme for incompressible flows and its applications[D]. Wuhan: Huazhong University of Science and Technology, 2016. (in Chinese) |
| [83] |
张浩龙, 陶实, 郭照立. 离散统一气体动理学格式的浸入边界方法[J]. 工程热物理学报, 2016, 37(3): 539-544. ZHANG H L, TAO S, GUO Z L. An immersed boundary method based on the discrete unified gas kinetic scheme[J]. Journal of Engineering Thermophysics, 2016, 37(3): 539-544. (in Chinese) |
| [84] |
朱炼华.基于非结构网格离散统一气体动理学格式的热驱流动数值研究[D].武汉: 华中科技大学, 2018. ZHU L H. Numerical study of thermally driven flows using unstructured mesh discrete unified gas kinetic scheme[D]. Wuhan: Huazhong University of Science and Technology, 2018. (in Chinese) |
| [85] |
张月.两组分气体多尺度流动的离散统一动理学方法研究[D].武汉: 华中科技大学, 2019.
|
| [86] |
陈玺君, 郭照立. 表征体元尺度渗流的离散统一动理学格式[J]. 计算物理, 2019, 36(4): 386-394. CHEN X J, GUO Z L. Discrete unified gas kinetic scheme for porous media flow at representative elementary volume scale[J]. Chinese Journal of Computational Physics, 2019, 36(4): 386-394. (in Chinese) |
| [87] |
姚博, 张创, 郭照立. 考虑分子转动自由度的离散统一气体动理学格式[J]. 航空学报, 2019, 40(7): 63-75. YAO B, ZHANG C, GUO Z L. Discrete unified gas kinetic scheme for diatomic gas with rotational degrees of freedom[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(7): 63-75. (in Chinese) |
| [88] |
ZHU Y J, LIU C, ZHONG C W, et al. Unified gas-kinetic wave-particle methods Ⅱ: multiscale simulation on unstructured mesh[EB/OL]. Computational Physics, 2019: arXiv: 1903.11861. https: //arxiv.org/abs/1903.11861.
|
| [89] |
LI W M, LIU C, ZHU Y J, et al. Unified gas-kinetic wave-particle methods Ⅲ:Multiscale photon transport[J]. Journal of Computational Physics, 2020, 408: 109280. |
| [90] |
LIU C, ZHU Y J, XU K. Unified gas-kinetic wave-particle methods I:Continuum and rarefied gas flow[J]. Journal of Computational Physics, 2020, 401: 108977. |
| [91] |
LIU C, XU K. A unified gas kinetic scheme for continuum and rarefied flows V:multiscale and multi-component plasma transport[J]. Communications in Computational Physics, 2017, 22(5): 1175-1223. |
| [92] |
LIU C, WANG Z, XU K. A unified gas-kinetic scheme for continuum and rarefied flows VI:Dilute disperse gas-particle multiphase system[J]. Journal of Computational Physics, 2019, 386: 264-295. |
| [93] |
SUN W J, JIANG S, XU K. An asymptotic preserving unified gas kinetic scheme for gray radiative transfer equations[J]. Journal of Computational Physics, 2015, 285: 265-279. |
| [94] |
SUN W J, JIANG S, XU K, et al. An asymptotic preserving unified gas kinetic scheme for frequency-dependent radiative transfer equations[J]. Journal of Computational Physics, 2015, 302: 222-238. |
| [95] |
SUN W J, JIANG S, XU K. A multidimensional unified gas-kinetic scheme for radiative transfer equations on unstructured mesh[J]. Journal of Computational Physics, 2017, 351: 455-472. |
| [96] |
SUN W, JIANG S, XU K, et al. An Asymptotic preserving unified gas kinetic scheme for requency-dependent radiative transfer equations[J]. Journal of Coputational Physics, 2015, 302: 222-238. |
| [97] |
TAN S, SUN W J, WEI J X, et al. A parallel unified gas kinetic scheme for three-dimensional multi-group neutron transport[J]. Journal of Computational Physics, 2019, 391: 37-58. |
| [98] |
GUO Z L, LI J Q, XU K. On unified preserving properties of kinetic schemes[EB/OL]. 2019: arXiv: 1909.04923[math. NA]. https: //arxiv.org/abs/1909.04923
|
| [99] |
WANG R J. Unified gas-kinetic scheme for the study of non-equilibrium flows[D]. The Hong Kong University of Science and Technology Library, Ph. D., 2015. DOI: 10.14711/thesis-b1514837
|
| [100] |
XIAO T B, CAI Q D, XU K. A well-balanced unified gas-kinetic scheme for multiscale flow transport under gravitational field[J]. Journal of Computational Physics, 2017, 332: 475-491. |
| [101] |
LIU S, YU P B, XU K, et al. Unified gas-kinetic scheme for diatomic molecular simulations in all flow regimes[J]. Journal of Computational Physics, 2014, 259: 96-113. |
| [102] |
WANG R, XU K. Unified gas-kinetic scheme for multi-species non-equilibrium flow[J]. AIP Conference Proceedings, 2014. |
| [103] |
ZHU L H, GUO Z L. Application of discrete unified gas kinetic scheme to thermally induced nonequilibrium flows[J]. Computers & Fluids, 2019, 193: 103613. |
| [104] |
WANG P, SU W, ZHANG Y. Oscillatory rarefied gas flow inside a three dimensional rectangular cavity[J]. Physics of Fluids, 2018, 30(10): 102002. |
| [105] |
ZHANG C H, YANG K, GUO Z L. A discrete unified gas-kinetic scheme for immiscible two-phase flows[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1326-1336. |
| [106] |
CHEN T, CHÉRON V, GUO Z, et al. Simulation of immiscible two-phase flows based on a kinetic diffuse interface approach[C]//ICMF 2019, Windsor Barra: 2019.
|
| [107] |
HUO Y T, RAO Z H. The discrete unified gas kinetic scheme for solid-liquid phase change problem[J]. International Communications in Heat and Mass Transfer, 2018, 91: 187-195. |
| [108] |
TAO S, ZHANG H L, GUO Z L, et al. A combined immersed boundary and discrete unified gas kinetic scheme for particle-fluid flows[J]. Journal of Computational Physics, 2018, 375: 498-518. |
| [109] |
SU Z G, LI T F, YI H L. Simulation of electroconvection in a dielectric liquid by DUGKS[J]. Computers & Fluids, 2019. |
| [110] |
LUO X P, WANG C H, ZHANG Y, et al. Multiscale solutions of radiative heat transfer by the discrete unified gas kinetic scheme[J]. Physical Review E, 2018, 97(6): 063302. |
| [111] |
ZHANG C, GUO Z L, CHEN S Z. Unified implicit kinetic scheme for steady multiscale heat transfer based on the phonon Boltzmann transport equation[J]. Physical Review E, 2017, 96(6): 063311. |
| [112] |
ZHANG C, GUO Z L. Discrete unified gas kinetic scheme for multiscale heat transfer with arbitrary temperature difference[J]. International Journal of Heat and Mass Transfer, 2019, 134: 1127-1136. |
| [113] |
BO Y T, WANG P, GUO Z L, et al. DUGKS simulations of three-dimensional Taylor-Green vortex flow and turbulent channel flow[J]. Computers & Fluids, 2017, 155: 9-21. |
| [114] |
CAO G Y, SU H M, XU J X, et al. Implicit high-order gas kinetic scheme for turbulence simulation[J]. Aerospace Science and Technology, 2019, 92: 958-971. |
| [115] |
CAO G Y, PAN L, XU K. Three dimensional high-order gas-kinetic scheme for supersonic isotropic turbulence I:Criterion for direct numerical simulation[J]. Computers & Fluids, 2019, 192: 104273. |
| [116] |
CHEN S Z, XU K, LEE C, et al. A unified gas kinetic scheme with moving mesh and velocity space adaptation[J]. Journal of Computational Physics, 2012, 231(20): 6643-6664. |
| [117] |
YUAN R F, ZHONG C W. A conservative implicit scheme for steady state solutions of diatomic gas flow in all flow regimes[J]. Computer Physics Communications, 2020, 247: 106972. |
 2019, Vol. 38
2019, Vol. 38


