0 引言

飞机设计初级阶段必须考虑飞机的起降性能, 而增升系统的设计是影响起降性能的最主要因素，它不但决定着飞机结构设计、操纵系统设计、载荷的大小和飞机重量，并且对增升系统的气动效率有着直接的影响^[1]。对于大型运输机，无论是高亚声速飞机，还是声速或者是超声速飞机，增升系统性能都是影响设计成败的一个重要因素^[2]。因此可以采用一些流动控制技术来改善飞机增升系统的气动性能，从而可以缩短起飞-着陆距离，提高起降性能^[3]。

流动控制技术通常可分为被动流动控制和主动流动控制两种方式。主动流动控制^[4-7]在增升方面的应用吸引了大量学者的关注，通过对机翼下表面进行喷气控制就是一个很好的应用，可以改变机翼上下表面的压力分布，从而达到增加升力的目的。目前对喷气控制效果研究主要实验和数值模拟两种手段^[8-9]。为了能够准确模拟喷气的增升效果，首先要能够准确、细致地模拟带有喷气控制的流场^[10-11]。由于带有喷气控制的流场非常复杂且带有强烈的干扰，数值模拟面临很多困难，因此目前大部分研究是以风洞实验为主。随着计算机技术的快速发展，使得数值模拟翼型大迎角绕流成为了可能^[12-13]。在此基础上可以对翼型喷气流场进行数值模拟，研究喷气增升的机理。

国外Krathapalli等^[14]最先是在一个基于NACA0018翼型的有限翼展模型的下表面0.5倍弦长处开一口，通过风洞实验的方法测出，机翼升力系数和弦向截面表面压力分布随喷气速度的变化。国内北京空气动力研究所李锋等^[15]在NACA0018翼型的基础上通过求解N-S方程，格式为Beam-worming格式的改进型，研究了喷气口位置、压强和喷气速度对翼型升力系数的影响。但鲜有人对三维机翼和飞机的喷气控制进行数值模拟研究。

本文基于NACA0012翼型和机翼对飞机下表面喷流增升效应做了全方面的研究。目前，对于喷气控制广泛应用的限制主要集中在两个方面。第一是要能获得稳定的气源，第二是在机翼全展向开口会对机翼结构安全性产生重大影响^[16]。通过从发动机引气的方法可以解决气源问题，然而第二个问题至今都没有得到很好地解决。本文提出只在机翼展向的某一段开口进行局部喷气控制来避免由于全展向开口带来的结构安全问题，并对喷气控制进行了数值研究，找出最合理的局部喷气展向分布，研究了不同喷气速度对机翼气动特性的影响。

1 喷气控制数值模拟方法 1.1 控制方程和湍流模型

本文采用不可压缩的雷诺时均N-S方程组^[17]，可表示为：

$ 连续方程：\frac{\partial u_{i}}{\partial x_{i}}=0 $

(1)

动量方程：

$ \frac{\partial u_{i}}{\partial t}+u_{j} \frac{\partial u_{i}}{\partial x_{j}}=-\frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+v \frac{\partial^{2} u_{i}}{\partial x_{j} \partial x_{i}}+\frac{\partial \tau_{i j}}{\partial x_{j}} $

(2)

采用有限体积法进行空间离散，对流项采用二阶迎风格式，扩散项采用中心差分格式，压力速度耦合采用基于压力的Simple算法处理，离散代数方程组采用Gauss-Seidel代数法求解^[18]。湍流模型采用Spalart-Allmaras模型。SA模型是一个相对简单的一方程模型，求解了一个有关涡黏性的运输方程。该模型比较适合具有壁面限制的流动问题，对于有逆压梯度的边界层问题能够给出一个很好地计算结果, 常常用于空气动力学问题中，例如飞行器、翼型等绕流流场分析^[19]。

1.2 边界条件

翼型和机翼表面采用物面边界条件，满足无滑移、绝热以及物面法向梯度为零的条件。喷气口采用质量流量边界条件，质量流量定义为：$ \dot{m}=\rho s v, \rho$是喷气流体密度，与来流大气密度一致，s是喷气口面积，v是喷气流体速度。对于机翼，在对称面采用对称边界条件。流场中除了物面、对称边界和喷气口外，所有边界条件均采用压力远场边界条件。

1.3 物理模型及网格划分

二维模型采用NACA0012翼型，翼型弦长为1 m。计算网格采用C-H型网格，如图 1所示。计算域四周边界条件距翼型表面距离均为20倍弦长，喷气口附近加密后的网格总数是43 586。最内层网格高度为10^-5 m，y⁺≈1。

三维模型采用基于NACA0012翼型的有限翼展模型，如图 2所示。翼根弦向截面(z=0)是对称面，半翼展的参考面积是3 m，计算域半展长是12 m，所以翼稍(z=3 m)处于流场之中，这样就考虑了翼尖涡的影响。

2 二维模型数值模拟结果和分析 2.1 算法验证及增升机理研究

NACA0012是最简单的对称低速模型，几十年来人们对它进行了大量的风洞实验^[20-21]和数值模拟。本算例采用Gregory和O’Reilly的实验设置和实验数据，此实验是1970年在美国NPL(National Physical Laboratory)实验室4.0 m×2.7 m的低速风洞中进行的。实验来流速度为55 m/s，模型弦长为0.76 m，雷诺数为Re＝2.88×10⁶，实验设备和细节可参考文献[20]。Gregory公布的实验数据仅有三个不同迎角下吸力面的压力系数，升力和阻力系数采用文献[21]提供的数据。

计算条件与实验条件相同，气体从翼型下表面垂直于物面吹出，喷气口参数为：下表面弦向位置$\Delta {{\bar x}_j} = {x_j}{\rm{ / }}c{\rm{ = 0}}{\rm{.5}} $，宽度$\Delta \bar{x}_{j}=0.04 $，喷气速度${{\bar v}_j} = {v_j}/{v_\infty } = 1 $。表 1和表 2是不同迎角下升力系数和阻力系数的实验结果和数值模拟计算结果。从表中可以看到，本文采用的数值方法在升力系数上很接近实验结果，阻力系数与其相当，误差在可以接受的范围。

翼型上下表面压力分布也是验证数值模拟准确性的一个重要参数。图 3所示为上述条件下NACA0012翼型数值模拟和实验得到的上下表面压力分布。由图可以看出数值模拟得到的结果和实验结果相差不大，在可接受的范围之内。

接下来对喷气增升机理展开讨论。从流场分布上来看，图 4是喷口和翼型附近流线图，从图中可以看出在喷气口上游产生一个分离泡，喷气口后游产生一对反向旋转的旋涡。喷气口的存在导致翼型后缘驻点移动到翼型的压力面上。Kutta条件的改变必然引起翼型后缘上下表面出现压差。对涡的存在使得上表面流速增加，压力变小，相对应的下表面流速减小，压力变大。

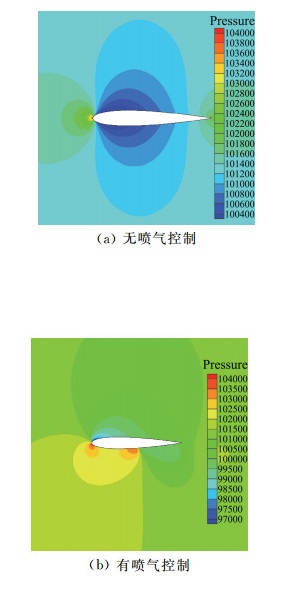
图 5是有无喷气控制时的翼型周围压力云图。从图中可以看出，没有喷气控制时翼型上下表面压力基本一样，采用喷气控制后翼型下表面的压力要大于翼型上表面的压力，对图 3中有喷气控制翼型的压强系数积分后有正升力(C_L=0.675 32)。

从外形上来看在翼型下表面进行喷气控制效果和在下表面加装Gurney襟翼类似，相当于增加了翼型的有效弯度，从而增加了绕翼型的典型环量，进而提高了翼型的升力系数。

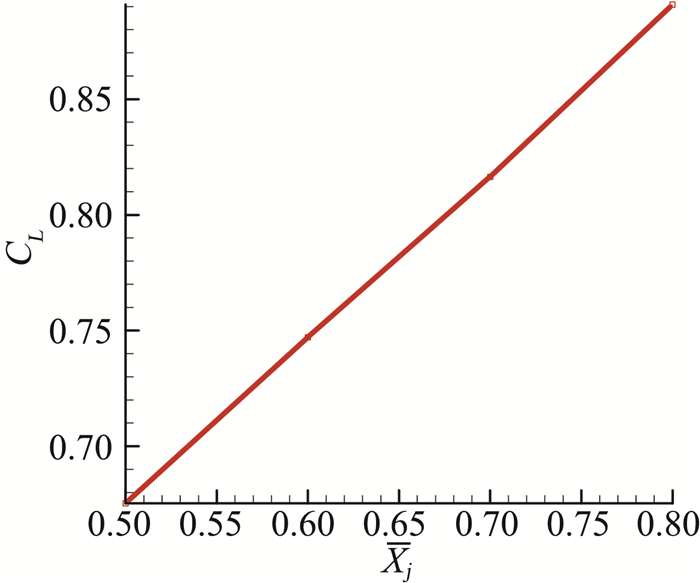
2.2 不同喷气位置的影响

基于上述研究，为了研究不同喷口弦向位置对增升效果的影响，只改变吹气口的弦向位置，其余计算条件和2.1节一样。得到的结果如图 6所示，图 7为不同喷气口位置时的C_p曲线图。

从图中可以看出在喷气控制作用下，下翼面喷气口前产生较大正压，喷气口后形成负压。并且随着喷气口后移，可以增大下翼面的正压区，较少负压区，这样有利于升力系数的增加。

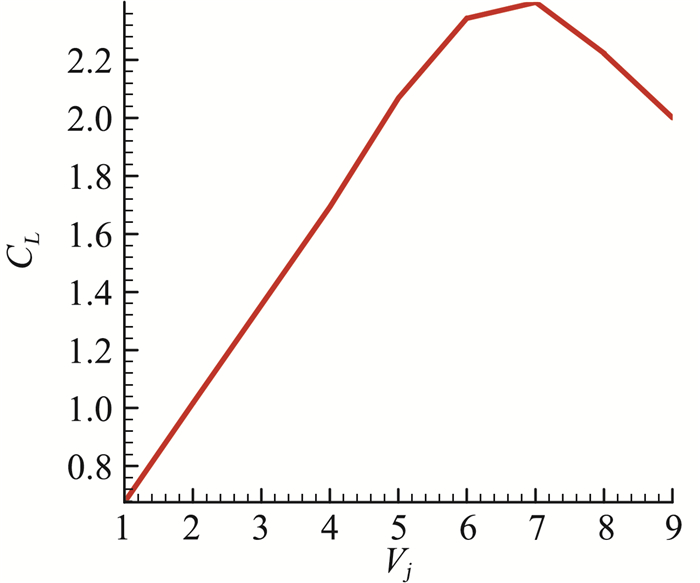
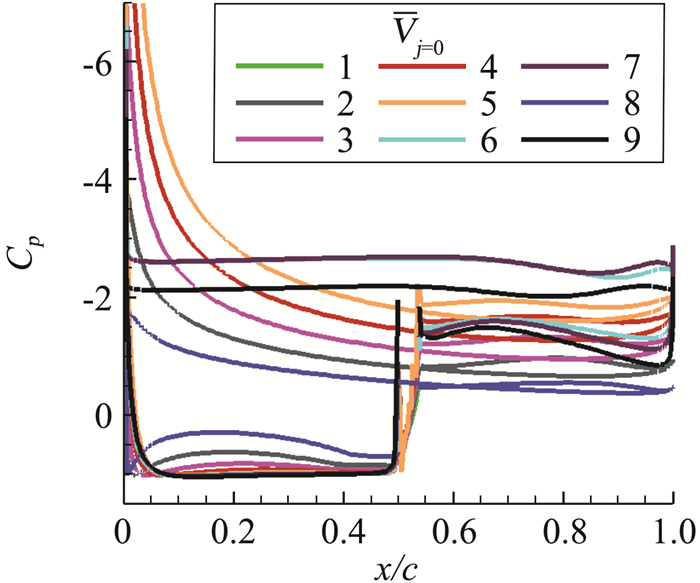
2.3 不同喷气速度的影响

为了研究不同喷气速度对增升效果的影响，只改变喷气速度，其他计算条件均不变。图 8和图 9是升力系数和压力系数随喷气速度变化曲线。

从图 8中可以看出当喷气速度小于某一个固定值时，随着喷气速度的增加升力系数也增加。但是超过这个值时，升力系数反而会减小。原因是当${{\bar v}_j} < 7 $时，随着喷气口速度的增加，喷气口前后上下表面压差都有所增加，而吹气口处压差变化不大，但是$ {{\bar v}_j} > 7$时，喷气口前后上下表面压差减少一点，而吹气口处压差变化剧烈，导致升力有所减小。

3 有限翼展模型数值模拟结果与分析

基于上述研究，本节将喷气口的弦向位置固定于0.7 c~0.74 c之间，研究不同展向位置和喷气速度的喷气控制对机翼气动特性的影响。当不采用喷气控制时，经数值模拟得到：C_L=-0.000016，C_D=0.00959。采用三维模型进行计算时得到的阻力系数稍微大于二维模型的计算结果，随着迎角增加，三维模型的升力系数会逐渐小于二维模型的计算结果。这是由于对于三维模型在下表面进行喷气控制时可以增加升力，但是湍流摩擦阻力和压差阻力也是增加的，而且三维模型会受到翼尖涡的影响，诱导阻力使得升力减小，升力越大诱导阻力也就越大。

将翼根到翼稍平均分为3段，每段的区域分别编号为1到3，每段展向长度均为1 m。本节按喷气口位置和喷气速度分为以下6种情况进行讨论：

① z=0-1 m，$ {{\bar v}_j}$ =1；② z=1-2 m，$ {{\bar v}_j}$=1；

③ z=2-3 m，$ {{\bar v}_j}$=1；④ z=0-3 m，$ {{\bar v}_j}$=1；

⑤ z=0-1 m，$ {{\bar v}_j}$=2；⑥ z=0-1 m，$ {{\bar v}_j}$=3。

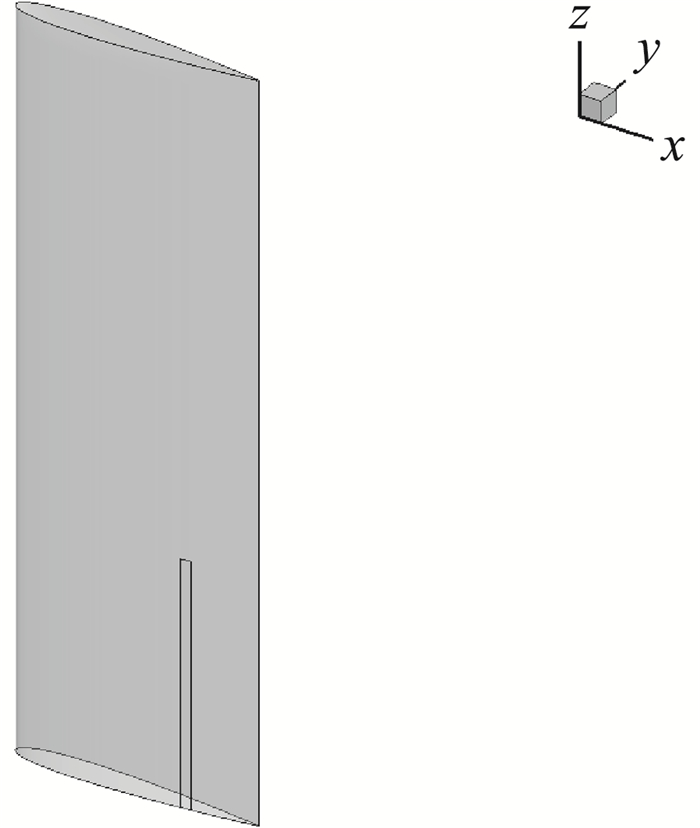
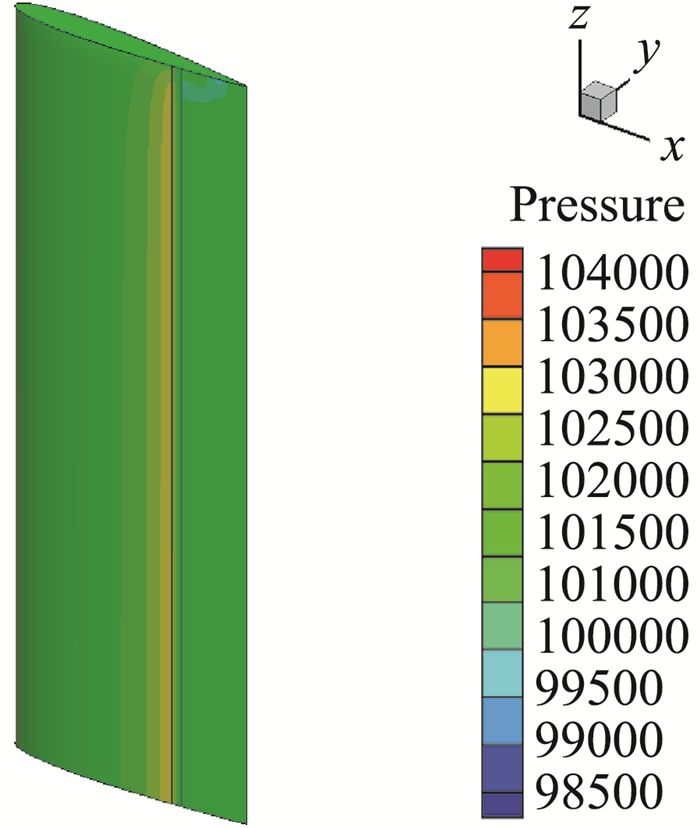
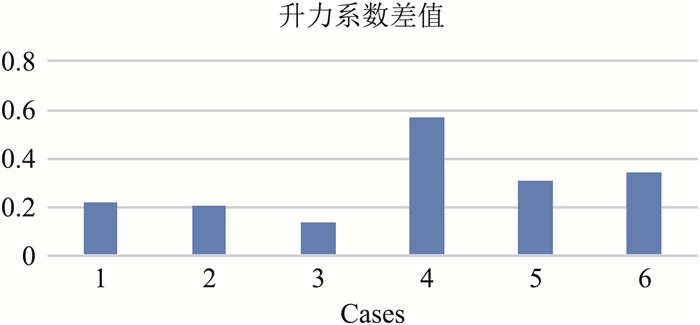
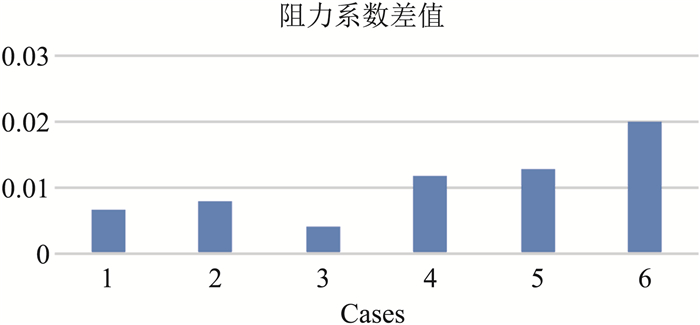
图 10为第①种情况下的物理模型图。图 11和图 12为没采用喷气控制和第④种情况下机翼下表面的压力云图。图 13和图 14为这6种情况下数值计算得到的的升力系数和阻力系数与不采用喷气控制时的差值。

从图 12可以明显看出采用喷气控制以后机翼的下表面压力会明显增大，这样使得机翼上下表面压力差增大，由此可以得出机翼的升力必然是变大的。从图 13和图 14中可以看到当整个展向都开口，$ {{\bar v}_j}$=3时可以获得最大的升力系数，此时的阻力系数值也是最大的。由此可见，在一定喷气速度范围内，随着喷气面积的增加，升力系数越大，阻力系数也越大。随着喷气速度增大，同样升力系数越大，阻力系数也越大。但是全翼展开口会对机翼结构的安全性产生一定的影响，一般会采用局部喷气控制。从图中可以看出，当$ {{\bar v}_j}$=1时，喷气口位于z=0-1m时，可以获得最大的升力系数(C_L=0.221)，但是阻力并不是最大值。相比之下升阻比也比不采用喷气控制也大很多。

下面构造量纲归一化的能量利用系数^[22]，具体形式如下:

$ E_{k}=\frac{A_{2} \Delta C_{D}+A_{1}}{A_{2} \Delta C_{L}} $

(3)

其中: $ A_{2}=\rho v^{2} s_{1}, s_{1}$是喷气口面积，表示单位时间喷气口吹出的气体的动量；${A_2} = \rho {v^2}{s_2}, {s_2} $是机翼参考面积，表示来流动量；$ {{A_2}\Delta {C_D}}$和${A_2}\Delta {C_L} $分别为阻力系数和升力系数增加所做的功。E_k的物理意义为单位时间内阻力系数增加值所做的功和将气流从初始速度加速到指定速度所做的功之和与升力系数增加值所做的功的比值。在相同控制效果下，E_k值越大，能量利用效率越低，表 3列出6种计算状态下的能量利用效率。

从表中可以看出当喷口展向分布固定于靠近翼根的1/3段时(z=0-1 m)，随着喷气速度的增大，E_k值也越大，则能量利用率越低，说明喷气速度越大喷出的气体能量越大, 使得增升效果越好，但是也会导致控制效率变低。若固定喷气速度为一个定值时($ {{\bar v}_j}$=1)，随着展向分布的扩大，E_k值越小，则能量利用率越高，说明扩大喷口面积虽然消耗更多的气体能量但是增升效果和控制效率会变得更好。但是全翼展开口会对机翼的整体结构来很大的不利影响，因此在实际应用时需要在结构安全性与气动优化之间做适当的协调。本文提出一种局部喷气控制的方法，只在机翼展向的一部分进行喷气控制，从上述结果可以看出当机翼沿展向平均分为三段时，相同喷气速度下当z=0-1 m时增升效果和能量利用率都是最好的。

4 DLRF6翼身组合体喷气增升效果

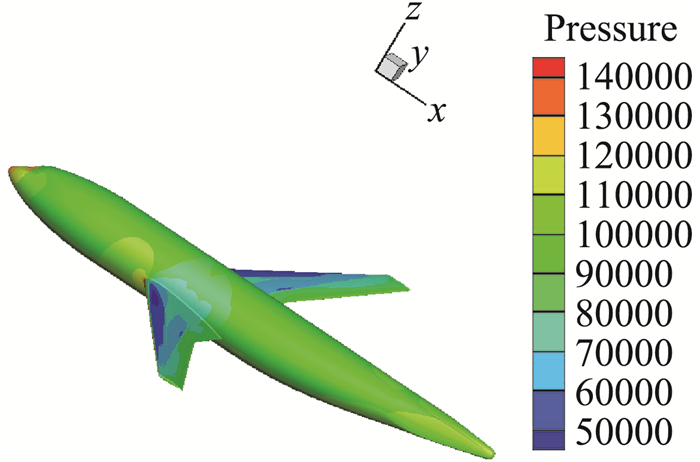
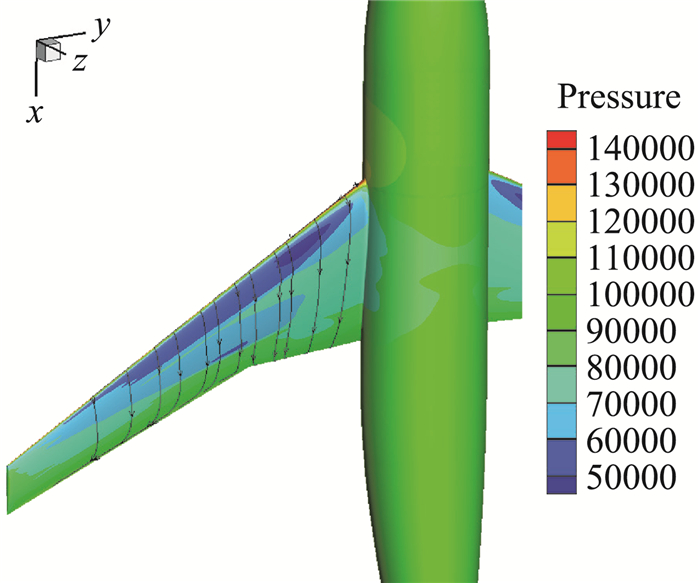
DLRF6翼身组合体是是一个经典的三维飞机模型，在国际上多次被用作标准算例。基于上述翼型和机翼的下表面喷气增升效应研究，将这种流动控制形式应用到DLRF6翼身组合体上，看是否也有相应的增升效果。来流条件：Ma=0.2，Re=5×10⁵。将喷口的弦向位置固定于0.7c~0.74c之间，在距翼根前1/3段进行喷气控制。只改变喷气速度大小$ {{\bar v}_j}$=0.25, 0.5, 1，研究不同迎角下的喷气控制效果。图 15和图 16是$ {{\bar v}_j}$=0.25喷气控制后的整机和翼身组合体表面压力分布。从图中明显可以看到上面存在一块低压区，机翼表面流线平滑向后缘流动。

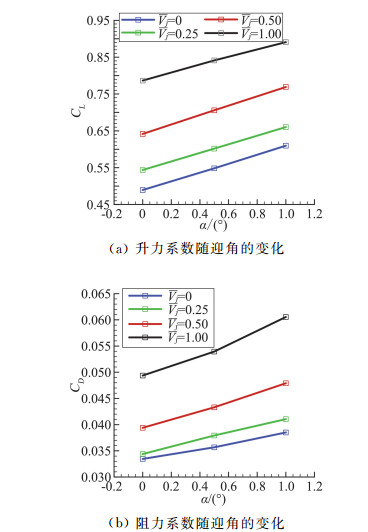
图 17是有无喷气控制作用时DLRF6翼身组合体气动力系数随迎角的变化。从图中可以看出迎角固定的情况下，升力系数和阻力系数都随着喷气速度增加，喷气速度固定的情况下，在一定范围内随着迎角增大，升力系数和阻力系数也增大，增加趋势大致相同。当喷气速度$ {{\bar v}_j}$=1时升力系数值最大可以增加0.298，整体变化和二维翼型模拟的结果趋势是相同的，由此可见增升效果还是非常明显的。如果此项加0.298，整体变化和二维翼型模拟的结果趋势是相同的，由此可见增升效果还是非常明显的。如果此项技术能够应用到飞机上，必定会对飞机的机动性能以及垂直起降性能有着明显的提升。

5 结论

本文以NACA0012翼型为基础，以增加升力为目的，对翼型和有限翼展模型下表面进行喷气控制研究, 得到以下主要结论：

1) 采用适当的设置，能够较好地模拟出翼型的气动特性，该方法对于工程应用的要求是满足的；

2) 在NACA0012翼型下表面喷气控制可以改变翼型上下表面压力分布，使得翼型升力系数增加，控制效果和喷气速度、喷气口宽度以及位置都有一定的关系, 在失速迎角之前随着迎角增大增升效果大致相同，最大升力系数明显增大许多；

3) 在三维有限翼展模型下表面进行喷气控制同样可以改变机翼上下表面的压力分布，使得机翼的升力增加，当$ {{\bar v}_j}$=1时，升力系数最高可达0.3095，升阻比也比不采用喷气控制时增加很多；

4) 随着喷气速度的增加，能量利用率在减小。当机翼沿展向平均分为三段时，喷气口应选在距离翼根1/3处(z=0-1 m)，此时可以获得最好的控制效果。