2. 南京理工大学 瞬态物理重点实验室, 江苏 南京 210094;
3. 上海航天技术研究院, 上海 201109
2. Key Laboratory of Transient Physics, Nanjing University of Science&Technology, Nanjing 210094, China;
3. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China
未来战争向空天一体化方向发展,如超声速远程制导火箭弹[1],其飞行高度大于60 km或平流层飞艇,以及高空低速太阳能无人机等,飞行高度约为20 km~30 km[2]。由于高空大气密度低、运动黏性系数大,飞行器工作环境处于低雷诺数范围,机翼或螺旋桨表面会出现层流分离[3]。当雷诺数降低时,流体黏性效应变强,边界层厚度变厚,脱落涡变大[4]。雷诺数在104~105时,光滑机翼气动性能急剧变坏,升力系数下降,阻力系数快速增大,稳定性和操纵性能都变差[5]。叶建等[6]采用高精度有限差分格式,对来流马赫数Ma=0.5、雷诺数Re=1×104、迎角α=3°下的二维翼型流动进行了直接数值模拟,发现在翼型上表面流动在强逆压梯度下发生分离,形成了包含驻留涡、脱落涡和二次涡的涡系结构,其尺度随时间不断变化,具有强烈的非定常性。王龙等[7]应用格子玻尔兹曼大涡模拟方法,对来流马赫数Ma=0.1、雷诺数Re=1×105、零迎角下的NACA0012翼型绕流进行了计算,结果表明在尾翼处形成卡门涡街,速度场不再对称,升力产生了振荡。因此,提高低雷诺数下翼型的升阻比以及减小飞行过程中流动扰动量尤为重要。
目前流动控制技术中,表面吹吸控制相对成熟且十分有效。LEBEAU等[8]对雷诺数Re=5×105,迎角α=18°下的NACA0012翼型进行了较为系统的吹吸控制,证明了对于吸气控制,在翼型前缘控制效果最佳,且随着吸气的增加,升力增大、阻力减小;对于吹气控制,在翼型后缘控制效果最佳,使得阻力减小,升力增大。然而,在较低雷诺数下,翼型的表面吹吸射流研究却少之又少。
李峰等[9-10]数值模拟了来流马赫数Ma=0.3、雷诺数Re=5×104下的大迎角翼型表面吸气对分离流动的控制及其增升机制,吸气孔位置在0.45c和0.80c。结果显示吸气可以将翼型头部非稳态涡稳定在翼面上,起到驻涡作用而提供涡升力,吸气孔位置在翼型中部附近时,增升效果较好。刘沛清[3]对Re=2×105、迎角α=0°下的Eppler387翼型表面层流分离泡的吹吸控制进行了数值模拟,并证明吹吸气可有效抑制低雷诺数下层流分离泡的发展,显著提高雷诺数下的翼型升阻比。吸气控制比吹气控制对层流分离泡的抑制作用更明显,且吸气位置在分离泡中部较佳。Wahidi等[11]在LA2574a翼型上表面设计了分布式抽吸结构,实验证明了在雷诺数Re=2.5×105下,分布式抽吸控制可有效控制分离泡大小,抑制流动分离。Zhao等[12]对雷诺数Re=1.17×106、迎角α=4°下E387翼型采用吸气控制,并采用多岛遗传算法,优化单孔吸气阻力系数最大可减小8.3%,同时证明了增多吸气孔数,可达到更好的减阻效果。
然而,现阶段吹吸气控制研究主要集中在雷诺数大于105的翼型绕流,缺乏对较低雷诺数下吹吸气射流对翼型绕流性能影响的对比分析。故本文在前人研究的基础上,采用基于大涡模拟算法的自编软件,在较低雷诺数下,射流孔位置在0.05c~0.95c、吹吸速度在0.1~0.5条件下研究吹吸气对二维NACA0012翼型的气动性能影响进行研究,为低雷诺数下翼型吹吸气得到最佳控制效果提供重要参考。
1 数值方法与模型 1.1 数值方法在笛卡尔坐标系下,基于Favre过滤的大涡模拟方程可表示为:
| $ {\frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_j}} \right)}}{{\partial {x_j}}} = 0} $ | (1) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_i}{{\tilde u}_j}} \right)}}{{\partial {x_j}}} = }\\ {\quad - \frac{{\partial \left( {\bar P{\delta _{ij}}} \right)}}{{\partial {x_i}}} + \frac{1}{{Re}}\frac{{\partial \left( {{\tau _{ij}}SGS + {{\bar \tau }_{ij}}} \right)}}{{\partial {x_j}}}} \end{array} $ | (2) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial (\bar \rho \tilde E)}}{{\partial t}} + \frac{{\partial (\bar \rho \tilde E + \bar P){{\tilde u}_j}}}{{\partial {x_j}}} = \frac{1}{{Re}}\frac{{\partial \left[ {{{\tilde u}_i}\left( {\tau _{ij}^{SGS} + {{\bar \tau }_{ij}}} \right)} \right]}}{{\partial {x_j}}} - }\\ {\frac{1}{{{\mathop{Re}\nolimits} (\gamma - 1)Ma_\infty ^2}}\frac{\partial }{{\partial {x_j}}}\left[ {{{\bar q}_j} + Q_j^{SGS}} \right]} \end{array} $ | (3) |
亚格子应力张量和亚格子热通量分别为:
| $ \tau_{i j}^{S G S}-\frac{1}{3} \tau_{k k}^{S G S} \delta_{i j}=2 \mu^{S G S} \widetilde{S}_{i j}-\frac{2}{3} \mu^{S G S} \widetilde{S}_{k k} \delta_{i j} $ | (4) |
| $ \begin{aligned} Q_{j}^{S G S} &=-\frac{\mu^{S G S} C_{p}}{P r_{T}} \frac{\partial \widetilde{T}}{\partial x_{j}} \\ &=-\frac{\mu^{S G S}}{(\gamma-1) M a^{2}_{\infty} R e_{\infty} P r_{T}} \frac{\partial \widetilde{T}}{\partial x_{j}} \end{aligned} $ | (5) |
其中,PrL和PrT分别为层流普朗特数和湍流普朗特数,γ为流体的比热比:
| $ P r_{L}=0.72, {Pr}_{T}=0.90, \gamma=1.4 $ |
亚格子模型采用WALE模型。控制方程采用有限元体积法进行离散。对流项采用AUSM+-up格式进行离散。黏性通量采用二阶中心差分格式离散。时间项则采用具有二阶精度的双时间步长(LU-SGS)全隐式算法。
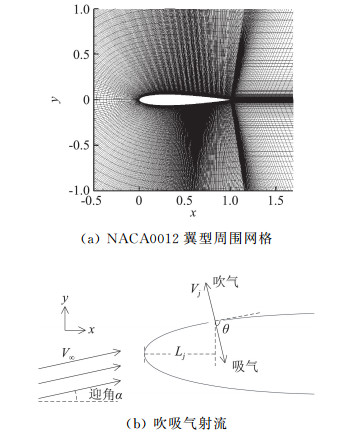
1.2 仿真模型本文选取Re=104,α=6°,Ma=0.2的低雷诺数流动下的NACA0012翼型为计算模型。采用椭圆方程生成“C”型网格,以翼型弦长c=1为参考长度,计算域左边界距离翼型前缘6.5c,上下边界距翼型弦线7.5c,右边界距翼型尾缘9c,为捕捉到翼型周围流场的涡系结构,采用渐变网格,靠近壁面网格加密,远离壁面后网格间距逐渐增大,在壁面第一层网格间距为10-4c,且满足y+ < 1.0。为了精确模拟抽吸控制对流场的影响,对射流孔周围网格进行了加密,如图 1(a)所示。当吸气孔宽度大于2.5%c时,翼型升力不再显著增加[13],故选取射流孔宽度为2.5%c。经网格收敛检测后,选取网格节点数为830×100。在文献[14, 15]中,均对本文数值计算方法进行了详细验证,证明了在低雷诺数下,该二维数值模拟方法具有较好的可靠性和准确性。
|
图 1 计算模型示意图 Fig.1 Schematic diagram of calculation model |
算例中,射流速度表达式为:
| $ u=\frac{V_{j}}{V_{\infty}} \cos \theta, \quad v=\frac{V_{j}}{V_{\infty}} \sin \theta $ | (6) |
其中,u为射流孔表面切向速度分量,v为垂直于射流孔的速度分量,Vj为射流速度,θ为射流孔表面与射流方向之间的夹角。θ为正代表吹气射流,θ为负代表吸气射流,本文仅考虑θ=±90°两种垂直射流情况。计算模型中,NACA0012翼型水平放置,坐标系x轴为翼型头部至尾部方向,y轴向上为正。来流与坐标系x轴之间的夹角即为翼型绕流迎角α,详细参见图 1(b)。
2 结果与分析 2.1 吸气射流为易于理解吹吸气射流对翼型附近流场的影响,引入边界层特征参数位移厚度δ*(定义为边界层上的主流被向外挤出的距离[16])和压力系数Cp,其表达式如下:
| $ \delta^{*}=\int_{0}^{\delta}\left(1-\frac{u_{x}(y)}{U}\right) \mathrm{d} y, \quad C_{p}=\frac{p-p_{\infty}}{\frac{1}{2} \rho_{\infty} U_{\infty}^{2}} $ | (7) |
其中,δ为边界层厚度,U为边界层外缘的势流速度,ux(y)为垂直距离翼面y处的切向速度分量。本文计算中,将翼型上表面流动速度达到0.995U时的边界层称为边界层外缘,边界层外缘到翼面的垂直距离为边界层厚度。
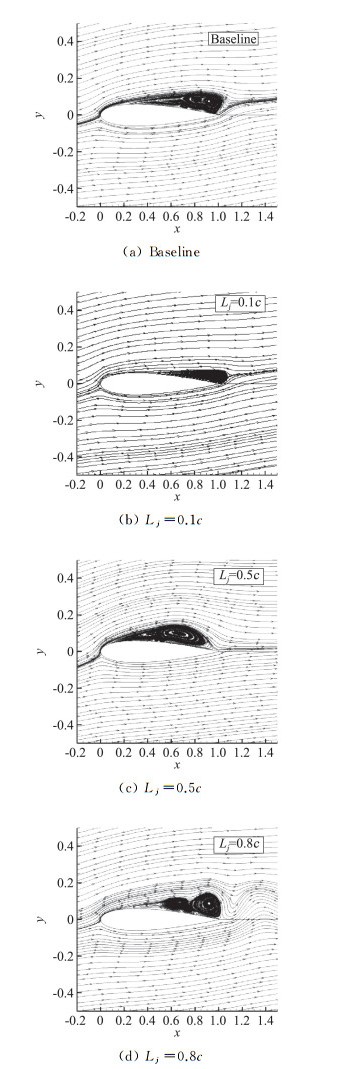
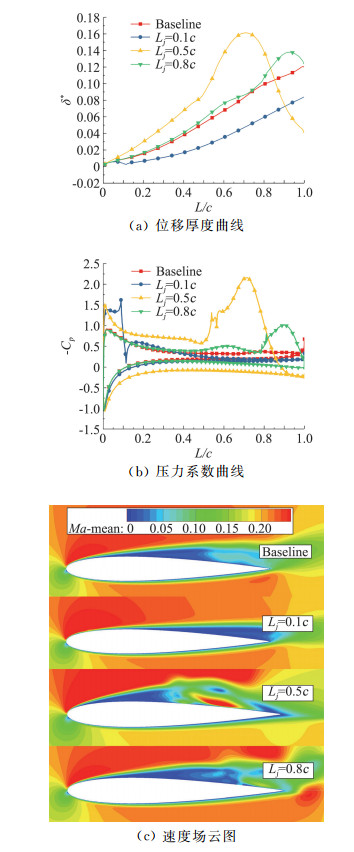
图 2、图 3为吸气Vj/V∞=0.2,作用位置在0.1c、0.5c、0.8c以及基准状态下,NACA0012翼型周围时均流场的流线图、位移厚度、翼型表面压力系数曲线以及速度场云图。相对于基准状态,当Lj=0.1c,翼型位移厚度减小(图 3(a)),表明该区域的质量流量损失减小,边界层内的低能流体被吸除,射流孔上游区域流速增大(图 3(c)), 翼型表面压力系数减小,但射流孔下游区流动速度明显降低,使得翼型表面压力系数增大,翼型抗逆压能力增强,分离区域明显得到抑制,如图 2(b)中的时均绕流流线图(流线图指在具体显示流动分离区域的大小)。当Lj=0.5c时,翼型背风面后半部存在高速区域,翼型背风面后半部的压力系数明显减小。在翼型上游处,虽然低能流体区域增大,但其速度大小相比较而言要稍稍增大。在翼型头部区域,流速增大较为明显,使得该条件下翼型上游区域的表面压力系数均减小,导致翼型抗逆压能力降低,流体分离区较大(图 2(c))。另外,翼型上表面几乎处于完全分离状态,涡脱落幅度较大,进而影响到翼型下表面的速度流场,比较发现,翼型下表面处流速比其他状态较低,翼型表面压力系数增大,使得翼型上下表面压力差增大,翼型升力急剧增加,如图 3所示。当Lj=0.8c时,在翼型后半缘处,位移厚度稍微增大(图 3(a)),射流孔附近低能流体被吸除,使得其流速增大,翼型表面压力系数减小,使得翼型抗逆压能力降低,流体分离区域波动大于基准状态。
|
图 2 不同吸气位置以及Vj/V∞=0.2下,NACA0012翼型时均流场流线图 Fig.2 Streamline of airfoil NACA0012 with different suction locations and Vj/V∞=0.2 |
|
图 3 不同吸气位置以及Vj/V∞=0.2下,NACA0012翼型周围时均流场参数变化 Fig.3 Flow field parameters of airfoil NACA0012 with different suction locations and Vj/V∞=0.2 |
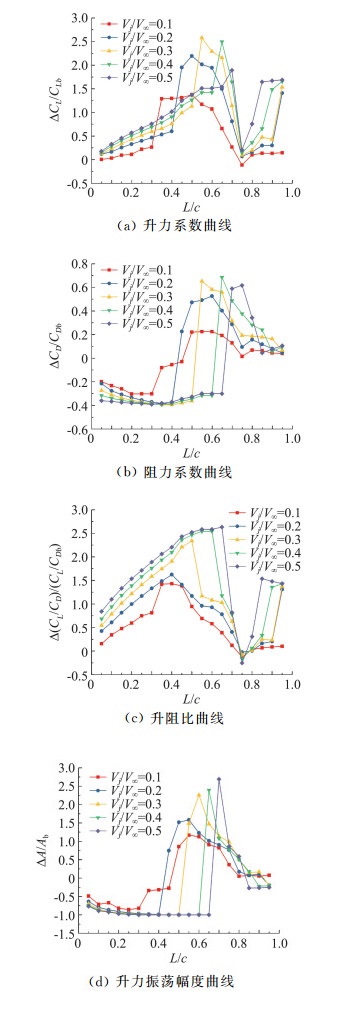
图 4比较了在吸气0.1≤Vj/V∞≤0.5、射流位置0.05c≤Lj≤0.95c下,翼型的时均升阻力变化情况(无射流控制下,翼型升力系数CLb=0.285,阻力系数CDb=0.080,升力系数振荡幅值Ab=0.370,流动分离点在0.2c~0.3c之间)。其中,
| $ \begin{array}{l} \Delta C_{D} / C_{D b}=\left(C_{D}-C_{D b}\right) / C_{D b} \\ \Delta C_{L} / C_{L b}=\left(C_{L}-C_{L b}\right) / C_{L b} \\ \frac{\Delta\left(C_{L} / C_{D}\right)}{\left(C_{L} / C_{D}\right)_{b}}=\left(C_{L} / C_{D}-C_{L b} / C_{D b}\right) /\left(C_{L b} / C_{D b}\right) \\ \Delta A / A_{b}=\left(A-A_{b}\right) / A_{b} \end{array} $ | (8) |
|
图 4 0.05c≤Lj≤0.95c、0.1≤Vj/V∞≤0.5吸气作用下,NACA0012翼型气动特性 Fig.4 The aerodynamic characteristics of airfoil NACA0012 with suction control, 0.05c≤Lj≤0.95c、0.1≤Vj/V∞≤0.5 |
可知,在翼型前部施加吸气控制,翼型的升力系数增加,阻力系数减小,该效果随着吸气比的增大而增大,表明分离流动逐渐得到抑制,流动分离点后移,例如在Lj=0.1c,Vj/V∞=0.1时,流动分离点为0.38c,当Vj/V∞=0.5时,流动分离点后移至0.52c。而且,其最佳吸气位置随着吸气的增大而逐渐后移,当Vj/V∞=0.2时,其最佳吸气位置Lj=0.4c,此时升阻比增大155%,升力的波动幅度降低100%,即分离流动得到完全控制,翼型气动扰动被控制;而当Vj/V∞=0.5时,其最佳吸气位置后移到Lj=0.65c,升阻比增大到261%且无分离流动,控制效果最好。
在翼型中部施加吸气时,因翼型上下表面压差增大,升力系数急剧增加,且该状态下翼型上表面流动几乎完全分离,阻力系数也随之增大,其升阻比反而降低。另外,升力波动幅值因脱落涡的影响而增大,导致气动扰动明显增大,翼型的气动性能变差。当射流位置处于0.75c时,射流对翼型下表面压力系数的影响可忽略,使其升力系数急剧降低(图 4a)。且从图 2可知,翼型尾部吸气使流动分离区域减小,脱落涡尺度减小,导致翼型表面脱落处压力振幅变小,其升力振动幅值降低,气动性能相对中部吸气得到改善,当射流位置进一步后移时,其升力波动和阻力系数逐渐降低,说明翼型上表面分离现象逐渐得到抑制。
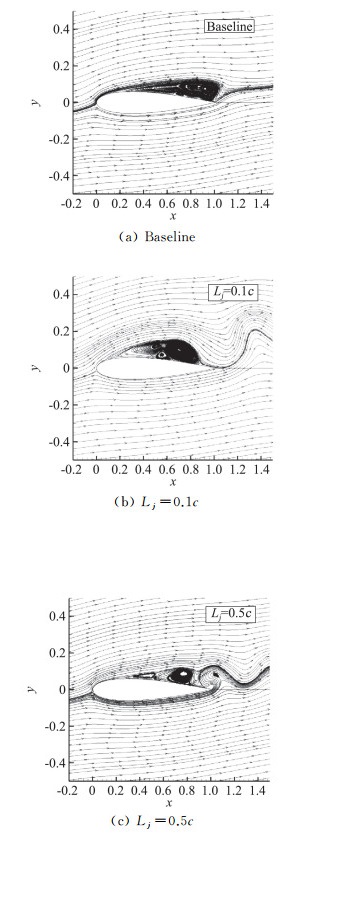
2.2 吹气射流图 5、图 6为吹气Vj/V∞=0.2,作用位置在0.1c、0.5c、0.8c以及基准状态下,NACA0012翼型周围时均流场的流线图、位移厚度、翼型表面压力系数曲线以及速度场云图。当Lj=0.1c,低能流体被注入到边界层内,位移厚度增大(图 6(a))。但在图 6(c)中发现,射流孔上游区域流速相对基准状态增加,使得翼型上表面压力系数在0~0.1c之间增大(图 6b),而在射流孔下游区域, 0.12c~0.83c,因低能流体的注入,使得翼型上表面压力系数减小,翼型抗逆压能力明显减弱,流动分离区域增大,如图 5(a)。
|
图 5 不同吹气位置以及Vj/V∞=0.2下,NACA0012翼型时均流场流线图 Fig.5 Streamline of airfoil NACA0012 with different blowing locations and Vj/V∞=0.2 |
|
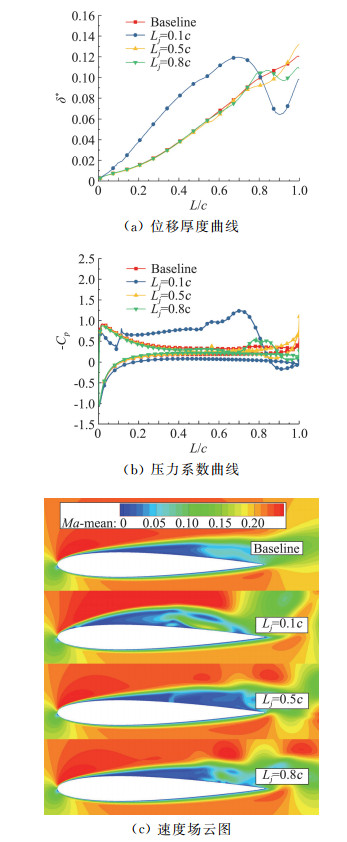
图 6 不同吹气位置以及Vj/V∞=0.2下,NACA0012翼型周围时均流场参数变化 Fig.6 Flow field parameters of airfoil NACA0012 with different suction locations and Vj/V∞=0.2 |
当Lj=0.5c或0.8c,从速度场和位移厚度曲线上看,吹气射流对翼型前缘影响较小,位移厚度与上下表面压力系数与基准状态基本相同,在上表面中后部,位移厚度减小,表明边界层内低能流体减小,流速增加(图 6(c)),使上表面压力系数增大,翼型上下表面压差减小,升力系数降低。在翼型尾部处,由于涡脱落的影响,位移厚度和压力系数出现不规则变化,但从位移厚度波动的幅度可以看出,前缘吹气射流下的脱落涡远大于中后部吹气(图 5),翼型气动参数扰动较大。
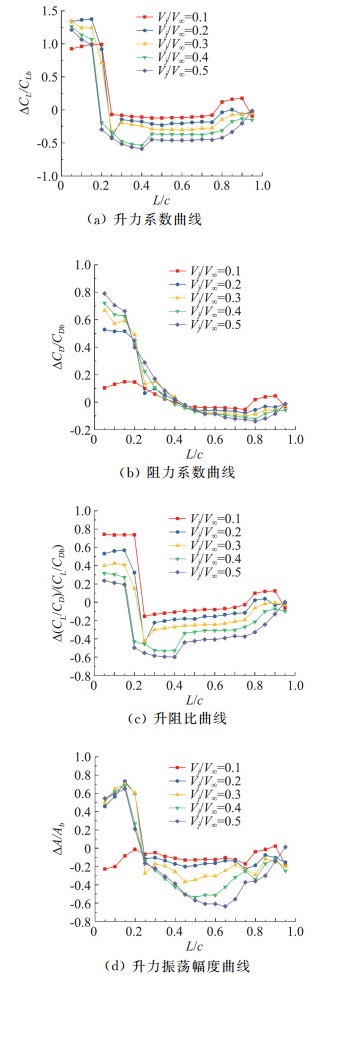
图 7比较了在吹气0.1≤Vj/V∞≤0.5、射流位置0.05c≤Lj≤0.95c下,翼型的时均升阻力变化情况。在流动分离点前施加吹气射流时,翼型的升力系数、阻力系数以及升阻比均增大。当吹气增大时,阻力系数的增长幅度要大于升力系数,翼型最大升阻比出现在较小吹气下,且较大的吹气使得升力振荡的幅度明显增大,即翼型飞行时,受到的气动扰动量会增加。例如,当Lj=0.1c,Vj/V∞=0.1时,翼型升阻比增大73%,升力波动幅度减小21%;当Vj/V∞=0.5时,翼型升阻比增大23%,而升力波动幅值增大59%。
|
图 7 0.05c≤Lj≤0.95c、0.1≤Vj/V∞≤0.5吹气作用下,NACA0012翼型气动特性 Fig.7 The aerodynamic characteristics of airfoil NACA0012 with blowing control, 0.05c≤Lj≤0.95c、0.1≤Vj/V∞≤0.5 |
在流动分离点后进行吹气射流时,翼型的升力系数、阻力系数以及升阻比明显下降,该效果随着吹气比的增大而增大。但值得注意的是,不同于翼型前部吹气,中后部吹气有利于抑制翼型飞行时的气动扰动量,且吹气越大,效果越明显。随着吹气位置移到翼型尾部时,升力系数、阻力系数以及升阻比都稍微增大,在较小的吹气下,均大于基准状态下的翼型气动性能,且其所受到的气动扰动量小于基准状态。
3 结论本文中采用大涡模拟方法,对低雷诺数,小迎角下的NACA0012翼型上表面吹吸气射流进行了数值模拟,从升阻力特性、上表面边界层位移厚度以及翼型压力系数等方面讨论了吹吸气位置以及速度变化对翼型气动性能的影响,从改善翼型气动系数以及抑制飞行受到的扰动上看,吸气射流要远远优于吹气射流。
对于同一射流速度,吸气射流存在最佳抽吸位置,可有效增升减阻,同时抑制飞行过程中受到的扰动量。如当Vj/V∞=0.2时,其最佳吸气位置Lj=0.4c,此时升阻比增大155%,升力的波动幅度降低100%,即分离流动得到完全控制,翼型气动扰动量被消除。当吸气速度增大,最佳吸气位置逐渐后移,如当Vj/V∞=0.5时,其最佳吸气位置Lj=0.65c。但若将吸气设置在其最佳位置后,吸气射流虽然吸收了射流孔附近的边界层内低能流体,但流动分离并没有消除,流场特性没有得到改善。
而吹气射流对翼型的气动性能影响较差,升阻比特性与其受到的气动扰动量之间相互冲突,须牺牲其中一个来满足特定要求,如在翼型前缘吹气,翼型升阻比明显增大,但此时翼型上表面几乎完全分离,涡脱落现象加剧,扰动量增加;在翼型中后缘吹气,翼型升阻比降低,但气动扰动量会降低。
| [1] |
王军波, 张军挪, 刘丽荣, 等. 雷诺数对高空飞行弹外弹道影响的规律研究[J]. 弹箭与制导学报, 2003(4): 150-152. WANG J B, ZHANG J N, LIU L R, et al. The study on the influence of Reynolds Number on the flight trajectory for projectile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003(4): 150-152. DOI:10.15892/j.cnki.djzdxb.2003.s4.013 (in Chinese) |
| [2] |
杜绵银, 陈培, 李光佳, 等. 临近空间低速飞行器螺旋桨技术[J]. 飞航导弹, 2011(7): 15-19. DU M Y, CHEN P, LI G J, et al. Propeller technology in the low-speed near-space maneuvering vehicles[J]. Aerodynamic Missile Journal, 2011(7): 15-19. DOI:10.16338/j.issn.1009-1319.2011.07.008 (in Chinese) |
| [3] |
刘沛清, 马利川, 屈秋林, 等. 低雷诺数下翼型层流分离泡及吹吸气控制数值研究[J]. 空气动力学学报, 2013, 31(4): 518-524. LIU P Q, MA L C, QU Q L, et al. Numerical investigation of the laminar separation bubble control by blowing/suction on an airfoil at low Re number[J]. Acta Aerodynamic Sinica, 2013, 31(4): 518-524. (in Chinese) |
| [4] |
LIN J C M, PAULEY L L. Low-Reynolds-number separation on an airfoil[J]. AIAA Journal, 1996, 34(8): 1570-1577. DOI:10.2514/3.13273 |
| [5] |
李峰, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257-268. LI F, BAI P, SHI W, et al. Low Reynolds number aerodynamics of micro air vehicles[J]. Advances in Mechanics, 2007, 37(2): 257-268. DOI:10.3321/j.issn:1000-0992.2007.02.009 (in Chinese) |
| [6] |
叶建, 邹正平, 陆利蓬, 等. 低雷诺数下翼型前缘流动分离机制的研究[J]. 北京航空航天大学学报, 2004, 30(8): 693-697. YE J, ZOU Z P, LU L P, et al. Investigation of separation mechnism for airfoil leading edge flow at low Reynolds number[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(8): 693-697. DOI:10.13700/j.bh.1001-5965.2004.08.001 (in Chinese) |
| [7] |
王龙, 宋文萍. 翼型绕流的LBM大涡模拟研究[J]. 西北工业大学学报, 2010, 28(3): 448-452. WANG L, SONG W P. Applying lattice Boltzmann method (LBM) to large eddy simulation (LES) of flow around airfoil at low Reynolds number[J]. Journal of Northwestern Polytechnical University, 2010, 28(3): 448-452. DOI:10.3969/j.issn.1000-2758.2010.03.026 (in Chinese) |
| [8] |
LEBEAU R P, HUANG L, HUANG P G, et al. Numerical study of blowing and suction control mechanism on NACA0012 airfoil[J]. Jounal of Airfoil, 2004, 41(5): 1005-1013. DOI:10.2514/1.2255 |
| [9] |
李峰, 王翼云, 崔尔杰. 表面吸气方法控制分离的数值模拟[J]. 空气动力学学报, 1994, 12(1): 36-42. LI F, WANG Y Y, CUI E J. Numerical simulation of separation control by suction[J]. Acta Aerodynamic Sinica, 1994, 12(1): 36-42. (in Chinese) |
| [10] |
李峰, 王翼云, 崔尔杰. 提高飞行器升力的若干方法研究[J]. 空气动力学学报, 1994, 12(3): 237-242. LI F, WANG Y Y, CUI E J. The investigation on some methods for increase lift force[J]. Acta Aerodynamic Sinica, 1994, 12(3): 237-242. (in Chinese) |
| [11] |
WAHIDI R, BRIDGES D. Effects of distributed suction on an airfoil at low Reynolds number[R]. AIAA 2010-4714. doi: 10.2514/1.J050913
|
| [12] |
ZHAO D J, WANG Y K, CAO W W, et al. Optimization of suction control on an airfoil using Multi-island genetic algorithm[J]. Procedia Engineering, 2015, 99: 696-702. DOI:10.1016/j.proeng.2014.12.591 |
| [13] |
DANNENBERG R E, WEIBERG J A. Section characteristics of a 10.5-percent thick airfoil with area suction as affected by chordwise distribution of permeability[R]. NASA TN-2847, 1952.
|
| [14] |
张旺龙.低雷诺数下附面层分离的抽吸控制及优化[D].南京: 南京理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10288-1016035477.htm
|
| [15] |
ZHANG W L, ZHANG Z Y, CHEN Z H, et al. Main characteristics of suction control of flow separation of an airfoil at low Reynolds numbers[J]. European Journal of Mechanics-B/Fluids, 2017, 65: 88-97. DOI:10.1016/j.euromechflu.2017.01.010 |
| [16] |
徐华舫. 空气动力学基础[M]. 北京: 北京航空学院出版社, 1987.
|
 2019, Vol. 38
2019, Vol. 38


