2. 南京航空航天大学 土木与机场工程系, 江苏 南京 210016
2. Department of Civil and Airport Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
1965年英国渡桥电厂的冷却塔群在5年一遇的强风中发生了严重的倒塌事故,调查结果[1-2]表明塔群干扰效应对冷却塔表面风荷载产生的极值放大作用是冷却塔倒塌的主要诱因之一。事故发生后,各国冷却塔规范[3-5]均对冷却塔的高度和塔群数量制定了严格规定。现阶段特大型冷却塔建设常以四塔组合形式出现,且随着高度增加不断突破规范限值,然而国内外相关规范均未明确给出典型四塔组合形式下冷却塔极值风荷载,更缺乏对此类典型四塔组合冷却塔群风致干扰机理的说明。
针对冷却塔群风荷载干扰效应,文献[6]基于系列测压试验,研究了不同塔间距下双塔塔群平均和脉动风荷载分布规律;文献[7]针对三塔塔群进行了测压风洞试验,探讨了三塔塔群干扰因子取值及其计算得到的冷却塔风致响应;文献[8]针对两组矩形四塔组合冷却塔群进行了测压风洞试验,探讨了受扰塔合力系数随风向角变化规律;文献[9]对考虑地形影响的斜L形四塔塔群进行了刚体测压和气弹测振风洞试验,并基于合力系数指标探讨了塔群干扰效应及其对冷却塔风致稳定性的影响。与此同时,国内外学者对单个冷却塔脉动风荷载进行了较为系统的研究[10-11],结果均表明大型冷却塔局部区域风压概率分布呈现出明显的非高斯特性,是导致冷却塔发生局部失稳和强度破坏的主要因素之一;文献[12]基于多种非高斯极值估计方法研究了单个冷却塔脉动风压的极值风压分布模式,研究认为基于Hermite法分析得到的风压极值具有较高保证率。上述研究大多基于简单塔群组合或特定工程的塔群组合进行分析,未形成可直接应用于四塔组合冷却塔群风荷载取值研究的规律性成果。近年来,随着不同四塔组合形式在火/核电厂的普遍应用,亟需针对多种常见四塔组合形式系统开展风荷载极值特性的定性和定量研究。
鉴于此,以目前世界最高特大型冷却塔为研究对象,进行了考虑串列、矩形、菱形、L形和斜L型五种典型四塔组合形式共320个工况的刚体测压风洞试验。分析了局部风压和整体力系数的非高斯和非平稳特征,研究了四塔干扰下特大型冷却塔的局部风压极值和整体力系数极值的分布规律。在此基础上,提出了考虑四塔组合形式的特大型冷却塔群局部风压谱和整体力系数谱估算公式,并验证了其精确度和有效性。其主要结论可为此类特大型冷却塔群四塔组合布置方案提供科学依据。
1 工程背景和典型四塔组合形式 1.1 工程背景以位于中国内陆地区某特大型冷却塔(高220 m)为工程背景,该塔目前为世界最高冷却塔(图 1),其喉部高度和底部直径分别为165 m和185 m。塔筒采用64对X型支柱支撑与环板基础连接,支柱采用矩形截面,环板基础为现浇钢筋混凝土结构。该特大型冷却塔位于B类地貌,基本风压为0.5 kPa。

|
图 1 目前世界最高冷却塔 Fig.1 Diagram of the world's highest cooling tower |
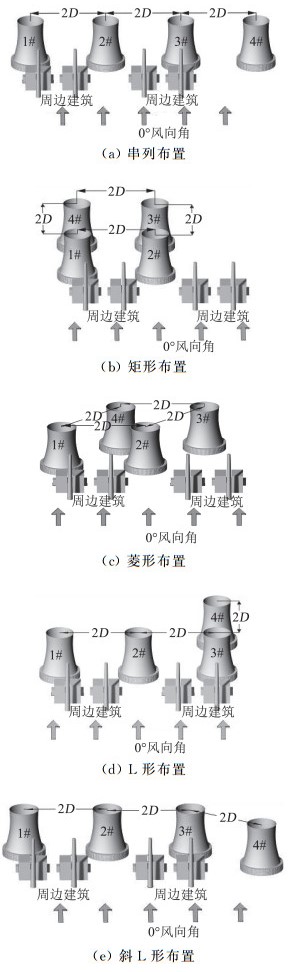
大型火/核电厂普遍采用的四塔组合形式主要有以下5种:串列、矩形、菱形、L形和斜L形布置方案。因此,本文针对这5种典型四塔组合形式进行冷却塔群风洞试验。试验过程中为反映特大型冷却塔在电厂中实际遭受的周边干扰,于特大型冷却塔附近布置厂房和烟囱等电厂常见设施,并采用目前实际工程中普遍选取的2D作为实验工况的塔间距设置标准[13],其中D为塔底直径。具体平面布置及冷却塔位置信息如图 2所示。
|
图 2 四塔组合形式布置示意图 Fig.2 Diagram of layouts of four-towers group |
试验风洞为闭口回流式矩形截面的大气边界层风洞,试验段宽度和高度分别为5.0 m和4.5 m。试验风场按中国《建筑结构荷载规范》中的B类地貌进行模拟[14]。风场模拟的主要指标为平均风速剖面、湍流度剖面和顺风向脉动风谱等,模拟效果见图 3所示,可见风场模拟效果较好,满足试验要求。

|
图 3 大气边界层风洞中的风场模拟结果 Fig.3 Simulation of wind characteristics in ABLWT |
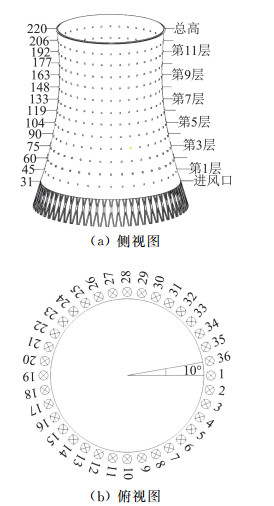
风洞试验模型的缩尺比选为1:450,采用亚克力材料制作实验模型以保证足够的刚度和强度。沿冷却塔塔筒外表面均匀布置12×36个风压测点,即子午向均匀布置12层测点,每一测点层沿环向顺时针均匀布置36个测点,模型测点布置如图 4所示。
|
图 4 试验模型测点布置示意图 Fig.4 Schematic of the measuring points of experimental model |
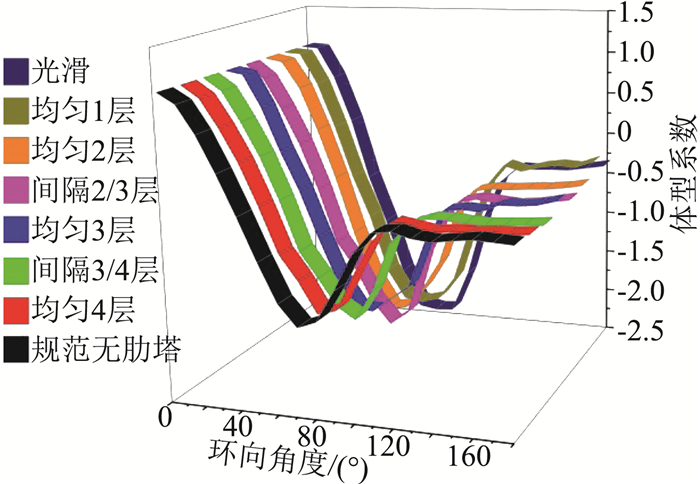
风洞试验中共测试了如下7种粗糙度工况以进行雷诺数效应修正:①表面光滑、②均匀粘贴1层、③均匀粘贴2层、④间隔粘贴2/3层、⑤均匀粘贴3层、⑥间隔粘贴3/4层、⑦均匀粘贴4层5 mm宽粗糙纸带。图 5给出了经归一化处理后的冷却塔喉部高度体型系数分布曲线,并与规范曲线[3]进行对比。由图可见,粘贴4层粗糙纸带可以较好地实现冷却塔雷诺数效应模拟,最终模拟措施如图 6所示。
|
图 5 风洞试验体型系数与目标曲线对比图 Fig.5 Comparison of μs between wind tunnel tests and target curve |

|
图 6 雷诺数效应措施示意图 Fig.6 Diagram of simulation for Reynolds number effect measure |
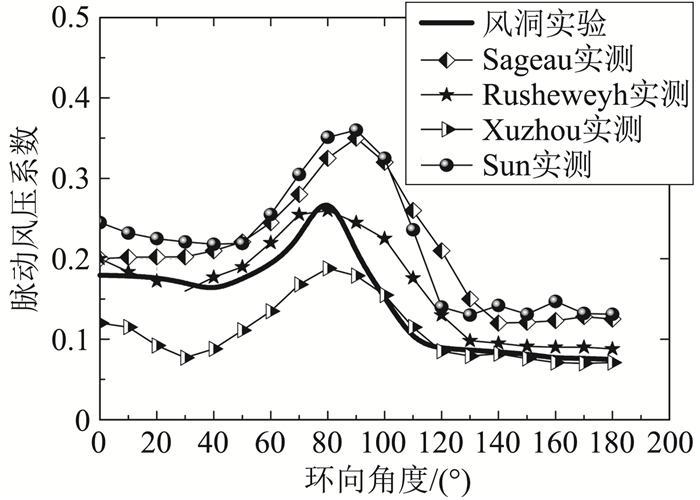
图 7给出了风洞试验测得的单塔脉动风压曲线和相关实测曲线[15-17]。冷却塔环向脉动风压分布可划分为三个区域:迎风区(0°≤θ≤40°)、侧风区(40°≤θ≤120°)和背风区(120°≤θ≤180°)。由于冷却塔脉动风压分布与所处地形、来流湍流、周边干扰和断面高度等密切相关,对比图中迎风区、侧风区和背风区数据,可以发现试验脉动风压沿环向分布规律与国内外实测曲线的分布趋势较为接近。
|
图 7 风洞试验脉动风压与实测数据对比示意图 Fig.7 Comparison between wind tunnel test results and actual measurements of pulsating wind pressure coefficient |
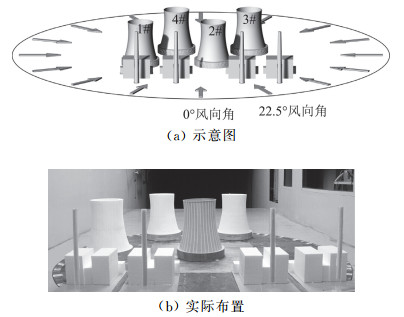
每种四塔布置形式在360°风向角范围内以22.5°增量逐一测量,共16个风向,总计320个风洞试验工况。图 8列举给出了菱形四塔布置时塔群风洞试验测量工况布置及其示意图,所有群塔工况的最大阻塞率为3.22%,满足现行风洞试验标准[18]中阻塞率小于8%的要求。
|
图 8 菱形塔群风洞试验测量工况布置及其示意图 Fig.8 The layout and schematic diagram of wind tunnel test of cooling tower group under rhombus arrangement |
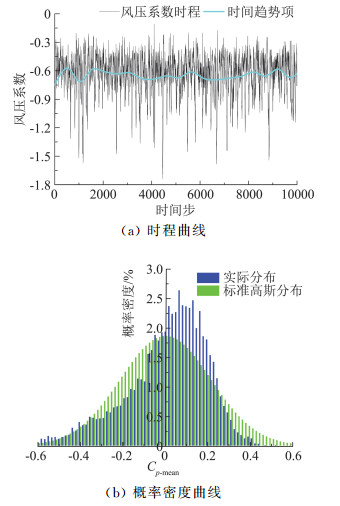
图 9给出了特大型冷却塔在矩形布置形式下喉部背风区风压系数时程及其概率密度曲线。图 9(a)中给出了风压时程曲线,并基于多尺度小波分析技术[19]提取了风压时程的时间趋势项,风压时程的斜度值和峰态值分别为-1.19和5.09。由图可知,从该风压时程的时程曲线和非高斯特征值(斜度值和峰态值)而言,该时程表现出显著的非高斯特征和一定的非平稳特征。
|
图 9 冷却塔风压系数时程及概率密度曲线 Fig.9 Wind pressure coefficient time history and probability density curve of cooling tower |
更多的统计结果表明,四塔干扰下的特大型冷却塔表面风压信号存在类似“大偏斜”和“高峰值”特征的风压信号比例较高。图 10列举了五种典型工况下特大型冷却塔风压系数信号的斜度和峰态关系图,参考已有研究[20]将-0.5≤μs sk≤0.5且2≤μs ku≤4的测点信号近似看作高斯信号(μs sk和μs ku分别代表风压信号的斜度值和峰态值)。分析可知,串列和斜L形方案下冷却塔各测点风压信号的斜度值和峰态值相对较为集中,矩形、菱形和L形四塔组合工况下特大型冷却塔风压信号中属于非高斯信号的占比接近50%。相对而言,特大型冷却塔的局部风压信号虽存在一定的非平稳特征,但基于轮次检验法[21]得到的非平稳信号比例显著低于非高斯信号比例。

|
图 10 五种典型工况下特大型冷却塔风压系数斜度-峰态关系图 Fig.10 Relationship between skewness and kurtosis of wind pressure coefficient under five typical conditions |
上述分析表明,四塔干扰下特大型冷却塔表面风压信号的非高斯特性不容忽视,后续风压极值研究均基于考虑非高斯特性影响的Hermite极值估计方法计算得到。
Kareem和Zhao[22]等在Davenport的工作基础上,将高斯随机变量表示为考虑高阶统计量(偏度和峰度)的非高斯随机变量的Hermite多项式,从而将Davenport仅仅适用于高斯过程的基于零值穿越理论的峰值因子法扩展到适用于估算非高斯过程的风压极值。非高斯随机变量x(t)和标准高斯过程u(t)的关系式:
| $ x=\alpha\left[u+h_{3}\left(u^{2}-1\right)+h_{4}\left(u^{3}-3 u\right)\right] $ | (1) |
式中:
通过Hermite多项式,可得非高斯过程的峰值因子:
| $ \begin{aligned} &g=\alpha\left\{\beta+\frac{\gamma}{\beta}+h_{3}\left(\beta^{2}+2 \gamma-1+\frac{1.98}{\beta^{2}}\right)+\right.\\ &\left.h_{4}\left[\beta^{3}+3 \beta(\gamma-1)+\frac{3}{\beta}\left(\frac{\pi^{2}}{6}-\gamma+\gamma^{2}\right)+\frac{5.44}{\beta^{3}}\right]\right\} \end{aligned} $ | (2) |
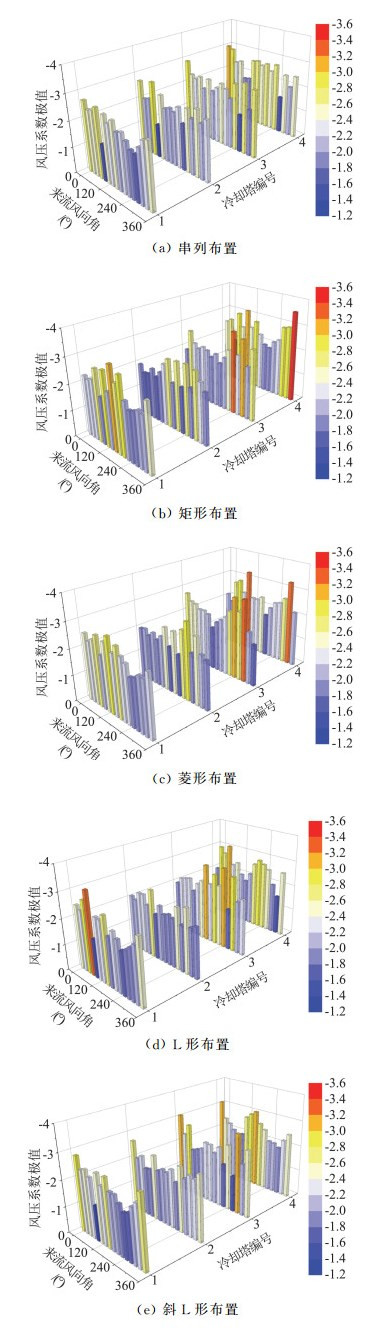
图 11给出了五种四塔组合形式共320个工况的冷却塔最大负压极值分布示意图,由Hermite法计算得到的风压极值保证率,均值为99.94%。由图可知,来流风向角对特大型冷却塔的最大负压极值存在决定性的影响作用,部分特定工况下特大型冷却塔的最大负压极值仅为-1.40左右,串列布置和斜L形布置出现此类工况的概率较高;五种布置形式中,矩形、菱形和L形布置均出现了负压极值小于-3.40的工况,其中矩形布置下负压极值最大,菱形布置下特大型冷却塔表面出现此类强吸力现象的可能性最高。
|
图 11 五种四塔组合形式最大负压极值分布示意图 Fig.11 Schematic diagram of the maximum negative pressure distribution under five kinds of four-tower groups |
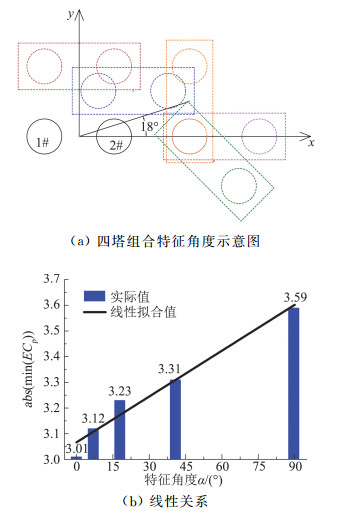
图 12(a)中汇总给出了五种四塔组合形式布置图,将1#塔和2#塔作为位置固定的特大型冷却塔,视为塔群A,3#塔和4#塔为塔群B。可以发现,五种四塔形式的不同在于塔群A与塔群B相对位置的改变。定义塔群A中心点与塔群B中心点连线相对X轴的夹角为四塔组合的特征角度α(取绝对值),图中L形方案α=18°。结合五种四塔组合形式320个工况下特大型冷却塔最大负压极值(ECp)发现,四塔组合特征角度α和该组合形式下的最大负压极值的绝对值存在明显的线性相关性,如图 12(b)所示。随着四塔组合特征角度α的增加,冷却塔群的局部负压极值效应愈加显著。该回归关系可表示为:
| $ a b s\left(\min \left(E C_{p}\right)\right)=3.06623+0.00595 \alpha $ | (3) |
|
图 12 四塔组合特征角度α与最大负压极值的相关性示意图 Fig.12 Schematic diagram of the linear correlation between α and the maximum of negative pressure extremum |
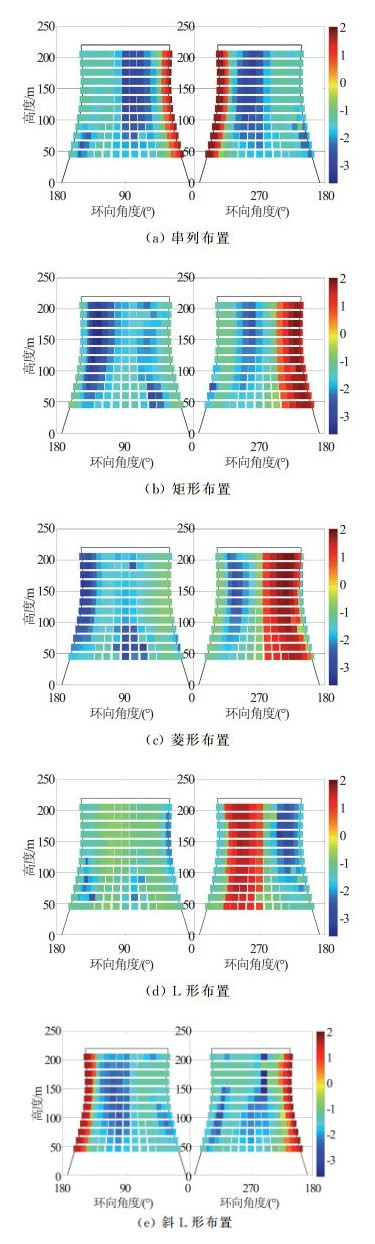
图 13给出了五种四塔组合最大负压极值工况冷却塔表面极值风压分布示意图,图中串列、矩形、菱形、L形和斜L形布置来流风向角分别为0°、337.5°、315°、67.5°和180°。不同四塔组合形式对正压极值影响微弱,主要影响区域为分离点附近的负压区,除串列布置外其它四塔组合形式表面极值风压分布均呈现出一定的非对称性(相对来流风向角),其中尤以矩形最为显著。
|
图 13 五种四塔组合形式冷却塔极值风压分布示意图 Fig.13 Distribution of extreme wind pressure of cooling tower under five kinds of four-tower groups |
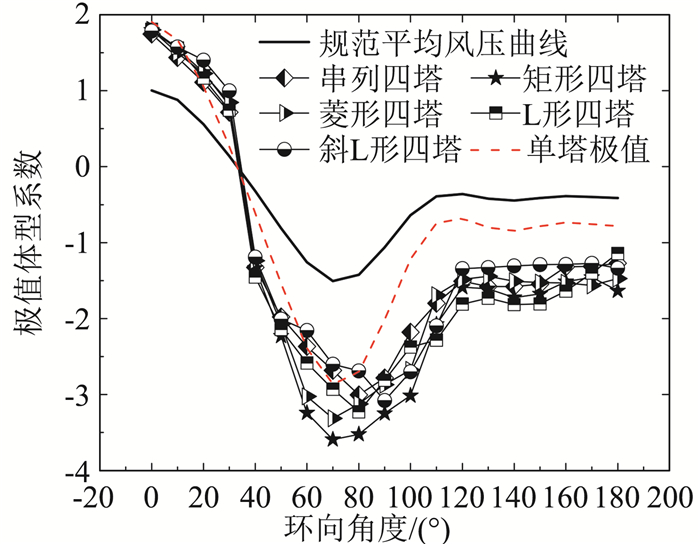
图 14汇总给出了五种组合形式特大型冷却塔喉部风压系数极值和单塔极值分布曲线。由图可知:迎风区内五种四塔组合形式极值风压较为接近;不同四塔方案下冷却塔风压系数极值分布曲线在侧风区和背风区分布趋势接近,且与规范给出的平均风压系数曲线分布规律类似,但组合形式对局部风压极值的幅值影响显著。
|
图 14 五种组合形式冷却塔风压系数极值分布曲线图 Fig.14 Distribution curves of extreme pressure coefficient of cooling tower under five arrangements |
结合规范[3]平均风压曲线的八项拟合式,引入四塔组合局部风压干扰系数β,提出了四塔组合特大型冷却塔群的一维风压系数极值估算公式,如下式:
| $ C_{p}(\theta)=\beta\left(\sum\limits_{k=0}^{m} a_{k} \cos k \theta\right) $ | (4) |
式中,θ(0≤θ≤360°)为局部区域的环向角度;ak为规范[3]平均风压系数的拟合参数。
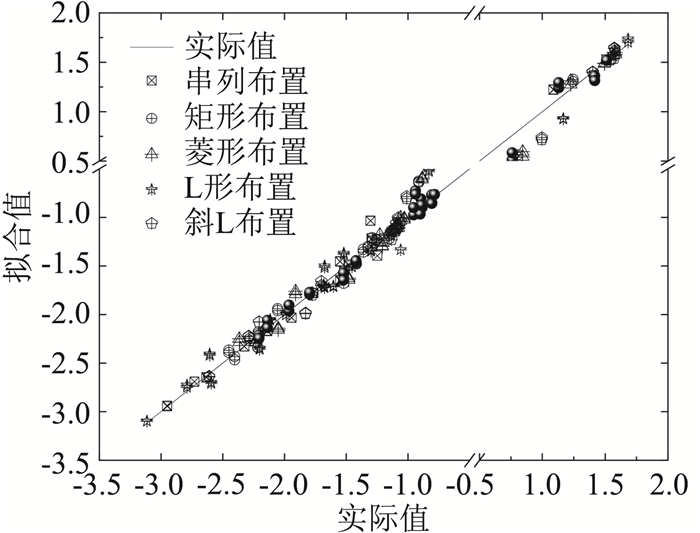
不同四塔组合形式的局部风压干扰系数β见表 1,拟合公式误差分析见图 15所示,试验值均匀地分布于代表拟合值附近,具有良好的预测效果。
| 表 1 四塔组合局部风压干扰系数β参数列表 Table 1 List of β (interference coefficient parameter of wind pressure) |
|
|
|
图 15 考虑四塔干扰效应的冷却塔极值风压拟合公式误差分析图 Fig.15 Schematic of error analysis on the fitted equations of extreme wind loads under the four-tower arrangements |
文献[13]研究表明合力系数可作为特大型冷却塔的整体气动力系数,计算公式如下:
| $ C_{D}(t)=\frac{\sum\limits_{i=1}^{n} C_{p i}(t) A_{i} \cos \theta_{i}}{A_{T}} $ | (5) |
| $ C_{L}(t)=\frac{\sum\limits_{i=1}^{n} C_{p i}(t) A_{i} \sin \theta_{i}}{A_{T}} $ | (6) |
| $ C_{T}=\sqrt{C_{D}^{2}+C_{L}^{2}} $ | (7) |
式中,CT、CD和CL分别为受扰冷却塔的合力、阻力和升力系数;Ai为测点i的压力等效面积,θi为该测点压力与来流风向的夹角,AT为冷却塔相对来流的投影面积。
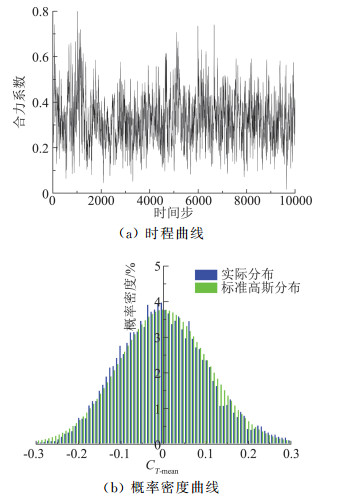
图 16列举给出了矩形四塔干扰工况下特大型冷却塔的合力系数时程及概率密度曲线。由图可知,该工况合力系数的斜度值和峰态值分别为0.43和3.45,且概率分布均与标准正态分布吻合良好。更多工况的合力系数时程统计表明,四塔干扰下特大型冷却塔合力系数均呈现出典型的高斯分布特征,可基于峰值因子法对四塔干扰下特大型冷却塔的合力系数极值(ECT)进行计算。
|
图 16 冷却塔合力系数时程及概率密度曲线 Fig.16 The time history and probability density curve of CT |
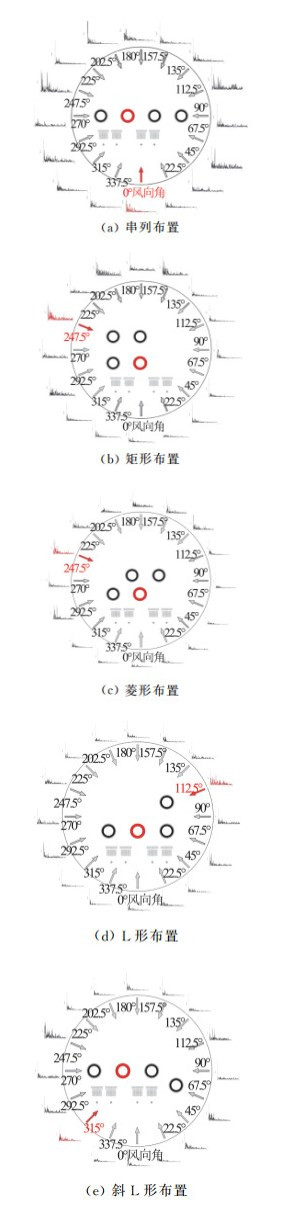
图 17给出了不同四塔组合下2#塔所有风向角工况的合力系数功率谱,图中红色工况即为最大合力系数极值工况。由图可知,最大合力系数极值工况合力系数功率谱均出现较明显的涡脱尖峰,且谱峰相对较窄,此时受扰塔除受自身分离流动的影响,周边干扰塔尾流对其影响显著。不同方案中,矩形和菱形布置在更多的风向角出现上述涡脱尖峰情况,这也说明了这两种方案属于干扰效应较为显著的四塔组合形式。
|
图 17 不同四塔组合2#塔所有风向角工况的合力系数功率谱 Fig.17 Spectrum of resultant force coefficient of 2# tower under different four-tower combinations |
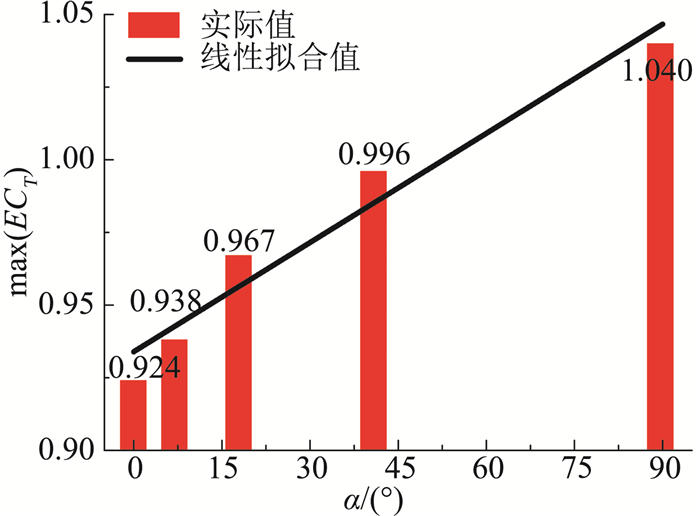
统计得出五种四塔组合形式的最大合力系数极值,并与特征角度α进行相关分析,二者相关系数为0.94,如图 18所示,图中回归关系如式(8)所示。与局部风压极值类似,四塔干扰下特大型冷却塔群的整体气动力极值与组合形式的特征角度α亦存在良好的线性相关性。
| $ \max \left(E C_{T}\right)=0.93393+0.00125 \alpha $ | (8) |
|
图 18 四塔组合特征角度与最大合力系数相关性示意图 Fig.18 Schematic diagram of the linear correlation between α and the maximum of extreme CT |
本文系统研究了四塔组合形式对冷却塔群风荷载极值分布特征的影响规律及其预测方法,主要涉及风洞试验、非高斯特性、极值估计、回归分析等内容。建议四塔组合布置方案应优先选择串列形式,并按斜L形、L形、菱形和矩形的顺序依次选择,具体研究结论如下:
1) 四塔干扰下特大型冷却塔局部风压信号呈现显著的非高斯特征,非高斯风压占比接近50%,局部风压极值估计应采取考虑非高斯特性的极值估计方法;特大型冷却塔的整体力系数是表面多点风压信号的统计值,避免了局部风压信号的奇异性,可基于峰值因子法直接进行极值估计。
2) 不同四塔组合形式对特大型冷却塔正压极值影响微弱,主要影响区域为流动分离点附近的负压区;五种布置形式均出现了负压极值小于-3.0的工况,矩形、菱形和L形布置最大负压极值均小于-3.40,矩形布置下特大型冷却塔的负压极值最大,菱形布置时出现此类强吸力现象的概率较高。
3) 四塔组合形式的特征角度α与塔群最大负压极值和最大合力系数极值之间均存在明确的线性相关性,可作为衡量四塔塔群风荷载干扰效应的有效指标;基于此,首次提出了适用于冷却塔四塔塔群最大负压极值和整体力系数极值的数学计算模型。
4) 结合规范的平均风压系数八项拟合式,并引入四塔组合局部风压干扰系数β,在上述基础上首次提出了适用于四塔组合特大型冷却塔群的一维风压系数极值差异化估算公式,可为此类四塔组合特大型冷却塔群极值风荷载取值提供参考依据。
| [1] |
SWARTZ S E, CHIEN C C, HU K K, et al. Tests on microconcrete model of hyperbolic cooling tower[J]. Experimental Mechanics, 1985, 25(1): 12-23. DOI:10.1007/BF02329121 |
| [2] |
POPE R A, et al. Structural deficiencies of natural draught cooling towers at uk power stations. Part 1: failures at ferrybridge and fiddlers ferry[J]. Structures & Buildings, 1994, 104(1): 1-10. |
| [3] |
GB/T 50102-2014.工业循环水冷却设计规范[S].北京: 中国计划出版社, 2014. GB/T 50102-2014. Code for design of cooling for industrial recirculating water[S]. Beijing: China Planning Press, 2014. (in Chinese) |
| [4] |
DL/T5339-2006.火力发电厂水工设计规范[S].北京: 中国电力出版社, 2006. DL/T5339-2006. The thermal power plant hydraulic design specification[S]. Beijing: China Electric Power Press, 2006. (in Chinese) |
| [5] |
VGB-R 610Ue, Structural design of cooling tower- technical guideline for the structural design, computation and execution of cooling towers[S]. BTRBautechnik bei Kühltürmen, Standard Essen, 2005. (in German)
|
| [6] |
NIEMANN H J, KOPPER H D. Influence of adjacent buildings on wind effects on cooling towers[J]. Engineering Structures, 1998, 20(10): 874-880. DOI:10.1016/S0141-0296(97)00131-4 |
| [7] |
张军锋, 葛耀君, 赵林. 群塔布置对冷却塔整体风荷载和风致响应的不同干扰效应[J]. 工程力学, 2016, 33(8): 15-23. ZHANG J F, GE Y J, ZHAO L. Interference effects on global wind loads and wind induced responses for group hyperboloidal cooling towers[J]. Engineering Mechanics, 2016, 33(8): 15-23. (in Chinese) |
| [8] |
程霄翔, 赵林, 葛耀君. 典型矩形八塔超大型冷却塔塔群风致干扰效应试验[J]. 中南大学学报(自然科学版), 2013, 44(1): 372-380. CHEN X X, ZHAO L, GE Y J. Wind tunnel investigation on interference effect of eight grouped super large cooling towers with rectangular arrangement[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 372-380. (in Chinese) |
| [9] |
KE S T, GE Y J, ZHAO L, et al. Stability and reinforcement analysis of super-large exhaust cooling towers based on a wind tunnel test[J]. Journal of Structural Engineering, ASCE, 2015, 141(12): 04015066. DOI:10.1061/(ASCE)ST.1943-541X.0001309 |
| [10] |
VILADKAR M N, KARISIDDAPP A, BHARGAVA P, et al. Static soil-structure interaction response of hyperbolic cooling towers to symmetrical wind loads[J]. Engineering Structures, 2006, 28(9): 1236-1251. DOI:10.1016/j.engstruct.2005.11.010 |
| [11] |
柯世堂, 葛耀君, 赵林. 大型双曲冷却塔表面脉动风压随机特性-非高斯特性研究[J]. 实验流体力学, 2010, 24(3): 12-18. KE S T, GE Y J, ZHAO L. Research on festures of fluctuating wind pressure on large hyperbolic cooling tower: features of non-Gaussian[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(3): 12-18. DOI:10.3969/j.issn.1672-9897.2010.03.003 (in Chinese) |
| [12] |
KE S T, WANG H, GE Y J. Non-Gaussian characteristics and extreme distribution of fluctuating wind pressures on large cylindrical-conical steel cooling towers[J]. Structural Design of Tall & Special Buildings, 2017, 9: 1-16. |
| [13] |
KE S T, WANG H, GE Y J. Interference effect and the working mechanism of wind loads in super-large cooling towers under typical four-tower arrangements[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2017, 170(1): 197-213. |
| [14] |
GB50009-2012.建筑结构荷载规范[S].北京: 中国建筑工业出版社, 2012. GB50009-2012. Load code for the design of building structures[S]. Beijing: China Building Industry Press, 2012. (in Chinese) |
| [15] |
CHENG X X, ZHAO L, GE Y J, et al. Wind pressures on a large cooling tower[J]. Advances in Structural Engineering, 2015, 18(2): 201-220. DOI:10.1260/1369-4332.18.2.201 |
| [16] |
RUSCHEWEYH H. Wind loadings on hyperbolic natural draught cooling towers[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1975, 1(5): 335-340. |
| [17] |
SUNA T F, ZHOUB L M. Wind pressure distribution around a ribless hyperbolic cooling tower[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 14(1): 181-192. |
| [18] |
JSJ/T 338-2014.建筑工程风洞试验方法标准[S].北京: 中国建筑工业出版社, 2014. JSJ/T 338-2014. Standard for wind tunnel test of buildings and structures[S]. Beijing: China Building Industry Press, 2014. (in Chinese) |
| [19] |
DAUBECHIES I. Ten lectures on wavelets[J]. Computers in Physics, 1992, 6(3): 1671-1671. |
| [20] |
ZAREIFARD H, KHALEDI M J. Non-Gaussian modeling of spatial data using scale mixing of a unified skew Gaussian process[J]. Journal of Multivariate Analysis, 2013, 114(114): 16-28. |
| [21] |
BENDAT J S, PIERSOL A G. Random data: Analysis and measurement procedures. (Izmerenie i analiz slucainyh processov.) Vbersetzung aus dem Englischen von G. V. Matusevskii und V. E. Prival'skii. Mit einem Vorwort von G. Ja. Mirskii[J]. IEEE Transactions on Signal Processing, 2010, 58(7): 3938-3945. DOI:10.1109/TSP.2010.2046636 |
| [22] |
KAREEM A, ZHAO J. Analysis of non-Gaussian surge response of tension leg platforms under wind loads[J]. Journal of Offshore Mechanics & Arctic Engineering, 1994, 116(3): 137-144. |
 2020, Vol. 38
2020, Vol. 38

