2. 中国空气动力研究与发展中心 结冰与防除冰重点实验室, 四川 绵阳 621050;
3. 澳大利亚新南威尔士大学 机械与制造工程学院, 悉尼 2052
2. Key laboratory of icing and de-icing research, China aerodynamics research and development center, Mianyang 621050, China;
3. Mechanical and Manufacturing School, University of New South Wales 2052, Sydney, Australia
由于热线风速仪具有很高的时间和空间分辨率,故热线比粒子图像测速(PIV)、激光多普勒仪(LDV)等更适合湍流流场的测量[1-3]。热线风速仪的工作原理为:通过仪器的内置电路(惠斯通电桥)加热微型金属丝,气体流动带走金属丝上的热量从而引起测量电阻的变化,惠斯通电桥对其进行补偿,补偿电阻的变化即反应了风速的变化[4-5]。热线风速仪主要有恒温(CTA)、恒压(CVA)和恒流(CCA)三种工作模式。根据热线丝的几何形状不同,热线探头有多种分类,并覆盖了从一维到三维流场的测量范围。本文主要研究恒温模式下的二维热线风速测量。为了得到真实的风速,需要先建立起热线电压与风速之间的校准关系,再将测量得到的电压值换算成风速值。一般情况下,热线的校准和测量过程是独立进行的,环境温度的变化将会给测量结果带来误差[6-8]。
假设环境温度变化足够小、气体的物理性质保持不变,Westphal[9]基于热线的温度系数、过热比、以及校准/测量之间的环境温度差,最早提出了一种温度效应修正的简化公式。Brunn[10]随后提出了一种改进的热线温度修正工程化方法,并在实际测量中得到了广泛的使用。但是当环境温度在短时间内变化较大或流体性质发生变化时,例如对于无冷却设备的低速回流式风洞、结冰风洞或增压风洞中的流场测量,Westphal和Brunn的修正方法会带来明显误差[11]。Cukurel[12]等考虑了气体的可压缩性,提出了一种用于测量跨声速喷流的二维热线校准方法。然而,Cukurel等没有考虑温度效应修正,故无法对诸如发动机热喷流之类的流场进行测量。Marcus[13]研究了强制对流中的热传递过程,提出了一种无量纲化的热线温度效应修正方法,并在高雷诺数气流的流场测量中得到了应用。
本文从热线风速仪的工作原理出发,结合气体物理参数之间的关系,提出了一种新的二维热线校准方法。该方法将温度效应修正隐式的包含在热线校准公式中,突破了传统方法对温度变化范围的限制,同时不受高压、低温等试验条件下气体物理参数变化的影响。本文的研究内容安排如下:第一节给出了二维热线校准的理论方法,并对隐式温度效应修正方法进行了阐述;第二节,对本文提出的校准方法进行了实验验证;第三节,对全文进行了总结。通过本文研究,以期提高二维热线的测量精度和拓展热线风速仪的应用范围。
1 理论方法根据Brunn提出的方法[10],热线测量的输出电压可以根据下式进行修正:
| $ {E_{w,c}} = {E_w}{\left[ {\frac{{{T_w} - {T_r}}}{{{T_w} - {T_a}}}} \right]^{0.5}} $ | (1) |
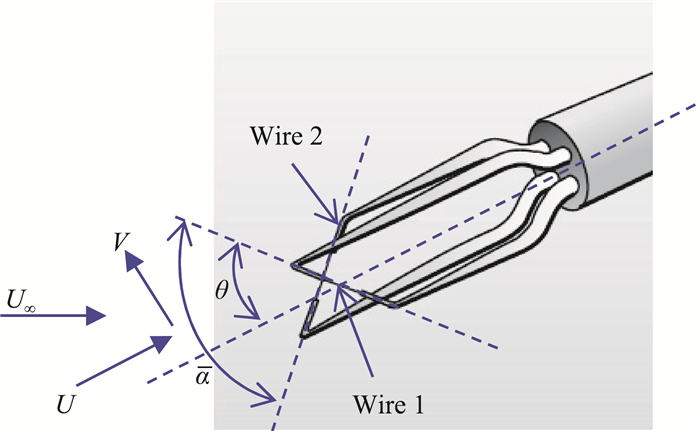
其中:Ewc、Ew分别表示经过修正后的结果和原始测量数据;Tw表示热线的工作温度;Ta表示环境温度;Tr表示热线校准时的环境温度。在标准大气条件下,式(1)是一个非常有用的经验修正公式。根据Jorgensen的研究结果[6],式(1)应在环境温度变化±5 ℃范围内使用。如果温度变化过大,则应多次重复进行校准。下文我们将推导一种新的用于二维热线风速测量的温度效应修正方法,图 1是二维热线风速仪探针示意图。
|
图 1 二维热线风速仪探针示意图[14] Fig.1 Schematic of a cross-hotwire probe |
试验测量过程中,热线暴露在气流当中,热线上的能量损失主要有三种方式:对流、辐射和传导。纵横比(长度与直径之比)大于200的热线主要以自由对流的方式耗散能量[15]。大部分用于科学研究的热线的纵横比大于200,故以下的分析中只考虑强制对流效应引起的能量损失。对于在恒温模式下工作的热线风速仪,惠斯通电桥使热线的温度或电阻值保持恒定。强制对流效应在热线电阻上产生的焦耳热可以用以下式表示:
| $ I_w^2{R_w} = \frac{{{E^2}}}{{{R_w}}} = {\rm{ \mathsf{ π} }}ld\left( {{T_w} - {T_a}} \right) \cdot h $ | (2) |
其中,Iw和E分别表示热线上的电流和电压;Rw、d和L分别表示电阻、热线丝的直径和长度;h=Nu·κ/d表示对流热传导系数,Nu表示努塞尔数,κ是气体的导热系数。根据Collis和Williams的研究结果[16],气体的努塞尔数Nu与雷诺数Re之间满足如下关系:
| $ Nu{\left( {\frac{T}{{{T_a}}}} \right)^{ - 0.17}} = A + B{\left( {Re} \right)^n} $ | (3) |
式中:T表示气流的温度;Ta表示参考温度;A、B和n是经验常数,通过实验确定。对于典型的微米直径的热线,式(3)在雷诺数Re=0.01~140范围内是成立的。根据式(3),式(2)可以改写为:
| $ \frac{{{E^2}}}{{\kappa \Delta T}}\left[ {\frac{1}{{{R_w}{\rm{ \mathsf{ π} }}l}}{{\left( {\frac{T}{{{T_a}}}} \right)}^{ - 0.17}}} \right] = A + B{\left( {\frac{{\rho ud}}{\mu }} \right)^n} $ | (4) |
其中:ΔT=Tw-Ta表示热线与周围气的温度差,ρ和μ分别表示气体的密度和运动粘滞系数。由于式(4)方括号中的量近似为常数,故可进一步简化为:
| $ \frac{{{E^2}}}{{\kappa \Delta T}} = \bar A + \bar B{\left( {\frac{{\rho u}}{\mu }} \right)^n} $ | (5) |
其中:A和B为新的待定常数。一般而言,对热线起冷却作用的气流速度主要在垂直于热线丝的方向上,但是平行于热线丝方向的气流速度也有一定的冷却作用。二维热线上的有效冷却速度写为[17]:
| $ {U_e} = {U_\infty }\sqrt {{{\cos }^2}\theta + k{{\sin }^2}\theta } $ | (6) |
式中:U∞表示自由来流速度;k表示冷却常数(与顺气流方向的气流速度相关);θ定义为气流方向与热线探针轴线之间的夹角,θ为正表示顺时针方向。联立方程(2)、(3)和(4),可得到气流速度和热线输出电压之间的关系式:
| $ \left( {\frac{{{E^2}}}{{\kappa \Delta T}}} \right) = A + B{\left[ {\left( {\frac{{\rho {U_\infty }}}{\mu }} \right)\sqrt {{{\cos }^2}\theta + k{{\sin }^2}\theta } } \right]^n} $ | (7) |
其中:κ、ρ和μ等气体物理参数与温度的变化密切相关。根据电压E、自由来流速度U∞和倾角θ的校准数据,通过方程(5)进行曲线拟合,可以给出A、B、n和k的校准值。在一定的温度和压力范围内,气体物理参数κ、ρ和μ的值可以通过下面的式子给出:
| $ \rho \left( T \right) = \frac{p}{{287.058T}} $ | (8a) |
| $ \kappa \left( T \right) = \frac{{2.334 \times {{10}^{ - 3}}{T^{\frac{3}{2}}}}}{{164.54 + T}} $ | (8b) |
| $ \mu \left( T \right) = \frac{{1.458 \times {{10}^{ - 6}}{T^{\frac{3}{2}}}}}{{110.4 + T}} $ | (8c) |
式中:p表示大气压力,T表示热线丝周围气体的温度。根据二维热线的角度和速度校准结果,结合试验测量得到的电压数据,使用Brunn给出方法可以得到二维流速分量Uc和Vc的估计值[10]:
| $ {U_c} = \frac{{{U_{e1}} + {U_{e2}}}}{{2f\left( {\bar \alpha } \right)}} $ | (9) |
| $ {V_c} = \frac{{{U_{e2}} - {U_{e1}}}}{{2f\left( {\bar \alpha } \right)g\left( {\bar \alpha } \right)}} $ | (10) |
| $ f\left( {\bar \alpha } \right) = {\left( {{{\cos }^2}\bar \alpha + {k^2}{{\sin }^2}\bar \alpha } \right)^{\frac{1}{2}}} $ | (11) |
| $ g\left( {\bar \alpha } \right) = \frac{{\left( {1 - {k^2}} \right){{\cos }^2}\bar \alpha }}{{{k^2} + \left( {1 - {k^2}} \right){\rm{co}}{{\rm{s}}^2}\bar \alpha }}\tan \bar \alpha $ | (12) |
其中:α是热线丝和探针轴线之间的角度。使用上述方法对热线丝的角度误差不敏感,角度误差在1°左右时,相对测量误差小于1%[1]。
2 实验研究 2.1 二维热线校准本文使用TSI公司的TSI1129校准器对一只新修复的TSI二维热线探针进行了校准。在校准过程中,使用Dantec54N80常温风速仪记录热线的电压模拟量输出,并用NI-9219数据卡将模拟量转换为数值量。设定CTA的过热比时,需要使用万用表测量热线探针、引线、支架和电缆的电阻值,然后将其作为参考值来计算过热比。实验过程中,数采卡的采样率设置为50 Hz (校准),采样时间是20 s。在标准大气压条件下,平均环境温度分别为21 ℃和25 ℃时,实验测量得到了两个校准数据集。其中一个数据集包含11个倾斜角度(从-30°到30°,步长为6°)和每个角度测点上包含30个流速值(从5 m/s到80 m/s)。另一个数据集包含相同的角度测量点和一半的流速测量点。
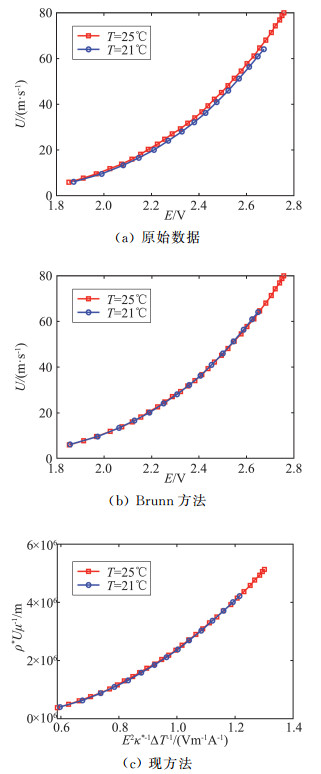
图 2给出了二维热线中的2#热线丝在零度倾斜角下的速度校准结果。由于结果非常类相似,文中没有重复给出该热线丝在其它俯仰角下的结果或1#热线丝的结果。图中的结果是由相同的热线丝在不同温度下(21 ℃和25 ℃)测量得到的。如图 2(a)所示,如果不进行温度修正,同一条热线在不同温度下的校准结果是不同的,特别是在流动速度较高的情况下更是如此。其对测量结果的影响主要表现在,通过电压输出和校准结果得到的流速的测量值将偏离真实值。取参考温度Tr=25 ℃,使用Brunn的方法或本方法修正21℃下获得的校准数据,可以发现两次校准得到的曲线完全重叠(见图 2(b)和图 2(c))。这表明两种方法都可以有效纠正温度效应。但是Brunn的方法要求温度变化小于几度,而本文提出的方法则没有这个限制。
|
图 2 标准大气压条件下的热线速度校准曲线 Fig.2 Velocity calibration curves for a cross hotwire under standard atmosphere pressure condition |
在高雷诺数条件下,气体的物理性质对温度变化敏感,使用Brunn的方法将会带来明显的误差,下文将进行说明。
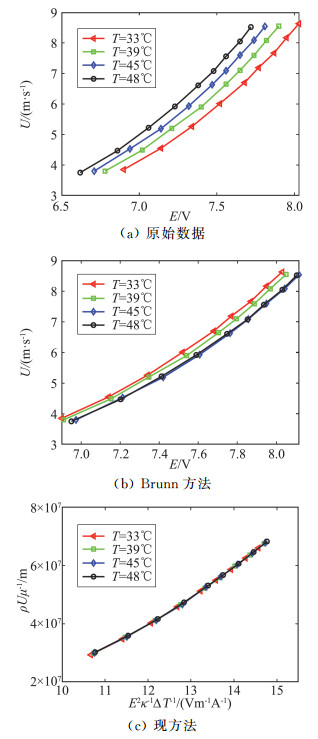
图 3(a)中给出了Marcus和Smits[13]在普林斯顿高雷诺数测试设备(HRTF)上对热线校准获得的原始数据。如果不开冷却设备,空气的温度在短时间内可以升高10 ℃以上。在高气压条件下,空气的密度、热传导系数和动力粘滞系数等必须相应地进行修正。从图 3(a)中可以看出,热线的输出电压随气流温度变化而改变,使用Brunn的方法进行修正后校准曲线仍然不重合(T=33 ℃被取为参考值,见图 3(b))。而使用本文提出的方法后,所有校准数据完全重叠(见图 3(c)),这表明温度变化对热线测量的影响可以通过本方法被准确地修正。
|
图 3 高压条件下的热线速度校准曲线 Fig.3 Velocity calibration curves for a cross hotwire under high-pressure condition |
表 1给出了TSI二维热线的校准常数A、B、n和k的值,其中k代表二维热线的角度校准结果。校准过程中的平环境温度为25 ℃,温度变化小于1 ℃。上述校准系数是根据式(5),采用曲面拟合的方法得到的,拟合的置信因子R2总是大于0.99。根据表中的结果,两种温度修正方法得到的k值大致相等,同时是否进行温度修正对k值的影响不明显。这表明冷却常数k主要由热线的几何形状决定,温度变化对二维热线的角度校准没有影响。
| 表 1 TSI二维热线的角度校准结果,25 ℃ Table 1 TSI cross-hotwire calibration results, 25 ℃ |
|
|
新南威尔士大学的UAT声学风洞是一座开口直流式风洞,风洞喷口尺寸为0.46 m×0.46 m[18]。2018年,UAT风洞进行了升级改造。风洞升级完成后,可以获得更高的风速,试验段的流场品质也有了较大的提升。风洞正式投入运营之前,使用二维热线风速仪进行了流场测试。
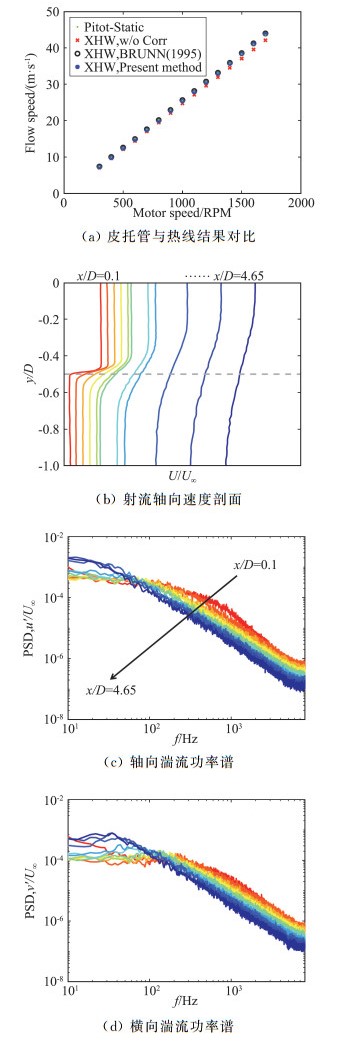
图 4给出了UAT风洞的流场测量结果。热线测量结果的准确性使用皮托管进行了验证。校准和试验测量之间的温度差为3 ℃。如果没有进行温度校正,热线测量结果将偏离皮托管的测量数据,最大相对误差可以达到5%(40 m/s,见图 4(a))。根据本文提出的方法进行温度修正之后,热线数据与皮托管的数据之间非常吻合。图 4(b)给出了40 m/s风速条件下的风洞自由射流的速度剖面曲线,其中y/D=0表示喷口中心线,y/D=-0.5表示风洞喷口边缘线(剪切层的位置),D=0.46 m表示风洞喷口的尺寸。从图上可以清楚地区分射流的核心区和混合区。图 4(c)和图 4(d),给出了沿流向几个不同位置的轴向(u′)和横向(v′)湍流功率谱(测点位于剪切层的中心位置,即y/D=-0.5)。湍流谱可以根据曲线斜率值被划分为三个区域:大的涡流区,惯性副区,能量耗散区;该测量结果与前人的实验结果是一致的[19]。
|
图 4 UAT风洞的流场测量结果 Fig.4 Sample results of flow field measurement of UAT wind tunnel |
热线风速仪主要用于湍流流场测量,热线测量的主要误差来源是由环境温度变化导致的热线校准参数的变化。通常使用的Brunn温度效应修正方法在温度变化较大的情况下会带来明显的误差。本文经过理论推导,提出了一种新的用于二维热线风速仪校准的温度修正方法,并开展了热线校准实验研究,结果表明:1)当环境温度变化在4 ℃以内时,本文提出的方法与Brunn方法的测量精度相当;2)当环境温度变化大于4 ℃时,本文提出的方法的测量精度远高于Brunn方法。与传统的Brunn方法相比,本文提出的方法可大大减少热线测量过程中的校准次数,对提高试验的质量和效率有意义。需要说明的是,现阶段受实验条件限制,本文没有开展温度变化范围较大条件下的湍流流场测量。待条件成熟后,作者将继续开展相关的研究工作。
致谢: 本文的实验部分工作是在澳大利亚新南威尔士大学做访问研究员期间完成的,感谢国家留学基金委(CSC)的资助,感谢Con. Doolan教授课题组提供实验设备支持。
| [1] |
BRUNN H H. Hot-wire anemometry[M]. Oxford: Oxford University Press, 1995.
|
| [2] |
HENBEST S M, JONES M B, WATMUFF J H. A technique for rapid calibration of cross-hot-wires[C]//20th Australian Fluid Mechanics Conference, Perth, Australia, 5-8 December 2016.
|
| [3] |
WALKER D A, WALKER M D. Experimental comparison of two hot-wire techniques in supersonic flow[J]. AIAA Journal, 1988, 27(8): 1074-1080. |
| [4] |
LUEPTOW R M, BREUER K S, HARITONIDIS J H. Computer-aided calibration of X-probes using a look-up table[J]. Experiments in Fluids, 1988, 6: 115-118. |
| [5] |
马护生, 时培杰, 李学臣, 等. 可压缩流体热线探针校准方法研究[J]. 空气动力学学报, 2019, 37(1): 55-60. MA H S, SHI P J, LI X C, et al. Investigation of calibration method for hot-wire probe incompressible flow[J]. Acta Aerodynamica Sinca, 2019, 37(1): 55-60. DOI:10.7638/kqdlxxb-2016.0093 (in Chinese) |
| [6] |
JORGENSEN F E. How to measure turbulence with hot-wire anemometers-a practical guide[R]. Dantec Dynamics, Denmark, 2002.
|
| [7] |
MORO J P, VUKOSLAVCEVIC P V, BLET V. A method to calibrate a hot-wire X-probe for applications in low-speed, variable-temperature flow[J]. Meas Sci Technol, 2003, 14: 1054-1062. DOI:10.1088/0957-0233/14/7/321 |
| [8] |
BRUNN H H, TROPEA C. Thecalibration of inclined hot-wires probes[J]. J Phys E: Sci Instrum, 1985, 18: 405-412. DOI:10.1088/0022-3735/18/5/011 |
| [9] |
WESTPHAL R V, MEHTA R D. Crossed hot-wire data acquisition and reduction system[R]. NASA TM-85881, 1984.
|
| [10] |
BRUNN H H, NABHANI N, FARDAD A A, et al. Calibraton and analysis of X hot-wire probe signals[J]. Meas Sci Technol, 1990, 1: 782-785. DOI:10.1088/0957-0233/1/8/019 |
| [11] |
YASA T, PANIAAGUA G, DENOS R. Hot-wire anemometry for non-isothermal flows and effect of aging of the sensor wire[R]. Data acquisition and signal processing for turbomachinery applications Von Karman Institute for Fluid Dynamics, 2005.
|
| [12] |
CUKUEL B, ACARER S, ARTS T. A novel perspective to high-speed cross-hot-wire calibration methodology[J]. Exp Fluids, 2012, 53: 1073-1085. DOI:10.1007/s00348-012-1344-y |
| [13] |
MARCUS H, ALEXANDER S. Temperature corrections for constant temperature and constant current hot-wire anemometry[J]. Meas Sci Technol, 2010, 21: 10540. |
| [14] |
COME B, SARMA G R. Constant voltage anemometer practice in supersonic flows[J]. AIAA Journal, 2001, 39: 261-270. DOI:10.2514/2.1321 |
| [15] |
SARMA G R. Automated constant voltage anemometer for measurements with fluid temperature drift[J]. Review of Scientific Instruments, 2002, 73: 1313. DOI:10.1063/1.1447303 |
| [16] |
COLLIS D C, WILLIAMS M J. Two-dimensional convection from heated wires at low Reynolds numbers[J]. Journal of Fluid Mechanics, 1959, 6: 357-384. DOI:10.1017/S0022112059000696 |
| [17] |
ALEXANDER S, MARK Z. Applications of dense gases to model testing for aeronautical and hydrodynamic applications[J]. Meas Sci Technol, 2005, 16: 1710-1715. DOI:10.1088/0957-0233/16/9/002 |
| [18] |
ZHANG J, WANG X N, ZHANG J L, et al. A study of shear-layer corrections and a tensioned fabric wall for the localization of sound sources in wind tunnel[C]//The 25th AIAA/CEAS aeroacoustics conference, Delft, the Netherlands, 20-24 May, 2019.
|
| [19] |
POPE S B. Turbulence flow[M]. United Kingdom: University Cambridge press, 2000.
|
 2020, Vol. 38
2020, Vol. 38

