在诸多实际问题中连续介质的物理构型往往表现为不规则的几何形态,例如旋转机械叶片之间的空间区域。从数学角度而言,曲线坐标系就是微分同胚,即同维数Euclid空间中两个开集之间的双射,并且正、反映照具有一定的正则性。因此,基于曲线坐标系可以将直接定义在几何不规则的物理区域上的偏微分方程变换至定义在几何规则的参数域上的偏微分方程。具体应用曲线坐标系可以分为二类:第一类仅利用曲线坐标系实现区域变换,守恒律等控制方程依然基于Cartesian空间中的典则基进行展开;第二类不仅进行区域变换,而且将控制方程等相对于曲线坐标系自身确定的局部协变基或者逆变基进行展开。一般曲线坐标系下的张量场场论[1-4]不仅为区域变换而且为方程变换提供了系统思想与方法,由此在数值计算与理论分析中应用广泛。
值得指出,曲线坐标系[5]的具体构造往往蕴含物理构型的几何特征,由此按曲线坐标系的局部基展开的分量方程更能清晰地展现构型几何特征与力学过程等之间的关系。例如研究圆周运动,一般按圆的局部基(切向量与法向量)展开速度与加速度,可以得知法向加速度表现了速率与圆周曲率之间的关系。物理构型的几何特征与力学等过程之间的关系是力学与数学之间关系的重要方面,一直为业界学者所关注[6-8]。
基准曲面与其邻域内的张量场场论具有极其广泛的工程背景[9-10]。例如, 旋转机械叶片邻域内的流动,飞行器、潜航器壁面邻域内的流动等流固耦合问题都对机械的运行效能起着基础性的作用。就此,基于曲面的半正交系被广泛使用,其主要思想为:以基准曲面为基础,沿法向进行空间延拓以构成基面曲面邻域内的曲线坐标系。基于曲面的半正交系依然隶属非正交曲线坐标系。非正交曲线坐标系指曲线坐标系自身诱导的局部协变或者逆变基向量之间非两两正交,此时基向量不仅具有自身的长度而且可能带有特定的量纲,由此物理量相对于非正交基的分量不仅在数值上而且在量纲上不甚清晰。由此,应用中往往希望采用正交系,诸如球坐标系、柱坐标系等。但是由微分同胚确定的局部基向量虽然两两正交但其长度并非单位长度,即其仅是正交基而非单位正交系。张量分析中将具有微分同胚的曲线坐标系与其诱导的基称为完整系与完整基,而非由微分同胚诱导的基称为非完整基[1]。张量分析中的非完整基理论利用基向量与张量分量之间的转换关系,为物理量相对于单位正交基的展开提供了系统方法。特别地,当完整基为正交基,非完整基为其单位化而得的单位正交基时,基于非完整基理论可以便捷且可靠地获得各种张量微分算子相对于单位正交基的展开式[1, 4]。
本文为基准曲面与其邻域建立了一种完整的正交系,在此基础上应用非完整基理论可为曲面与其邻域内的张量场场论提供一种有效的方法,能够展现曲面几何与力学行为之间的联系。本文结构为:第1节阐述基于曲面主方向的正交系的非完整基理论,包括基于曲面主方向的正交系的构造、单位正交基的运动方程、基于非完整基理论开展场论以及具体应用方法等;第2节阐述本文所提场论方法的相关应用,包括可变形边界上的涡量动力学、曲面上的流体边界层方程、曲面介质的相关理论等;第3节为总结。本文另含附录,包括:曲面主方向单位正交基的运动方程、曲面主方向单位正交基下的基本场论运算、曲面主方向单位正交基下的曲面介质动量方程、曲面梯度算子的相关处理等。
1 基于曲面主方向的正交系的非完整基理论 1.1 曲面的基本几何量ℝ3中的光滑曲面,有如下的向量值映照表示:
| $ \sum {(\mathit{\boldsymbol{x}})} :{\mathbb{R}^2} \ni \mathit{\boldsymbol{x}} \mapsto \sum {(\mathit{\boldsymbol{x}})} \in {\mathbb{R}^3} $ |
可以定义曲面的局部协变基向量:
| $ {\mathit{\boldsymbol{g}}_\mathit{\boldsymbol{i}}}(\mathit{\boldsymbol{x}}) = \frac{{\partial \sum }}{{\partial {x^i}}}(\mathit{\boldsymbol{x}}) \in {\mathbb{R}^3},i = 1,2 $ |
对应为曲面上坐标线xi的切向量。对于曲面上的正则点(指{ g1(x), g2(x)}线性无关),可引入单位法向量:
| $ \mathit{\boldsymbol{n}}(\mathit{\boldsymbol{x}}) = \frac{{{\mathit{\boldsymbol{g}}_1} \times {\mathit{\boldsymbol{g}}_2}}}{{{{\left| {{\mathit{\boldsymbol{g}}_1} \times {\mathit{\boldsymbol{g}}_2}} \right|}_{{\mathbb{R}^3}}}}}(\mathit{\boldsymbol{x}}) \in {\mathbb{R}^3} $ |
就此,{ g1(x), g2(x), n (x)}构成曲面的局部协变基,按对偶关系则可确定局部逆变基{ g1(x), g2(x), n (x)}。
基于曲面上的局部基,可以引入曲面的度量张量
| $ \mathit{\boldsymbol{I}} \buildrel \Delta \over = {g_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^i} = {g^{ij}}{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}_j} = \delta _j^i{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} $ |
式中gij= gi· gj、gij= gi· gj分别为度量张量的协变与逆变分量。曲面的曲率张量
| $ \mathit{\boldsymbol{K}} \buildrel \Delta \over = {b_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^j} = {b^{ij}}{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}_j} = b_j^i{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} $ |
式中bij=
将线性代数中的同时对角化应用于度量张量的协变分量矩阵[gij](对称正定阵)与曲率张量的协变分量矩阵[bij](对称阵), 则有存在且唯一存在非奇异阵G ∈ℝ2×2, 使得
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{G}}^{\rm{T}}}\left[ {{g_{ij}}} \right]\mathit{\boldsymbol{G}} = \left[ {{\delta _{ij}}} \right]}\\ {{\mathit{\boldsymbol{G}}^{\rm{T}}}\left[ {{b_{ij}}} \right]\mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} {{\lambda _1}}&0\\ 0&{{\lambda _2}} \end{array}} \right)} \end{array}} \right. $ |
式中λi、λ2为特征多项式| B -λ I |=0的两个实数根,称为曲面的主曲率。根据GT[gij] G =[δij], 可引入单位正交基
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{ }}{\mathit{\boldsymbol{g}}_1}}&{{\mathit{\boldsymbol{g}}_2}} \end{array}} \right]\mathit{\boldsymbol{G}} $ |
e1及e2确定了曲面的两个主方向。根据Frobenius定理[5, 11],对曲面上每一点必存在一个邻域U,在U上存在新的正交参数系{ξ, η},使得新参数系对应的协变基向量gi(ξ, η)与曲面主方向ei平行,即(本文全文采用指标的Einstein求和约定, 指标带有下划线表示不参与求和)
| $ {\mathit{\boldsymbol{e}}_i} = \frac{1}{{\sqrt {{g_{\underline {ii} }}} }}{\mathit{\boldsymbol{g}}_i} = \sqrt {{g_{\underline {ii} }}} {\mathit{\boldsymbol{g}}^i},\;\;\;i = 1,2 $ |
值得指出,现有的协变基向量gi(ξ, η)、逆变基向量gi(ξ, η)都与对应的主方向ei平行,但一般而言不能三者相同。曲率张量相对于正交基{ g1(ξ, η), g2(ξ, η)}或者单位正交基{ e1(ξ, η), e2(ξ, η)}可以表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{K}} = {b^{ij}}(\xi ,\eta ){\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}_j}(\xi ,\eta ) = {b^{ij}}\left( {\sqrt {{g_{\underline {ii} }}} {\mathit{\boldsymbol{e}}_i}} \right) \otimes \\ \;\;\;\;\;\;\;\left( {\sqrt {{g_{\underline {ii} }}} {\mathit{\boldsymbol{e}}_j}} \right) = {\lambda _{\underline i }}{\mathit{\boldsymbol{e}}_i} \otimes {\mathit{\boldsymbol{e}}_i} \end{array} $ |
曲率张量的迹, tr K =λ1+λ2,定义为平均曲率,记为H;曲率张量的行列式,det K =λ1λ2,定义为Gauss曲率,记为KG。
1.2 正交基的标架运动方程对于曲面的一般基向量有标架运动方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{g}}_i}}}{{\partial {x_j}}} = \mathit{\Gamma }_{ji}^s{\mathit{\boldsymbol{g}}_s} + {b_{ji}}\mathit{\boldsymbol{n}}}\\ {\frac{{\partial {\mathit{\boldsymbol{g}}^i}}}{{\partial {x_j}}} = - \mathit{\Gamma }_{js}^i{\mathit{\boldsymbol{g}}^s} + b_j^i\mathit{\boldsymbol{n}}}\\ {\frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial {x_j}}} = - b_j^s{\mathit{\boldsymbol{g}}_s}} \end{array}} \right. $ |
此处引入第一类与第二类Christoffel符号
| $ \mathit{\Gamma }_{ji}^s = \frac{{\partial {\mathit{\boldsymbol{g}}_i}}}{{\partial {x_j}}} \cdot {\mathit{\boldsymbol{g}}^s},{\mathit{\Gamma }_{ji,s}} = \frac{{\partial {\mathit{\boldsymbol{g}}_i}}}{{\partial {x^j}}} \cdot {\mathit{\boldsymbol{g}}_s},\;i,j,s = 1,2 $ |
考虑曲面上的光滑曲线
| $ \left[ {0,L} \right] \ni S \mapsto r\left( S \right) = \sum {(\mathit{\boldsymbol{x}}(} s)) \in \Sigma $ |
式中S为弧长参数。r (S)在S点的无限小增量公式
| $ \begin{array}{l} \mathit{\boldsymbol{r}}(S + \Delta S) - \mathit{\boldsymbol{r}}(S) = \\ \;\;\;\mathit{\boldsymbol{\dot r}}(S) + \frac{1}{2}\mathit{\boldsymbol{\ddot r}}(S){(\Delta S)^2} + o\left( {{{(\Delta S)}^2}} \right) \end{array} $ |
式中
| $ \mathit{\boldsymbol{\dot r}}(S) = \frac{{\partial \Sigma }}{{\partial {x^i}}}\left( {\mathit{\boldsymbol{x}}\left( S \right)} \right){{\dot x}^i}\left( S \right) = {{\dot x}^i}{\mathit{\boldsymbol{g}}_i} = :{\mathit{\boldsymbol{e}}_1}\left( S \right); $ |
| $ \begin{array}{l} \mathit{\boldsymbol{\ddot r}}(S) = {{\ddot x}^i}{\mathit{\boldsymbol{g}}_i} + {{\dot x}^i}{{\dot x}^j}\frac{{\partial {\mathit{\boldsymbol{g}}_i}}}{{\partial {x^j}}}(\mathit{\boldsymbol{x}}(S)) = \\ \;\;\;\;\;\;\;\;\;\left( {{{\ddot x}^k} + \mathit{\Gamma }_{ij}^k{{\dot x}^i}{{\dot x}^j}} \right){\mathit{\boldsymbol{g}}_k} + {b_{ij}}{{\dot x}^i}{{\dot x}^j}\mathit{\boldsymbol{n}} = :\\ \;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\ddot r}}}_\parallel }(S) + {{\mathit{\boldsymbol{\ddot r}}}_ \bot }(S) \end{array} $ |
| $ {\mathit{\boldsymbol{e}}_1} = \mathit{\boldsymbol{\dot r}}(S),{\mathit{\boldsymbol{e}}_3} = \mathit{\boldsymbol{n}}(S),{\mathit{\boldsymbol{e}}_2} = {\mathit{\boldsymbol{e}}_3}(S) \times {\mathit{\boldsymbol{e}}_1}(S) $ |
并建立Cartesian坐标系(ξ, η,ζ},则有r (S+ΔS)- r (S)的参数有
| $ \left\{ \begin{gathered} \xi = \Delta S + \frac{1}{2}|{{\mathit{\boldsymbol{\ddot r}}}_\parallel }(S){|_{{\mathbb{R}^3}}}\cos \theta {(\Delta S)^2} + o\left( {{{(\Delta S)}^2}} \right); \hfill \\ \eta = \frac{1}{2}|{{\mathit{\boldsymbol{\ddot r}}}_\parallel }(S){|_{{\mathbb{R}^3}}}\sin \theta {(\Delta S)^2} + o\left( {{{(\Delta S)}^2}} \right); \hfill \\ \zeta = \frac{1}{2}{b_{ij}}{{\dot x}^i}{{\ddot x}^j}{(\Delta S)^2} + o\left( {{{(\Delta S)}^2}} \right) \hfill \\ \end{gathered} \right. $ |
式中θ为e1与
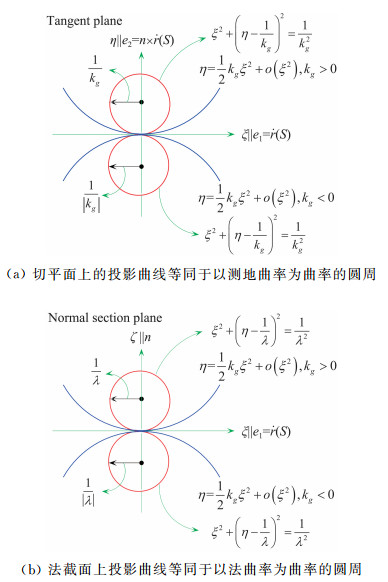
| $ \eta = \frac{1}{2}{\left| {{{\mathit{\boldsymbol{\ddot r}}}_\parallel }(S)} \right|_{{\mathbb{R}^3}}}\sin \theta \cdot {\xi ^2} + o\left( {{\xi ^2}} \right) = :\frac{1}{2}{k_g}{\xi ^2} + o\left( {{\xi ^2}} \right), $ |
表明r (S+ΔS)- r (S)在切平面的投影曲线(在二阶精度下)对应曲率为kg的圆周,kg称为曲线r (S)的测地曲率,如图 1(a)所示。类似地,
| $ \zeta = \frac{1}{2}\left( {{b_{ij}}{{\dot x}^i}{{\dot x}^j}} \right){\xi ^2} + o\left( {{\xi ^2}} \right) = :\frac{1}{2}\lambda {\xi ^2} + o\left( {{\xi ^2}} \right), $ |
|
图 1 曲面上的曲线 Fig.1 Curve on surface |
表明r (S+ΔS)- r (S)在由{ e1(S), e3(S)}构成的法截面上的投影曲线对应曲率为λ的圆周,λ称为曲线r (S)的法曲线,如图 1(b)所示。
综上所述,在二阶精度下,曲面上曲线在切平面的投影曲线对应以测地曲率为曲率的圆周;在法截面的投影曲线对应对法曲率为曲率的圆周。
对于曲面主方向的单位正交基{ eξ, eη, n }, 我们可以获得如下标架运动方程(详见附录:基于曲面主方向的单位正交基的标架运动方程)。
定理1.1 曲面主方向单位正交基的运动方程。
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\xi }}} = {\kappa _{g,\xi }}{\mathit{\boldsymbol{e}}_\eta } + {\lambda _\xi }\mathit{\boldsymbol{n}}}\\ {\frac{{\partial {\mathit{\boldsymbol{e}}_\eta }}}{{\partial {S_\eta }}} = {\kappa _{g,\eta }}{\mathit{\boldsymbol{e}}_\xi } + {\lambda _\eta }\mathit{\boldsymbol{n}}} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\eta }}} = - {\kappa _{g,\eta }}{\mathit{\boldsymbol{e}}_\eta }}\\ {\frac{{\partial {\mathit{\boldsymbol{e}}_\eta }}}{{\partial {S_\xi }}} = - {\kappa _{g,\xi }}{\mathit{\boldsymbol{e}}_\xi }} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial {S_\xi }}} = - {\lambda _{\hat \xi }}{\mathit{\boldsymbol{e}}_\xi }}\\ {\frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial {S_\eta }}} = - {\lambda _\eta }{\mathit{\boldsymbol{e}}_\eta }} \end{array}} \right. $ |
式中Sξ与Sη分别表示坐标曲线ξ与η的弧长坐标。值得指出,上述表达式中基向量相对于曲面弧长坐标的变化率都表现为与其正交的平面中以测地曲率或者主曲率为曲率的圆周运动。
基于单参数向量值映照的无限小展开(Taylor公式),并利用上述标架运动方程,可得
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_\xi }\left( {{S_\xi } + \Delta {S_\xi }} \right) - {\mathit{\boldsymbol{r}}_\xi }\left( {{S_\xi }} \right) = \Delta {S_\xi }{\mathit{\boldsymbol{e}}_\xi } + \\ \;\;\;\;\;\frac{1}{2}{\kappa _{g,\xi }}{\left( {\Delta {S_\xi }} \right)^2}{\mathit{\boldsymbol{e}}_\eta } + \frac{1}{2}{\lambda _\xi }{\left( {\Delta {S_\xi }} \right)^2}\mathit{\boldsymbol{n}} + {\rm{o}}\left( {{{\left( {\Delta {S_\xi }} \right)}^2}} \right)\\ {\mathit{\boldsymbol{r}}_\eta }\left( {{S_\eta } + \Delta {S_\eta }} \right) - {\mathit{\boldsymbol{r}}_\eta }\left( {{S_\eta }} \right) = \Delta {S_\eta }{\mathit{\boldsymbol{e}}_\eta } + \\ \;\;\;\;\frac{1}{2}{\kappa _{g,\eta }}{\left( {\Delta {S_\eta }} \right)^2}{\mathit{\boldsymbol{e}}_\xi } + \frac{1}{2}{\lambda _\eta }{\left( {\Delta {S_\eta }} \right)^2}\mathit{\boldsymbol{n}} + o\left( {{{\left( {\Delta {S_\eta }} \right)}^2}} \right) \end{array} \right. $ |
式中rξ(Sξ)与rη(Sη)分别为ξ-线与η-线的弧长参数表示。由此,主曲率λη可以理解为η-线在eη对应的主法截面上的投影曲线所对应的曲率圆的曲率;测地曲率κg, η为η-线在切平面上的投影曲线所对应的曲率圆的曲率,如图 2所示。类似地,主曲率λξ可以理解为ξ-线在eξ对应的主法截面上的投影曲线所对应的曲率圆的曲率;κg, ξ为ξ-线在切平面上的投影曲线所对应的曲率圆的曲率。

|
图 2 主曲率与测地曲率的几何意义 Fig.2 Geometric meaning of principal curvatures and geodesic curvatures |
利用上述曲面主方向的单位正交基的运动方程, 可以获得向量场物质导数的表达式。
定理1.2 曲面主方向单位正交基下向量场物质导数的表示。
设b为定义在质点上的向量值,其物质导数具有如下表达式
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{b}}}}{{{\rm{d}}t}} = \frac{{\mathop {\rm{d}}\limits^e \mathit{\boldsymbol{b}}}}{{{\rm{d}}t}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{b}} $ |
式中
| $ \frac{{\mathop {\rm{d}}\limits^e \mathit{\boldsymbol{b}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}b\langle \xi \rangle }}{{{\rm{d}}t}}{\mathit{\boldsymbol{e}}_\xi } + \frac{{{\rm{d}}b\langle \eta \rangle }}{{{\rm{d}}t}}{\mathit{\boldsymbol{e}}_\eta } + \frac{{{\rm{d}}b\langle \zeta \rangle }}{{{\rm{d}}t}}{\mathit{\boldsymbol{e}}_\zeta }; $ |
Ω定义为:
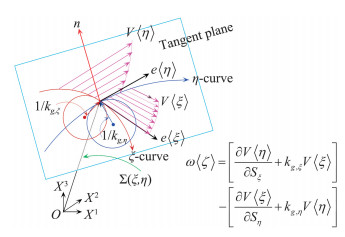
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}: = {\lambda _\eta }V\langle \eta \rangle {\mathit{\boldsymbol{e}}_\xi } - {\lambda _\xi }V\langle \xi \rangle {\mathit{\boldsymbol{e}}_\eta } + \left( {{\kappa _{g,\xi }}V\langle \xi \rangle - {\kappa _{g,\eta }}V\langle \eta \rangle } \right){\mathit{\boldsymbol{e}}_\zeta } $ |
Ω可称为曲面主方向单位正交基的角速度向量,表现为切平面与主法截面中各圆周运动的角速度向量的叠加。角速度向量由当地曲面的曲率与当地速度确定,如果在变形壁面上则完全由壁面曲率与壁面速度确定。
将质点轨迹上的曲面单位正交基作为随时间变化的运动基,上述基本结构建立了向量场的绝对变换率与相对于运动基的相对变换率之间的关系。以此,可获得速度与加速度关于曲面主方向单位正交基的合成形式。
定理1.3 速度与加速度关于曲面主方向单位正交基的合成形式。
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{V}} = \mathop {\mathit{\boldsymbol{V}}}\limits^e + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{r}}},\\ {\mathit{\boldsymbol{a}} = \mathop {\mathit{\boldsymbol{a}}}\limits^e + 2\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathop {\mathit{\boldsymbol{V}}}\limits^e + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times (\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{r}}) + \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} \times \mathit{\boldsymbol{r}}} \end{array}} \right. $ |
式中
对于张量场的微分算子,由于涉及对曲线坐标求偏导数故需要在完整基中展开,但运算后所得的新张量却可以在任意基下进行展开,所对应的张量分量满足坐标转换关系。考虑ℝ3中的非完整协变基{g(μ)}μ=13与逆变基{g(μ)}μ=13,二者之间依然满足对偶关系(g(α),g(β)) ℝ3=δαβ,(α, β=1, 2, 3)。非完整基自然可以由完整基线性表示,由此可以建立基向量之间的转换关系:
| $ {\mathit{\boldsymbol{g}}_{\left( \mu \right)}} = \left( {{\mathit{\boldsymbol{g}}_{(\mu )}} \cdot {\mathit{\boldsymbol{g}}^\gamma }} \right){\mathit{\boldsymbol{g}}_\gamma } = :C_{(\mu )}^\gamma {\mathit{\boldsymbol{g}}_\gamma } $ |
| $ {\mathit{\boldsymbol{g}}^{(\mu )}} = \left( {{\mathit{\boldsymbol{g}}^{(\mu )}} \cdot {\mathit{\boldsymbol{g}}_\gamma }} \right){\mathit{\boldsymbol{g}}^\gamma } = :C_\gamma ^{(\mu )}{\mathit{\boldsymbol{g}}^\gamma } $ |
考虑三阶张量在完整基与非完整基下的表示:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma }{\mathit{\boldsymbol{g}}_\alpha } \otimes {\mathit{\boldsymbol{g}}^\beta } \otimes {\mathit{\boldsymbol{g}}_\gamma } = \mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )}{\mathit{\boldsymbol{g}}_{(\lambda )}} \otimes {\mathit{\boldsymbol{g}}^{(\mu )}} \otimes {\mathit{\boldsymbol{g}}_{(\theta )}} $ |
式中张量分量定义为:
| $ \mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma } = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{g}}^\alpha },{\mathit{\boldsymbol{g}}_\beta },{\mathit{\boldsymbol{g}}^\gamma }} \right), $ |
| $ \mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{g}}^{(\lambda )}},{\mathit{\boldsymbol{g}}_{(\mu )}},{\mathit{\boldsymbol{g}}^{(\theta )}}} \right) $ |
按张量的多重线性函数的定义,则有张量分量之间满足坐标转换关系:
| $ \mathit{\Phi }_{ \cdot \beta }^{a \cdot \gamma } = C_{(\lambda )}^\alpha C_\beta ^{(\mu )}C_{(\theta )}^\gamma \mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )}, $ |
| $ \mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )} = C_\alpha ^{(\lambda )}C_{(\mu )}^\beta C_\gamma ^{(\theta )}\mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma } $ |
考虑张量场在完整基下的梯度运算
| $ \nabla \otimes \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\nabla _\xi }\mathit{\Phi }_{ \cdot \beta }^{a \cdot \gamma }{\mathit{\boldsymbol{g}}^\zeta } \otimes {\mathit{\boldsymbol{g}}_a} \otimes {\mathit{\boldsymbol{g}}^\beta } \otimes {\mathit{\boldsymbol{g}}_\gamma } $ |
式中张量分量的协变导数为:
| $ {\nabla _\zeta }\mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma } = \frac{{\partial \mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma }}}{{\partial \zeta }} + \mathit{\Gamma }_{\zeta \mu }^\alpha \mathit{\Phi }_{ \cdot \beta }^{\mu \cdot \gamma } - \mathit{\Gamma }_{\xi \beta }^\mu \mathit{\Phi }_{ \cdot \mu }^{\alpha \cdot \gamma } + \mathit{\Gamma }_{\zeta \mu }^\gamma \mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \mu } $ |
在完整基中定义的张量梯度作为新的张量可以在非完整基下表示, 记有如下形式:
| $ \nabla \otimes \mathit{\Phi } = {\nabla _{(\xi )}}\mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )}{\mathit{\boldsymbol{g}}^{(\xi )}} \otimes {\mathit{\boldsymbol{g}}_{(\lambda )}} \otimes {\mathit{\boldsymbol{g}}^{(\mu )}} \otimes {\mathit{\boldsymbol{g}}_{(\theta )}} $ |
式中非完整基下的张量分量按坐标转换关系由完整基下的分量确定,即:
| $ {\nabla _{(\xi )}}\mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )} = C_{(\xi )}^\zeta C_\alpha ^{(\lambda )}C_{(\mu )}^\beta C_\gamma ^{(\theta )}{\nabla _\zeta }\mathit{\Phi }_{ \cdot \beta }^{\alpha \cdot \gamma } $ |
非完整基理论的基本思想为在非完整基下定义形式偏导数、形式Christoffel符号以及形式协变导数, 由此间接性地获得张量梯度在非完整基下的表示, 如下所述:
| $ \left\{ \begin{array}{l} \frac{\partial }{{\partial {x^{(\mu )}}}} = C_{(\mu )}^\gamma \frac{\partial }{{\partial {x^\gamma }}}\\ \mathit{\Gamma }_{(a)(\beta )}^{(\mu )} = C_\gamma ^{(\mu )}C_{(a)}^\lambda C_{(\beta )}^\theta \mathit{\Gamma }_{\lambda \theta }^\gamma - C_{(\alpha )}^\lambda C_{(\beta )}^\theta \frac{{\partial C_{{\theta ^\mu }}^{(\mu )}}}{{\partial {x^\lambda }}} \ne \mathit{\Gamma }_{(\beta )\left( \alpha \right)}^{(\mu )}\\ {\nabla _{(\xi )}}\mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )} = \frac{\partial }{{\partial {x^{(\xi )}}}}\mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\theta )} + \mathit{\Gamma }_{(\hat \xi )(\eta )}^{(\lambda )}\mathit{\Phi }_{ \cdot (\mu )}^{(\eta ) \cdot (\theta )} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Gamma }_{(\xi )(\mu )}^{(\eta )}\mathit{\Phi }_{ \cdot (\eta )}^{(\lambda ) \cdot (\theta )} + \mathit{\Gamma }_{(\xi )(\eta )}^{(\theta )}\mathit{\Phi }_{ \cdot (\mu )}^{(\lambda ) \cdot (\eta )} \end{array} \right. $ |
式中
值得指出, 如果完整基为正交基,而非完整基为其单位化, 则形式偏导数、形式Christoffel符号与形式协变导数具有最为简单的形式, 如下所述:
| $ \left\{ \begin{array}{l} \frac{\partial }{{\partial {x^{(\theta )}}}} = \frac{1}{{\sqrt {{g_{\underline {\theta \theta } }}} }}\frac{\partial }{{\partial {x^\theta }}};\\ \mathit{\Gamma }\langle \alpha \beta \alpha \rangle = - \mathit{\Gamma }\langle \alpha \alpha \beta \rangle = \frac{1}{{\sqrt {{g_{\underline {\beta \beta } }}} }}\frac{{\partial \ln \sqrt {{g_{\underline {\alpha \alpha } }}} }}{{\partial {x^\beta }}},\\ \;\;\;\;\;\;\;\;\;\;\;\;此处\;\alpha \ne \beta ;\\ \nabla \langle \mu \rangle \mathit{\Phi }\langle \alpha \beta \gamma \rangle = \frac{{\partial \mathit{\Phi }\langle \alpha \beta \gamma \rangle }}{{\partial {x^{(\mu )}}}} + \mathit{\Gamma }\langle \mu \theta \alpha \rangle \mathit{\Phi }\langle \theta \beta \gamma \rangle + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Gamma }\langle \mu \theta \beta \rangle \mathit{\Phi }\langle \alpha \theta \gamma \rangle + \mathit{\Gamma }\langle \mu \theta \gamma \rangle \mathit{\Phi }\langle \alpha \beta \theta \rangle \end{array} \right. $ |
由于单位正交基的协变基向量值与逆变基向量一致, 由此单位正交基下张量分量的逆变与协变分量一致。就此情形, 本文将指标都写在同一行, 如上所示。
1.4 曲面与其邻域内适用的非完整基理论力学研究中常需要在一张基准曲面及其邻域内开展张量场场论。因此,常基于基准曲面的法向进行三维延拓,构造三维曲线坐标系{ x, ζ}:
| $ \begin{gathered} \mathit{\boldsymbol{X}}(\mathit{\boldsymbol{x}},\zeta ):{\mathscr{D}_x} \times ( - \delta ,\delta ) \ni \left( {\begin{array}{*{20}{l}} x \\ \zeta \end{array}} \right) \mapsto \hfill \\ \;\;\;\mathit{\boldsymbol{X}}(\mathit{\boldsymbol{x}},\zeta ) = \sum {(\mathit{\boldsymbol{x}})} + \zeta \mathit{\boldsymbol{n}}(\mathit{\boldsymbol{x}}) \in {\mathbb{R}^3} \hfill \\ \end{gathered} $ |
其局部协变基{gα(x, ζ)}α=13为
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\bar g}}}_i} \buildrel \Delta \over = \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial {x^i}}}(\mathit{\boldsymbol{x}},\zeta ) = {\mathit{\boldsymbol{g}}_i}(\mathit{\boldsymbol{x}}) + \zeta \frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial {x^i}}}(\mathit{\boldsymbol{x}})\\ \;\;\;\; = \left( {\delta _i^j - \zeta b_i^j} \right){\mathit{\boldsymbol{g}}_j}(\mathit{\boldsymbol{x}}),\;\;\;\;\;\;i = 1,2\\ {{\mathit{\boldsymbol{\bar g}}}_3} \buildrel \Delta \over = \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial \zeta }}(\mathit{\boldsymbol{x}},\zeta ) = \mathit{\boldsymbol{n}}(\mathit{\boldsymbol{x}}) \end{array} \right. $ |
此处{gi(x, ζ)}i=12亦为当地曲面∑ζ:
| $ \sum\nolimits_\zeta {(\mathit{\boldsymbol{x}})} :{\mathscr{D}_x} \ni \mathit{\boldsymbol{x}} \mapsto \sum\nolimits_\zeta {(\mathit{\boldsymbol{x}})} = \sum {(\mathit{\boldsymbol{x}})} + \zeta \mathit{\boldsymbol{n}}(\mathit{\boldsymbol{x}}) \in {\mathbb{R}^3} $ |
的局部协变基。由于,一般的曲面坐标系对应的协变基向量不一定正交,由此上述三维曲线坐标系仅有第三个基向量(法向量)与前二个基向量(当地曲面的协变基向量)正交,故常称为基于基准曲面的半正交系。按微积分中全局微分同胚的存在性定理[5],存在基于曲面的半正交系需要满足如下条件:
| $ \begin{array}{l} {\rm det}\left( {{{\mathit{\boldsymbol{\bar g}}}_1},{{\mathit{\boldsymbol{\bar g}}}_2},{{\bar g}_3}} \right) = \left[ {1 + {I_1}(\mathit{\boldsymbol{K}})( - \zeta ) + {I_2}(\mathit{\boldsymbol{K}}){{( - \zeta )}^2}} \right] \cdot \sqrt g \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left[ {1 - H\zeta + {K_G}{\zeta ^2}} \right] \cdot \sqrt g \ne 0 \end{array} $ |
式中{Ir(K)}r=12表示基准曲面的曲率张量K的主不变量,
如果基准曲面采用基于主方向的正交系{ξ, η}, 则有当地曲面的向量值映照表示:
| $ \begin{gathered} \sum\nolimits_\zeta {(\xi ,\eta )} :{\mathscr{D}_{\xi \eta }} \ni \{ \xi ,\eta \} \mapsto \hfill \\ \;\;\;\;\sum\nolimits_\zeta {(\xi ,\eta )} = \sum {(\xi ,\eta )} + \zeta \mathit{\boldsymbol{n}}(\xi ,\eta ) \in {\mathbb{R}^3} \hfill \\ \end{gathered} $ |
其局部协变基为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\bar g}}}_\xi }(\xi ,\eta ,\zeta ) = \left( {1 - \zeta {\lambda _{\hat \xi }}} \right){\mathit{\boldsymbol{g}}_\xi }(\xi ,\eta )\\ {{\mathit{\boldsymbol{\bar g}}}_\eta }(\xi ,\eta ,\zeta ) = \left( {1 - \zeta {\lambda _\eta }} \right){\mathit{\boldsymbol{g}}_\eta }(\xi ,\eta )\\ {{\mathit{\boldsymbol{\bar g}}}_\zeta }(\xi ,\eta ,\zeta ) = \mathit{\boldsymbol{n}}(\xi ,\eta ) \end{array} \right. $ |
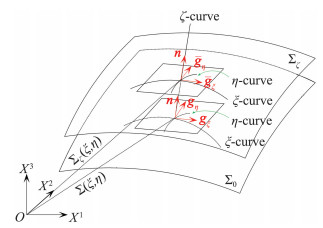
可见沿法向不同当地曲面的协变基向量{gξ(ξ, η, ζ), gη(ξ, η, ζ)}与基准曲面的协变基向量{ gξ(ξ, η), gη(ξ, η)}保持平行, 以此构成曲面及其邻域内的正交基, 如图 3所示。
|
图 3 基于曲面主方向的正交系 Fig.3 The orthogonal coordinate system based on the principal directions of the surface ∑代表基面,∑ζ代表当地曲面,其沿法向偏离基准曲面∑的距离为ζ |
对完整的正交基{gξ(ξ, η, ζ), gη(ξ, η, ζ); n (ξ, η)}进行单位化, 则获得非完整的单位正交基{ e 〈ξ〉, e 〈η〉, e 〈ζ〉}。按完整基理论, 可以计算得非自然为零的Christoffel符号, 如下所示:
| $ \left\{ \begin{array}{l} \mathit{\bar \Gamma }\langle \xi \eta \xi \rangle = \frac{1}{{\sqrt {{{\bar g}_{\eta \eta }}} }}\frac{{\partial \ln \sqrt {{{\bar g}_{\xi \xi }}} }}{{\partial \eta }} = - {{\bar \kappa }_{g,\xi }}\\ \mathit{\bar \Gamma }\langle \eta \xi \eta \rangle = \frac{1}{{\sqrt {{{\bar g}_{\xi \xi }}} }}\frac{{\partial \ln \sqrt {{{\bar g}_{\eta \eta }}} }}{{\partial \xi }} = - {{\bar \kappa }_{g,\eta }} \end{array} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\bar \Gamma }\langle \xi \zeta \xi \rangle = \frac{1}{{\sqrt {{{\bar g}_{\zeta \zeta }}} }}\frac{{\partial \ln \sqrt {{{\bar g}_{\xi \xi }}} }}{{\partial \zeta }} = - {{\bar \lambda }_\xi }}\\ {\mathit{\bar \Gamma }\langle \eta \zeta \eta \rangle = \frac{1}{{\sqrt {{{\bar g}_{\zeta \zeta }}} }}\frac{{\partial \ln \sqrt {{{\bar g}_{\eta \eta }}} }}{{\partial \zeta }} = - {{\bar \lambda }_\eta }} \end{array}} \right. $ |
式中κg, ξ与κg, η为当地曲面∑ζ相对于主方向gξ与gη的测地曲率; λξ与λη为当地曲面∑ζ相对于正交系ξ与η的主曲率。进一步可以计算得到, 当地曲面与基准曲面的测地曲率、主曲率之间的联系,如下所示:
| $ \left\{ \begin{array}{l} {{\bar \kappa }_{g,\xi }} = \frac{{{\kappa _{g,\xi }}}}{{1 - \zeta {\lambda _\eta }}} + \frac{\zeta }{{\left( {1 - \zeta {\lambda _\eta }} \right)\left( {1 - \zeta {\lambda _\xi }} \right)\sqrt {{g_{\eta \eta }}} }}\frac{{\partial {\lambda _\xi }}}{{\partial \eta }}\\ {{\bar \kappa }_{g,\eta }} = \frac{{{\kappa _{g,\eta }}}}{{1 - \zeta {\lambda _\xi }}} + \frac{\zeta }{{\left( {1 - \zeta {\lambda _\xi }} \right)\left( {1 - \zeta {\lambda _\eta }} \right)\sqrt {{g_{\xi \xi }}} }}\frac{{\partial {\lambda _\eta }}}{{\partial \xi }} \end{array} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar \lambda }_\xi } = \frac{{{\lambda _\xi }}}{{1 - \zeta {\lambda _\xi }}}}\\ {{{\bar \lambda }_\eta } = \frac{{{\lambda _\eta }}}{{1 - \zeta {\lambda _\eta }}}} \end{array}} \right. $ |
至此, 按非完整基理论[1, 4],我们可以便捷地获得张量场微分算子的分量表示。考虑向量场
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = {A^\xi }{{\mathit{\boldsymbol{\bar g}}}_\xi } + {A^\eta }{{\mathit{\boldsymbol{\bar g}}}_\eta } + {A^\zeta }n\\ \;\;\; = A\langle \xi \rangle \mathit{\boldsymbol{e}}\langle \xi \rangle + A\langle \eta \rangle \mathit{\boldsymbol{e}}\langle \eta \rangle + A\langle \zeta \rangle \mathit{\boldsymbol{e}}\langle \zeta \rangle \end{array} $ |
其左梯度可以表示为
| $ \nabla \otimes \mathit{\boldsymbol{A}} = \nabla \langle \alpha \rangle \mathit{\boldsymbol{A}}\langle \beta \rangle \mathit{\boldsymbol{e}}\langle \alpha \rangle \otimes \mathit{\boldsymbol{e}}\langle \beta \rangle $ |
各分量可以计算如下:
| $ \left\{ \begin{array}{l} \nabla \langle \xi \rangle A\langle \xi \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\xi \xi }}} }}\frac{{\partial A\langle \xi \rangle }}{{\partial \xi }} - {{\bar \kappa }_{g,\xi }}A\langle \eta \rangle - {{\bar \lambda }_\xi }A\langle \zeta \rangle \\ \nabla \langle \xi \rangle A\langle \eta \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\xi \xi }}} }}\frac{{\partial A\langle \eta \rangle }}{{\partial \xi }} + {{\bar \kappa }_{g,\xi }}A\langle \xi \rangle \\ \nabla \langle \xi \rangle A\langle \zeta \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\xi \xi }}} }}\frac{{\partial A\langle \zeta \rangle }}{{\partial \xi }} + {{\bar \lambda }_\xi }A\langle \xi \rangle \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \nabla \langle \eta \rangle A\langle \xi \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\eta \eta }}} }}\frac{{\partial A\langle \xi \rangle }}{{\partial \eta }} + {{\bar \kappa }_{g,\eta }}A\langle \eta \rangle \\ \nabla \langle \eta \rangle A\langle \eta \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\eta \eta }}} }}\frac{{\partial A\langle \eta \rangle }}{{\partial \eta }} - {{\bar \kappa }_{g,\eta }}A\langle \xi \rangle - {{\bar \lambda }_\eta }A\langle \zeta \rangle \\ \nabla \langle \eta \rangle A\langle \zeta \rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\eta \eta }}} }}\frac{{\partial A\langle \zeta \rangle }}{{\partial \eta }} + {{\bar \lambda }_\eta }A\langle \eta \rangle \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \nabla \langle \zeta \rangle A\langle \xi \rangle = \frac{{\partial A\langle \xi \rangle }}{{\partial \zeta }}\\ \nabla \langle \zeta \rangle A\langle \eta \rangle = \frac{{\partial A\langle \eta \rangle }}{{\partial \zeta }}\\ \nabla \langle \zeta \rangle A\langle \zeta \rangle = \frac{{\partial A\langle \zeta \rangle }}{{\partial \zeta }} \end{array} \right. $ |
基于非完整基理论,可以可靠且便捷地获得向量场的散度、旋度、对流项与Laplace项等在曲面主方向单位正交基下的表达式(详见附录:曲面主方向单位正交基下的基本场论运算)。值得指出,柱坐标系、球坐标系等都可以理解为设定基准曲面上的法向延拓,并且正交的协变基向量正好平行于当地曲面的主方向与法方向,由此基于曲面方向的非完整基理论可以统一相关曲线坐标系下的场论。
值得指出,数学上虽然存在曲面的参数坐标使得参数曲线的切向量平行于主方向,但是仅有局部存在性而无一般的显式表达形式。由此,基于曲面主方向的正交系的非完整基理论并不能直接应用于计算流体力学等方面。然而,我们可以利用相对于完整基与非完整基的张量分量之间的转化关系解决上述问题。具体可以分为以下两个方面。
(1) 基于Christoffel符号之间的转化关系,可以确定出曲面的测地曲率与主曲率。由一般的转换关系式:
| $ \begin{array}{l} \mathit{\Gamma }\langle \alpha \beta \alpha \rangle = C_\theta ^{(\alpha )}C_{(\alpha )}^\lambda C_{(\beta )}^\mu \mathit{\Gamma }_{\lambda \mu }^\theta - C_{(\alpha )}^\lambda C_{(\beta )}^\mu \frac{{\partial C_\mu ^{(\alpha )}}}{{\partial {x^\lambda }}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \ne \beta \end{array} $ |
对应有确定测地曲率的转换关系:
| $ \left\{ \begin{array}{l} \mathit{\bar \Gamma }\langle \xi \eta \xi \rangle = - {{\bar \kappa }_{g,\xi }} = C_\theta ^{(\xi )}C_{(\xi )}^\lambda C_{(\eta )}^\mu \mathit{\Gamma }_{\lambda \mu }^\theta - \\ \;\;\;\;\;\;\;\;\;\;\;\;C_{(\xi )}^\lambda C_{(\eta )}^\mu \frac{{\partial C_\mu ^{(\xi )}}}{{\partial {x^\lambda }}}\\ \mathit{\bar \Gamma }\langle \eta \xi \eta \rangle = - {{\bar \kappa }_{k,\eta }} = C_\theta ^{(\eta )}C_{(\eta )}^\lambda C_{(\xi )}^\mu \mathit{\Gamma }_{\lambda \mu }^\theta - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;C_{(\eta )}^\lambda C_{(\xi )}^\mu \frac{{\partial C_\mu ^{(\eta )}}}{{\partial {x^\lambda }}} \end{array} \right. $ |
确定主曲率的转换关系:
| $ \left\{ \begin{array}{l} \mathit{\bar \Gamma }\langle \xi \zeta \xi \rangle = - {{\bar \lambda }_\xi } = C_\theta ^{(\xi )}C_{(\xi )}^\lambda C_{(\zeta )}^\mu \mathit{\Gamma }_{\lambda \mu }^\theta - \\ \;\;\;\;\;\;\;\;\;\;\;\;C_{(\xi )}^\lambda C_{(\zeta )}^\mu \frac{{\partial C_\mu ^{(\xi )}}}{{\partial {x^\lambda }}}\\ \mathit{\bar \Gamma }\langle \eta \zeta \eta \rangle = - {{\bar \lambda }_\eta } = C_\theta ^{(\eta )}C_{(\eta )}^\lambda C_{(\zeta )}^\mu \mathit{\Gamma }_{\lambda \mu }^\theta - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;C_{(\eta )}^\lambda C_{(\zeta )}^\mu \frac{{\partial C_\mu ^{(\eta )}}}{{\partial {x^\lambda }}} \end{array} \right. $ |
式中Cβ(α)= e 〈α〉 · gβ,C(α)β= e 〈α〉 · gβ为非完整基与完整基之间的转换系数。基于曲面的向量值映照(参数曲线无需与主方向平行)就可以确定主方向, 结合实际计算中采用的曲线坐标系所确定的局部基就可以确定基转换系数, 以此按上述转换关系可以间接性地确定测地曲率与主曲率。
(2) 基于曲面主方向的正交系的非完整基理论, 可以推导力学中诸多物理量的表达式,以期建立曲面几何与力学行为之间的关系。可以通过张量分量之间的转换关系, 由实际计算所采用的坐标系下的分量间接性地获得非完整基下的分量。
综上所述, 基于非完整基与非完整基之间Christoffel符号与张量分量之间的转化关系, 实际计算时可以采用适合的曲线坐标系(完整基), 然后再通过转换关系获得曲面曲率与张量相对基于曲面主方向的单位正交基(非完整基)的表达式。
值得指出, 诸多文献对于完整的正交系的处理往往引入Lame系数hα=
| $ \frac{{\partial \mathit{\boldsymbol{e}}\langle \alpha \rangle }}{{\partial {x^\beta }}} = \left\{ \begin{array}{l} \frac{1}{{{h_\alpha }}}\frac{{\partial {h_\beta }}}{{\partial {x^\alpha }}}\mathit{\boldsymbol{e}}\langle \beta \rangle \;\;\;\;\;\;\;\;\;\alpha \ne \beta \\ - \sum\limits_{\gamma \ne \alpha } {\frac{1}{{{h_\gamma }}}} \frac{{\partial {h_\alpha }}}{{\partial {x^\gamma }}}\mathit{\boldsymbol{e}}\langle \gamma \rangle \quad \alpha = \beta \end{array} \right. $ |
式中Lame系数相对于坐标的偏导数可以联系与测地曲率或者主曲率,但并不是直接的联系。本文推导了平行于主方向的单位正交基的运动方程,可见只有基向量对坐标曲线的弧长求偏导数才有完全的曲率表示。原则上,为获得张量场微分算子的分量表示,可以首先将张量场相对于单位正交基展开,然后求关于曲线坐标的偏导数,涉及基向量的偏导数就利用上述标架运动方程。但是,如此操作易使得Lame系数的相关项越来越复杂,而且整个操作是步骤型的,不能直接写出张量场微分算子的表达式,曲面曲率也未能直接显现。
1.5 曲面半正交基的相关性质如果基准曲面采用的参数坐标{ x }非正交, 则基于基准曲面的法向进行空拓延拓所得的完整系{ x, ζ}为半正交系, 并且当地曲面的参数坐标依然为{ x },
| $ \begin{gathered} \sum\nolimits_\zeta {\left( {{x^1},{x^2}} \right)} :{\mathscr{D}_x} \ni \left\{ {{x^1},{x^2}} \right\} \mapsto \hfill \\ \;\;\;\;\;\;\;\sum\nolimits_\zeta {\left( {{x^1},{x^2}} \right)} = \sum {\left( {{x^1},{x^2}} \right)} + \zeta \mathit{\boldsymbol{n}}\left( {{x^1},{x^2}} \right) \in {\mathbb{R}^3} \hfill \\ \end{gathered} $ |
此处ζ作为参数。
以下确定当地曲面∑ζ的坐标曲线的测度曲率与法截线曲率。设其局部协变基为{ g1, g2}考虑
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{g}}_1} = \frac{{\partial {\Sigma _\zeta }}}{{\partial {x^1}}} = :{h_1}{\mathit{\boldsymbol{e}}_1}\\ {\mathit{\boldsymbol{g}}_2} = \frac{{\partial {\Sigma _\zeta }}}{{\partial {x^2}}} = :{h_2}{\mathit{\boldsymbol{e}}_2} \end{array} \right. $ |
则有:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{e}}_1}}}{{\partial {S_1}}} = \frac{\partial }{{\partial {S_1}}}\left( {\frac{1}{{{h_1}}}{\mathit{\boldsymbol{g}}_1}} \right) = - \frac{1}{{h_1^2}}\frac{{\partial {h_1}}}{{\partial {S_1}}}{\mathit{\boldsymbol{g}}_1} + \frac{1}{{{h_1}}}\frac{{\partial {\mathit{\boldsymbol{g}}_1}}}{{\partial {S_1}}}\\ = - \frac{{\partial \ln {h_1}}}{{\partial {S_1}}}{\mathit{\boldsymbol{e}}_1} + \frac{1}{{h_1^2}}\frac{{\partial {\mathit{\boldsymbol{g}}_1}}}{{\partial {x^1}}}\\ = - \frac{{\partial \ln {h_1}}}{{\partial {S_1}}}{\mathit{\boldsymbol{e}}_1} + \frac{1}{{h_1^2}}\left( {\Gamma _{11}^S{\mathit{\boldsymbol{g}}_S} + {b_{11}}\mathit{\boldsymbol{n}}} \right)\\ = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}&\mathit{\boldsymbol{n}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} { - \frac{{\partial \ln {h_1}}}{{\partial {S_1}}} + \frac{{\mathit{\Gamma }_{11}^1}}{{{h_1}}}}\\ {\frac{{{h_2}\mathit{\Gamma }_{11}^2}}{{h_1^2}}}\\ {\frac{{{b_{11}}}}{{h_1^2}}} \end{array}} \right] \end{array} $ |
结合x1-坐标曲线关于其弧长的无限小展开
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_1}\left( {{S_1} + \Delta {S_1}} \right) - {\mathit{\boldsymbol{r}}_1}\left( {{S_1}} \right) = \\ \;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot r}}}_1}\left( {{S_1}} \right)\Delta {S_1} + \frac{1}{2}{{\mathit{\boldsymbol{\ddot r}}}_1}\left( {{S_1}} \right){\left( {\Delta {S_1}} \right)^2} + o\left( {{{\left( {\Delta {S_1}} \right)}^2}} \right)\\ \;\;\;\;\;\;\;\; = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}&\mathit{\boldsymbol{n}} \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\Delta {S_1} + \frac{1}{2}\left( { - \frac{{\partial \ln {h_1}}}{{\partial {S_1}}} + \frac{{\mathit{\Gamma }_{11}^1}}{{{h_1}}}} \right){{\left( {\Delta {S_1}} \right)}^2} + o\left( {{{\left( {\Delta {S_1}} \right)}^2}} \right)}\\ {\frac{1}{2}\frac{{{h_2}\mathit{\Gamma }_{11}^2}}{{h_1^2}}{{\left( {\Delta {S_1}} \right)}^2} + o\left( {{{\left( {\Delta {S_1}} \right)}^2}} \right)}\\ {\frac{1}{2}\frac{{{b_{11}}}}{{h_1^2}}{{\left( {\Delta {S_1}} \right)}^2} + o\left( {{{\left( {\Delta {S_1}} \right)}^2}} \right)} \end{array}} \right] \end{array} $ |
x2-坐标曲线可作类似展开,可确定坐标曲线的测地曲率{κg, i}i=12与法截线曲率{λi}i=12
| $ \left\{ {\begin{array}{*{20}{l}} {{\kappa _{g,1}} = \frac{{{h_2}}}{{h_1^2}}\mathit{\Gamma }_{11}^2\sin \theta }\\ {{\kappa _{g,2}} = \frac{{{h_1}}}{{h_2^2}}\mathit{\Gamma }_{22}^1\sin \theta } \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _1} = \frac{{{b_{11}}}}{{h_1^2}}}\\ {{\lambda _2} = \frac{{{b_{22}}}}{{h_2^2}}} \end{array}} \right. $ |
此处θ为坐标曲线之间的夹角, {bij}与{Γijk}分别为当地曲面的曲率张量与Christoffel符号。
计算当地曲面度量张量的协变分量:
| $ \left[ {\begin{array}{*{20}{l}} {{g_{11}}}&{{g_{12}}}\\ {{g_{21}}}&{{g_{22}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {h_1^2}&{{h_1}{h_2}\cos \theta }\\ {{h_1}{h_2}\cos \theta }&{h_2^2} \end{array}} \right] $ |
可得度量张量的逆变分量:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{g^{11}}}&{{g^{12}}}\\ {{g^{21}}}&{{g^{22}}} \end{array}} \right] = \frac{1}{{h_1^2h_2^2\sin \theta }}\left[ {\begin{array}{*{20}{c}} {h_2^2}&{ - {h_1}{h_2}\cos \theta }\\ { - {h_1}{h_2}\cos \theta }&{h_1^2} \end{array}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{h_1^2{{\sin }^2}\theta }}}&{ - \frac{{\cos \theta }}{{{h_1}{h_2}{{\sin }^2}\theta }}}\\ { - \frac{{\cos \theta }}{{{h_1}{h_2}{{\sin }^2}\theta }}}&{\frac{1}{{h_2^2{{\sin }^2}\theta }}} \end{array}} \right] \end{array} $ |
现有当地曲面曲率张量的协变分量:
| $ \left[ {\begin{array}{*{20}{l}} {{b_{11}}}&{{b_{12}}}\\ {{b_{21}}}&{{b_{22}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}h_1^2}&{{b_{12}}}\\ {{b_{21}}}&{{\lambda _2}h_2^2} \end{array}} \right] $ |
则可得曲率张量的混合分量:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {b_1^1}&{b_2^1}\\ {b_1^2}&{b_2^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{g^{11}}}&{{g^{12}}}\\ {{g^{21}}}&{{g^{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{b_{11}}}&{{b_{12}}}\\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]\\ \;\;\; = \left[ {\begin{array}{*{20}{c}} {\frac{{{\lambda _1}}}{{{{\sin }^2}\theta }} - \frac{{\cos \theta }}{{{h_1}{h_2}{{\sin }^2}\theta }}{b_{12}}}&{ - \frac{{{h_2}\cos \theta }}{{{h_1}{{\sin }^2}\theta }}{\lambda _2} + \frac{{{b_{12}}}}{{h_1^2{{\sin }^2}\theta }}}\\ { - \frac{{{h_2}\cos \theta }}{{{h_1}{{\sin }^2}\theta }}{\lambda _1} + \frac{{{b_{12}}}}{{h_2^2{{\sin }^2}\theta }}}&{\frac{{{\lambda _2}}}{{{{\sin }^2}\theta }} - \frac{{\cos \theta }}{{{h_1}{h_2}{{\sin }^2}\theta }}{b_{12}}} \end{array}} \right] \end{array} $ |
基于曲率张量的混合分量,可以确定当地曲面的Gauss曲率KG=det[bji]与平均曲率H=tr[bji](当地曲面的一般坐标曲线的法截线曲率{λ1, λ2}不同于主法截线曲率{λξ, λη};但有KG=λξλη,H=λξ+λη),就此可确定
| $ {b_{12}} = \frac{{\left( {{\lambda _1} + {\lambda _2} - H{{\sin }^2}\theta } \right){h_1}{h_2}}}{{2\cos \theta }} $ |
至此, 可以获得曲率张量的混合分量与坐标曲线对应的法截线曲率之间的关系:
| $ \left\{ \begin{array}{l} b_1^1 = \frac{1}{{{{\sin }^2}\theta }}\frac{{{\lambda _1} - {\lambda _2} + H{{\sin }^2}\theta }}{2}\\ b_2^2 = \frac{1}{{{{\sin }^2}\theta }}\frac{{{\lambda _2} - {\lambda _1} + H{{\sin }^2}\theta }}{2}\\ b_2^1 = \frac{1}{{{{\sin }^2}\theta \cos \theta }}\frac{{{h_2}}}{{{h_1}}} \cdot \\ \;\;\;\;\;\;\left[ { - {\lambda _2}{{\cos }^2}\theta + \frac{{{\lambda _1} + {\lambda _2} - H{{\sin }^2}\theta }}{2}} \right]\\ b_1^2 = \frac{1}{{{{\sin }^2}\theta \cos \theta }}\frac{{{h_1}}}{{{h_2}}} \cdot \\ \;\;\;\;\;\;\;\left[ { - {\lambda _1}{{\cos }^2}\theta + \frac{{{\lambda _1} + {\lambda _2} - H{{\sin }^2}\theta }}{2}} \right] \end{array} \right. $ |
可见, 当参数曲线为平行于主方向的正交系{ξ, η}, 则有b11=λξ, b22=λη, b21=b12=0。
综上所述, 可获得当地曲面的部分第二类Christoffel符号与坐标曲线的测度曲率与主曲率之间的关系。
| $ \left\{ \begin{array}{l} \mathit{\Gamma }_{12}^3 = \mathit{\Gamma }_{21}^3 = {b_{12}} = \frac{{{\lambda _1} + {\lambda _2} - H{{\sin }^2}\theta }}{{2\cos \theta }}{h_1}{h_2}\\ \mathit{\Gamma }_{11}^3 = {b_{11}} = {\lambda _1}h_1^2\\ \mathit{\Gamma }_{22}^3 = {b_{22}} = {\lambda _2}h_2^2\\ \mathit{\Gamma }_{13}^3 = \mathit{\Gamma }_{23}^3 = \mathit{\Gamma }_{33}^3 = 0 \end{array} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }_{11}^2 = \frac{{h_1^2}}{{{h_2}\sin \theta }}{\kappa _{g,1}}}\\ {\mathit{\Gamma }_{22}^1 = \frac{{h_2^2}}{{{h_1}\sin \theta }}{\kappa _{g,2}}} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }_{13}^i = - b_1^i,}&{i = 1,2}\\ {\mathit{\Gamma }_{23}^i = - b_2^i,}&{i = 1,2} \end{array}} \right. $ |
对于其他第二类Christoffel符号, 可基于一般关系式:
| $ \mathit{\Gamma }_{jk}^i = {g^{is}}{\mathit{\Gamma }_{jk,s}} = {g^{is}}\frac{1}{2}\left( {\frac{{\partial {g_{js}}}}{{\partial {x^k}}} + \frac{{\partial {g_{ks}}}}{{\partial {x^j}}} - \frac{{\partial {g_{jk}}}}{{\partial {x^s}}}} \right) $ |
一般曲线坐标系下的张量场场论, 张量场相对于曲线坐标的变化率可以由张量分量的协变导数表述, 而协变导数联系与第二类Christoffel符号。将有关第二类Christoffel符号用曲面曲率表示,则分量表达式可能同时含有曲面曲率与Lame系数。以下考虑对流项的展开:
| $ \begin{array}{l} \mathit{\boldsymbol{V}} \cdot (\nabla \otimes \mathit{\boldsymbol{V}}) = {V^\alpha }{\nabla _\alpha }{V^\beta }{\mathit{\boldsymbol{g}}_\beta } = {h_{\underline \beta }}{V^\alpha }{\nabla _\alpha }{V^\beta }{\mathit{\boldsymbol{e}}_\beta }\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}{h_{\underline \beta }}{V^\alpha }\left( {\frac{{\partial {V^\beta }}}{{\partial {x^\alpha }}} + \mathit{\Gamma }_{\alpha \gamma }^\beta {V^\gamma }} \right){\mathit{\boldsymbol{e}}_\beta }\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {h_{\underline \beta }}\left( {{V^\alpha }\frac{{\partial {V^\beta }}}{{\partial {x^\alpha }}} + {V^\alpha }{V^\gamma }\mathit{\Gamma }_{\alpha \gamma }^\beta } \right){\mathit{\boldsymbol{e}}_\beta } \end{array} $ |
计算对流项相对于e1的分量:
| $ \begin{array}{l} {h_1}{V^\alpha }{V^\gamma }\mathit{\Gamma }_{\alpha \gamma }^1 = {h_1}\left[ {\frac{{V\langle 1\rangle }}{{{h_1}}}\quad \frac{{V\langle 2\rangle }}{{{h_2}}}\quad V\langle 3\rangle } \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\mathit{\Gamma }_{11}^1}&{\mathit{\Gamma }_{12}^1}&{\mathit{\Gamma }_{13}^1}\\ {\mathit{\Gamma }_{21}^1}&{\mathit{\Gamma }_{22}^1}&{\mathit{\Gamma }_{23}^1}\\ {\mathit{\Gamma }_{31}^1}&{\mathit{\Gamma }_{32}^1}&{\mathit{\Gamma }_{33}^1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{V\langle 1\rangle }}{{{h_1}}}}\\ {\frac{{V\langle 2\rangle }}{{{h_2}}}}\\ {V\langle 3\rangle } \end{array}} \right] \end{array} $ |
此处
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\Gamma }_{11}^1}&{\mathit{\Gamma }_{12}^1}&{\mathit{\Gamma }_{13}^1}\\ {\mathit{\Gamma }_{21}^1}&{\mathit{\Gamma }_{22}^1}&{\mathit{\Gamma }_{23}^1}\\ {\mathit{\Gamma }_{31}^1}&{\mathit{\Gamma }_{32}^1}&{\mathit{\Gamma }_{33}^1} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\Gamma }_{11}^1}&{\mathit{\Gamma }_{12}^1}&{ - b_1^1}\\ {\mathit{\Gamma }_{21}^1}&{\frac{{2h_2^2}}{{{h_1}\sin \theta }}{\kappa _{g,2}}}&{ - b_2^1}\\ { - b_1^1}&{ - b_2^1}&0 \end{array}} \right] $ |
式中Γ111、Γ121可由度量/Lame系数表示;b11、b21由坐标曲线的法截线曲率以及曲面的平均曲率表示。
比较曲面半正交系与曲面主方向单位正交基下的张量场场论,后者所有的Christoffel符号直接对应(仅差一个负号)为曲面的主曲率与主方向对应的测地曲率。进一步,由于曲面的主方向是唯一确定的,从而主曲率与主方向对应的测地曲率也是唯一确定的,所以曲面主方向单位正交基下的张量场场论可认为是曲面与其邻域内最为清晰地展现曲面几何特征并且形式上最为简单的场论方法。
2 场论中的应用 2.1 可变形壁面上的涡量动力学 2.1.1 涡量分解众所周知, 涡量在流体力学中具有基础性的意义。本小节研究可变形壁面上涡量相对于曲面主方向单位正交基{ e 〈ξ〉, e 〈η〉, e 〈ζ〉}的分解。
涡量定义为速度的旋度, 亦即
| $ \mathit{\boldsymbol{\omega }} = \nabla \times \mathit{\boldsymbol{V}} = e\langle \alpha \beta \gamma \rangle \nabla \langle \alpha \rangle V\langle \beta \rangle \mathit{\boldsymbol{e}}\langle \gamma \rangle $ |
首先, 涡量相对于法向e 〈ζ〉的分量可以推导为:
| $ \begin{array}{l} \omega \langle \zeta \rangle = \mathit{\boldsymbol{e}}\langle \zeta \alpha \beta \rangle \nabla \langle \alpha \rangle V\langle \beta \rangle \\ \;\;\;\;\;\;\;\; = \nabla \langle \xi \rangle V\langle \eta \rangle - \nabla \langle \eta \rangle V\langle \xi \rangle \\ = \left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + \mathit{\bar \Gamma }\langle \xi \xi \eta \rangle V\langle \xi \rangle } \right) - \left( {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + \mathit{\bar \Gamma }\langle \eta \eta \xi \rangle V\langle \eta \rangle } \right)\\ = \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} - \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + {{\bar \kappa }_{g,\xi }}V\langle \xi \rangle - {{\bar \kappa }_{g,\eta }}V\langle \eta \rangle \end{array} $ |
此处
|
图 4 可变形壁面上, 相对于e 〈ζ〉的涡量分量ω〈ζ〉 Fig.4 Normal component of vorticity ω〈ζ〉 on deformable wall |
涡量在当地曲面∑ζ的切平面上的分量,如下所示:
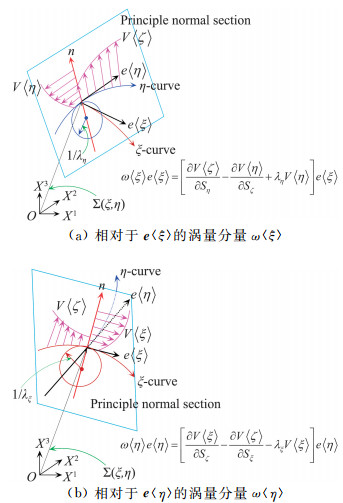
| $ \begin{array}{l} \omega \langle \xi \rangle = e\langle \xi \alpha \beta \rangle \nabla \langle \alpha \rangle V\langle \beta \rangle \\ \;\;\;\;\;\;\;\; = \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} - \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}} + {{\bar \lambda }_\eta }V\langle \eta \rangle \end{array} $ |
| $ \begin{array}{l} \omega \langle \eta \rangle = e\langle \eta \alpha \beta \rangle \nabla \langle \alpha \rangle V\langle \beta \rangle \\ \;\;\;\;\;\;\;\; = \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - {{\bar \lambda }_\xi }V\langle \xi \rangle \end{array} $ |
分量均表现为对应法截面上的两个剪切作用与沿坐标线的圆周运动的复合,如图 5所示。相对于平面壁面,弯曲壁面对于切平面上涡量的贡献由法截面上沿坐标线的圆周运动表征,圆周运动的曲率半径为法截线的曲率。
|
图 5 可变形壁面上,涡量在切平面上的分量 Fig.5 Components of vorticity on deformable wall on tangent plane |
将上述涡量的分量表达式联系与曲面主方向单位正交基的角速度向量,则有:
| $ \begin{array}{l} \mathit{\boldsymbol{\omega }} = \left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} - \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}} \right)\mathit{\boldsymbol{e}}\langle \xi \rangle + \\ \;\;\;\;\;\left( {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}}} \right)\mathit{\boldsymbol{e}}\langle \eta \rangle + \left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} - \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}}} \right)\mathit{\boldsymbol{e}}\langle \zeta \rangle + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ |
即涡量可以分解为纯粹剪切运动项与曲面主方向单位正交基的角速度向量之和。
综上所述,本文得到曲面主方向单位正交基下涡量的表示。
定理2.1 曲面主方向单位正交基下涡量的表示。当地曲面上涡量的法向分量可以分解为两种运动,其一为切平面中的两个剪切运动,其二为切平面中以二个测地曲率为曲率的圆周运动。切面上的涡量分量亦可以分为两个部分,其一为相对于法向与另一主方向的两个剪切运动,其二为主法向截面中以主曲率为曲率的圆周运动。进一步,可以将涡量分解为纯粹剪切运动与曲面主方向单位正交基的角速度向量之和。
2.1.2 可变形壁面上的涡量法向梯度一般地,涡量在可变形壁面上的法向梯度
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{\omega }}}}{{\partial \mathit{\boldsymbol{n}}}} = \mathit{\boldsymbol{n}} \cdot (\nabla \otimes \mathit{\boldsymbol{\omega }}) = n\langle \alpha \rangle \nabla \langle \alpha \rangle \omega \langle \beta \rangle \mathit{\boldsymbol{e}}\langle \beta \rangle \\ \;\;\;\;\;\; = \nabla \langle 3\rangle \omega \langle \xi \rangle \mathit{\boldsymbol{e}}\langle \xi \rangle + \nabla \langle 3\rangle \omega \langle \eta \rangle \mathit{\boldsymbol{e}}\langle \eta \rangle + \\ \;\;\;\;\;\;\nabla \langle 3\rangle \omega \langle \zeta \rangle \mathit{\boldsymbol{e}}\langle \zeta \rangle , \end{array} $ |
式中
| $ \left\{ \begin{array}{l} \nabla \langle 3\rangle \omega \langle \xi \rangle = \frac{{\partial \omega \langle \xi \rangle }}{{\partial {S_\zeta }}} + \mathit{\Gamma }\langle 3\mu \xi \rangle \omega \langle \mu \rangle = \frac{{\partial \omega \langle \xi \rangle }}{{\partial {S_\zeta }}}\\ \nabla \langle 3\rangle \omega \langle \eta \rangle = \frac{{\partial \omega \langle \eta \rangle }}{{\partial {S_\zeta }}} + \mathit{\Gamma }\langle 3\mu \eta \rangle \omega \langle \mu \rangle = \frac{{\partial \omega \langle \eta \rangle }}{{\partial {S_\zeta }}}\\ \nabla \langle 3\rangle \omega \langle \zeta \rangle = \frac{{\partial \omega \langle \zeta \rangle }}{{\partial {S_\zeta }}} + \mathit{\Gamma }\langle 3\mu \zeta \rangle \omega \langle \mu \rangle = \frac{{\partial \omega \langle \zeta \rangle }}{{\partial {S_\zeta }}} \end{array} \right. $ |
即有
| $ \frac{{\partial \mathit{\boldsymbol{\omega }}}}{{\partial \mathit{\boldsymbol{n}}}} = \frac{{\partial \omega \langle \xi \rangle }}{{\partial {S_\zeta }}}\mathit{\boldsymbol{e}}\langle \xi \rangle + \frac{{\partial \omega \langle \eta \rangle }}{{\partial {S_\zeta }}}\mathit{\boldsymbol{e}}\langle \eta \rangle + \frac{{\partial \omega \langle \zeta \rangle }}{{\partial {S_\zeta }}}\mathit{\boldsymbol{n}} $ |
因此,边界涡量流可以分成两部分,其一为切平面边界涡量流
| $ \frac{{\partial \mathit{\boldsymbol{\omega }}}}{{\partial \mathit{\boldsymbol{n}}}} = \frac{{\partial {\mathit{\boldsymbol{\omega }}_\parallel }}}{{\partial {S_\zeta }}} + \frac{{\partial {\mathit{\boldsymbol{\omega }}_ \bot }}}{{\partial {S_\zeta }}} $ |
| $ \frac{{\partial {\mathit{\boldsymbol{\omega }}_\parallel }}}{{\partial {S_\zeta }}} \in T\sum $ |
| $ \frac{{\partial {\mathit{\boldsymbol{\omega }}_ \bot }}}{{\partial {S_\zeta }}} \in {\left( {T\sum } \right)^ \bot } $ |
此处ω‖=ω〈ξ〉 e 〈ξ〉+ω〈η〉 e 〈η〉∈T∑, ω⊥=ω〈ζ〉 e 〈ζ〉∈(T∑)⊥。
将涡量表达式带入上式,可得可变形壁面上边界涡量流动的表示。
定理2.2 可变形壁面上的边界涡量流。 可变形壁面上的边界涡量流, 可以分解为:切平面边界涡量流与法向边界涡量流, 且分别具有如下表达式
| $ \left\{ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{\omega }}_\parallel }}}{{\partial \zeta }} = \left[ { - {\lambda _\eta }\omega \langle \xi \rangle + 2\lambda _\eta ^2V\langle \eta \rangle + \lambda \langle \eta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\zeta ^2}} + \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial {S_\eta }\partial {S_\zeta }}}} \right]\mathit{\boldsymbol{e}}\langle \xi \rangle + \\ \;\;\;\;\;\;\;\;\;\left[ { - {\lambda _\xi }\omega \langle \eta \rangle - 2\lambda _\xi ^2V\langle \xi \rangle - \lambda \langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\zeta ^2}} - \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial {S_\xi }\partial {S_\zeta }}}} \right]e\langle \eta \rangle \\ \frac{{\partial {\mathit{\boldsymbol{\omega }}_ \bot }}}{{\partial {S_\zeta }}} = \left[ {{\kappa _{g,\eta }}\omega \langle \xi \rangle + {\kappa _{g,\xi }}\omega \langle \eta \rangle + H\omega \langle \zeta \rangle - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\partial {\omega _\xi }}}{{\partial {S_\xi }}} - \frac{{\partial {\omega _\eta }}}{{\partial {S_\eta }}}} \right]\mathit{\boldsymbol{n}} \end{array} \right. $ |
基于上述可变形壁面上涡量与边界涡量流的表达式,可以一定程度上研究壁面几何与边界拟涡能流之间的关系。例如在壁面变形的最大位置,此时壁面速度为零,对不可压缩流动有切平面涡量拟涡能流的表示
| $ \begin{gathered} \frac{\partial }{{\partial {S_\zeta }}}\frac{{\left| {{\mathit{\boldsymbol{\omega }}_\parallel }} \right|_{{\mathbb{R}^3}}^2}}{2} = - {\lambda _\eta }\omega {\langle \xi \rangle ^2} - {\lambda _\xi }\omega {\langle \eta \rangle ^2} + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\zeta ^2}} + \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}\frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\zeta ^2}} \hfill \\ \end{gathered} $ |
可见:一方面,正的主曲率(对应壁面凹陷的情形)伴随切平面涡量起涡量源(涡量由壁面注入流体)的作用;负的主曲率(对应壁面凸起的情形)起涡量汇(壁面吸取流体中涡量)的作用。另一方面,切向速度剖面的凹凸性也对壁面起源或者汇的作用有影响。现有研究发现[13-14],尽管主曲率项有一定的贡献,但往往是速度剖面的凹凸性项起主要作用。对于法向涡量的拟涡能流
关于可变形壁面上的变形率张量,Wu等[6]提出了一种基于切平面涡量与法向量的分解形式。以此为基础,谢等[15]提出了如下表达式:
| $ \begin{array}{l} \mathit{\boldsymbol{D}} - \mathop {\mathit{\boldsymbol{D}}}\limits^\Sigma = \left( {\theta - \mathop \nabla \limits^\Sigma \cdot \mathit{\boldsymbol{V}}} \right)\mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}} + \\ \;\;\;\;\;\;\frac{1}{2}\left[ {\left( {{\mathit{\boldsymbol{\omega }}_\parallel } + \mathit{\boldsymbol{W}}} \right) \times \mathit{\boldsymbol{n}}} \right] \otimes \mathit{\boldsymbol{n}} + \frac{1}{2}\mathit{\boldsymbol{n}} \otimes \left[ {\left( {{\mathit{\boldsymbol{\omega }}_\parallel } + \mathit{\boldsymbol{W}}} \right) \times \mathit{\boldsymbol{n}}} \right] \end{array} $ |
此处
基于可变形壁面上切平面涡量的表达式:
| $ \begin{array}{l} {\mathit{\boldsymbol{\omega }}_\parallel } = \omega \langle \xi \rangle \mathit{\boldsymbol{e}}\langle \xi \rangle + \omega \langle \eta \rangle \mathit{\boldsymbol{e}}\langle \eta \rangle \\ \;\;\;\; = \left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} + {\lambda _\eta }V\langle \eta \rangle - \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}} \right)\mathit{\boldsymbol{e}}\langle \xi \rangle + \\ \;\;\;\;\left( { - \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - {\lambda _\xi }V\langle \xi \rangle + \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}} \right)\mathit{\boldsymbol{e}}\langle \eta \rangle \end{array} $ |
以及
| $ \begin{array}{l} \mathit{\boldsymbol{W}} = - (\mathop \nabla \limits^\Sigma V\langle \zeta \rangle + \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{K}}) \times \mathit{\boldsymbol{n}}\\ \;\;\;\; = - \left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} + {\lambda _\eta }V\langle \eta \rangle } \right)\mathit{\boldsymbol{e}}\langle \xi \rangle + \left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + {\lambda _\xi }V\langle \xi \rangle } \right)\mathit{\boldsymbol{e}}\langle \eta \rangle \end{array} $ |
则有
| $ {\mathit{\boldsymbol{\omega }}_\parallel } + \mathit{\boldsymbol{W}} = - \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}\mathit{\boldsymbol{e}}\langle \xi \rangle + \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}\mathit{\boldsymbol{e}}\langle \eta \rangle $ |
由此,本文获得相对变形率张量相对于曲面主方向{ e 〈ξ〉,e 〈η〉, e 〈ζ〉}的单位正交基的表达式。
定理2.3 可变形壁面上相对变形率张量的表示。可变形壁面上, 相对变形率张量
| $ \left( {\begin{array}{*{20}{c}} 0&0&{\frac{1}{2}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}}\\ 0&0&{\frac{1}{2}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}}\\ {\frac{1}{2}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}}&{\frac{1}{2}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}}&{\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}}} \end{array}} \right) $ |
仅含有沿法向ζ的剪切作用。
基于上述表达式, 可以简洁地获得相对变形率张量
| $ \begin{array}{l} {\lambda _{1,2}} = \\ \begin{array}{*{20}{c}} {\frac{1}{2}\left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} \pm \sqrt {{{\left( {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}} \right)}^2} + {{\left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}} \right)}^2} + {{\left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}}} \right)}^2}} } \right),}\\ {{\lambda _3} = 0} \end{array} \end{array} $ |
可见相对变形率张量的行列式为零, 迹为
| $ \cos {\theta _1} = \frac{{\sqrt 2 }}{2}\sqrt {1 + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}}\frac{1}{M}} $ |
| $ \cos {\theta _2} = \frac{{\sqrt 2 }}{2}\sqrt {1 - \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}}\frac{1}{M}} $ |
式中M:=
值得指出, 本部分理论推导所得的可变形壁面上的涡量、涡量法向梯度、相对变形率张量的表达式不仅可以用来分析边界变形与涡量在壁面产生并进入流场的机制,而且可以用来自我检查数值方法的正确性[13, 16]。
2.2 流体边界层方程 2.2.1 一般光滑曲面上的边界层方程经典的不可压缩流动的Naiver-Stokes系统, 如下所示
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot \mathit{\boldsymbol{V}} = 0}\\ {\rho \frac{{{\rm{D}}\mathit{\boldsymbol{V}}}}{{{\rm{D}}t}} = \rho \left[ {\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial t}} + \mathit{\boldsymbol{V}} \cdot (\nabla \otimes \mathit{\boldsymbol{V}})} \right] = - \nabla p + \mu \Delta \mathit{\boldsymbol{V}}} \end{array}} \right. $ |
为了说明上的简化,上述动量方程中没有包括体积力项。基于曲面主方向单位正交基下的基本场论运算,可以获得上述连续性方程与动量方程的完整分量方程。为了获得流体边界层,首先根据物理事实做量级估计,然后忽略完整分量方程中量级低的项[17-18]。另外,可以利用匹配渐近展开导出边界层方程[19]。
首先, 获得不可压缩流动的连续性方程
| $ \begin{array}{l} \nabla \cdot \mathit{\boldsymbol{V}} = \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} - {\kappa _{g,\xi }}V\langle \eta \rangle - \\ \;\;\;\;\;\;\;\;\;\;{\kappa _{g,\eta }}V\langle \xi \rangle - HV\langle \zeta \rangle = 0 \end{array} $ |
可见测地曲率联系与切平面速度,而主曲率联系与法向速度。因此,可以借鉴利用微元法获得连续性方程的方法。考虑沿ξ-坐标曲线方向的流量增量
| $ \begin{array}{l} \frac{\partial }{{\partial {S_{\xi \xi }}}}(V\langle \xi \rangle \sqrt {{g_{\eta \eta }}} \sqrt {{g_{\xi \xi }}} \Delta \eta \Delta \zeta )\sqrt {{g_{\xi \xi }}} \Delta \xi \\ \;\;\;\; = \left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + V\langle \xi \rangle \frac{{\partial \ln \sqrt {{g_{\eta \eta }}} }}{{\partial {S_\xi }}}} \right]\sqrt {{g_{\xi \xi }}} \sqrt {{g_{\eta \eta }}} \sqrt {{g_{\zeta \zeta }}} \Delta \xi \Delta \eta \Delta \zeta \\ \;\;\;\; = \left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\eta }}V\langle \xi \rangle } \right]\sqrt {{g_{\xi \xi }}} \sqrt {{g_{\eta \eta }}} \sqrt {{g_{\zeta \zeta }}} \Delta \xi \Delta \eta \Delta \zeta \end{array} $ |
可见ξ方向速度与η方向测地曲率的耦合,源于ξ方向的流量沿ξ方向的变化率,η方向的测地曲率表现了η方向的弧长微元(弧长度量)沿ξ方向的变化率。
设切平面上的特征尺度的量级为
| $ \left\{ {\begin{array}{*{20}{l}} {V\langle \xi \rangle ,V\langle \eta \rangle = \mathscr{O}(U)}\\ {V\langle \zeta \rangle = \mathscr{O}\left( {\frac{\delta }{L}U} \right)} \end{array}} \right. $ |
测地曲率与主曲率分别为平行于主方向的坐标线在切平面与法截面上的投影曲线所对应的圆周运动的曲率。设二者有如下的量级估计:
| $ \left\{ {\begin{array}{*{20}{l}} {{\kappa _{g,\xi }},{\kappa _{g,\eta }} = \mathscr{O}\left( {\frac{1}{L}} \right)}\\ {{\lambda _\xi },{\lambda _\eta } = \mathscr{O}\left( {\frac{1}{\delta }} \right)} \end{array}} \right. $ |
则连续性方程中测地曲率与主曲率的相关项均保留。
考虑切平面上的Navier-Stokes方程,以相对于e 〈ξ〉的分量方程为例:
| $ \begin{array}{l} \rho \left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial t}} + V\langle \xi \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}}} \right.\\ \;\;\;\;\;\;\;\;\; + V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - {\kappa _{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle \\ \;\;\;\;\;\;\;\;\left. { + {\kappa _{g,\eta }}V{{\langle \eta \rangle }^2} - {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle } \right]\\ = - \frac{{\partial p}}{{\partial {S_\xi }}} + \mu \left[ {\Delta V\langle \xi \rangle - 2{\lambda _\xi }\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - } \right.\\ 2{\kappa _{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + 2{\kappa _{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + \\ V\langle \xi \rangle \left( { - \kappa _{g,\xi }^2 - \kappa _{g,\eta }^2 - \lambda _\xi ^2} \right) + V\langle \eta \rangle \left( { - \frac{{\partial {\kappa _{g,\xi }}}}{{\partial {S_\xi }}} + \frac{{\partial {\kappa _{g,\eta }}}}{{\partial {S_\eta }}}} \right) + \\ \left. {V\langle \zeta \rangle \left( { - \frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} + {\kappa _{g,\eta }}\left( {{\lambda _\xi } - {\lambda _\eta }} \right)} \right)} \right] \end{array} $ |
式中
| $ \begin{array}{l} \Delta V\langle \xi \rangle = \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\xi ^2}} + \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\eta ^2}} + \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\zeta ^2}} - \\ \;\;\;\;\;\;\;{\kappa _{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - H\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} \end{array} $ |
将上述方程应用于二维弯曲壁面, 所得到的不可压缩流动的Navier-Stokes方程与文献[17]给出的方程完全一致。
首先, 考虑Euler观点下的加速度表示。将曲面主方向单位正交基下物质导数的表示应用于速度,
| $ \mathit{\boldsymbol{V}} = V\langle \xi \rangle \mathit{\boldsymbol{e}}(\xi ) + V\langle \eta \rangle \mathit{\boldsymbol{e}}(\eta ) + V\langle \zeta \rangle \mathit{\boldsymbol{e}}(\zeta ) $ |
则有:
| $ \mathit{\boldsymbol{a}} = \frac{{{\rm{d}}\mathit{\boldsymbol{V}}}}{{{\rm{d}}t}} = \frac{{\mathop {\rm{d}}\limits^e \mathit{\boldsymbol{V}}}}{{{\rm{d}}t}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{V}}, $ |
式中
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{V}} = [\mathit{\boldsymbol{e}}\langle \xi \rangle \quad \mathit{\boldsymbol{e}}\langle \eta \rangle \quad \mathit{\boldsymbol{e}}\langle \zeta \rangle ] \cdot \\ \left[ {\begin{array}{*{20}{c}} { - {\kappa _{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\eta }}V{{\langle \eta \rangle }^2} - {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle }\\ { - {\kappa _{g,\eta }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\xi }}V{{\langle \xi \rangle }^2} - {\lambda _\eta }V\langle \eta \rangle V\langle \zeta \rangle }\\ {{\lambda _\xi }V{{\langle \xi \rangle }^2} + {\lambda _\eta }V{{\langle \eta \rangle }^2}} \end{array}} \right] \end{array} $ |
值得指出,上述V是绝对速度(基于曲面主方向单位正交基表示),而非相对速度;
综上所述,可以获得曲面主方向单位正交基下的加速度表示。
定理2.4 曲面主方向单位正交基下的加速度表示。将加速度相对于基于曲面主方向的单位正交基进行分解,可以获得三个部分:(1)速度的非定常项;(2)速度的对流项;(3)因局部基随空间位置变化而增加的附加项,可表示为曲面主方向单位正交基角速度向量与速度的叉乘。
文献[18]给出了完全由Lame系数表示的Navier-Stokes方程的一般分量表达式。为获得张量场微分算子在具体正交系下的表示,首先计算正交基的Lame系数,然后代入相应的分量表达式。本文所研究的曲面主方向单位正交基的非完整基理论,可以将基于Lame系数一般表达式中的Lame系数相关项对应至当地曲面的主曲率或者测地曲率,并且可以通过非完整基的方法直接推导张量场微分算子的表达式。
以下对切平面上Navier-Stokes方程的分量方程,进行量级估计。
(1) 估计对流项。有
| $ \left\{ \begin{array}{l} V\langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}},V\langle \eta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} = \mathscr{O}\left( {\frac{{{U^2}}}{L}} \right)\\ V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} = \mathscr{O}\left( {\frac{{{U^2}}}{L}} \right) \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\kappa _{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle ,{\kappa _{g,\eta }}V{\langle \eta \rangle ^2} = \mathscr{O}\left( {\frac{{{U^2}}}{L}} \right)\\ {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle = \mathscr{O}\left( {\frac{{{U^2}}}{L}} \right) \end{array} \right. $ |
故对流项全部保留。
(2) 估计黏性项中的Laplace项。有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\xi ^2}},\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\eta ^2}} = \mathscr{O}\left( {\frac{U}{{{L^2}}}} \right)}\\ {\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\zeta ^2}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}} \right)} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {{\kappa _{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}},{\kappa _{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} = \mathscr{O}\left( {\frac{U}{{{L^2}}}} \right)}\\ {H\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}} \right)} \end{array}} \right. $ |
其它附加项的量级估计:
| $ \left\{ {\begin{array}{*{20}{l}} {V\langle \xi \rangle \kappa _{g,\xi }^2,V\langle \xi \rangle \kappa _{g,\eta }^2 = \mathscr{O}\left( {\frac{U}{{{L^2}}}} \right)}\\ {V\langle \xi \rangle \lambda _\xi ^2 = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}} \right)} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {V\langle \eta \rangle \frac{{\partial {\kappa _{g,\xi }}}}{{\partial {S_\xi }}},V\langle \eta \rangle \frac{{\partial {\kappa _{g,\eta }}}}{{\partial {S_\eta }}},V\langle \zeta \rangle \frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} = \mathscr{O}\left( {\frac{U}{{{L^2}}}} \right)}\\ {V\langle \zeta \rangle {\kappa _{g,\eta }}{\lambda _\xi },V\langle \zeta \rangle {\kappa _{g,\eta }}{\lambda _\eta } = \mathscr{O}\left( {\frac{U}{{{L^2}}}} \right)} \end{array}} \right. $ |
故黏性项中保留量级为
考虑指标对称性, 就可以由相对于e 〈ξ〉的方程, 获得相对于e 〈η〉的方程。
考虑Navier-Stokes方程的法向e 〈ζ〉分量方程:
| $ \begin{array}{l} \rho \left[ {\frac{{\partial V\langle \zeta \rangle }}{{\partial t}} + V\langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}}} \right.\\ \;\;\;\;\;\;\;\;\left. { + V\langle \zeta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} + {\lambda _\xi }V{{\langle \xi \rangle }^2} + {\lambda _\eta }V{{\langle \eta \rangle }^2}} \right]\\ \;\;\;\;\; = - \frac{{\partial p}}{{\partial {S_\zeta }}} + \mu \left[ {\Delta V\langle \zeta \rangle + 2{\lambda _\xi }\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + 2{\lambda _\eta }\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + } \right.\\ \;\;\;\;\;V\langle \xi \rangle \left( {\frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} - {\kappa _{g,\eta }}H} \right) + \\ \;\;\;\;\;\left. {V\langle \eta \rangle \left( {\frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} - {\kappa _{g,\xi }}H} \right) - V\langle \zeta \rangle \left( {\lambda _\xi ^2 + \lambda _\eta ^2} \right)} \right] \end{array} $ |
式中,
| $ \begin{array}{l} \Delta V\langle \zeta \rangle = \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\xi ^2}} + \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\eta ^2}} + \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\zeta ^2}} - \\ \;\;\;\;\;\;\;\;\;\;{\kappa _{g,\xi }}\frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}\frac{{\partial V\langle \zeta \rangle }}{{\partial S_\xi ^2}} - H\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} \end{array} $ |
(1) 估计对流项。有
| $ \left\{ \begin{array}{l} V\langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}},V\langle \eta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} = \mathscr{O}\left( {\frac{{{U^2}}}{\delta }\frac{{{\delta ^2}}}{{{L^2}}}} \right)\\ V\langle \zeta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} = \mathscr{O}\left( {\frac{{{U^2}}}{\delta }\frac{{{\delta ^2}}}{{{L^2}}}} \right) \end{array} \right. $ |
| $ {\lambda _\xi }V{\langle \xi \rangle ^2},{\lambda _\eta }V{\langle \eta \rangle ^2} = \mathscr{O}\left( {\frac{{{U^2}}}{\delta }} \right) $ |
故对流项中量级为
(2) 估计黏性项中的Laplace项。有
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\xi ^2}},\frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\eta ^2}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{{{\delta ^3}}}{{{L^3}}}} \right)\\ \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\zeta ^2}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{\delta }{L}} \right) \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\kappa _{g,\xi }}\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}},{\kappa _{g,\eta }}\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{{{\delta ^3}}}{{{L^3}}}} \right)\\ H\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{\delta }{L}} \right) \end{array} \right. $ |
其它附加项的量级估计:
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _\xi }\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}},{\lambda _\eta }\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{\delta }{L}} \right)}\\ {V\langle \xi \rangle \left( {\frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} - {\kappa _{g,\eta }}H} \right),V\langle \eta \rangle \left( {\frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} - {\kappa _{g,\xi }}H} \right) = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{\delta }{L}} \right)} \end{array}} \right. $ |
| $ V\langle \zeta \rangle \left( {\lambda _\xi ^2 + \lambda _\eta ^2} \right) = \mathscr{O}\left( {\frac{U}{{{\delta ^2}}}\frac{\delta }{L}} \right) $ |
故黏性项中量级为
考虑压力项的量级,按上述切平面中的动量平衡,可有
| $ p = \mathscr{O}\left( {\rho {U^2}} \right) = \mathscr{O}\left( {\mu \frac{U}{{{\delta ^2}}}L} \right) $ |
因此,可有
| $ \frac{{\partial p}}{{\partial {S_\zeta }}} = \mathscr{O}\left( {\frac{{\rho {U^2}}}{\delta }} \right) = \mathscr{O}\left( {\mu \frac{U}{{{\delta ^2}}}\frac{L}{\delta }} \right) $ |
综上所述,本文获得曲率项保留的不可压缩流动的边界层方程。
定理2.5 光滑曲面上曲率项保留的不可压缩流动的边界层方程。当设定测地曲率为切平面/展向特征尺度倒数的量级,主曲率为法向尺度倒数的量级,则有如下曲率项都保留的边界层方程。
(1) 连续性方程
| $ \begin{array}{l} \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} - {\kappa _{g,\xi }}V\langle \eta \rangle \\ \;\;\;\;\;\; - {\kappa _{g,\eta }}V\langle \xi \rangle - HV\langle \zeta \rangle = 0 \end{array} $ |
(2) 动量方程
| $ \left\{ \begin{array}{l} \frac{{\partial V\langle \xi \rangle }}{{\partial t}} + V\langle \xi \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}}\\ \;\;\;\;\; - {\kappa _{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\eta }}V{\langle \eta \rangle ^2} - {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle \\ \;\;\;\;\; = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_\xi }}} + \frac{\mu }{\rho }\left[ {\frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial {S^2}}} - H\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - \lambda _\xi ^2V\langle \xi \rangle } \right];\\ \frac{{\partial V\langle \eta \rangle }}{{\partial t}} + V\langle \xi \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}}\\ \;\;\;\;\; - {\kappa _{g,\eta }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\xi }}V{\langle \xi \rangle ^2} - {\lambda _\eta }V\langle \eta \rangle V\langle \zeta \rangle \\ \;\;\;\;\; = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_\eta }}} + \frac{\mu }{\rho }\left[ {\frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\zeta ^2}} - H\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}} - \lambda _\eta ^2V\langle \eta \rangle } \right];\\ {\lambda _\xi }V{\langle \xi \rangle ^2} + {\lambda _\eta }V{\langle \eta \rangle ^2} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_\zeta }}} \end{array} \right. $ |
当设定测地曲率与主曲率都是展向特征尺度倒数的量级,则上述边界层方程中去除含有主曲率的项。值得指出,两个测地曲率或者主曲率的量级可以独立进行估计,而无关联性。
对比平面壁面上的流体边界层方程,可见弯曲壁面的测地曲率与主曲率都在控制方程中起着一定的作用:测地曲率的量级一般为切平面特征尺度的倒数,在边界层方程中保留;主曲率的量级只有达到法向尺度的倒数,才在边界层方程中保留。如果为进行流动控制等,在壁面上引入局部的凹凸性(振幅等同于边界层厚度),则边界层方程中需要保留主曲率项。如果上述方程中忽略主曲率相关项,则与文献[20]中的方程一致。文献[20]引用了E.J.Watson关于曲面上层流边界层的推导,此种推导基于Lame系数表达式的Navier-Stokes方程,并利用基准曲面与当地曲面上梯度算子之间的近似关系,行文中未将有关Lame系数项对应为测地曲率。
如果基准曲面采用一般的非正交参数坐标,并且沿法向进行空间延拓则形成半正交系,可以基于一般曲线坐标系下张量场场论推导边界层方程,并且可将度量/Lame系数项联系于当地曲面的参数曲线的测地曲率[19, 21]。值得指出,相对于曲面半正交系展开的分量方程往往同时含有Lame系数与曲面曲率,而非仅含有曲面曲率,如1.5节所述。另一方面,基于曲面的半正交系(完整基)可以直接应用于计算,而基于曲面单位正交基(非完整基)无法直接用于计算,但基于张量分量的坐标转换关系可以理论分析采用曲面单位正交基而实际计算所用适合的完整的曲线坐标系(甚至不需要半正交系),如1.4节所述。
2.2.2 旋成曲面上的相关结论本小节将上述一般光滑曲面上的场论应用至旋成曲面,具体获得涡量与边界层方程的表达式。
旋成曲面的向量值映照可构造如下:
| $ \begin{gathered} \sum {(\mathit{\boldsymbol{x}})} :{\mathscr{D}_{\theta z}} \ni \left( {\begin{array}{*{20}{l}} \theta \\ z \end{array}} \right) \mapsto \hfill \\ \sum {(\theta ,z) = R(z)} \cos \theta \mathit{\boldsymbol{i}} + R(z)\sin \theta \mathit{\boldsymbol{j}} + z\mathit{\boldsymbol{k}} \in {\mathbb{R}^3} \hfill \\ \end{gathered} $ |
此处z表示沿中心轴的坐标,R(z)表示圆形截面的半径,θ表示极角,如图 6所示。旋成曲面的局部基可以确定如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{g}}_\theta } = \frac{{\partial \Sigma }}{{\partial \theta }} = - R(z)\sin \theta \mathit{\boldsymbol{i}} + R(z)\cos \theta \mathit{\boldsymbol{j}}\\ {\mathit{\boldsymbol{g}}_z} = \frac{{\partial \sum }}{{\partial z}} = {R_z}\cos \theta \mathit{\boldsymbol{i}} + {R_z}\sin \theta \mathit{\boldsymbol{j}} + \mathit{\boldsymbol{k}}\\ n = \frac{{{\mathit{\boldsymbol{g}}_\theta } \times {\mathit{\boldsymbol{g}}_z}}}{{\left| {{\mathit{\boldsymbol{g}}_\theta } \times {\mathit{\boldsymbol{g}}_z}} \right|}} = \frac{1}{{\sqrt {R_z^2 + 1} }}\left( {\cos \theta \mathit{\boldsymbol{i}} + \sin \theta \mathit{\boldsymbol{j}} - {R_z}\mathit{\boldsymbol{k}}} \right) \end{array} \right. $ |
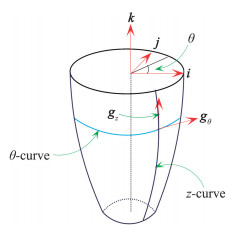
|
图 6 旋成曲面的参数坐标及其诱导的局部协变基 Fig.6 Parameter coordinates of a revolved surfaces and the induced local covariant basis |
式中Rz=
由此,可计算旋成曲面度量张量的协变分量与主曲率张量混合分量,
| $ \left( {{g_{ij}}} \right) = \left( {\begin{array}{*{20}{c}} {R{{(z)}^2}}&0\\ 0&{1 + R_z^2} \end{array}} \right) $ |
| $ \left( {b_i^j} \right) = \left( {\begin{array}{*{20}{c}} { - \frac{1}{{R{{\left( {1 + R_z^2} \right)}^{\frac{1}{2}}}}}}&0\\ 0&{\frac{{{R_{zz}}}}{{{{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}}}}} \end{array}} \right) $ |
由此可得,测地曲率κg, θ=
旋成曲面邻域内的曲线坐标系,可构造如下:
| $ {\mathscr{D}_{\theta z\zeta }} \ni \left( {\begin{array}{*{20}{l}} \theta \\ z \\ \zeta \end{array}} \right) \mapsto \mathit{\boldsymbol{X}}\left( {\theta ,z,\zeta } \right) = \sum {(\theta ,z)} + \zeta \mathit{\boldsymbol{n}}(\theta ,z) \in {\mathbb{R}^3}, $ |
其诱导的局部协变基
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\bar g}}}_\theta }(z,\theta ,\zeta ) = \left( {1 - \zeta {\lambda _\theta }} \right){\mathit{\boldsymbol{g}}_\theta } = \left( {1 + \frac{\zeta }{{R{{\left( {1 + R_z^2} \right)}^{\frac{1}{2}}}}}} \right){\mathit{\boldsymbol{g}}_\theta }\\ {{\mathit{\boldsymbol{\bar g}}}_z}(z,\theta ,\zeta ) = \left( {1 - \zeta {\lambda _z}} \right){\mathit{\boldsymbol{g}}_z} = \left( {1 + \frac{{\zeta {R_{zz}}}}{{{{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}}}}} \right){\mathit{\boldsymbol{g}}_z}\\ {{\mathit{\boldsymbol{\bar g}}}_\zeta }(z,\theta ,\zeta ) = n \end{array} \right. $ |
为正交基,如图 6所示。度量张量的协变分量为
| $ \begin{array}{l} \left( {{{\mathit{\boldsymbol{\bar g}}}_{ij}}} \right) = \\ \;\;\;\left( {\begin{array}{*{20}{c}} {{{\left( {R + \frac{\zeta }{{{{\left( {1 + R_z^2} \right)}^{\frac{1}{2}}}}}} \right)}^2}}&{}&{}\\ {}&{{{\left( {\sqrt {1 + R_z^2} - \frac{{\zeta {R_{zz}}}}{{1 + R_z^2}}} \right)}^2}}&{}\\ {}&{}&1 \end{array}} \right) \end{array} $ |
以此可计算非完整的单位正交基{ e (z), e (θ), e (ζ)}的形式Christoffel符号:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\bar \Gamma }\langle z\theta z\rangle = - {{\bar \kappa }_{g,z}} = 0,}\\ {\mathit{\bar \Gamma }\langle \theta z\theta \rangle = - {{\bar \kappa }_{g,\theta }} = \frac{{{R_z}}}{{R{{\left( {1 + R_z^2} \right)}^{\frac{1}{2}}} + \zeta }};} \end{array}} \right. $ |
| $ \left\{ \begin{array}{l} \mathit{\bar \Gamma }\langle z\zeta z\rangle = - {{\bar \lambda }_z} = \frac{{{R_{zz}}}}{{\zeta {R_{zz}} - {{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}}}},\\ \mathit{\bar \Gamma }\langle \theta \zeta \theta \rangle = - {{\bar \lambda }_\theta } = \frac{1}{{R{{\left( {1 + R_z^2} \right)}^{\frac{1}{2}}} + \zeta }} \end{array} \right. $ |
因此可确定当地曲面的测地曲率与主曲率,此时无需计算当地曲面的曲率张量。
按场论,可以获得涡量相对于法向n的分量表达式:
| $ \begin{array}{l} \omega \langle \zeta \rangle = \frac{1}{{\sqrt {{{\bar g}_{zz}}} }}\frac{{\partial V\langle \theta \rangle }}{{\partial z}} - \frac{1}{{\sqrt {{{\bar g}_{\theta \theta }}} }}\frac{{\partial V\langle z\rangle }}{{\partial \theta }} + \\ \;\;\;\;\;\;\;\;\;\;\;{{\bar \kappa }_{g,z}}V\langle z\rangle - {{\bar \kappa }_{g,\theta }}V\langle \theta \rangle \\ = \frac{{1 + R_z^2}}{{{{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}} - \zeta {R_{zz}}}}\frac{{\partial V\langle \theta \rangle }}{{\partial z}} - \frac{{\sqrt {1 + R_z^2} }}{{R\sqrt {1 + R_z^2} + \zeta }}\frac{{\partial V\langle z\rangle }}{{\partial \theta }} + \\ \;\;\;\;\frac{{{R_z}}}{{R\sqrt {1 + R_z^2} + \zeta }}V\langle \theta \rangle \end{array} $ |
涡量在切平面上的分量为:
| $ \begin{array}{l} \omega \langle \theta \rangle = \frac{{\partial V\langle z\rangle }}{{\partial \zeta }} - \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{zz}}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial z}} - {{\bar \lambda }_z}V\langle z\rangle \\ \;\;\;\;\;\;\;\; = \frac{{\partial V\langle z\rangle }}{{\partial \zeta }} - \frac{{1 + R_z^2}}{{{{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}} - \zeta {R_{zz}}}}\frac{{\partial V\langle \zeta \rangle }}{{\partial z}} - \\ \;\;\;\;\;\;\;\frac{{{R_{zz}}}}{{{{\left( {1 + R_z^2} \right)}^{\frac{3}{2}}} - \zeta {R_{zz}}}}V\langle z\rangle ; \end{array} $ |
| $ \begin{array}{l} \omega \langle z\rangle = \frac{1}{{\sqrt {{{\mathit{\boldsymbol{\bar g}}}_{\theta \theta }}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \theta }} - \frac{{\partial V\langle \theta \rangle }}{{\partial \zeta }} + {{\bar \lambda }_\theta }V\langle \theta \rangle \\ \;\;\;\;\;\;\; = \frac{{\sqrt {1 + R_z^2} }}{{R\sqrt {1 + R_z^2} + \zeta }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \theta }} - \frac{{\partial V\langle \theta \rangle }}{{\partial \zeta }} - \\ \;\;\;\;\;\;\;\;\;\frac{1}{{R\sqrt {1 + R_z^2} + \zeta }}V\langle \theta \rangle \end{array} $ |
按一般理论,可得旋成曲面上测地曲率与主曲率都保留的不可压缩流动的边界层方程。连续性方程,具有如下形式
| $ \frac{{\partial V\langle \theta \rangle }}{{\partial {S_\theta }}} + \frac{{\partial V\langle z\rangle }}{{\partial {S_z}}} + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} - {{\bar k}_{g,\theta }}V\langle z\rangle = \bar HV\langle \zeta \rangle = 0 $ |
动量方程,如下所示
| $ \left\{ \begin{array}{l} \frac{{\partial V\langle \theta \rangle }}{{\partial t}} + V\langle \theta \rangle \frac{{\partial V\langle \theta \rangle }}{{\partial {S_\theta }}} + V\langle z\rangle \frac{{\partial V\langle \theta \rangle }}{{\partial {S_z}}} + \\ \;\;\;V\langle \zeta \rangle \frac{{\partial V\langle \theta \rangle }}{{\partial {S_\zeta }}} - {{\bar k}_{g,\theta }}V\langle \theta \rangle V\langle z\rangle - {{\bar \lambda }_\theta }V\langle \theta \rangle V\langle \zeta \rangle \\ \;\;\; = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_\theta }}} + \frac{\mu }{\rho }\left[ {\frac{{{\partial ^2}V\langle \theta \rangle }}{{\partial S_\zeta ^2}} - \bar H\frac{{\partial V\langle \theta \rangle }}{{\partial {S_\zeta }}} - \bar \lambda _\theta ^2V\langle \theta \rangle } \right]\\ \frac{{\partial V\langle z\rangle }}{{\partial t}} + V\langle \theta \rangle \frac{{\partial V\langle z\rangle }}{{\partial {S_\theta }}} + V\langle z\rangle \frac{{\partial V\langle z\rangle }}{{\partial {S_z}}} + \\ \;\;\;\;\;V\langle \zeta \rangle \frac{{\partial V\langle z\rangle }}{{\partial {S_\xi }}} - {{\bar k}_{g,\theta }}{V^2}\langle \theta \rangle - {{\bar \lambda }_z}V\langle z\rangle V\langle \zeta \rangle \\ \;\;\;\; = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_z}}} + \frac{\mu }{\rho }\left[ {\frac{{{\partial ^2}V\langle z\rangle }}{{\partial S_\zeta ^2}} - \bar H\frac{{\partial V\langle z\rangle }}{{\partial {S_\zeta }}} - \bar \lambda _z^2V\langle z\rangle } \right]\\ {{\bar \lambda }_\theta }{V^2}\langle \theta \rangle + {{\bar \lambda }_z}{V^2}\langle z\rangle = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {S_\zeta }}} \end{array} \right. $ |
对于旋成曲面,往往可认为主曲率λθ与测地曲率kg, θ与具有相同的量级,故含有λθ的项可以去除。如果z-曲线在局部有波动/震荡,使得主曲率λz的量级为法向特征尺度的倒数,则保留含有λz项;如果λz的量级为切平面尺度的倒数,则含有λz的项可去除。如果去除所有的主曲率项,忽略关于θ的偏导数项,并且测地曲率取壁面上的值,则上述边界层方程与文献[20]所述的一致。
2.3 曲面介质的相关理论涉及曲面的研究中常涉及曲面上张量场的曲面梯度算子,按一般理论[4]有:
| $ \begin{array}{l} \mathit{\Phi } \otimes \mathop \nabla \limits^\Sigma = \frac{\partial }{{\partial {x^l}}}\left( {\mathit{\Phi }_{ \cdot j3}^i{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} \otimes \mathit{\boldsymbol{n}}} \right) \otimes {\mathit{\boldsymbol{g}}^l}\\ \;\;\;\;\;\;\; = \left[ {{\nabla _l}\mathit{\Phi }_{ \cdot j3}^i{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} \otimes \mathit{\boldsymbol{n}} + \mathit{\Phi }_{ \cdot j3}^i{b_{li}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j} \otimes \mathit{\boldsymbol{n}} + } \right.\\ \;\;\;\;\;\;\;\left. {\mathit{\Phi }_{ \cdot j3}^ib_l^j{\mathit{\boldsymbol{g}}_i} \otimes \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}} - \mathit{\Phi }_{ \cdot j3}^ib_l^s{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} \otimes {\mathit{\boldsymbol{g}}_s}} \right] \otimes {\mathit{\boldsymbol{g}}^l} \end{array} $ |
式中张量分量关于切平面指标的协变导数定义为:
| $ {\nabla _l}\mathit{\Phi }_{ \cdot j3}^i = \frac{{\partial \mathit{\Phi }_{ \cdot j3}^i}}{{\partial {x^l}}} + \mathit{\Gamma }_{ls}^i\mathit{\Phi }_{ \cdot j3}^s - \mathit{\Gamma }_{lj}^s\mathit{\Phi }_{ \cdot s3}^i $ |
对张量分量的切平面指标可以利用切平面上的非完整基理论。曲面主方向单位正交基下的曲面梯度算子,可以处理如下:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \otimes \mathop \nabla \limits^\Sigma = [\nabla \langle l\rangle \mathit{\Phi }\langle ij3\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{n}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Phi }\langle ij3\rangle b\langle li\rangle \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{n}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Phi }\langle ij3\rangle b\langle jl\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Phi }\langle ij3\rangle b\langle sl\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{e}}\langle s\rangle ] \otimes \mathit{\boldsymbol{e}}\langle l\rangle \\ \;\;\; = [\nabla \langle l\rangle \mathit{\Phi }\langle ij3\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{n}} + \\ \;\;\;\;\;{\lambda _l}\mathit{\Phi }\langle lj3\rangle \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{n}} + {\lambda _l}\mathit{\Phi }\langle il3\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}} - \\ \left. {\;\;\;\;\;{\lambda _l}\mathit{\Phi }\langle ij3\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{e}}\langle j\rangle \otimes \mathit{\boldsymbol{e}}\langle l\rangle } \right] \otimes \mathit{\boldsymbol{e}}\langle l\rangle \end{array} $ |
式中张量分量关于切平面指标的形式协变导数定义为:
| $ \nabla \langle l\rangle \mathit{\Phi }\langle ij3\rangle = \frac{{\partial \mathit{\Phi }\langle ij3\rangle }}{{\partial {S_l}}} + \mathit{\Gamma }\langle lsi\rangle \mathit{\Phi }\langle sj3\rangle + \mathit{\Gamma }\langle lsj\rangle \mathit{\Phi }\langle is3\rangle $ |
我们考虑一种特殊的流动形态,称为曲面流动,总体上连续介质的几何形态为曲面,流层的法向尺度远远小于切平面尺度。就此,物理建模上设定:(1)所有物理量沿法向的变化率可以忽略,即沿法向做均匀性设定;(2)引入面密度,指单位面积上的质量,以此刻画流面厚度的时空演化。在此物理设定下,可以建立曲面形态连续介质的有限变形理论[4, 22]。本小节研究曲面介质的Euler型质量与动量守恒方程在曲面主方向单位正交基下的展开。
设运动曲面的向量值映照
| $ {\mathscr{D}_x} \ni \left\{ {\mathit{\boldsymbol{x}},t} \right\} \mapsto \sum {(\mathit{\boldsymbol{x}},t)} , $ |
则有曲面介质质点的Euler表示
| $ \mathit{\boldsymbol{V}} = \frac{{\partial \Sigma }}{{\partial t}}\left( {\mathit{\boldsymbol{x}},t} \right) + {V^i}{\mathit{\boldsymbol{g}}_i}\left( {\mathit{\boldsymbol{x}},t} \right) = :\mathop {\mathit{\boldsymbol{V}}}\limits^\Sigma + {\mathit{\boldsymbol{V}}_\parallel } $ |
式中
| $ a = \frac{{{\rm{d}}\mathop {\mathit{\boldsymbol{V}}}\limits^\Sigma }}{{{\rm{d}}t}} + \frac{{{\rm{d}}{\mathit{\boldsymbol{V}}_\parallel }}}{{{\rm{d}}t}}. $ |
进一步,可将相对运动的加速度表示为
| $ \begin{array}{l} \frac{{{\rm{d}}{\mathit{\boldsymbol{V}}_\parallel }}}{{{\rm{d}}t}} = \frac{{\mathop {\rm{d}}\limits^e {\mathit{\boldsymbol{V}}_\parallel }}}{{{\rm{d}}t}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{V}}_\parallel } + \\ V\langle \xi \rangle \frac{{\partial e}}{{\partial t}}\left( {\mathit{\boldsymbol{x}},t} \right) + V\langle \eta \rangle \frac{{\partial e}}{{\partial t}}\left( {\mathit{\boldsymbol{x}},t} \right) \end{array} $ |
式中
| $ \frac{{\mathop {\rm{d}}\limits^e {\mathit{\boldsymbol{V}}_\parallel }}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\mathit{\boldsymbol{V}}\langle \xi \rangle }}{{{\rm{d}}t}}e\langle \xi \rangle + \frac{{{\rm{d}}V\langle \eta \rangle }}{{{\rm{d}}t}}e\langle \eta \rangle ; $ |
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{V}}_\parallel } = \left[ {\begin{array}{*{20}{c}} {e\langle \xi \rangle }&{e\langle \eta \rangle }&{e\langle \zeta \rangle } \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} { - {k_{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle + {k_{g,\eta }}{V^2}\langle \eta \rangle }\\ { - {k_{g,\eta }}V\langle \eta \rangle V\langle \xi \rangle + {k_{g,\xi }}{V^2}\langle \xi \rangle }\\ {{\lambda _\xi }{V^2}\langle \xi \rangle + {\lambda _\eta }{V^2}\langle \eta \rangle } \end{array}} \right] \end{array} $ |
Ω × V‖中的项kg, ηV2〈η〉 e 〈ξ〉、kg, ξV2〈ξ〉 e 〈η〉与(λξV2〈ξ〉+ληV2〈η〉) e 〈ζ〉可以理解切平面与法截面内圆周运动的向心加速度;而(-kg, ξV〈ξ〉V〈η〉) e 〈ξ〉、(-kg, ηV〈η〉V〈ξ〉) e 〈η〉可以理解为类似Coriolis加速度。切平面上的圆周运动以测地曲率为曲率,如图 7(a)所示;主法截面上的圆周运动以主曲率为曲率,如图 7(b)所示。
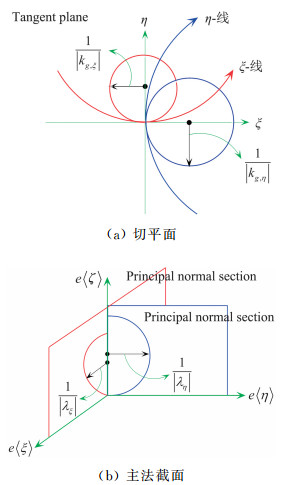
|
图 7 切平面与主法截面上的圆周运动 Fig.7 Circular motions on tangent plane and principal normal sections |
考虑积分形式的质量守恒方程
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\int_{\mathop \Sigma \limits^t } {{\rho _\Sigma }{\rm{d}}S} = 0 $ |
式中
| $ \frac{{{\rm{d}}{\rho _\Sigma }}}{{{\rm{d}}t}} + \rho \mathop \nabla \limits^\Sigma \cdot \mathit{\boldsymbol{V}} = \frac{{\partial {\rho _\Sigma }}}{{\partial t}} + \mathop \nabla \limits^\Sigma \cdot \left( {{\rho _\Sigma }\mathit{\boldsymbol{V}}} \right) $ |
由此,可得曲面主方向单位正交基下的曲面介质连续性方程。
定理2.6 曲面主方向单位正交基下的曲面介质连续性方程。
| $ \begin{array}{l} \frac{{\partial {\rho _\Sigma }}}{{\partial t}} + \frac{{\partial \left( {{\rho _\Sigma }V\langle \xi \rangle } \right)}}{{\partial {S_\xi }}} + \frac{{\partial \left( {{\rho _\Sigma }V\langle \eta \rangle } \right)}}{{\partial {S_\eta }}} - \\ {\kappa _{g,\xi }}{\rho _\Sigma }V\langle \eta \rangle - {\kappa _{g,\eta }}{\rho _\Sigma }V\langle \xi \rangle - H{\rho _\Sigma }V\langle \zeta \rangle = 0 \end{array} $ |
考虑积分形式的动量守恒
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\int_{\mathop \Sigma \limits^t } {{\rho _\Sigma }\mathit{\boldsymbol{V}}{\rm{d}}S} = \\ \;\;\;\;\;\oint \mathit{\boldsymbol{t}} \cdot (\mathit{\boldsymbol{\tau }} \times \mathit{\boldsymbol{n}}){\rm{d}}s + \int_{\mathop \Sigma \limits^t } {{\rho _\Sigma }\mathit{\boldsymbol{f}}{\rm{d}}S} , \end{array} $ |
式中τ为曲面边界曲线的切向量,由此τ × n为切平面上与边界曲线正交的方向且指向朝外, f表示曲面介质所受的面力。t代表曲面应力,设有一般形式:
| $ \mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_\parallel } + {\mathit{\boldsymbol{t}}_ \bot } = {\mathit{\boldsymbol{t}}_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^j} + {t_{3j}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j} $ |
结合物质面输运方程与第二类内蕴形式Stokes公式[15],可得曲面介质微分形式的动量方程
| $ {\rho _\Sigma }\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{t}} \cdot \mathop \nabla \limits^\Sigma + {\rho _\Sigma }\mathit{\boldsymbol{f}} $ |
利用主方向单位正交基的非完整基理论,可以获得基于主方向单位正交基展开的曲面介质动量方程(详见附录:曲面主方向单位正交基下的曲面介质动量方程)。
定理2.7 基于主方向单位正交基展开的曲面介质动量方程。
| $ \left\{ \begin{array}{l} {\rho _\Sigma }a\langle \xi \rangle = \frac{{\partial t\langle \xi \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial t\langle \xi \eta \rangle }}{{\partial {S_\eta }}} - \\ \;\;\;\;{\kappa _{g,\xi }}(t\langle \xi \eta \rangle + t\langle \eta \xi \rangle ) - {\kappa _{g \cdot \eta }}(t\langle \xi \xi \rangle - \\ \;\;\;\;\;t\langle \eta \eta \rangle ) - {\lambda _\xi }t\langle \zeta \xi \rangle + {\rho _\Sigma }f\langle \xi \rangle \\ {\rho _\Sigma }a\langle \eta \rangle = \frac{{\partial t\langle \eta \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial t\langle \eta \eta \rangle }}{{\partial {S_\eta }}} - \\ \;\;\;{\kappa _{g,\eta }}(t\langle \xi \eta \rangle + t\langle \eta \xi \rangle ) - {\kappa _{g,\xi }}(t\langle \eta \eta \rangle - \\ \;\;\;t\langle \xi \xi \rangle ) - {\lambda _\eta }t\langle \zeta \eta \rangle + {\rho _\Sigma }f\langle \eta \rangle \\ {\rho _\Sigma }a\langle \zeta \rangle = \frac{{\partial t\langle \zeta \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial t\langle \zeta \eta \rangle }}{{\partial {S_\eta }}} - \\ \;\;\;\;{\kappa _{g,\xi }}t\langle \zeta \eta \rangle - {\kappa _{g,\eta }}t\langle \zeta \xi \rangle + \\ \;\;\;\;{\lambda _\xi }t\langle \xi \xi \rangle + {\lambda _\eta }t\langle \eta \eta \rangle + {\rho _\Sigma }f\langle \zeta \rangle \end{array} \right. $ |
此处力的作用由曲面应力表示。上述动量方程适用于任意曲面形态连续介质,包括液体膜与固体膜。
值得指出,曲面形态连续介质的曲面应力可以基于相关作用形式而获得。以下考虑液膜。设想液膜内部的压力作用(包含表面张力),具有如下形式:
| $ \oint_{\partial \mathop \sum \limits^t } - p\mathit{\boldsymbol{I}} \cdot (\mathit{\boldsymbol{\tau }} \times \mathit{\boldsymbol{n}}){\rm{d}}s = \int_{\mathop \Sigma \limits^t } { - (p\mathit{\boldsymbol{I}}) \cdot \mathop \nabla \limits^\Sigma {\rm{d}}s} $ |
式中
| $ \begin{array}{l} p\mathit{\boldsymbol{I}} \cdot \mathop \nabla \limits^\Sigma = \frac{\partial }{{\partial {x^l}}}\left( {p\delta _j^i{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j}} \right) \cdot {\mathit{\boldsymbol{g}}^l}\\ = \left[ {{\nabla _l}\left( {p\delta _j^i} \right){\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^j} + p\delta _j^i{b_{li}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j} + } \right.\\ \left. {p\delta _i^jb_i^j{\mathit{\boldsymbol{g}}_i} \otimes \mathit{\boldsymbol{n}}} \right] \cdot {\mathit{\boldsymbol{g}}^l}\\ = \nabla \langle l\rangle (p\delta \langle il\rangle )\mathit{\boldsymbol{e}}\langle i\rangle + p\delta \langle ij\rangle b\langle ij\rangle \mathit{\boldsymbol{n}} \end{array} $ |
则有:
| $ - (p\mathit{\boldsymbol{I}}) \cdot \mathop \nabla \limits^\Sigma = - \frac{{\partial p}}{{\partial {S_\xi }}}{\mathit{\boldsymbol{e}}_\xi } - \frac{{\partial p}}{{\partial {S_\eta }}}{\mathit{\boldsymbol{e}}_\eta } - pH\mathit{\boldsymbol{n}} $ |
设想液膜自身流动而产生的黏性作用(此处设定粘性作用正比于切平面上的“法向”速度梯度,实际情况可以根据具体的实验或者模型来决定),具有如下作用形式:
| $ \begin{array}{l} \oint_{\partial \mathop \Sigma \limits^t } {\mu \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right)} \cdot (\mathit{\boldsymbol{\tau }} \times \mathit{\boldsymbol{n}}){\rm{d}}s = \\ \;\;\;\int_{\mathop \Sigma \limits^t } {\mu \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma {\rm{d}}S} \end{array} $ |
式中
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma = \left( {{V^i}{\mathit{\boldsymbol{g}}_i}} \right) \otimes \mathop \nabla \limits^\Sigma \\ \;\;\; = \frac{\partial }{{\partial {x^l}}}\left( {{V^i}{\mathit{\boldsymbol{g}}_i}} \right) \otimes {\mathit{\boldsymbol{g}}^l}\\ \;\;\; = \left[ {{\nabla _l}{V^i}{\mathit{\boldsymbol{g}}_i} + {V^i}{b_{li}}\mathit{\boldsymbol{n}}} \right] \otimes {\mathit{\boldsymbol{g}}^l}\\ \;\;\; = \nabla \langle l\rangle V\langle i\rangle \mathit{\boldsymbol{e}}\langle i\rangle \otimes \mathit{\boldsymbol{e}}\langle l\rangle + V\langle i\rangle b\langle li\rangle \mathit{\boldsymbol{e}}\langle 3\rangle \otimes \mathit{\boldsymbol{e}}\langle l\rangle \end{array} $ |
V‖=Vigi称为切平面速度,则有:
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma = \\ \;\;\;\left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\xi }}V\langle \eta \rangle } \right]\mathit{\boldsymbol{e}}\langle \xi \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle + \\ \;\;\;\left[ {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}V\langle \xi \rangle } \right]\mathit{\boldsymbol{e}}\langle \eta \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle + \\ \;\;\;\left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + {\kappa _{g \cdot \eta }}V\langle \eta \rangle } \right]\mathit{\boldsymbol{e}}\langle \xi \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle + \\ \;\;\;\left[ {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + {\kappa _{g,\xi }}V\langle \xi \rangle } \right]\mathit{\boldsymbol{e}}\langle \eta \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle + \\ {\lambda _\xi }V\langle \xi \rangle \mathit{\boldsymbol{e}}\langle \zeta \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle + {\lambda _\eta }V\langle \eta \rangle \mathit{\boldsymbol{e}}\langle \zeta \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle \end{array} $ |
综上所述,考虑压力与摩擦作用的曲面应力具有如下形式:
| $ \mathit{\boldsymbol{t}} = - p\mathit{\boldsymbol{I}} + \mu {\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma $ |
且已获得其相对于曲面主方向单位正交基的分量表示,代入应力表示的动量方程则可获得具体的动量方程。或者通过非完整基理论,直接计算曲面应力关于曲面梯度的右散度,可得如下表达式:
| $ \begin{array}{l} \mathit{\boldsymbol{t}} \cdot \mathop \nabla \limits^\Sigma = - \mathop \nabla \limits^\Sigma p + \mu \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma \\ = \left\{ { - \frac{{\partial p}}{{\partial {S_\xi }}} + \mu [\Delta V\langle \xi \rangle - 2{k_{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + 2{k_{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}}} \right.\\ \;\;\; - \left( {k_{g,\xi }^2 + k_{g,\eta }^2 + \lambda _\xi ^2} \right)V\langle \xi \rangle \\ \;\;\;\left. {\left. { + \left( { - \frac{{\partial {k_{g,\xi }}}}{{\partial {S_\xi }}} + \frac{{\partial {k_{g,\eta }}}}{{\partial {S_\eta }}}} \right)V\langle \eta \rangle } \right]} \right\}\mathit{\boldsymbol{e}}\langle \xi \rangle \\ = \left\{ { - \frac{{\partial p}}{{\partial {S_\eta }}} + \mu \left[ {\Delta V\langle \eta \rangle - 2{k_{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + 2{k_{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}}} \right.} \right.\\ \;\;\;\; - \left( {k_{g,\xi }^2 + k_{g,\eta }^2 + \lambda _\eta ^2} \right)V\langle \eta \rangle \\ \;\;\;\;\left. {\left. { + \left( {\frac{{\partial {k_{g,\xi }}}}{{\partial {S_\xi }}} - \frac{{\partial {k_{g,\eta }}}}{{\partial {S_\eta }}}} \right)V\langle \xi \rangle } \right]} \right\}\mathit{\boldsymbol{e}}\langle \eta \rangle \\ = \left\{ { - pH + \mu \left[ {2{\lambda _\xi }\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + 2{\lambda _\eta }\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}}} \right.} \right.\\ \;\;\; + \left( {\frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} - {k_{g,\eta }}H} \right)V\langle \xi \rangle \\ \;\;\;\left. {\left. { + \left( {\frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} - {k_{g,\xi }}H} \right)V\langle \eta \rangle } \right]} \right\}\mathit{\boldsymbol{e}}\langle \zeta \rangle \end{array} $ |
引入如下算子,并计算可得
| $ \begin{array}{l} \left[ {\left( {{k_{g,\xi }}\frac{\partial }{{\partial {S_\xi }}} - {k_{g,\eta }}\frac{\partial }{{\partial {S_\eta }}}} \right){\mathit{\boldsymbol{e}}_\zeta }} \right] \times {\mathit{\boldsymbol{V}}_\parallel } \buildrel \Delta \over = {\mathit{\boldsymbol{e}}_\zeta } \times \\ \;\;\;\left( {{k_{g,\xi }}\frac{{\partial {\mathit{\boldsymbol{V}}_\parallel }}}{{\partial {S_\xi }}} - {k_{g,\eta }}\frac{{\partial {\mathit{\boldsymbol{V}}_\parallel }}}{{\partial {S_\eta }}}} \right)\\ = \left[ {\left( {{k_{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {k_{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}}} \right) - \left( {k_{g,\xi }^2 + k_{g,\eta }^2} \right)V\langle \xi \rangle } \right]{\mathit{\boldsymbol{e}}_\xi } + \\ \left[ {\left( {{k_{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - {k_{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}}} \right) - \left( {k_{g,\xi }^2 + k_{g,\eta }^2} \right)V\langle \eta \rangle } \right]{\mathit{\boldsymbol{e}}_\eta }, \end{array} $ |
则有
| $ \begin{array}{l} \mathit{\boldsymbol{t}} \cdot \mathop \nabla \limits^\Sigma = - \mathop \nabla \limits^\Sigma p + \mu \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma \\ = - \left( {\frac{{\partial p}}{{\partial {S_\xi }}}{\mathit{\boldsymbol{e}}_\xi } + \frac{{\partial p}}{{\partial {S_\eta }}}\mathit{\boldsymbol{e}}\langle \eta \rangle } \right) + \\ \;\;\;\;\mu (\Delta V\langle \xi \rangle e\langle \xi \rangle + \Delta V\langle \eta \rangle \mathit{\boldsymbol{e}}\langle \eta \rangle ) - \mu {\mathit{\boldsymbol{K}}^2} \cdot {\mathit{\boldsymbol{V}}_\parallel } + \\ \;\;\;\;\mu \left\{ {2\left[ {\left( {{k_{g,\xi }}\frac{\partial }{{\partial {S_\xi }}} - {k_{g,\eta }}\frac{\partial }{{\partial {S_\eta }}}} \right)\mathit{\boldsymbol{e}}\langle \zeta \rangle } \right] \times } \right.\\ \;\;\;\;\left. {{\mathit{\boldsymbol{V}}_\parallel } + \left( {k_{g,\xi }^2 + k_{g,\eta }^2} \right){\mathit{\boldsymbol{V}}_\parallel }} \right\}\\ \;\;\;\; + \left\{ { - pH + \mu \left[ {2{\lambda _\xi }\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + 2{\lambda _\eta }\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}}} \right.} \right.\\ \;\;\;\; + \left( {\frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} - {k_{g,\eta }}H} \right)V\langle \xi \rangle + \\ \;\;\;\;\left. {\left. {\left( {\frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} - {k_{g,\xi }}H} \right)V\langle \eta \rangle } \right]} \right\}e\langle \zeta \rangle \end{array} $ |
式中
| $ {\mathit{\boldsymbol{K}}^2} = \lambda _\xi ^2\mathit{\boldsymbol{e}}\langle \xi \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle + \lambda _\eta ^2\mathit{\boldsymbol{e}}\langle \eta \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle $ |
按上述表达式可见,黏性作用中主曲率起恢复力的作用;测地曲率的作用包括驱动力与类似Coriolis力的作用。
另一方面,对于曲面介质成立
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \nabla } \right) \cdot \nabla = \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma ;}\\ {\left( {{\mathit{\boldsymbol{V}}_ \bot } \otimes \nabla } \right) \cdot \nabla = \left( {{\mathit{\boldsymbol{V}}_ \bot } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma } \end{array}} \right. $ |
式中V‖=V〈ζ〉e〈ζ〉称为法向速度。故有
| $ \left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma = (\mathit{\boldsymbol{V}} \otimes \nabla ) \cdot \nabla - \left( {{\mathit{\boldsymbol{V}}_ \bot } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma , $ |
式中
| $ \begin{array}{l} \left( {{\mathit{\boldsymbol{V}}_ \bot } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma \\ = \left[ { - 2{\lambda _\xi }\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - \frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}}V\langle \zeta \rangle + {k_{g,\eta }}\left( {{\lambda _\xi } - {\lambda _\eta }} \right)V\langle \zeta \rangle } \right]e\langle \xi \rangle + \\ \left[ { - 2{\lambda _\eta }\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} - \frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}}V\langle \zeta \rangle + {k_{g,\xi }}\left( {{\lambda _\eta } - {\lambda _\xi }} \right)V\langle \zeta \rangle } \right]\mathit{\boldsymbol{e}}\langle \eta \rangle + \\ \left[ {\Delta V\langle \zeta \rangle - V\langle \zeta \rangle \left( {\lambda _\xi ^2 + \lambda _\eta ^2} \right)} \right]e\langle \zeta \rangle \end{array} $ |
按上式并基于(V⊗∇)·∇=Δ⊗ V的表达式可以重新获得t·
值得指出,上述形式的切平面应力非对称,故存在液膜内存在面力偶[4, 22]。根据力学模型的设定,对于考虑切平面应力对称、无法向应力分量的本构关系,本文方法亦可便捷地获得曲面主方向单位正交系下的分量方程[4, 23]。
3 总结本文利用微分几何中光滑曲面上局部存在的参数曲线平行于主方向的参数坐标,按法向进行空间延拓获得基准曲面与其邻域内的完整的正交系,并将非完整基理论应用于此种基于曲面的正交系,以此获得了一种新颖的适用于曲面及其邻域的场论方法,称之为基于曲面主方向的正交系的非完整基理论,简称为曲面主方向单位正交基的非完整基理论。值得指出,平行于主方向与法方向的单位正交基的形式Christoffel符号完全地对应至基准或者当地曲面的测地曲率与主曲率,并且可以建立当地与基准曲面的测地曲率与主曲率之间的关系。就此,张量场微分算子相对于曲面主方向单位正交基的展开仅含有物理量与曲率,及物理量与曲率关于参数曲线弧长坐标的变化率。常用的基于基准曲面的半正交系下的场论,无法将第二类Christoffel符号完全对应至曲面曲率,张量场微分算子的展开式往往同时含有参数曲线的度量/Lame系数、测地曲率、法截线曲率与曲面的平均曲率。基于曲面主方向的正交系是曲面半正交系的一种特殊情形,由于主方向由曲面自身唯一确定,所以此种参数坐标也具有唯一性; 并且曲面主方向单位正交基下的场论不仅最为清晰地展现曲面的几何特性,而且形式上最为简单。
本文从三个方面实践与检验曲面主方向正交基的非完整基理论:
1) 推导了可变形曲面上涡量、涡量法向梯度、相对变形率张量的表达式。涡量可以分解为纯剪切与曲面主方向单位正交基角速度向量的和;涡量法向梯度的表达式反映了壁面主曲率与测地曲率的作用;相对变形张量可以完全由沿法向的速度剖面/剪切作用决定。
2) 推导了基准曲面上的流体边界层方程。绝对加速度可以分解为相对于曲面主方向单位正交基的时间变化率项与曲面主方向单位正交基的角速度向量与速度的叉乘,也可以对曲面主方向单位正交基进行速度与角速度的分解。一般而言,测地曲率的量级为切平面尺度的倒数,故在边界层方程中保留测地曲率相关项;对于主曲率,如果其量级是切平面尺度的倒数则略去主曲率相关项,如果其量级是法向尺度的倒数则需保留主曲率相关项。如果动量方程中保留了主曲率相关项,则存在法向压力梯度以平衡主法截面中以主曲率的圆周运动。
3) 推导了曲面介质连续性方程、动量方程。此方面研究涉及曲面上张量场的曲面梯度算子,就此对张量的切平面指标可以利用曲面主方向单位正交基的非完整基理论。对于曲面形态的流动,曲面单位正交基因空间位置变化对加速度的贡献表现为切平面与主法截面上的圆周运动,前者的曲率为测地曲率,后者的曲率为主曲率。但设定剪切导致黏性作用,则其对切平面中流动的影响含有主曲率的恢复力效应,测地曲率的驱动力与类似Coriolis力效应。
由于基于曲面主方向的正交系只有数学上的存在性,故对应的非完整基理论可直接应用于理论分析。本文提出,基于不同基之间的Christoffel符号的转换关系可以间接性地确定曲面的测地曲率与主曲率。此外,基于不同基下张量分量之间的转化关系,实际计算与理论分析所用的曲线坐标系可分离,由此对实际计算所采用的曲线坐标系没有限制。需指出,光滑曲面上存在坐标线平行于主方向的参数坐标不仅仅只有局部(邻域)意义的存在性,而且未能够提供直接方法以获得其解析表达式。由此,在实际应用中需要将计算用的一般曲线坐标系与理论分析用的曲面主方向单位基分离。
本文提出的曲面主方向单位正交基的非完整基理论,作为一种场论方法也适用于固体力学等领域。
附录AA.1 曲面主方向单位正交基的运动方程
类似地,考虑曲面上基于主方向单位正交基的标架运动方程(下将两个参数分别记为ξ和η,不再以哑标形式出现)。引入弧长参数:
| $ {S_\xi } = \int_{{\xi _0}}^\xi {\left| {{\mathit{\boldsymbol{g}}_\xi }} \right|} {\rm{d}}\xi = \int_{{\xi _0}}^\xi {\sqrt {{g_{\xi \xi }}} } {\rm{d}}\xi $ |
则
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\xi }}} = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial \xi }}\\ \;\;\;\;\;\; = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{\partial }{{\partial \xi }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}{\mathit{\boldsymbol{g}}_\xi }} \right)\\ \;\;\;\;\;\; = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{\partial }{{\partial \xi }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}} \right){\mathit{\boldsymbol{g}}_\xi } + \frac{1}{{{g_{\xi \xi }}}}\frac{{\partial {\mathit{\boldsymbol{g}}_\xi }}}{{\partial \xi }} \end{array} $ |
式中,
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{g}}_\xi }}}{{\partial \xi }} = \mathit{\Gamma }_{\xi \xi }^\xi {\mathit{\boldsymbol{g}}_\xi } + \mathit{\Gamma }_{\xi \xi }^\eta {\mathit{\boldsymbol{g}}_\eta } + {b_{\xi \xi }}\mathit{\boldsymbol{n}}\\ \;\;\;\;\;\;\; = \sqrt {{g_{\xi \xi }}} \frac{{\partial \ln \sqrt {{g_{\xi \xi }}} }}{{\partial \xi }}{\mathit{\boldsymbol{e}}_\xi } - \frac{1}{{2\sqrt {{g_{\eta \eta }}} }}\frac{{\partial {g_{\xi \xi }}}}{{\partial \eta }}{\mathit{\boldsymbol{e}}_\eta } + {b_{\xi \xi }}\mathit{\boldsymbol{n}} \end{array} $ |
代入原式有:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\xi }}} = \frac{\partial }{{\partial \xi }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}} \right){\mathit{\boldsymbol{e}}_\xi } + \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial \ln \sqrt {{g_{\xi \xi }}} }}{{\partial \xi }}{\mathit{\boldsymbol{e}}_\xi } - \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{2{g_{\xi \xi }}\sqrt {{g_{\eta \eta }}} }}\frac{{\partial {g_{\xi \xi }}}}{{\partial \eta }}{\mathit{\boldsymbol{e}}_\eta } + \frac{1}{{{g_{\xi \xi }}}}{b_{\xi \xi }}\mathit{\boldsymbol{n}}\\ \;\;\;\;\;\;\;\;\;\; = - \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial \ln \sqrt {{g_{\xi \xi }}} }}{{\partial \eta }}{\mathit{\boldsymbol{e}}_\eta } + b_\xi ^\xi \mathit{\boldsymbol{n}} = {\kappa _{g,\xi }}{\mathit{\boldsymbol{e}}_\eta } + {\lambda _\xi }\mathit{\boldsymbol{n}} \end{array} $ |
对
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\eta }}} = \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial \eta }}\\ \;\;\;\;\;\;\; = \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{\partial }{{\partial \eta }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}{\mathit{\boldsymbol{g}}_\xi }} \right)\\ \;\;\;\;\;\;\; = \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{\partial }{{\partial \eta }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}} \right){\mathit{\boldsymbol{g}}_\xi } + \frac{1}{{\sqrt {{g_{\xi \xi }}} \sqrt {{g_{\eta \eta }}} }}\frac{{\partial {\mathit{\boldsymbol{g}}_\xi }}}{{\partial \eta }} \end{array} $ |
式中
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{g}}_\xi }}}{{\partial \eta }} = \mathit{\Gamma }_{\xi \eta }^\xi {\mathit{\boldsymbol{g}}_\xi } + \mathit{\Gamma }_{\xi \eta }^\eta {\mathit{\boldsymbol{g}}_\eta }\\ \;\;\;\;\;\; = \frac{1}{{2{g_{\xi \xi }}}}\frac{{\partial {g_{\xi \xi }}}}{{\partial \eta }}{\mathit{\boldsymbol{g}}_\xi } + \frac{1}{{2{g_{\eta \eta }}}}\frac{{\partial {g_{\eta \eta }}}}{{\partial \xi }}{\mathit{\boldsymbol{g}}_\eta } \end{array} $ |
代入原式有:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{e}}_\xi }}}{{\partial {S_\eta }}} = \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{\partial }{{\partial \eta }}\left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}} \right){\mathit{\boldsymbol{g}}_\xi } + \\ \;\;\;\;\frac{1}{{\sqrt {{g_{\xi \xi }}} \sqrt {{g_{\eta \eta }}} }}\left( {\frac{1}{{2\sqrt {{g_{\xi \xi }}} }}\frac{{\partial {g_{\xi \xi }}}}{{\partial \eta }}{\mathit{\boldsymbol{e}}_\xi } + \frac{1}{{2\sqrt {{g_{\eta \eta }}} }}\frac{{\partial {g_{\eta \eta }}}}{{\partial \xi }}{\mathit{\boldsymbol{e}}_\eta }} \right)\\ \;\;\;\;\; = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial \ln \sqrt {{g_{\eta \eta }}} }}{{\partial \xi }}{\mathit{\boldsymbol{e}}_\eta } = - {\kappa _{g,\eta }}{\mathit{\boldsymbol{e}}_\eta } \end{array} $ |
对
| $ \frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial {S_\xi }}} = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial \mathit{\boldsymbol{n}}}}{{\partial \xi }} = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\left( { - b_\xi ^\xi {\mathit{\boldsymbol{g}}_\xi }} \right) = - {\lambda _\xi }{\mathit{\boldsymbol{e}}_\xi } $ |
根据ξ和η的对称性容易得到对η的相关结果。
上述Christoffel符号的计算, 利用一般的计算方法
| $ \begin{array}{l} \mathit{\Gamma }_{\alpha \beta }^\gamma = {g^{\gamma \mu }}{\mathit{\Gamma }_{\alpha \beta ,\mu }}\\ \;\;\;\;\; = {g^{\gamma \mu }}\frac{1}{2}\left( {\frac{{\partial {g_{\alpha \mu }}}}{{\partial {x^\beta }}} + \frac{{\partial {g_{\beta \mu }}}}{{\partial {x^\alpha }}} - \frac{{\partial {g_{\alpha \beta }}}}{{\partial {x^\mu }}}} \right), \end{array} $ |
此处{xα}α=13为曲线坐标。
A.2 曲面主方向单位正交基下的基本场论运算
基于主方向的非完整基下的形式Christoffel符号:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }\langle \xi \eta \xi \rangle = \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial \ln \sqrt {{g_{\xi \xi }}} }}{{\partial \eta }} = - {\kappa _{g,\xi }}}\\ {\mathit{\Gamma }\langle \eta \xi \eta \rangle = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial \ln \sqrt {{g_{\eta \eta }}} }}{{\partial \xi }} = - {\kappa _{g,\eta }}} \end{array}} \right. $ |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }\langle \xi \zeta \xi \rangle = - {\lambda _\xi }}\\ {\mathit{\Gamma }\langle \eta \zeta \eta \rangle = - {\lambda _\eta }} \end{array}} \right. $ |
A.2.1 向量场的散度
| $ \begin{array}{l} \nabla \cdot \mathit{\boldsymbol{V}} = \nabla \langle \alpha \rangle V\langle \alpha \rangle = \nabla \langle 1\rangle V\langle 1\rangle + \nabla \langle 2\rangle V\langle 2\rangle + \\ \;\;\;\;\;\;\;\;\;\nabla \langle 3\rangle V\langle 3\rangle \\ = \partial \langle 1\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 121\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 131\rangle V\langle 3\rangle + \\ \;\;\partial \langle 2\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 212\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 232\rangle V\langle 3\rangle + \\ \;\;\partial \langle 3\rangle V\langle 3\rangle \\ = \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \xi \rangle }}{{\partial \xi }} - {\kappa _{g,\xi }}V\langle \eta \rangle - {\lambda _\xi }V\langle \zeta \rangle + \\ \;\;\;\frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V\langle \eta \rangle }}{{\partial \eta }} - {\kappa _{g,\eta }}V\langle \xi \rangle - {\lambda _\eta }V\langle \zeta \rangle + \frac{{\partial V\langle \zeta \rangle }}{{\partial \zeta }}\\ = \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} - \\ {\kappa _{g,\xi }}V\langle \eta \rangle - {\kappa _{g,\eta }}V\langle \xi \rangle - HV\langle \zeta \rangle \end{array} $ |
A.2.2 向量场的旋度
| $ \begin{array}{l} \nabla \times \mathit{\boldsymbol{V}} = \varepsilon \langle \alpha \beta \gamma \rangle \nabla \langle \beta \rangle V\langle \gamma \rangle \mathit{\boldsymbol{e}}\langle \alpha \rangle \\ \;\;\;\;\; = [\mathit{\boldsymbol{e}}\langle \xi \rangle \quad \mathit{\boldsymbol{e}}\langle \eta \rangle \quad \mathit{\boldsymbol{e}}\langle \zeta \rangle ] \cdot \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} {\nabla \langle 2\rangle V\langle 3\rangle - \nabla \langle 3\rangle V\langle 2\rangle }\\ {\nabla \langle 3\rangle V\langle 1\rangle - \nabla \langle 1\rangle V\langle 3\rangle }\\ {\nabla \langle 1\rangle V\langle 2\rangle - \nabla \langle 2\rangle V\langle 1\rangle } \end{array}} \right]\\ \;\;\;\;\; = [\mathit{\boldsymbol{e}}\langle \xi \rangle \quad \mathit{\boldsymbol{e}}\langle \eta \rangle \quad \mathit{\boldsymbol{e}}\langle \zeta \rangle ] \cdot \\ \left[ {\begin{array}{*{20}{c}} {\partial \langle 2\rangle V\langle 3\rangle + \mathit{\Gamma }\langle 223\rangle V\langle 2\rangle - \partial \langle 3\rangle V\langle 2\rangle }\\ {\partial \langle 3\rangle V\langle 1\rangle - \partial \langle 1\rangle V\langle 3\rangle - \mathit{\Gamma }\langle 113\rangle V\langle 1\rangle }\\ {\partial \langle 1\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 112\rangle V\langle 1\rangle - \partial \langle 2\rangle V\langle 1\rangle - \mathit{\Gamma }\langle 221\rangle V\langle 2\rangle } \end{array}} \right]\\ \;\;\;\;\; = [\mathit{\boldsymbol{e}}\langle \xi \rangle \quad \mathit{\boldsymbol{e}}\langle \eta \rangle \quad \mathit{\boldsymbol{e}}\langle \zeta \rangle ] \cdot \\ \left[ {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \eta }} + {\lambda _\eta }V\langle \eta \rangle - \frac{{\partial V\langle \eta \rangle }}{{\partial \zeta }}}\\ {\frac{{\partial V\langle \xi \rangle }}{{\partial \zeta }} - \frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \xi }} - {\lambda _\xi }V\langle \xi \rangle }\\ {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \eta \rangle }}{{\partial \xi }} - \frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V(\xi )}}{{\partial \eta }} + {\kappa _{g,\xi }}V\langle \xi \rangle - {\kappa _{g,\eta }}V\langle \eta \rangle } \end{array}} \right] \end{array} $ |
A.2.3 向量场的对流项
| $ \begin{array}{l} \mathit{\boldsymbol{V}} \cdot (\nabla \otimes \mathit{\boldsymbol{V}}) = V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle \beta \rangle )\mathit{\boldsymbol{e}}\langle \beta \rangle \\ \;\;\;\;\; = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{e}}\langle \xi \rangle }&{\mathit{\boldsymbol{e}}\langle \eta \rangle }&{\mathit{\boldsymbol{e}}\langle \zeta \rangle } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 1\rangle )}\\ {V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 2\rangle )}\\ {V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 3\rangle )} \end{array}} \right] \end{array} $ |
其中,
| $ \begin{array}{l} V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 1\rangle )\\ \;\;\;\; = V\langle 1\rangle (\nabla \langle 1\rangle V\langle 1\rangle ) + \\ \;\;\;\;\;\;\;V\langle 2\rangle (\nabla \langle 2\rangle V\langle 1\rangle ) + V\langle 3\rangle (\nabla \langle 3\rangle V\langle 1\rangle )\\ \;\;\;\; = V\langle 1\rangle (\partial \langle 1\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 121\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 131\rangle V\langle 3\rangle ) + \\ \;\;\;\;\;\;\;V\langle 2\rangle (\partial \langle 2\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 221\rangle V\langle 2\rangle ) + V\langle 3\rangle \partial \langle 3\rangle V\langle 1\rangle \\ \;\;\;\;\; = V\langle \xi \rangle \left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \xi \rangle }}{{\partial \xi }} - {\kappa _{g,\xi }}V\langle \eta \rangle - {\lambda _\xi }V\langle \zeta \rangle } \right) + \\ \;\;\;\;\;\;\;V\langle \eta \rangle \left( {\frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V\langle \xi \rangle }}{{\partial \eta }} + {\kappa _{g,\eta }}V\langle \eta \rangle } \right) + V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial \zeta }}\\ \;\;\;\;\;\; = V\langle \xi \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - \\ \;\;\;\;\;\;\;\;\;{\kappa _{g,\xi }}V\langle \eta \rangle V\langle \xi \rangle + {\kappa _{g,\eta }}V{\langle \eta \rangle ^2} - {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle \end{array} $ |
| $ \begin{array}{l} V\langle \alpha \rangle \left( {\nabla \langle \alpha \rangle V\langle 2\rangle } \right)\\ \;\;\;\; = V\langle 1\rangle \left( {\nabla \langle 1\rangle V\langle 2\rangle } \right) + \\ \;\;\;\;V\langle 2\rangle \left( {\nabla \langle 2\rangle V\langle 2\rangle } \right) + V\langle 3\rangle \left( {\nabla \langle 3\rangle V\langle 2\rangle } \right)\\ = V\langle 1\rangle (\partial \langle 1\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 112\rangle V\langle 1\rangle ) + V\langle 2\rangle (\partial \langle 2\rangle V\langle 2\rangle + \\ \;\;\;\;\mathit{\Gamma }\langle 212\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 232\rangle V\langle 3\rangle ) + V\langle 3\rangle \partial \langle 3\rangle V\langle 2\rangle \\ = V\langle \xi \rangle \left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \eta \rangle }}{{\partial \xi }} + {\kappa _{g,\xi }}V\langle \xi \rangle } \right) + \\ V\langle \eta \rangle \left( {\frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V\langle \eta \rangle }}{{\partial \eta }} - {\kappa _{g,\eta }}V\langle \xi \rangle - {\lambda _\eta }V\langle \zeta \rangle } \right) + \\ V\langle \zeta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial \zeta }}\\ = V\langle \xi \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}} + \\ {\kappa _{g,\xi }}V{\langle \xi \rangle ^2} - {\kappa _{g,\eta }}V\langle \xi \rangle V\langle \eta \rangle - {\lambda _\eta }V\langle \eta \rangle V\langle \zeta \rangle \end{array} $ |
| $ \begin{array}{l} V\langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 3\rangle )\\ = V\langle 1\rangle (\nabla \langle 1\rangle V\langle 3\rangle ) + \\ V\langle 2\rangle (\nabla \langle 2\rangle V\langle 3\rangle ) + V\langle 3\rangle (\nabla \langle 3\rangle V\langle 3\rangle )\\ = V\langle 1\rangle (\partial \langle 1\rangle V\langle 3\rangle + \mathit{\Gamma }\langle 113\rangle V\langle 1\rangle ) + V\langle 2\rangle (\partial \langle 2\rangle V\langle 3\rangle + \\ \mathit{\Gamma }\langle 223\rangle V\langle 2\rangle ) + V\langle 3\rangle \partial \langle 3\rangle V\langle 3\rangle \\ = V\langle \xi \rangle \left( {\frac{1}{{\sqrt {{g_{\xi \xi }}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \xi }} + {\lambda _\xi }V\langle \xi \rangle } \right) + \\ V\langle \eta \rangle \left( {\frac{1}{{\sqrt {{g_{\eta \eta }}} }}\frac{{\partial V\langle \zeta \rangle }}{{\partial \eta }} + {\lambda _\eta }V\langle \eta \rangle } \right) + V\langle \zeta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial \zeta }}\\ = V\langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} + \\ {\lambda _\xi }V{\langle \xi \rangle ^2} + {\lambda _\eta }V{\langle \eta \rangle ^2} \end{array} $ |
综上,向量场的对流项具有如下表达式:
| $ \begin{array}{l} \mathit{\boldsymbol{V}} \cdot \left( {\nabla \otimes \mathit{\boldsymbol{V}}} \right) = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{e}}\langle \xi \rangle }&{\mathit{\boldsymbol{e}}\langle \eta \rangle \quad \mathit{\boldsymbol{e}}\langle \zeta \rangle } \end{array}} \right]\\ \;\;\;\left[ \begin{array}{l} V\langle \xi \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \xi \rangle }}{{\partial {S_\zeta }}} - \\ \;\;\;{\kappa _{g,\xi }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\eta }}V{\langle \eta \rangle ^2} - {\lambda _\xi }V\langle \xi \rangle V\langle \zeta \rangle \\ V\langle \xi \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \eta \rangle }}{{\partial {S_\zeta }}} - \\ \;\;\;{\kappa _{g,\eta }}V\langle \xi \rangle V\langle \eta \rangle + {\kappa _{g,\xi }}V{\langle \xi \rangle ^2} - {\lambda _\eta }V\langle \eta \rangle V\langle \zeta \rangle \\ V\langle \xi \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + V\langle \eta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} + V\langle \zeta \rangle \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} + \\ \;\;\;{\lambda _\xi }V{\langle \xi \rangle ^2} + {\lambda _\eta }V{\langle \eta \rangle ^2} \end{array} \right] \end{array} $ |
A.2.4 向量场的Laplace项
基于标量场Laplace算子的一般表达式
| $ \begin{array}{l} \Delta \psi = \nabla \langle \alpha \rangle (\nabla \langle \alpha \rangle \psi )\\ \;\;\;\;\;\; = \partial \langle \alpha \rangle (\partial \langle \alpha \rangle \psi ) + \mathit{\Gamma }\langle \alpha \mu \alpha \rangle (\partial \langle \mu \rangle \psi ) \end{array} $ |
可以较为清晰地计算向量场的Laplace项,如下所示:
| $ \begin{array}{l} \nabla \langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle \beta \rangle )\\ = \partial \langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle \beta \rangle ) + \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \nabla \langle \mu \rangle V\langle \beta \rangle + \\ \mathit{\Gamma }\langle \alpha \mu \beta \rangle \nabla \langle \alpha \rangle V\langle \mu \rangle \\ = [\partial \langle \alpha \rangle (\partial \langle \alpha \rangle V\langle \beta \rangle ) + \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \partial \langle \mu \rangle V\langle \beta \rangle ] + \\ \partial \langle \alpha \rangle (\mathit{\Gamma }\langle \alpha \mu \beta \rangle V\langle \mu \rangle ) + \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \mathit{\Gamma }\langle \mu \theta \beta \rangle V\langle \theta \rangle + \\ \mathit{\Gamma }\langle \alpha \mu \beta \rangle \nabla \langle \alpha \rangle V\langle \mu \rangle \\ = \Delta V\langle \beta \rangle + \partial \langle \alpha \rangle (\mathit{\Gamma }\langle \alpha \mu \beta \rangle V\langle \mu \rangle ) + \\ \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \mathit{\Gamma }\langle \mu \theta \beta \rangle V\langle \theta \rangle + \mathit{\Gamma }\langle \alpha \mu \beta \rangle \nabla \langle \alpha \rangle V\langle \mu \rangle \end{array} $ |
(1) 当β=1时,计算
| $ \begin{array}{l} \mathit{\Gamma }\langle \alpha \mu 1\rangle \nabla \langle \alpha \rangle V\langle \mu \rangle \\ = \mathit{\Gamma }\langle 1\mu 1\rangle \nabla \langle 1\rangle V\langle \mu \rangle + \mathit{\Gamma }\langle 2\mu 1\rangle \nabla \langle 2\rangle V\langle \mu \rangle \\ = - {\kappa _{g,\xi }}\nabla \langle 1\rangle V\langle 2\rangle - {\lambda _\xi }\nabla \langle 1\rangle V\langle 3\rangle + \\ {\kappa _{g,\eta }}\nabla \langle 2\rangle V\langle 2\rangle \\ = - {\kappa _{g,\xi }}(\partial \langle 1\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 1\mu 2\rangle V\langle \mu \rangle ) - \\ {\lambda _\xi }(\partial \langle 1\rangle V\langle 3\rangle + \mathit{\Gamma }\langle 1\mu 3\rangle V\langle \mu \rangle ) + \\ {\kappa _{g,\eta }}(\partial \langle 2\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 2\mu 2\rangle V\langle \mu \rangle )\\ = - {\kappa _{g,\xi }}\left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + {\kappa _{g,\xi }}V\langle \xi \rangle } \right) - \\ {\lambda _\xi }\left( {\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} + {\lambda _\xi }V\langle \xi \rangle } \right) + \\ {\kappa _{g,\eta }}\left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}V\langle \xi \rangle - {\lambda _\eta }V\langle \zeta \rangle } \right) \end{array} $ |
| $ \begin{array}{l} \partial \langle \alpha \rangle (\mathit{\Gamma }\langle \alpha \mu 1\rangle V\langle \mu \rangle )\\ \;\;\;\;\; = \partial \langle 1\rangle (\mathit{\Gamma }\langle 1\mu 1\rangle V\langle \mu \rangle ) + \partial \langle 2\rangle (\mathit{\Gamma }\langle 2\mu 1\rangle V\langle \mu \rangle )\\ \;\;\;\;\; = \frac{\partial }{{\partial {S_\xi }}}\left( { - {\kappa _{g,\xi }}V\langle \eta \rangle - {\lambda _\xi }V\langle \zeta \rangle } \right) + \frac{\partial }{{\partial {S_\eta }}}\left( {{\kappa _{g,\eta }}V\langle \eta \rangle } \right) \end{array} $ |
| $ \begin{array}{l} \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \mathit{\Gamma }\langle \mu \theta 1\rangle V\langle \theta \rangle \\ = \mathit{\Gamma }\langle 1\mu 1\rangle \mathit{\Gamma }\langle \mu \theta 1\rangle V\langle \theta \rangle + \mathit{\Gamma }\langle 2\mu 2\rangle \mathit{\Gamma }\langle \mu \theta 1\rangle V\langle \theta \rangle \\ = - {\kappa _{g,\xi }}\mathit{\Gamma }\langle 2\theta 1\rangle V\langle \theta \rangle - {\kappa _{g,\eta }}\mathit{\Gamma }\langle 1\theta 1\rangle V\langle \theta \rangle \\ = - {\kappa _{g,\xi }}{\kappa _{g,\eta }}V\langle \eta \rangle + {\kappa _{g,\eta }}\left( {{\kappa _{g,\xi }}V\langle \eta \rangle + {\lambda _\xi }V\langle \zeta \rangle } \right)\\ = {\lambda _\xi }{\kappa _{g,\eta }}V\langle \zeta \rangle \end{array} $ |
综上,有向量场的Laplace项关于e 〈ξ〉的表达式:
| $ \begin{array}{l} \nabla \langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 1\rangle )\\ \;\;\;\; = \Delta V\langle \xi \rangle - 2{\lambda _\xi }\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - 2{\kappa _{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + \\ \;\;\;\;\;\;2{\kappa _{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + V\langle \xi \rangle \left( { - k_{g,\xi }^2 - k_{g,\eta }^2 - \lambda _\xi ^2} \right) + \\ \;\;\;\;\;\;V\langle \eta \rangle \left( { - \frac{{\partial {\kappa _{g,\xi }}}}{{\partial {S_\xi }}} + \frac{{\partial {\kappa _{g,\eta }}}}{{\partial {S_\eta }}}} \right) + \\ \;\;\;\;\;\;V\langle \zeta \rangle \left( { - \frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} + {\kappa _{g,\eta }}\left( {{\lambda _\xi } - {\lambda _\eta }} \right)} \right) \end{array} $ |
(2) 当β=2时,利用指标对称性,可直接获得向量场的Laplace项关于e 〈η〉的表达式
| $ \begin{array}{l} \nabla \langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 2\rangle )\\ \;\;\; = \Delta V\langle \eta \rangle - 2{\lambda _\eta }\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} + 2{\kappa _{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - \\ \;\;\;\;\;2{\kappa _{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} + V\langle \xi \rangle \left( {\frac{{\partial {\kappa _{g,\xi }}}}{{\partial {S_\xi }}} - \frac{{\partial {\kappa _{g,\eta }}}}{{\partial {S_\eta }}}} \right) + \\ \;\;\;\;\;V\langle \eta \rangle \left( { - k_{g,\xi }^2 - k_{g,\eta }^2 - \lambda _\eta ^2} \right) + \\ \;\;\;\;\;V\langle \zeta \rangle \left( { - \frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} + {\kappa _{g,\xi }}\left( {{\lambda _\eta } - {\lambda _\xi }} \right)} \right) \end{array} $ |
(3) 当β=3时,计算
| $ \begin{array}{l} \mathit{\Gamma }\langle \alpha \mu 3\rangle \nabla \langle \alpha \rangle V\langle \mu \rangle \\ \;\;\;\; = \mathit{\Gamma }\langle 113\rangle \nabla \langle 1\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 223\rangle \nabla \langle 2\rangle V\langle 2\rangle \\ \;\;\;\; = {\lambda _\xi }(\partial \langle 1\rangle V\langle 1\rangle + \mathit{\Gamma }\langle 1\mu 1\rangle V\langle \mu \rangle ) + \\ {\lambda _\eta }(\partial \langle 2\rangle V\langle 2\rangle + \mathit{\Gamma }\langle 2\mu 2\rangle V\langle \mu \rangle )\\ \left. { = {\lambda _\xi }\left( {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\xi }}V\langle \eta \rangle - {\lambda _\xi }V\langle \zeta \rangle } \right)} \right) + \\ \left. {{\lambda _\eta }\left( {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}V\langle \xi \rangle - {\lambda _\eta }V\langle \zeta \rangle } \right)} \right) \end{array} $ |
| $ \begin{array}{l} \partial \langle \alpha \rangle (\mathit{\Gamma }\langle \alpha \mu 3\rangle V\langle \mu \rangle )\\ \;\;\; = \partial \langle 1\rangle (\mathit{\Gamma }\langle 1\mu 3\rangle V\langle \mu \rangle ) + \partial \langle 2\rangle (\mathit{\Gamma }\langle 2\mu 3\rangle V\langle \mu \rangle )\\ \;\;\; = \frac{\partial }{{\partial {S_\xi }}}\left( {{\lambda _\xi }V\langle \xi \rangle } \right) + \frac{\partial }{{\partial {S_\eta }}}\left( {{\lambda _\eta }V\langle \eta \rangle } \right) \end{array} $ |
| $ \begin{array}{l} \mathit{\Gamma }\langle \alpha \mu \alpha \rangle \mathit{\Gamma }\langle \mu \theta 3\rangle V\langle \theta \rangle \\ \;\;\; = \mathit{\Gamma }\langle 1\mu 1\rangle \mathit{\Gamma }\langle \mu \theta 3\rangle V\langle \theta \rangle + \mathit{\Gamma }\langle 2\mu 2\rangle \mathit{\Gamma }\langle \mu \theta 3\rangle V\langle \theta \rangle \\ \;\;\; = - {\kappa _{g,\xi }}\mathit{\Gamma }\langle 2\theta 3\rangle V\langle \theta \rangle - {\kappa _{g,\eta }}\mathit{\Gamma }\langle 1\theta 3\rangle V\langle \theta \rangle \\ \;\;\; = - {\kappa _{g,\xi }}{\lambda _\eta }V\langle \eta \rangle - {\kappa _{g,\eta }}{\lambda _\xi }V\langle \xi \rangle \end{array} $ |
综上,有向量场的Laplace项关于e 〈ζ〉的表达式:
| $ \begin{array}{l} \nabla \langle \alpha \rangle (\nabla \langle \alpha \rangle V\langle 3\rangle )\\ \;\;\; = \Delta V\langle \zeta \rangle + 2{\lambda _\xi }\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} + 2{\lambda _\eta }\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} + \\ \;\;\;\;V\langle \xi \rangle \left( {\frac{{\partial {\lambda _\xi }}}{{\partial {S_\xi }}} - {\kappa _{g,\eta }}H} \right) + V\langle \eta \rangle \left( {\frac{{\partial {\lambda _\eta }}}{{\partial {S_\eta }}} - {\kappa _{g,\xi }}H} \right) - \\ \;\;\;\;V\langle \zeta \rangle \left( {\lambda _\xi ^2 + \lambda _\eta ^2} \right) \end{array} $ |
上述向量场Laplace项各分量的表达式中含有向量场各分量的Laplace项,具有如下表达式:
| $ \left\{ \begin{array}{l} \Delta V\langle \xi \rangle = \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\xi ^2}} + \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\eta ^2}} + \frac{{{\partial ^2}V\langle \xi \rangle }}{{\partial S_\zeta ^2}} - \\ \;\;\;\;{\kappa _{g,\xi }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - H\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}}\\ \Delta V\langle \eta \rangle = \frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\xi ^2}} + \frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\eta ^2}} + \frac{{{\partial ^2}V\langle \eta \rangle }}{{\partial S_\zeta ^2}} - \\ \;\;\;\;{\kappa _{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} - H\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}}\\ \Delta V\langle \zeta \rangle = \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\xi ^2}} + \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\eta ^2}} + \frac{{{\partial ^2}V\langle \zeta \rangle }}{{\partial S_\zeta ^2}} - \\ \;\;\;{\kappa _{g,\zeta }}\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\xi }}} - H\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\zeta }}} \end{array} \right. $ |
A.2.5 经典正交系
对于经典正交系,诸如柱坐标系、球坐标系等,如果可以理解为基于某个基面的沿法向延拓的曲线坐标系,此时两个参数坐标作为基面的参数并且协变基向量正好对应主方向,另一个坐标对应法向坐标,则可以利用曲面主方向单位正交基的非完整基理论获得经典坐标系下张量场微分算子的分量表达式。
(1) 柱坐标系。按柱坐标系的定义
| $ \left\{ {\begin{array}{*{20}{l}} {X = R\cos \theta }\\ {Y = R\sin \theta }\\ {Z = Z} \end{array}} \right. $ |
考虑曲面
| $ \sum\nolimits_R {(\theta ,z)} :\{ \theta ,z\} \to \sum\nolimits_R {(\theta ,z)} = \left( {\begin{array}{*{20}{c}} {R\cos \theta }\\ {R\sin \theta }\\ z \end{array}} \right) $ |
式中下标z作为参数。令θ、z分别对应ξ、η、e对应ζ,则有:
| $ {\mathit{\boldsymbol{g}}_\xi } = {\mathit{\boldsymbol{g}}_\theta } = \left( {\begin{array}{*{20}{c}} { - R\sin \theta }\\ {R\cos \theta }\\ 0 \end{array}} \right) $ |
| $ {\mathit{\boldsymbol{g}}_\eta } = {\mathit{\boldsymbol{g}}_z} = \left( {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right) $ |
| $ {\mathit{\boldsymbol{g}}_\zeta } = \mathit{\boldsymbol{n}} = \left( {\begin{array}{*{20}{c}} {\cos \theta }\\ {\sin \theta }\\ 0 \end{array}} \right) $ |
度量张量协变分量矩阵
| $ \left[ {{G_{ij}}} \right] = \left( {\begin{array}{*{20}{l}} {{g_{\xi \xi }}}&{{g_{\xi \eta }}}\\ {{g_{\eta \xi }}}&{{g_{\eta \eta }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{g_{\theta \theta }}}&0\\ 0&{{g_{zz}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{R^2}}&0\\ 0&1 \end{array}} \right) $ |
为对角阵,说明曲面上协变基为正交基。
曲面协变基对θ、z的不为零的偏导数仅有
| $ \frac{{\partial {\mathit{\boldsymbol{g}}_\theta }}}{{\partial \theta }} = \left( {\begin{array}{*{20}{c}} { - R\cos \theta } \\ { - R\sin \theta } \\ 0 \end{array}} \right),\quad {b_{\theta \theta }} = {\left( {\mathit{\boldsymbol{n}},\frac{{\partial {\mathit{\boldsymbol{g}}_\theta }}}{{\partial \theta }}} \right)_{{\mathbb{R}^3}}} = - R $ |
故有,曲率张量协变分量矩阵
| $ \left[ {{b_{ij}}} \right] = \left( {\begin{array}{*{20}{l}} {{b_{\xi \xi }}}&{{b_{\xi \eta }}}\\ {{b_{\eta \xi }}}&{{b_{\eta \eta }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_{\theta \theta }}}&0\\ 0&0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - R}&0\\ 0&0 \end{array}} \right) $ |
为对角阵。
综上,有gξ= gθ,gη= gz为曲面的主方向,而gζ= n为法向量。由此,按曲率张量混合分量矩阵
| $ \left[ {b_j^i} \right] = {\left[ {{g_{ij}}} \right]^{ - 1}} \cdot \left[ {{b_{ij}}} \right] = \left( {\begin{array}{*{20}{c}} { - \frac{1}{R}}&0\\ 0&0 \end{array}} \right) $ |
可得主曲率
| $ {\lambda _\xi } = {\lambda _\theta } = - \frac{1}{R},\quad {\lambda _\eta } = {\lambda _z} = 0 $ |
按度量张量协变分量矩阵,可有测地曲率
| $ \begin{array}{l} {\kappa _{g,\xi }} = {\kappa _{g,\theta }} = - \frac{1}{{\sqrt {{g_{zz}}} }}\frac{{\partial \ln \sqrt {{g_{\theta \theta }}} }}{{\partial z}} = 0\\ {\kappa _{g,\eta }} = {\kappa _{g,z}} = - \frac{1}{{\sqrt {{g_{\theta \theta }}} }}\frac{{\partial \ln \sqrt {{g_{zz}}} }}{{\partial \theta }} = 0 \end{array} $ |
(2) 球坐标系。按球坐标系的定义
| $ \left\{ {\begin{array}{*{20}{l}} {X = R\cos \phi \sin \theta }\\ {Y = R\sin \phi \sin \theta }\\ {Z = R\cos \theta } \end{array}} \right. $ |
考虑曲面
| $ \begin{array}{l} \sum\nolimits_R {(\theta ,\phi )} ;\{ \theta ,\phi \} \to \\ \;\;\;\;\;\sum\nolimits_R {(\theta ,\phi )} = \left( {\begin{array}{*{20}{c}} {R\cos \phi \sin \theta }\\ {R\sin \phi \sin \theta }\\ {R\cos \theta } \end{array}} \right) \end{array} $ |
式中下标z作为参数。令θ与ϕ分别对应ξ与η,R对应ζ,则有:
| $ {\mathit{\boldsymbol{g}}_\theta } = \left( {\begin{array}{*{20}{c}} {R\cos \phi \cos \theta }\\ {R\sin \phi \cos \theta }\\ { - R\sin \theta } \end{array}} \right) $ |
| $ {\mathit{\boldsymbol{g}}_\phi } = \left( {\begin{array}{*{20}{c}} { - R\sin \phi \sin \theta }\\ {R\cos \phi \sin \theta }\\ 0 \end{array}} \right) $ |
| $ \mathit{\boldsymbol{n}} = \left( {\begin{array}{*{20}{c}} {\cos \phi \sin \theta }\\ {\sin \phi \sin \theta }\\ {\cos \theta } \end{array}} \right) $ |
度量张量协变分量矩阵
| $ \left[ {{G_{ij}}} \right] = \left( {\begin{array}{*{20}{l}} {{g_{\hat f\hat \xi }}}&{{g_{\hat \xi \eta }}}\\ {{g_{\eta \xi }}}&{{g_{\eta \eta }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{g_{\theta \theta }}}&0\\ 0&{{g_{\phi \phi }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{R^2}}&0\\ 0&{{R^2}{{\sin }^2}\theta } \end{array}} \right) $ |
为对角阵,说明曲面上协变基为正交基。
曲面协变基对θ、ϕ的偏导数为:
| $ \frac{{\partial {\mathit{\boldsymbol{g}}_\theta }}}{{\partial \theta }} = \left( {\begin{array}{*{20}{c}} { - R\cos \phi \sin \theta }\\ { - R\sin \phi \sin \theta }\\ { - R\cos \theta } \end{array}} \right) $ |
| $ \frac{{\partial {\mathit{\boldsymbol{g}}_\theta }}}{{\partial \phi }} = \left( {\begin{array}{*{20}{c}} { - R\sin \phi \cos \theta }\\ {R\cos \phi \cos \theta }\\ 0 \end{array}} \right) $ |
| $ \frac{{\partial {\mathit{\boldsymbol{g}}_\phi }}}{{\partial \theta }} = \left( {\begin{array}{*{20}{c}} { - R\sin \phi \cos \theta }\\ {R\cos \phi \cos \theta }\\ 0 \end{array}} \right) $ |
| $ \frac{{\partial {\mathit{\boldsymbol{g}}_\phi }}}{{\partial \phi }} = \left( {\begin{array}{*{20}{c}} { - R\cos \phi \sin \theta }\\ {R\sin \phi \sin \theta }\\ 0 \end{array}} \right) $ |
故有,曲率张量协变分量矩阵
| $ \left[ {{b_{ij}}} \right] = \left( {\begin{array}{*{20}{l}} {{b_{\theta \theta }}}&{{b_{\theta \phi }}}\\ {{b_{\phi \theta }}}&{{b_{\phi \phi }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_{\theta \theta }}}&0\\ 0&{{b_{\phi \phi }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - R}&0\\ 0&{ - R{{\sin }^2}\theta } \end{array}} \right) $ |
为对角阵。
综上可有,gξ= gθ, gη= gz为曲面的主方向,而gζ= n为法向量。由此, 按曲率张量混合分量矩阵
| $ \left[ {b_j^i} \right] = {\left[ {{g_{ij}}} \right]^{ - 1}} \cdot \left[ {{b_{ij}}} \right] = \left( {\begin{array}{*{20}{c}} { - \frac{1}{R}}&0\\ 0&0 \end{array}} \right) $ |
可得主曲率
| $ {\lambda _\xi } = {\lambda _\theta } = - \frac{1}{R},\quad {\lambda _\eta } = {\lambda _\phi } = - \frac{1}{R} $ |
按度量张量协变分量矩阵,可有测地曲率
| $ {\kappa _{g,\xi }} = {\kappa _{g,\theta }} = - \frac{1}{{\sqrt {{g_{\phi \phi }}} }}\frac{{\partial \ln \sqrt {{g_{\theta \theta }}} }}{{\partial \phi }} = 0 $ |
| $ {\kappa _{g,\eta }} = {\kappa _{g,\phi }} = - \frac{1}{{\sqrt {{g_{\theta \theta }}} }}\frac{{\partial \ln \sqrt {{g_{\phi \phi }}} }}{{\partial \theta }} = - \frac{1}{R}\cot \theta $ |
A.3 曲面主方向单位正交基下的曲面介质动量方程
| $ \begin{array}{l} {\mathit{\boldsymbol{t}}_\parallel } \cdot \mathop \nabla \limits^\Sigma = \left( {{t_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^j}} \right) \cdot \mathop \nabla \limits^\Sigma \\ \;\;\; = \frac{\partial }{{\partial {x^l}}}\left( {{t_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^j}} \right) \cdot {\mathit{\boldsymbol{g}}^l}\\ \;\;\;\left. { = \left[ {{\nabla _l}{t_{ij}}{\mathit{\boldsymbol{g}}^i} \otimes {\mathit{\boldsymbol{g}}^j} + {t_{ij}}b_l^i\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j} + {t_{ij}}b_l^j{\mathit{\boldsymbol{g}}^i} \otimes \mathit{\boldsymbol{n}}} \right]} \right) \cdot {\mathit{\boldsymbol{g}}^l}\\ \;\;\; = \nabla \langle l\rangle t\langle il\rangle \mathit{\boldsymbol{e}}\langle i\rangle + t\langle ij\rangle b\langle ij\rangle \mathit{\boldsymbol{n}} \end{array} $ |
式中,
| $ \begin{array}{l} \nabla \langle l\rangle t\langle 1l\rangle = \nabla \langle 1\rangle t\langle 11\rangle + \nabla \langle 2\rangle t\langle 12\rangle \\ \;\;\;\; = \partial \langle 1\rangle t\langle 11\rangle + \mathit{\Gamma }\langle 1s1\rangle t\langle s1\rangle + \mathit{\Gamma }\langle 1s1\rangle t\langle 1s\rangle + \\ \;\;\;\;\partial \langle 2\rangle t\langle 12\rangle + \mathit{\Gamma }\langle 2s1\rangle t\langle s2\rangle + \mathit{\Gamma }\langle 2s2\rangle t\langle 1s\rangle \end{array} $ |
则有,
| $ \begin{array}{l} \nabla \langle l\rangle t\langle 1l\rangle = \frac{{\partial t\langle \xi \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\xi }}t\langle \eta \xi \rangle - {\kappa _{g,\xi }}t\langle \xi \eta \rangle + \\ \;\;\;\;\;\;\frac{{\partial t\langle \xi \eta \rangle }}{{\partial {S_\eta }}} + {\kappa _{g,\eta }}t\langle \eta \eta \rangle - {\kappa _{g,\eta }}t\langle \xi \xi \rangle \\ \;\;\; = \frac{{\partial t\langle \xi \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial t\langle \xi \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\xi }}(t\langle \xi \eta \rangle + t\langle \eta \xi \rangle ) - \\ \;\;\;\;\;{\kappa _{g,\eta }}(t\langle \xi \xi \rangle - t\langle \eta \eta \rangle ) \end{array} $ |
式中,
| $ \begin{array}{l} \nabla \langle l\rangle t\langle 2l\rangle = \nabla \langle 1\rangle t\langle 21\rangle + \nabla \langle 2\rangle t\langle 22\rangle \\ \;\;\;\; = \partial \langle 1\rangle t\langle 21\rangle + \mathit{\Gamma }\langle 1s2\rangle t\langle s1\rangle + \mathit{\Gamma }\langle 1s1\rangle t\langle 2s\rangle + \\ \;\;\;\;\;\partial \langle 2\rangle t\langle 22\rangle + \mathit{\Gamma }\langle 2s2\rangle t\langle s2\rangle + \mathit{\Gamma }\langle 2s2\rangle t\langle 2s\rangle \end{array} $ |
则有:
| $ \begin{array}{l} \nabla \langle j\rangle t\langle 2j\rangle = \frac{{\partial t\langle \eta \xi \rangle }}{{\partial {S_\xi }}} + {\kappa _{g,\varepsilon }}t\langle \xi \xi \rangle - {\kappa _{g,\xi }}t\langle \eta \eta \rangle + \\ \;\;\;\;\frac{{\partial t\langle \eta \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}t\langle \xi \eta \rangle - {\kappa _{g,\eta }}t\langle \eta \xi \rangle \\ \;\;\;\; = \frac{{\partial t\langle \eta \eta \rangle }}{{\partial {S_\eta }}} + \frac{{\partial t\langle \eta \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\eta }}(t\langle \xi \eta \rangle + t\langle \eta \xi \rangle ) - \\ \;\;\;\;\;\;\;{\kappa _{g,\xi }}(t\langle \eta \eta \rangle - t\langle \xi \xi \rangle ) \end{array} $ |
式中t〈ij〉b〈ij〉 n =(λξt〈ξξ〉+ληt〈ηη〉) n
| $ \begin{array}{l} {t_ \bot } \cdot \mathop \nabla \limits^\Sigma = \left( {{t_{3j}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j}} \right) \cdot \mathop \nabla \limits^\Sigma \\ \;\;\; = \frac{\partial }{{\partial {x^l}}}\left( {{t_{3j}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j}} \right) \cdot {\mathit{\boldsymbol{g}}^l}\\ \;\;\; = \left[ {{\nabla _l}{t_{3j}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^j} - {t_{3j}}b_l^s{\mathit{\boldsymbol{g}}_s} \otimes {\mathit{\boldsymbol{g}}^j} + {t_{3j}}b_l^j\mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}}} \right] \cdot {\mathit{\boldsymbol{g}}^l}\\ \;\;\; = \nabla \langle l\rangle t\langle 3l\rangle n - t\langle 3l\rangle b\langle sl\rangle {\mathit{\boldsymbol{e}}_s} \end{array} $ |
式中,
| $ \begin{array}{l} \nabla \langle j\rangle t\langle 3j\rangle = \nabla \langle 1\rangle t\langle 31\rangle + \nabla \langle 2\rangle t\langle 32\rangle \\ \;\;\; = \partial \langle 1\rangle t\langle 31\rangle + \mathit{\Gamma }\langle 1s1\rangle t\langle 3s\rangle \\ \;\;\; + \partial \langle 2\rangle t\langle 32\rangle + \mathit{\Gamma }\langle 2s2\rangle t\langle 3s\rangle \end{array} $ |
则有:
| $ \begin{array}{*{20}{c}} {\nabla \langle j\rangle t\langle 3j\rangle = \frac{{\partial t\langle \zeta \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\xi }}t\langle \zeta \eta \rangle + \frac{{\partial t\langle \zeta \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g \cdot \eta }}t\langle \zeta \xi \rangle }\\ { = \frac{{\partial t\langle \zeta \xi \rangle }}{{\partial {S_\xi }}} + \frac{{\partial t\langle \zeta \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\xi }}t\langle \zeta \eta \rangle - {\kappa _{g,\eta }}t\langle \zeta \xi \rangle } \end{array} $ |
式中-t〈3l〉b〈sl〉es=-λξt〈ζξ〉 eξ-ληt〈ζη〉 eη。
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_ \bot } \otimes \mathop \nabla \limits^\Sigma = \left( {{V^3}{\mathit{\boldsymbol{g}}_3}} \right) \otimes \mathop \nabla \limits^\Sigma = \frac{\partial }{{\partial {x^l}}}\left( {{V^3}{\mathit{\boldsymbol{g}}_3}} \right) \otimes {\mathit{\boldsymbol{g}}^l}\\ \; = \left[ {{\nabla _l}{V^3}{\mathit{\boldsymbol{g}}_3} - {V^3}b_l^s{g_s}} \right] \otimes {\mathit{\boldsymbol{g}}^l}\\ \; = \nabla \langle l\rangle V\langle 3\rangle \mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{e}}\langle l\rangle - V\langle 3\rangle b\langle ls\rangle \mathit{\boldsymbol{e}}\langle s\rangle \otimes \mathit{\boldsymbol{e}}\langle l\rangle \end{array} $ |
则有
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_ \bot } \otimes \mathop \nabla \limits^\Sigma = \\ \;\;\;\frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\varepsilon }}}\mathit{\boldsymbol{e}}\langle \zeta \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle + \frac{{\partial V\langle \zeta \rangle }}{{\partial {S_\eta }}}\mathit{\boldsymbol{e}}\langle \zeta \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle - \\ \;\;\;{\lambda _\xi }V\langle \zeta \rangle \mathit{\boldsymbol{e}}\langle \xi \rangle \otimes \mathit{\boldsymbol{e}}\langle \xi \rangle - {\lambda _\eta }V\langle \zeta \rangle \mathit{\boldsymbol{e}}\langle \eta \rangle \otimes \mathit{\boldsymbol{e}}\langle \eta \rangle \end{array} $ |
A.4 曲面梯度算子的相关处理
| $ \begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{V}}_\parallel } \otimes \mathop \nabla \limits^\Sigma } \right) \cdot \mathop \nabla \limits^\Sigma = \left[ {{\nabla _l}{V^i}{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^l} + {V^i}{b_{li}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^l}} \right] \cdot \mathop \nabla \limits^\Sigma }\\ { = \frac{\partial }{{\partial {x^q}}}\left[ {{\nabla _l}{V^i}{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^l} + {V^i}{b_{li}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^l}} \right] \cdot {\mathit{\boldsymbol{g}}^q}} \end{array} $ |
式中,
| $ \begin{array}{l} \frac{\partial }{{\partial {x^q}}}\left[ {{\nabla _l}{V^i}{\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^l}} \right] \cdot {\mathit{\boldsymbol{g}}^q}\\ \;\;\; = \left[ {{\nabla _q}\left( {\nabla ,{V^i}} \right){\mathit{\boldsymbol{g}}_i} \otimes {\mathit{\boldsymbol{g}}^l} + \left( {{\nabla _l}{V^i}} \right){b_{qi}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^l} + } \right.\\ \;\;\;\;\;\left. {\left( {{\nabla _l}{V^i}} \right)b_q^l{\mathit{\boldsymbol{g}}_i} \otimes \mathit{\boldsymbol{n}}} \right] \cdot {\mathit{\boldsymbol{g}}^q}\\ \;\;\; = {\nabla _q}\left( {{\nabla ^q}{V^i}} \right){\mathit{\boldsymbol{g}}_i} + \left( {{\nabla _l}{V^i}} \right)b_i^l\mathit{\boldsymbol{n}}\\ \;\;\; = \nabla \langle q\rangle (\nabla \langle q\rangle V\langle i\rangle )\mathit{\boldsymbol{e}}\langle i\rangle + (\nabla \langle l\rangle V\langle i\rangle )b\langle li\rangle \mathit{\boldsymbol{e}}\langle 3\rangle \end{array} $ |
| $ \begin{array}{l} \frac{\partial }{{\partial {x^q}}}\left[ {{V^i}{b_{li}}\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^l}} \right] \cdot {\mathit{\boldsymbol{g}}^q}\\ = \left[ {{\nabla _q}\left( {{V^i}{b_{li}}} \right)\mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{g}}^l} - {V^i}{b_{li}}b_q^s{\mathit{\boldsymbol{g}}_s} \otimes {\mathit{\boldsymbol{g}}^l} + } \right.\\ \;\;\left. {{V^i}{b_{li}}b_q^l\mathit{\boldsymbol{n}} \otimes \mathit{\boldsymbol{n}}} \right] \cdot {\mathit{\boldsymbol{g}}^q}\\ = {\nabla _q}\left( {{V^i}b_i^q} \right)\mathit{\boldsymbol{n}} - {V^i}b_i^qb_q^s{\mathit{\boldsymbol{g}}_s}\\ = - V\langle i\rangle b\langle iq\rangle b\langle qs\rangle \mathit{\boldsymbol{e}}\langle s\rangle + \nabla \langle q\rangle (V\langle i\rangle b\langle i\rangle )\mathit{\boldsymbol{e}}\langle 3\rangle \end{array} $ |
V‖⊗
| $ \begin{array}{l} (\nabla \langle l\rangle V\langle i\rangle )b\langle li\rangle \\ \;\;\; = (\nabla \langle 1\rangle V\langle i\rangle )b\langle 1i\rangle + (\nabla \langle 2\rangle V\langle i\rangle )b\langle 2i\rangle \\ \;\;\; = {\lambda _\xi }\nabla \langle 1\rangle V\langle 1\rangle + {\lambda _\eta }\nabla \langle 2\rangle V\langle 2\rangle \\ = \left\{ {\begin{array}{*{20}{l}} {{\lambda _\xi }\left[ {\frac{{\partial V\langle \xi \rangle }}{{\partial {S_\xi }}} - {\kappa _{g,\delta }}V\langle \eta \rangle } \right] + }\\ {{\lambda _\eta }\left[ {\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - {\kappa _{g,\eta }}V\langle \xi \rangle } \right]} \end{array}} \right. \end{array} $ |
| $ \begin{array}{l} \nabla \langle q\rangle (V\langle i\rangle b\langle qi\rangle \\ \;\;\; = (\nabla \langle 1\rangle V\langle i\rangle )b\langle 1i\rangle ) + \nabla \langle 2\rangle (V\langle i\rangle b\langle 2i\rangle )\\ \;\;\; = \left\{ {\begin{array}{*{20}{l}} {\partial \langle 1\rangle (V\langle i\rangle b\langle 1i\rangle ) + \mathit{\Gamma }\langle 121\rangle (V\langle i\rangle b\langle 2i\rangle ) + }\\ {\partial \langle 2\rangle (V\langle i\rangle b\langle 2i\rangle ) + \mathit{\Gamma }\langle 212\rangle (V\langle i\rangle b\langle 1i\rangle )} \end{array}} \right.\\ \;\;\; = \left\{ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial {S_\xi }}}\left( {{\lambda _\xi }V\langle \xi \rangle } \right) - {\kappa _{g,\xi }}{\lambda _\eta }V\langle \eta \rangle + }\\ {\frac{\partial }{{\partial {S_\eta }}}\left( {{\lambda _\eta }V\langle \eta \rangle } \right) - {\kappa _{g,\eta }}{\lambda _\xi }V\langle \xi \rangle } \end{array}} \right. \end{array} $ |
V‖⊗
| $ - V\langle i\rangle b\langle iq\rangle b\langle qs\rangle \mathit{\boldsymbol{e}}\langle s\rangle , $ |
当s=1, 有
| $ \begin{array}{l} - V\langle i\rangle b\langle iq\rangle b\langle q1\rangle = - V\langle i\rangle b\langle i1\rangle b\langle 11\rangle = \\ - \lambda _\xi ^2V\langle \xi \rangle ; \end{array} $ |
| $ \begin{array}{l} \nabla \langle q\rangle (\nabla \langle q\rangle V\langle i\rangle )\\ \;\;\; = \partial \langle q\rangle (\nabla \langle q\rangle V\langle i\rangle ) + \mathit{\Gamma }\langle qsq\rangle (\nabla \langle s\rangle V\langle i\rangle ) + \\ \;\;\;\mathit{\Gamma }\langle qsi\rangle \nabla \langle q\rangle V\langle s\rangle )\\ \;\;\; = \left\{ {\begin{array}{*{20}{l}} {\partial \langle q\rangle (\partial \langle q\rangle V\langle i\rangle + \mathit{\Gamma }\langle qsi\rangle V\langle s\rangle ) + }\\ {\mathit{\Gamma }\langle qsq\rangle (\partial \langle s\rangle V\langle i\rangle + \mathit{\Gamma }\langle ski\rangle V\langle k\rangle ) + }\\ {\mathit{\Gamma }\langle qsi\rangle (\nabla \langle q\rangle V\langle s\rangle )} \end{array}} \right.\\ \;\;\; = \left\{ {\begin{array}{*{20}{l}} {\Delta V\langle i\rangle + \partial \langle q\rangle (\mathit{\Gamma }\langle qsi\rangle V\langle s\rangle ) + }\\ {\mathit{\Gamma }\langle qsq\rangle \mathit{\Gamma }\langle ski\rangle V\langle k\rangle + }\\ {\mathit{\Gamma }\langle qsi\rangle (\nabla \langle q\rangle V\langle s\rangle )} \end{array}} \right. \end{array} $ |
当i=1, 有
| $ \begin{array}{l} \partial \langle q\rangle (\mathit{\Gamma }\langle qs1\rangle V\langle s\rangle )\\ \;\;\;\; = \partial \langle 1\rangle (\mathit{\Gamma }\langle 1s1\rangle V\langle s\rangle ) + \partial \langle 2\rangle (\mathit{\Gamma }\langle 2s1\rangle V\langle s\rangle )\\ \;\;\;\; = \frac{\partial }{{\partial {S_\xi }}}\left( { - {k_{g,\xi }}V\langle \eta \rangle } \right) + \frac{\partial }{{\partial {S_\eta }}}\left( {{k_{g,\eta }}V\langle \eta \rangle } \right); \end{array} $ |
| $ \begin{array}{l} \mathit{\Gamma }\langle qsq\rangle \mathit{\Gamma }\langle sk1\rangle V\langle k\rangle = \mathit{\Gamma }\langle qsq\rangle \mathit{\Gamma }\langle s21\rangle V\langle 2\rangle \\ \;\;\;\; = \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }\langle q1q\rangle \mathit{\Gamma }\langle 121\rangle V\langle 2\rangle + }\\ {\mathit{\Gamma }\langle q2q\rangle \mathit{\Gamma }\langle 221\rangle V\langle 2\rangle } \end{array}} \right.\\ \;\;\;\; = \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }\langle 212\rangle \mathit{\Gamma }\langle 121\rangle V\langle 2\rangle + }\\ {\mathit{\Gamma }\langle 121\rangle \mathit{\Gamma }\langle 221\rangle V\langle 2\rangle } \end{array} = 0} \right.; \end{array} $ |
| $ \begin{array}{l} \mathit{\Gamma }\langle qs1\rangle (\nabla \langle q\rangle V\langle s\rangle )\\ \;\;\;\; = \mathit{\Gamma }\langle 1s1\rangle (\nabla \langle 1\rangle V\langle s\rangle ) + \mathit{\Gamma }\langle 2s1\rangle (\nabla \langle 2\rangle V\langle s\rangle )\\ \;\;\;\; = - {k_{g,\xi }}(\nabla \langle 1\rangle V\langle 2\rangle ) + {k_{g,\eta }}(\nabla \langle 2\rangle V\langle 2\rangle )\\ \;\;\;\; = - {k_{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + {k_{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - \left( {k_{g,\xi }^2 + k_{g,\eta }^2} \right)V\langle \xi \rangle \end{array} $ |
综上,有
| $ \begin{array}{l} \nabla \langle q\rangle (\nabla \langle q\rangle V\langle 1\rangle )\\ \;\;\; = \left\{ \begin{array}{l} \Delta V\langle \xi \rangle - 2{k_{g,\xi }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\xi }}} + 2{k_{g,\eta }}\frac{{\partial V\langle \eta \rangle }}{{\partial {S_\eta }}} - \\ \left( {k_{g,\xi }^2 + k_{g,\eta }^2} \right)V\langle \xi \rangle + \left( { - \frac{{\partial {k_{g,\xi }}}}{{\partial {S_\xi }}} + \frac{{\partial {k_{g,\eta }}}}{{\partial {S_\eta }}}} \right)V\langle \eta \rangle \end{array} \right. \end{array} $ |
上述表达式交换ξ、η,则可得∇〈q〉(∇〈q〉V〈2〉)的表达式。
致谢: 感谢北京大学吴介之教授、苏卫东副教授等就本文相关内容进行的有益讨论。感谢课题组傅渊、陈玉竹等就相关推导的验证与讨论等。本文将张量分析中的非完整基理论应用至基准曲面与其邻域,期待能为相关领域的研究提供有效的场论方法,也谨以此怀念我国理性力学先驱之一的郭仲衡先生。
| [1] |
郭仲衡. 张量理论与应用[M]. 北京: 科学出版社, 1988. GUO Z H. Tensor (theory and application)[M]. Beijing: Science Press, 1988. (in Chinese) |
| [2] |
郭仲衡. 非线性弹性理论[M]. 北京: 科学出版社, 1988. GUO Z H. Nonlinear theory of elasticity[M]. Beijing: Science Press, 1988. (in Chinese) |
| [3] |
黄克智, 薛明德, 陆明万. 张量分析[M]. 北京: 清华大学出版社, 2003. HUANG K Z, XUE M De, LU M W. Tensor analysis[M]. Beijing: Tsinghua University Press, 2003. (in Chinese) |
| [4] |
谢锡麟. 现代张量分析及其在连续介质力学中的应用[M]. 上海: 复旦大学出版社, 2014. XIE X L. Modern tensor analysis and application in continuum mechanics[M]. Shanghai: Fudan University Express, 2014. (in Chinese) |
| [5] |
谢锡麟. 微积分讲稿:高维微积分[M]. 上海: 复旦大学出版社, 2017. XIE X L. Lectures on calculus:high dimensional calculus[M]. Shanghai: Fudan University Express, 2017. (in Chinese) |
| [6] |
WU J Z, YANG Y T, LUO Y B, et al. Fluid kinematics on a deformable surface[J]. Journal of Fluid Mechanics, 2005, 541: 371-381. DOI:10.1017/S0022112005005963 |
| [7] |
SUN B H. Incompatible deformation field and Riemann curvature tensor[J]. Applied Mathematics and Mechanics, 2017, 38(3): 311-332. DOI:10.1007/s10483-017-2176-8 |
| [8] |
YIN Y J, CHEN C, LV C J, et al. Shape gradient and classical gradient of curvatures:driving forces on micro/nano curved surfaces[J]. Applied Mathematics and Mechanics, 2011, 32(5): 533-550. DOI:10.1007/s10483-011-1436-6 |
| [9] |
王仲奇. 透平机械三元流动计算及其数学和气动力学基础[M]. 北京: 机械工业出版社, 1983. WANG Z Q. Ternary flow calculation of turbine machinery and its mathematical and aerodynamic basis[M]. Beijing: Machinery Industry Press, 1983. (in Chinese) |
| [10] |
李开泰, 黄艾香. 张量分析与应用[M]. 北京: 科学出版社, 2004. LI K T, HUANG A X. Tensor analysis and applications[M]. Beijing: Science Press, 2004. (in Chinese) |
| [11] |
陈维桓. 微分几何[M]. 北京: 北京大学出版社, 2006. CHEN W H. Differential geometry[M]. Beijing: Peking University Press, 2006. (in Chinese) |
| [12] |
WU J Z, MA H Y, ZHOU M D. Vorticity and vortex dynamics[M]. Springer, 2005.
|
| [13] |
ZHANG D P, CHEN Y Z, XIE X L. A study of boundary vorticity dynamics and identification of large-scale structures in flow field based on two-dimensional flow around a bluff body[J]. Journal of Hydrodynamics, 2019, 31(2): 1-18. |
| [14] |
FU Y, ZHANG D P, XIE X L. Vorticity vector-potential method based on time-dependent curvilinear coordinates for two-dimensional rotating flows in closed con-figurations[J]. Journal of Hydrodynamics, 2018, 30(2): 1-17. |
| [15] |
XIE X L. On two kinds of differntial operators on general smooth surfaces[J]. Journal of Fudan University Natural Science, 2013, 52(5): 688-711. |
| [16] |
CHEN Y, XIE X L. Vorticity vector-potential method for 3d viscous incompressible flows in time-dependent curvilinear coordinates[J]. Journal of Computational Physics, 2016, 312: 50-81. DOI:10.1016/j.jcp.2016.02.020 |
| [17] |
郭永怀. 边界层理论讲议[M]. 北京: 中国科学技术大学出版社, 2008.
|
| [18] |
吴望一. 流体力学[M]. 北京: 北京大学出版社, 2008. WU W Y. Fluid mechanics[M]. Beijing: Peking University Press, 2008. (in Chinese) |
| [19] |
孙茂. 非惯性正交曲线坐标系中的边界层方程[J]. 航空学报, 1996, 17(2): 208-212. SUN M. Boundary layer equations in noinertial curvilinear coordinate system[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(2): 208-212. DOI:10.3321/j.issn:1000-6893.1996.02.016 (in Chinese) |
| [20] |
ROSENHEAD L. Laminar boundary layers[M]. Oxford University Press, 1963.
|
| [21] |
CEBECI T, KAUPS K, RAMSEY J A. A general method for calculationg three-dimensional compressible laminar and turbulent boundary layers on arbitrary wings[R]. NASA CR 1977-2777.
|
| [22] |
XIE X L, CHEN Y, SHI Q. Some studies on mechanics of continuous medi-ums viewed as differential manifolds[J]. Sci China-Phys Mech Astron, 2013, 56(2): 432-456. DOI:10.1007/s11433-012-4983-3 |
| [23] |
ARIS R. Vectors, tensors, and the basic equations of fluid mechanics[M]. Dover Pub-lications, INC, 1989.
|
 2020, Vol. 38
2020, Vol. 38

