湍流不只局限于中性流体,非中性流体,比如导电流体同样可以展现湍流特性。导电流体中的流体脉动会引起磁场的波动,而磁场的波动也会强烈的影响流体运动,因此磁流体的湍流流动并不遵守Navier-Stokes方程,而是遵守磁流体方程。相对来说,在地球上,湍流运动中的磁流体很少;但是,在广阔的外太空,大部分气体都被离子化,强的湍流非常普遍,并且湍流强度往往比地球上的湍流现象强很多个数量级。空间等离子体流,例如太阳风,在大尺度上可以用磁流体模型来描述[1],因此研究磁流体湍流对研究天体物理、空间物理和等离子体物理有重要的作用[2]。不仅如此,磁流体湍流在磁约束聚变、快中子堆和聚变堆、工业中液体金属流动、航空航天等领域都有着重大的应用[3-10]。
湍流的一个基本特征是存在不同尺度的涡旋结构(相干结构),而这些涡旋的相互作用使得能量在不同尺度间传递。磁流体湍流较中性流体湍流复杂之处,除了增加了磁场的作用,还出现了电流相干结构,因为这些原因,磁流体湍流中不同尺度之间,除了不同涡旋之间的动能传输,还有磁能传输,以及动能与磁能之间的互相耦合[2]。
早在20世纪70年代,Orszag和Tang[11]使用直接数值模拟对二维磁流体湍流中的电流和涡旋相干结构进行了研究,揭示了磁流体湍流中相干结构产生的过程;因为强烈的电流片结构的产生,磁流体湍流展现出比中性湍流更强的间歇性。之后大量的研究探讨了磁流体湍流中的相干结构产生机理以及它们与能量传输、耗散和磁重联等的关系。Matthaeus[12]采用数值模拟研究了磁流体重联点附近电流片和“四极子”形状涡旋结构的生成和演化。Carbone等[13]研究了磁流体湍流中片状或条状结构的形成,以及不稳定性的影响,并指出了其与尺度间能量传递的联系。Politano等[14]研究了三维磁流体湍流中电流和涡旋结构的生成和演化,指出了磁流体湍流中这些结构与中性湍流中涡旋结构的不同。Kinney等[15]研究了衰减二维磁流体湍流的自相似演化,探讨了相干结构的演化和尺度间的能量传输的关联。Cowley等[16]研究了磁流体湍流中电流片结构的产生和湮灭,讨论了电流片结构产生位置的限制。
早期对磁流体湍流中相干结构的研究,由于计算和观测条件的局限,往往所研究的湍流雷诺数不高。进入21世纪以来,随着超级计算机的发展和高精度观测卫星的使用,对磁流体湍流中结构和跨尺度能量传输的研究取得更多的进展。本文主要介绍近几年有关磁流体湍流相干结构和能量传输的一些工作。文章的主要结构如下:第一部分介绍磁流体基本方程;第二部分介绍均匀各向同性磁流体湍流中的相干结构和能量传输;第三部分是对均匀各向同性湍流的拓展,主要讨论各向异性和可压缩等情况下的影响;最后是文章的结论。
1 磁流体力学基本方程磁流体力学(magnetohydrodynamics,MHD)是以连续介质的观点研究导电流体和电磁场的相互作用, 需考察流体运动的速度场u与介质内部电磁场b的耦合, 即存在流体力学方程和麦克斯韦(Maxwell)方程耦合。不可压磁流体力学的方程为:
| $ {\partial _t}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{u}}{\rm{ }}\cdot\nabla {\rm{ }}\mathit{\boldsymbol{u}}{\rm{ }} = - {\rm{ }}\frac{1}{\rho }{\rm{ }}\nabla {p_t} + {\rm{ }}\frac{1}{{\rho {\mu _e}}}{\rm{ }}\mathit{\boldsymbol{b}}{\rm{ }}\cdot\nabla {\rm{ }}\mathit{\boldsymbol{b}}{\rm{ }} + \nu {\nabla ^2}\mathit{\boldsymbol{u}} $ | (1) |
| $ {\partial _t}\mathit{\boldsymbol{b}}{\rm{ }} = \nabla \times \left( {{\rm{ }}\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{b}}{\rm{ }}} \right) + \eta {\nabla ^2}\mathit{\boldsymbol{b}} $ | (2) |
| $ \partial \cdot{\rm{ }}\mathit{\boldsymbol{u}}{\rm{ }} = \nabla \cdot{\rm{ }}\mathit{\boldsymbol{b}}{\rm{ }} = 0 $ | (3) |
式中, 密度ρ为常数, 总压pt=p+ b2/2μe为流体压力和磁压之和, μe为磁导率, 洛伦兹力分解为j × b=(b ·∇)(b /μe)-∇(b 2/2μe), ν为黏性系数, η为磁扩散系数。
磁流体力学有两类不同的雷诺数, 一类是流体力学雷诺数Re=UL/ν(其中U为特征速度, L为特征长度), 其度量了流体运动的惯性力和黏性力的相对大小; 一类是磁流体力学特有的磁雷诺数Rem=UL/η, 其描述了磁场对流效应和磁场扩散效应的相对重要性。两者之比为磁普朗特数Prm=Rem/Re=ν/η, 它描述了黏性耗散和电阻耗散的相对重要性。在边界层理论中, 层流速度边界层和磁边界层分别正比于Re-1/2和Rem-1/2[17], 因此磁普朗特数代表了两种边界层的相对厚度.此外, 两种耗散尺度, ld∝ν3/4[18-20]及lmd∝η3/4的相对大小也和磁普朗特数有关。实际中, 磁普朗特数的取值可以跨越多个量级, 例如, 液态金属磁流体发电机Prm~10-5[21], 星际介质Prm~1014[22]。
不同的磁普朗特数对于流场和电磁场的性质会产生一定的影响[23],本文中如无特别说明, 主要讨论Prm~1的情况。当Re及Rem足够大时,磁流体呈湍流态。电磁场和流场之间的非线性相互作用,使得磁流体湍流相较于中性流体湍流,具有更多自由度,也更加复杂,因此中性流体的湍流理论是否适用于磁流体湍流是一个值得关注的问题。
2 均匀各向同性磁流体湍流 2.1 相干结构磁流体湍流中存在多种相干结构, 如电流和涡旋,分别对应电流密度μe j =∇× b和涡量ω =∇× u。不同于中性流体湍流中的管状结构[24-26],磁流体湍流多呈现片状结构[14, 27-28],如图 1所示的电流密度的三维等值图[29],在强电流片附近存在强涡片结构[14]。湍流场具有间歇性, 图 2所示的z方向电流密度的概率密度明显偏离高斯分布[30-31],将概率分布函数分为Ⅰ、Ⅱ、Ⅲ三个部分, 分别对应的概率密度函数的靠近中心、中部、尾部三个部分,可画出每个部分的电流密度在空间的分布(如图 2所示)。区域Ⅰ对应的弱电流密度集中分布在磁岛间的连通区域,区域Ⅱ对应的中等电流密度主要分布在靠近磁岛中心的位置,而区域Ⅲ对应的强电流密度呈片状结构,可看成相邻磁岛的边界。

|
图 1 磁流体湍流数值模拟中, 电流密度随时间变化(依次从左到右, 从上到下)的三维等值图(摘自文献[29]) Fig.1 Contour maps of current density at four different times (from left to right and top to bottom) in a 15263 simulation of MHD turbulence (Adapted from Ref.[29]) |

|
图 2 二维磁流体湍流数值模拟中, z方向电流密度Jz的概率分布, 其中黑实线为高斯分布。概率分布图的Ⅰ, Ⅱ, Ⅲ区域对应的电流密度的空间分布位置以红色区域标出, 而磁力线(磁势的等值线)以黑色线标出(摘自文献[30]) Fig.2 PDF of the electric current density Jz from a 2D MHD simulation, compared to a reference Gaussian. For each region Ⅰ, Ⅱ, and Ⅲ, magnetic field lines (contours of constant magnetic potential) are shown in black; the red regions are places where the selected band (Ⅰ, Ⅱ, or Ⅲ) contributes (Adapted from Ref.[30]) |
湍流场的小尺度结构一般可以由速度梯度张量来描述, 速度梯度张量∇ u 又可以进一步分解为变形速度张量(对称部分)和旋转速度张量(反对称部分):
| $ \nabla \mathit{\boldsymbol{u}}{\rm{ }} = {\rm{ }}\mathit{\boldsymbol{S}}{\rm{ }} + {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (4) |
其中S =
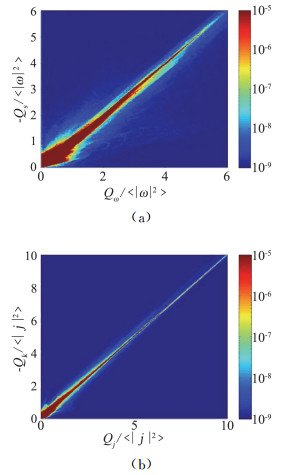
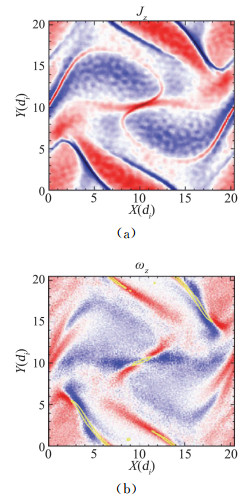
在许多流体湍流中, 通常充满了涡管结构, 在这些涡管中, 具有强拟涡能, 但变形拉伸项往往很小, 所以Qs和Qω的联合概率分布函数会分散开[26, 36]。与上述情况不同, 图 3中画出了磁流体湍流中Qs和Qω的联合概率密度以及Qk和Qj的联合概率密度, 可以看到联合概率密度集中在对角线上, 意味着两个量之间存在强的正相关性[37-38],可以理解为流场中Qs~Qω, 则强涡结构是片状的, 类似的情况也适用于磁流体湍流中电流片的结构。图 4为二维Orszag-Tang问题的全粒子模拟(PIC)中, 电流密度和涡量的等值图, 从图上可以看出两者的空间分布很相似, 但中间位置的强涡结构和强电流密度大致可以看出两者不是完全重合的, 而是会略有偏移, 而更多定量的分析[12, 14, 38-39]也表明强涡结构倾向于在强电流结构周围形成。
|
图 3 磁流体湍流数值模拟中, Qs和Qω的联合概率密度以及Qk和Qj的联合概率密度(摘自文献[37]) Fig.3 Joint PDFs of the second invariants of strain rate and rotation rate tensors normalized by the mean enstrophy and the second invariants of magnetic strain rate and current density rate tensors normalized by the mean squared current density for a 3D MHD simulation (Adapted from Ref.[37]) |
|
图 4 二维Orszag-Tang问题的全粒子模拟(PIC)中, 电流密度和涡量的等值图(摘自文献[39]) Fig.4 Contour maps of current density and vorticity from a PIC simulation of 2D Orszag-Tang problem (Adapted from Ref.[39]) |
对于磁流体湍流的研究, 除了理论、数值模拟和实验(如磁约束的受控热核反应装置), 卫星观测是天体物理中一个非常有利的手段, 太阳风是人类唯一可以直接探测的恒星风, 是研究磁流体湍流的一个天然实验室。在空间观测数据中, 与磁流体湍流相干结构直接相关的是间断的出现[40-41],因为电流使得切向磁场间断。有多种方法可用以捕捉观测数据的间断, 例如PVI (partial variance of increments)[42]、小波分析[43]等, 其中PVI因其简洁有效性而被广泛使用。
| $ {\rm{PVI}}\left( {s,\tau } \right) = \frac{{\Delta \mathit{\boldsymbol{b}}{\rm{ }}\left( {s,\tau } \right)}}{{\sqrt {\left\langle {|\Delta \mathit{\boldsymbol{b}}{\rm{ }}\left( {s,\tau } \right){|^2}} \right\rangle } }} $ | (5) |
式中, Δ b (s, τ)= b (s+τ)- b (s)
2.2 能量传输能谱是湍流能量传输过程的一个基础的亦是非常重要的统计量, 例如各向同性湍流典型的-5/3湍动能谱(Kolmogorov谱)。然而对于磁流体湍流的能谱, 学术界一直存在争议。如果将能量传输过程看成一系列涡的畸变, 对应的时间尺度为涡翻转时间, 便得到Kolmogorov -5/3谱[44-45]:
| $ {E_k} = {C_k}{\varepsilon ^{2/3}}{k^{ - 5/3}} $ | (6) |
式中, Ck为Kolmogorov常数, ε为能量耗散率。阿尔芬波是磁流体的基本波模态。在20世纪70年代, 空间飞船的观测发现太阳风脉动具有某些阿尔芬波的特性[46],如磁场变化和速度变化相关, 于是学术界开始相信小尺度的脉动其实是沿磁场方向传播的阿尔芬波包, 而级串过程是由传播方向相反的阿尔芬波包之间的非线性相互作用导致。以阿尔芬时间作为特征时间,便得到Iroshnikov-Kraichnan -3/2谱[47-48]:
| $ {E_k} = {C_{IK}}{(\varepsilon {V_A})^{1/2}}{k^{ - 3/2}} $ | (7) |
式中, CIK为常数, VA为阿尔芬波速。目前学术界对能谱服从Kolmogorov k-5/3或者Iroshnikov-Kraichnan k-3/2并没有定论, 实际可能是涡畸变与阿尔芬波包两者之间相互竞争的结果, 于是将两者结合得到特征时间[49-50]。
经典的能量级串的概念提供了唯象理论中导出Kolmogorov谱或者Iroshnikov-Kraichnan谱的简捷方法, 但能谱并不是惯性区行为的充分标志, 能谱仅是2阶统计矩。Kolmogorov局部各向同性湍流理论提出惯性区的高阶速度结构函数的线性标度律, 然而湍流场的间歇性使得线性标度律只对于低阶结构函数(p≤3)成立。Kolmogorov-Yaglom定律[20, 51]将三阶结构函数和能量耗散率关联, Politano和Pouquet[52]将其推广至不可压各向同性磁流体湍流:
| $ S_{||}^ \pm \left( r \right) = \left\langle {\delta {z^ \mp }_{||}\delta z_i^ \pm \delta z_i^ \pm } \right\rangle = - {\rm{ }}\frac{4}{d}{\varepsilon ^ \pm }r $ | (8) |
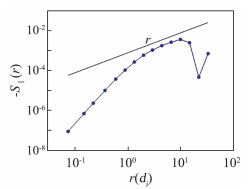
式中, z ±= u ± b为Elsasser变量, δz ±(r)= z ±(x+r)- z ±(x)为增量, δz ‖±=δz ±· r / r为沿r方向的投影, ε±为Elsasser变量对应的耗散率, ε=(ε++ε-)/2为总的黏性和磁阻耗散, d为空间维度(三维时, d=3;二维时, d=2)。卫星观测[53-55]以及数值模拟[56-57]均对该定律进行了验证, 图 5画出了Elsasser变量三阶结构函数与距离r之间的关系, 可以看出在一段区域(惯性区)内, 该定律成立。
|
图 5 二维等离子体湍流全粒子模拟中, Elsasser变量三阶结构函数S‖=(S‖++S‖-)/2随间距r的变化, 其中黑实线表示线性关系(摘自文献[57]). Fig.5 Mixed third-order moments of Elsasser fields increments S‖=(S‖++S‖-)/2, as a function of separation length r for a PIC simulation of 2D plasma turbulence. A linear fit is also indicated as a black solid line (Adapted from Ref.[57]) |
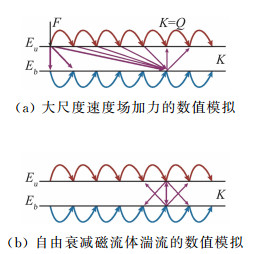
湍流不同尺度间的能量传输是诸多湍流理论和湍流模型的基础, 尽管实验可以测量从所有尺度传递给某一给定尺度的总能量, 但却很难测量能量传递过程的细节, 如两个给定尺度间的能量传输。根据Eyink[58]对能量传输局部性的定义, 对于通过尺度l的能流, 如果尺度Δ>>l对其贡献可忽略, 则能量传输为红外局部的(infrared local);如果尺度δ < < l对其贡献可忽略, 则能量传输为紫外局部的(ultraviolet local)。值得注意, 这里的能量传输的局部性不同于相互作用的局部性。Kraichnan[59]指出能量传输是由3个波数(k, p, q)的脉动共同作用引起的, 波数满足 k+p+q =0, 称为三波作用(triadic interaction)。如果相互作用的三个波数的模在同一范围, 则为局部三波作用;否则为非局部三波作用。局部三波作用必然产生局部能量传输, 这里仅限于讨论能量传输的局部性。对流体湍流的能量传输过程, 已有很多研究[60-63]表明动能传输是局部的, 类似的研究在磁流体湍流中相对少, 一方面, 除了动能, 还需要考虑磁能, 以及两者之间的转化。另一方面, 背景磁场没法通过伽利略变换消除, 因此可能导致大尺度和小尺度之间的相互作用。学者们采用谱空间的球壳模型[64-65]讨论了不可压磁流体湍流能量传输的局部性, 研究表明同场间(如动能到动能, 磁能到磁能)能量传输是局部的, 而不同场间(如动能到磁能)能量传输的局部性依赖于是否有外力驱动、是否有外加磁场等。图 6是由球壳模型得到的动能、磁能各尺度间的能量传输示意图, 可以看到如果在大尺度速度场加力, 动能和磁能之间的传输明显是非局部的; 如果是衰减湍流, 则动能和磁能之间的传输是局部的。Aluie和Eyink[67]采用滤波方法对该问题进行研究, 指出动能和磁能之间的传输亦是局部的, 与球壳模型的结果不一致是因为两者波数带的选取方式不一样。
|
图 6 均匀各向同性磁流体湍流中谱空间球壳间能量传输示意图, 红色线表示动能传输, 蓝色线表示磁能传输, 紫色线表示动能和磁能间的传输. (摘自文献[66]) Fig.6 Sketch of several shell-to-shell energy transfers identified in simulations of isotropic and homogeneous magnetohydrodynamic turbulence. The kinetic energy transfers are shown in red, magnetic energy transfers in blue, and kinetic-magnetic energy transfers in purple. (Adapted from Ref.[66]) |
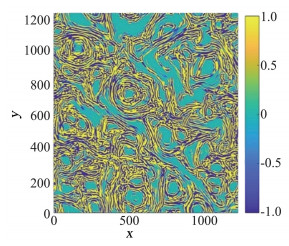
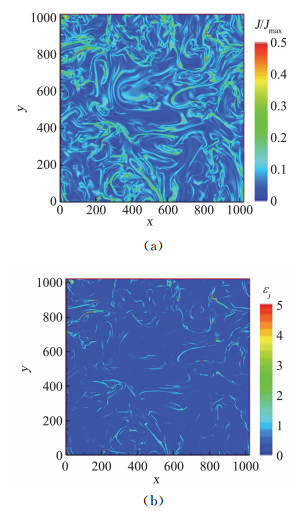
通过尺度l的能流率是能量传输过程的最基本的量, 在经典的能量级串中, 能量在无穷大Reynolds数下的惯性区的传输是守恒的, 这意味着能流是常数。如果能流为正, 则级串为正向的(即从大尺度流向小尺度); 如果能流为负, 则级串为逆向的(即从小尺度流向大尺度)。值得注意的是, 这里的能流率指的是净能量传递, 即全场平均值, 但是局部的能量传输很可能与平均值有很大偏离。为了给出局部的能量传输率, 采用滤波的方法[68]可以得到通过尺度l的亚格子能流Πl。在中性流体湍流中亚格子能流Πl=-(uu- u u):∇ u -的空间分布具有间歇性[69-70],并且局部的亚格子能流可正可负, 可以理解为从局部来看能量可能从大(小)尺度传向小(大)尺度。有关磁流体湍流局部的亚格子能流的研究[38, 71-73]中有讨论, 图 7画出了Hall磁流体湍流的亚格子能流, 研究表明, 亚格子能流具有间歇性, 极值集中在较小区域范围, 且与相干结构存在关联。传输的能量最终被耗散成热, 黏性耗散为εν=2ν S 2, 磁阻耗散为εj=η j 2。根据定义可看出局部的耗散率和相关结构有关[74]。图 8为三维磁流体湍流的某一截面的电流密度及磁阻耗散的等值图, 两者的空间分布非常相似, 也就是说强电流密度对应着强磁阻耗散。
|
图 7 二维Hall磁流体湍流的亚格子能流的等值图(摘自文献[72]) Fig.7 Contour map of subgrid-scale energy flux in a simulation of 2D Hall magnetohydrodynamic turbulence (Adapted from[72]) |
|
图 8 三维磁流体湍流某一截面上电流密度(a)及磁阻耗散(b)的等值图(摘自文献[74]) Fig.8 Contour maps of current density (a) and magnetic dissipation (b) from one 2D slice of 3D MHD simulation. (Adapted from[74]) |
该部分主要讨论, 不可压、各向同性等条件不满足的情况下的性质。
3.1 各向异性各向异性相对各向同性更为复杂, 然而非各向同性磁流体湍流的研究是非常由必要的。例如, 宇宙空间中普遍存在的天体磁场(行星磁场、太阳磁场、行星际磁场等), 背景磁场会导致非各向同性的产生, 从而影响湍流的结构及能量传输, 其效果在一定程度上类似于2011年Lamriben等[75]第一次从实验中发现旋转湍流中能量传输的各向异性。这里介绍背景磁场下两种各向异性:
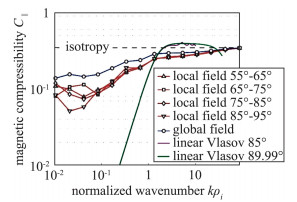
(1) 方差各向异性(variance anisotropy)[76-77],各方向的能量不相等。以磁场脉动b为例, 可以用磁压缩性C‖=〈b‖2〉/〈b‖2+b⊥2〉(〈·〉表示平均值, b⊥、b‖分别是垂直、平行于背景磁场的磁场脉动)来衡量方差各向异性[78]。图 9为磁压缩性随波数的变化, 可以看到背景磁场使得大部分尺度的磁压缩性明显小于1/3, 平行于背景磁场方向的发展明显受到抑制。
|
图 9 采用太阳风湍流的Cluster卫星观测数据, 分析磁压缩性C‖随波数的变化.水平虚线表示的各向同性情况下, 磁压缩性C‖为1/3 (摘自文献[78]) Fig.9 Magnetic compressibility C‖, computed by using high cadence in situ magnetic field measurements from the Cluster spacecraft missions, against the normalized wavenumber. The horizontal dashed line at C‖=1/3 indicates the isotropic state (Adapted from Ref.[78]) |
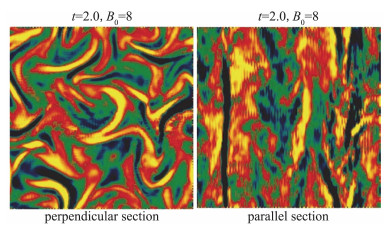
(2) 波矢各向异性(wavevector anisotropy)[76-77],给定波数的能量在谱空间分布非各向同性。以能谱E(kx, ky, k‖)为例,背景磁场沿z方向, 波矢各向异性可以表现为E(k, 0, 0)>>E(0, 0, k)。以结构函数R(r)=〈 b ( x)· b (x + r)〉为例, 波矢各向异性可以表现为
|
图 10 背景磁场B0/δb=8的三维磁流体湍流, 垂直于背景磁场(左)及平行于背景磁场(右)的截面上电流密度等值图(摘自文献[81]) Fig.10 Contour maps of current density in perpendicular (left) and parallel (right) cross sections from 3D simulation of MHD turbulence with an applied background magnetic field B0/δb=8 (Adapted from Ref.[81]) |
在讨论磁流体湍流的各向异性时,一个需要注意的问题是,磁场是局部平均磁场还是全局平均磁场。对磁场在尺度l进行平均,〈 B 〉l=〈 b+B 0〉l,称为局部平均磁场;对磁场进行全场平均,B 0,称为全局平均磁场。二阶结构函数S2=(S2++S2-)/2(其中S2±(l)=〈δzi±δzi±〉)常用于研究各向异性的尺度相关性,l‖、l⊥分别为二阶结构函数相等时对应的平行、垂直于磁场方向的间距,即S2(l‖, 0)=S2(0, l⊥)。如果各向异性是尺度无关的,则l‖∝l⊥,即l⊥/l‖不随尺度变化;如果各向异性是尺度相关的,则l‖∝l⊥p(其中p<1),即l⊥/l‖随尺度减小而增大。研究表明,如果采用局部平均磁场来确定平行与垂直磁场方向,则各向异性是尺度相关的[82-83],而采用全局平均磁场来确定平行与垂直磁场方向,则各向异性是尺度无关的[84-85]。如图 11所示,尽管没有背景磁场,B0=0,采用局部平均磁场时,l‖和l⊥满足临界平衡关系l‖∝l⊥2/3,表明各向异性是尺度相关的。
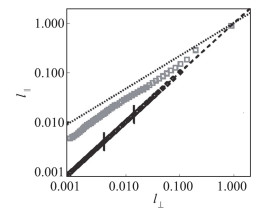
|
图 11 利用二阶结构函数得到的平行及垂直于磁场的尺度l‖及l⊥之间的关系.黑色棱形点对应全局平均磁场情形; 灰色方形点对应局部平均磁场情形.图中虚线为l‖=l⊥, 代表尺度无关的各向异性, 点线为l‖=l⊥2/3, 代表临界平衡尺度相关的各向异性(摘自文献[86]) Fig.11 Increments l‖ and l⊥obtained by identifying the scales at which the second-order structure functions have the same value. Black diamonds and grey squares indicate the anisotropy with respect to the global or the local mean magnetic field, respectively. The two reference straight lines indicate scale-independent anisotropy (l‖=l⊥, dashed line) and the critical balance scale-dependent anisotropy (l‖=l⊥2/3, dotted line) (Adapted from Ref.[86]) |
当马赫数很小时, 磁流体湍流可以近似看做不可压的, 大多实验室等离子体即是近似不可压的。大部分的空间和天体等离子体是可压的, 例如星际物质, 因为温度很低, 所以其对应的马赫数往往很大, 可以达到几十的量级甚至更大。流场的压缩性可以通过∇· u来衡量, 运用Helmholtz分解, 将速度场分解为剪切部分和胀压部分, 进而讨论剪切过程、胀压过程及两者之间的相互作用[70, 87]。在磁流体力学中, 还需要考虑磁场的作用。相较于不可压磁流体湍流, 可压缩磁流体湍流中压强做功是非常有效的增加热能的方式[71]。
气体动力学中压缩性使非均匀密度的扰动发展为激波, 其中主要波动过程为声波; 在磁流体力学中,磁声波的叠起也会形成快、慢激波, 不过此时既有流体和磁压的压缩效应, 也有磁力的剪切效应, 磁流体力学激波的关系[88-89]比气体动力学激波更复杂。激波是不同于涡或者电流片的另一类相干结构,涡片或者电流片可以看成切向间断, 而激波会有法向间断, 这类强间断会对湍流的性质产生很大影响, 比如激波处的能量传输显著增强[71, 90]。激波的出现带来了很强的间歇性, 标度律远远偏离线性标度关系, 并且随着阶数的增加, 结构函数的标度指数会达到饱和值[71, 87]。图 12(a)给出了密度结构函数Spρ(r)=〈|δρ(r)|p〉随间距r的变化。为了简洁, 图中只画出了四阶到七阶的结构函数。从图中可看出, 在一段区域内密度结构函数和间距之间存在明显的幂律关系, 即Spρ(r)~rζρp。图 12(b)为局部标度指数ζpρ随间距的变化, 采用黑色水平线标注的区域(该区域局部标度指数变化很小), 计算标度指数及误差。如图 12(c)所示, 标度指数ζpρ在阶数增大时, 会趋于饱和, 饱和值为ζ∞ρ=1.31±0.06, 这是由于激波引起了密度间断的缘故[91-92]。根据重分形理论, 这些激波结构的分形维度Dρ=3-ζ∞ρ < 2, 所以这些激波不是单片的正激波面, 而是会有变形和破碎。
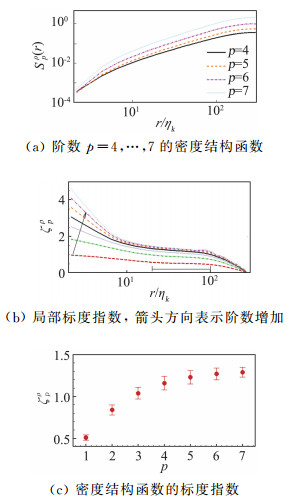
|
图 12 可压缩磁流体湍流密度标度律(摘自文献[71]) Fig.12 Scaling properties of density fluctuations in compressible MHD turbulence (Adapted from Ref.[71]) |
等离子体湍流中, 带电粒子和电磁场的相互作用非常复杂, 因此要精确地描述等离子体湍流极其困难。为了研究等离子体流, 更完善的模型可以给出等离子体流更全面的性质。然而一个模型是否合适, 取决于限制条件、应用范围、计算能力等多个因素, 实际只能根据不同的研究问题, 采用不同的近似方法进行描述。磁流体是描述等离子体的一个模型, 只有在所考虑的问题满足一定的条件时, 等离子体可简化为磁流体, 比如研究问题的尺度远大于带电粒子的轨道半径, 只讨论低频过程。磁流体力学利用从宏观到微观的决定论, 侧重于等离子体宏观大尺度流体属性。
在磁流体工程应用中,磁雷诺数Rem < < 1,感应磁场可忽略,即认为外加磁场未受到流动的干扰,其控制方程实际是经过了电磁效应源项修正后的N-S方程,在一定程度上简化了文中采用的方程(考虑了流场与磁场的双向作用)。尽管如此,低磁雷诺数磁流体湍流也表现出非常重要的特性,如磁诱导的各向异性[93-94]、k-3的能谱[95]、能量的反向传递[96]等,有关低磁雷诺数更全面的综述可参见文献[97],我们文中主要概述了在空间、天体物理常见的高磁雷诺数磁流体湍流的部分研究。
和磁流体湍流理论相比,中性流体湍流理论的发展更完备,但中性流体湍流的很多理论并不能直接推广至磁流体湍流。为了研究磁流体湍流这一复杂系统,须借助实验、卫星观测、数值模拟和理论分析等多种手段,例如,实验方面,受控热核反应问题对其发展起了关键作用;观测方面,高时空分辨率的卫星计划(如NASA在2015年实施的Magnetospheric Multiscale卫星计划)为我们提供了一个天然实验室。
磁流体湍流是一个时间多尺度、空间多尺度的物理现象, 而各尺度间的能量传输是将多尺度联合起来的关键, 文章也正是围绕能量传输以及与能量传输相关的结构展开。需要指出的是,本文仅介绍了小部分和磁流体湍流结构与能量传输相关的工作。另一方方面,尽管在磁流体湍流理论、实验、观测、数值模拟方面已有长足的发展, 但还有许多问题有待进一步研究, 如对于磁流体湍流模型和高超声速磁流体湍流的研究相对较少;又比如对速度场和磁场非平衡、存在交叉螺旋度的湍流缺乏足够的认识,甚至对其能谱和标度率都存在争议。
| [1] |
GOLDSTEIN M L, ROBERTS D A, MATTHAEUS W H. Magnetohydrodynamic turbulence in the solar wind[J]. Annual Review of Astronomy and Astrophysics, 1995, 33(1): 283-325. |
| [2] |
BISKAMP D. Magnetohydrodynamic turbulence[M]. Cambridge: Cambridge University Press, 2003.
|
| [3] |
徐复. 原子核聚变反应堆中的力学问题[J]. 力学进展, 1994, 24(3): 301-314. XU F. Various problems of mechanics in nuclear fusion reactors[J]. Advances in Mechanics, 1994, 24(3): 301-314. (in Chinese) |
| [4] |
赫新, 陈坚强, 邓小刚. NND格式在多维理想磁流体方程组中的应用[J]. 空气动力学学报, 2005, 23(3): 267-273. HE X, CHEN J Q, DENG X G. NND scheme's application in multi-dimensional ideal magnetohydrodynamic equations[J]. Acta Aerodynamica Sinica, 2005, 23(3): 267-273. (in Chinese) |
| [5] |
李茂, 周孑民, 王长宏. 300 kA铝电解槽电、磁、流多物理场耦合仿真[J]. 过程工程学报, 2007, 7(2): 354-359. LI M, ZHOU J M, WANG C H. Coupled simulation of multiple physical fields in a 300kA aluminum electrolysis cell[J]. The Chinese Journal of Process Engineering, 2007, 7(2): 354-359. (in Chinese) |
| [6] |
张康平, 田正雨, 冯定华, 等. 三维磁流体动力学管道流动加减速控制数值研究[J]. 空气动力学学报, 2009, 27(4): 474-479. ZHANG K P, TIAN Z Y, FENG D H, et al. Numerical study of acceleration/deceleration control of three-dimensional magnetohydrodynamic flow in channel[J]. Acta Aerodynamica Sinica, 2009, 27(4): 474-479. (in Chinese) |
| [7] |
苏纬仪, 陈立红, 张新宇. MHD控制超声速边界层的理论研究和数值分析[J]. 力学学报, 2010, 42(4): 782-788. SU W Y, CHEN L H, ZHANG X Y. Physics and numerical simulations of MHD accelerated supersonic boundary layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 782-788. (in Chinese) |
| [8] |
候俊, 毛洁, 潘华辰. 磁流体管流的层流与湍流模型数值模拟[J]. 核聚变与等离子体物理, 2013, 33(1): 7-12. HOU J, MAO J, PAN H C. Numerical simulation of MHD duct flow about laminar and turbulence model[J]. Nuclear Fusion and Plasma Physics, 2013, 33(1): 7-12. (in Chinese) |
| [9] |
孟宣市, 宋科, 龙玥霄, 等. NS-SDBD等离子体流动控制研究现状与展望[J]. 空气动力学学报, 2018, 36(6): 901-916. MENG X S, SONG K, LONG Y X, et al. Airflow control by NS-SDBD plasma actuators[J]. Acta Aerodynamica Sinica, 2018, 36(6): 901-916. (in Chinese) |
| [10] |
薛明, 高超, 刘峰, 等. 非定常激励下等离子体DBD诱导涡特性研究[J]. 空气动力学学报, 2019, 37(1): 83-88. XUE M, GAO C, LIU F, et al. Characteristics of vortex induced by DBD plasma actuator under unsteady excitation in quiescent air[J]. Acta Aerodynamica Sinica, 2019, 37(1): 83-88. (in Chinese) |
| [11] |
ORSZAG S A, TANG C M. Small-scale structure of two-dimensional magnetohydrodynamic turbulence[J]. Journal of Fluid Mechanics, 1979, 90(1): 129-143. |
| [12] |
MATTHAEUS W H. Reconnection in two dimensions:localization of vorticity and current near magnetic X-points[J]. Geophysical Research Letter, 1982, 9(6): 660-663. |
| [13] |
CARBONE V, VELTRI P, MANGENEY A. Coherent structure formation and magnetic field line reconnection in magnetohydrodynamic turbulence[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(8): 1487-1496. |
| [14] |
POLITANO H, POUQUET A, SULEM P L. Current and vorticity dynamics in three-dimensional magnetohydrodynamic turbulence[J]. Physics of Plasmas, 1995, 2: 2931-2939. |
| [15] |
KINNEY R, MCWILLIAMS J C, TAJIMA T. Coherent structures and turbulent cascades in two-dimensional incompressible magnetohydrodynamic turbulence[J]. Physics of Plasmas, 1995, 2(10): 3623-3639. |
| [16] |
COWLEY S C, LONGCOPE D W, SUDAN R N. Current sheets in MHD turbulence[J]. Physics Reports, 1997, 283(1-4): 227-251. |
| [17] |
GLAUERT M B. A study of the magnetohydrodynamic boundary layer on a flat plate[J]. Journal of Fluid Mechanics, 1961, 10: 276-288. |
| [18] |
KOLMOGOROV A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]. Proceedings of the Royal Society of London. Series A:Mathematical and Physical Sciences, 1991, 434(1890): 9-13. |
| [19] |
KOLMOGOROV A N. Dissipation of energy in the locally isotropic turbulence[J]. Proceedings of the Royal Society of London. Series A:Mathematical and Physical Sciences, 1991, 434(1890): 15-17. |
| [20] |
FRISCH U. Turbulence:the legacy of A. N. Kolmogorov[M]. Cambridge: Cambridge University Press, 1995.
|
| [21] |
GAILITIS A, LIELAUSIS O, PLATACIS E, et al. Colloquium:Laboratory experiments on hydromagnetic dynamos[J]. Reviews of Modern Physics, 2002, 74(4): 973. |
| [22] |
ELMEGREEN B G, SCALO J. Interstellar turbulence I:observations and processes[J]. Annual Review of Astronomy and Astrophysics, 2004, 42: 211-273. |
| [23] |
SAHOO G, PERLEKAR P, PANDIT R. Systematics of the magnetic-Prandtl-number dependence of homogeneous, isotropic magnetohydrodynamic turbulence[J]. New Journal of Physics, 2011, 13: 013036. |
| [24] |
SHE Z S, JACJSON E, ORSZAG S A. Intermittent vortex structures in homogeneous isotropic turbulence[J]. Nature, 1990, 344(6263): 226. |
| [25] |
VINCENT A, MENEGUZZI M. The spatial structure and statistical properties of homogeneous turbulence[J]. Journal of Fluid Mechanics, 1991, 225: 1-20. |
| [26] |
JIMÉNEZ J, WRAY A A, SAFFMAN P G, et al. The structures of intense vorticity in isotropic turbulence[J]. Journal of Fluid Mechanics, 1993, 255: 65-90. |
| [27] |
ZIKANOV O, THESS A. Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number[J]. Journal of Fluid Mechanics, 1998, 358: 299-333. |
| [28] |
MININNI P D, POUQUET A G, MONTGOMERY D C. Small-scale structures in three-dimensional magnetohydrodynamic turbulence[J]. Physical Review Letters, 2006, 97: 244503. |
| [29] |
MININNI P, LEE E, NORTON A, et al. Flow visualization and field line advection in computational fluid dynamics:application to magnetic fields and turbulent flows[J]. New Journal of Physics, 2008, 10: 125007. |
| [30] |
GRECO A, MATTHAEUS W H, SERVIDIO S, et al. Statistical analysis of discontinuities in solar wind ACE data and comparison with intermittent MHD turbulence[J]. The Astrophysical Journal, 2009, 691: L111-L114. |
| [31] |
MATTHAEUS W H, WAN M P, SERVIDIO S, et al. Intermittency, nonlinear dynamics and dissipation in solar wind and astrophysical plasmas[J]. Philosophical Transaction of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2015, 373(2041): 20140154. |
| [32] |
CHONG M S, PERRY A E, CANTWELL B J. A general classification of three-dimensional flow fields[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(5): 765-777. |
| [33] |
OOI A, MARTIN J, SORIA J, et al. A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence[J]. Journal of Fluid Mechanics, 1999, 381: 141-174. |
| [34] |
WANG J C, SHI Y P, WANG L P, et al. Effect of compressibility on the small-scale structures in isotropic turbulence[J]. Journal of Fluid Mechanics, 2012, 713: 588-631. |
| [35] |
CANTWELL B J. Introduction of symmetry analysis[M]. Cambridge: Cambridge University Press, 2002.
|
| [36] |
BLACK H M, MANSOUR N N, CANTWELL B J. Topology of fine-scale motions in turbulent channel flow[J]. Journal of Fluid Mechanics, 1996, 310: 269-292. |
| [37] |
DALLAS V, ALEXAKIS A. Structures and dynamics of small scales in decaying magnetohydrodynamic turbulence[J]. Physics of Fluids, 2013, 25: 105106. |
| [38] |
YANG Y, MATTHAEUS W H, PARASHAR T N, et al. Energy transfer, pressure tensor, and heating of kinetic plasma[J]. Physics of Plasmas, 2017, 24: 072306. |
| [39] |
PARASHAR T N, MATTHAEUS W H. Propinquity of current and vortex structures:effects on collisionless plasma heating[J]. The Astrophysical Journal, 2016, 832: 57. |
| [40] |
BURLAGA L F, NORMAN F N. Macro-and micro-structure of the interplanetary magnetic field[J]. Canadian Journal of Physics, 1968, 46(10): S962-S965. |
| [41] |
TSURUTANI B T, SMITH E J. Interplanetary discontinuities:Temporal variations and the radial gradient from 1 to 8.5 AU[J]. Journal of Geophysical Research:Space Physics, 1979, 84(A6): 2773-2787. |
| [42] |
GRECO A, CHUYCHAI P, MATTHAEUS W H, et al. Intermittent MHD structures and classical discontinuities[J]. Geophysical Research Letters, 2008, 35: L19111. |
| [43] |
BRUNO R, CARBONE V, VELTRI P, et al. Identifying intermittency events in the solar wind[J]. Planetary and Space Science, 2001, 49(12): 1201-1210. |
| [44] |
MATTHAEUS W H, GOLDSTEIN M L. Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind[J]. Journal of Geophysical Research:Space Physics, 1982, 87(A8): 6011-6028. |
| [45] |
MVLLER W C, GRAPPIN R. Spectral energy dynamics in magnetohydrodynamic turbulence[J]. Physical Review Letters, 2005, 95(11): 114502. |
| [46] |
BELCHER J W, DAVIS L. Large-amplitude Alfvén waves in the interplanetary medium, 2[J]. Journal of Geophysical Research, 1971, 76(16): 3534-3563. |
| [47] |
IROSHNIKOV P. Turbulence of a conducting fluid in a strong magnetic field[J]. Soviet Astronomy, 1964, 7: 566. |
| [48] |
KRAICHNAN R H. Inertial-range spectrum of hydromagnetic turbulence[J]. Physics of Fluids, 1965, 8(7): 1385-1387. |
| [49] |
TU C Y. The damping of interplanetary Alfvénic fluctuations and the heating of the solar wind[J]. Journal of Geophysical Research:Space Physics, 1988, 93(A1): 7-20. |
| [50] |
MATTHAEUS W H, ZHOU Y. Extended inertial range phenomenology of magnetohydrodynamic turbulence[J]. Physics of Fluids B:Plasma Physics, 1989, 1(9): 1929-1931. |
| [51] |
MONIN A S, YAGLOM A M. Statistical fluid mechanics:mechanics of turbulence, volume 2[M]. Cambridge, MA: MIT Press, 1975.
|
| [52] |
POLITANO H, POUQUET A. Von Kármán-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions[J]. Physics Review E, 1998, 57: R21-R24. |
| [53] |
SORRISO-VALVO L, MARINO R, CARBONE V, et al. Observation of inertial energy cascade in interplanetary space plasma[J]. Physical Review Letters, 2007, 99(11): 115001. |
| [54] |
COBURN J T, FORMAN M A, SMITH C W, et al. Third-moment descriptions of the interplanetary turbulent cascade, intermittency and back transfer[J]. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2015, 373(2041): 20140150. |
| [55] |
BANDYOPADHYAY R, CHASAPIS A, CHHIBER R, et al. Solar wind turbulence studies using MMS fast plasma investigation data[J]. The Astrophysical Journal, 2018, 866(2): 81. |
| [56] |
SORRISO-VALVO L, CARBONE V, NOULLEZ A, et al. Analysis of cancellation in two-dimensional magnetohydrodynamic turbulence[J]. Physics of Plasmas, 2002, 9(1): 89-95. |
| [57] |
YANG Y, WAN M P, MATTHAEUS W H, et al. Scale dependence of energy transfer in turbulent plasma[J]. Monthly Notices of the Royal Astronomical Society, 2019, 482: 4933-4940. |
| [58] |
EYINK G L. Locality of turbulent cascades[J]. Physica D:Nonlinear Phenomena, 2005, 207(1-2): 91-116. |
| [59] |
KRAICHNAN R H. Inertial-range transfer in two-and three-dimensional turbulence[J]. Journal of Fluid Mechanics, 1971, 47(3): 525-535. |
| [60] |
OHKITANI K, KIDA S. Triad interactions in a forced turbulence[J]. Physics of Fluids A:Fluid Dynamics, 1992, 4(4): 794-802. |
| [61] |
ZHOU Y. Degrees of locality of energy transfer in the inertial range[J]. Physics of Fluids A:Fluid Dynamics, 1993, 5(5): 1092-1094. |
| [62] |
DOMARADZKI J A, CARATI D. An analysis of the energy transfer and the locality of nonlinear interactions in turbulence[J]. Physics of Fluids, 2007, 19(8): 085112. |
| [63] |
EYINK G L, ALUIE H. Localness of energy cascade in hydrodynamic turbulence[J]. Physics of Fluids, 2009, 21(11): 115107. |
| [64] |
VERMA M K, AYYER A, CHANDRA A V. Energy transfers and locality in magnetohydrodynamic turbulence[J]. Physics of Plasmas, 2005, 12(8): 082307. |
| [65] |
ALEXAKIS A, MININNI P D, POUQUET A. Shell-to-shell energy transfer in magnetohydrodynamics. I. Steady state turbulence[J]. Physical Review E, 2005, 72(4): 046301. |
| [66] |
MININNI P D. Scale interactions in magnetohydrodynamic turbulence[J]. Annual Review of Fluid Mechanics, 2011, 43: 377-397. |
| [67] |
ALUIE H, EYINK G L. Scale locality of magnetohydrodynamic turbulence[J]. Physical Review Letters, 2010, 104(8): 081101. |
| [68] |
GERMANO M. Turbulence:the filtering approach[J]. Journal of Fluid Mechanics, 1992, 238: 325-336. |
| [69] |
CHEN S Y, ECKE R E, EYINK G L, et al. Physical mechanism of the two-dimensional inverse energy cascade[J]. Physical Review Letters, 2006, 96(8): 084502. |
| [70] |
WANG J C, YANG Y T, SHI Y P, et al. Cascade of kinetic energy in three-dimensional compressible turbulence[J]. Physical Review Letters, 2013, 110: 214505. |
| [71] |
YANG Y, MATTHAEUS W H, SHI Y P, et al. Compressibility effect on coherent structures, energy transfer, and scaling in magnetohydrodynamic turbulence[J]. Physics of Fluids, 2017, 29: 035105. |
| [72] |
CAMPOREALE E, SORRISO-VALVO L, CALIFANO F, et al. Coherent structures and spectral energy transfer in turbulent plasma:a space-filter approach[J]. Physical Review Letters, 2018, 120(12): 125101. |
| [73] |
YANG Y. Energy transfer and dissipation in plasma turbulence:from compressible MHD to collisionless plasma[M]. Singapore: Springer Singapore, 2019.
|
| [74] |
WAN M P, MATTHAEUS W H, ROYTERSHTEYN V, et al. Intermittency, coherent structures and dissipation in plasma turbulence[J]. Physics of Plasmas, 2016, 23: 042307. |
| [75] |
LAMRIBEN C, CORTET P P, MOISY F. Direct measurements of anisotropic energy transfers in a rotating turbulence experiment[J]. Physical Review Letters, 2011, 107(2): 024503. |
| [76] |
HORBURY T S, WICKS R T, CHEN C H K. Anisotropy in space plasma turbulence:solar wind observations[J]. Space Science Reviews, 2012, 172: 325-342. |
| [77] |
OUGHTON S, MATTHAEUS W H, WAN M P, et al. Anisotropy in solar wind plasma turbulence[J]. Philosophical Transaction of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2015, 373(2041): 20140152. |
| [78] |
KIYANI K H, CHAPMAN S C, SAHRAOUI F, et al. Enhanced magnetic compressibility and isotropic scale invariance at sub-ion Larmor scales in solar wind turbulence[J]. The Astrophysical Journal, 2012, 763(1): 10. |
| [79] |
LUO Q Y, WU D J. Observations of anisotropic scaling of solar wind turbulence[J]. The Astrophysical Journal Letters, 2010, 714(1): L138. |
| [80] |
SHEBALIN J V, MATTHAUES W H, MONTGOMERY D C. Anisotropy in MHD turbulence due to a mean magnetic field[J]. Journal of Plasma Physics, 1983, 29(3): 525-547. |
| [81] |
ZHOU Y, MATTHAEUS W H, DMITRUK P. Colloquium:Magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas[J]. Reviews of Modern Physics, 2004, 76(4): 1015. |
| [82] |
CHO J, VISHNIAC E T. The anisotropy of magnetohydrodynamic Alfvénic turbulence[J]. The Astrophysical Journal, 2000, 539(1): 273. |
| [83] |
CHEN C H K, MALLET A, SCHEKOCHIHIN A A, et al. Three-dimensional structure of solar wind turbulence[J]. The Astrophysical Journal, 2012, 758(2): 120. |
| [84] |
CHEN C H K, MALLET A, YOUSEF T A, et al. Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations[J]. Monthly Notices of the Royal Astronomical Society, 2011, 415(4): 3219-3226. |
| [85] |
BERESNYAK A. Basic properties of magnetohydrodynamic turbulence in inertial range[J]. Monthly Notices of the Royal Astronomical Society, 2012, 422(4): 3495-3502. |
| [86] |
VERDINI A, GRAPPIN R, HELLINGER P, et al. Anisotropy of third-order structure functions in MHD turbulence[J]. The Astrophysical Journal, 2015, 804(2): 119. |
| [87] |
WANG J C, SHI Y P, WANG L P, et al. Scaling and statistics in three-dimensional compressible turbulence[J]. Physical Review Letters, 2012, 108: 214505. |
| [88] |
MYONG R S, ROE P L. Shock waves and rarefaction waves in magnetohydrodynamics. Part 2. The MHD system[J]. Jourmal of Plasma Physics, 1997, 58(3): 521-552. |
| [89] |
胡文瑞. 宇宙磁流体力学[M]. 北京: 科学出版社, 1987.
|
| [90] |
YANG Y, SHI Y P, WAN M P, et al. Energy cascade and its locality in compressible magnetohydrodynamic turbulence[J]. Physical Review E, 2016, 93: 061102. |
| [91] |
CELANI A, LANOTTE A, MAZZINO A, et al. Fronts in passive scalar turbulence[J]. Physics of Fluids, 2001, 13(6): 1768-1783. |
| [92] |
BENZI R, BIFERALE L, FISHER R T, et al. Intermittency and universality in fully developed inviscid and weakly compressible turbulent flows[J]. Physical Review Letters, 2008, 100(23): 234503. |
| [93] |
VOROBEV A, ZIKANOV O, DAVIDSON P A, et al. Anisotropy of magnetohydrodynamic turbulence at low magnetic Reynolds number[J]. Physics of Fluids, 2005, 17: 125105. |
| [94] |
ZHAI X M, YEUNG P K. Evolution of anisotropy in direct numerical simulations of MHD turbulence in a strong magnetic field on elongated periodic domains[J]. Physical Review Fluids, 2018, 3: 084602. |
| [95] |
BURATTINI P, KINET M, CARATI D, et al. Anisotropy of velocity spectra in quasistatic magnetohydrodynamic turbulence[J]. Physics of Fluids, 2008, 20: 065110. |
| [96] |
BAKER N T, POTHERAT A, DAVOUST L, et al. Inverse and direct cascades in three-dimensional magnetohydrodynamic turbulence at low magnetic Reynolds number[J]. Physical Review Letters, 2018, 120: 224502. |
| [97] |
KNAEPEN B, MOREAU R. Magnetohydrodynamic turbulence at low magnetic Reynolds number[J]. Annual Review of Fluid Mechanics, 2008, 40: 25-45. |
 2020, Vol. 38
2020, Vol. 38

