边界层转捩是空气动力学中的一个重要难题,特别是在超声速和高超声速条件下的边界层转捩问题更为复杂,相关认知更加欠缺。高超声速边界层转捩广泛存在于工程应用中, 例如高超声速飞行器的舵面绕流、发动机进气道内流动等.它对高超声速飞行器的气动力、气动热以及发动机启动等关键问题都有着重要的影响。研究表明[1],湍流状态下,飞行器表面的摩擦阻力系数和传热系数大约是层流状态下的3-5倍,且随着飞行器的飞行速度的增加,湍流和层流状态下的结果差异会更大。因此边界层转捩对超声速、高超声速飞行器的气动特性和结构设计具有重要的影响。Mack[2-3]在20世纪80~90年代对边界层中扰动波的线性发展进行了系统的研究,他发现当Ma>4时,边界层中密度和速度的组合剖面会产生拐点,在当地声速线和壁面之间会出现纵向辐射声扰动波,并且认为这种由压力脉动引起的扰动波(即第二模态波)在边界层转捩中起着主导作用。这之后,美国加利福利亚大学的Zhong等人[4]以及Kendall[5]和Stetson[6]等诸多学者[7-8]分别通过数值模拟和风洞实验的方法都证明了第二模态波对高超声速边界层转捩具有十分重要的影响。然而在飞行器真实飞行过程中,流动往往是非对称的,此时边界层速度剖面是三维的[9],横流不稳定性就是主导三维边界层转捩的典型模态,存在于后掠翼[10]、椭圆锥[11]以及有迎角圆锥[12]流动中。Craig等人[13]利用热线技术对带迎角圆锥展向定常横流涡进行了研究,并且测得了中心频率为110 kHz的I型二次不稳定波。Moyes等人[14]通过数值模拟方法,得到了70~155 kHz和140~300 kHz的两种二次不稳定模态。这两种不稳定模态迅速增长,并且随着定常横流的饱和而变成主导模态。
本文首先通过对高超声速条件下的圆锥边界层进行实验研究,对边界层中的第二模态不稳定波进行分析。然后选择三角翼非对称三维流动,对边界层中的横流不稳定性进行了研究。
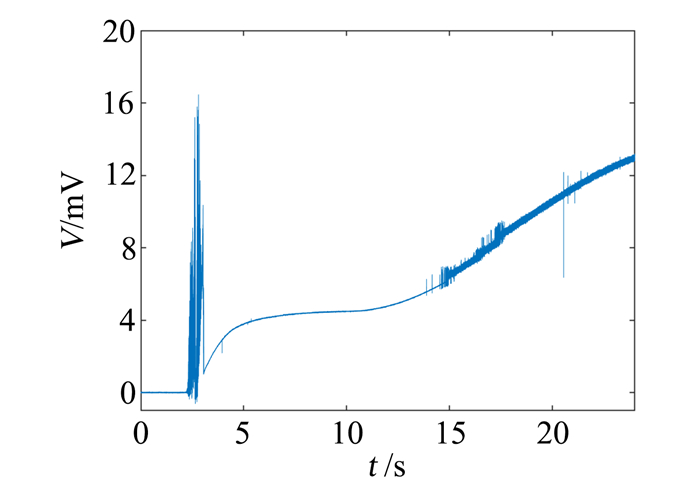
1 实验设备与测试技术 1.1 高超声速静音风洞图 1所示为国防科技大学空气动力学实验室高超声速静音风洞,它采用了上吹下吸的运行方式,喷管出口尺寸为Ф300 mm。为了提供低湍流度的自由来流,该风洞除了在稳定段设置了多孔倒锥、阻尼网和消音夹层等整流装置之外,还在喷管喉道上游附近设计了抽吸装置,其目的是抽走喉道壁面附近的边界层,从而使喷管壁面边界层尽量保持层流状态,减小边界层中涡结构产生的声幅噪声。通过控制抽吸阀门,可以改变风洞自由来流的湍流度水平。采用Kulite传感器进行了风洞来流噪声水平测量,典型结果如图 2所示,最低湍流度约为千分之一,达到静音风洞标准[15]。

|
图 1 高超声速静音风洞 Fig.1 Hypersonic quiet wind tunnel |
|
图 2 风洞来流噪声水平测量典型结果 Fig.2 Typical result of the freestream noise-level measurement |
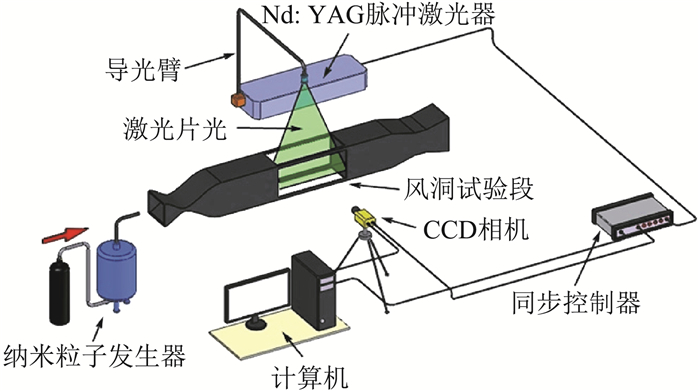
基于纳米示踪的平面激光散射技术(Nano-tracer-based Planar Laser Scattering,NPLS)是本文作者自主研发的流动精细测试技术。NPLS系统组成如图 3所示,主要包括:纳米粒子发生器,Nd:YAG双腔脉冲激光器,同步控制器,CCD相机和计算机等。文献[16-18]对NPLS技术的原理和适用性进行了详细的阐述,前期研究证明NPLS技术具有高时空分辨率和高信噪比,适用于超声速、高超声速流场的精细结构研究。
|
图 3 NPLS系统组成 Fig.3 Schematic diagram of NPLS system |
温敏漆(Temperature-Sensitive Paints,TSP)技术的原理是基于荧光分子的热猝灭效应。荧光分子受到LED光源激发会发出长波的光线,光强会随温度的升高而降低,根据这个特性来进行温度以及热流测量。硬件包括TSP涂料、LED光源、CCD相机系统、滤光片。本系统选用了单波长为365 nm的UV-LED等作为激励光源,灯头有两个,总功率40 W,同时,结合TSP分子发光特性,选用规格为460 nm长波通的滤光片。所选用的CCD相机分辨率为2058 pixel×2456 pixel。
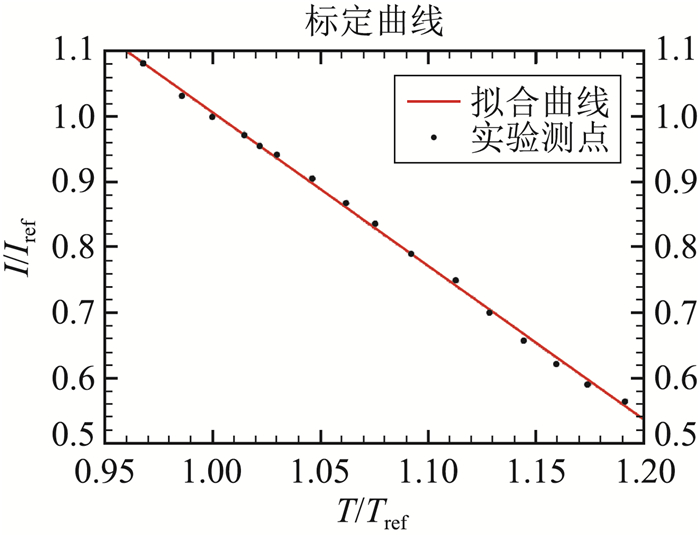
对TSP涂层的静态标定在恒温箱中进行,将喷涂TSP涂料的标定板放入恒温箱,粘贴热电偶测量准确温度,同时采集对应温度的TSP光强数据。标定的温度范围为10 ℃~80 ℃,每隔5 ℃采集一次数据。得到的标定曲线如图 4所示。
2 第二模态不稳定波研究 2.1 直圆锥边界层中第二模态波研究在半锥角7°的直圆锥上进行了边界层流动稳定性实验研究。如图 5所示,圆锥头部为R=0.1mm的尖前缘,圆锥总长L=536mm,底部直径D=132 mm。在X方向上共布置了7个PCB高频脉动压力传感器测点,1~7号测点具体位置分别为:X1=140 mm,X2=200 mm,X3=260 mm,X4=320 mm,X5=380 mm,X6=440 mm,X7=500 mm。图 6中给出单位雷诺数Re=0.5×107 m-1时的脉动压力功率谱结果。此时在X=380 mm和X=440 mm处观察到了明显的第二模态波,第二模态波的特征频率从137.9 kHz降到127.1 kHz,此时第二模态波的幅值表现为明显增加。但在X=500 mm处第二模态波消失,此时低频成分所占能量比例大幅增加,并且在该位置处没有观察到明显的高频谐波成分出现,说明边界层中的扰动波从X=440 mm发展到X=500 mm的位置时,扰动已经完成了非线性的增长过程,此时边界层开始由层流状态向湍流状态转捩。

|
图 5 直圆锥示意图 Fig.5 Schematic diagram of straight cone |

|
图 6 脉动压力功率谱结果(Re=0.5×107 m-1) Fig.6 Power spectrum density of the fluctuation pressure (Re=0.5×107 m-1) |
图 7所示为在雷诺数Re=0.5×107 m-1条件下得到的圆锥边界层NPLS结果。图片分辨率为40 μm/pixel。此时从NPLS结果中能够观察到清晰的绳状第二模态波结构。对比近年来相关学者采用基于二氧化碳冷凝散射等技术测量得到的第二模态波流动结果,NPLS采用二氧化钛纳米粒子作为示踪粒子,受壁面温度影响较小,能够更加准确的反应出边界层近壁面位置处的密度分布。

|
图 7 马赫数6圆锥边界层二次模态波NPLS测量结果(Re=0.5×107 m-1) Fig.7 The NPLS result of the second mode wave in the Mach 6 boundary layer on the cone |
单幅NPLS图片只能够反应流场结构的瞬态结果,为了进一步对边界层中流动结构进行定量的分析,选取具有时间相关性的两幅NPLS图片进行进一步的分析。图 8所示为单位雷诺数Re=0.75×107 m-1条件下得到的两幅时间相关NPLS结果,其间隔时间Δt=5 μs。选取图中的绳状第二模态波结构作为特征结构,通过从两幅图片相应位置可以量出特征结构的移动距离ΔS1=3.72 mm,从而可以计算出对应的第二模态波的传播速度Vc=ΔS1/(cos7°×Δt)=750 m/s。根据该雷诺数条件下的总温总压条件,可以计算主流速度约为810 m/s,所以此时第二模态波的传播速度约为主流速度的0.93倍。同时对该雷诺数条件下得到的所有第二模态波的波长进行统计平均得到第二模态波的统计波长λ约为2.99 mm,根据公式f=Vc/λ可以得到该工况条件下第二模态波的特征频率f=251 kHz。

|
图 8 边界层二次模态波时间相关NPLS测量结果 Fig.8 Temporal-correlated NPLS results of the second mode waves in the boundary layer |
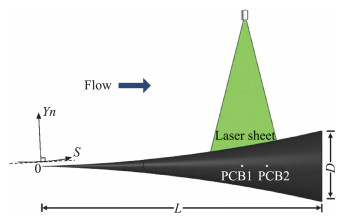
由于上述直锥边界层中第二模态波发展演化较快,为了进一步对高超声速边界层转捩过程中的第二模态不稳定性进行研究,继续在如图 9所示的裙锥模型上开展流动稳定性相关研究。相比于母线为直线的直锥而言,它通过提供额外的逆压梯度,使边界层中扰动波的幅值放大倍数更大,这样的外形也更有利于在实验中对边界层中的不稳定扰动波进行测量和分析。裙锥模型总长L=562 mm,圆锥底部直径D =133 mm,圆锥母线曲率半径R=3000 mm。圆锥头部为r=0.1 mm的尖前缘。以圆锥顶点为坐标原点,S方向代表圆锥母线方向,而Yn方向代表壁面法向方向。
|
图 9 裙锥示意图 Fig.9 Schematic diagram of the flared cone |
图 10所示分别为Re=0.9×107 m-1和Re=1.2 ×107 m-1条件下裙锥边界层的典型NPLS结果。从图中可以清晰分辨出相互交织的绳状第二模态扰动波以及下游相应的湍流精细涡结构。对比2.1节中的结果,在裙锥边界层中,第二模态波分布的流向范围比直锥边界层中第二模态波的分布范围明显更长,在边界层转捩之前,第二模态波增长和衰减过程都更加缓慢,这样有利于基于NPLS结果,对边界层中第二模态波发展的线性阶段进行进一步的定量分析。

|
图 10 高超声速裙锥边界层转捩NPLS照片(Ma=6) Fig.10 NPLS results of the hypersonic boundary layer on the flared cone (Ma=6) |
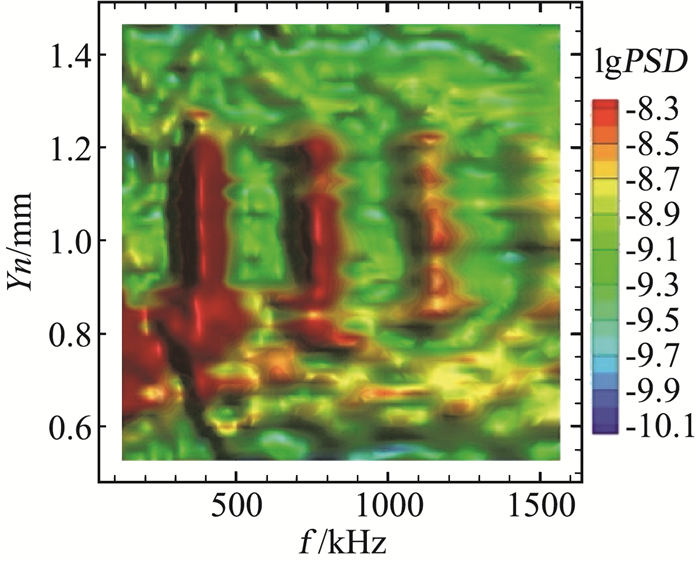
NPLS图片反映了流场中的密度信息在空间位置上的分布情况,为了对扰动波的频域成分进行分析,首先需要把NPLS图片反映出的密度的空间分布信息转化为特定空间位置上随时间变化的密度信息。基于边界层中第二模态波等特征结构,通过互相关算法首先求得第二模态波的传播速度,然后将图 11所示时间相关的NPLS结果转换为空间固定位置上的时序结果。图 12是基于时间相关NPLS结果计算得到的S=505 mm位置处功率谱分析云图。结果表明基于NPLS结果不仅可以测量到第二模态波,同时也能准确捕捉到边界层中高次谐波信息。

|
图 11 边界层转捩第二模态波时间相关NPLS照片 Fig.11 Temporal-correlated NPLS images of the second mode waves in the boundary layer |
|
图 12 S=505 mm位置处功率谱分布云图 Fig.12 The power spectrum density at the position S=505 mm |
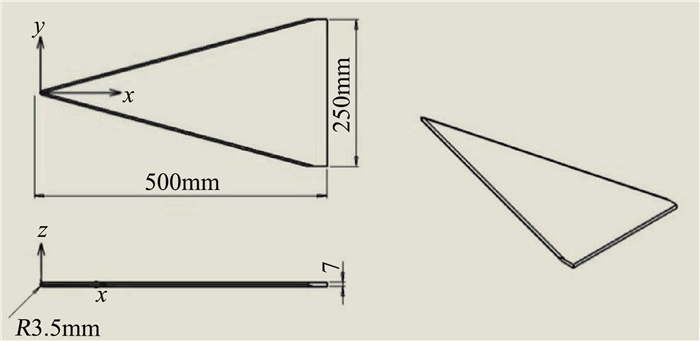
对于横流不稳定性的研究,是在三角平板翼上进行的。实验模型如图 13所示,长度为500 mm,宽度为250 mm,厚度为7 mm,头部和前缘半径为3.5 mm钝前缘。定义的坐标系原点O位于模型头部,沿流向方向为x轴,展向方向为y轴,垂直于展向平面向上为z轴。
|
图 13 三角平板翼实验模型 Fig.13 Schematic diagram of triangular flat wing |
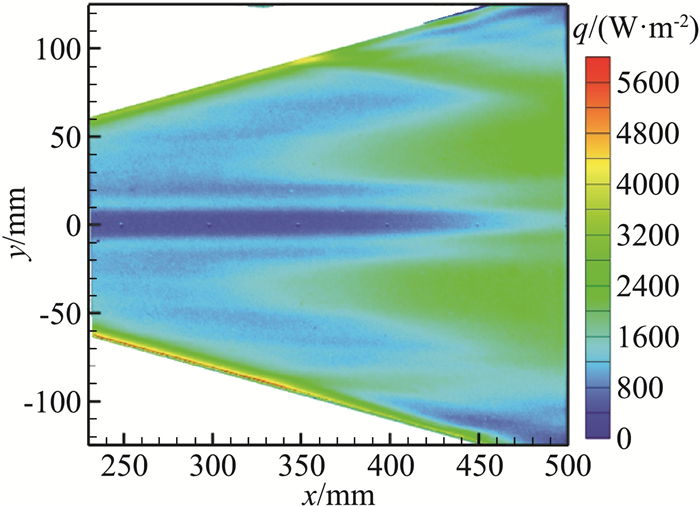
如图 14为单位雷诺数3×106 m-1,迎角为10°时的三角翼迎风面TSP结果。由图 14可知,在x=300~500 mm范围内,出现了“肺叶状”的高温区,为边界层转捩引起。在靠近三角翼前缘的位置,转捩阵面与前缘平行,此性质与后掠翼边界层转捩特性相同,属于典型的横流主导的边界层转捩。并且,转捩阵面光滑而非锯齿状,说明此状态下的主导模态是行进横流波而非定常横流模态。
|
图 14 三角翼迎风面TSP测量结果 Fig.14 TSP results on windward side of delta wing |
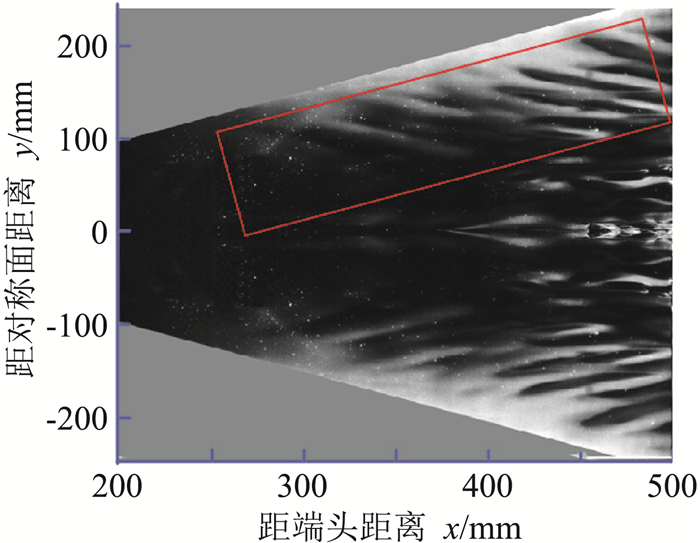
利用NPLS技术,我们可以得到行进横流波的精细流场显示图像,分析行进横流波特性。图 15是对应状态的NPLS图像。由图可知,在x=300~500 mm范围内存在大量近似平行的大尺度横流波结构,结构角方向为从三角平板的前缘偏离向对称面。并且,涡结构的边缘光滑,说明此时为首次横流不稳定性,未发生二次失稳。
|
图 15 三角翼行进横流波NPLS测量结果 Fig.15 NPLS results of the traveling cross-flow wave on the delta wing |
为了方便分析,我们将图 14中红色框圈起来的部分取出,并进行二值化处理,得到涡结构的边界,从而分析横流波的波长和传播速度。如图 16所示,两帧图像的跨帧时间为10 μs,红线为t0时刻的横流波下游边缘,蓝线为t0+10 μs时刻的横流波边缘。可以得到,该6个波的平均移动距离为3.83 mm,移动速度为383 m/s,而在平行于三角平板前缘方向的平均波长为26.65 mm。由公式f=Vc/λ,计算得到横流行波的特征频率为14.37 kHz。

|
图 16 时间相关行进横流波二值化结果 Fig.16 Temporal-correlated binarization results of the traveling cross-flow wave |
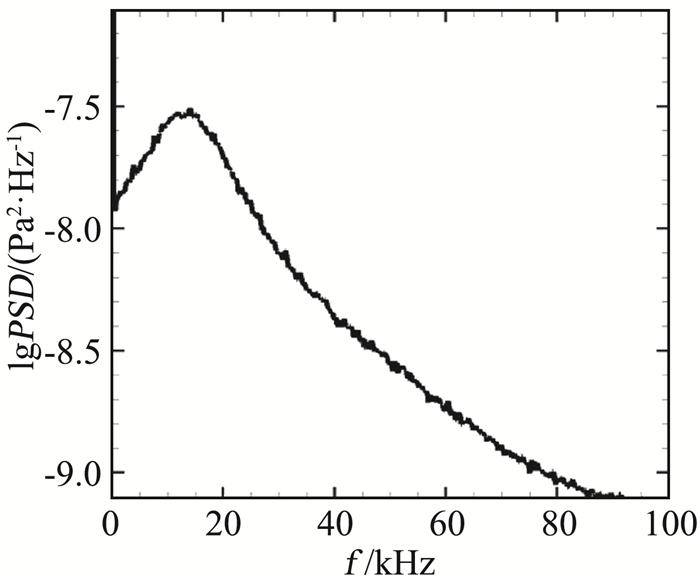
为了验证由NPLS图像得到的行进横流波特性,我们在x=400,距前缘45 mm位置处布置了一个Kulite传感器,得到的PSD结果如图 17所示,由图可知,存在f=14 kHz附近的横流行波信号,与NPLS图像得到的结果互相验证。进一步说明在靠近三角翼前缘部分,边界层转捩的主导模态为中心频率约14 kHz的行进横流模态。
|
图 17 Kulite测得脉动压力的PSD结果 Fig.17 The PSD results of pressure measured by the Kulite transducer |
本文主要通过NPLS等技术对圆锥和三角翼边界层流动稳定性开展了风洞实验研究。结果表明利用NPLS技术能够测量得到边界层中绳状第二模态波的精细流动结构,且通过将NPLS照片得到的密度空间信息转化为特定位置上的时序信号,可以进一步基于NPLS结果对扰动波进行定量研究,通过频谱分析能够测量到相应的高频谐波成分。对于三角翼边界层,在迎风面前缘的边界层流动中,主导边界层转捩的模态为行进横流模态。通过NPLS结果,得到了横流波的结构角方向由前缘偏向对称面,移动速度为383 m/s,平均波长为26.65 mm,中心频率为14 kHz左右,与Kulite传感器测到的压力信号的PSD结果相一致。
| [1] |
李锋, 解少飞, 毕志献, 等. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 1-7. LI F, XIE S F, BI Z X, et al. Experimental study of several aerodynamic problems on hypersonic vehicles[J]. Modern Defence Technology, 2014, 42(5): 1-7. DOI:10.3969/j.issn.1009-086x.2014.05.001 (in Chinese) |
| [2] |
MACK L M. Linear stability theory and the problem of supersonic boundary-layer transition[J]. AIAA Journal, 1975, 13(3): 278-289. DOI:10.2514/3.49693 |
| [3] |
MACK L M. Boundary layer linear stability theory[R]. AGARD Report, 1984, No. 709(709).
|
| [4] |
ZHONG X L. Direct numerical simulation of 3-D hypersonic boundary layer receptivity to freestream disturbances[C]//36th AIAA Aerospace Sciences Meeting and Exhibit: American Institute of Aeronautics and Astronautics, 1998. doi: 10.2514/6.1998-533
|
| [5] |
KENDALL J M. Wind tunnel experiments relating to supersonic and hypersonic boundary layer transition[C]//AIAA-74-0133, 1974. doi: 10.2514/3.49694
|
| [6] |
STETSON K, KIMMEL R. On hypersonic boundary-layer stability[C]//30th Aerospace Sciences Meeting and Exhibit, AIAA-92-0737, 1992. doi: 10.2514/6.1992-737
|
| [7] |
MALIK MUJEEB. Prediction and control of transition in supersonic and hypersonic boundary layers[J]. AIAA Journal, 1989, 27(11): 1487-1493. DOI:10.2514/3.10292 |
| [8] |
KENDALL JAMES M. Boundary layer receptivity to freestream turbulence[C]//AIAA 21st Fluid Dynamics, Plasma Dynamics and Lasers Conference, AIAA-90-1504, 1990. doi: 10.2514/6.1990-1504
|
| [9] |
SARIC W S, CARRILLO R B, REIBERT M S. Nonlinear stability and transition in 3-D boundary layers[J]. Meccanica, 1998, 33(5): 469-487. DOI:10.1023/a:1004368526215 |
| [10] |
RADEZTSK Y, RONALD H, REIBERT M S, et al. Effect of micron-sized roughness on transition in swept-wing flows[J]. AIAA J, 1993, 93(11): 1370-1377. DOI:10.2514/6.1993-76 |
| [11] |
THOMAS J, BORG M P, SCHNEIDER S P. Quiet tunnel measurements of HIFiRE-5 boundary-layer transition[J]. AIAAJ, 2015, 53(4): 832-846. DOI:10.2514/1.J053189 |
| [12] |
WARD C, HENDERSON R, SCHNEIDERS P. Secondary instability of stationary crossflow vortices on an inclined cone at Mach 6[C]//AIAA Fluid Dynamics Conference, 2015. doi: 10.2514/6.2015-2773
|
| [13] |
CRAIG S A, SARIC W S. Crossflow instability in a hypersonic boundary layer[J]. Journal of Fluid Mechanics, 2016, 808: 224-244. DOI:10.1017/jfm.2016.643 |
| [14] |
MOYES A J, PAREDES P, KOCIAN T S, et al. Secondary instability analysis of crossflow on a hypersonic yawed straight circular cone[J]. Journal of Fluid Mechanics, 2016, 812: 370-397. DOI:10.1017/jfm.2016.793 |
| [15] |
GANG D D, YI S H, LU X G. Design and performance of a hypersonic quiet wind tunnel at NUDT[C]//21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 2017. doi: 10.2514/6.2017-2305
|
| [16] |
ZHAO Y X, YI S H, TIAN L F, et al. Supersonic flow imaging via nanoparticles[J]. Science in China Series E-Technological Sciences, 2009, 52(12): 3640-3648. DOI:10.1007/s11431-009-0281-3 |
| [17] |
刘小林, 易仕和, 牛海波, 等. 高超声速条件下7°直圆锥边界层转捩实验研究[J]. 物理学报, 2018, 67(17): 175-186. LIU X L, YI S H, NIU H B, et al. Experimental investigation of the hypersonic boundary layer transition on a 7 degrees straight cone[J]. Acta Physica Sinica, 2018, 67(17): 175-186. DOI:10.7498/aps.67.20180531 (in Chinese) |
| [18] |
LIU X L, YI S H, XU X W, et al. Experimental study of second-mode wave on a flared cone at Mach 6[J]. Physics of Fluids, 2019, 31(7): 074108. DOI:10.1063/1.5103192 |
| [19] |
牛海波, 易仕和, 刘小林, 等. 压缩拐角流动中Gortler涡特性及热流分布实验研究[J]. 气体物理, 2018, 3(5): 48-55. NIU H B, YI S H, LIU X L, et al. Experimental investigation of the G rtler vortex and heat flux distribution on the compression ramp flow[J]. Physics of Gases, 2018, 3(5): 48-55. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38