转捩是指流动从层流态转变为湍流态的过程,是生产生活中的常见现象。由于层流和湍流的动量、能量、质量传输特性有着很大不同,在工程设计中为了减阻、隔热、降噪需要流场尽量保持在层流状态,而在增混、促燃和强化换热时又需要促进转捩过程。因此,航空航天航海以及能源化工设备的优化设计同层流-湍流转捩的高效控制是密不可分的。转捩研究可追溯至雷诺的管流实验,而转捩的起始与流场的失稳密不可分[1]。亥姆霍兹、凯尔文、瑞利等人的早期稳定性研究专注于流场对无穷小扰动的响应,通过线性化的控制方程求解不稳定的简正模态(normal mode), 从而确定临界控制参数。黏性剪切流最重要的控制参数即为雷诺数。对于小幅值扰动,一些流动如瑞利-贝纳尔对流随着控制参数的增加可经历一系列的超临界分岔过程,分岔的临界参数是可以精确确定的[2]。但对于边界层流、黏性剪切驱动的槽流或压差驱动的管流和槽流,其转捩行为可明显不同。它们的层流速度型在中等雷诺数时对小幅值扰动(线性扰动)是稳定的[3-4],但扰动幅值足够大时可变为湍流,即发生亚临界转捩[5-6]。以管流为例,对于不同形式和强度的扰动,其转捩临界雷诺数的变化范围可很大,如1700~100 000 [7-8]。剪切流的亚临界转捩过程对外部扰动的敏感性给转捩预测带来极大困难。
在边界层流中,人们发现一对斜Tollmien-Schlichting(TS)波的非线性演化对边界层流的转捩至关重要[9-10];基于对转捩过程中湍流间歇性的认识,构造了基于间歇因子输运方程和当地流动变量的转捩模式[11];实验研究了壁湍流转捩中的三维非线性波和二次涡环等结构[12]。对于光滑壁的平行剪切流,如管流,人们发现初始人为引入的大幅值流向涡扰动并不会完全衰减掉[13],随后的实验研究显示局地湍流(puff)[14-18]的瞬态增长特性和分裂对管流的亚临界转捩过程有重要意义。Eckhardt等和Mullin分别于2007年[19]和2011年[20]在流体力学年鉴(Annu. Rev. Fluid Mech.)中对管流亚临界转捩的研究进展进行了综述,不断涌现的成果相继发表在了Science[21-23]和Nature[24-25],引起广泛关注。本文将重点讨论平行平板间压差驱动的平板泊肃叶流(plane-Poiseuille flow,PPF)的亚临界转捩过程,同时简述剪切驱动的平板库埃特流(plane-Couette flow,PCF)和压差驱动的圆管流动(Hagen-Poiseuille flow,管流)的相关研究进展。
1 槽流的亚临界转捩现象能量稳定性分析或能量法可以给出基本流失稳的必要条件。对于槽流这类黏性剪切流而言,能量法所定义的临界阈值远远低于实际的转捩雷诺数[26-28]。由于线性稳定性分析所得特征函数并不一定是两两正交的,初始扰动有可能经历瞬态增长[3, 29],因此人们寄希望于经瞬态增长机制将小扰动放大至有限幅值后的非线性阶段,也研究了槽流的最大瞬态增长模态和三维扰动瞬态增长的最大能量放大倍数[30-32]。需指出的是,由于扰动能量的增长机制是线性的,能量法和针对扰动方程线性算子的瞬态增长分析均与扰动的初始幅值无关。采用同伦分析的方法[33-36]、在小尺度周期盒子中用迭代法[37-38]或通过二分的边界追踪(edge-tracking)[39-40]等数值方法,人们可求得空间上有严格周期性的非线性解和有局地特性的边界态(localized edge state)。尽管这些Navier-Stokes方程的解在中低雷诺数时会衰减掉,其流动结构、动力学和统计学特性对人们认识低雷诺数湍流是有益的[41]。近年来的一个重要研究进展是发现倾斜的大尺度的湍流带同槽流的亚临界转捩进程直接相关。
对于平板泊肃叶流(PPF),常用的雷诺数定义为Re=3Umh/(2ν),其中h为半槽高,Um为截面平均流速,ν为运动学黏性系数。1928年,Davies和White实验测量了不同横截面宽高比的槽道流的壁面摩擦阻力系数与雷诺数的关系[42]。实验结果显示,摩阻系数在小雷诺数时同层流解相符,在Re高于某临界值时开始高于层流解。更大的宽高比意味着更小的侧壁影响,数据显示临界雷诺数随着宽高比的增大而增大,当宽高比足够大后则不再增加,维持在Re=667.5附近。这一临界值在此前一直未受重视,因为随后实验发现的转捩临界值要高得多。1969年,Patel和Head [43]的槽流实验发现当Re < 1035时,流动维持在层流状态;当1035 < Re < 1350时,流场内存在间歇性的湍流猝发;当Re>1350后流动变为持续的湍流状态。Nishioka和Asai [44]的实验研究也发现在Re < 1000时湍流态难以自维持。
Carlson等人通过流动显示[45]发现,雷诺数在1000左右时壁面小孔的脉冲射流可激发出湍斑结构(见图 1a),在往下游的发展过程中湍斑会发生分裂,如图 1(b)所示。当Re大于1200时,无需人工激励即可由背景扰动随机地形成湍斑。在Re < 840时,激励触发的湍斑无法充分发展,最终衰减掉。由于这些实验结果显示可自维持的湍流要求雷诺数高于1000,随后大量的实验、理论和数值模拟工作主要集中在了Re>1000的湍斑研究上[46-50]。Alavyoon等人在实验中也采用壁面小孔射流来激发湍斑[51],他们发现在Re=1100附近可以观察到未发展完全的湍斑;当Re < 1100时,任意大幅值的扰动都无法产生湍斑;直到Re>1200时,才能观察到完整的湍斑,即在展向有对称的两个分支的湍斑。随着计算能力的提高,人们在Re≥1070的数值模拟中发现存在规则排列的被层流区间隔的湍流带(turbulent stripe或turbulent band)结构[52, 53],随后的实验也证实了湍流带结构的存在[54](见图 2)。实验显示在Re < 1275时湍流带会断裂;在Re=1200时仅发现一两个湍斑;在Re=975时流场为稳定的层流[55]。以Re≥1567的层流场叠加扰动涡对作为初始场,分别在保持净压力梯度不变[56]和保持流量不变[57]的条件下进行的数值模拟发现,初始扰动诱发的湍斑均会扩展、演化。

|
图 1 PPF在Re=1000时的湍斑(a)以及湍斑的分裂(b)[45] Fig.1 Turbulent spot (a) and its split (b) at Re=1000 for PPF[45] |
|
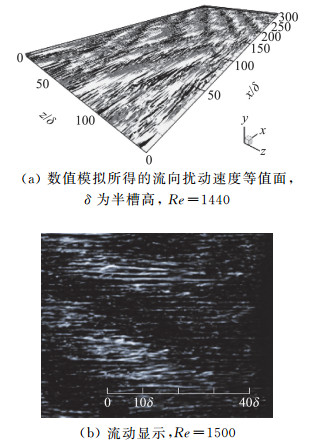
图 2 PPF的数值模拟和实验在较高雷诺数时所获得的湍流带结构[54] Fig.2 The turbulent bands obtained at relatively high Reynolds numbers in a simulation and an experiment for PPF [54] |
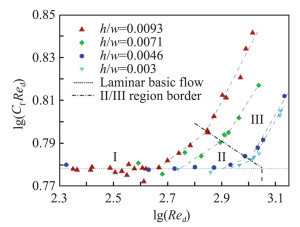
Tao等人重新分析了Davies和White的实验数据[42]并将其分为三个区(见图 3)[58]。Ⅰ区对应于层流,Ⅱ区和Ⅲ区的斜率明显不同。Ⅱ区随着槽道高宽比的减小而减小,而Ⅲ区的斜率并不随高宽比变化,反映了在该区间不受高宽比影响的内在的动力学特性。Ⅱ、Ⅲ区的分界线外插至层流态的临界值估计为Red=1127或Re=845。采用大计算域的初步的数值模拟也显示在雷诺数低至900时存在增长的湍斑,因此该阈值被解释为可发展湍斑的临界值[58]。这一阈值的提出提示人们在Re < 1000的情况下,PPF有可能存在着可自维持的湍流态。
Tuckerman对PPF用倾斜的狭小计算域进行了数值模拟[59],发现在雷诺数大于850时存在湍流带。需注意的是,采用狭小计算域虽可大为节省计算资源并定性模拟局地湍流结构,但人为设定的计算域倾角和展向的周期边界条件对转捩过程及临界阈值的确定有显著影响[60]。为减少周期边界条件对局地湍流结构的影响,2013年Tao等采用流向和展向尺度均很大的计算域数值模拟了PPF的亚临界转捩过程,发现存在湍流带的雷诺数可低至720[61];得到了孤立的湍流带(见图 4),即在计算域内湍流带周围为层流,没有其他的湍流结构。由于孤立的湍流带远离其他局地湍流结构从而大大减弱了同它们的相互影响,其存在为研究湍流带自身的时空演化特性提供了可能。
|
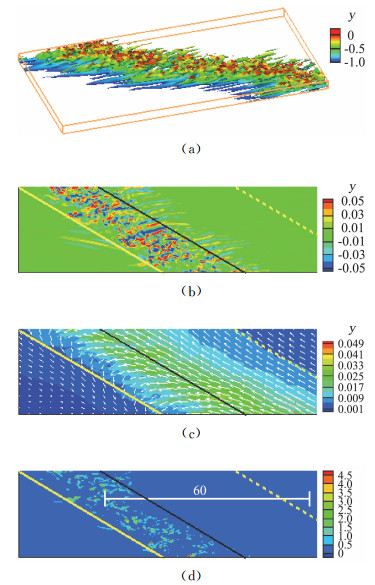
图 4 中等雷诺数的PPF湍流带在下半槽内(a)及中平面(b-d)的特征。(a)湍流带的脉动涡量等值面,以及中平面处的(b)脉动法向速度云图, (c)平动坐标系(速度为0.75倍的层流中平面速度)内的平均脉动动能云图和平均速度场(d)预乘了雷诺数的能量耗散率云图。Re=950[61] Fig.4 Characteristics of the PPF turbulent band in the lower half domain (a) and the middle plane (b)-(d) at moderate Re. (a) Iso-surface of the amplitude of disturbance vorticity in the lower half domain. (b) Iso-contours of the disturbing transverse velocity. (c) Iso-contours of the disturbing kinetic energy averaged in a moving reference frame of speed 0.75Uc, where Uc is the midplane velocity of the base flow. The in-plane mean flow is shown by arrows. (d) Iso-contours of the kinetic-energy dissipation rate multiplied by Re. Re=950[61] |
根据数值模拟结果,存在统计定常态的转捩阶段被定义为平衡局地湍流态(equilibrium localized turbulence)[61]。根据全流场的耗散率特性定义的平衡局地湍流态的临界值为Re=859,该阈值同之前分析Davies和White实验结果所得阈值845[58]基本一致。数值模拟还发现在Re>950时湍流带发生分裂的频次增加从而大为促进湍流的扩展,由层流区间隔开的湍流带结构最终会铺满整个流场;在Re>1300时层流区不再明显,此时流态被定义为均匀湍流(uniform turbulence)[61],如图 5所示。随后,人们开始重视PPF在雷诺数低于1000的转捩特性[62-63]。
|
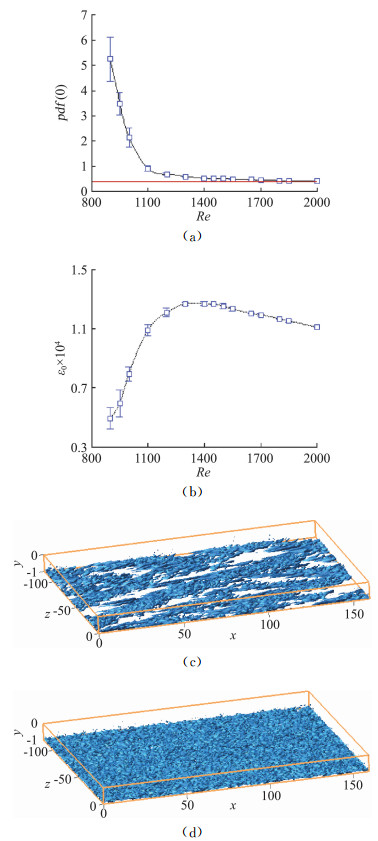
图 5 (a) 中平面归一化法向速度v/σ (σ为法向速度标准差)的概率密度函数pdf(0), (b)中平面平均的能量耗散率ε0随Re的变化。在Re=1300 (c)和Re=1800 (d)时八分之一计算域内的脉动涡量等值面图( ω =9)[61] Fig.5 (a) pdf(0) of the normalized transverse velocity v/σ in the midplane, where σ is the standard error of v. (b) Kinetic-energy dissipation rate averaged in the middle plane ε0 as a function of Re. The iso-surfaces of the disturbance vorticity ω =9 in one eighth of the computational domain at Re=1300 and 1800 are shown in (c) and (d), respectively.[61] |
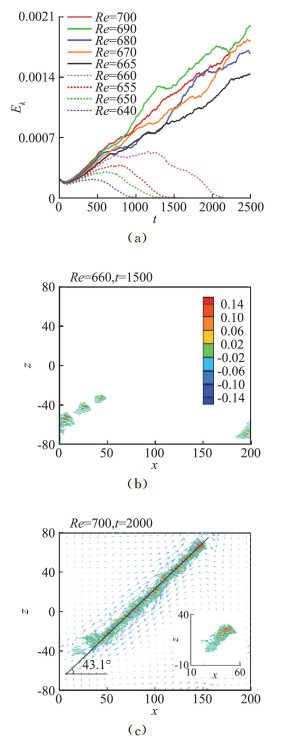
通过对PPF在大计算域(流向和展向计算域尺度均为102h量级)进行系统的直接数值模拟,Xiong等人[64]发现,局地扰动诱发的湍斑要么演化为湍流带,要么衰减掉,因此其自维持时间远远小于湍流带的自维持时间;在中等雷诺数时,孤立的湍流带会倾斜伸长(见图 6);当Re < 660时湍流带扰动动能经瞬态增长后会衰减掉,见图 6(a)(b)。另外,湍流带周围存在大尺度环流(见图 6c),这些环流之间的相互作用会导致湍流带的断裂和衰减,而在适当的条件下断裂的湍流带还会发生重连现象[65]。倾斜狭长的计算域无法模拟湍流带的伸长现象,而小的计算域由边界条件带来的较强的环流相互作用会导致湍流带的断裂和衰减,从而无法准确获得可自维持湍流带的下临界雷诺数。比如近期人们发现用小展向尺度的计算域进行的数值模拟只能得到最终衰减的类似于管流中puff的局地湍流结构[66]。综上所述,在中低雷诺数发现的湍流带结构使人们对槽流亚临界转捩的认识进入了一个新阶段。
|
图 6 PPF扰动动能曲线和中平面法向速度等值线图。(a)不同雷诺数下相同初始扰动的扰动动能随时间的变化;(b) Re=660,中平面法向速度;(c) Re=700,中平面法向速度及y=0.514平面内湍流带周围的环流,小图为初始扰动[64] Fig.6 (a) Time series of the volume-averaged disturbance kinetic energy Ek at different Reynolds numbers and for the same initial condition. The iso-contours of the transverse velocity in the midplane for Re=600 and 700 are shown in (b) and (c), respetively where the initial perturbation pattern is added as an inset. The mean velocity of disturbance in the plane at y=0.514 is depicted by vectors on a coarse mesh to show the large-scale flow.[64] |
为了理解亚临界转捩中局地湍流结构的生成与演化机理,人们建立了多种动力学模型。Barkley等借用化学中的反应扩散模型和生命科学中的神经元模型来定性描述管流从puff的瞬态增长到最后全场湍流的整个亚临界转捩过程[67-70]。金融领域的极值理论(Extreme Value Theory)和生态捕食模型(predator-prey model)也分别被用来分析平板库艾特流亚临界转捩阈值问题[71]和管流转捩现象[72]。Pomeau在1986年将转捩过程与定向逾渗(Directed Percolation,DP)的相变类型联系了起来[73]。在定向逾渗理论中,一个活跃状态可以通过相邻的节点以一定概率p进行传播。随后人们对管流和平板库艾特流转捩过程的实验和数值模拟数据用DP模型进行了拟合分析[74-76]。
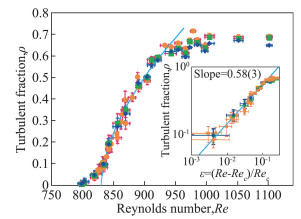
对于PPF,2016年Sano和Tamai通过增加多孔板的方式提高试验段入口流场的湍流度,并利用流动显示技术观测下游流动结构的变化,计算了流场中湍流占比与Reynolds数的关系[77],如图 7所示,发现湍流占比(湍流区域所占的面积百分比)与参数ε = (Re-Rec)/Rec呈幂次分布,同DP模型相符,并通过外插法定义了PPF亚临界转捩的临界雷诺数为830。但从图 7可以看出,在Re < 830时湍流占比并不是零,即转捩已经开始,这是DP模型无法解释的。实际上,用DP幂次关系外插实验数据所得的转捩阈值同之前依据早期实验数据外插所得的阈值845[58]和由数值模拟数据定义的平衡局地湍流态的临界值859[61]是符合的,反映的是存在统计定常态的局地湍流的临界性质。在雷诺数低于830时,之前的数值模拟已经表明湍流带是可以增长演化的(如图 6)。近期在Re= 660~800范围内的数值模拟进一步表明,大计算域中的周期湍流带是可以自维持的,这一阶段每一雷诺数对应的湍流占比不唯一但存在一个统计上的最大值,即PPF在转捩之初存在一种稀疏湍流态[65]。
|
图 7 实验所得PPF湍流占比随雷诺数的变化[77] Fig.7 Turbulent fraction obtained experimentally for PPF at different Reynolds numbers[77] |
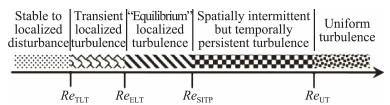
无论对管流还是槽流,如平板库艾特流和平板泊肃叶流,局地湍流结构的产生与时空演化特征显示亚临界转捩过程可包括不同的阶段(见图 8),而不同黏性剪切流的转捩阶段之间的相似性似乎预示它们遵循着相同的转捩路径[78-79]。但对这种相似性的量化分析是困难的,比如不同流动发生转捩的雷诺数可相差巨大,因为雷诺数的定义中选取的特征长度和特征速度因流动不同而不同。那么不同的黏性剪切流是否可定义统一的稳定性控制参数呢?对这一问题的研究已有六十年的历史。
|
图 8 平行剪切流的亚临界转捩阶段[79] Fig.8 Transition stages of the subcritical transition of parallel shear flows[79] |
人们分别尝试依据平均流特性[80-81]和流场的局部特性来定义有普适性的稳定性参数。1959年,Ryan和Johnson [82]依据线性化的二维能量方程为管流提出了一个稳定性参数Zmax,是“流体微团的能量输入与能量耗散之比的函数”。Zmax代表着横截面内该能量比值的最大值。管流实验数据显示牛顿流体和几种假塑性流体的转捩临界Zmax值是一致的,这在一定程度上证实了一个观念:流态是由具有最大能量输入与能量耗散之比的流体微团或局地稳定性参数Zmax决定的。由于Zmax不依赖于边界条件,仅取决于流场的局地特性,因此相较于传统的雷诺数定义Zmax更能反映不同流场转捩过程的共性。随后Hanks [83]基于Navier-Stokes (NS)方程将这一观念扩展到了槽流(PPF),并给出了另一个局地控制参数K,其对压力驱动管流和槽流的定义分别为:
| $ K = \frac{1}{2}\rho \frac{{{\rm{d}}({U^2})/{\rm{d}}r}}{{{\rm{d}}p/{\rm{d}}x}}{\rm{ }}及{\rm{ }}K = \frac{1}{2}\rho \frac{{{\rm{d}}({U^2})/{\rm{d}}y}}{{{\rm{d}}p/{\rm{d}}x}} $ | (1) |
其中U是基本流速度。对于管流,Zmax =2K, K为K在横截面内的最大值。需提及的是K参数无法应用于剪切驱动的流动,如平板库艾特流,因其基本流的流向压力梯度dp/dx=0。后来的“能量梯度法”[84]提出的控制参数也称为K,对于管流和PPF其定义式是把公式(1)中的压力梯度dp/dx替换为μ∇2U。对于定常的平行剪切流,NS方程可简化为μ∇2U=dp/dx。因此对于管流和PPF“能量梯度法”定义的K同Hanks定义的K形式相同。但对于平板库艾特流,“能量梯度法”则更换了其K的定义式,把分母μ∇2U换为∂W/∂s,而W被称为“外部对单位体积流体所做的功”,并认为库艾特流的W有非零值而泊肃叶流中的W为零[85], 这一人为设定与库艾特流和泊肃叶流中的流体微团遵从相同的动力学控制方程这一事实相违背。
普适的转捩或稳定性控制参数对不同的流动应具有统一的定义式。依据NS方程定义的局地雷诺数Rem反映了局地的非线性对流与黏性扩散效应之比[58]。与之前的稳定性参数定义中的分母(dp/dx或μ∇2U)仅由基本流决定的情况不同,Rem定义中的基于物理模型所表征的黏性扩散项为ν
| $ R{e_L} = {\left| {\rho {R_h}U\frac{{{\rm{d}}U}}{{{\rm{d}}{x_2}}}/{\tau _w}} \right|_{{\rm{max}}}} $ | (2) |
Rh 是水力半径(截面积与湿周之比), τw是壁面切应力,x2是壁面法向坐标,“max”代表截面内最大值。传统雷诺数的定义式包含的是反映流场平均特征的量,如截面平均流速和槽高,但这些平均量难以反映具有不同边界条件的流场特性(如PCF和PPF)。尽管不同形式的流动有不同的边界条件,但流体微团的动力学行为是统一的,其动量与能量控制方程是相同的,因此反映流体微团能量输入与耗散特性的局地雷诺数ReL相较于传统的雷诺数定义具有更好的普适性。另外,不同于之前的局地控制参数Zmax和K,ReL既适用于压差驱动的泊肃叶流,又适用于黏性剪切驱动的库艾特流,而且具有统一的定义形式。将管流、平板库艾特流和平板泊肃叶流的基本流代入公式(2)所得的各类流动的ReL表达式同Rem的表达式是一致的;管流和平板泊肃叶流的ReL表达式同Hanks定义的K也是一致的[79]。
通过分析管流、PPF和PCF以往的实验和数值模拟结果[79]并整理近期结果[77, 86],三种不同剪切流亚临界转捩的不同阶段的ReL阈值基本相符,分别为:255~290(稀疏湍流)、320~340(平衡局地湍流)、380~394(空间间歇性分布但可自维持湍流)、500~520(均匀湍流)。采用传统雷诺数定义的阈值则相差巨大,比如对于管流和平板库艾特流,其平衡局地湍流的阈值分别为1750和325左右。显然,采用基于流场局地信息定义的稳定性参数是可以定量表征不同剪切流亚临界转捩过程的相似性的。当然,需要提及的是不同流动的转捩过程也会有其特殊性。比如在转捩的最初阶段,管流中的puff结构是瞬态的,平板泊肃叶流中的湍流带结构在较狭窄的流道或计算域中也是瞬态的[66],但当这些局地湍流结构相距很远时是可以维持倾斜伸长的。因此,亚临界转捩的最初阶段被称为稀疏湍流态。
4 结论与展望剪切流的亚临界转捩是一个剧烈的过程,但人们通过研究局地湍流结构的产生、演化(如湍流带的断裂、伸长、分裂、重连),认识到该过程仍可细分为不同的阶段,而不同流动的转捩阶段是存在相似性的。这种内在的相似性来自于流体微团受控于相同的动力学规律(方程)这一事实,而基于局地流场特性所定义的稳定性参数揭示了不同流动在不同的转捩阶段具有相符合的临界阈值,从而定量地反映了黏性剪切流亚临界转捩的统一性。尽管人们已经取得了许多可喜的进展,但对于剪切流的亚临界转捩过程仍有许多重要问题有待解决。首先,对于槽道流亚临界转捩的实验研究仍是不充分的,目前的认识多是来自于大规模的并行计算,局地湍流结构在各转捩阶段的临界阈值仍需实验确认,局地结构的演化特征(如湍流带的倾斜伸长、分裂、重连)仍需相应的实验研究[87]。其次,局地湍流结构的产生和演化机理仍需更为深入的探索。目前的动力学模型分析多是从类比、形似的定性角度来解释现象,仍需直接根植于流动控制方程的机理研究[88]。另外,目前的亚临界转捩研究多是由强初始扰动触发的,由复杂边界触发的亚临界转捩过程的相关研究仍有待深入。相信随着实验技术、计算能力、数值方法和稳定性理论的发展,这些挑战性的问题在不久的将来会被一一攻克,从而进一步优化人们的转捩控制方法、加强人们在工程实践中的流动控制能力。
| [1] |
周恒, 赵耕夫. 流动稳定性[M]. 北京: 国防工业出版社, 2004. ZHOU H, ZHAO G F. Hydrodynamic stability[M]. Beijing: National Defence Industry Press, 2004. (in Chinese) |
| [2] |
BUSSE F H. The sequence-of-bifurcations approach towards understanding turbulent fluid flow[J]. Surveys in Geophysics, 2003, 24: 269-288. DOI:10.1023/A:1024860722683 |
| [3] |
SCHMID P J, HENNINGSON D S. Stability and transition in shear flows[M]. New York, NY: Springer, 2001.
|
| [4] |
MESEGUER A, TREFETHEN L N. Linearized pipe flow to Reynolds numbers 107[J]. J Comp Phys, 2003, 186: 178-197. DOI:10.1016/S0021-9991(03)00029-9 |
| [5] |
MANNEVILLE P. Laminar-turbulent patterning in transitional flows[J]. Entropy, 2017, 19: 316. DOI:10.3390/e19070316 |
| [6] |
TUCKERMAN L S, CHANTRY M, BARKLEY D. Patterns in wall-bounded shear flows[J]. Annu Rev Fluid Mech, 2020, 52: 343-367. DOI:10.1146/annurev-fluid-010719-060221 |
| [7] |
PFENNINGER W. Transition experiments in the inlet length of tubes at high Reynolds numbers[M]//LACHMANN G, In Boundary Layer and Flow Control: Its Principles and Application, 2: 970-980. New York, NY: Pergamon(1961).
|
| [8] |
PEIXINHO J, MULLIN T. Finite-amplitude thresholds for transition in pipe flow[J]. J Fluid Mech, 2007, 582: 169-178. DOI:10.1017/S0022112007006398 |
| [9] |
WU X, LEIB S J, GOLDSTEIN M E. On the nonlinear evolution of a pair of oblique Tollmien-Schlichting waves in boundary layers[J]. J Fluid Mech, 1997, 340: 361-394. DOI:10.1017/S0022112097005557 |
| [10] |
WU X. Nonlinear theories for shear flow instabilities:physical insights and practical implications[J]. Annu Rev Fluid Mech, 2019, 51: 451-485. DOI:10.1146/annurev-fluid-122316-045252 |
| [11] |
FU S, WANG L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory[J]. Progress in Aerospace Sciences, 2013, 58: 36-59. DOI:10.1016/j.paerosci.2012.08.004 |
| [12] |
LEE C B, WU J Z. Transition in wall-bounded flows[J]. Appl Mech Rev, 2008, 61: 030802. DOI:10.1115/1.2909605 |
| [13] |
FAISST H, ECKHARDT B. Traveling waves in pipe flow[J]. Phys Rev Lett, 2003, 91: 224502. DOI:10.1103/PhysRevLett.91.224502 |
| [14] |
REYNOLDS O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels[J]. Proc. R. Soc. London, 1883, 35: 84-99. DOI:10.1098/rspl.1883.0018 |
| [15] |
WYGNANSKI I J, CHAMPAGNE F H. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug[J]. J Fluid Mech, 1973, 59(2): 281-335. DOI:10.1017/S0022112073001576 |
| [16] |
WYGNANSKI I, SOKOLOV M, FRIEDMAN D. On transition in a pipe. Part 2. The equilibrium puff[J]. J Fluid Mech, 1975, 69(2): 283-304. DOI:10.1017/S0022112075001449 |
| [17] |
HOF B, DELOZAR A, KUIK D J, et al. Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow[J]. Phys Rev Lett, 2008, 101: 214501. DOI:10.1103/PhysRevLett.101.214501 |
| [18] |
AVILA K, MOXEY D, DE LOZAR A, et al. The onset of turbulence in pipe flow[J]. Science, 2011, 333: 192-196. DOI:10.1126/science.1203223 |
| [19] |
ECKHARDT B, SCHNEIDER T M, HOF B, et al. Turbulence transition in pipe flow[J]. Annu Rev Fluid Mech, 2007, 39: 447-468. DOI:10.1146/annurev.fluid.39.050905.110308 |
| [20] |
MULLIN T. Experimental studies of transition to turbulence in a pipe[J]. Annu Rev Fluid Mech, 2011, 43: 1-24. DOI:10.1146/annurev-fluid-122109-160652 |
| [21] |
HOF B, DOORNE C W H, WESTERWEEL J, et al. Experimental observation of nonlinear traveling waves in turbulent pipe flow[J]. Science, 2004, 305: 1594-1598. DOI:10.1126/science.1100393 |
| [22] |
HOF B, De LOZAR A, AVILA M, et al. Eliminating turbulence in spatially intermittent flows[J]. Science, 2010, 327: 1491-1494. DOI:10.1126/science.1186091 |
| [23] |
ECKHARDT B. A critical point for turbulence[J]. Science, 2011, 333: 165-166. DOI:10.1126/science.1208261 |
| [24] |
HOF B, WESTERWEEL J, SCHNEIDER T M, et al. Finite lifetime of turbulence in shear flows[J]. Nature Physics, 2006, 443: 59-62. DOI:10.1038/nature05089 |
| [25] |
BARKLEY D, SONG B, MUKUND V., et al. The rise of fully turbulent flow[J]. Nature Physics, 2015, 526: 550-553. DOI:10.1038/nature15701 |
| [26] |
JOSEPH D D, CARMI S. Stability of Poiseuille flow in pipes, annuli, and channels[J]. Quarterly of Applied Mathematics, 1969, 26: 575-599. DOI:10.1090/qam/99836 |
| [27] |
BUSSE F H. Bounds on the transport of mass and momentum by turbulent flow between parallel plates[J]. Zeitschrift für angewandte Mathematik und Physik ZAMP, 1969, 20(1): 1-14. DOI:10.1007/BF01591113 |
| [28] |
JOSEPH D D. Nonlinear stability of the Boussinesq equations by the method of energy[J]. Archive for Rational Mechanics and Analysis, 1966, 22(3): 163-184. DOI:10.1007/BF00266474 |
| [29] |
XIONG X, TAO J. Lower bound for transient growth of inclined buoyancy layer[J]. Appl Math Mech (Engl Ed), 2017, 38: 779-796. DOI:10.1007/s10483-017-2202-8 |
| [30] |
BUTLER K M, FARRELL B F. Three-dimensional optimal perturbations in viscous shear flow[J]. Physics of Fluids A, 1992, 4(8): 1637-1650. DOI:10.1063/1.858386 |
| [31] |
TREFETHEN L N, TREFETHEN A E, REDDY S C, et al. Hydrodynamic stability without eigenvalues[J]. Science, 1993, 261: 578-584. DOI:10.1126/science.261.5121.578 |
| [32] |
REDDY S C, HENNINGSON D S. Energy growth in viscous channel flows[J]. J Fluid Mech, 1993, 252: 209-238. DOI:10.1017/S0022112093003738 |
| [33] |
NAGATA M. Three-dimensional finite-amplitude solutions in plane Couette flow:bifurcation from infinity[J]. J Fluid Mech, 1990, 217: 519-527. DOI:10.1017/S0022112090000829 |
| [34] |
CLEVER R M, BUSSE F H. Three-dimensional convection in a horizontal fluid layer subjected to a constant shear[J]. J Fluid Mech, 1992, 234: 511-527. DOI:10.1017/S0022112092000892 |
| [35] |
WALEFFE F. Three-dimensional coherent states in plane shear flows[J]. Phys Rev Lett, 1998, 81: 4140-4143. DOI:10.1103/PhysRevLett.81.4140 |
| [36] |
WEDIN H, KERSWELL R R. Exact coherent structures in pipe flow:travelling wave solutions[J]. J Fluid Mech, 2004, 508: 333-371. DOI:10.1017/S0022112004009346 |
| [37] |
KAWAHARA G, KIDA S. Periodic motion embedded in plane Couette turbulence:regeneration cycle and burst[J]. J Fluid Mech, 2001, 449: 291-300. DOI:10.1017/S0022112001006243 |
| [38] |
GIBSON J F, HALCROW J, CVITANOVIC P. Visualizing the geometry of state space in plane Couette flow[J]. J Fluid Mech, 2008, 611: 107-130. DOI:10.1017/S002211200800267X |
| [39] |
SCHNEIDER T M, MARINC D, ECKHARDT B. Localized edge states nucleate turbulence in extended plane Couette cells[J]. J Fluid Mech, 2010, 646: 441-451. DOI:10.1017/S0022112009993144 |
| [40] |
ZAMMERT S, ECKHARDT B. Streamwise and doubly-localised periodic orbits in plane Poiseuille flow[J]. J Fluid Mech, 2014, 761: 348-359. DOI:10.1017/jfm.2014.633 |
| [41] |
KAWAHARA G, UHLMANN M, VAN VEEN L. The significance of simple invariant solutions in turbulent flows[J]. Annu Rev Fluid Mech, 2012, 44: 203-225. DOI:10.1146/annurev-fluid-120710-101228 |
| [42] |
DAVIES S J, WHITE C M. An experimental study of the flow of water in pipes of rectangular section[C]//Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1928, 119(781): 92-107.
|
| [43] |
PATEL V C, HEAD M R. Some observations on skin friction and velocity profiles in fully developed pipe and channel flows[J]. J Fluid Mech, 1969, 38(1): 181-201. DOI:10.1017/S0022112069000115 |
| [44] |
NISHIOKA M, ASAI M. Some observations of the subcritical transition in plane Poiseuille flow[J]. J Fluid Mech, 1985, 150: 441-450. DOI:10.1017/S0022112085000210 |
| [45] |
CARLSON D R, WIDNALL S E, PEETERS M F. A flow-visualization study of transition in plane Poiseuille flow[J]. J Fluid Mech, 1982, 121: 487-505. DOI:10.1017/S0022112082002006 |
| [46] |
HENNINGSON D, SPALART P, KIM J. Numerical simulations of turbulent spots in plane Poiseuille and boundary-layer flow[J]. Phys Fluids, 1987, 30(10): 2914-2917. DOI:10.1063/1.866067 |
| [47] |
HENNINGSON D S, ALFREDSSON P H. The wave structure of turbulent spots in plane Poiseuille flow[J]. J Fluid Mech, 1987, 178: 405-421. DOI:10.1017/S0022112087001289 |
| [48] |
LI F, WIDNALL S E. Wave patterns in plane Poiseuille flow created by concentrated disturbances[J]. J Fluid Mech, 1989, 208: 639-656. DOI:10.1017/S0022112089002971 |
| [49] |
HENNINGSON D S, KIM J. On turbulent spots in plane Poiseuille flow[J]. J Fluid Mech, 1991, 228: 183-205. |
| [50] |
HENNINGSON D S, JOHANSSON A V, ALFREDSSON P H. Turbulent spots in channel flows[J]. J Eng Math, 1994, 28: 21-42. DOI:10.1007/BF02383603 |
| [51] |
ALAVYOON F, HENNINGSON D S, ALFREDSSON P H. Turbulent spots in plane Poiseuille flow-flow visualization[J]. Phys Fluids, 1986, 29(4): 1328-1331. DOI:10.1063/1.865884 |
| [52] |
TSUKAHARA T, SEKI Y, KAWAMURA H, et al. DNS of turbulent channel flow at very low Reynolds numbers[C]//Proceedings of the 4th International Symposium on Turbulence and Shear Flow Phenomena, Williamsburg, 27-29 June 2005(unpublished), pp. 935-940, arXiv: 1406. 0248[physics. flu-dyn].
|
| [53] |
TSUKAHARA T, IWAMOTO K, KAWAMURA H, et al. DNS of heat transfer in a transitional channel flow accompanied by a turbulent puff-like structure[C]//Turbulent, Heat and Mass Transfer 5, 2006, Sept, 25-29, Dubrovnik, Croatia.
|
| [54] |
TSUKAHARA T, KAWAGUCHI Y, KAWAMURA H, et al. Turbulence stripe in transitional channel flow with/without system rotation[C]//Proceedings of the IUTAM Symposium on Laminar-Turbulent Transition, 2009, Stockholm, Sweden.
|
| [55] |
HASHIMOTO S, HASOBE A, TSUKAHARA T, et al. An experimental study on turbulent-stripe structure in transitional channel flow[C]//Turbulence, heat and Mass Transfer 6, 2009, 14-18 September, Rome, Italy.
|
| [56] |
AIDA H, TSUKAHARA T, KAWAGUCHI Y. Development of a turbulent spot into stripe pattern in plane Poiseuille flow[C]//Proceedings of Seventh International Symposium on Turbulence & Shear Flow Phenomena, 2011, July, 28-31, Ottawa, Canada.
|
| [57] |
TSUKAHARA T, ISHIDA T, DUGUET Y. Turbulent-spot development in constant-mass-flux channel flow[C]//14th European Turbulence Conference 2013, Sept. 1-4, Lyon, France.
|
| [58] |
TAO J, CHEN S Y, SU W D. Universal threshold of the transition to localized turbulence in shear flows[J]. Theor Appl Mech Lett, 2011, 1(5): 052002. DOI:10.1063/2.1105202 |
| [59] |
TUCKERMAN L. Turbulent-laminar banded patterns in plane Poiseuille flow[C]//23rd ICTAM, 2012, Aug. 19-24, Beijing, China.
|
| [60] |
TUCKERMAN L S, BARKLEY D. Patterns and dynamics in transitional plane Couette flow[J]. Phys Fluids, 2011, 23: 041301. DOI:10.1063/1.3580263 |
| [61] |
TAO J, XIONG X. The unified transition stages in linearly stable shear flows[C]//Proc 14th Asian Congress of Fluid Mechanics, 2013, Oct. 15-19, Hanoi and Halong, Vietnam.
|
| [62] |
TSUKAHARA T, ISHIDA T. The lower bound of subcritical transition in plane Poiseuille flow[C]//Euromech Colloquium EC565, 2014, May 6-9, Cargese, France.
|
| [63] |
TUCKERMAN L S, KREILOS T, SCHROBSDORFF H, et al. Turbulent-laminar patterns in plane Poiseuille flow[J]. Phys Fluids, 2014, 26(11): 114103. DOI:10.1063/1.4900874 |
| [64] |
XIONG X, TAO J, CHEN S Y, et al. Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers[J]. Phys Fluids, 2015, 27(4): 041702. DOI:10.1063/1.4917173 |
| [65] |
TAO J J, ECKHARDT B, XIONG X M. Extended localized structures and the onset of turbulence in channel flow[J]. Phys Rev Fluids, 2018, 3(1): 011902. DOI:10.1103/PhysRevFluids.3.011902 |
| [66] |
SHIMIZU M, KANAZAWA T, KAWAHARA G. Exponential growth of lifetime of localized turbulence with its extent in channel flow[J]. Fluid Dyn Res, 2019, 51: 011404. DOI:10.1088/1873-7005/aaa73c |
| [67] |
BARKLEY D. Simplifying the complexity of pipe flow[J]. Phys Rev E, 2011, 84: 016309. DOI:10.1103/PhysRevE.84.016309 |
| [68] |
BARKLEY D. Modeling the transition to turbulence in shear flows[J]. J Phys:Conf Ser, 2011, 38: 032001. |
| [69] |
SONG B F, BARKLEY D, HOF B, et al. Speed and structure of turbulent fronts in pipe flow[J]. J Fluid Mech, 2017, 813: 1045-1059. DOI:10.1017/jfm.2017.14 |
| [70] |
BARKLEY D. Theoretical perspective on the route to turbulence in a pipe[J]. J Fluid Mech, 2016, 803: P1. DOI:10.1017/jfm.2016.465 |
| [71] |
FARANDA D, LUCARINI V, MANNEVILLE P, et al. On using extreme values to detect global stability thresholds in multi-stable systems:The case of transitional plane Couette flow[J]. Chaos, Solitons & Fractals, 2014, 64: 26-35. |
| [72] |
SHIH H Y, HSIEH T L, GOLDENFELD N. Ecological collapse and the emergence of travelling waves at the onset of shear turbulence[J]. Nature Phys, 2016, 12: 245-248. DOI:10.1038/nphys3548 |
| [73] |
POMEAU Y. Front motion, meta stability and subcritical bifurcations in hydrodynamics[J]. Physica D, 1986, 23: 3-11. DOI:10.1016/0167-2789(86)90104-1 |
| [74] |
SIPOS M, GOLDENFELD N. Directed percolation describes lifetime and growth of turbulent puffs and slugs[J]. Phys Rev E, 2011, 84: 035304. |
| [75] |
LEMOULT G, SHI L, AVILA K, et al. Directed percolation phase transition to sustained turbulence in Couette flow[J]. Nature Phys, 2016, 12(3): 254-258. DOI:10.1038/nphys3675 |
| [76] |
CHANTRY M, TUCKERMAN L S, BARKLEY D. Universal continuous transition to turbulence in a planar shear flow[J]. J Fluid Mech, 2017, 824: R1. DOI:10.1017/jfm.2017.405 |
| [77] |
SANO M, TAMAI K. A universal transition to turbulence in channel flow[J]. Nature Phys, 2016, 12(3): 249-253. DOI:10.1038/nphys3659 |
| [78] |
ECKHARDT B. Turbulence transition in pipe flow:some open questions[J]. Nonlinearity, 2008, 21: T1-T11. DOI:10.1088/0951-7715/21/1/T01 |
| [79] |
TAO J J, CHEN S Y, SU W D. Local Reynolds number and thresholds of transition in shear flows[J]. Sci China-Phys Mech Astron, 2013, 56(2): 263-269. DOI:10.1007/s11433-012-4955-7 |
| [80] |
ALFREDSSON P H, MATSUBARA M. Free-stream turbulence, streaky structures and transition in boundary layer flows[R]. AIAA 2000-2534, 2000.
|
| [81] |
MANNEVILLE P, PRIGENT A, DAUCHOT O. Banded turbulence in Taylor-Couette and plane Couette flow[C]//APS/DFD meeting. Bull Am Phys Soc, 2001, 46: 35.
|
| [82] |
RYANN W, JOHNSON M M. Transition from laminar to turbulent flow in pipes[J]. AIChE J, 1959, 5: 433-435. DOI:10.1002/aic.690050407 |
| [83] |
HANKS R W. The laminar-turbulent transition for flow in pipes, concentric annuli, and parallel plates[J]. AIChE J, 1963, 9: 45-48. DOI:10.1002/aic.690090110 |
| [84] |
DOU H S. Mechanism of flow instability and transition to turbulence[J]. International J Non-Linear Mechanics, 2006, 41: 512-517. DOI:10.1016/j.ijnonlinmec.2005.12.002 |
| [85] |
DOU H S, KHOO B C, YEO K S. Instability of Taylor-Couette flow between concentric rotating cylinders[J]. Inter J of Thermal Science, 2008, 47: 1422-1435. DOI:10.1016/j.ijthermalsci.2007.12.012 |
| [86] |
LU J Z, TAO J J, ZHOU W T, et al. Threshold and decay properties of transient isolated turbulent band in plane Couette flow[J]. Appl Math Mech, 2019, 40(10): 1449-1456. DOI:10.1007/s10483-019-2531-6 |
| [87] |
LIU J S, XIAO Y, LI M G, et al. Measurement of localized turbulent structures in a plane Poiseuille flow[C]//Reynolds number effect: implications on understanding and control turbulence, Mar, 28-30, 2019, Shenzhen, China.
|
| [88] |
XIAO X K, SONG B F. The growth mechanism of turbulent bands in channel flow at low Reynolds numbers[J]. J Fluid Mech, 2020, 883: R1. |
 2020, Vol. 38
2020, Vol. 38