2. 飞机/发动机综合系统安全北京市重点实验室, 北京 100191
2. Aircraft/Engine Integrated System Safety Beijing Key Laboratory, Beijing 100191, China
飞机/发动机结冰会严重影响飞机性能和操稳特性,甚至危害飞行安全[1-3],因此防除冰系统设计非常重要。水滴撞击特性是部件防除冰系统设计的基础和关键[4-5],主要计算研究方法包括拉格朗日法[6-8]和欧拉法[9-11]。拉格朗日法是将过冷水滴当作离散系,对单个水滴建立控制方程,追踪水滴运动轨迹。欧拉法则是把过冷水滴视作连续流体,在欧拉坐标系下建立水滴相控制方程,使用同一套网格求解过冷水滴流场和空气流场,避免了拉格朗日法的大量插值问题,可获得各网格单元内水滴体积份额和表面撞击水滴的质量。对比研究[12-14]表明二者都能在特定情况下很好分析物面水滴收集规律。
借助数值模拟工具,国内外对常规防冰系统和部件水滴收集规律开展了大量研究。赵勇等[15]发现飞机三维水平尾翼从翼根到翼尖局部水滴撞击系数逐渐增加;易贤等[16]发现三段翼最大收集率会出现在缝翼,而水滴撞击范围最大的是襟翼,T型尾翼平尾上水滴收集率要整体大于立尾。杨胜华等[17]发现在多段翼后方存在水滴无法撞击的遮蔽区。杨军等[18]发现随着飞行高度、来流速度及水滴直径的增加,水滴撞击极限、总收集系数和局部收集系均增加。申晓斌等[19]发现进气道唇口附近水滴撞击区和撞击量都受进气流量的影响,水滴撞击特性受到整流罩影响较小。
鉴于冲击换热具有高的对流传热系数,常规热气防冰系统中通常利用热气射流冲击防冰部件内表面来提升加热效率,近年来也有研究人员直接利用热气射流除冰和防冰。例如,罗振兵等[20-21]开展了合成热射流机翼除冰实验,发现合成热射流能有效促进热能的扩散,缩短除冰时间,出口通道开缝角度与表面积冰越垂直,加速除冰效果越明显。柯鹏等[22]发展了一种针对复合材料帽罩的热气膜防冰系统,采用数值模拟和实验方法研究了其内部冲击换热和外部气膜加热效果,发现射流气膜能大幅提高缝后外壁面温度,在前缘开设气膜缝还会提升前缘内部的冲击换热效果。
外部射流直接加热待防护表面的同时还会影响近壁区的外部流场[23],改变物面水滴撞击特性。例如,柯鹏等[24]计算发现气膜缝位置和热气吹风比等都影响开缝支板表面局部水滴撞击系数分布,吹风比越大,水滴撞击系数越小。刘华等[25]计算了不同气膜缝出流位置、射流角度等结构参数下,支板表面水滴撞击特性,发现气膜缝位置会影响局部水滴撞击系数和总撞击效率。但目前射流对结构水滴撞击特性影响的研究仍十分有限,尤其是对于飞机/航空发动机的典型防冰部件,如机翼、进气道、帽罩和支板等。
本文选取了双开孔的三维圆柱作为基本构型,采用基于欧拉-欧拉方法的数值模拟算法对不同吹风比和来流速度下的水滴撞击系数进行了数值模拟,揭示射流对开孔圆柱表面不同位置水滴撞击系数分布、最大水滴收集系数和撞击极限的影响规律,并分析原因,为结冰预测与防冰设计提供参考。
1 考虑数值扩散的水滴相模型一般防冰工况下可认为空气和水滴之间单向耦合,只考虑空气流场对水滴运动的影响。基本假设如下:
(1) 水滴运动过程保持常物性、无变形、无破碎、无碰撞;
(2) 水滴撞击壁面后无飞溅;
(3) 忽略水滴与空气之间的传热传质;
(4) 只考虑作用在水滴上的空气阻力和重力。
1.1 水滴相控制方程Slater[26]指出速度方向不同的水滴相交后形成一个无限大的密度脉冲,会导致欧拉法计算发散,为此建议在水滴连续性方程中加入数值扩散项,详细分析参见文献[27-28]等。
考虑数值扩散后水滴相控制方程如下:
| $ \nabla \cdot\left(\rho_{w} \alpha \boldsymbol{V}\right)=b \nabla^{2} \alpha \rho_{w} $ | (1) |
| $ \nabla \cdot\left(\rho_{w} \alpha \boldsymbol{V} \boldsymbol{V}\right)=\rho_{w} \alpha K\left(\boldsymbol{V}_{a}-\boldsymbol{V}\right)+\rho_{w} \alpha \boldsymbol{G} $ | (2) |
其中b为数值扩散系数,ρw为水滴密度,α为局部水滴体积分数,V为水滴速度矢量,Va为气流运动速度矢量,G是重力加速度矢量。K为空气-水滴作用因子,
| $ K=\frac{18 \mu_{a} f}{\rho_{w} D_{w}^{2}} $ | (3) |
其中μa是空气动力黏度,Dw是水滴直径,f为水滴阻力系数。
1.2 边界条件基于假设(2),撞击到壁面的水滴应从计算域中排除。设n为撞击壁面的单位法向量,n · V < 0即表明水滴撞击到了壁面。壁面水滴容积分数和速度都取紧贴壁面网格的中心点的值。
1.3 局部水滴撞击系数计算局部水滴撞击系数β定义为微元表面上的实际水收集量与该微元表面上最大可能的收集量之比,计算式为:
| $ \beta=\alpha(\boldsymbol{V} \cdot \boldsymbol{n}) /\left(\alpha_{\infty}\left|\boldsymbol{V}_{\infty}\right|\right) $ | (4) |
其中α∞为来流体积分数,V∞为来流速度。
定义吹风比M来表征射流强度,
| $ M=\rho_{j} \boldsymbol{V}_{j} / \rho_{\infty} \boldsymbol{V}_{\infty} $ | (5) |
其中ρj为射流气体密度,Vj为射流气体速度。
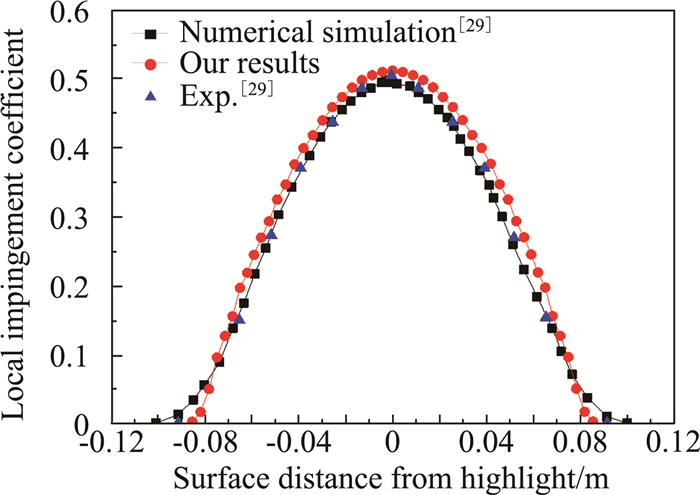
1.4 算法验证选取文献[29]中三维圆柱算例,圆柱直径101.6 mm,来流速度80 m/s,压力89867 Pa,水滴直径16 μm。计算边界采用速度入口,压力出口。图 1给出了中心截面上水滴撞击系数对比结果。可以发现,本文计算结果中水滴撞击系数分布与文献中数值模拟和实验结果吻合良好,撞击极限和实验结果相比误差大约为6.5%,最大水滴撞击系数和实验结果相比误差大约为1%。更多验证结果见文献[14, 28]。
|
图 1 三维圆柱验证算例 Fig.1 Algorithm verification(3D cylinder) |
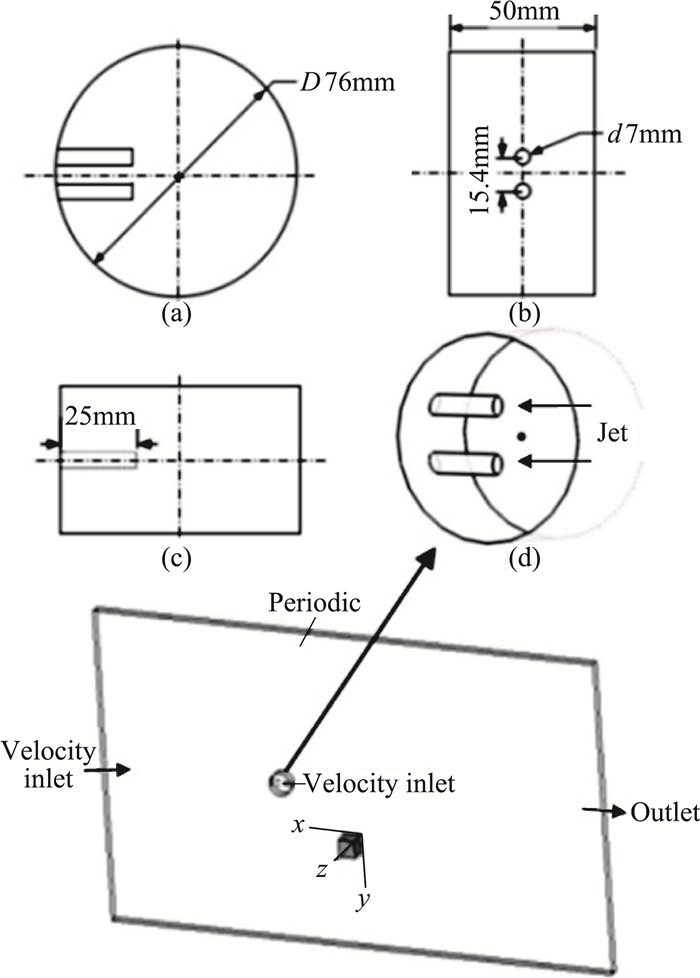
研究构型为开直孔的三维圆柱,几何模型和计算域如图 2所示,直径D取76 mm。射流孔为上下对称分布,水平方向,直径d为7 mm,孔间距为15.4 mm。计算域为前场8D,后场14D,上下各7D。其中图 2(d)为局部放大图,图 2(a)、图 2(b)和图 2(c)分别图 2(d)的正视图、左视图和俯视图。
|
图 2 计算域 Fig.2 Computational domain |
计算网格为三维结构化网格,通过网格无关性验证后,最终网格数约300万,如图 3所示,其中近壁网格进行了加密,y+≈1。

|
图 3 计算网格 Fig.3 Computational mesh |
来流入口采用速度入口边界条件,出口采用压力出口边界条件,射流采用速度入口边界条件,展向两侧采用周期性边界条件,圆柱表面采用1.2节定义的边界条件,其他壁面为无滑移壁面边界。
利用Fluent软件求解空气流场,水滴流场通过用户自定义函数求解。采用标准k-ε湍流模型和增强型壁面函数,使用基于压力的分离式求解器,各项参数均采用二阶精度的空间离散方法。
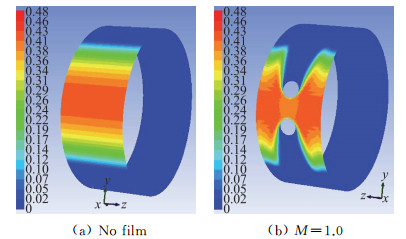
2.3 计算结果及分析选取典型水滴大小(单一直径20 μm)在来流速度(30 m/s)和射流吹风比(M=1.0)条件下进行计算,发现射流对水滴撞击特性存在显著影响,无射流孔圆柱和有射流孔圆柱的表面水滴撞击系数分布对比如图 4所示。
|
图 4 水滴撞击系数云图 Fig.4 Contours of droplet impingement coefficient |
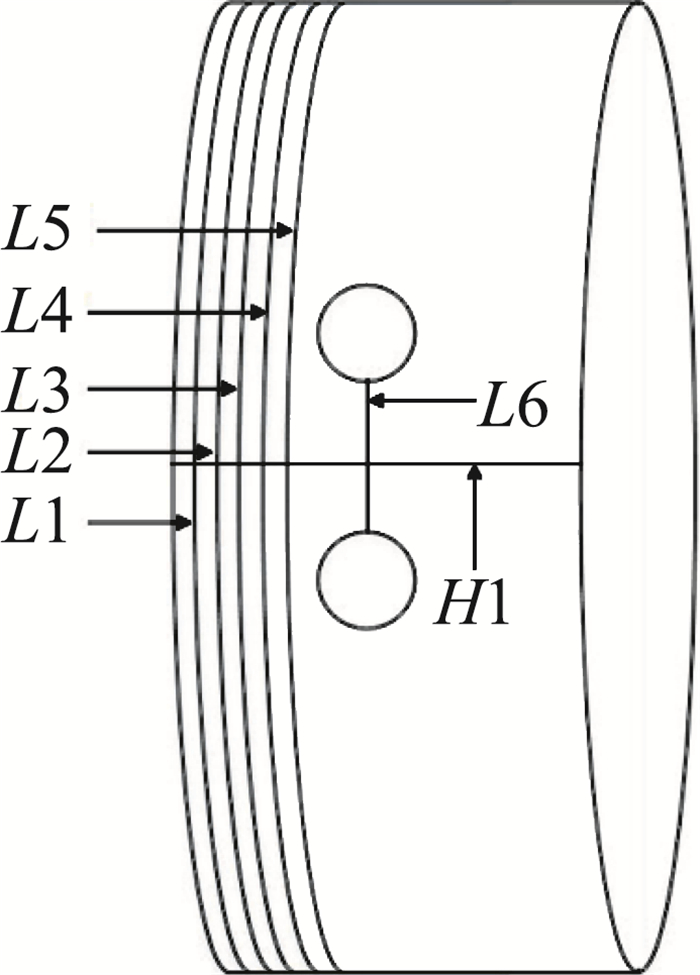
对比图 4(a)、图 4(b)可见,射流孔出口下游水滴被完全吹散,小孔附近则随表面位置不同而呈现出不同变化规律。为此,进一步选取几个特征截面来分析不同位置水滴撞击特性。各截面对应位置关系如图 5所示,展向从左往右依次为截面L1~L6,中心截面L6通过两个射流孔中线,弦向中心截面H1则为二个射流孔上下方向的正中间截面。各个截面的无量纲位置坐标如表 1所示,其中,s表示截面到二孔中心线的距离,r为射流孔半径。
|
图 5 截面位置示意图 Fig.5 Section positions |
| 表 1 各截面位置 Table 1 Parameters in section positions |
|
|
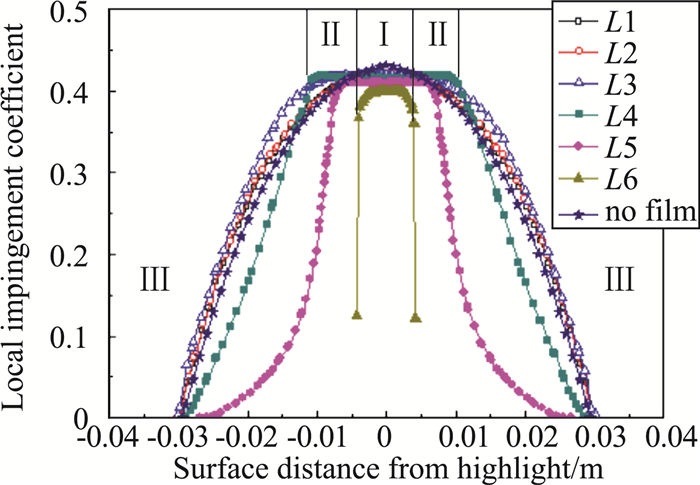
各弦向截面在吹风比为1.0时的水滴撞击系数分布如图 6所示, 射流对水滴撞击系数分布规律影响较为复杂。例如,中心截面L6的水滴撞击系数显著小于无气膜情况,撞击极限终止于孔边缘,最大水滴撞击系数降低了6.88%。近孔截面L5的水滴撞击系数分布曲线呈现显著不同的凹曲线,在前缘的一小段范围内曲线保持水平,之后呈现为快速下降的凹曲线,到撞击边缘附近时降幅趋缓。水滴撞击系数变化最剧烈的区域(距离中心-0.015~-0.008 m和0.008~0.015 m)正是射流吹袭作用最强的区域。最大水滴撞击系数相比于无气膜时减少了5%,撞击极限减少了8%。中间截面L4上最大水滴撞击系数和撞击极限都略小于无气膜情况,但是水滴撞击系数曲线从撞击极限到驻点前缘(距离中心-0.030~-0.012 m和0.012~0.030 m)几乎呈线性分布,与无射流情况下差异不大。在前缘一小段范围内(距离中心-0.012~0.012 m)曲线几乎保持水平。
|
图 6 吹风比为1.0时的水滴撞击系数 Fig.6 Droplet impingement coefficient for blowing ratio 1.0 |
为分析水滴撞击系数变化的原因,将图 6中圆柱表面沿弦向划分为三个区域,Ⅰ区、Ⅱ区和Ⅲ区,对应表面的孔间、孔两侧和孔后区域,图 7进一步给出与三个区相应的水滴速度矢量图。

|
图 7 吹风比为1.0时的水滴速度矢量 Fig.7 Velocity vector of droplet for blowing ratio 1.0 |
Ⅰ区所有截面的水滴撞击系数均小于无气膜作用情况,从图 7中Ⅰ区水滴速度矢量图可以明显看出,水滴有向展向和弦向外侧运动的趋势,这是在射流展向扩散和弦向吹袭共同作用下的结果。
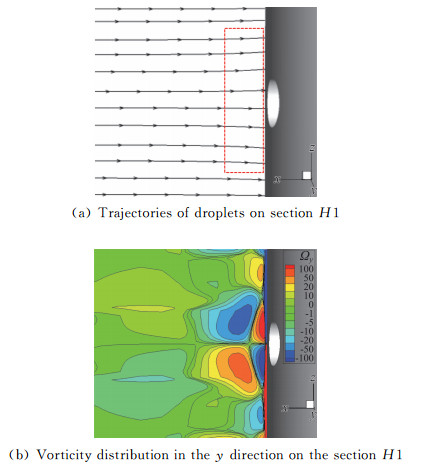
1) 展向射流扩散作用可以从图 8的H1剖面上来流水滴轨迹和流场y方向涡量场可以明显看出,两射流孔间的水滴被吹向展向外侧,造成Ⅰ区的来流水量减少。
|
图 8 吹风比为1.5时H截面水滴运动轨迹和y方向流场涡量 Fig.8 Droplet trajectories and vorticity distribution in y direction on section H1 for blowing ratio 1.5 |
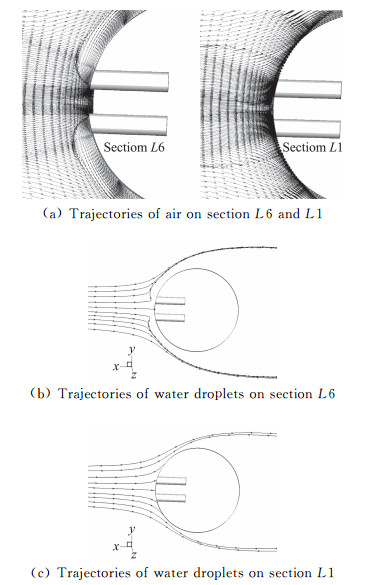
2) 弦向射流吹袭作用,由图 9中L6和L1截面吹风比为1.0时空气运动轨迹和水滴运动轨迹可以看出,水滴轨迹有明显的上扬,被吹向弦向后侧,而且对比图 9(b)、图 9(c)发现,近流孔截面受到射流吹袭作用更强,所以L6截面上水滴撞击特性变化更为剧烈。
|
图 9 L6和L1截面吹风比为1.0时空气运动轨迹和水滴运动轨迹 Fig.9 The trajectories of air and droplets on section L6 and L1 for blowing ratio 1.0 |
Ⅱ区为射流孔侧区域,在气流吹袭和扩散作用下(如图 7中Ⅱ区水滴速度矢量图)下,水滴撞击系数会下降。近孔截面L5和L6则受射流吹袭作用影响更大,下降最为显著,而外侧截面L1和L2则影响不大;但是,对于L3和L4截面,由于射流扩散作用将Ⅰ区的水滴吹过来,导致来流水量增加,所以水滴撞击系数反而会增大。
Ⅲ区为射流孔后的区域,与Ⅱ区受到的作用力类似,即在射流吹袭和射流扩散的共同作用下,水滴向孔后、向外侧方向运动(如图 7中Ⅲ区水滴速度矢量图),射流影响范围仅局限在近孔截面L4~L6。
3 射流强度影响分析射流强度会影响圆柱表面的水滴撞击特性分布规律,为此,进一步分析了吹风比(0.5和1.5)对典型截面位置的水滴撞击系数的分布特征和最大水滴撞击系数的影响。
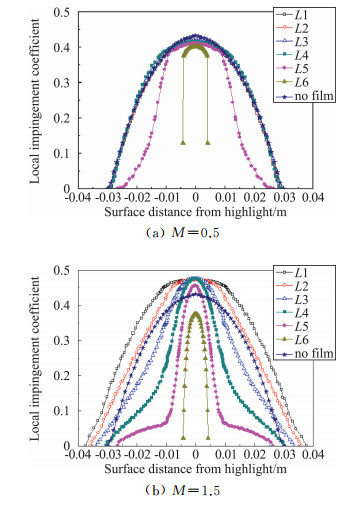
图 10给出了不同吹风比条件下表面水滴撞击系数的分布规律。总体来说,吹风比对不同位置的水滴撞击系数的影响规律类似,孔后基本无水滴,孔间和近孔位置受影响最为显著,差异也很明显。
|
图 10 吹风比为0.5和1.5时水滴撞击系数对比 Fig.10 Comparison of droplet impingement coefficient for different blowing ratios(0.5, 1.5) |
当吹风比减小到0.5时,由图 10(a)可以看到,总体分布规律与吹风比为1.0时基本一致,是射流吹袭和射流扩散共同作用下的结果。由于吹风比小,射流孔气流吹袭影响仅限于近孔侧截面L5和孔间截面L6。对其他截面的影响较小,基本限于孔间Ⅰ区范围。
当吹风比增大到1.5时,图 10(b)显示了射流的显著影响。外侧截面L1和L2的水滴撞击系数都明显高于无气膜情况,其他截面变化与吹风比1.0的情况类似,但是孔间Ⅰ区的水滴撞击系数也明显增加,高于无气膜状态。原因在于当吹风比大于1.0时,射流吹袭和扩散作用更加强烈,来自两孔间(Ⅰ区)的水滴沿展向被吹向外侧,造成近孔截面L6水滴量减少,小于无气膜结果,而远孔各截面上增加,在不同程度上高于无气膜情况。
各截面水滴撞击系数变化规律的差异,主要来源于物面局部流场的巨大差异。图 11给出了吹风比为1.5时的物面涡量分布情况,近壁区域存在射流诱发的复杂涡流场,会对水滴撞击轨迹产生显著影响。接下来针对不同截面来具体分析。
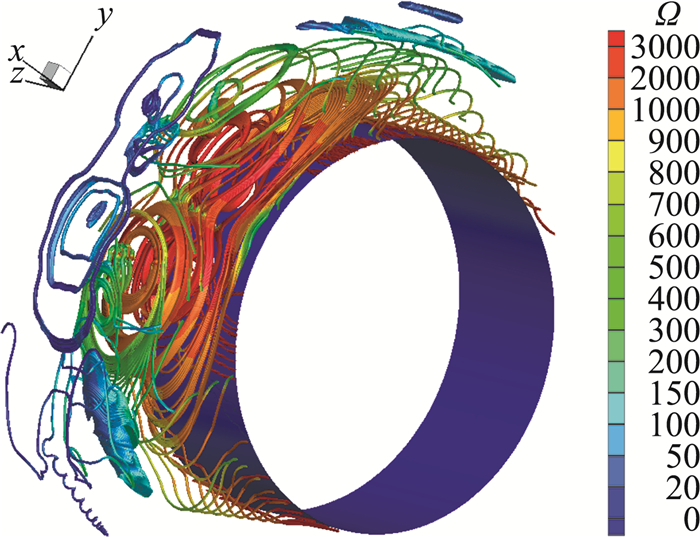
|
图 11 吹风比为1.5时的涡量分布 Fig.11 Vorticity distribution for blowing ratio 1.5 |
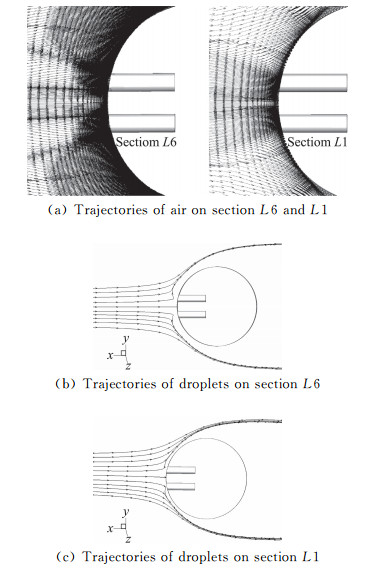
图 12为吹风比为1.5时L6和L1截面水滴运动轨迹。对比图 12(b)和图 9(b)可明显看出吹风比增大时,中心截面L6处射流吹袭作用加强,减小了局部水滴撞击系数。综上,在近孔截面射流吹袭作用和远孔截面射流扩散作用的综合影响下,会出现图 10(b)中的水滴撞击系数分布规律。
|
图 12 L6和L1截面吹风比为1.5时的水滴运动轨迹 Fig.12 Trajectories of water droplets on section L6 and section L1 for different blowing ratios 1.5 |
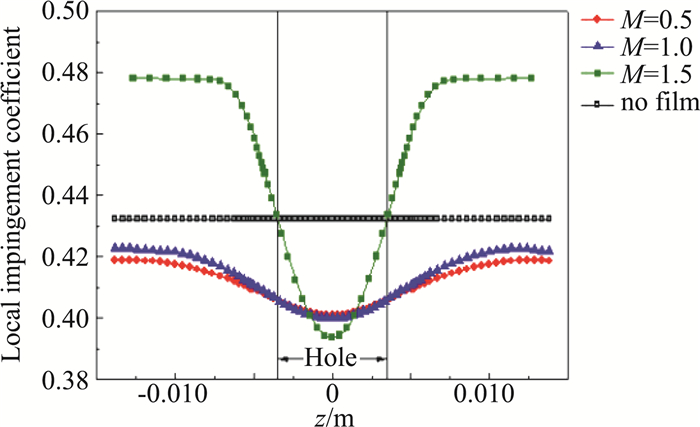
展向位置上的最大水滴撞击系数的分布结果能更好的显示射流在不同区域的综合作用。图 13给出了三个吹风比下, 截面H1的水滴撞击系数。吹风比较小时(0.5和1.0),总体水滴撞击系数分布低于无气膜工况,孔间区域水滴撞击系数相比于无气膜工况最大下降了7.51%,吹风比增大到1.5时,射流动量大大增强,对孔间主气流吹袭作用更为强烈,导致孔间水滴撞击系数比无气膜工况最大下降了8.95%。但水滴撞击系数从展向外侧截面向孔间截面呈下降趋势,最大降幅约17.65%。
|
图 13 三吹风比下水滴撞击系数分布 Fig.13 Distribution of droplet impingement coefficient on section H1 at three blowing ratios(0.5, 1.0, 1.5) |
采用基于欧拉-欧拉模型的水滴撞击算法,针对典型水滴直径,分析了射流对三维带双开孔射流的圆柱表面水滴撞击特性的影响规律和内在机理,得出以下结论:
1) 射流与主流之间存在的强耦合作用会显著改变来流的流动规律,进而会影响开孔圆柱物面的水滴撞击特性。在物面的不同区域,射流与水滴之间存在吹袭作用和扩散作用等不同的作用关系,且其强度随物面区域变化而差异很大。例如,吹风比为1.0时,弦向孔后区域影响最大,完全没有水滴撞击,展向向外区域影响逐渐减小。
2) 射流和来流水滴间的吹袭和扩散作用不仅与物面位置有关,与射流强度也密切相关。水滴直径为20 μm,在小吹风比(0.5和1.0)时,射流仅对展向近孔截面有影响,孔间水滴撞击系数相比于无气膜工况最大下降7.51%;吹风比为1.5时,射流吹袭和扩散作用进一步加强,孔间的水滴沿展向被吹向外侧,造成近孔截面水滴量减少而远孔截面增加,孔间截面水滴撞击系数比无气膜工况最大下降了8.95%,水滴撞击系数从展向外侧向孔间最大降幅约17.65%。
本文初步研究了射流对三维开孔圆柱物面不同区域水滴撞击特性的影响规律,分析了其内在机理。虽然所得规律在相同工况下对多种结构具有一定普遍性,但仅针对了特定的水滴直径(20 μm)和开孔布置方式,而射流对水滴撞击特性的影响程度会随水滴直径减小进一步增强,具体规律还有待后续进一步研究。
| [1] |
LYNCH F T, KHODADOUSTB A. Effects of ice accretions on aircraft aerodynamics[J]. Progress in Aerospace Sciences, 2001, 37(8): 669-767. DOI:10.1016/S0376-0421(01)00018-5 |
| [2] |
CAO Y H, TAN W Y, WU Z L. Aircraft icing: An ongoing threat to aviation safety[J]. Aerospace Science and Technology, 2018, 75: 353-385. DOI:10.1016/j.ast.2017.12.028 |
| [3] |
杜雁霞, 李明, 桂业伟, 等. 飞机结冰热力学行为研究综述[J]. 航空学报, 2017, 38(2): 25-36. DU Y X, LI M, GUI Y W, et al. Review of thermodynamic behavior studies in aircraft icing process[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 25-36. (in Chinese) |
| [4] |
郁嘉, 卜雪琴, 林桂平, 等. 非结冰气象条件下机翼热气防冰系统数值模拟[J]. 空气动力学学报, 2016, 34(5): 562-567. YU J, BU X Q, LIN G P, et al. Numerical simulation of a wing hot air anti-icing system in dry air conditions[J]. Acta Aerodynamica Sinica, 2016, 34(5): 562-567. (in Chinese) |
| [5] |
SAEED F, MORENCY F, PARASCHIVOIU I. Numerical simulation of a hot-air anti-icing system[C]//Aerospace Sciences Meeting and Exhibit, 2013.
|
| [6] |
WANG C, CHANG S, WU H. Lagrangian approach for simulating supercooled large droplets' impingement effect[J]. Journal of Aircraft, 2015, 52(2): 1-14. |
| [7] |
桑为民, 胡少华, 鲁天. 过冷大水滴动力学特性对结冰影响数值研究[J]. 空气动力学学报, 2016, 34(5): 549-555. SANG W M, HU S H, LU T. Numerical investigation of ice accretion effects at supercooled large droplet conditions[J]. Acta Aerodynamica Sinica, 2016, 34(5): 549-555. (in Chinese) |
| [8] |
YANG H, KE P, YANG C. Analysis of droplet impingement characteristics of aero-engine nose cone with hot air film[C]//ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition.
|
| [9] |
申晓斌, 张志强, 林贵平, 等. 旋转部件复杂表面水滴撞击计算[J]. 空气动力学学报, 2016, 34(6): 709-713. SHEN X B, ZHANG Z Q, LIN G P, et al. Droplet impingement calculation on complex suface of rotating part[J]. Acta Aerodynamica Sinica, 2016, 34(6): 709-713. DOI:10.7638/kqdlxxb-2015.0213 (in Chinese) |
| [10] |
郭宇翔, 刘荫泽, 董威, 等. 大水滴撞击壁面的动态特性数值模拟[J]. 空气动力学学报, 2016, 34(5): 573-580. GUO Y X, LIU Y Z, DONG W, et al. Numerical investigation on dynamic characteristics of large droplet impacting on surface[J]. Acta Aerodynamica Sinica, 2016, 34(5): 573-580. (in Chinese) |
| [11] |
KIM J, P GARZA DENNIS, et al. Ice accretion modeling using an eulerian approach for droplet impingement[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2013.
|
| [12] |
KIND R J, POTAPCZUK M G, FEO A, et al. Experimental and computational simulation of in-flight icing phenomena[J]. Progress in Aerospace Sciences, 1998, 34(5-6): 257-345. DOI:10.1016/S0376-0421(98)80001-8 |
| [13] |
IULIANO E, BRANDI V, MINGIONE G. Water impingement prediction on multi-element airfoils by means of eulerian and lagrangian approach with viscous and inviscid air flow[R]. AIAA 2006-1270, 2006.
|
| [14] |
YU C, KE P, YU G, et al. Investigation of water impingement on a multi-element high-lift airfoil by Lagrangian and Eulerian approach[J]. Propulsion and Power Research, 2015, 4(3): 161-168. DOI:10.1016/j.jppr.2015.07.001 |
| [15] |
赵勇, 杨新亮. 飞机水平尾翼水滴撞击特性及防冰热载荷计算[J]. 航空动力学报, 2012, 27(11): 2402-2407. ZHAO Y, YANG X L. Impingement characteristics and anti-icing heat load calculation of certain tail plane[J]. Journal of Aerospace Power, 2012, 27(11): 2402-2407. (in Chinese) |
| [16] |
易贤, 王开春, 桂业伟, 等. 结冰面水滴收集率欧拉计算方法研究及应用[J]. 空气动力学学报, 2010, 28(5): 97-601. YI X, WANG K C, GUI Y W, et al. Investigation to Scheme of 2DPIV field of view[J]. Acta Aerodynamica Sinica, 2010, 28(5): 597-601. (in Chinese) |
| [17] |
杨胜华, 林贵平, 申晓斌. 三维复杂表面水滴撞击特性计算[J]. 航空动力学报, 2010, 25(2): 285-90. YANG S H, LIN G P, SHEN X B. Water droplet Impingement prediction for three-dimensional complex surfaces[J]. Journal of Aerospace Power, 2010, 25(2): 290. (in Chinese) |
| [18] |
杨军, 郭文, 娄德仓. 发动机防冰支板水滴撞击特性的数值研究[J]. 燃气涡轮试验与研究, 2011, 24(1): 19-24. YANG J, GUO W, LOU D C. Numerical analysis of trajectories of water droplets on the anti-icing vane of an Engine[J]. China Gas Turbine Establishment, 2011, 24(1): 19-24. DOI:10.3969/j.issn.1672-2620.2011.01.004 (in Chinese) |
| [19] |
申晓斌, 林贵平, 杨胜华. 三维发动机进气道水滴撞击特性分析[J]. 北京航空航天大学学报, 2011, 37(1): 1-5. SHEN X B, LIN G Y, SHENG H F, et al. Analysis on three dimensional water droplets impingement characteristics of engine inlet[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(1): 1-5. (in Chinese) |
| [20] |
蒋浩, 金龙, 牛上维, 等. 基于合成热射流的机翼除冰实验研究[J]. 实验流体力学, 2017, 31(3): 94-100. JIAN G H, JIN L, NIU S W, et al. Experimental analysis of de-icing on airfoil using heated dual synthetic jet actuators[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(3): 94-100. (in Chinese) |
| [21] |
李玉杰, 罗振兵. 水滴结冰结霜及合成双射流除霜除冰实验研究[J]. 实验流体力学, 2016, 30(3): 27-32. LI Y J, LUO Z B. An experimental investigation on the process of droplet icing frosting and defrosting decing using dual synthetic jet[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 27-32. (in Chinese) |
| [22] |
柯鹏, 杨慧赟, 王俊凯, 等. 航空发动机帽罩热气膜防冰的加热特性研究[J]. 航空动力学报, 2018, 33(3): 530-539. KE P, YANG H Y, WANG J K, et al. Investigation of heating characteristics of aero-engine nose cone with film-heating anti-icing system[J]. Journal of Aerospace Power, 2018, 33(3): 530-539. (in Chinese) |
| [23] |
王旭东, 高峰, 朱柏银, 等. 超声速来流下混合流动控制射流角度影响数值研究[J]. 空气动力学学报, 2018, 36(4): 670-676. WANG X D, GAO F, ZHU B Y, et al. Investigation on the influence of injection angle in supersonic flow with hybrid flow control[J]. Acta Aerodynamica Sinica, 2018, 36(4): 670-676. DOI:10.7638/kqdlxxb-2016.0076 (in Chinese) |
| [24] |
柯鹏, 张韵, 于广锋, 等. 航空发动机进口支板外部热气膜对水滴撞击特性的影响[J]. 航空动力学报, 2017, 32(3): 621-629. KE P, ZHANG Y, YU G F, et al. Influence of exterior hot-film on droplet impingement characteristics over aero-engine inlet strut[J]. Journal of Aerospace Power, 2017, 32(3): 621-629. (in Chinese) |
| [25] |
刘华, 杨军. 防冰支板气膜缝出流对水滴撞击特性的影响[J]. 燃气涡轮试验与研究, 2017, 30(2): 51-57. LIU H, YANG J. Effect of film gap outflow on water droplets impingement characteristics of the anti-icing vane[J]. Gas Turbine Experiment and Research, 2017, 30(2): 51-57. DOI:10.3969/j.issn.1672-2620.2017.02.009 (in Chinese) |
| [26] |
SLATER S A, YOUNG J B. The calculation of inertransport in dilute gas-particle flows[J]. International Journal of Multiphase Flow, 2001, 27(1): 61-87. DOI:10.1016/S0301-9322(99)00122-6 |
| [27] |
TONG X, LUKE E. An Eulerian simulations of icing collection efficiency using a singularity diffusion model[R]. AIAA, 2003-1073, 2003.
|
| [28] |
刘兵, 柯鹏. 三维圆柱水滴撞击特性分析[J]. 应用力学学报, 2016, 33(3): 389-393. LIU B, KE P. Analysis of droplet impingement characteristics of three dimensional cylinder[J]. Chinese Journal of Applied Mechanics, 2016, 33(3): 389-393. (in Chinese) |
| [29] |
WIRIGO S, SRIRAMBHATLA S. An Eulerian method to calculate the collection efficiency on two and three dimensional bodies[R]. AIAA 2003-1073, 2003.
|
 2019, Vol. 37
2019, Vol. 37


