高超声速飞行器在大气层中持续飞行时,飞行器表面将经受严峻的气动加热[1]。高超声速气动热会导致飞行器结构温度急剧升高,严重时局部高温还可能导致飞行器结构材料的物理属性和刚度发生改变,对飞行器的飞行安全造成极大隐患。因此快速预测气动加热与结构传热的物理过程,对高超声速飞行器设计的初步选型和热防护系统轻量化设计,具有重要作用[2]。
高超声速气动加热问题[3]的主要研究方法包括:数值模拟方法[4]、工程计算方法[5-6]、地面风洞试验[7]及飞行试验等,其中后两种方法因代价高昂等因素不适于工程设计的初期选型阶段。
数值模拟方法主要是对N-S(Navier-Stokes)方程及相关简化形式的控制方程进行求解,具有计算精度高、可处理复杂流动和全机外形等优点,但在气动热与结构传热耦合问题的求解方面对计算资源需求巨大且非常耗时。在这方面的研究,相关学者做了大量工作,主要工作集中在计算效率与精度等方面。董维中[8]等开展了高超声速飞行器气动加热与飞行器表面温度耦合的数值模拟研究,结果表明在气动热环境的预测中,应采用表面温度分布与气动热耦合计算的方法,以减小表面温度分布对气动热计算结果的影响。杨恺[9]等采用基于点隐式的二阶精度迎风TVD格式的N-S方程有限体积法,开展了高温热化学非平衡条件下球锥和RAM-CII模型的气动热数值模拟计算,分析了不同非平衡模型在热化学非平衡条件下流场的影响。计算结果表明建立的数值模拟方法具有较高的精度。夏刚[10]等依据流场特征时间步长远小于结构传热时间步长的特点,提出了一种松耦合的流-固-热耦合计算方法,并采用二维高超声速圆管绕流与结构传热的非定常算例对方法进行了验证。耿湘人[11]等基于Levelset方法和有限差分方法,将流场与固体结构统一到同一组控制方程中进行求解,计算结果与试验值吻合良好,探索了流-固-热一体化计算的可行性。张胜涛[12]等针对高超声速流场-热-结构松耦合分析策略框架,采用自适应耦合计算时间步长、混合插值策略等方法,建立了多场耦合分析平台。由于流-固-热物理问题复杂,该问题的求解在数值计算技术及计算设备硬件条件等方面要求甚高,采用全流场黏性数值模拟方法难以快速得到工程设计初期选型所需的参考数据。
气动加热工程计算方法[13]对简单外形的气动热求解具有高效、准确的特点,因此在实际工程应用中率先得到发展。但在复杂气动外形的气动热分析方面适应性较差,并且需要基于大量试验数据对计算方法与结果进行人工修正。在这方面比较著名的是NASA兰利研究中心研发的一套气动加热预测程序(MINIVER)[14],该程序中驻点区域使用经典的Fay-Riddle公式,采用参考焓方法来计算高速流动压缩性效应,另外可对过渡流区气动热进行计算。Hamilton[15]针对三维钝头体发展了一种适用于空气平衡气体的高超声速流动热流密度计算方法,该方法可计算不同高速流动状态(层流、转捩、湍流)下的热流密度。Zoby[16]等人开发了LATCH方法,该方法基于参考焓和修正雷诺比拟计算热流密度,可用于有化学反应参与的钝头体气动热计算。乐嘉陵[17]针对高超声速流动的黏性效应,利用边界层近似方法和工程方法对高超声速飞行器的传热系数和表面摩擦阻力进行了相应计算。李建林[18]等人对气动热工程计算方法进行拓展应用,对乘波体构型高速飞行器进行气动热快速估算,得到较好结果。总体而言,工程计算方法的缺陷在于需要大量人工干涉以及庞大试验数据,在处理复杂外形飞行器方面的通用性上仍需完善。
综上,本文依据高超声速边界层[19]理论,利用数值计算方法与工程算法的各自优势,将气动热的计算简化为绕飞行器的无黏外流(边界层以外)数值解和边界层内热流求解两个部分,同时耦合防热系统结构传热计算模型,考虑了高温化学非平衡效应,发展了一种可用于快速计算三维复杂外形飞行器气动加热与结构传热特性的方法,实现了复杂飞行条件下飞行器全机表面热流密度与防热结构温度场时变特性的快速计算。
该方法的优点在于:综合了全流场数值模拟与工程算法各自的优势,可以快速、高效地对三维复杂外形高速飞行器的多种飞行状态下的气动加热与结构耦合传热特性进行计算与分析,给出热流密度与防热结构层内温度等参数分布,弥补了全流场黏性数值模拟方法计算代价高、效率低、周期长等缺陷,同时拓展了气动热工程算法的应用范围。
1 无黏外流场数值计算方法气动加热与结构传热耦合数值计算技术考虑了瞬态气动加热、巡航状态长时传热和弹道状态长时传热三种模型。根据不同飞行状态完成无黏流场的求解,取无黏流场解结果中的物面参数(如表 1所示)作为边界层外缘参数提供给工程方法中的边界层简化算法作为输入条件,之后可得到用于防热系统中结构传热计算所需的飞行器表面热流及传热系数等参数。
| 表 1 无黏外流解物面输出参数 Table 1 Surface parameters of inviscid outflow |
|
|
在无黏外流场求解方面,本文采用基于块结构网格技术及分布式并行计算技术的三维流场数值计算方法,为气动热工程估算方法提供如表 1所列的物面流动参数。
2 物面热流与结构传热工程估算方法 2.1 物面热流密度计算物面热流的计算采用工程中简化求解边界层方程的方法。将该工程方法所需的边界层外缘参数设定为无黏流场解的物面流动参数(见表 1),计算输出结果为物面热流密度。
本文研究针对的是全机外形,因此根据热流密度工程计算方法将飞行器表面热流的计算划分为驻点区和非驻点区两个区域。驻点区热流计算采用目前广泛使用的Fay-Riddell公式[20]:
| $ \begin{array}{l} {q_{ws}} = 0.763P{r^{ - 0.6}}{\left( {\frac{{{\rho _w}{\mu _w}}}{{{\rho _s}{\mu _s}}}} \right)^{0.1}}\sqrt {{\rho _s}{\mu _s}{{\left( {\frac{{{\rm{d}}{u_e}}}{{{\rm{d}}x}}} \right)}_s}} \cdot \\ \left[ {1 + \left( {L{e^{0.52}} - 1} \right)\frac{{{h_D}}}{{{h_s}}}} \right]\left( {{h_s} - {h_w}} \right) \end{array} $ | (1) |
式中ρw、μw、hw分别表示物面上气体的密度、黏性系数和焓,ρs和μs分别表示驻点处的气体密度及气体黏性系数,hD为平均空气电离焓。计算中取普朗特数Pr=0.71,路易斯数Le=1.0。非驻点区的热流密度计算公式参见文献[21]。
2.2 结构传热耦合计算方法采用工程中常用的平板传热模型进行结构传热计算。传热方程为一维热传导方程,热防护结构内表面采用绝热壁边界条件,采用差分法进行求解。在传热计算模型的选取上,根据式(2)定义的防热结构材料的毕奥数Bi的取值来选取[22]。
| $ B_{i}=\frac{\alpha \delta}{\lambda_{\delta}} $ | (2) |
式中α为传热系数,δ为材料结构厚度,λδ为当前材料热传导系数。
当Bi≤0.1时,采用式(3)所示的热薄壁传热模型:
| $ \rho_{\delta} c_{\delta} \delta \frac{\mathrm{d} T}{\mathrm{d} t}=\alpha\left(T_{a w}-T_{w}\right)-\varepsilon \delta T_{w}^{4} $ | (3) |
初始条件为:
| $ \left.T_{w}\right|_{t=0}=T_{0} $ | (4) |
式中ρδ、cδ和ε分别表示防热材料的密度、比热容和表面辐射系数。采用差分方法对式(3)进行时间t的推进求解,即可得到热薄壁条件下热防护结构层温度随时间的变化。
当Bi>0.1时,采用热厚壁传热模型。在具体计算时,将热厚壁由内向外分为j层进行逐层推进求解。计算方程为:
表层:
| $ c_{m} \rho_{m} \delta_{m j} \frac{\mathrm{d} T_{j}}{\mathrm{d} t}=\alpha\left(T_{a w}-T_{j}\right)-\varepsilon \sigma T_{j}^{4}-\lambda_{m} \frac{T_{j}-T_{j-1}}{\delta_{m j}} $ | (5) |
最内层:
| $ c_{m} \rho_{m} \delta_{m 1} \frac{\mathrm{d} T_{1}}{\mathrm{d} t}=\lambda_{m} \frac{T_{2}-T_{1}}{\delta_{m 2}} $ | (6) |
中间层:
| $ c_{m} \rho_{m} \delta_{m n} \frac{\mathrm{d} T_{n}}{\mathrm{d} t}=\lambda_{m} \frac{T_{n+1}-T_{n}}{\delta_{m n}}-\lambda_{m} \frac{T_{n}-T_{n-1}}{\delta_{m n}} $ | (7) |
初始条件为:
| $ \left.T_{j}\right|_{t=0}=\left.T_{1}\right|_{t=0}=\left.T_{n}\right|_{t=0}=T_{0} $ | (8) |
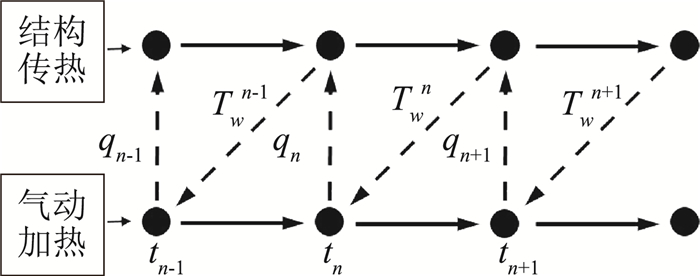
式中下标m为材料类型,n表示结构材料的分层数,λm为材料m的热传导系数,该计算方法可用于计算多种材料组成的热防护结构的传热情况。将式(5)~式(7)进行差分离散并按时间步长推进求解,可以计算得出各层材料温度随时间的变化。气动加热与结构传热过程的耦合计算[23-27]比较复杂,在求解气动热参数时,需要以物面温度Tw作为物面边界输入条件,然后通过简化边界层工程方法计算得到表面热流密度qn;而在计算结构传热时,又以表面热流密度qn作为热边界输入条件,计算得到壁面温度。因此,本文采用图 1所示的耦合迭代计算思路[23]。
|
图 1 气动加热与结构传热耦合求解示意图 Fig.1 Flowchart of aerodynamic heating coupled with structure heat-transferring |
在时间步tn的求解中,以上一时间步tn-1的物面温度Twn-1作为本时间步的物面温度边界条件,采用工程算法进行边界层的气动加热计算,得出tn时间步的热流密度qwn;然后,以qwn作为热边界输入条件提供给结构传热计算模块,计算得到tn时间步的物面温度Twn,如此循环以实现结构传热和气动热环境的耦合计算。
3 弹道状态动态插值方法文中所述的弹道状态是指飞行器在真实飞行中随飞行时间改变飞行高度、迎角、马赫数三个参数的状态(暂不考虑侧滑角)。
根据第2小节中所述的物面热流与结构传热工程计算方法的特点,将其扩展到随时间变化非定常弹道(飞行包线)状态下的气动加热与结构传热耦合计算,此时需要足够多的无黏外流的数值解作为输入参数。为了在满足工程设计误差要求前提下提高耦合算法的计算效率,提出了一种无黏外流解动态插值方法:即通过已经预先完成的有限个无黏外流解的流场结果,插值得到当前弹道时间点上飞行条件下的流场解,以供气动加热与结构传热耦合计算使用。
由于高超声速飞行器飞行高度跨度大,通常涵盖整个大气层高度,若针对飞行高度H进行插值,必须要先构建飞行器在各个飞行高度条件下的流场数据库,其计算量非常庞大,难以达到快速计算的目的。针对该问题,参考国内外有关大气参数随大气高度的变化特征及拟合方法,采用如下方法对飞行高度参数的插值进行简化。
首先,在飞行高度H对流场参数的影响规律方面,研究发现飞行器物面上的当地流场参数与来流参数的比值在不同飞行高度下几乎保持不变[28]。根据这一规律,对同一飞行器,若已知某高度H0下的边界层外缘参数(以P0表示)以及该高度下的流动参数Pinf, 0,且已知任意高度下的大气参数Pinf, x,那么就可以通过Px=Pinf, xP0/Pinf, 0计算获得该飞行器在任意高度上的边界层外缘参数[24, 28]。
由此一来,无黏外流解的计算可仅考虑马赫数和迎角两个参数。具体方法为:在对整个弹道状态进行计算时,无黏外流的求解只需计算设定参考飞行高度下的两个马赫数和两个迎角,共四个飞行状态,其他飞行状态可根据插值方法快速得到。这四个计算状态分别为设定飞行高度下的两个马赫数和两个迎角的组合,即:(Ma1, α1), (Ma1, α2), (Ma2, α1), (Ma2, α2)。与这四个状态所对应的飞行器表面上任一点处的流动参数的值分别记作P11、P12、P21和P22,则某个弹道时间点上飞行条件(Max, αx)状态下的飞行器表面同一位置处的流动参数Pxx可通过如下插值算法得到:
| $ \begin{aligned} &P_{x 1}=P_{11} \frac{M_{2}-M_{x}}{M a_{2}-M a_{1}}+P_{21} \frac{M_{x}-M_{1}}{M a_{2}-M a_{1}}\\ &P_{x 2}=P_{12} \frac{M_{2}-M_{x}}{M a_{2}-M a_{1}}+P_{22} \frac{M_{x}-M_{1}}{M a_{2}-M a_{1}}\\ &P_{x x}=P_{x 1} \frac{\alpha_{2}-\alpha_{x}}{\alpha_{2}-\alpha_{1}}+P_{x 2} \frac{\alpha_{x}-\alpha_{1}}{\alpha_{2}-\alpha_{1}} \end{aligned} $ | (9) |
构造该插值算法的目的在于减少弹道状态无黏外流解的计算次数以提高数值仿真效率,该算法具有简单可行、易实现等特点。由式(9)表示的插值算法可看出,在流场参数的插值精度方面主要依赖于已经求得的无黏外流解的精度及插值变量间距(即马赫数与迎角的增量值)。因此在实际计算中根据弹道参数特征合理建立插值状态数据库及采用高精度无黏外流求解器将有利于提高流场参数的插值精度,能够最大程度地满足工程设计中的误差要求。该方法在插值精度与误差分析方面的详细分析参见文献[23]。
4 高温化学非平衡效应估算计算模型中,将无黏外流解得到的物面流动参数作为边界层外缘参数,即该无黏流的物面流动参数不是实际黏性流场中飞行器的物面参数。由前述可知,实际物面的热流密度是由Fay-Riddell热流密度计算公式(1)得到的[29]。需要说明的是,该公式是在平衡边界层的前提条件下推导得出的,因而未考虑高温条件下的空气化学非平衡效应。在实际高超声速飞行条件下,空气的高温非平衡效应对气动热影响显著,因此对于实际高温化学非平衡流动,需要对Fay-Riddell驻点热流密度计算公式进行修正。式(10)给出了高温空气非平衡边界层驻点传热与平衡边界层驻点传热表面热通量的关系式[30]:
| $ \begin{array}{l} {\left( {\frac{{{q_{{\rm{ne}}}}}}{{{q_{{\rm{eq}}}}}}} \right)_s} = \\ \frac{{{{\left( {1 + \left( {Le{\phi _{\rm{O}}} - 1} \right)\frac{{h_{\rm{O}}^0{C_{{\rm{O}},s}}}}{{{h_s} - {h_w}}} + \left( {Le{\phi _{\rm{N}}} - 1} \right)\frac{{h_{\rm{N}}^{\rm{0}}{C_{{\rm{N}}, s}}}}{{{h_s} - {h_w}}}} \right]}^{0.5}}}}{{{{\left[ {1 + (Le - 1)\frac{{{h_D}}}{{{h_s} - {h_w}}}} \right]}^{0.5}}}} \end{array} $ | (10) |
式中,下标O、N分别表示氧原子和氮原子,ϕ为壁面催化因子,h0为生成焓,CO, s和CN, s分别为氧原子和氮原子的质量浓度,Le为路易斯数。
通过式(10)可看出,求解高温化学非平衡流状态下的驻点热流,需要确定驻点位置氧原子和氮原子的质量浓度。本文主要发展的是一种面向工程应用的快速气动加热计算技术,因此在组元参数特性的获取方面,使用目前国内外广泛认可的组元参数简化计算模型,而不使用耗费资源巨大的精确多组元N-S方程数值解。依据Dunn和Kang[31]发展的各组元浓度计算模型,在流场温度9000 K以下时,可以只考虑O2、O、O+、N2、N、N+、NO、NO+、e-等九种组元及以下六个化学反应式:
| $ \begin{aligned} ①&\mathrm{O}_{2} \leftrightarrows \mathrm{O}+\mathrm{O}, K_{1}=\frac{[\mathrm{O}]^{2}}{\left[\mathrm{O}_{2}\right]}\\ ②&\mathrm{N}_{2} \leftrightarrows \mathrm{N}+\mathrm{N}, K_{2}=\frac{[\mathrm{N}]^{2}}{\left[\mathrm{N}_{2}\right]}\\ ③&\mathrm{NO} \leftrightarrows \mathrm{N}+\mathrm{O}, K_{3}=\frac{[\mathrm{N}][\mathrm{O}]}{[\mathrm{NO}]}\\ ④&\mathrm{NO} \leftrightarrows \mathrm{NO}^{+}+\mathrm{e}^{-}, K_{4}=\frac{\left[\mathrm{NO}^{+}\right]\left[\mathrm{e}^{-}\right]}{[\mathrm{NO}]}\\ ⑤&\mathrm{O} \leftrightarrows \mathrm{O}^{+}+\mathrm{e}^{-}, K_{5}=\frac{\left[\mathrm{O}^{+}\right]\left[\mathrm{e}^{-}\right]}{\mathrm{O}}\\ ⑥&\mathrm{N} \leftrightarrows \mathrm{N}^{+}+\mathrm{e}^{-}, K_{6}=\frac{\left[\mathrm{N}^{+}\right]\left[\mathrm{e}^{-}\right]}{[\mathrm{N}]} \end{aligned} $ |
其中Ki为摩尔密度平衡常数,对于不同的化学反应式,取值可由文献[31]附表查得。
由高温空气化学反应特性可知:当高温空气在9000 K以下时化学反应以离解反应为主,电离反应可忽略,在混合气体组成中,NO、NO+、e-、N+、O+的浓度比O2、O、N2、N的浓度小得多,即:
| $ \left[\mathrm{O}_{2}\right]+\frac{1}{2}[\mathrm{O}]>\frac{1}{2}[\mathrm{O}]+\frac{1}{2}\left[\mathrm{NO}^{+}\right]+\frac{1}{2}\left[\mathrm{O}^{+}\right] $ | (11) |
| $ \left[\mathrm{N}_{2}\right]+\frac{1}{2}[\mathrm{N}]>\frac{1}{2}[\mathrm{NO}]+\frac{1}{2}\left[\mathrm{NO}^{+}\right]+\frac{1}{2}\left[\mathrm{N}^{+}\right] $ | (12) |
因此,在化学反应效应对气动加热的影响特性分析方面,暂不考虑NO、NO+、N+、O+、e-等5种组元。同时,氧原子和氮原子的壁面催化因子有如下关系成立:
| $ {\phi _{\rm{O}}} = \frac{{\frac{1}{2}[{\rm{NO}}] + \frac{1}{2}\left[ {{\rm{N}}{{\rm{O}}^ + }} \right] + \frac{1}{2}\left[ {{{\rm{O}}^ + }} \right]}}{{{{\left[ {{{\rm{O}}_2}} \right]}_0}}}( \ll 1) $ | (13) |
| $ {\phi _{\rm{N}}} = \frac{{\frac{1}{2}[{\rm{NO}}] + \frac{1}{2}\left[ {{\rm{N}}{{\rm{O}}^ + }} \right] + \frac{1}{2}\left[ {{{\rm{N}}^ + }} \right]}}{{{{\left[ {{{\rm{N}}_2}} \right]}_0}}}( \ll 1) $ | (14) |
其中[O2]0、[N2]0分别表示为空气中氧分子和氮分子的摩尔密度。联立式(13)、式(14)与反应方程①②求解,可以分别得到氧原子和氮原子的摩尔密度为:
| $ [{\rm{O}}] = \frac{{{K_1}}}{4}[ - 1 + \sqrt {1 + \frac{{16\left( {1 - {\phi _{\rm{O}}}} \right){{\left[ {{{\rm{O}}_2}} \right]}_0}}}{{{K_1}}}} ] $ | (15) |
| $ [N]=\frac{K_{2}}{4}[-1+\sqrt{1+\frac{16\left(1-\phi_{\mathrm{N}}\right)\left[\mathrm{N}_{2}\right]_{0}}{K_{2}}}] $ | (16) |
由于ϕO、ϕN远小于1,因此在一级近似时可以取ϕO=ϕN=0。然后联立反应方程①~③,可得到[O2]、[N2]和[NO]的摩尔密度计算式为:
| $ \left[\mathrm{O}_{2}\right]=\frac{[\mathrm{O}]^{2}}{K_{1}}, \left[\mathrm{N}_{2}\right]=\frac{[\mathrm{N}]^{2}}{K_{2}}, [\mathrm{NO}]=\frac{[\mathrm{N}][\mathrm{O}]}{K_{3}} $ | (17) |
最后联立反应方程④~⑥和电荷守恒方程[19]可以得到电子的摩尔密度为:
| $ \left[\mathrm{e}^{-}\right]=\sqrt{K_{4}[\mathrm{NO}]+K_{5}[\mathrm{O}]+K_{6}[\mathrm{N}]} $ | (18) |
在气动加热计算中,各组元质量分数需根据外流流动特征采用时间历程相关的迭代方法计算获得。由此,考虑高温化学非平衡效应下的气动加热计算方法可修正为:首先由Fay-Riddell驻点热流密度计算式(1),得到平衡条件下热流密度qeq,然后根据化学反应计算模型得到各组元摩尔密度和质量分数,最后由驻点化学非平衡边界层与平衡边界层热流密度关系式(10),求得高温非平衡条件下的热流密度qne。
研究中将如上所述的高温空气化学非平衡多组元效应嵌入到所发展的全机外形飞行器弹道飞行状态下的气动加热与结构传热数值计算方法中,使得计算模型更接近于高超声速飞行器真实飞行条件下的热环境。
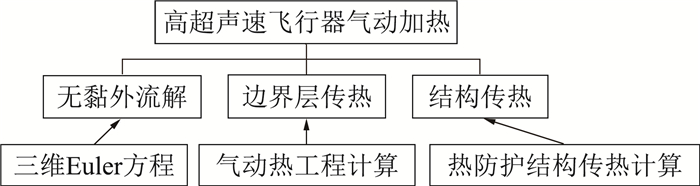
5 算例与分析根据以上理论分析与数值建模过程,发展了一种复杂飞行器气动加热与结构传热耦合计算技术。该技术主要由无黏外流解、气动热工程计算和结构传热三部分构成,如图 2所示。
|
图 2 高超声速气动加热方法示意图 Fig.2 Calculation modules of aero-heating and structure heat transfer |
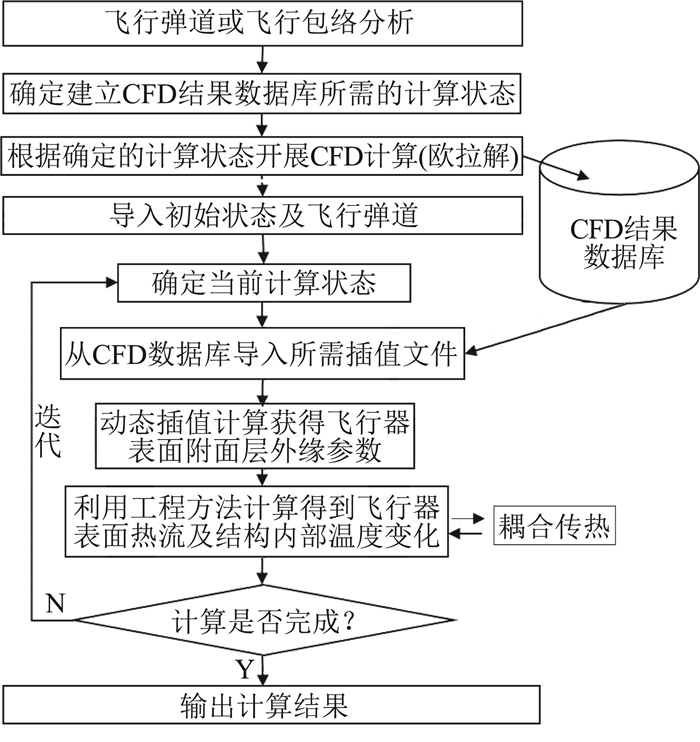
在实际计算中,无黏外流解模块需根据计算任务要求完成所需无黏流动状态的计算,并形成后续计算所需的外流解数据库。边界层加热和结构传热的计算可根据飞行器实际飞行时间进行耦合求解。图 3给出了计算技术总体流程示意图。
|
图 3 求解流程示意图 Fig.3 Flow chart of the coupled method |
下面采用三类典型的高超声速气动加热与结构传热算例来对所发展的耦合计算方法的效率、功能及精度进行具体分析。
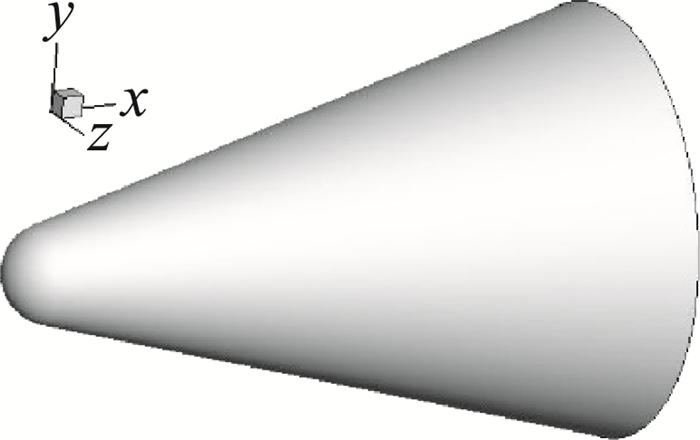
5.1 典型外形气动加热验证 5.1.1 钝头体瞬态气动加热本算例计算模型(图 4)选取NASA报告[32]中的三维钝锥模型,模型长为0.352 m,头部半径0.02794 m,锥角30°。无黏外流求解所用的计算网格为块结构网格,网格总单元数约32万,物面网格单元约1.1万。来流条件设定为:马赫数Ma∞=10.6,迎角α=20°,压强P∞=132.1 Pa,温度T∞=47.3 K;设定钝头体壁温Tw=294.44 K。
|
图 4 计算模型 Fig.4 Calculation model |
该算例在普通微机(3.3 GHz/4 GB,下同)上约在8 s CPU机时(不包含无黏外流解计算时间,下同)内即可完成瞬态气动加热的计算并输出飞行器表面热流分布。
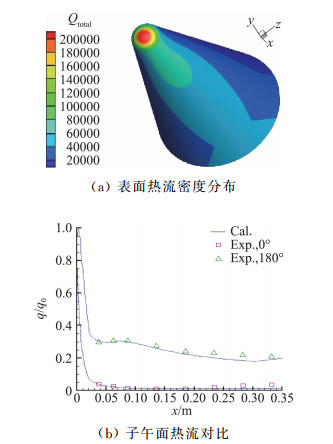
图 5为该算例物面热流密度计算结果。图 5(a)为模型表面总热流密度分布云图。可见在有迎角情况下,计算所得的沿子午面热流密度分布具有很好的对称性,而且热流密度等值线图分布均匀,没有出现明显的锯齿、跳跃等现象。图 5(b)为采用驻点热流值进行归一化处理后的子午面(截面方位角0°与180°)上热流密度分布与试验值[32]的比较,可以看到计算结果与试验值相符。由于飞行器大面积气动热数据的试验值难以获得,因此在热流具体数值的对比方面,取驻点作为对比验证点。表 2给出了当前流动状态下驻点热流密度的计算结果与参考试验值对比,相对误差小于10%,基本满足气动热工程设计的误差要求。
|
图 5 瞬态气动加热计算结果 Fig.5 Transient calculation results of aerodynamic heating |
| 表 2 驻点热流值对比 Table 2 Comparison of the stagnation heat flux |
|
|
计算外形采用典型高速飞行器RAM-CII球锥体试验模型,几何参数为:头部曲率半径0.152 m,半顶角9°,模型长度1.3 m。无黏外流场解的计算网格为块结构网格,总单元数约40万,物面单元约1.5万。设定的巡航状态为:飞行高度H=60 km,迎角α=0°,Ma∞=6.0,初始壁温Tw=247 K,飞行时间t=1000 s。长时加热中考虑结构传热,飞行器热防护结构材料为金属Ti,厚度2 mm,表面发射率为0.8。结构传热计算中,时间步长取为0.05 s(即总时间推进步数为2万步),采用热薄壁传热模型。该算例在普通微机上计算耗时约1020 s(17 min) CPU机时。
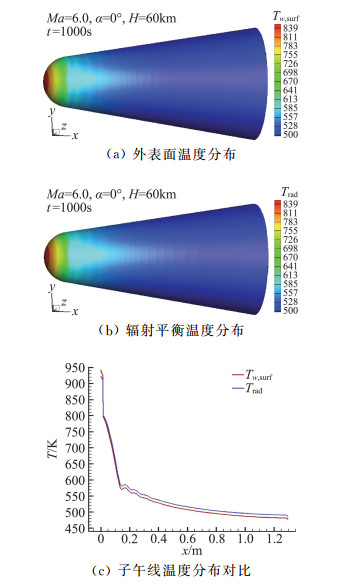
图 6(a)、图 6(b)分别为第1000 s时飞行器外表面温度及辐射平衡温度分布图,图 6(c)为子午面温度分布曲线对比,计算所得的第1000 s时驻点温度为945 K。图中Tw, surf表示物面温度,Trad表示采用同一无黏外流解直接计算所得的辐射平衡温度。依据Stefan-Boltzmann定律[33],计算辐射平衡温度时,飞行器表面和来流之间的对流传热Qw, c与辐射传热Qw, r之间的关系有
|
图 6 巡航状态长时加热第1000 s计算结果 Fig.6 Calculation results in cruising state(t=1000 s) |
通过图 6(c)中的对比可以看出,在子午线温度分布上,计算结果与辐射平衡温度吻合较好,当时间足够长时,表面温度计算结果愈趋近于辐射平衡温度,与理论分析一致。
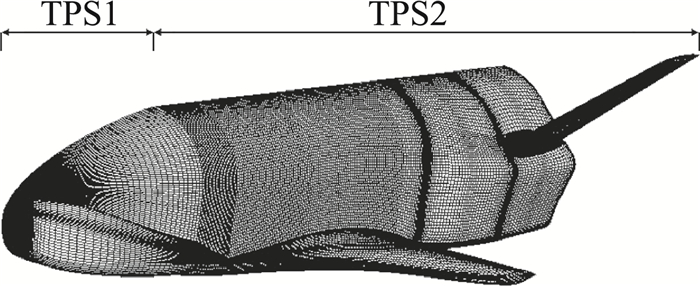
5.2 复杂飞行器巡航状态长时传热计算模型为如图 7所示的类X-37B外形,图中同时给出了计算所用的表面网格。计算状态为巡航状态长时传热:Ma∞=5,迎角α=3°,飞行高度H=40 km,飞行时间t=1000 s。用于无黏外流求解的块结构网格总单元数约512万,物面网格单元约25.1万。在热防护结构方面,该算例进行了更接近于工程设计的复杂方案,即飞行器头部区域设定为热防护区1,以TPS1表示,全机其他部位设为热防护区2,以TPS2表示(见图 7),不同的热防护区域使用表 3给出的不同的热防护方案,其中热防护结构材料的最外层(飞行器表面)和最内层温度初值设为飞行高度上的大气环境温度245 K。根据该算例的飞行条件,不考虑高温非平衡效应影响特性。该算例耗时约1680 s (28 min) CPU机时。
|
图 7 计算模型与TPS方案 Fig.7 Aircraft configuration and TPS definition |
| 表 3 热防护系统参数设置 Table 3 Thermal protection system parameters |
|
|
图 8给出了计算结果,其中图 8(a)和图 8(b)分别为第1000 s时飞行器防热层外表面(Tw, surf)和内表面(Tw, in)温度分布,飞行器在计算初始时刻(第0 s)和计算结束时(第1000 s)的防护层外表面热流密度分布如图 8(c)、图 8(d)所示。由计算结果可见,巡航1000 s时,类X-37B热防护层内表面温度在不同的热防护区域出现明显差异(图 8(b)),而热防护层整个外表面温度分布均匀。这是由于TPS1区使用的是热薄壁与隔热层的组合防热结构,并且隔热层采用热沉性好的二氧化硅(SiO2)材料,故在该热防护区域内表面温度出现显著降低,大部分区域温度在410 K左右,说明防热层隔热效果良好。而TPS2区仅采用了热薄壁结构,防热材料为厚度0.002 m的金属Ti,其热传导性很好,故防护层内外表面温度很快达到平衡,与外表面温度差别很小,且防护区域热流密度很小,该区域温度大部分在600 K以上。图 8(e)、8(f)分别为驻点内外层温度与热流密度随时间变化曲线,可以发现TPS1区域内外表面温度变化差别较大,计算结果显示驻点区域防热层外表面最高温度约为979 K,内表面最高温度约为521 K,造成此温度值差异的原因仍然是由于在这个区域使用了SiO2隔热层。算例计算与分析结果表明,发展的复杂飞行器气动加热与结构传热耦合计算方法可用于复杂外形及多种热防护方案问题的求解。

|
图 8 巡航状态长时传热计算结果 Fig.8 Aerodynamic heating variables distribution |
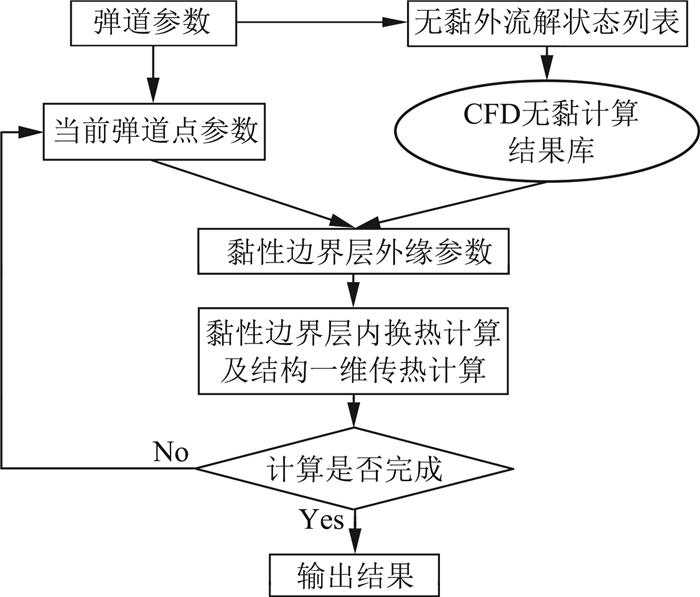
文中的弹道状态长时加热指的是飞行器按照给定的弹道状态(变高度、迎角、马赫数)飞行时的气动加热与结构传热特性,弹道计算状态更接近飞行器实际飞行包线状态。计算模型采用算例5.2的模型及计算网格。由于考虑的是弹道状态,因此使用了前文中的弹道状态动态插值方法。具体计算方法流程如图 9所示。
|
图 9 弹道状态长时加热计算流程 Fig.9 Flow chart of the present solver for trajectory state |
由于缺乏相关弹道参数数据,本文根据相关文献设定的弹道参数如表 4所示。弹道参数考虑了马赫数、飞行高速及迎角的变化,弹道飞行时间1000 s,在此期间飞行高度由60 km降至30 km,飞行马赫数由Ma=6降至Ma=4,迎角变化范围为±5°。该算例全机表面采用同一种组合热防护方案模型,具体参数与算例5.2中TPS1区相同。该算例耗时约1860 s(31 min) CPU机时。
| 表 4 弹道参数 Table 4 Trajectory parameters |
|
|
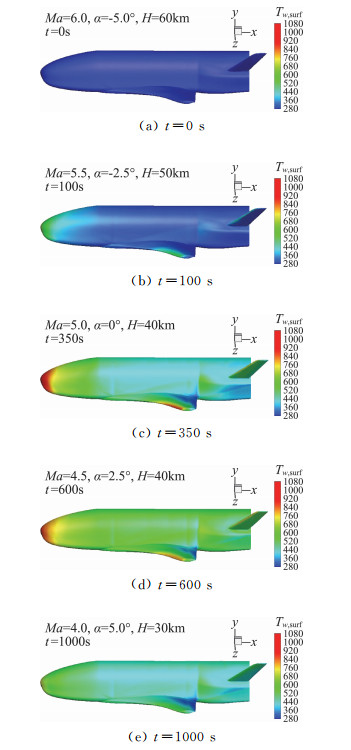
图 10给出了该算例计算结果。从图 10中可以清晰地看到飞行器表面沿弹道飞行时逐渐加热到平衡状态的过程,并且随迎角从-5°至5°变化过程中, 飞行器头部与机翼前缘处的高温区往下表面移动,第1000 s时,最高温出现在飞行器头部下表面,约为1050 K,这与高超声速飞行器防热结构材料特性理论分析相符。由于没有在公开发表文献中找到与此类似的算例进行对比,因此这里仅给出本文算例计算结果的分析。该算例表明所发展的计算方法可对复杂高超声速飞行器在弹道飞行状态下的气动加热与结构传热耦合进行快速高效计算与分析,可为高速飞行器的热防护设计与初期选型提供技术参考。
|
图 10 弹道状态不同时刻表面温度分布 Fig.10 Surface temperature distribution at different flight time |
针对复杂外形飞行器在复杂飞行条件下的气动加热与结构传热耦合问题,发展了一种基于耦合边界层外无黏流场解与气动热工程方法的高超声速全机外形气动加热与结构传热快速计算方法。对典型外形及典型状态进行了数值计算与分析,得到了与理论分析及文献相符的计算结果。结论如下:
1) 以边界层理论为基础,综合数值计算方法与工程算法各自的优势,将高超声速飞行器气动热的计算简化为飞行器无黏外流欧拉数值解和边界层内热流求解,并考虑了热化学非平衡效应。同时在计算方法中嵌入不同防热模型(热薄壁、热厚壁)的结构传热计算方法,可用于快速数值计算分析热防护系统中防热材料的温度场时变特性。
2) 所发展的计算方法避开了全流场黏性数值模拟所需的巨大计算量,同时拓展了气动热工程估算方法的应用范围,计算精度可满足工程设计初期方案论证要求,另外嵌入弹道状态动态插值方法,可方便地应用于高超声速复杂全机外形在复杂弹道飞行条件下的气动加热与结构传热多场耦合问题的快速计算分析。
3) 所发展的方法具有较好的可移植性,在后续研究中将考虑不同防热材料及材料烧蚀效应对高超声速飞行器气动加热特性的影响。
| [1] |
王江峰, 伍贻兆. 高超声速复杂气动问题数值方法研究进展[J]. 航空学报, 2015, 36(1): 159-175. WANG J F, WU Y Z. Progress in numerical simulation techniques of hypersonic aerodynamic problems[J]. Acta Aeronautics et Astronautics Sinica, 2015, 36(1): 159-175. (in Chinese) |
| [2] |
程克明, 吕英伟. 飞行器持续气动加热的耦合性分析[J]. 南京航空航天大学学报, 2000, 32(2): 150-155. CHENG K M, LYU Y W. An analysis of coupling feature in continuing gasdynamic heating over flight vehicles[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2000, 32(2): 150-155. (in Chinese) |
| [3] |
卞荫贵, 徐立功. 气动热力学[M]. 合肥: 中国科技大学出版社, 1997: 15-20.
|
| [4] |
SINHA K K, REDDY D S. Effect of chemical reaction rates on aeroheating predictions of reentry flows[J]. Journal of Thermophysics and Heat Transfer, 2011, 25(1): 21-33. |
| [5] |
HAMILTON H H, WEILMUENSTER K J, DEJARNETTE F R. Approximate method for computing convective heating on hypersonic vehicles using unstructured grids[J]. Journal of Spacecraft and Rockets, 2014, 1288: 1305. |
| [6] |
ZOBY E V, MOSS J N, SUTTON K. Approximate convective-heating equations for hypersonic flows[J]. Journal of Spacecraft and Rockets, 1981, 18(1): 64-70. DOI:10.2514/3.57788 |
| [7] |
田旭昂, 王成鹏, 程克明. Ma5斜激波串动态特性实验研究[J]. 推进技术, 2014, 35(8): 1030-1039. TIAN X A, WANG C P, CHENG K M. Experimental investigation of dynamic characteristics of oblique shock train in Mach 5 flow[J]. Journal of Propulsion Technology, 2014, 35(8): 1030-1039. (in Chinese) |
| [8] |
董维中, 高铁锁, 丁明松. 高超声速飞行器表面温度分布与气动热耦合数值研究[J]. 航空学报, 2015, 36(1): 311-324. DONG W Z, GAO T S, DING M S. Numerical study of coupled surface temperature distribution and aerodynamic heat for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 311-324. (in Chinese) |
| [9] |
杨恺, 原志超, 朱强华, 等. 高超声速热化学非平衡钝体绕流数值模拟[J]. 推进技术, 2014, 35(12): 1585-1591. YANG K, YUAN Z C, ZHU Q H, et al. Numerical simulation of hypersonic thermochemical nonequilibrium blunt body flows[J]. Journal of Propulsion Technology, 2014, 35(12): 1585-1591. (in Chinese) |
| [10] |
夏刚, 刘新建, 程文科, 等. 钝头体超声速气动加热与结构传热耦合的数值计算[J]. 国防科技大学学报, 2003, 25(1): 35-39. XIA G, LIU X J, CHENG W K, et al. Numerical simulation of coupled aeroheating and solid heat penetration for a hypersonic blunt body[J]. Journal of National University of Defense Technology, 2003, 25(1): 35-39. DOI:10.3969/j.issn.1001-2486.2003.01.008 (in Chinese) |
| [11] |
耿湘人, 张涵信, 沈清, 等. 高超飞行器流场和固体结构温度场一体化计算新方法的初步研究[J]. 空气动力学学报, 2002, 20(4): 422-427. GENG X R, ZHANG H X, SHEN Q, et al. Study on an integrat-ed algorithm for the flowfields of high speed vehicles and the heat transfer in solid structures[J]. Acta Aerodynamica Sinica, 2002, 20(4): 422-427. DOI:10.3969/j.issn.0258-1825.2002.04.008 (in Chinese) |
| [12] |
张胜涛, 陈方, 刘洪. 高超声速进气道前缘流场-热-结构耦合分析[J]. 空气动力学学报, 2017, 35(3): 436-443. ZHANG S T, CHEN F, LIU H. Fluid-thermal-structural coupling analysis on leading edge of hypersonic inlets[J]. Acta Aerodynamica Sinica, 2017, 35(3): 436-443. DOI:10.7638/kqdlxxb-2017.0036 (in Chinese) |
| [13] |
ZHAO J S, GU L X, MA H Z. A rapid approach to convective aeroheating prediction of hypersonic vehicles[J]. Science China Technological Sciences, 2013, 56(8): 2010-2024. DOI:10.1007/s11431-013-5258-6 |
| [14] |
李会萍.高超声速飞行器气动加热特性及其计算方法研究[D].上海: 上海交通大学, 2010. LI H P. The calculation and analysis of aerodynamic heating distributions for the hypersonic aircrafts[D]. Shanghai: Shanghai Jiao Tong University, 2010. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10248-2010204232.htm |
| [15] |
HAMILTON H H, WEILMUENSTER K J, DEJARNETTE F R. Approximate method for computing laminar and turbulent convective heating on hypersonic vehicles using unstructured grids[C]//41st Annual AIAA Thermophysics Conference, 2009. AIAA 2009-4310.
|
| [16] |
ZOBY E V, SIMMONDS A L. Engineering flowfield method with angle-of-attack applications[J]. Journal of Spacecraft and Rockets, 1985, 22(4): 398-404. DOI:10.2514/3.25764 |
| [17] |
乐嘉陵, 詹妮迈德芙, 曼彻娜娅. 高超声速飞行器表面气动热和黏性摩擦力计算[J]. 实验流体力学, 2002, 16(1): 8-20. LE J L, GANIMEDOV V L, MUCHNAJA M I, et al. The calculations of aerodynamic heating and viscous friction forces on the surface of hypersonic flight vehicle[J]. Journal of Experiments in Fluid Mechanics, 2002, 16(1): 8-20. DOI:10.3969/j.issn.1672-9897.2002.01.002 (in Chinese) |
| [18] |
李建林, 唐乾刚, 霍霖, 等. 复杂外形高超声速飞行器气动热快速工程估算[J]. 国防科技大学学报, 2012, 34(6): 89-93. LIJ L, TANG Q G, HUO L, et al. The rapid engineering aero-heating calculation method for complex shaped hypersonic vehicles[J]. Journal of National University of Defense Technology, 2012, 34(6): 89-93. DOI:10.3969/j.issn.1001-2486.2012.06.015 (in Chinese) |
| [19] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersonic boundary layer transition: what we know[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. DOI:10.7638/kqdlxxb-2017.0030 (in Chinese) |
| [20] |
张志成, 主编. 高超声速气动热和热防护[M]. 北京: 国防工业出版社, 2003: 46-136.
|
| [21] |
卞荫贵, 钟家康. 高温边界层传热[M]. 科学出版社, 1986.
|
| [22] |
航天工业部.战术导弹气动加热工程计算方法[S]. QJ1734-89, 1989. |
| [23] |
施昆, 王江峰, 李佳伟.带烧蚀效应的高超声速气动加热计算技术[C]//第二届中国航空科学技术大会论文集, 2015. SHI K, WANG J F, LI J W. Numerical method of aerodynamic heating with heating with ablation effects for hypersonic vehicles[C]//2th China Aviation Science and Technology Conference, 2015. |
| [24] |
唐国庆.高超声速多体分离动态气动加热计算技术[D].南京: 南京航空航天大学, 2013. TANG G Q. Calculating method of aerodynamic heating for hypersonic multi-body separation process[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese) |
| [25] |
吴洁, 阎超. 气动热与热响应的耦合研究[J]. 导弹与航天运载技术, 2009(4): 35-39. WU J, YAN C. Research on the coupling of aero-dynamic heating and thermal response[J]. Journal of Missiles and Space Vehicles, 2009(4): 35-39. DOI:10.3969/j.issn.1004-7182.2009.04.009 (in Chinese) |
| [26] |
季卫栋, 王江峰, 唐国庆. 高超声速多体分离过程气动加热计算技术[J]. 空气动力学学报, 2014, 32(6): 761-766. JI W D, WANG J F, TANG G Q. Calculating method of aerodynamic heating for hypersonic multi-body separation process[J]. Acta Aerodynamica Sinica, 2014, 32(6): 761-766. DOI:10.7638/kqdlxxb-2014.0080 (in Chinese) |
| [27] |
BOVA S W, HOWARD M A. Coupling strategies for high-speed aeroheating problems[R]. Sandia National Laboratories, 2011.
|
| [28] |
王杰.高超声速飞行器气动加热计算技术[D].南京: 南京航空航天大学, 2012. WANG J. Calculating method of aerodynamic heating for hypersonic aircrafts[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese) |
| [29] |
FAY J A. Theory of stagnation point heat transfer in dissociated air[J]. Journal of the Aerospace Sciences, 1958, 25(2): 73-85. DOI:10.2514/8.7517 |
| [30] |
欧阳水吾, 谢中强. 高温非平衡空气扰流[M]. 北京: 国防工业出版社, 2003.
|
| [31] |
DUNN M G. Theoretical and experimental studies of reentry plasmas[R]. NASA CR-2232, 1973.
|
| [32] |
JOSEPB W C. Effect of angle of attack and blunt ness on laminar heating-rate distributions of a 15° cone at mach number of 10.6[R]. NASA TN D-5450, 1969.
|
| [33] |
周金伟, 李吉成, 石志广, 等. 高超声速飞行器红外可探测性能研究[J]. 光学学报, 2015, 35(5): 1-8. ZHOU J W, LI J C, SHI Z G, et al. Research of infrared detectability of hypersonic vehicle[J]. Journal of Acta Optica Sinica, 2015, 35(5): 1-8. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


