2. 中国空气动力研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
热传导逆问题是相对于热传导正问题而言的。一般的正问题是给定其物理模型及其外形、物性参数等模型参数,分析模型对边界或内部扰动的响应;而热传导逆问题,是利用测得的系统响应(即温度),来辨识边界、内部扰动或模型的结构参数(如外形、物性参数等)。辨识表面热流是在已知传热模型结构参数的情况下,由温度测量结果辨识外表面热流,是经典的热传导逆问题, 它可以为航空航天飞行器表面热环境研究提供技术支撑[1]。美国20世纪60年代进行Reentry-F飞行试验项目[2-3]利用近壁热电偶测温来计算表面热流并由此判断转捩。X15/X17[4-5]则在金属壳体内安装了热电偶测量温度来计算表面热流。“FIRE”[6-8]飞行器采用了多层烧蚀防热结构,并在其中3层金属薄壳中埋入多个热电偶来测量温度计算热流。而国内研究者也开展一些研究并应用于地面试验,钱炜祺[9]等人开展了表面热流辨识的原理性实验,张石玉[10]在高超声速气动热风洞试验中利用试验件内部温度辨识了表面热流,张聪[11]建立利用温度计算超声速燃烧室的内壁面热流方法并应用于地面试验台。
“MF-1”飞行试验是中国空气动力研究与发展中心首次开展的航天飞行试验,其目的是进行技术验证并开展相关的空气动力学研究。飞行试验成功获取了飞行器表面压力和测点温度数据。本文计划利用这些测点温度计算表面热流。由温度数据计算表面热流关键在于建立与传感器相匹配的辨识模型,考虑传感器对结构传热的影响。据此先后建立了一维、三维辨识模型,并利用气动热环境数值计算所得的恢复焓考虑了传感器表面温度分布对壁面传热状态的影响,获得了较为精确的表面热流数据。辨识结果可以为确定边界层流态变化(再层流化、转捩)提供依据,并为更详尽的气动热环境数据对比提供数据支撑。
1 测温结构MF-1是典型的头锥、柱外型,具体结构见文献[12-13]。根据试验的目标以及气动力热、边界层流态变化(再层流化、转捩)计算结果,试验飞行器温度测点总体布置方案如下:在测量锥舱和测量直舱沿流向布置了4条的测温带,分别位于0°~180°的4个子午线上,一共58个测点,主要集中在锥段以得到边界层流态变化试验数据。考虑到结构强度以及重心位置,各舱段的壁厚不同,其中锥舱前段不锈钢壁厚为22 mm,测量锥舱后段不锈钢壁厚为12 mm,测量直段的厚度为4.5 mm。由于壳体的热传导系数较低,直接用内壁温度来辨识飞行器外壁面热流的精度较低。因此需要设计灵敏度较高即厚度较薄测温部件,提高辨识精度。较薄测温部件与旁边较厚的壳体结构之间必然存在相互传热,使得测温部件传热相对复杂。而基于三维导热模型进行热流辨识工作量大,也会引入边界误差。因此在设计测温部件结构时,主要考虑减小横向导热效应,使测温部件的导热接近一维导热,期望利用一维热流辨识方法获得较好的辨识效果。
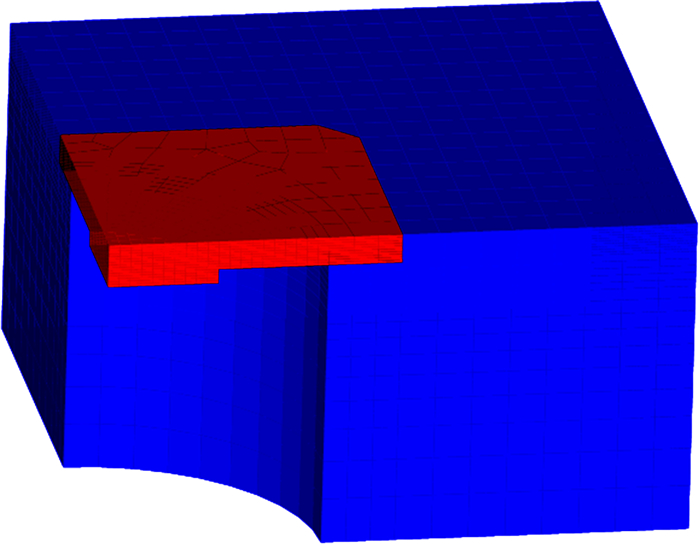
为减少横向导热效应[12],结合结构热载荷设计与工艺的要求,将测温部件结构设计为整体厚2 mm,边长40 mm的正方形平板,平板中间凸起直径15 mm相对高1 mm的圆台,而温度测点在圆台底面中心位置。对应的在飞行器壳体外表面铣出与正方形平板匹配、深2 mm的方形槽,方形槽中心挖出直径为30 mm的圆孔穿透金属结构层。装配时将测温薄板扣入方形槽,薄板四周与方形槽利用激光焊接成一体,热电偶导线由方形槽圆孔中穿过导入飞行器内部。结构有限元模型(1/4模型)如图 1所示,图中蓝色部分为飞行器壳体,红色部分为测温薄壁结构,上表面为飞行器外表面,即加热面。
|
图 1 测量部件计算模型 Fig.1 Model of measurement units |
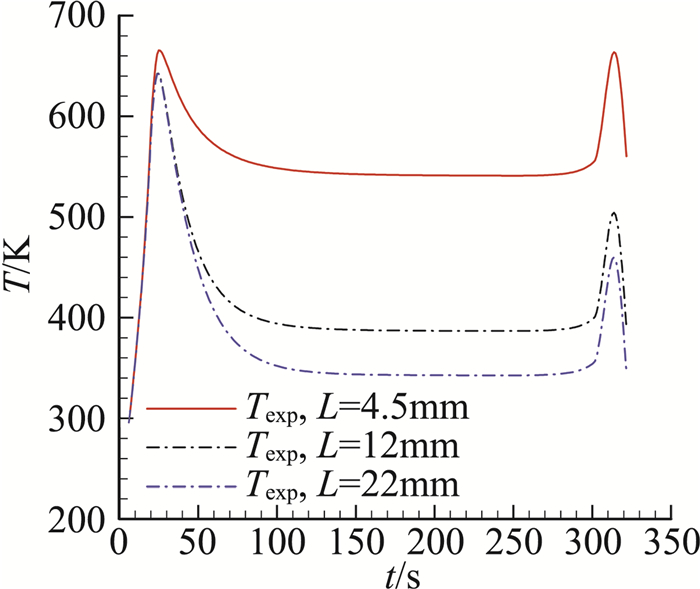
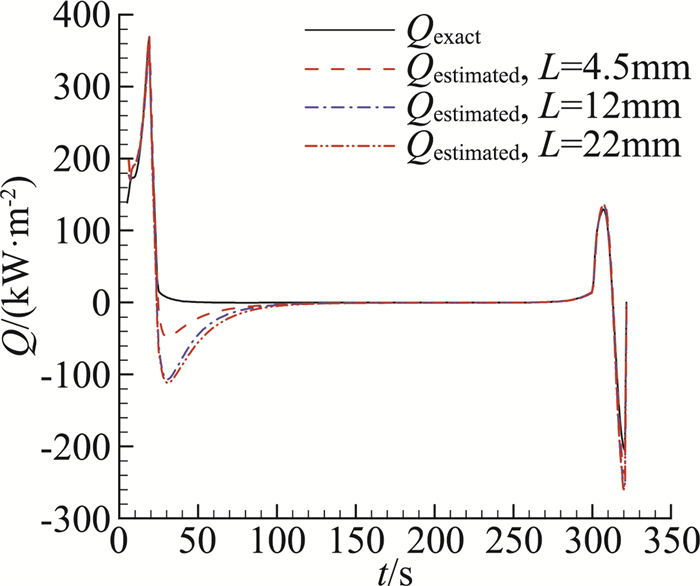
下面利用有限元模型分析测温结构在沿弹道热环境下的热响应。计算时假设加热面的热流均匀分布,加载的热流为根据设计弹道利用数值方法计算得到的典型热流,如图 2中的“Qexact”所示。图 3为计算所得温度历程。以此计算值采用一维表面热流辨识方法辨识表面热流。文献[14-15]中有一维表面热流辨识算法详细的介绍,这里不再详述。图 2中“Qestimated”为仿真辨识结果。飞行器壳体厚4.5 mm时辨识所得热流峰值与真值相比误差在1%左右,而壳体厚12 mm和22 mm时辨识所得热流峰值误差都在5%左右。由此可以看出:一维辨识结果峰值与真值偏差较小,可以为边界层流态变化分析提供依据。但由于目前的计算模型没有考虑飞行器壳体和测温部件之间传热,辨识结果在20 s至100 s出现了明显的负热流,这与理论预期明显不符。因此为了能够获得更精细的辨识结果,需要建立多维辨识模型,考虑测温结构和飞行器壳体之间的传热。
|
图 2 热流辨识结果 Fig.2 Estimation of heat flux |
|
图 3 有限元模型温度计算结果 Fig.3 Calculated temperature of finite element model |
三维热传导控制方程:
| $ \rho {C_p}\frac{{\partial T}}{{\partial t}} = k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) $ | (1) |
受热表面:
接触热阻边界条件:
| $ - {\left. {k\frac{{\partial T}}{{\partial n}}} \right|_{\mathit{\Gamma }2}} = \frac{{{T_{\mathit{\Gamma }2}} - {T_{\mathit{\Gamma }3}}}}{R} = {\left. {k\frac{{\partial T}}{{\partial n}}} \right|_{\mathit{\Gamma }3}}; $ |
其余边界设为绝热,即:
初始条件:t=0时T=T0。
设观测方程为:
| $ \begin{array}{l} {T_m}\left( {x_m^s,y_m^s,z_m^s,t} \right) = T\left( {x_m^s,y_m^s,z_m^s,t} \right) + v\left( t \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {0,{t_f}} \right];s = 1,S \end{array} $ | (2) |
其中下标“m”表示测量点,上标s表示测点序号,S为测点总数,tf为末时刻值。
给出待辨识表面热流初始值后, 采用有限元方法求解温度场,可得出各测点的温度变化历程。通过对比温度计算结果和实测值的差异就可以对表面热流进行优化辨识。即求解表面热流以使得下式中的代价函数J极小:
| $ J = \sum\limits_s {\int_0^{{t_f}} {{{\left[ {T\left( {x_m^s,y_m^s,z_m^s,t} \right) - {T_m}\left( {x_m^s,y_m^s,z_m^s,t} \right)} \right]}^2}} } {\rm{d}}t $ | (3) |
采用拉格朗日乘数法后,代价函数可取为:
| $ \begin{array}{l} J = \sum\limits_s {\int_0^{{t_f}} {\left[ {T\left( {x_m^s,y_m^s,z_m^s,t} \right) - } \right.} } \\ \;\;\;\;\;\;{\left. {{T_m}\left( {x_m^s,y_m^s,z_m^s,t} \right)} \right]^2}{\rm{d}}t + \\ \;\;\;\int\limits_0^{{t_f}} {\int\limits_\mathit{\Omega } {\left[ {k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) - \rho {C_p}\frac{{\partial T}}{{\partial t}}} \right]\lambda \left( {x,y,z,t} \right){\rm{d}}\mathit{\Omega }{\rm{d}}t} } \end{array} $ | (4) |
式中λ为拉格朗日乘子,通过变换可以得到当λ满足如下伴随方程:
| $ k\left( {\frac{{{\partial ^2}\lambda }}{{\partial {x^2}}} + \frac{{{\partial ^2}\lambda }}{{\partial {y^2}}} + \frac{{{\partial ^2}\lambda }}{{\partial {z^2}}}} \right) + \rho {C_p}\frac{{\partial \lambda }}{{\partial t}} = 0 $ | (5) |
测点处:
| $ \begin{array}{l} k\frac{{\partial \lambda }}{{\partial n}} = 2\left( {T - {T_m}} \right)\delta \left( {x - x_m^s} \right)\delta \left( {y - y_m^s} \right)\delta \left( {z - z_m^s} \right),\\ s = 1,S; \end{array} $ |
接触热阻边界条件:
| $ - {\left. {k\frac{{\partial \lambda }}{{\partial n}}} \right|_{\mathit{\Gamma }2}} = \frac{{{\lambda _{\mathit{\Gamma }2}} - {\lambda _{\mathit{\Gamma }3}}}}{R} = {\left. {k\frac{{\partial \lambda }}{{\partial n}}} \right|_{\mathit{\Gamma }3}}; $ |
其余边界:
时域边界条件:t =tf, λ(tf) = 0。
可导出目标函数对Q的导数为:
| $ \frac{{\partial J}}{{\partial Q}} = {\left. {\lambda \left( {x,y,z,t} \right)} \right|_{\mathit{\Gamma }1}} $ | (6) |
由伴随方程求得梯度后可以利用牛顿类梯度法进行迭代计算,在这里我们采用最为常用的共轭梯度法。
共轭梯度法的计算公式如下:
| $ \hat Q_i^{n + 1} = \hat Q_i^n - {\beta ^n}P_i^n $ | (7) |
式中:
| $ P_i^n = {{J'}^n} + {\gamma ^n}P_i^{n - 1};{{J'}^n} = {\left( {\partial J/\partial {Q_i}} \right)^n}; $ |
| $ {\gamma ^n} = \frac{{\int\limits_{t = 0}^{{t_f}} {\int_{\mathit{\Gamma }1} {{{\left( {{{J'}^n}} \right)}^2}{\rm{d}}\mathit{\Gamma }1{\rm{d}}t} } }}{{\int\limits_{t = 0}^{{t_f}} {\int_{\mathit{\Gamma }1} {{{\left( {{{J'}^{n - 1}}} \right)}^2}{\rm{d}}\mathit{\Gamma }1{\rm{d}}t} } }}; $ |
| $ \begin{array}{l} {\beta ^n} = \\ \frac{{\sum\limits_s {\int_0^{{t_f}} {\left[ {T\left( {x_m^s,y_m^s,z_m^s,t} \right) - {T_m}\left( {x_m^s,y_m^s,z_m^s,t} \right)} \right]{U^s}\left( t \right){\rm{d}}t} } }}{{\sum\limits_s {\int_0^{{t_f}} {{U^s}{{\left( t \right)}^2}{\rm{d}}t} } }} \end{array} $ |
其中U满足:
| $ k\left( {\frac{{{\partial ^2}U}}{{\partial {x^2}}} + \frac{{{\partial ^2}U}}{{\partial {y^2}}} + \frac{{{\partial ^2}U}}{{\partial {z^2}}}} \right) = \rho {C_p}\frac{{\partial U}}{{\partial t}} $ | (8) |
受热表面:
接触热阻边界条件:
| $ - {\left. {k\frac{{\partial U}}{{\partial n}}} \right|_{\mathit{\Gamma }2}} = \frac{{{U_{\mathit{\Gamma }2}} - {U_{\mathit{\Gamma }3}}}}{R} = {\left. {k\frac{{\partial U}}{{\partial n}}} \right|_{\mathit{\Gamma }3}}; $ |
初始条件:t=0时U=0。
3 飞行试验的热流辨识结果 3.1 基于一维模型的辨识结果首先利用一维辨识模型分析了飞行试验温度测量数据。图 4给出了头锥段三个测点的温升历程和辨识所得的测点温度,可以看到两者符合很好,这说明了优化算法的有效性。

|
图 4 飞行测量温度与辨识所得温度对比 Fig.4 Estimation and flight test data |
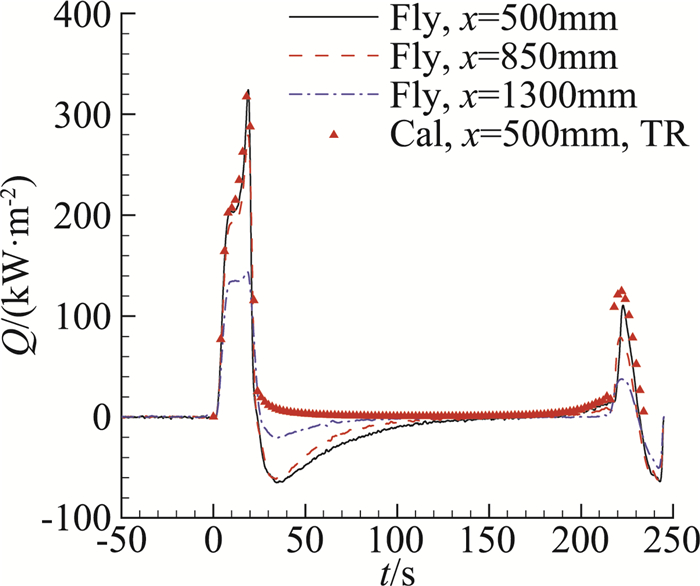
图 5给出了利用θ=0°子午线上几个测点辨识所得的热流,Fly为一维模型辨识结果,Cal为工程数值计算结果,后标TR表示边界层再层流化、转捩。由图 5可以看辨识结果与工程数值计算结果在大部分区域符合较好;但辨识结果在20 s~100 s出现了明显的负热流,而工程数值模拟结果为正热流。辨识结果如此反常是因为一维辨识模型没有考虑测温结构和飞行器壳体之间的横向传热。
|
图 5 一维模型辨识所得表面热流 |
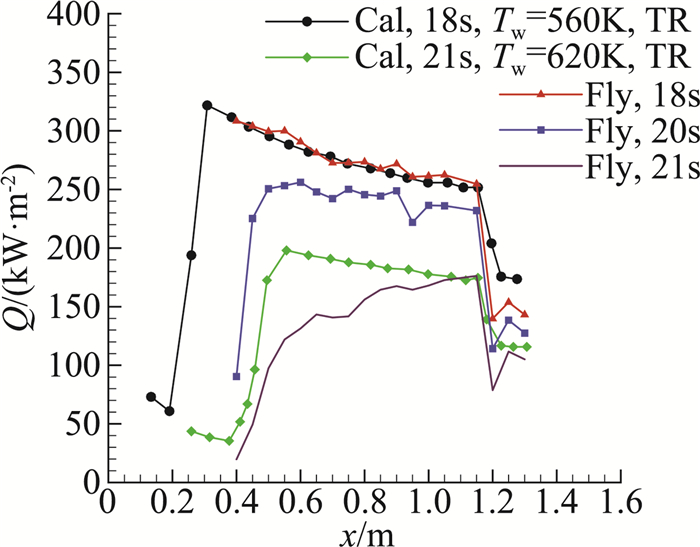
图 6、图 7为不同时刻θ=0°子午线上热流分布,Cal为数值模拟所得热流,其中后标CL、TL、TR表示数值模拟时气体流动状态,分别对应完全层流状态、完全湍流状态、层流-湍流之间转化的状态;Tw为数值模拟时所采用的壁温;Fly为一维模型辨识结果。辨识结果结合数值模拟结果可以判断实际飞行时的边界层流态变化发生的时间与位置。特别是在图 6中的20 s和图 7中220 s和222 s,辨识结果清晰地捕捉到了边界层流态变化发生的区域。
|
图 6 18 s~20 s热流空间分布对比 Fig.6 Comparison of heat flux space distribution from 18 s to 20 s |

|
图 7 218 s~222 s热流空间分布对比 Fig.7 Comparison of the heat flux space distribution from 218 s to 222 s |
为了能够获得更精细的辨识结果,需要建立能够考虑测温结构和飞行器壳体之间传热的多维辨识模型。如图 1所示飞行器壳体选取的区域过大会导致计算量过大,但壳体选取的区域过小又会影响计算精度。因此局部模型精度还需通过仿真验证。
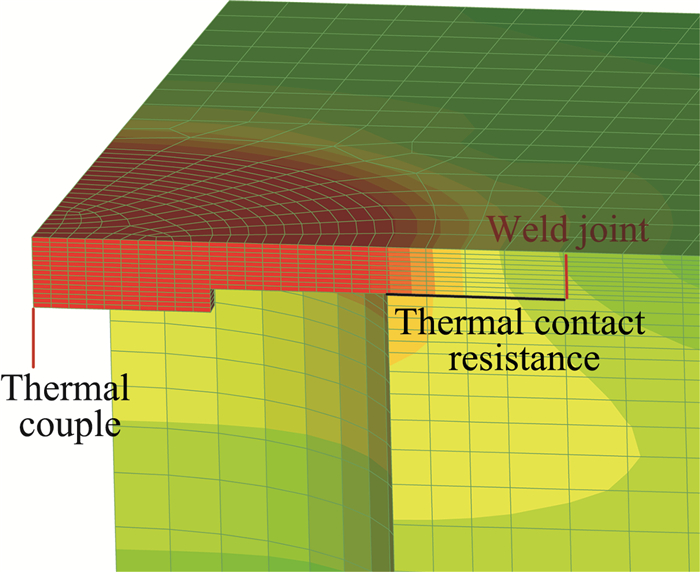
图 8为计算采用的有限元模型局部示意图。图中红线所示为薄壁测温结构与飞行器壳体的激光焊接面; 黑线所示为测温结构与壳体的无焊接接触面,接触面为内圆外方的环形面,存在接触热阻。当认为接触面完美接触即接触热阻为0时,三维模型可退化为轴对称模型, 即二维模型。图 9为轴对称模型,y轴为对称轴,测点位于x=0处。其中二维模选取的壳体影响区域较大。二维、三维模型辨识表面热流时均假设加热面热流均匀分布,其余各边界绝热。图 10给出了不同模型辨识所得飞行器直段测点表面热流。图中Qestimated(2D)标示的是二维模型辨识所得热流,Qestimated(3D,TCR=0)标示的是接触热阻为0时三维模型辨识所得热流。同时图 10还给出了二维加密网格情况下辨识的结果。通过对比可以看到三者符合较好,这验证了计算所使用的网格较为合适,网格带来的误差较小,而三维模型选取的传热影响区域也比较合适。
|
图 8 三维有限元模型 Fig.8 Three dimensional finite element model |

|
图 9 二维轴对称有限元模型 Fig.9 Two dimensional axisymmetric finite element model |

|
图 10 二维三维模型辨识所得表面热流 Fig.10 Estimated heat flux from 2D and 3D model |
图 8薄壁测温结构与飞行器壳体存在接触热阻,而接触热阻与接触面粗糙度、压力、温度和材料有关。文献[16]通过试验测量了不同压强下不锈钢接触面的换热系数(接触热阻系数的倒数)。根据文献的结果可以看到,接触热阻随温度和压强升高而降低,在界面压强为2.96 MPa时,换热系数降至8000 W/m2K左右。而薄壁测温结构与飞行器壳体接触面压强大小不确定,因此在辨识中为了覆盖接触热阻可能的取值范围,分别考虑了接触热阻系数R为0,0.0001,0.001,0.01 m2 K/W的情况,分析不同热阻对辨识的影响,其中R为0.01对应接触热阻的极大值。图 11给出了辨识结果的对比。比较几组辨识结果可以看到,随着接触热阻变大,热流峰值不断降低。三维的辨识结果没有再出现反常的负热流,与工程数值模拟比较接近,有效地改善了辨识结果。进一步在图 12、图 13给出了不同模型辨识所得热流峰值对比。

|
图 11 考虑接触热阻影响辨识所得的表面热流 Fig.11 Heat flux estimated with influence of thermal contact resistance |
|
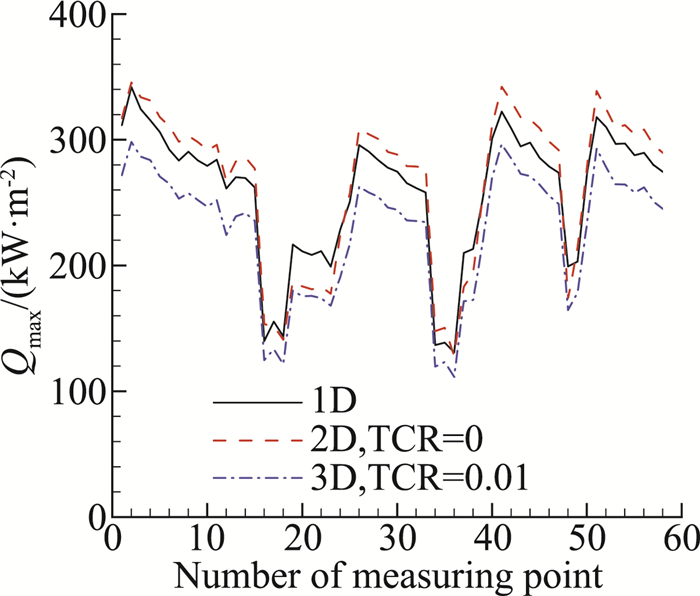
图 12 不同模型辨识所得热流峰值对比(上升段) Fig.12 Comparison of the peak of heat flux between different models (ascent stage) |
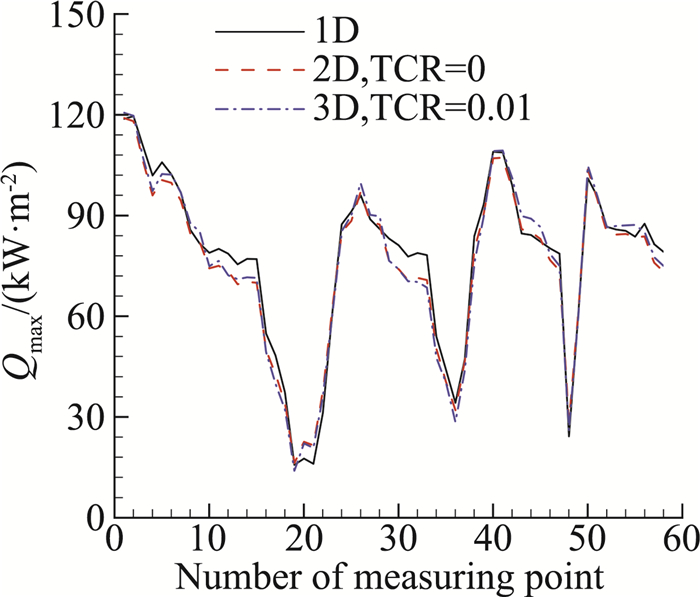
|
图 13 不同模型辨识所得热流峰值对比(下降段) Fig.13 Comparison of the peak of heat flux between different models (descent stage) |
通过对比分析可以看到:在上升段试验窗口期,二维模型辨识结果峰值较高而三维模型辨识结果峰值较低。这是由于测温结构中间较厚的圆形区域和飞行器壳体之间的环形槽温度较高,而二维模型的横向传热较强,环形槽温度不足以补偿壳体的低温,测点所在圆形区域会通过环形槽壳体传热,因此二维辨识结果峰值较高。三维模型中接触热阻阻碍了环形槽向飞行器壳体的传热,环形槽同时向测点所在圆形区域和飞行器壳体传入热量,此时三维模型辨识结果峰值较低。接触热阻为0和0.01 m2K/W分别对应的接触热阻影响较小和较大的情况,其辨识结果也对应了考虑接触热阻情况下的辨识上下界。
3.4 测点局部热流空间分布对辨识结果的影响上述辨识计算都假设了表面热流均匀分布,而表面热流与当地表面壁温有关,测温薄壁表面温度明显高于周围飞行器的外壳,壁温不同传热状态亦不同。本节利用局部的表面热流分布与表面温度分布的关系,分析局部热流空间分布对辨识结果的影响。
对于简单外形利用雷诺比拟关系可以将表面热流密度写为:
| $ q \cong S{t^*}{\rho ^*}{u_e}\left( {{h_{\rm{r}}} - {h_{\rm{w}}}} \right) $ |
其中hr为恢复焓,hw为壁面焓。hr可以根据弹道以及飞行器外形计算,计算精度也相对较高。这样结合壁面温度就可给出表面热流密度的空间分布。将事先算好的气体恢复焓代入传热方程,则式(1)边界条件可以改写为:
受热表面:
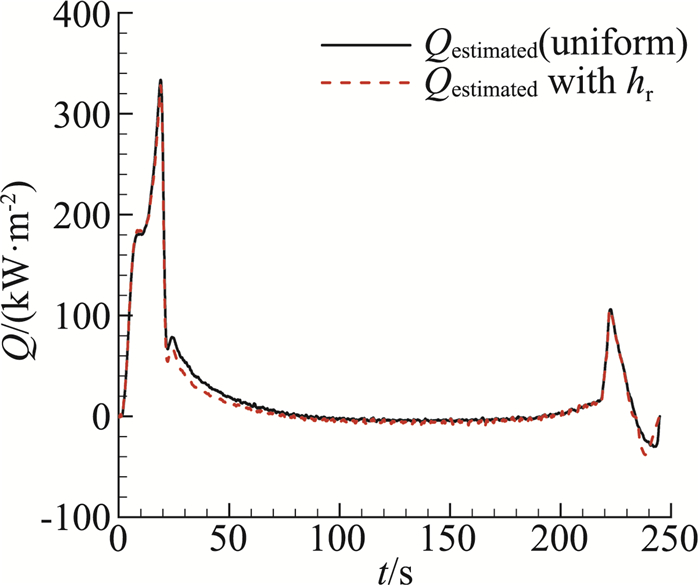
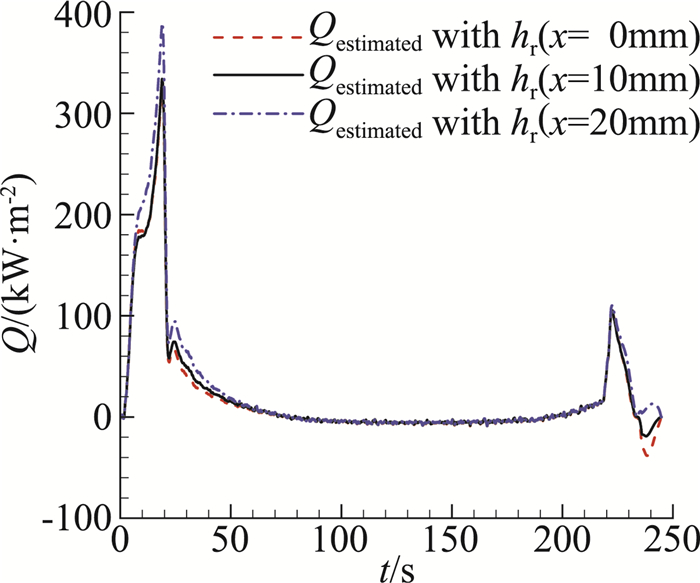
此时辨识表面热流密度变为辨识传热系数C,并合理假设在计算区域C均匀分布,由此辨识所得热流如图 14,图中Qestimated with hr为考虑壁温对热流密度影响时辨识所得的表面热流。通过对比可以看到, 3.3节不考虑壁温影响时辨识所得热流稍稍高于考虑壁温影响时辨识所得热流,但两者相差不大。图 15还给出了测温薄壁结构表面不同位置的热流密度,x=0 mm、10 mm、20 mm分别对应图 9中的位置。由图 9可以看到飞行器壳体表面热流密度(接近于20 mm处)的结果明显高于测温薄壁结构的表面热流(0 mm处)的结果。这说明测温部件感受到的热流与飞行壳体的热流略有不同。同时这也说明,在对比分析热流的测量结果和理论计算结果时,需要注意其对应的状态。
|
图 14 考虑空间分布辨识所得表面热流对比 Fig.14 Comparison of the heat flux estimation between different distributions |
|
图 15 同一测温结构不同位置表面热流 Fig.15 Heat flux with different positions |
本文根据MF-1飞行试验,利用表面热流辨识方法处理了飞行试验的温度测量数据,并将辨识所得的热流与工程数值模拟预测的结果相比较。得出以下结论:
1) 辨识结果与数值模拟结果比较接近,可以有效地判断边界层流态变化的发生。
2) 合理简化的二维、三维辨识模型可以有效模拟飞行器壳体与测温薄壁结构之间的横向传热从而提高辨识精度。
3) 由于缺乏相应的先验知识,飞行器壳体与测温薄壁之间的接触热阻不确定度较高。本文在辨识计算中分别考虑了接触热阻相对较小和较大的情况,给出了相应的辨识结果及影响规律。
4) 飞行器壳体与测温薄壁表面温度不一致会导致壳体与测温薄壁表面热流有明显差别。本文利用热环境数值计算的结果,在辨识模型中考虑了壁温对气动传热的影响,给出了相对应的表面热流分布。
综上所述,目前所采用温度测量和分析处理方法满足了此次飞行试验的要求,成功地获取了真实飞行环境下气动热数据,为边界层流态变化等高超声速关键气动问题研究提供了数据支撑。
致谢: 中国空气动力研究与发展中心欧朝助理研究员、何坤副研究员、吉洪亮副研究员、张毅峰副研究员对本文工作亦有贡献,在此表示感谢。
| [1] |
BECK J V, BLACKWELL B, Jr CLAIR C R S. Inverse heat conduction-ill-posed problems[M]. John Wiley&Sons, 1985.
|
| [2] |
ILIFE K W, SHAFER M F. A comparison of hypersonic vehicle flight and prediction results[R]. NASA TM-104313, 1995.
|
| [3] |
WRIGHT R L, ZOBY E V. Flight boundary layer transition measurements on a slender cone at Mach 20[R]. AIAA 77-719, 1977.
|
| [4] |
ROBERT D Q, FRANK V O. Heat transfer measurement obtained on the X-15 airplane including correlation with windtunnel result[R]. NASA TM-X-1705, 1969.
|
| [5] |
BALGEMAN E J, CASSELL G. X-17 Re-entry test vehicle R-2 final flight report[R]. NASA AD-127785, 1957.
|
| [6] |
SCALLION W I, LEWIS J H. Flight parameters and vehicle performance for project FIRE flight 1 launched April 14, 1964[R]. NASA TN-D-2996, 1965.
|
| [7] |
ANON. Project FIRE integrated post flight evaluation report flight No.Ⅱ[R]. NASA CR-66000, 1965.
|
| [8] |
CAUCHON D L. Project FIRE flight 1 radiative heating experiment[R]. NASA TM-X-1222, 1965.
|
| [9] |
钱炜祺, 吴世见, 卜海涛, 等. 气动热参数辨识原理性实验初步研究[J]. 实验流体力学, 2009, 23(2): 59-62. QIAN W Q, WU S J, BU H T, et al. Preliminary investigation of principle experiment for aerothermodynamic parameter estimation[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(2): 59-62. DOI:10.3969/j.issn.1672-9897.2009.02.013 (in Chinese) |
| [10] |
张石玉, 赵学军, 陈则霖. 采用内部测温估计表面热流在高超声速风洞试验中的应用[J]. 实验流体力学, 2015, 29(2): 61-67. ZHANG S Y, ZHAO X J, CHEN Z L. Application of surface-heat-flux estimation by measuring model interior temperature in hypersonic wind tunnel tests[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(2): 61-67. (in Chinese) |
| [11] |
张聪.高超声速燃烧室壁面热流辨识方法研究[D].哈尔滨: 哈尔滨工业大学, 2011. ZHANG C. Identification method investigation of supersonic combustor wall heat flux[D]. Harbin: Harbin Institute of Technology, 2011. (in Chinese) http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=1012003178.nh |
| [12] |
杨庆涛, 周宇, 袁先旭, 等. MF-1模型飞行试验表面压力与温度测量技术研究[J]. 空气动力学学报, 2017, 35(5): 732-741. YANG Q T, ZHOU Y, YUAN X X, et al. Surface pressure and temperature measurement technology in MF-1 modeling flight test[J]. Acta Aerodynamica Sinica, 2017, 35(5): 732-741. DOI:10.7638/kqdlxxb-2017.0167 (in Chinese) |
| [13] |
欧朝, 吉洪亮, 肖涵山, 等. MF-1模型飞行试验结构与热防护关键问题研究[J]. 空气动力学学报, 2017, 35(5): 742-749. OU C, JI H L, XIAO H S, et al. Key problems in structure and thermal protection for MF-1 model testing flight vehicle[J]. Acta Aerodynamica Sinica, 2017, 35(5): 742-749. DOI:10.7638/kqdlxxb-2017.0170 (in Chinese) |
| [14] |
ALIFANOV O M. Inverse heat transfer problems[M]. Berlin: Springer-Verlag, 1994.
|
| [15] |
钱炜祺, 周宇, 何开锋, 等. 非线性热传导逆问题的表面热流辨识方法[J]. 空气动力学学报, 2012, 30(2): 145-150. QIAN W Q, ZHOU Y, HE K F, et al. Estimation of surface heat flux for nonlinear inverse heat conduction problem[J]. Acta Aerodynamica Sinica, 2012, 30(2): 145-150. DOI:10.3969/j.issn.0258-1825.2012.02.002 (in Chinese) |
| [16] |
朱德才.固体界面接触换热系数的实验研究[D].大连: 大连理工大学, 2007. ZHU D C. Experiment research on solid interface thermal contact conductance coefficient[D]. Dalian: Dalian University of Technology, 2007. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10141-2007211209.htm |
 2019, Vol. 37
2019, Vol. 37


