高温热密封结构是各种航天运载火箭及空天飞行器的关键零部件之一[1],比如在美国的Apollo航天器[2]与大力神洲际导弹[3]就大量采用了此类结构。目前,国内外已有较多的研究关注了飞行器外部高超声速流场与结构温度场的耦合问题。当前最常用的两类方法为耦合方法[4-7]与同步方法[8-9]。耦合方法与同步计算方法的区别在于:耦合方法一般忽略特征时间较小一方随时间变化的细节,具有较高的计算效率;而同步计算方法考虑连续变化的过程,理论上比耦合方法更符合实际物理过程,对流场的非定常效应模拟更加精准。耦合方法的每一个时间步需要在边界处交换物理信息。因而当计算流场(结构温度场)的时候,需要“冻结”结构温度场(流场)。同步方法则通过构建统一的控制方程,避免了耦合过程中边界条件的反复迭代,实现了流场和结构温度场同步求解。以上研究只包含高超声速流场与结构温度场,未涉及空腔结构。实际上,高温热密封结构在外部高温气流的作用下会受热导致温度不均,进而引起密封结构内气体的流动。
目前数值计算空腔内气体热对流的方法主要分为两种:一种是求解基于Bossinesq假设[10-11]的不可压Navier-Stokes (N-S)方程,另一种是通过引入预处理矩阵[12-16]求解可压缩N-S方程。当冷热源温差低于30 K的时候,采用Bossinesq假设计算得到的结果与真实情况相符[11]。然而,在高温差情况下,采用求解不可压方程的方法将带来数值计算上的困难[12]。Paillere等人[13]采用预处理方法对一个温差比较小的二维封闭空间热对流问题进行模拟,结果表明,采用该方法得到的结果与求解不可压方程得到的结果基本一致,但是对于温差较大的情形,结果差异较为明显。Weiss和Simth[14]采用预处理方法对一个二维同心圆环热对流问题进行了模拟,结果表明采用该方法能够精确高效地得到流场特性。
综合已有文献来看,目前国内外对同时考虑高超声速气动环境、结构传热以及空腔内低速流动的瞬态同步数值模拟研究仍然较少。鉴于此,本文基于已发展的高超声速外流场/结构温度场同步数值模拟方法,进一步将其拓展至能够模拟包含空腔热对流的多区域耦合问题。通过在相邻场交界面引入虚拟单元实现不同计算区域之间的物理量交换。通过与文献对比,验证了方法在求解单独气动热/结构热传导问题中的有效性,同时也验证了引入预处理矩阵方法在空腔自然对流问题中的精度。分别对封闭和带开孔的两种高超声速运动圆环进行多区域同步数值模拟,最终对计算得到的空腔内流动、气体输运特性以及结构温度分布随时间变化历程进行了分析研究。
1 控制方程与离散方法 1.1 控制方程内部空腔流动从无到有的产生过程是内壁面温度连续变化导致的。随着内壁面温度升高,空腔内气体流动速度加快,输运特性发生变化,特征时间尺度也发生变化。同时为了能够精确模拟空腔内部流动导致的结构温度场分布变化,本文采用同步计算方法。流场(包含外流场与空腔内流场)与结构温度场控制方程可以写成直角坐标系下的统一形式:
| $ \frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{f}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{q}}}}{{\partial z}} = \frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{T}}}}{{\partial z}} + \mathit{\boldsymbol{Q}} $ | (1) |
式中,W为守恒变量。f、q为对流通量项。R、T为黏性通量项,Q为源项,这里特指空腔内热对流计算时出现的重力项。各量定义如下:
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho w}\\ {\rho E} \end{array}} \right];\;\;\;\mathit{\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho {u^2}}\\ {\rho uw}\\ {\left( {\rho E + p} \right)u} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{q}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u\tau v}\\ {\rho {\tau ^2}}\\ {\left( {\rho E + p} \right)w} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{xx}}}\\ {{\tau _{zx}}}\\ {u{\tau _{xx}} + \tau v{\tau _{zx}} + k\frac{{\partial T}}{{\partial x}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{xz}}}\\ {{\tau _{zz}}}\\ {u{\tau _{xz}} + w{\tau _{zz}} + k\frac{{\partial T}}{{\partial z}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - \left( {\rho - {\rho _0}} \right)g}\\ { - \left( {\rho - {\rho _0}} \right)gw} \end{array}} \right] $ | (2) |
其中,p为气体压强,ρ为气体密度,ρ0为参考气体密度,E为单位质量混合气体的总能,k为气体导热系数,T为温度,u、v、w为气体速度在直角坐标系下的速度分量,τ为应力张量,g为重力加速度。对于理想气体介质有:
| $ p = \rho RT $ | (3) |
| $ \rho E = \frac{p}{{\left( {\gamma - 1} \right)}} + \frac{1}{2}\rho \left( {{u^2} + {w^2}} \right) $ | (4) |
气体介质的黏性系数与热传导系数由温度决定:
| $ \begin{array}{l} \mu \left( T \right) = {\mu _0}{\left( {\frac{T}{{{T_0}}}} \right)^{\frac{3}{2}}}\left[ {\frac{{{T_0} + 110.4}}{{T + 110.4}}} \right]\\ k\left( T \right) = \frac{{\mu \left( T \right)\gamma R}}{{(\gamma - 1)Pr}} \end{array} $ | (5) |
其中μ0为海平面空气黏度值,Pr为普朗特数。
对于固体介质有:
| $ {\rho _{\rm{s}}}{E_{\rm{s}}} = {\rho _{\rm{s}}}{C_{\rm{s}}}{T_{\rm{s}}} $ | (6) |
其中,ρs为固体密度,Cs为固体比热容,ks为固体导热系数。在固体区域中,显然有u=w=0,因而方程组(2)中的前三个方程自然满足。
1.2 数值方法整个计算空间包含三个区域,分别为外部高超声速流动区域、结构热传导区域与空腔内气体热对流区域。
对于外部高超声速流动区域,对流通量采用AUSM+格式进行离散,可以保证计算的稳定性与精度。黏性通量采用中心格式离散。结构热传导方程本质与黏性扩散方程相同,因此也采用中心格式离散。对于空腔内部热对流区域,通过求解带预处理矩阵的可压缩N-S方程来模拟。时间离散采用双时间步长推进的方法。气体介质内迭代时间步长的确定方法为:
| $ \Delta {t_I} = \sigma \frac{{{\mathit{\Omega }_I}}}{{{{\left( {\mathit{\hat \Lambda }_c^I + \mathit{\hat \Lambda }_c^K} \right)}_I} + 4{{\left( {\mathit{\hat \Lambda }_v^I + \mathit{\hat \Lambda }_v^K} \right)}_I}}} $ | (7) |
其中,σ为CFL数。
| $ \mathit{\hat \Lambda }_c^I = \left( {\left| {{V^I}} \right| + c} \right)\Delta {S^I} $ | (8) |
VI代表网格单元格心处在I方向上的法向速度。ΔSI代表I方向上的面积。c是当地声速。
| $ \mathit{\hat \Lambda }_v^I = \max \left( {\frac{4}{{3{\rho _{\rm{f}}}}},\frac{\gamma }{{{\rho _{\rm{f}}}}}} \right)\left( {\frac{{{\mu _L}}}{{P{r_L}}} + \frac{{{\mu _T}}}{{P{r_T}}}} \right)\frac{{{{\left( {\Delta {S^I}} \right)}^2}}}{{{\mathit{\Omega }_I}}} $ | (9) |
其中,μL和μT分别表示层流和湍流黏性系数,PrL和PrT分别表示层流和湍流普朗特数。对于气体的热传导系数有:
| $ {k_f} = \frac{{\gamma R{\mu _L}}}{{\mathit{P}{\mathit{r}_L}\left( {\gamma - 1} \right)}} + \frac{{\gamma R{\mu _T}}}{{\mathit{P}{\mathit{r}_L}\left( {\gamma - 1} \right)}} = {C_p}\left( {\frac{{{\mu _L}}}{{\mathit{P}{\mathit{r}_L}}} + \frac{{{\mu _T}}}{{\mathit{P}{\mathit{r}_T}}}} \right) $ | (10) |
由式(10)可以得到:
| $ \frac{{{\mu _L}}}{{\mathit{P}{\mathit{r}_L}}} + \frac{{{\mu _T}}}{{\mathit{P}{\mathit{r}_T}}} = \frac{{{k_{\rm{f}}}}}{{{C_p}}} $ | (11) |
热传导的控制方程为抛物型方程,其本质与黏性扩散方程相同。因此,当地时间步长的确定方法与黏性扩散方程的方法类似。对于固体介质,对流通量谱半径
| $ \Delta {t_I} = \sigma \frac{{{\mathit{\Omega }_I}}}{{4{{\left( {\mathit{\hat \Lambda }_{v,{\rm{s}}}^I + \mathit{\hat \Lambda }_{v,{\rm{s}}}^K} \right)}_I}}} $ | (12) |
根据黏性谱半径的定义与式(11),确定了固体介质热传导谱半径:
| $ \mathit{\hat \Lambda }_{v,{\rm{s}}}^I = \frac{{{k_{\rm{s}}}}}{{{\rho _{\rm{s}}}{C_{\rm{s}}}}}\frac{{{{\left( {\Delta {S^I}} \right)}^2}}}{{{\mathit{\Omega }_I}}} $ | (13) |
采用热传导谱半径的方法确定当地时间步长,相当于在固体介质中的定义了热传导的“黏性”,能够保证气体介质和固体介质在计算热传导的方法上保持一致。气体和固体介质边界信息在每个虚拟迭代时间步都保持同步更新,不存在耦合时间,无需冻结流场和温度场。
在进行同步计算之前,需要规定全部区域物理场的初始条件与边界条件。对于外部高超声速流动区域,采用定常方法计算得到的结果作为初始流场,将等温壁作为交界面的边界条件;对于结构温度场,规定一个均匀的温度场作为初始条件,同时规定交界面处温度相等、热流密度连续;空腔内区域初场速度为0,初始温度场与结构温度场相同,将等温壁作为交界面的边界条件。
由于气体介质和固体介质在边界处的物理性质相差较大,本文采用引入虚拟单元的方法来高效处理固体域和流体域之间的交界面。虚拟单元物理属性与对应的真实单元物理属性相同,单元内的温度采用插值方法求得:
| $ {T_0} = 2{T_{\rm{w}}} - {T_1} $ | (14) |
式中T0、T1分别为虚拟单元与第一层单元的温度,Tw为交界面温度。交界面的温度Tw根据热流密度连续公式确定:
| $ {k_{\rm{f}}}\frac{{{T_{\rm{f}}} - {T_{\rm{w}}}}}{{{d_{\rm{f}}}}} = {k_{\rm{s}}}\frac{{{T_{\rm{w}}} - {T_{\rm{s}}}}}{{{d_{\rm{s}}}}} $ | (15) |
式中df和ds分别为气体和固体介质第一层单元中心到交界面之间的距离。Tf为气体介质第一层单元温度,Ts为固体介质第一层单元温度。ks和kf分别为固体和气体介质的热传导系数。在交界面处,气体介质还需满足物面法向压力梯度为0以及无滑移边界条件。
2 方法验证 2.1 高超声速流场/结构温度场同步计算方法模型为一厚度为12.7 mm、外径为76.2 mm的不锈钢半圆环。流场参数为:Ma∞=6.47,α=0°,T∞=241.5 K,Tw=294.4 K,p∞=701.8 Pa。流场网格包含12 000个单元,半圆环网格包含3000个单元,在交界面沿周向有着相同的分布规律。流体域与固体域内法向第一层网格高度均取为1.016×10-5 m。圆环的内壁采用绝热壁边界条件。
在进行数值计算之前,需要对初始时刻的流场进行计算。本文计算得到的驻点热流密度为494.030 kW/m2,与文献[5]符合较好。
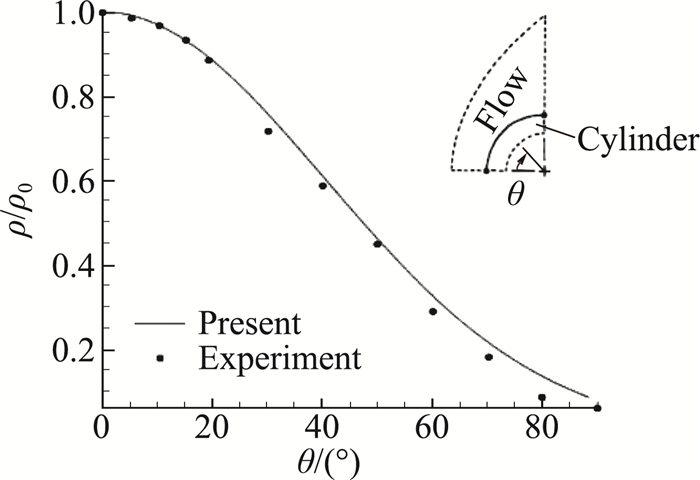
表面压强分布与文献[17]对比如图 1所示,结果符合良好。最终同步计算方法计算得到的驻点温度为390.227 K (702.408 R), 文献[5]计算得到的驻点温度为388.889 K (约700 R),计算结果与文献符合较好。
|
图 1 同步计算方法计算得到的表面压强分布与试验值对比 Fig.1 Comparison of computed pressure distribution with experimental data |
该算例方腔的水平壁面为绝热壁,垂直壁面为等温壁。左侧壁面为高温壁Th=303 K,右侧壁面为低温壁Tc=283 K,初始流场温度为293 K。由于存在温差,空间内各处气体的密度会发生变化。在重力的作用下,方腔内气体会产生流动。对Ra=1×103和Ra=1×105两种瑞利数的情况进行了模拟。验证算例中流动为层流,Pr取0.72。无量纲量(u*, w*, T*)为:T*=(T-Tc)/ΔT,
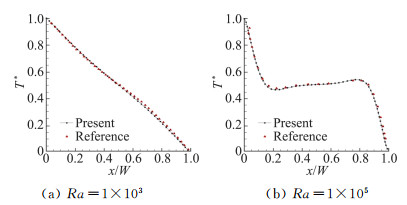
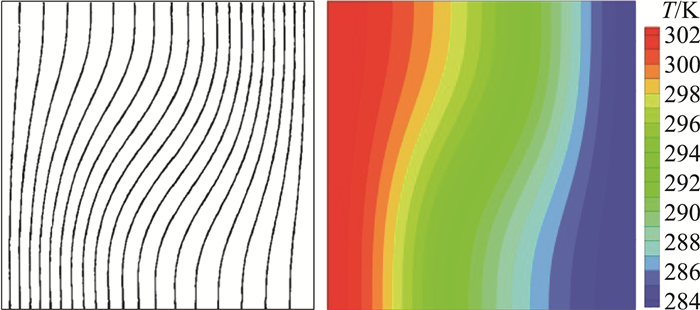
通过与文献对比温度在半高度位置沿水平方向分布(图 2)可知,引入预处理矩阵的可压缩N-S方程得到的数值模拟结果与文献符合很好。图 3、图 4给出了不同瑞利数温度云图与文献[10]对比。
|
图 2 不同瑞利数下,空腔半高度处温度沿水平方向分布对比 Fig.2 Distributions of temperature at mid-height of cavity for different values of Ra |
|
图 3 Ra=1×103温度云图对比 Fig.3 Comparison of temperature contours at Ra=1×103 |

|
图 4 Ra=1×105温度云图对比 Fig.4 Comparison of temperature contours at Ra=1×105 |
模型为一厚度为3.81 mm,外径为76.2 mm的不锈钢圆环。流场参数为Ma∞=7,α=0°,T∞=216.65 K,Tw=294.4 K,p∞=5.529×103 Pa,Tin=294.4 K,pin=1.01325×105 Pa。
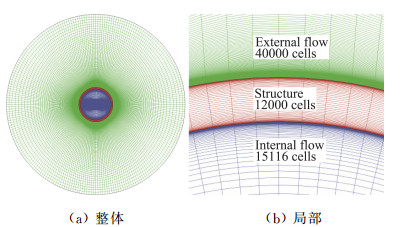
Tin为空腔内气体初始温度,pin为空腔内气体初始压强。图 5为计算网格,其中外部高超声速流动区域包含48 000个单元,结构热传导区域包含12 000个单元,空腔内部热对流区域包含15 116个单元,边界处网格沿周向分布一致。
|
图 5 计算网格 Fig.5 Computational grids |
在高超声速气动加热的作用下,外部流动前缘驻点处的温度会急剧上升,此处的热流密度达到最大,结构传热效果最明显。随着结构传热过程的进行,结构内壁前缘最先升温,造成空腔内流场温度分布不均匀,从而产生热对流现象。
图 6、图 7显示,当t=5 s时,由于空腔前后缘内壁温度均有增加,高温气流上升,低温气流下降,气流分别在前后缘处产生了旋涡;当t=15 s时,腔内空气的流动逐渐显著,流速增加,气体的输运特性也越发明显,前缘高温气流不断上升,后缘处旋涡消失,旋涡中心距离前缘较近;在t=25 s后的流动中,旋涡中心向空腔中心移动,旋涡形状与涡核位置逐渐稳定。
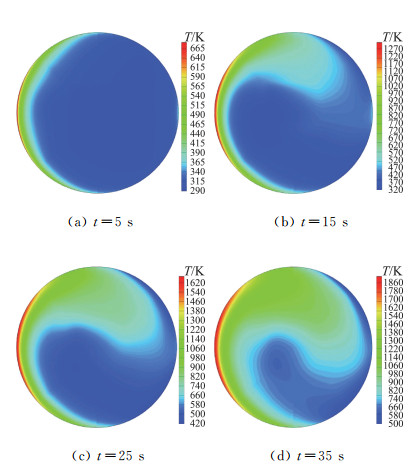
|
图 6 不同时刻内部流场温度云图 Fig.6 Internal temperature distributions at different time |
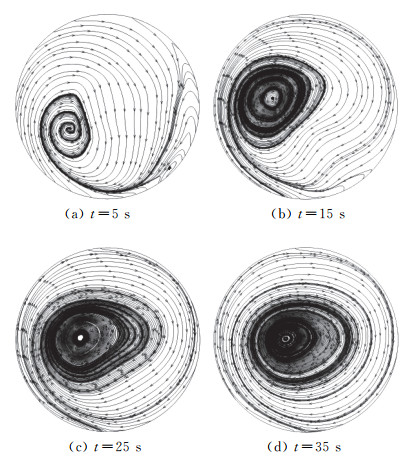
|
图 7 不同时刻空腔内流线 Fig.7 Internal streamlines at different time |
图 8为不同时刻是否考虑空腔内气体流动的结构温度差,即将不考虑空腔气体流动情形下的结构单元温度减去考虑空腔气体流动情形下相应单元的温度。当t=5 s时,最大差别点出现在近空腔前缘附近,原因是对于后者,该处结构与空腔内气体温差最大,结构向空腔气体传热最明显。随着时间推进,由重力驱动的高温气体将能量从驻点向其他地方输送,高温气体上升,对上半圆环进行加热,上半圆环温度升高,结构温差减小;而低温气体下降,在涡流作用下经过后半圆环向下运动,吸收下半圆环的热量,下半圆环温度降低,导致下半圆环结构温差增加。
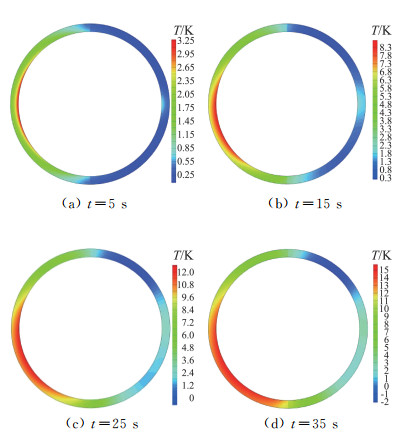
|
图 8 不同时刻是否考虑空腔内气体流动的结构温度场差别 Fig.8 Structural temperature differences between simulations with and without consideration of cavity flow at different time |
在上文模型的基础上对开孔空腔模型进行同步数值模拟进行研究。如图 9所示,开孔位置位于来流方向逆时针旋转90°方向,开孔内壁两端点与圆心连线夹角为3.31°。初始外部流场和初始空腔内部流场与上一节相同。
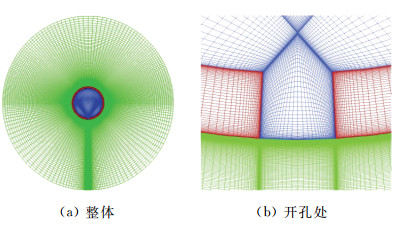
|
图 9 整体网格与开孔处局部放大图 Fig.9 Overall view and partial enlarged view of computational grids |
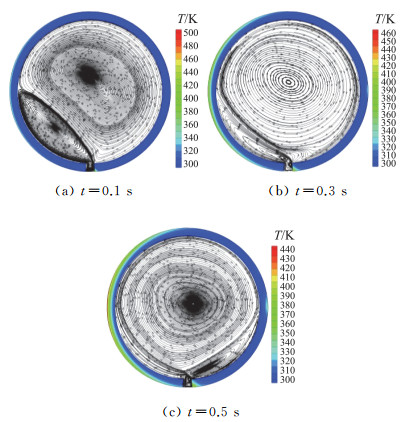
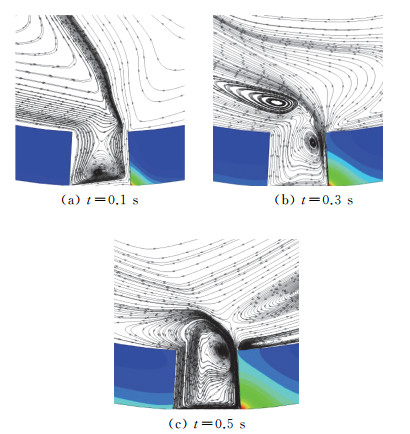
空腔内流场不同时刻流线如图 10所示。通过不同时刻流线图可以看出,在流动初期,由于流速较快,在开孔处形成旋涡,堵塞流动,外部气体沿着右侧孔壁流入腔内。受到开孔壁面影响,气体成一定角度流入空腔,空腔内气流被流入气流分成两个部分,形成两个旋涡。经过一段时间后,空腔内气流流速增加,与流入的气流形成干扰。孔左侧的旋涡逐渐减小,在孔右侧形成了一个新的旋涡。此外,如图 11所示,开孔的存在对于结构温度场影响较大,主要体现在孔附近的壁面。t=0.1 s时,外部流场驻点温度为361.29 K,开孔边缘温度为508.11 K;t=0.3 s时,驻点温度为413.01 K,开孔边缘温度为468.53 K;t=0.5 s时,驻点温度为446.99 K,开孔边缘温度为451.86 K。可以看出,短时间内开孔边缘温度可以超过外部流场驻点温度。由此可见,当密封结构存在开孔时会出现局部过热的现象,其附近结构瞬时温度甚至会超过驻点温度,可能造成结构破坏。
|
图 10 不同时刻空腔内流线 Fig.10 Internal streamlines at different time |
|
图 11 不同时刻结构温度场与开孔处流线 Fig.11 Temperature distributions of structure and streamlines near the hole at different time |
本文在已发展的高超声速外流场/结构温度场同步计算方法基础上,进一步发展了考虑了空腔内低速流动的同步数值模拟方法。通过对不同时刻空腔内流动特征和结构温度场分布进行对比分析,研究了结构温度场不均匀分布引起的空腔内对流流动反作用于结构温度场的影响,以及开孔对结构温度分布的影响。总结得出以下结论:
1) 封闭空腔内气体由于结构温度分布不均匀产生了流动。在空腔内气体流动的影响下,封闭圆环前缘温度在35 s内最多下降0.8%左右。
2) 开孔空腔的开孔处边缘温度在0.5 s内能够超过外流驻点温度。
由此可以看出,高超声速飞行器封闭结构内空腔气体流动对结构温度场影响较小,而结构间隙对结构温度场的影响不容忽视。未来可以进一步深入研究缝隙大小对结构温度场影响。所发展的方法为未来薄壁、带空腔的高超声速飞行器空腔内部流动数值模拟,以及高温热密封结构与热防护设计提供一种有效手段。
| [1] |
吴国庭. 载人飞船舷窗防热与密封结构的设计与试验[J]. 航天器工程, 2007, 16(3): 99-105. WU G T. Design and test for window thermal protection and sealed structure of ShenZhou spaceship[J]. Spacecraft Engineering, 2007, 16(3): 99-105. DOI:10.3969/j.issn.1673-8748.2007.03.019 (in Chinese) |
| [2] |
FINKBEINER J R, DUNLAP P H, STEINETZ B M, et al. Review of seal designs on the Apollo spacecraft[J]. Journal of Spacecraft & Rockets, 2008, 45(5): 900-910. |
| [3] |
FOOTE J O, FOOTE J. Titan Ⅳ solid rocket motor upgrade program at Alliant Techsystems Inc[R]. AIAA 97-2991.
|
| [4] |
CLEMENTE M D, RUFOLO G, IANIRO A, et al. Hypersonic test analysis by means of aerothermal coupling methodology and infrared thermography[J]. AIAA Journal, 2013, 51(7): 1755-1769. DOI:10.2514/1.J052234 |
| [5] |
PRAMOTE D, EARL A T, ALLAN R W. Flow-thermal-structural study of aerodynamically heated leading edges[J]. Journal of Spacecraft, 1989, 26(4): 201-209. DOI:10.2514/3.26055 |
| [6] |
季卫栋, 王江峰, 唐国庆. 高超声速多体分离过程气动加热计算技术[J]. 空气动力学学报, 2014, 32(6): 761-766. JI W D, WANG J F, TANG G Q. Calculating method of aerodynamic heating for hypersonic multi-body separation process[J]. Acta Aerodynamica Sinica, 2014, 32(6): 761-766. DOI:10.7638/kqdlxxb-2014.0080 (in Chinese) |
| [7] |
CROWELL A R, MILLER B A, MCNAMARA J J. Computational modeling for conjugate heat transfer of shock-surface interactions on compliant skin panels[R]. AIAA 2011-2017, 2011.
|
| [8] |
耿湘人, 张涵信, 沈清, 等. 高速飞行器流场和固体结构温度场一体化计算新方法的初步研究[J]. 空气动力学学报, 2002, 20(4): 422-427. GENG X R, ZHANG H X, SHEN Q, et al. Study on an integrated algorithm for the flow fields of high speed vehicles and the heat transfer in solid structures[J]. Acta Aerodynamica Sinica, 2002, 20(4): 422-427. DOI:10.3969/j.issn.0258-1825.2002.04.008 (in Chinese) |
| [9] |
DUCHAINE F, CORPRON A, PONS L, et al. Development and assessment of a coupled strategy for conjugate heat transfer with large eddy simulation: Application to a cooled turbine blade[J]. International Journal of Heat and Fluid Flow, 2009, 30(6): 1129-1141. DOI:10.1016/j.ijheatfluidflow.2009.07.004 |
| [10] |
BARAKOS G, MITSOULIS E, ASSIMACOPOULOS D. Natural convection flow in a square cavity revisited: Laminar and turbulent models with wall functions[J]. International Journal for Numerical Methods in Fluids, 1994, 18(7): 695-719. DOI:10.1002/fld.1650180705 |
| [11] |
GRAY D D, GIORGINI A. The validity of the boussinesq approximation for Liquids and gases[J]. International Journal of Heat & Mass Transfer, 1976, 19(5): 545-551. |
| [12] |
FU W S, LI C G, HUANG C P, et al. An investigation of a high temperature difference natural convection in a finite length channel without Bossinesq assumption[J]. International Journal of Heat & Mass Transfer, 2009, 52(11-12): 2571-2580. |
| [13] |
PAILLERE H, VIOZAT C, KUMBARO A, et al. Comparison of low Mach number models for natural convection problems[J]. Heat and Mass Transfer, 2000, 36(6): 567-573. DOI:10.1007/s002310000116 |
| [14] |
WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flows[J]. AIAA Journal, 1995, 33(11): 2050-2057. DOI:10.2514/3.12946 |
| [15] |
MERCI B, VIERENDEELS J, DICK E. Numerical study of natural convective heat transfer with large temperature differences[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2001, 11(4): 329-341. |
| [16] |
SENAPATI J R, DASH S K, ROY S. 3D numerical study of the effect of eccentricity on heat transfer characteristics over horizontal cylinder fitted with annular fins[J]. International Journal of Thermal Sciences, 2016, 108: 28-39. DOI:10.1016/j.ijthermalsci.2016.04.021 |
| [17] |
WIETING A R, HOLDEN M S. Experimental study of shock wave interference heating on a cylindrical leading edge at Mach 6 and 8[R]. AIAA 87-1511.
|
 2019, Vol. 37
2019, Vol. 37


