2. 北京航空航天大学 国家计算流体力学实验室, 北京 100191;
3. 北京大学 物理学院, 北京 100871;
4. 香港科技大学 数学系, 香港
2. National Laboratory for Computational Fluid Dynamics, Beihang University, Beijing 100191, China;
3. School of Physics, Peking University, Beijing 100871, China;
4. Department of Mathematics, The Hong Kong University of Science and Technology, Hong Kong, China
嫦娥奔月的美丽传说千百年来激励着人类对月球的深切向往,现代火箭技术的发展则将这一美好梦想变为现实。自1950年以来,人类向月球发射了100余个飞行器,特别是阿波罗飞船的登月成功,极大拓展了人类足迹范围[1]。20世纪以来,随着中国等新兴国家的加入和美国再次登月的提出,探月成为大国之间竞争的焦点之一。据维基百科统计,2010年至2014年间, 中美等国家共进行了8次探月飞行,而2018年至2024年列入计划的发射任务多达13项。
按照我国探月工程的“绕”、“落”、“回”三步走方案,载人登月最为关键的是“回”。探月面临一系列关键技术问题[2]。以我国2014年10月24日发射并于11月1日成功返回的探月返回试验器为例,研究人员围绕再入角变化特征[3]、轨道设计[4-5]、制导与控制[6-7]、烧蚀[8]以及末端伞降[9]开展了大量工作,特别是文献[10]在分析探月返回器稀薄气体效应时考虑了热化学非平衡特性,认为80 km高度再入时气体分子发生剧烈的化学反应且流场呈现化学非平衡状态。
与飞船返回舱等以第一宇宙速度返回的航天器不同,探月返回试验器以接近第二宇宙速度再入,面临的气动问题更为复杂,特别是绕流气体发生严重的化学反应和电离过程,传统上发生在连续流区的通信黑障大幅向稀薄区域延伸。然而,至今尚无探月返回试验器气体稀薄流区电离特性的分析结果,其原因是地面试验设备无法再现极高速再入稀薄段的高温、高速、稀薄、非平衡环境,基于NS方程的高温真实气体效应研究[11]对稀薄流失效,而适用于稀薄气体流动的DSMC方法在三维真实外形情况下的研究仍在发展之中。
最早将DSMC方法应用于稀薄气体电离过程的是Bird G A[12],他将传统连续流动化学反应Arrhenius方程常数与DSMC的碰撞概率相关联,将电子与伴随生成的带电粒子强制关联,以此避免弱电离电场的复杂计算。受限于当时的计算机能力,Bird的工作仅能处理一维驻点线流动,没有成功实现与试验结果的比较[13]。后续Carlson[14]等人的工作虽然在弱等离子体建模上有所进步,也没有突破一维驻点线的束缚。
近年来,稀薄气体电离过程的二维/轴对称模拟结果陆续发表,但鲜有三维复杂外形的公开报导。Ozawa[15]采用轴对称的Stardust外形,比较了Stardust极高速再入状态下电离的DSMC和CFD计算结果。Boyd[13]基于轴对称程序,采用稀有组分追踪算法和电离与离子强制关联的方法模拟分析了RAM-C Ⅱ的再入电离情况。樊菁[16]采用稀有组分分离方法、基于轴对称程序模拟了RAM-C Ⅱ的再入电离过程。Morsa [17]基于DS2V程序,针对Orin外形,比较了不同化学反应模型涉及电离计算的结果。上述工作均基于二维或轴对称程序,仅适用于简单轴对称外形。
三维真实外形航天器极高速再入稀薄气体电离过程DSMC模拟的核心困难有两点,一是弱电离过程产生的离子和电子数目与气体分子存在若干数量级的差异,DSMC方法的统计本质导致计算得到的稀有组分数密度涨落巨大,进而得不到真实的化学反应计算;二是电子与其它组分在质量上存在4到5个数量级的差异,同时电子运动受到弱等离子体环境的约束,导致电子的运动模拟极为困难。
文献[18]提出用增大电子质量的方法处理稀薄弱等离子体效应,建立了三维复杂外形航天器极高速再入条件下稀薄气体电离效应模拟的基本框架,开发了并行的计算代码,以RAM-C Ⅱ和Stardust等外形初步验证了基本算法的有效性。文献[19]发展了含电离化学反应稀有组分的权重因子方法,算例表明该方法能大幅改善电子数密度等稀有组分数密度等值线的光滑性,证实能获得三维复杂外形航天器电子数密度满足工程需求的结果。本文是上述工作的延续,基于作者开发的稀有组分权重因子方法的DSMC计算平台,采用公开的外形和与探月返回试验器相似的飞行条件,重点分析类探月返回试验器的稀薄电离特性,结果可为其通信设计提供依据。
1 第一次再入的稀薄气体电离特性分析据媒体公开报导,探月返回试验器与神舟飞船具有相似的外形,尺寸为神舟飞船的一半。本文计算外形如图 1所示。耳片等控制机构和攻角的存在,使得类探月返回试验器的电离特性计算分析超出了轴对称程序的处理范围,必须采用三维算法和配套程序。

|
图 1 类探月返回试验器计算外形 Fig.1 Configuration of lunar exploration type capsule |
按照我国探月返回试验器“蛙跳式”的再入方式,返回器第一次再入的速度超过10 km/s,具有明显的极高超声速特征,其稀薄气体电离特性计算分析是返回过程通信设计的关键所在。
参考探月返回试验器的飞行轨迹,第一次再入时稀薄气体电离特性分析的计算状态如表 1所示。所有计算采用240×250×250的网格、使用60个进程在x方向上分区并行计算。初始化时来流空气由79%的N2和21%的O2构成,每个网格约放置5个仿真分子。采用沿返回器轴向方向分区并行。取稀有组分权重因子为0.1。为确保流场稳定且得到足够光滑的电子数密度曲线,取时间步长为1×10-7 s,在40000步时开始抽样。
| 表 1 类探月返回试验器第一次再入对应的计算条件 Table 1 Computing states of lunar exploration type capsule for the first re-entry |
|
|
本研究关注的核心问题是类探月返回试验器绕流的电子数密度分布。90 km、95 km和97 km三个不同高度的电子数密度分布如图 2所示。三种状态下的最大电子数密度分别为5.216×1019/m3、5.047×1018/m3、1.988×1018/m3,对应处的分子数密度分别为9.35×1021/m3、3.19×1021/m3和2.05×1021/m3。由于电离程度较低,电离度可以定义为电子数目与所在网格总的分子数目之比,可见上述三种状态下的电离度在1%至1‰量级。
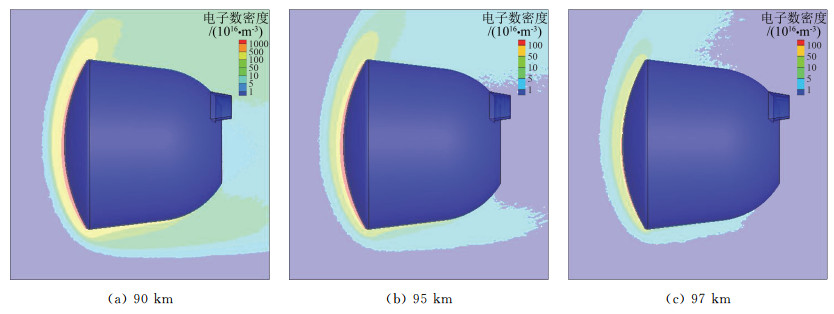
|
图 2 类探月返回试验器第一次再入时不同高度的电子数密度 Fig.2 Electron number density distributions of lunar exploration type capsule at different altitudes for the first re-entry |
从通信设计的角度而言,工程实际应用最为关心的是飞行器周围等离子体对通信信号的屏蔽作用。对于极高超声速电离热化学反应形成的稀薄弱等离子体,其等离子体电子振荡频率为[20]:
| $ \omega_{p e}=\sqrt{\frac{n_{e} e^{2}}{m_{e} \varepsilon_{0}}} $ | (1) |
其中,ne为电子数密度,e为电子电量,me为电子质量,ε0为真空中的介电常数。对于以cm-3为单位的ne,计算等离子体电子振荡频率对应电磁波频率的近似公式为:
| $ f_{p e}=\frac{\omega}{2 \pi} \approx 9000 \sqrt{n_{e}} $ | (2) |
类探月返回试验器在上述状态下的再入角在20°到25°之间,考虑地面雷达与试验器之间也有一定夹角,在分析等离子体对电磁信号的屏蔽作用时不应取整个流场的电子数密度最大值,而应该取包裹整个返回试验器头部及前部区域的电子数密度等值线。上述三种状态电子数密度对应的电磁波频率如图 3所示,表明对于S波段(2.3 GHz),完全通信中断的高度接近于97 km,或者说在95~97 km之间。
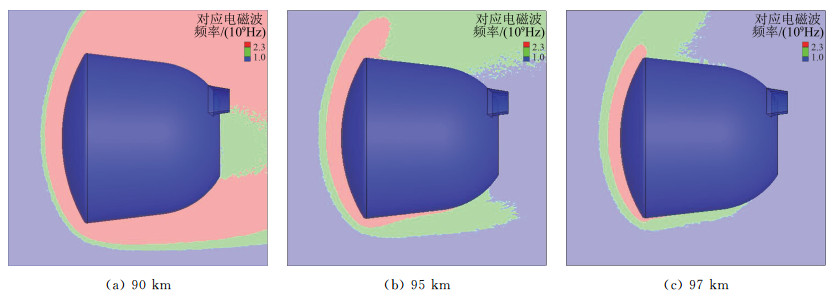
|
图 3 类探月返回试验器第一次再入时不同高度电子数密度对应的电磁波频率 Fig.3 Corresponding electromagnetic wave frequency of lunar exploration type capsule at different altitudes for the first re-entry |
与RAM-C Ⅱ在81 km处的电离情况不同,类探月返回试验器第一次再入时在稀薄流区的主要电离源是N和O原子与中性分子/原子碰撞导致的直接电离,这一点可以从图 4给出的N+和O+的数密度分布得到证明。图中N+和O+的数密度之和几乎完全等于电子数密度,NO+贡献率在1%量级,而N2+和O2+的贡献率比N+和O+至少低一个数量级(限于文章篇幅,NO+、N2+和O2+的数密度分布图并未给出)。
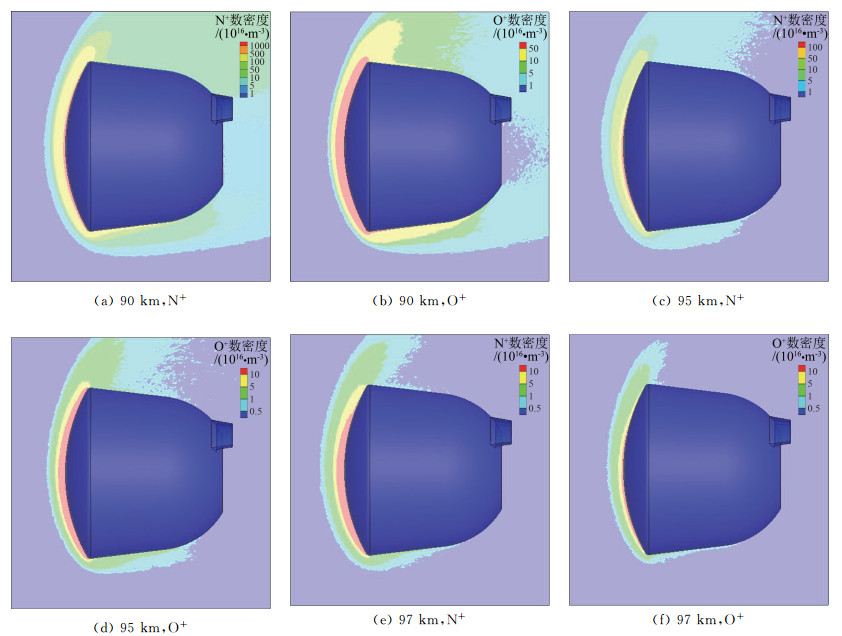
|
图 4 类探月返回试验器第一次再入时不同高度的N+、O+数密度 Fig.4 Number density of N+、O+ at different altitudes for the first re-entry |
第一次跳出时稀薄气体电离特性分析的计算状态如表 2所示。网格设置、进程数使用、初始化、时间步长设置及抽样方法与第1节相同,稀有组分权重因子为0.01。
| 表 2 类探月返回试验器第一次跳出时稀薄气体电离特性计算条件 Table 2 Computing states of lunar exploration type capsule for the first jump-out |
|
|
需要指出的是,80 km高度的来流气体分子平均自由程为4.4×10-3 m,小于计算采用的网格宽度8×10-3 m,这在DSMC计算中是不推荐的。但是,由于计算过程中采用了亚网格技术,碰撞分子对的选择在亚网格或者临近的亚网格内,上述网格设置不会导致显著的问题。关于网格和亚网格技术,不是本文的重点,故不在此处细致论述。
与图 2对应的电子数密度及与图 3对应的电磁波频率分别如图 5和图 6所示。由于再入速度从超过10 km/s降低到第一宇宙速度以下,第一次跳出时对应的电子数密度也显著降低,90 km高度对应的电子数密度差异超过1个数量级,与之对应的电离程度也明显降低,对于稀有组分权重因子的需求更为强烈,也是权重因子减小的根本原因。对于S波段(2.3 GHz),90 km处的信号受到较为强烈的干扰,但是通信并不会完全中断。图 6表明,通信完全中断的高度接近于85 km,或者略高。
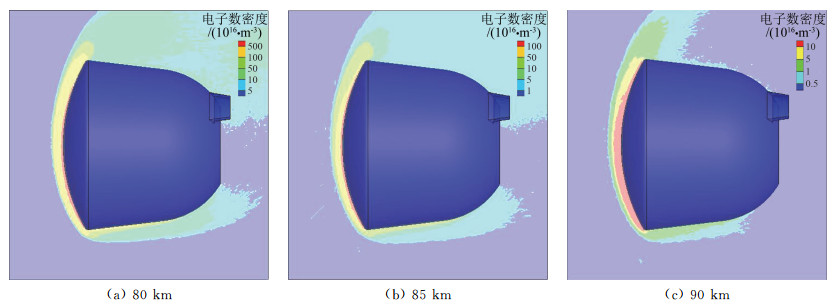
|
图 5 类探月返回试验器第一次跳出不同高度的电子数密度 Fig.5 Electron number density distributions of lunar exploration type capsule at different altitudes for the first jump-out |
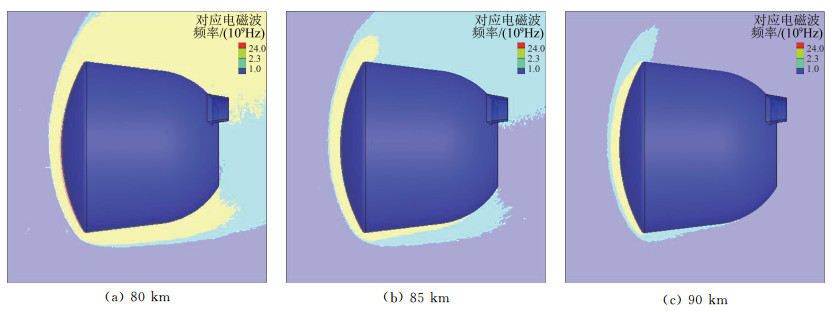
|
图 6 类探月返回试验器第一次跳出时不同高度电子数密度对应的电磁波频率 Fig.6 The corresponding electromagnetic wave frequency of lunar exploration type capsule at different altitudes for the first jump-out |
第一次跳出时的主要电离源依然是N和O原子与中性分子/原子碰撞导致的直接电离,限于文章篇幅,此处不再详细给出N+和O+的数密度分布图。为进一步考察主要电离源问题,我们计算分析了神舟飞船返回舱在80 km和85 km的再入电离特性,其再入速度亦略低于第一宇宙速度,发现主要电离源依然是N和O原子与中性分子/原子碰撞导致的直接电离。限于文章篇幅,此处亦不再细致论述。
3 第二次再入的稀薄气体电离特性分析第二次再入时稀薄气体电离特性分析的计算状态如表 3所示。网格设置、进程数使用、初始化、时间步长设置、抽样方法及权重因子设置与第2节相同。
| 表 3 类探月返回试验器第二次再入时稀薄气体电离特性计算条件 Table 3 Computing states of lunar exploration type capsule for the second re-entry |
|
|
上述计算状态下的电子数密度及对应的电磁波频率分别如图 7和图 8所示。图 7中的电子数密度与图 5中的电子数密度差异并不是太大,是因为相对于第一次跳出,第二次再入在同一高度的速度差异并不明显。图 8表明,第二次再入时S波段(2.3 GHz)的完全通信中断发生高度应该接近于85 km,或者略低。主要电离源的结论与第1节相同。
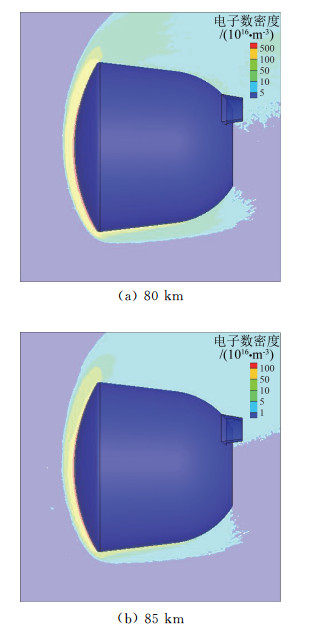
|
图 7 类探月返回试验器第二次再入不同高度的电子数密度 Fig.7 Electron number density distributions of lunar exploration type capsule at different altitudes for the first re-entry |
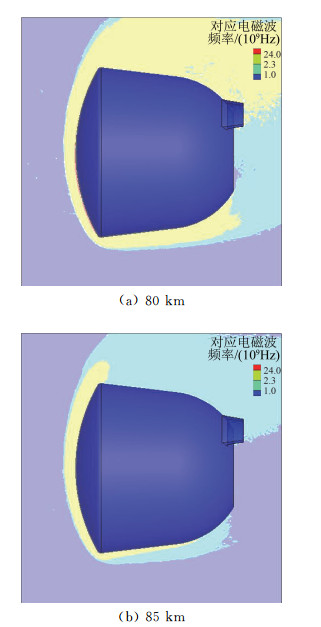
|
图 8 类探月返回试验器第二次再入不同高度电子数密度对应的电磁波频率 Fig.8 Corresponding electromagnetic wave frequency of lunar exploration type capsule at different altitudes for the second re-entry |
对于S波段(2.3 GHz)的电磁波,上述第一次再入、第一次跳出、第二次再入时的通信完全中断发生高度预测值与飞行试验观测值的对比结果见表 4。可以看出,基于本文的计算结果,给出的类探月返回试验器在S波段(2.3 GHz)的通信中断发生高度预测值与飞行试验观测值误差在2 km以内,证明电子数密度的计算具有较高的精度。这一结果不仅填补了该类飞行器稀薄气体电离特性分析的空白,且通信中断发生高度预测值较之连续流的5 km精度也显著提高。
| 表 4 类探月返回试验器通信中断发生高度预测值与飞行试验观测值之比较 Table 4 Comparison of black-out starting altitude of lunar exploration type capsule between prediction and flight observation |
|
|
本文基于稀有组分权重因子的含电离化学反应DSMC方法,考察了类探月返回试验器的稀薄气体电离特性,主要结论有:
1) 基于发展的稀有组分权重因子方法和计算平台,首次分析了类探月返回试验器的稀薄气体电离特性,无论是第一次再入、第一次跳出还是第二次再入时,S波段(2.3 GHz)通信中断都发生在80 km以上的稀薄流区;给出的通信中断发生高度预测值与飞行试验观测值误差在2 km以内,证明电子数密度的计算具有较高的精度。
2) 与RAM C-Ⅱ的细长体外形飞行器再入的主要来源是N和O的联合电离不同,对于类探月返回试验器的大钝头体再入,稀薄气体电离的主要来源是N、O与中性分子/原子碰撞导致的直接电离。
| [1] |
龙乐豪. 关于中国载人登月工程若干问题的思考[J]. 导弹与航天运载技术, 2010(6): 1-5. LONG L H. On issue of China manned lunar exploration[J]. Missiles and Space Vehicles, 2010(6): 1-5. DOI:10.3969/j.issn.1004-7182.2010.06.001 (in Chinese) |
| [2] |
吴伟仁, 于登云. 深空探测发展与未来关键技术[J]. 深空探测学报, 2014(1): 5-17. WU W R, YU D Y. Development of deep space exploration and its future key technologies[J]. Journal of Deep Space Exploration, 2014(1): 5-17. (in Chinese) |
| [3] |
赵玉辉, 侯锡云, 刘林.探月返回轨道再入角的变化特征[C]//中国宇航学会深空探测技术专业委员会第六届学术年会暨863计划"深空探测与空间实验技术"重大项目学术研讨会论文集, 2009.
|
| [4] |
周文勇, 王传魁, 陈益, 等. 一种模拟探月返回器再入条件的轨道设计方案[J]. 导弹与航天运载技术, 2015(6): 13-16. |
| [5] |
田浩.探月飞行器再入地球大气层的轨道设计[D].哈尔滨: 哈尔滨工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013037358.htm
|
| [6] |
于萍, 王鹏基, 胡洪凯, 等. 飞行器GNC试验子系统新技术及验证[J]. 中国科学:技术科学, 2015(2): 193-197. |
| [7] |
苏杭.探月飞船返回跳跃式再入轨迹规划与制导研究[D].哈尔滨: 哈尔滨工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013038882.htm
|
| [8] |
顾征, 陈丽平, 王彤, 等. 一种返回器烧蚀温度在轨测量方法[J]. 航天器工程, 2015(2): 129-133. DOI:10.3969/j.issn.1673-8748.2015.02.020 |
| [9] |
贾贺, 荣伟, 江长虹, 等. 探月三期月地高速再入返回器降落伞减速系统设计与实现[J]. 中国科学:技术科学, 2015(2): 185-192. |
| [10] |
梁杰, 李志辉, 杜波强, 等. 探月返回器稀薄气体热化学非平衡特性数值模拟[J]. 载人航天, 2015, 21: 295-302. DOI:10.3969/j.issn.1674-5825.2015.03.014 |
| [11] |
乐嘉陵. 再入物理[M]. 国防工业出版社, 2005.
|
| [12] |
BIRD G A. Nonequilibrium radiation during re-entry at 10 km/s[R]. AIAA 87-1543, 1987.
|
| [13] |
BOYD I D. Modeling of plasma formulation in rarefied hypersonic entry flows[R]. AIAA 2007-206, 2007.
|
| [14] |
CARLSON A B, HASSAN H A. Direct simulation of re-entry flows with ionization[J]. Journal of Thermophysics and Heat Transfer, 1992(6): 400-404. |
| [15] |
OZAWA T, ZHONG J, LEVIN D A, et al. Modeling of Stardust reentry flows with ionization in DSMC[R]. AIAA 2007-611.
|
| [16] |
FAN J, ZHANG Y H, JIANG J Z. Monte Carlo modeling of electron density in hypersonic rarefied gas flows[C]//29th International Symposium on Rarefied Gas Dynamics, 2014.
|
| [17] |
MORSA L, ZUPPARDI G. Influence of ionization on the Gupta and on the Park chemical models[C]//29th International Symposium on Rarefied Gas Dynamics, 2014.
|
| [18] |
方明, 李志辉, 李中华, 等. 球锥钝头体再入稀薄气体电离过程三维DSMC模拟与验证[J]. 空气动力学学报, 2017, 35(1): 39-45. FANG M, LI Z H, LI Z H, et al. Three dimensional DSMC simulation and validation of rarefied air ionization process for sphere-cone blunt body reentry[J]. Acta Aerodynamica Sinica, 2017, 35(1): 39-45. DOI:10.7638/kqdlxxb-2015.0086 (in Chinese) |
| [19] |
方明, 杜波强, 李志辉, 等. 含电离化学反应DSMC模拟的稀有组分权重因子方法[J]. 空气动力学学报, 2018, 36(5): 856-882. FANG M, DU B Q, LI Z H, et al. Weighting scheme for rare species in DSMC simulation involving ionization chemical reactions[J]. Acta Aerodynamica Sinica, 2018, 36(5): 856-882. DOI:10.7638/kqdlxxb-2016.0090 (in Chinese) |
| [20] |
庄钊文, 袁乃昌, 刘少斌, 等. 等离子体隐身技术[M]. 科学出版社, 2005.
|
 2019, Vol. 37
2019, Vol. 37

