随着近年来临近空间低速飞行器和高性能微小型飞行器的快速发展,翼型在低雷诺数范围内的气动问题日益受到关注。低雷诺数条件下(1×104~1×105)翼型绕流流动会出现层流分离现象,其形成和演化会严重损害翼型气动性能,并直接影响飞行器续航能力以及操纵性和稳定性[1]。准确预测翼型层流分离流动现象,并分析认识其气动特性及流动机理,对于低速临近空间飞行器和微型飞行器的设计研制具有重要意义。
对翼型层流分离流动的研究可追溯至20世纪60年代,Gaster和Horton提出了经典层流分离泡模型[2-3], 认为层流附面层在逆压梯度作用下分离,在空间发生转捩后,外部高能量气流的引入导致再附,形成层流分离泡。大量的风洞试验[4-5]和数值模拟[6-7]研究发现,翼型层流分离流动存在显著的非定常特征和非线性效应。层流分离流场中存在流动分离、转捩、再附等非定常流动结构,并不存在稳定的分离泡,而是一系列的大尺度旋涡结构时均结果。
基于雷诺平均假设的RANS(Reynolds Averaged Navier-Stokes)方法难以准确预测层流分离流动中的转捩现象。为此,Yuan[8]、Radespiel[9], Lian[10]分别发展了基于稳定性分析的eN方法与RANS联合求解的方法,用于预测工程问题中的低雷诺数转捩过程;此外,Choudhry[11]等采用γ-Reθ和k-kL-ω转捩模型模拟了NACA0021翼型低雷诺数流动,对翼型层流分离泡结构、特性及随迎角、雷诺数、湍流度的变化规律展开了细致的研究。这类基于RANS的方法虽然计算量较小,但受模型限制,能否准确描述层流分离和转捩的三维非定常过程仍存在质疑[12]。
翼型低雷诺数风洞试验方面尽管已经开展了大量研究工作[13-14],但获取流场精细化非定常流场信息方面的试验还比较缺乏,并且试验结果难以吻合一致;OL等[15]分析了三座不同试验设备中采用PIV技术得到的SD7003翼型层流分离流场平均流向速度和雷诺应力等结果,为三维精细数值模拟提供了较为细致的验证数据。
随着计算机性能的迅速提高和数值方法的发展,对该类问题的研究趋于采用大涡模拟(Large Eddy Simulation, LES)或直接数值模拟(Direct Numerical Simulation, DNS)方法。Shan等[16]对NACA0012翼型层流分离流动现象开展了直接数值模拟研究,并分析了流场结构特征及其演化机理。Galbraith和Visbal[17]在重叠网格上采用ILES方法模拟了SD7003翼型低雷诺数层流分离流动,并将计算结果与试验数据进行了对比。Vilem和Miyaji等[18]采用不同精度的通量重构格式及不同密度网格,开展了SD7003翼型在不同迎角下的层流分离现象的隐式大涡模拟计算,验证了高阶通量重构格式对于这一复杂流动的应用效果。艾国远等[19]采用基于四阶中心格式以及动态亚格子模型的大涡模拟方法,对NACA0025不同分离流态的层流分离流动开展了模拟研究。
上述研究工作验证了这类精细数值模拟方法对于层流分离现象的模拟预测能力,但所采用亚格子模型、数值格式、计算网格各有不同。此外,严格意义的直接数值模拟因计算量过大难以应用于翼型层流分离现象的模拟分析;大涡模拟中网格尺度、数值格式、亚格子模型是影响其准确性的关键因素,并且三者间存在相互影响。大涡模拟方法及其关键技术在翼型低雷诺数层流分离流动模拟中的适用性有待进一步验证评估。
因此,本文发展基于结构化拼接网格的大涡模拟方法,针对SD7003翼型在雷诺数60000及4°迎角下的层流分离流动开展数值模拟,对比分析数值格式、亚格子模型以及网格尺度对流场预测结果的影响,并与转捩模型计算结果进行对比,验证发展的大涡模拟方法对于该类问题的适用性,为下一步研究工作奠定基础。
1 数值方法 1.1 控制方程本文大涡模拟方法求解Favre滤波形式的三维可压缩Navier-Stokes方程,其守恒形式如下:
| $ \begin{array}{l} \frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}}{{\partial {x_i}}} = 0\\ \frac{{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_i}{{\tilde u}_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{{\partial \left( {{{\tilde \tau }_{ij}} - \tau _{ij}^{{\rm{SGS}}} + D_{ij}^{{\rm{SGS}}}} \right)}}{{\partial {x_j}}}\\ \frac{{\partial \bar \rho \tilde E}}{{\partial t}} + \frac{{\partial \left[ {\left( {\bar \rho \tilde E + \bar p} \right){{\tilde u}_i}} \right]}}{{\partial {x_i}}} = \\ \frac{\partial }{{\partial {x_j}}}\left( { - {{\tilde q}_i} + {{\tilde u}_j}{{\tilde \tau }_{ij}} + \psi _i^{{\rm{SGS}}} + \sigma _i^{{\rm{SGS}}} - Q_i^{{\rm{SGS}}} - H_i^{{\rm{SGS}}}} \right) \end{array} $ | (1) |
其中,f表示空间滤波变量,
| $ {{\tilde \tau }_{ij}} = \tilde \mu \left( {2{{\tilde S}_{ij}} - \frac{2}{3}{\delta _{ij}}{{\tilde S}_{kk}}} \right) $ | (2) |
| $ {{\tilde q}_i} = - \frac{{\tilde \mu {c_p}}}{{\mathit{Pr}}}\frac{{\partial \tilde T}}{{\partial {x_i}}} $ | (3) |
其中,
| $ {S_{ij}} = \left( {\partial {{\tilde u}_i}/\partial {x_j} + \partial {{\tilde u}_j}/\partial {x_i}} \right)/2 $ | (4) |
式(1)中由于滤波运算引入的待封闭亚格子项(Sub-Grid Scale, SGS)定义如下:
| $ \tau _{ij}^{{\rm{SGS}}} = \bar \rho \left( {\widetilde {{u_i}{u_j}} - {{\tilde u}_i}{{\tilde u}_j}} \right),\;\;\;\;{\rm{SGS}}扩散通量 $ |
| $ D_{i j}^{\mathrm{SGS}}=\left(\bar{\tau}_{i j}-\tilde{\tau}_{i j}\right),\;\;\;黏性应力非线性项 $ |
| $ \psi _i^{{\rm{SGS}}} = - \frac{1}{2}\bar \rho \left( {\widetilde {{u_i}{u_k}{u_k}} - {{\tilde u}_i}\widetilde {{u_k}{u_k}}} \right),\;\;\;{\rm{SGS}}湍流扩散项 $ |
| $ Q_{i}^{\mathrm{SGS}}=\bar{q}_{i}-\tilde{q}_{i},\;\;热通量非线性项 $ |
| $ H_i^{{\rm{SGS}}} = {C_P}\left( {\bar \rho \widetilde {{u_i}T} - \bar \rho {{\tilde u}_i}\tilde T} \right),\;\;\;{\rm{SGS}}能量项 $ |
| $ \sigma_{i}^{\mathrm{SGS}}=\left(\overline{u_{j} \tau_{i j}}-\tilde{u}_{j} \tilde{\tau}_{i j}\right), \quad \mathrm{SGS}黏性扩散项 $ |
上述未封闭项中,黏性应力非线性项DijSGS和亚格子黏性扩散项σiSGS由于对能量方程贡献较小,故可忽略;其余项通过构造亚格子模型黏性系数μt进行近似,使方程封闭,形式如下[20-21]:
| $ Q_i^{{\rm{SGS}}} = - \frac{{{\mu _t}{C_P}}}{{\mathit{Pr}}}\frac{{\partial \tilde T}}{{\partial {x_i}}} $ | (5) |
| $ \tilde \tau _{ij}^{{\rm{SGS}}} = {\mu _t}\left( {2{{\tilde S}_{ij}} - \frac{{\rm{2}}}{3}{\delta _{ij}}{{\tilde S}_{kk}}} \right) $ | (6) |
| $ H_i^{{\rm{SGS}}} = - \frac{{{\mu _t}{C_P}}}{{P{r_t}}}\frac{{\partial \tilde T}}{{\partial {x_i}}} $ | (7) |
| $ \psi _i^{{\rm{SGS}}} = {{\tilde u}_j}\tau _{ij}^{{\rm{SGS}}} $ | (8) |
亚格子模型可分为两类:显式模型和隐式模型。隐式大涡模拟方法MILES(Monotone Integrated LES)和ILES(Implicit LES)[20, 22],基于数值格式耗散作用可代替显式亚格子模型的假设,该类方法已广泛应用于非定常复杂流场的精细数值模拟。
显式模型通常假定小尺度结构是相对各向同性的,并普遍基于Boussinesq应力/应变关系建立涡黏性模型。目前被广泛应用的亚格子模型有:SM模型(Smagorinsky Model)[23],DSM模型(Dynamic Smagorinsky Model)[24]和WALE模型(Wall Adapting Local Eddy-Viscosity Model)[25]。
1.2.1 Smagorinsky模型SM模型(Smagorinsky)基于混合长度假设,将湍流涡黏性系数正比于亚格子尺度和滤波后的速度张量的二阶不变量,即
| $ {\mu _t} = C_S^2\bar \rho {\Delta ^2}\sqrt {2{{\tilde S}_{ij}}{{\tilde S}_{ij}}} $ | (9) |
其中,模型系数CS为0.1,Δ为涡黏性长度尺度,它对应网格滤波函数在物理空间的宽度,取Δ=V1/3(V为网格单元体积)。由于近壁区域流动受到壁面限制,需进行修正减小近壁区域耗散,提高计算精度。
1.2.2 DSM模型SM模型主要缺陷是将模型系数CS作为常数。DSM模型建立了随时间与空间变化的亚尺度黏性系数公式,通过两个不同的亚尺度应变率张量从已求解的区域信息计算得到CS,计算公式如下:
| $ {L_{ij}} = \widetilde {{{\bar u}_i}{{\bar u}_j}} - \widetilde {{{\bar u}_i}}\widetilde {{{\bar u}_j}} $ | (10) |
| $ {M_{ij}} = {{\bar \Delta }^2}\left( {{\alpha ^2}\widetilde {\left| {\bar S} \right|}\widetilde {\overline {S_{ij}^k} } - \widetilde {\left| {\bar S} \right|}\widetilde {\overline {S_{ij}^k} }} \right) $ | (11) |
| $ {\left( {{C_S}\bar \Delta } \right)^2} = \frac{1}{2}\frac{{{{\left\langle {{L_{ij}}{M_{ij}}} \right\rangle }_h}}}{{{{\left\langle {{M_{ij}}{M_{ij}}} \right\rangle }_h}}} $ | (12) |
其中,Lij和Mij为速度矢量的二阶张量,k和h为常数,α为滤波宽度比;Δ为格子过滤尺寸。在准二维流动中,为保证计算稳定,通常将模型系数CS在空间沿均匀流动方向进行平均处理。
1.2.3 WALE模型WALE模型同样基于混合长度假设,但是包含形变率张量和旋度率张量的混合运算,以充分探测与湍动能耗散有关的所有湍流结构;此外,WALE模型可根据当地流动信息,再现流动从层流到湍流的转捩。其亚格子黏性系数计算如下:
| $ {\mu _t} = \bar \rho {\left( {{C_w}\Delta } \right)^2}\frac{{{{\left( {S_{ij}^dS_{ij}^d} \right)}^{\frac{3}{2}}}}}{{{{\left( {{{\tilde S}_{ij}}{{\tilde S}_{ij}}} \right)}^{\frac{5}{2}}} + {{\left( {S_{ij}^dS_{ij}^d} \right)}^{\frac{3}{4}}}}} $ | (13) |
| $ S_{ij}^d = \frac{1}{2}\left( {\frac{{\partial {{\tilde u}_i}}}{{\partial {x_l}}}\frac{{\partial {{\tilde u}_l}}}{{\partial {x_j}}} + \frac{{\partial {{\tilde u}_j}}}{{\partial {x_l}}}\frac{{\partial {{\tilde u}_l}}}{{\partial {x_i}}}} \right) - \frac{1}{3}\frac{{\partial {{\tilde u}_m}}}{{\partial {x_l}}}\frac{{\partial {{\tilde u}_l}}}{{\partial {x_m}}}{\delta _{ij}} $ | (14) |
其中,模型常数Cw在各向同性湍流中可取0.45,在壁湍流中取为0.5。
1.3 数值格式 1.3.1 空间离散格式对流通量离散选用AUSM+(Advection Upstream Splitting Method)格式[26], 以及前期发展的满足几何守恒律WENO格式[27]。AUSM+格式具有高分辨率和高计算效率的优点,为提高计算精度,网格单元界面两侧原始变量插值采用WENO[28-29]格式。满足几何守恒律的WENO格式采用守恒型网格导数计算方法,并将标准的WENO格式分解为中心差分部分和数值耗散部分。该格式能够消除网格导数计算误差, 保证来流保持性,并具有较高的精度和分辨率,能够精细捕捉小尺度流场结构。黏性通量计算中的导数项采用二阶中心差分格式计算。
1.3.2 时间推进方法本文发展的非定常时间推进方法包括显式Runge-Kutta格式以及隐式亚迭代[30]和双时间步方法[31]。显式格式具有精度高、物理问题相容性好等优点,但时间步长小、计算耗时长;而隐式方法则具有计算效率高的特点,但存在离散近似、收敛判据影响计算精度等问题,在层流分离非定常现象中的应用有待验证确认。双时间步隐式迭代推进方法的物理时间步长可根据物理问题来选取,不受稳定性条件的限制,并具有计算效率高、简单可靠等优点。
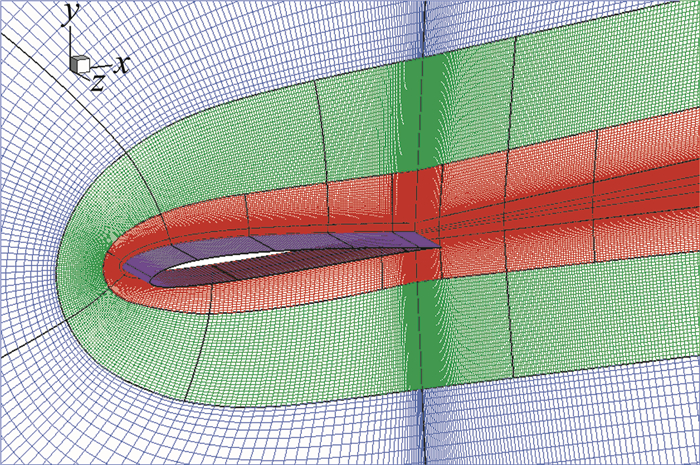
1.4 计算网格及边界条件采用C型结构化网格对计算域进行划分,网格坐标原点位于翼型前缘点,流向和法向计算域设为40倍弦长。为提高网格效率,节省总计算量,采用三维拼接技术在翼型附近区域(图 1中红色部分)分布较多的网格点,而在远离翼型的外围区域(图 1中蓝色部分)分布较少的网格点,中间区域(图 1中绿色部分)为过渡区。基准网格展向宽度设为0.2,物面法向第一层网格间距1×10-4,网格单元总量为7 704 000。
|
图 1 基准计算网格 Fig.1 Baseline computational mesh |
计算域远场边界设为特征边界条件,物面边界层采用绝热无滑移条件,展向设为周期边界条件。
2 结果分析SD7003翼型计算状态为Re=60000(基于来流速度和翼型弦长)、迎角4°,来流马赫数设为0.2。为减小计算量,将二维层流定常计算结果展向延拓作为三维非定常计算初始流场。流场发展稳定后做统计平均计算,统计100000步,平均流场结果由时间平均结果作展向平均计算得到。将计算结果与OL等[15]在布伦瑞克工业大学(TUBS)的低雷诺数风洞和美国空军研究实验室的水平自由水面水洞(HFWT)获得的试验数据以及Galbraith和Visbal[17]的隐式大涡模拟计算结果进行对比分析。本文中将以在基准网格上采用AUSM格式和双时间步方法以及隐式模型作为基准方法,对比分析数值格式、亚格子模型、网格尺度对流场预测结果的影响。
2.1 数值格式影响大涡模拟要求采用了高精度计算格式以精细分辨流场非定常小尺度结构,因此首先在基准网格上,基于隐式大涡模拟方法,对比分析不同空间离散格式和时间推进方法对计算结果影响。
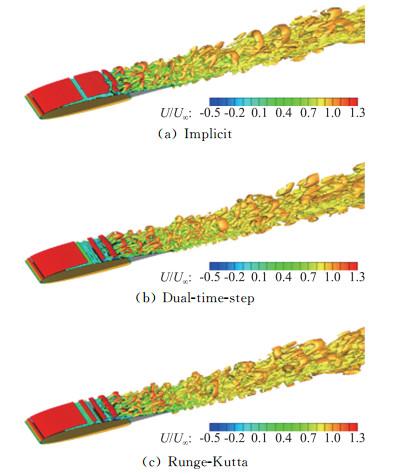
2.1.1 时间推进方法分别采用隐式亚迭代(Implicit)、双时间步(Dual-time-step)和显式Runge-Kutta推进方法,隐式和显式格式无量纲时间步长分别为1×10-4和1×10-5,对流通量计算格式采用AUSM格式。结果对比如下:从图 2给出的瞬时涡系结构(Q准则显示、流向速度着色)可以看到,不同时间推进方法均能捕捉到流动发生分离和转捩的复杂流动结构,双时间步长方法和显式格式分辨的涡结构更为精细。
|
图 2 不同时间推进方法瞬时涡系结构对比 Fig.2 Instantaneous vortex by different time advancing methods |
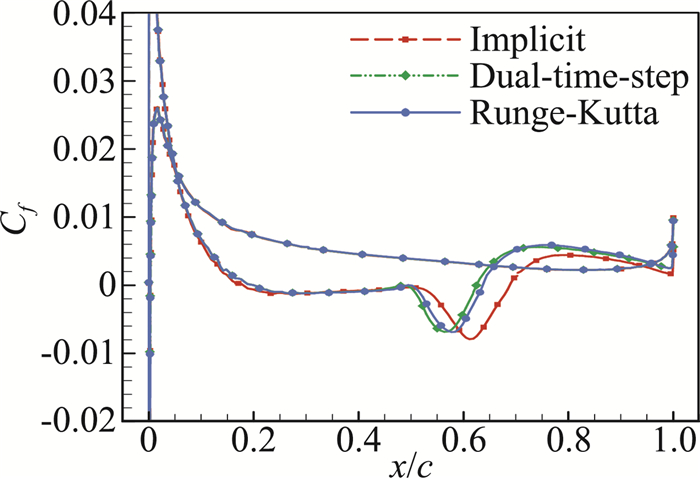
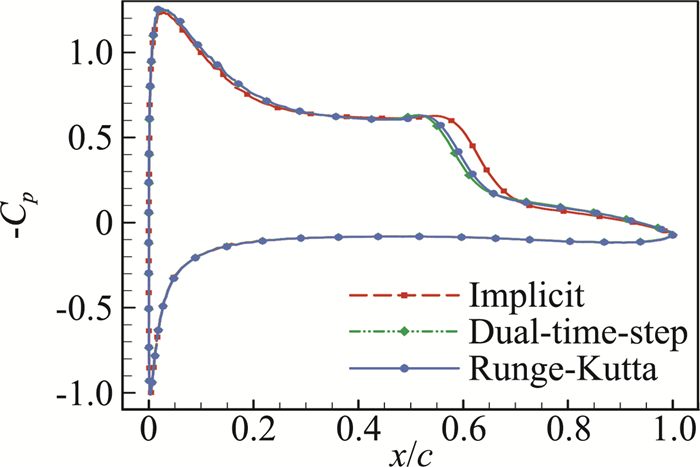
图 3和图 4分别对比了统计平均摩阻系数和压强系数,可以看到,双时间步长方法与显式格式计算得到的分布曲线非常接近,而隐式亚迭代方法偏差较大。表 1所示的分离点(xs)、转捩点(xt)、再附点(xr)位置的对比进一步表明,双时间步方法计算结果与显式格式接近。此外,双时间步方法的时间步长可取为显式格式的十倍,总的计算量约为显式格式二分之一。因此,在后续计算中均采用双时间步方法进行时间推进。
|
图 3 不同时间推进方法平均摩阻系数对比 Fig.3 Comparison of mean Cf by different time advancing methods |
|
图 4 不同时间推进方法平均压强系数对比 Fig.4 Comparison of mean Cp by different time advancing methods |
| 表 1 不同时间推进方法分离、转捩、再附点位置对比 Table 1 Locations of separation, transition and reattachment by different time advancing methods |
|
|
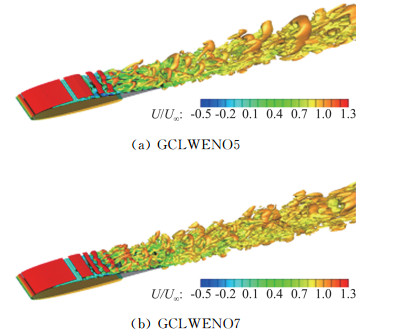
分别采用基于5阶原始变量插值的AUSM+格式,以及满足几何守恒律的通量型5阶(GCLWENO5)和7阶WENO格式(GCLWENO7)对比分析空间离散格式对计算结果影响。图 5给出了不同离散格式得到的瞬时涡系结构。结合基准方法结果(图 2a)对比可发现,不同格式得到的非定常流动特征一致,其中7阶WENO格式对小尺度流动结构的捕捉最为精细。
|
图 5 不同空间离散格式瞬时涡系结构对比 Fig.5 Instantaneous vortex by different spatial schemes |
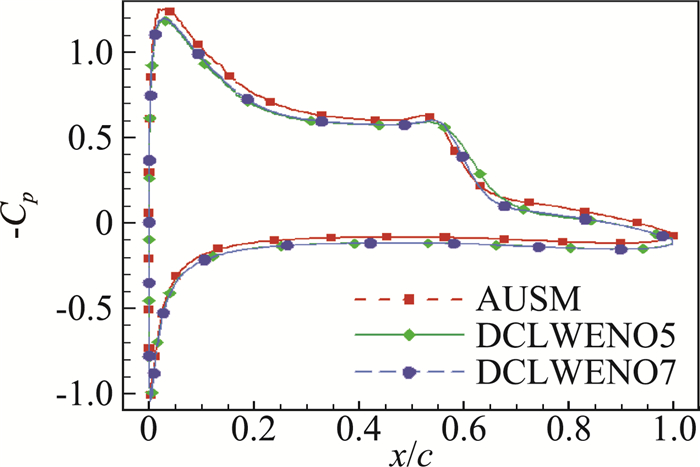
从图 6所示的平均压强系数对比可以看出,不同离散格式计算得到的压力系数接近,分布规律一致:在翼型上表面靠近前缘区域存在明显的逆压梯度,在时均化分离区内压强趋于恒定,再附点后压强迅速升高。
|
图 6 不同空间离散格式平均压强系数对比 Fig.6 Comparison of mean Cp by different spatial schemes |
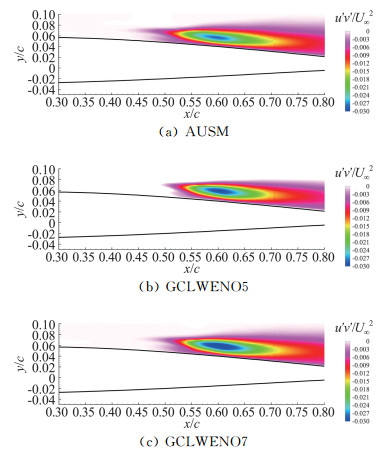
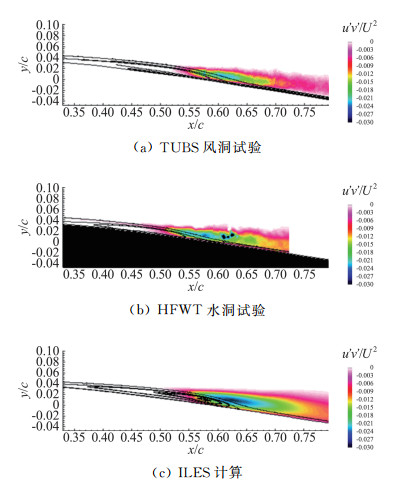
图 7给出了不同计算格式获得的平均雷诺应力分布,文献中试验和计算结果如图 8所示。对比可发现,本文数值计算结果与文献中雷诺应力分布形态一致,数值略有差异,AUSM格式和5阶WENO格式与试验和ILES计算结果更为接近。
|
图 7 不同空间离散格式雷诺应力对比 Fig.7 Comparison of Reynolds shear stress by different spatial schemes |
|
图 8 雷诺应力文献结果 Fig.8 Reynolds stress in reference |
综上,本文不同空间离散格式计算结果均能够精细刻画翼型层流分离现象中的小尺度非定常流动结构,雷诺应力分布与文献试验和计算数据均吻合较好。基于5阶原始变量插值的AUSM格式具有较高的分辨率,并且鲁棒性更好、计算量小,在实际应用中更具优势。
2.2 亚格子模型影响基于隐式亚格子模型(MILES)以及不同显式模型计算结果对比如下。从表 2的分离、转捩、再附点位置对比可以看到,隐式模型计算结果与DSM模型和WALE模型较为接近,且与文献[15]中的试验数据接近。而SM模型计算得到再附点明显靠后,时均化分离泡范围更大。
| 表 2 不同亚格子模型分离、转捩、再附点位置对比 Table 2 Locations of separation, transition and reattachment by different SGS models |
|
|
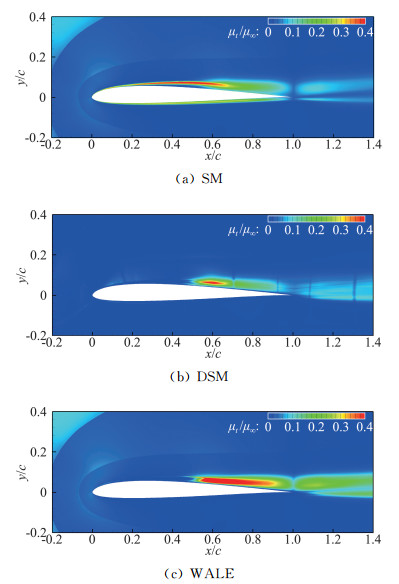
图 9为不同显式模型平均亚格子黏性系数的对比。可以发现,不同显式模型计算得到的亚格子黏性系数数值较小,表明亚格子黏性对流场影响较弱。在其形态分布方面,SM模型与DSM模型和WALE模型存在明显差异——DSM和WALE模型预测得到的湍流黏性在“分离泡”区域数值较大,而SM模型从翼型头部开始在整个翼型附面层均发挥作用,表明SM模型无法准确预测转捩。
|
图 9 不同亚格子模型黏性系数对比 Fig.9 Comparison of turbulence viscosity coefficient by different sub-grid scale models |
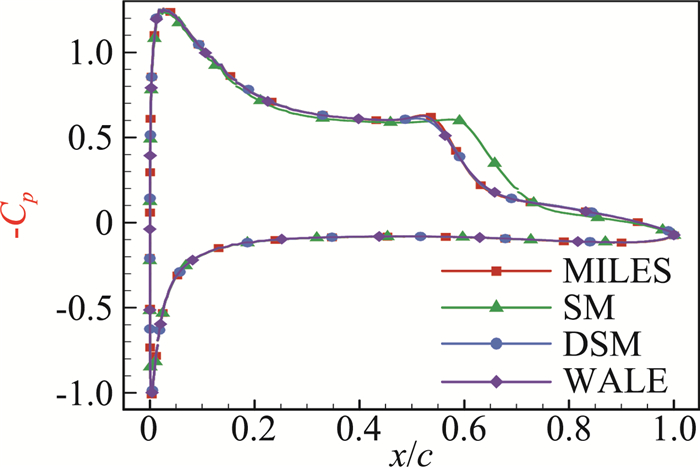
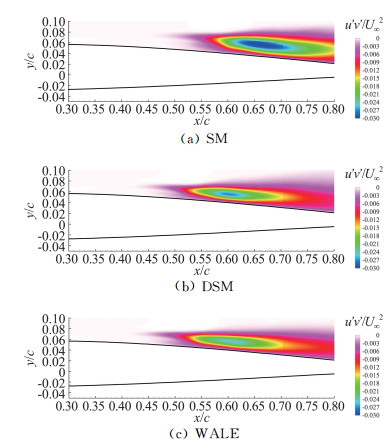
图 10给出了不同亚格子模型平均压强系数。对比可发现,SM模型在翼型上表面再附点附近压强升高起始位置显著偏后。此外,图 11列出了显式亚格子模型得到的雷诺应力分布,结合隐式模型结果(图 7a)对比可发现,SM模型得到的雷诺应力幅值较大,并且雷诺应力分布位置更靠下游,而隐式模型与DSM、WALE显式模型计算结果非常接近,并与文献试验和计算结果一致。以上结果表明:SM模型无法准确预测流动发生分离与转捩相互影响的物理现象;亚格子模型对大涡模拟计算结果影响较小;隐式大涡模拟方法可用于该类现象的模拟分析。
|
图 10 不同亚格子模型压强系数对比 Fig.10 Comparison of mean Cp by different sub-grid scale models |
|
图 11 不同亚格子模型雷诺应力对比 Fig.11 Comparison of Reynolds shear stress by different sub-grid scale models |
计算中展向取周期边界,展向可认为是无限延伸,但实际展向范围限制了流动流向涡的尺度;另一方面,网格尺度直接决定了计算所能解析的最小流动尺度。因此,分别在基准网格(Basic)上进行展向延拓(0.3倍弦长)和流向加密(Dense),加密网格单元总量1128万,以对比分析网格尺度对计算结果影响。数值方法基于隐式亚格子模型,采用AUSM格式和双时间步长方法计算求解。
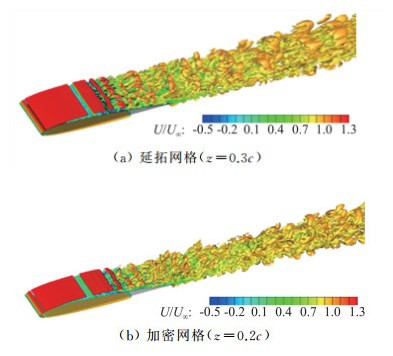
基于修改后的网格计算得到的瞬时涡系结构如图 12所示。与基准网格结果(图 2a)对比可以看到,不同展向范围和网格密度下,瞬时涡系结构形态一致,加密网格计算结果显示的流动结构更为精细。
|
图 12 不同网格瞬时涡系结构对比 Fig.12 Instantaneous vortex by different meshes |
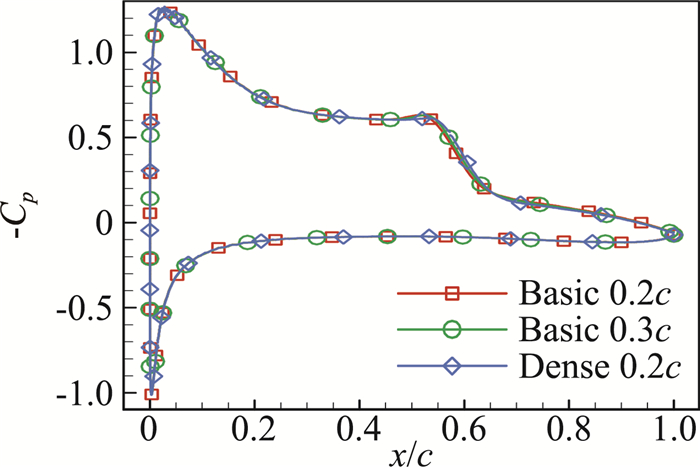
从平均压强系数对比(图 13)可看到,不同计算网格得到压强系数分布曲线近乎重合。以上结果表明,0.2倍弦长展向计算范围对于准确捕捉该类三维非定常流动结构已足够;基准网格已能解析绝大多数的流动结构;本文所采用的计算网格已达到大涡模拟计算要求。
|
图 13 不同网格平均压强系数对比 Fig.13 Comparison of mean Cp by different meshes |
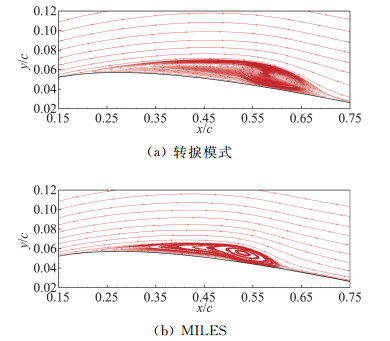
采用基于SST k-ω湍流模型的γ-Reθ转捩模式对该问题进行了数值模拟,计算得到定常解。图 14为转捩模式得到的层流分离泡与大涡模拟时均化结果的对比。可以看到,二者形态相似,但转捩模式得到的分离泡外形尺寸较大,再附点位置较试验数据(0.62和0.58)显著靠后。
|
图 14 分离泡形态对比 Fig.14 Comparison of laminar separation bubble by LES and transition model |
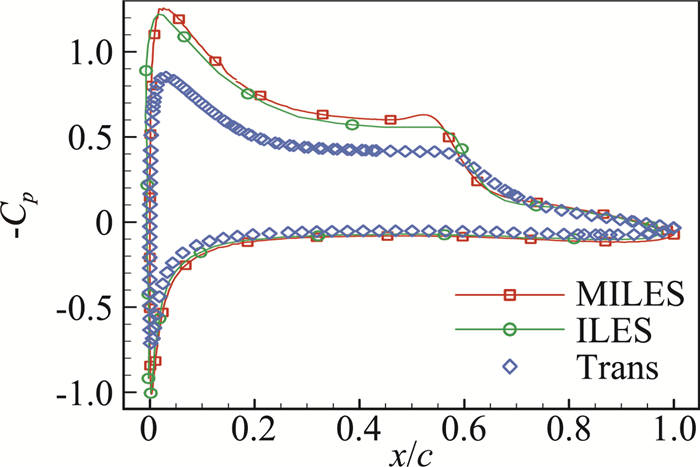
从压强系数对比(图 15)可以看到,本文大涡模拟结果(MILES)与文献中ILES结果吻合较好, 而转捩模式计算得到的翼型上表面压强分布存在较大偏差。此外,转捩模式升阻力系数计算结果分别为0.6001和0.02505,与大涡模拟计算结果(0.6160、0.02199)相对误差为2.6%和13.9%。以上结果表明,转捩模式难以对该类非定常复杂流动现象进行准确预测,获得的气动力参数存在较大偏差。
|
图 15 转捩模式与大涡模拟压强系数对比 Fig.15 Comparison of mean Cp by LES and transition model |
本文发展了基于结构化拼接网格的大涡模拟方法,对SD7003翼型层流分离流动开展了数值模拟研究,对比分析了数值格式、亚格子模型和网格尺度对计算结果影响,并与转捩模式计算结果进行了对比,得到如下结论:
1) 翼型低雷诺数层流分离流动中存在分离、转捩及再附等多尺度复杂流动结构,并具有强烈的非定常运动特征。
2) 大涡模拟方法能够精细分辨翼型层流分离流动中涡系结构的时空演化过程,并可获得时均化流场以及雷诺应力等脉动参数分布特征,计算结果与试验数据吻合较好,对于低雷诺数条件下的翼型气动特性的准确预测以及流动机理分析具有重要应用价值。
3) 对大涡模拟方法中的网格划分、数值格式、亚格子模型等关键技术的对比分析表明,采用的拼接网格能够有效解析层流分离现象中的小尺度结构;AUSM格式和双时间步方法具有较高的精度,并且计算量相对较小;隐式亚格子模型适用于低雷诺数层流分离现象的模拟预测。
4 下一步工作拟采用发展的大涡模拟方法对不同迎角及雷诺数条件下翼型层流分离现象进行数值模拟,进一步分析翼型层流分离现象中分离诱发转捩的物理机理,并对迎角和雷诺数的影响规律和作用机制开展研究。
| [1] |
李锋, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257-268. LI F, BAI P, SHI W, et al. Micro air vehicle aerodynamics at low Reynolds number[J]. Advances in Mechanics, 2007, 37(2): 257-268. DOI:10.3321/j.issn:1000-0992.2007.02.009 (in Chinese) |
| [2] |
GASTER M. The structure and behavior of laminar separation bubbles[R]. AGARD CP-4, 1966: 813-854.
|
| [3] |
HORTON H P. Laminar separation bubbles in two-and three-dimensional incompressible flow[D]. University of London, 1968.
|
| [4] |
SELIG M S, GUGLIELMO J J, et al. Experiments on airfoils at low Reynolds numbers[R]. AIAA 96-0062.
|
| [5] |
BREHM C, MACK S, GROSS A, et al. Investigations of an airfoil at low Reynolds number conditions[C]//4th AIAA Flow Control Conference. Seattle, Washington, 2008.
|
| [6] |
GROSS A, FASEL H F. Numerical investigation of separation for airfoils at low Reynolds numbers[C]//40th AIAA Fluid Dynamics Conference and Exhibit. Chicago, Illinois, 2010.
|
| [7] |
白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 416-424. BAI P, CUI E J, ZHOU W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J]. Acta Aerodynamic Sinica, 2006, 24(4): 416-424. DOI:10.3969/j.issn.0258-1825.2006.04.004 (in Chinese) |
| [8] |
YUAN W X, KHALID M, WINDTE J, et al. An investigation of low-Reynolds-number flows past airfoils[C]//23rd AIAA Applied Aerodynamics Conference. Toronto, AIAA 2005-4607.
|
| [9] |
RADESPIEL R, WINDTE J, SCHOLZ U. Numerical and experimental flow analysis of moving airfoils with laminar separation bubbles[J]. 2007, AIAA Journal, 45(6): 1346-1356.
|
| [10] |
LIAN Y S, WEI S. Laminar-turbulent transition of a low Reynolds number rigid or flexible airfoil[C]//36th AIAA Fluid Dynamics Conference and Exhibit. San Francisco, California, 2006.
|
| [11] |
CHOUDHRY A, ARJOMANDI M, KELSO R. A study of long separation bubble on thick airfoils and its consequent effects[J]. International Journal of Heat & Fluid Flow, 2015, 52: 84-96. |
| [12] |
ARNAL D, CASALIS G, JUILLEN J C. A survey of the transition prediction methods: From analytical criteria to PSE and DNS[C]//UTAM Symposia. Sendai, Japan, 1994.
|
| [13] |
YANG Z, HAAN F L, HUI H, et al. An experimental investigation on the flow separation on a low-reynolds-number airfoil[J]. AIAA Paper, AIAA-2007-0275.
|
| [14] |
ANANDA G K, SUKUMAR P P, SELIG M S. Measured aerodynamic characteristics of wings at low Reynolds numbers[J]. Aerospace Science & Technology, 2015, 42: 392-406. |
| [15] |
OL V, MCAULIFFE B R, HANFF E S, et al. Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities[C]//35th AIAA Fluid Dynamics Conference and Exhibit. Toronto, Ontario Canada, 2005. AIAA 2005-5149.
|
| [16] |
SHAN H, JIANG L, LIU C R. Direct numerical simulation of flow separation around a NACA 0012 airfoil[J]. Computers and Fluids, 2005, 34(9): 1096-1114. DOI:10.1016/j.compfluid.2004.09.003 |
| [17] |
GALBRAITH M C, VISBAL M R. Implicit large eddy simulation of low Reynolds number flow past the SD7003 airfoil[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2007.
|
| [18] |
VILEM S, MIYAJI K. Transitional flow over a SD7003 wing using flux reconstruction scheme[C]//52nd AIAA Sci Tech. National Harbor. MD, United States, 2014. AIAA 2014-0250.
|
| [19] |
艾国远, 叶建. 低雷诺数下翼型不同分离流态的大涡模拟[J]. 空气动力学学报, 2017, 35(2): 299-304. AI G Y, YE J. Large-eddy simulation of low Reynolds number airfoil with different separating flow[J]. Acta Aerodynamica Sinica, 2017, 35(2): 299-304. DOI:10.7638/kqdlxxb-2016.0159 (in Chinese) |
| [20] |
GARNIER E, ADAMS N, SAGAUT P. Large eddy simulation for compressible flows[M]. Scientific Computation, Springer Netherlands, 2009: 22-30.
|
| [21] |
LU X Y, WANG S W, SUNG H Y, et al. Large eddy simulations of turbulent swirling flows injected into a dump chamber[J]. J Fluid Mech, 2005, 527: 171-195. DOI:10.1017/S0022112004002927 |
| [22] |
BORIS J P, GRINSTEIN F F, ORAN E S, et al. New insights into large eddy simulation[J]. Fluid Dynamics Research, 1992, 10(4): 199-228. |
| [23] |
SMAGORINSKY J. General circulation experiments with the primitive equation Ⅰ: The basic experiment[J]. Monthly Weather Review, 1963, 91(3): 99-164. DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
| [24] |
GERMANO M, PIOMELLI U, MOIN P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids A: Fluid Dynamic, 1991, 3(7): 1760-1765. DOI:10.1063/1.857955 |
| [25] |
NICOUD F, FUCROS F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J]. Flow Turbulence and Combusition, 1999, 62(3): 183-200. DOI:10.1023/A:1009995426001 |
| [26] |
LIU M S. Progress towards an improved CFD method: AUSM+[R]. AIAA 95-1701, 1995.
|
| [27] |
朱志斌, 杨武兵, 禹旻. 满足几何守恒率的WENO格式及其应用[J]. 计算力学学报, 2017, 34(6): 779-784. ZHU Z B, YANG W V, YU M. A WENO scheme with geometric conservation law and its application[J]. Chinese Journal of Computational Mechanics, 2017, 34(6): 779-784. (in Chinese) |
| [28] |
LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory scheme[J]. Journal of Computational Physics, 1994, 115: 200-212. DOI:10.1006/jcph.1994.1187 |
| [29] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [30] |
DENG S T, JIANG L, LIU C Q. DNS for flow separation control around airfoil by steady and pulsed jets[J]. Computer & Fluid, 2007, 36(6): 1040-1060. |
| [31] |
ANTONY J. Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings[C]//AIAA 10th Computational Fluid Dynamics Conference. Honolulu, HI, 1991.
|
 2019, Vol. 37
2019, Vol. 37


