钝体绕流是流体力学研究中的经典课题。研究表征其尾流场特点的参数(如临界雷诺数、阻力系数、斯特劳哈尔数等)与流场结构的关系, 可以为工程问题提供可靠的理论依据。
目前学者对圆柱、矩形柱绕流进行了大量研究,而对三棱柱绕流流场的研究相对较少。研究中发现柱体的截面形状、尺度比以及来流工况都会对绕流流场产生影响。在数值模拟研究方面,刘聪等[1]利用格子Boltzmann方法对比了低雷诺数20≤Re≤100下方柱、1/4圆柱和棱柱的绕流流场,得出方柱的阻力系数最大,棱柱次之。Ganga Prasath等[2]研究发现,三棱柱尺度比H(H=h/D=0.5~5.0, h为三棱柱截面底边所对的高,D为截面底边长)的增加会提高临界雷诺数,这个现象在顶点背风时表现得尤为显著。Bao Y等[3]研究了来流攻角对正三棱柱尾流场的影响,指出当Re=100、三棱柱沿流向不对称放置时其阻力系数变化有两个主频率。同时众多国外学者针对低雷诺数下三棱柱对流传热课题进行研究,总结出尾流场形态及其特征参数同雷诺数之间的变化关系[4-7]。国内陆建洲等人[8]研究了低雷诺数Re≤160时三棱柱尺度比(H=0.2~3)对临界雷诺数、升阻力系数、尾涡强度等参数的影响,但缺乏对流场结构的深入分析。在实验研究方面,Buresti等[9]通过风洞实验分析了在高雷诺数Re=1.2×105时,不同尺度比(H=1.0~3.0)、来流攻角下三棱柱的尾流特点,发现尺度比越小时旋涡脱落越快。Srigrarom等[10]利用流动显示和PIV实验探究了正三棱柱在二维不可压缩流中的流动情况,结果显示Re=7500时三棱柱沿流向不对称放置时两个侧面的流动状态不同,会形成自激振荡,使三棱柱发生交替旋转运动。目前国外学者对三棱柱绕流的研究居多,以数值模拟方法为主,并且研究缺少三棱柱在低雷诺数Re=200~800工况的数据。同时三棱柱绕流流场具有其特殊性,在某些领域三棱柱比圆柱和矩形柱更加适用,如涡街流量计中的旋涡发生体[11]、航空涡轮发动机和冲压发动机燃烧室内的火焰稳定器[12]。因此,对三棱柱绕流问题有必要进行更加细致的实验研究。
本文利用粒子成像测速技术(Particle Image Velocimetry, PIV)对三棱柱实验件在雷诺数Re=500条件下的流场进行二维平面的研究,结合本征正交分解法和时间空间关联法,探讨尾流宽度、尾涡形成长度、旋涡平均输运速率、阻力系数等重要尾流参数的变化情况,得到三棱柱尺度比对尾流场的作用机理。
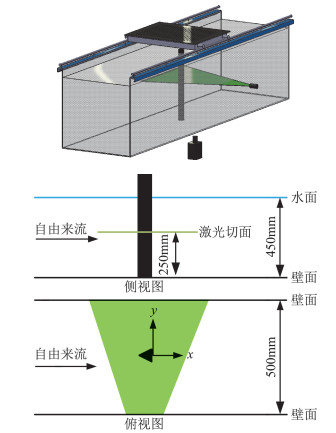
1 实验模型及设备本文的实验测量工作均在厦门大学流体&PIV实验室[13]的多功能流体力学实验平台上完成。PIV实验采样方案如图 1所示,三棱柱垂直固定在水槽底端,激光从水槽右侧水平打入,高速相机固定在水槽底部,确保片光源与高速相机拍摄平面垂直。三棱柱柱体长480 mm。水槽液面高度L=450 mm,此时激光切面距离水槽底面250 mm。三棱柱柱体截面底边中心和坐标原点重合,x轴正方向与来流方向一致。
|
图 1 实验方案 Fig.1 Experiment scheme |
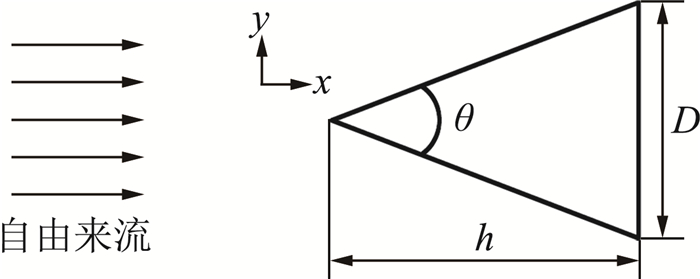
实验研究不同尺度比H的三棱柱在雷诺数Re=500来流工况下的绕流流场。如图 2所示,三棱柱截面底边长为D=12mm,长细比为L/D=37.5;高为h,尺度比H=h/D。研究柱体截面顶角θ分别为15°、30°、45°、60°、75°,尺度比H相应为3.8、1.9、1.2、0.9、0.7。雷诺数
|
图 2 流场工况定义 Fig.2 Definition of flow field conditions |
粒子成像测速技术(PIV)是通过在流场中散布跟随性和反光性良好的示踪粒子,用高速相机对激光片光照亮的特定测量区域连续曝光记录两次,得到粒子在时间t和t+Δt的两幅图像,再利用专业的图像分析处理技术对这两幅图像进行互相关分析,就能得到该区域流场内部的二维速度矢量场[14]。在PIV图像处理过程中,本文用Dantec公司开发的Dynamic Studio 2016a软件对相机连续拍摄得到的两帧粒子图像进行互相关处理分析,系统误差在1%以内。实验中所用的PIV相机为高速CMOS相机,分辨率200万像素。采样频率为50 Hz, 采集1542幅原始图片,保证采样时间足够长,从而利用PIV数据测得的速度信号进行频谱分析,得到尾流场中大尺度旋涡结构运动频率。
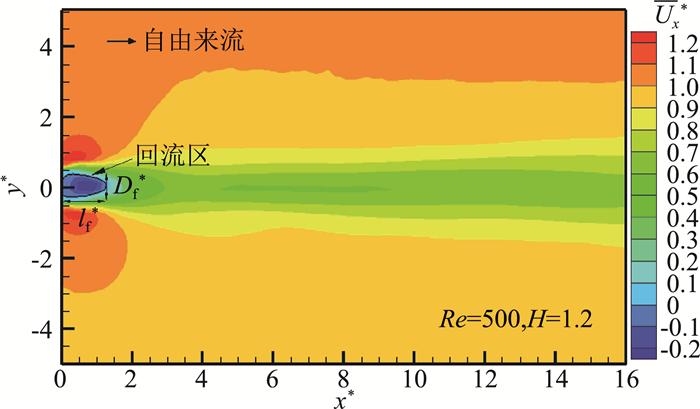
2 PIV实验结果及分析 2.1 不同截面尺度比H的三棱柱绕流流场定常分析在Re=500来流工况下进行尾流场定常分析。选取截面底边D作为特征长度无量纲化长度单位,分别有x*=x/D,y*=y/D。图 3是实验雷诺数Re=500时,尺度比H=1.2工况下无量纲化流向时均速度
|
图 3 流向时均速度 |
| 表 1 不同尺度比H下尾涡参数 Table 1 Parameters of the wake vortex with different aspect ratios H |
|
|
Schlichting首次利用动量方程(1979)估算不同工况下尾流场的阻力系数的变化。利用上述方法能得到较精确的平均阻力系数CD,计算公式[16]如下:
| $ \begin{aligned} C_{D}=& 2 \int_{-\infty}^{\infty} \frac{U}{U_{\infty}} \frac{\left(U_{\infty}-U\right)}{U_{\infty}} \mathrm{d}\left(\frac{y}{D}\right)+\\ & 2 \int_{-\infty}^{\infty} \frac{\overline{v^{\prime 2}}-\overline{u^{\prime 2}}}{U_{\infty}^{2}} \mathrm{d}\left(\frac{y}{D}\right) \end{aligned} $ | (1) |
式中u′、v′分别为流向和法向脉动速度,U=U(x*,y*)选取x*=16处展向速度分布,计算结果如表 2所示。雷诺数Re=500时,三棱柱压差阻力所占比重更大,截面更接近流线型,使得抑制尾流分离的作用明显大于黏性作用。因此尾流场阻力系数CD随着三棱柱尺度比H的增大而减小。
| 表 2 不同尺度比H下,尾流场平均阻力系数CD Table 2 Variation of mean drag coefficient CD with different aspect ratios H |
|
|
雷诺应力并不是严格意义上的表面应力,它是对真实的脉动运动进行平均处理时,将脉动引起的动量交换折算在想象的平均运动界面上的作用力。无量纲化的雷诺应力可由式(2)表示。
| $ -\left\langle u^{\prime} v^{\prime}\right\rangle / U_{\infty}^{2} $ | (2) |
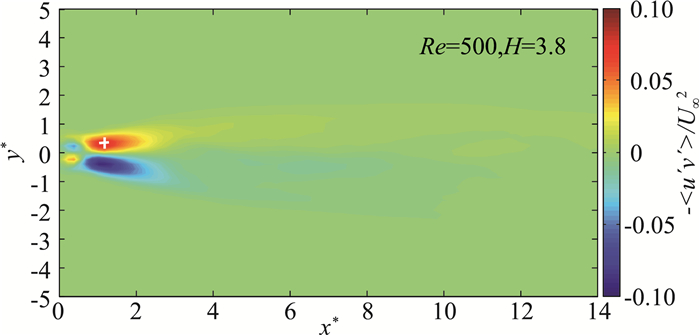
图 4为雷诺数Re=500、尺度比H=3.8工况下,无量纲化雷诺应力-〈u′v′〉/U∞2的分布。雷诺应力密集区代表强剪切作用,该区域与涡旋形成有关(图 4中雷诺应力峰值点由符号“+”标记)。
|
图 4 无量纲化雷诺应力分布 Fig.4 Distribution of the dimensionless Reynolds stress -〈u′v′〉/U∞2 |
Re=500时,在x*=1.26、y*=±0.3处雷诺应力最大。取无量纲雷诺应力峰值稍偏后处(x*=2,y*=0.3)为速度监测点,对其流向速度信号进行频谱分析,即得出涡脱频率fs。根据式(3),可进一步得到不同尺度比H下尾流场的斯特劳哈尔数St,见表 3。发现,Re=500时,St随尺度比H的减小而小,即三棱柱尺度比H越小,旋涡脱落越慢,流场非定常性变弱,这和高雷诺数下的特点不同[9]。
| $ S t=\frac{f_{\rm s} D}{U_{\infty}} $ | (3) |
| 表 3 不同尺度比H下斯特劳哈尔数St Table 3 Variation of Strouhal number St with different aspect ratios H |
|
|
利用空间时间关联分析法(即空间分离和时间延迟),对其法向脉动速度进行时空分析,得出稳定区域内的涡旋平均输运速率Ulocal。计算公式为[17]:
空间关联:
| $ R\left(r_{1}, r_{2}\right)=\frac{\overline{u^{\prime}(x) u^{\prime}(x+r)}}{\overline{u^{\prime 2}(x)}} $ | (4) |
时间空间关联:
| $ R\left(r_{1}, r_{2}, t\right)=\frac{\overline{u^{\prime}\left(r_{1}, t\right) u^{\prime}\left(r_{2}, t\right)}}{\sqrt{u^{\prime}\left(r_{1}, t\right)^{2} u^{\prime}\left(r_{2}, t\right)^{2}}} $ | (5) |
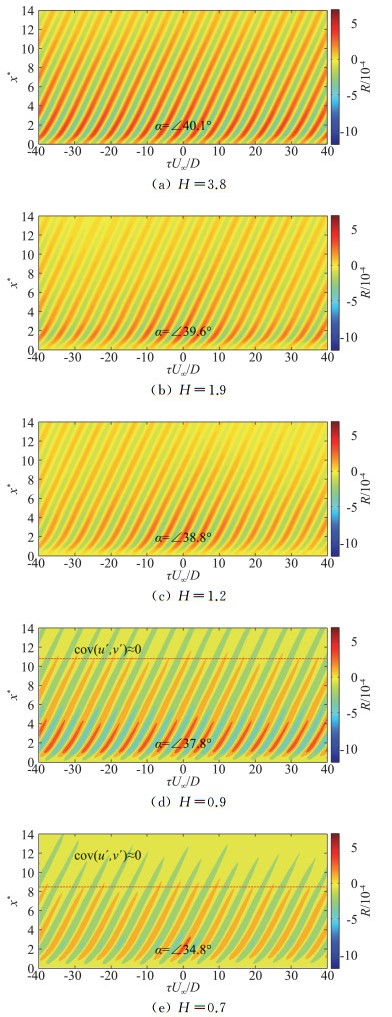
图 5是不同尺度比H、以(x*=2,y*=0.3)为参考点,流体法向脉动速度的时空分布图。图中横坐标为无量纲化的延迟时间
|
图 5 法向脉动速度时空分布 Fig.5 Time-space distribution of vertical velocity |
|
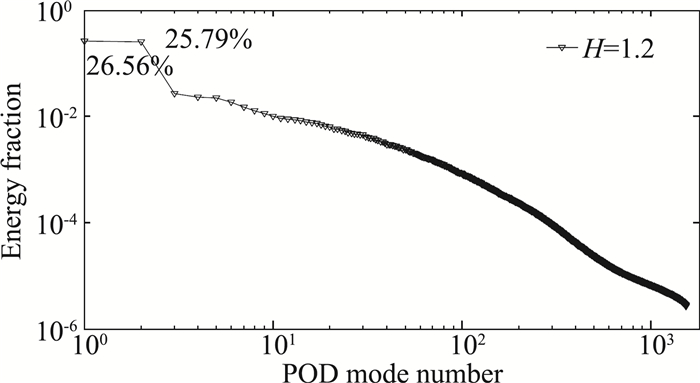
图 6 各阶模态湍动能占比 Fig.6 Turbulent kinetic energy fraction in different POD modes |
| 表 4 不同尺度比H下涡街平均输运速率Ulocal/U∞ Table 4 Variation of Ulocal/U∞ with different aspect ratios H |
|
|
利用Sirovich提出的快照POD(Snapshot POD)算法[18-20]进行PIV数据的本征正交分解分析。如图 6所示通过比较不同尺度比下各模态湍动能占比可以发现,1、2阶模态能量占比最大,而表征流场小尺度结构特征的高阶模态所含有的湍动能随模态阶数增加而骤降。并且从统计得到的表 5不同尺度比下前10阶模态能量分布中可以发现,小尺度比下高阶模态湍动能占比之和有所增加,流场不稳定性增加,使得尾流场中的大尺度涡旋结构越容易变成小尺度的涡旋结构。
| 表 5 不同尺度比H下前10阶模态的能量分布 Table 5 Energy distribution of first ten modes with different aspect ratios H |
|
|
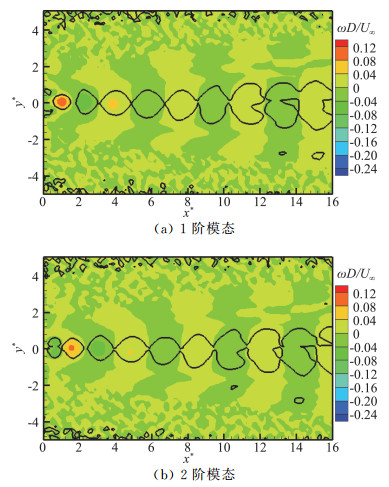
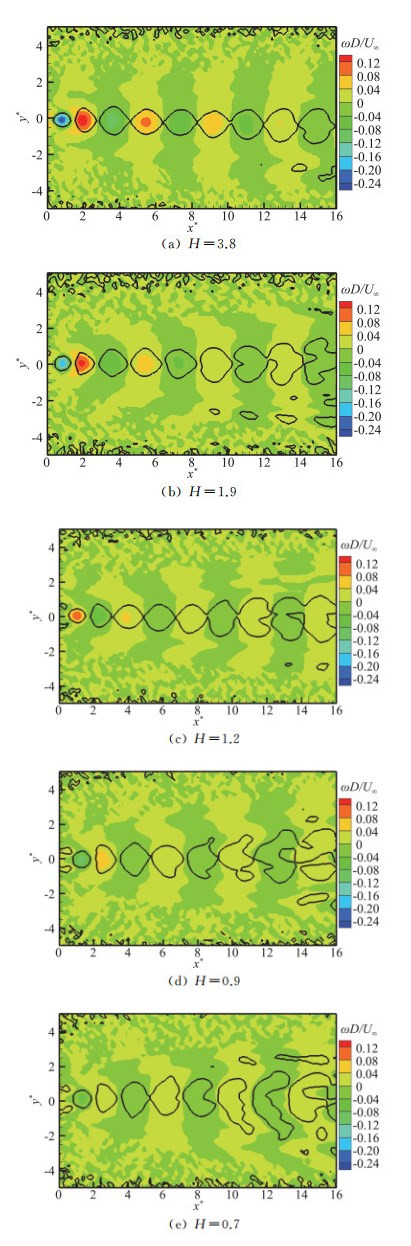
如图 7所示,通过比较尺度比H=1.2时的前两阶模态流场结构,发现利用1或2阶模态流场结构可直观地看出卡门涡街拖动剪切层向下游输运过程中的较稳定区域以及涡街失稳区域。图 8为雷诺数Re=500、不同尺度比H工况下1阶模态无量纲涡量云图(图中黑色封闭轮廓线为应用λ2算法[21]识别出的流场中涡旋结构)。结合图 5时空分布和表 6的模态能量分布可以发现,对于Re=500工况,随着三棱柱尺度比H的减小,尾流场愈加不稳定,涡街稳定向下游运输的区域开始减小,表现为同一涡旋涡量不集中,涡街更容易出现撕裂、合并吞噬等现象。上述现象在H=0.9、0.7工况下尤为明显。具体表现如下:对于H=3.8、1.9、1.2工况,涡旋在流向x*=0~16区域均保持规则结构;而对于H=0.9、0.7工况,涡旋结构分别仅在x*=0~11和x*=0~9区域保持相对规则,但在尾流场远端涡旋涡量也不再集中,并向展向扩散,导致整体尾流宽度增大,从而引起流体对三棱柱柱体阻力的增加。
|
图 7 三棱柱绕流流场前2阶模态图(H=1.2) Fig.7 First two modes of the proper orthogonal decomposition (H=1.2) |
|
图 8 三棱柱绕流流场1阶模态图 Fig.8 First mode of the proper orthogonal decomposition |
通过对低雷诺数Re=500时,不同尺度比工况下的三棱柱尾流场进行实验分析,得出以下结论:
1) 三棱柱尺度比H的减小,对尾流场的尾流宽度、尾涡形成长度都有明显的促进作用,旋涡脱落变慢。
2) 三棱柱尾流场中涡街稳定运输区域和涡街向下游平均运输速率均随三棱柱尺度比H的减小而减小。
3) 三棱柱尺度比H的减小使尾流场愈加不稳定,涡街难以保持规则结构。尾流场远端涡旋涡量也不再集中,并向展向扩散,导致整体尾流宽度增大,从而引起流体对三棱柱柱体阻力的增加。
| [1] |
刘聪, 李艳, 梅宁. 低雷诺数下钝体绕流的流动特性研究[J]. 中国科技纵横, 2013(19): 157-158. LIU C, LI Y, MEI N. Study on the flow characteristics of low reynolds number flow over a bluff body[J]. China Science & Technology Overview, 2013(19): 157-158. DOI:10.3969/j.issn.1671-2064.2013.19.104 (in Chinese) |
| [2] |
GANGAPRASATH S, SUDHARSAN M, VINODH KUMAR V, et al. Effects of aspect ratio and orientation on the wake characteristics of low Reynolds number flow over a triangular prism[J]. Journal of Fluids and Structures, 2014, 46: 59-76. DOI:10.1016/j.jfluidstructs.2013.12.008 |
| [3] |
BAO Y, ZHOU D, ZHAO Y J. A two-step Taylor-characteristic-based Galerkin method for incompressible flows and its application to flow over triangular cylinder with different incidence angles[J]. International Journal for Numerical Methods in Fluids, 2010, 62(11): 1181-1208. DOI:10.1002/fld2054 |
| [4] |
SRIKANTH S, DHIMAN A K, BIJJAM S. Confined flow and heat transfer across a triangular cylinder in a channel[J]. International Journal of Thermal Sciences, 2010, 49(11): 2191-2200. DOI:10.1016/j.ijthermalsci.2010.06.010 |
| [5] |
ZEITOUN O, ALI M, NUHAIT A. Convective heat transfer around a triangular cylinder in an air cross flow[J]. International Journal of Thermal Sciences, 2011, 50(9): 1685-1697. DOI:10.1016/j.ijthermalsci.2011.04.011 |
| [6] |
DE A K, DALAL A. Numerical study of laminar forced convection fluid flow and heat transfer from a triangular cylinder placed in a channel[J]. Journal of Heat Transfer, 2007, 129(5): 646-656. DOI:10.1115/1.2712848 |
| [7] |
ABBASSI H, TURKI S, NASRALLAH S B. Numerical investigation of forced convection in a plane channel with a built-in triangular prism[J]. International Journal of Thermal Sciences, 2001, 40(7): 649-658. DOI:10.1016/S1290-0729(01)01254-6 |
| [8] |
陆建洲, 陶建军. 三棱柱的低雷诺数绕流研究[J]. 航空动力学报, 2016, 31(5): 1226-1233. LU J Z, TAO J J. Low-Reynolds-number wake flows of a triangular prism[J]. Journal of Aerospace Power, 2016, 31(5): 1226-1233. DOI:10.13224/j.cnki.jasp.2016.05.026 (in Chinese) |
| [9] |
IUNGO G V, BURESTI G. Experimental investigation on the aerodynamic loads and wake flow features of low aspect-ratio triangular prisms at different wind directions[J]. Journal of Fluids and Structures, 2009, 25(7): 1119-1135. DOI:10.1016/j.jfluidstructs.2009.06.004 |
| [10] |
SRIGRAROM S, KOH A K G. Flow field of self-excited rotationally oscillating equilateral triangular cylinder[J]. Journal of Fluids and Structures, 2008, 24(5): 750-755. DOI:10.1016/j.jfluidstructs.2007.10.015 |
| [11] |
苏彦勋, 盛健.流量计量和测试[M].北京: 中国计量出版社, 2007, 87-103. SU Y X, SHENG J. Flow measurement and testing[M]. China Metrology Publishing House, 2007, 87-103.(in Chinese) |
| [12] |
金莉, 谭永华. 火焰稳定器综述[J]. 火箭推进, 2006, 32(1): 30-34. JIN L, TAN Y H. Study on flameholders[J]. Journal of Rocket Propulsion, 2006, 32(1): 30-34. DOI:10.3969/j.issn.1672-9374.2006.01.006 (in Chinese) |
| [13] |
刘锦生, 邹赫, 刘志荣, 等. 开缝圆柱缝隙倾斜角对脱落涡的影响[J]. 北京航空航天大学学报, 2017, 43(1): 128-135. LIU J S, ZOU H, LIU Z R, et al. Performance of vortex shedding behind a slotted circular cylinder with different angles of attack[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1): 128-135. DOI:10.13700/j.bh.1001-5965.2016.0058 (in Chinese) |
| [14] |
刘玥, 梁忠生, 鲍锋. 粒子成像测速-非介入式全场技术[J]. 中国科技信息, 2010, 13(11): 37-40. LIU Y, LIANG Z S, BAO F. Particle image velocimetry-a whole fields technology without disturbs the flow[J]. Chinese Science and Technology Information, 2010, 13(11): 37-40. DOI:10.3969/j.issn.1001-8972.2010.13.011 (in Chinese) |
| [15] |
ROSHKO A. On the wake and drag of bluff bodies[J]. Journal of the Aeronautical Sciences, 1955, 22(2): 124-132. DOI:10.2514/8.3286 |
| [16] |
QU Y, WANG J, SUN M, et al. Wake vortex evolution of square cylinder with a slot synthetic jet positioned at the rear surface[J]. Journal of Fluid Mechanics, 2017, 812: 940-965. DOI:10.1017/jfm.2016.833 |
| [17] |
陈懋章. 粘性流体动力学基础[M]. 高等教育出版社, 2006: 275-278. CHEN M Z. Fundamentals of viscous fluid dynamics[M]. Higher Education Press, 2006: 275-278. (in Chinese) |
| [18] |
MA X, KARNIADAKIS G E, PARK H, et al. DPIV-driven flow simulation:a new computational paradigm[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2003, 459(2031): 547-565. DOI:10.1098/rspa.2002.0981 |
| [19] |
VENTURI, DANIELE. On proper orthogonal decomposition of randomly perturbed fields with applications to flow past a cylinder and natural convection over a horizontal plate[J]. Journal of Fluid Mechanics, 2006, 559: 215-254. DOI:10.1017/S0022112006000346 |
| [20] |
KONSTANTINIDIS E, BALABANI S, YIANNESKIS M. Bimodal vortex shedding in a perturbed cylinder wake[J]. Physics Fluids, 2007, 19(1): 011701-011704. DOI:10.1063/1.2432152 |
| [21] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285(1): 69-94. DOI:10.1017/S0022112095000462 |
 2019, Vol. 37
2019, Vol. 37


