减阻是外流空气动力学的基本任务之一,大飞机减阻是当代航空技术的一个迫切需求。减阻的前提是对阻力主要组分做出正确的物理解释和准确的理论预测。在传统流场诊断和减阻方案中采用的原则是线性分解、各个击破和线性叠加,并据此选定合适的阻力分类方式,追溯阻力各组分的物理来源,寻找对应的减阻措施[1]。例如,采用改变壁面条件来控制摩擦阻力[2],采用吹吸气抑制流场分离来控制压差阻力[3],采用翼梢小翼来控制诱导阻力,等等。在实际工程应用中则把对各个阻力的相应减阻方案结合起来以达到总体减阻的目标。
但是,如我们最近的研究[4]评述的,当前国内外的减阻思路存在若干根本性弊病,普遍的问题包括:阻力分类不唯一,阻力成分占比预测不精确,总体减阻结果也并非各减阻措施的简单线性叠加。
其实,对于任意构型的定常绕流(包括雷诺时均定常湍流),在亚声速情况下只有两种阻力分解方式具有严格的理论基础[5]:第一种把物面应力积分得到的总阻力D分解成压差阻力Dp和摩擦阻力Df,其物理意义是清晰而无歧义的;第二种则用流场动量平衡的体积分得到诱导阻力Di和型阻DP。这里的流场体积分可以转换为外边界的面积分,再通过选取合适的控制面简化为适当尾流截面的积分。第一种分解方式是普适的,对任何物体在任何流动条件下都成立,但无法将阻力与实际流场中的结构联系起来,故需转向基于动量平衡积分的第二种分解方式。可是,由于CFD和EFD都无法分别单独测量Di和DP,它们中至少一个必须先给出精确的理论定义(另一个可由总阻力推出)才知道要测量或计算什么,其可靠性完全取决于理论的可靠性。理论好,则定义合理可信;若理论过于简化,则定义不准,减阻措施打不中要害,而毛病何在却是根据定义算不出测不到的。现在工程中常用的诱导阻力公式均基于线化尾流模型,引入Trefftz平面假设,通过展向升力[6]或者尾流面上流向涡量分布[7]来确定诱导阻力。这些公式对小攻角大展弦比薄翼的附着流基本适用,但对真实的复杂流动却偏差很大。为此,Zou等[4]对该问题进行了深入的研究,提出了三维不可压缩定常黏性流动中基于尾流积分的气动力分量精确理论。
这个理论仍基于传统的线性思维,却揭示了两个无法回避的问题。一是在给定构型和流动条件下,型阻和诱导阻力不再是纯数而是尾流截面位置的函数。Zou等[4]从理论和数值上确认了该变化的趋势,并查明了其随尾流截面位置变化的物理根源。型阻和诱导阻力客观性的丧失,使得寻找合适阻力分量测量位置、确认减阻措施的有效性成了无法解决的难题。二是升力、型阻和诱导阻力是物理上同源的,可分别采用Lamb矢量的体积分或其矩的面积分来定义。Lamb矢量是所有气动力的核心。这个观察在Wu等[8]的书中已初现端倪,但未系统追究。它的结论是:若要通过线性思维减少某阻力分量,必会对其余气动力分量产生影响。气动力分量的非客观性和同源性使得原有的基于线性分解、各个击破、线性叠加的传统流动诊断和减阻方案无法应对真实非线性流场。
针对上述问题,我们提出了两种不同的解决方案。方案一保留传统气动力分解框架,给出附着流的诱导阻力中场近似。该方案兼顾了阻力分解的精确性和公式的易用性,适用于常规的大飞机气动设计。方案二突破传统的阻力分解框架,构造面向任意复杂构型气动力诊断的新型断层扫描技术,可称为空气动力学CT,其理念来源于现代空气动力学理论。Wu等[9]述评了关于黏性可压缩复杂流动的现代空气动力学基础理论及其CFD/EFD检验,其中提出了现代空气动力学理论在近场可以分为三个不同的层次:速度压力层次、结构层次以及因果层次。所有这些层次的理论相互丰富,而非相互排斥。对于复杂流动,不同层次的理论应该联合使用,并与CFD/EFD紧密结合。结合CFD/EFD的现实情况可知,非线性近场得到的数据是最为准确的,也是利用有限的CFD/EFD数据进行局部动力学诊断和优化的最佳场所。若需要,甚至可以将截面切入物体内部.这种观念上的解放,意味着不再纠结于寻找“客观”的阻力分类方式,而是转向研究流场结构与气动力的直接联系并追溯其在壁面的产生根源。
本文介绍笔者的课题组基于上述认识的研究成果。为叙述方便完整起见,本文第1节回顾Zou等[4]的研究成果,第2节系统阐述气动力分量的同源性及其本征机理,第3节提出空气动力学CT技术,展示新的进展。本文仅限于不可压流。
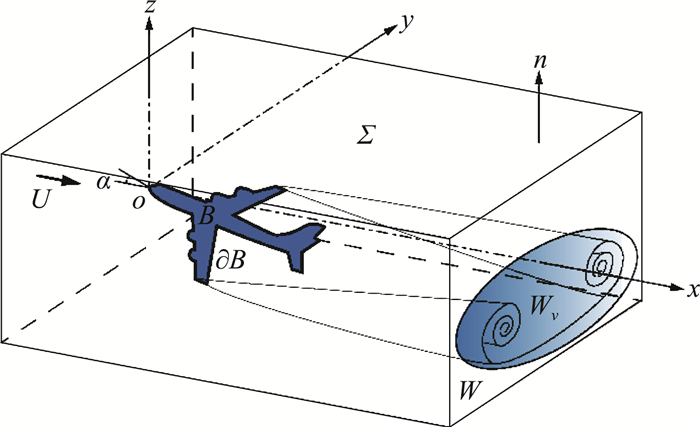
1 定常黏性不可压外流的气动力分解理论及紧致中场近似考虑一个绕任意飞行器的三维定常黏性流动,均匀来流速度为U=Uex,飞行器B的外边界为∂B。图 1定义了固定于飞行器的坐标系(x, y, z),流向坐标x的原点位于机翼前缘,并列出了下面将用到的标记:控制面∑包围了流体区域Vf以及飞行器B,因此V=Vf∪B。流体域外边界∂Vf的单位法向量指向流体外部。在大雷诺数下,∑上的黏性力可以忽略。控制面∑仅在尾流处切割涡量场,其前面和侧面上的流动是无黏无旋的。尾流中的涡量ω ≠0仅仅在尾流面上很小的一个区域Wv
|
图 1 流体分析区域以及标记 Fig.1 Flow domain to be analyzed and notations |
首先回顾当前常用的定常不可压层流诱导阻力和型阻公式(时均湍流中的公式只需略加修改),再简述精确的一般理论,探讨气动力客观性丧失的物理根源,最后提出保留传统气动力分解框架的诱导阻力中场近似。
1.1 常用型阻和诱导阻力公式采用尾流积分(W-积分)定义的型阻是清晰且明确的[10-11]:
| $ {D_P} = \int_W {\left( {{P_\infty } - P} \right){\rm{d}}S} $ | (1) |
其中P=p+ρ|u|2/2是总压,p、ρ和u分别是压强、密度和速度。式(1)适用于任何飞行器的定常绕流。与此相反,诱导阻力Di的尾流积分表达式却并不唯一。在当前的工程应用中,有两个简单的Di定义公式。一个是经典的Prandtl[6, 12]公式,无黏且DP=0,
| $ {D_i} = \frac{{{L^2}}}{{{\rm{ \mathsf{ π} }}\mathit{\Lambda }}}\left( {1 + \delta } \right),\;\;\;\delta = \sum\limits_{n = 2}^\infty n {\left( {\frac{{{A_n}}}{{{A_1}}}} \right)^2} $ | (2) |
其中Λ和An分别是展弦比和升力展向分布的Fourier展开系数。对于椭圆升力分布,δ=0,从而得到单个机翼的最小诱导阻力。另一个是Maskell公式[7],可用于黏流:
| $ \begin{array}{l} {D_i} = - \frac{\rho }{2}\int_T {{\omega _x}} {\psi _x}{\rm{d}}S\\ \;\;\;\; = - \frac{\rho }{2}\int_T {\int_T {\frac{{{\omega _x}\omega _x^\prime }}{{\rm{ \mathsf{ π} }}}} } \ln \left| {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}^\prime }} \right|{\rm{d}}S{\rm{d}}S' \end{array} $ | (3) |
其中ωx是流向涡量, ▽2ψx=-ωx, r =yey+zez是远场Trefftz平面T上的位置矢量。公式(2)和公式(3)均基于线化尾流模型,在尾流截面上只保留流向涡量ω =(ωx, 0, 0)。该假设使得公式(2)和公式(3)在小攻角大展弦比薄翼的附着流中基本适用[13],但Zou等[4]指出它们在真实复杂流动中有较大偏差。
过去30年中,如何定义一般流动情况下的诱导阻力一直是个非常活跃的研究领域[5, 14-22]。在这些讨论中,Di的另一个通用公式常作为研究的起点。令u = U + v =(U+u′, v, w),有[5, 16-22]
| $ \begin{array}{l} {D_i} = \rho \int_W {\left( {k - {{u'}^2}} \right){\rm{d}}S} \\ \;\;\;\; = \frac{\rho }{2}\int_W {\left( {{v^2} + {w^2} - {{u'}^2}} \right){\rm{d}}S} \end{array} $ | (4) |
其中k=|v|2/2是扰动动能。然而,公式(4)仅仅意味着诱导阻力可以表示为被尾流对流带走的扰动动能减去流向扰动动量,物理含义含糊,而且被积函数在尾流中弥散。这个公式不适用于实际的尾流测量。现有的理论推导(可压缩流动)主要采用摄动方法,Maskell公式(3)则被证明是个一阶近似[16]。总的来看,在非线性黏性流动中如何精确定义诱导阻力并解释其物理含义,一直没有显著的进展,这也导致了对整个诱导阻力预测理论“长期存在的不满” (Spalart[22])。
1.2 型阻与诱导阻力的精确定义为精确定义基于尾流积分的阻力分量,通常从动量方程出发,方程(4)就是其中的一个结果。其实,诱导阻力的概念和理论源于Prandtl[6],但很少人注意到在同一篇论文中,Prandtl已经给出了定常无黏流升阻力的一般涡力理论,其诱导阻力公式仅是这个理论在升力线近似下简化到最低阶的解析表示。Wu等[8]在Prandtl涡力理论的基础上,将其进一步拓展到了黏性流动中,并采用体积分以及尾流截面积分,分别给出了诱导阻力和型阻的精确的一般定义式:
| $ {D_i} = \rho \int_V {{\mathit{\boldsymbol{e}}_x}} \cdot \left( {\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}} \right){\rm{d}}V $ | (5) |
| $ \begin{array}{l} {D_P} = \frac{\rho }{2}\int_{{W_v}} \mathit{\boldsymbol{r}} \cdot \left( {\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{\omega }}} \right){\rm{d}}S\\ \;\;\;\;\; = \frac{\rho }{2}\mathit{\boldsymbol{U}} \cdot \int_{{W_v}} \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{r}}{\rm{d}}S + \frac{\rho }{2}\int_{{W_v}} \mathit{\boldsymbol{r}} \cdot \left( {\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}} \right){\rm{d}}S\\ \;\;\;\;\; \equiv {D_{P0}} + {D_{P1}} \end{array} $ | (6) |
公式(5)是一个具有明确物理意义的紧致积分,Marongiu等[13]已用数值计算验证了它的正确性。它可以严格地转换为公式(4),说明诱导阻力的体积分定义和W上的非紧致积分等价。公式(6)则是从公式(1)直接通过导数矩变换得来,两者也等价。此式表明,型阻的物理载体是物体定常运动产生的Lamb矢量场的矩,积分区域是紧致的。这对于物理理解、精确计算测量和流动诊断具有极其重要的作用。
为了实际计算和测量的方便,积分区域应越小越好。型阻的一般定义式(6)满足该需求,而诱导阻力的一般定义式(5)可进一步转换为尾流截面积分,但留下明显依赖于x的非紧致项:
| $ \begin{array}{*{20}{c}} {{D_i} = \frac{\rho }{2}\int_{{W_v}} \mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{\psi }}{\rm{d}}S + \rho \int_{{W_v}} \mathit{\boldsymbol{r}} \cdot \left( {\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}} \right){\rm{d}}S + }\\ {\frac{\rho }{2}\frac{{\rm{d}}}{{{\rm{d}}x}}\int_{{W_v}} {\left[ {{\mathit{\boldsymbol{e}}_x} \cdot (\mathit{\boldsymbol{\psi }} \times \mathit{\boldsymbol{v}}) + 2u'\mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{r}}} \right]{\rm{d}}S} } \end{array} $ | (7) |
其中▽2ψ =- ω。我们称方程(7)为诱导阻力的(ω, ψ)表述,它显然是Maskell公式(3)在三维非线性流动中的一个扩展。值得注意的是,第二项紧致积分正是型阻公式(6)中的2DP1,这意味着至少在(ω, ψ)表述中,诱导阻力和型阻在本质上(在目前是运动学上)相关或者耦合。非紧致积分中对x的导数来自于三维向量f的散度▽· f在W上的积分,它明确显示了诱导阻力的x依赖性。与简洁优雅的诱导阻力体积分定义式(5)相比,W积分公式(7)不够自然,还残留着物理上模糊的非紧致项。
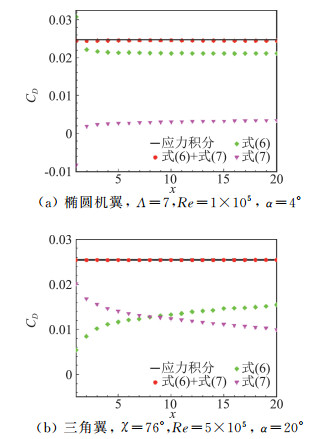
对于上述严格的三维黏性尾流截面积分理论,Zou等[4]的论文中采用两个典型的定常流计算结果——雷诺Re=1×105、攻角α=4°的绕Xt=1.0椭圆机翼的附着流以及Re=5×105、α=20°的绕后掠角χ=76°细长三角翼的分离流——分别验证了其在附着流和分离流中的准确性与有效性。具体细节可以参阅该论文,在此我们只关注型阻DP和诱导阻力Di与总阻力D随x的演化关系,如图 2所示。由公式(6)+公式(7)计算出的总阻力与壁面应力积分计算出的结果符合得很好,两者最大的相对误差小于2%。我们发现在近尾流区域,Di和DP都是x相关的。椭圆机翼的Di和DP在机翼尾缘随x变化较大,但随后便基本保持不变。但是,三角翼的DP一直单调上升,而Di最初占据了D的绝大部分并在后缘附近达最大值,然后单调减少,这导致在中场以后DP占了D的绝大部分。已有理论证明[14, 23-25],随x→∞,有Di→0, DP→D。
|
图 2 总阻力D的x依赖性 Fig.2 The x-dependency of D for the elliptic wing and delta wing |
1.2节从理论和数值两个方面确认了:气动力分量总是具有x依赖性;这种依赖性在附着流中比较弱,即在近尾流比较明显,而在远尾流基本可以认为不存在;但在定常分离流中却很强:在近尾流和远尾流都有着明显的体现。
进而,Zou等[4]找到Di和DP的x依赖性根源。在运动学上,对公式(5)沿x方向求导,可得:
| $ \frac{{{\rm{d}}{D_i}}}{{{\rm{d}}x}} = \rho \int_{{W_v}(x)} {{\mathit{\boldsymbol{e}}_x}} \cdot (\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}){\rm{d}}S $ | (8) |
这表明诱导阻力随x的变化取决于尾流截面上的扰动Lamb矢量的x分量积分。若将扰动速度和涡量分解为v =vxex+ vπ, ω =ωxex+ ωπ,下标π代表着尾流W截面上的切向向量,有
| $ {\mathit{\boldsymbol{e}}_x} \cdot \left( {\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}} \right) = {\mathit{\boldsymbol{e}}_x} \cdot \left( {{\mathit{\boldsymbol{v}}_{\rm{ \mathsf{ π} }}} \times {\mathit{\boldsymbol{\omega }}_{\rm{ \mathsf{ π} }}}} \right) $ | (9) |
因此,只要在W(x)上vπ× ωπ≠0,从尾流平面上算得的诱导阻力肯定是x依赖的。在动力学上,x依赖性可从物体做功和流体区域Vf的动能变化求得:
| $ \begin{array}{l} \frac{{{\rm{d}}{D_i}}}{{{\rm{d}}x}} = - \frac{1}{{\rho \left( {U + \overline {u'} } \right)}} \cdot \\ \left[ {\int_{{W_v}\left( x \right)} \mu {\omega ^2}{\rm{d}}S - \mu \frac{{\rm{d}}}{{{\rm{d}}x}}\int_{{W_v}(x)} {{\mathit{\boldsymbol{e}}_x}} \cdot (\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}){\rm{d}}S} \right] \end{array} $ | (10) |
其中u′为截面平均扰动流向速度。因此,对所有有限雷诺数的黏性层流、所有带分离的复杂流动和所有湍流都有dDi/dx≠0。甚至在Re→∞,当自由面涡卷绕成为有黏性子核的翼尖涡[26],流动仍然是有耗散的。显然,对于黏性流动,Di和DP的x无关性以及Prandtl和Maskell的公式,都只是粗略的工程近似。
现在的问题是:在可接受的误差范围内是否存在一个尾流区间,使dDi/dx=-dDp/dx
前已说明,x依赖性的存在使得选取合适的位置测量诱导阻力和型阻成了一个关键问题。由式(10)可知,在此尾流位置上必须忽略耗散。根据上述分析,这在近尾流和远尾流都是不可能的,唯一的选择是两者之间的弱非线性区域,称之为中场尾流区。在其中的尾流平面W上,诱导阻力所固有的核心非线性效应即扰动Lamb矢量v × ω应该保留下来。最终可把公式(7)简化为比公式(2)和公式(3)准确的紧致中场近似:
| $ {D_i} \simeq \frac{\rho }{2}\int_{{W_v}} {\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{\tilde \psi }}{\rm{d}}S} + \rho \int_{{W_v}} \mathit{\boldsymbol{r}} \cdot (\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}){\rm{d}}S $ | (11) |
其中
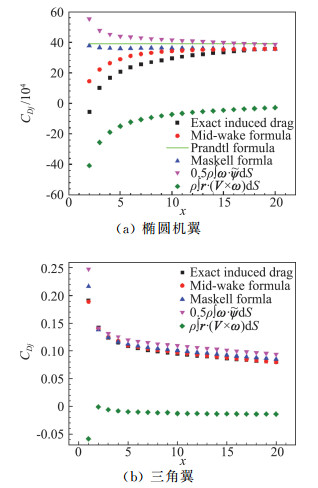
以相同的椭圆机翼和细长三角翼流场为例,可粗略认为中场尾流区域位于x∈(3, 20)。公式(7)、公式(11)、公式(2)和公式(3)计算出的诱导阻力随x的演化如图 3所示(计算参数与图 2一致)。我们只在椭圆机翼中考虑Prandtl公式(2),其中δ=0,并得到一条直线。方程(3)表现好些,但在近尾迹区域(x=2)中有很大的误差。对于椭圆机翼,当x增加时,Maskell公式(3)的误差变小,并且当x>18时与精确解以及中场近似几乎重叠。对于三角翼,x>4以后,尾流截面上的切向涡量ωπ不会显著下降且无法忽略。因此,公式(3)的误差逐渐增加,当x=20时误差达到了9%。同时,产生诱导阻力的核心非线性项r ·(v × ω)修正了
|
图 3 椭圆机翼与三角翼的诱导阻力随x的变化曲线 Fig.3 x-dependency of induced drag for the elliptic wing and delta wing |
回顾诱导阻力公式(5)和型阻公式(6),并考虑涡力理论中升力的公式
| $ \begin{array}{l} L = {L_0} + {L_1}\\ \;\;\; = \rho \int_V {{\mathit{\boldsymbol{e}}_z}} \cdot (\mathit{\boldsymbol{U}} \times \mathit{\boldsymbol{\omega }}){\rm{d}}V + \rho \int_V {{\mathit{\boldsymbol{e}}_z}} \cdot (\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{w}}){\rm{d}}V \end{array} $ | (12) |
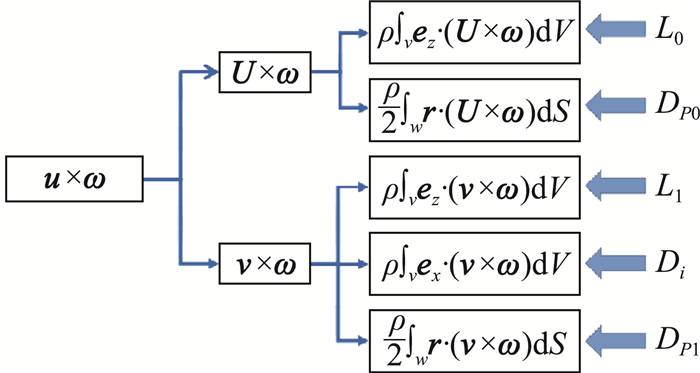
可以看出,型阻的线性项DP0和线性升力L0一样,来自线化Lamb矢量U × ω;型阻的非线性项DP1与非线性升力L1以及诱导阻力Di一样,来自非线性Lamb矢量v × ω。它们之间的关系如图 4所示。
|
图 4 合力各组分的物理同源性示意图 Fig.4 Sketch of physical homology of force components |
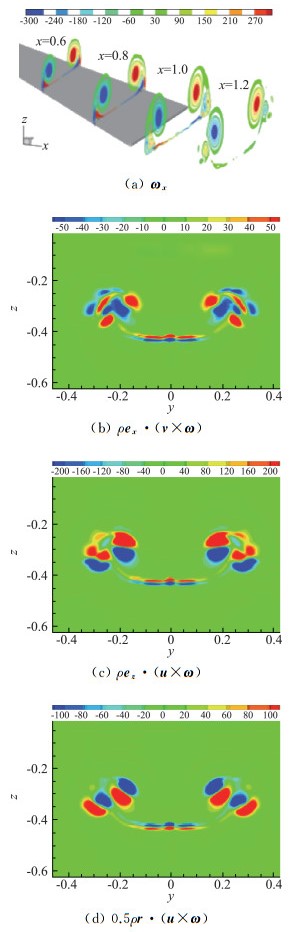
这个观察表明,定常物体运动产生的Lamb矢量场u × ω及其演化是理解所有气动力分量的关键。诱导阻力与升力和型阻本征相关,说明对它们必须做一体化考虑,很难分割开来实施优化。以三角翼尾流为例,如图 5所示,在x=1.2截面,尾涡对不仅提供了升力,也同时提供了Di和Dp。
|
图 5 三角翼尾流涡不同合力分量云图 Fig.5 Contour of force components of slender delta wing trailing vortex |
为了深入理解升阻力各分量的同源性和本征关联,我们从Lamb矢量的纵横分解以及其发展演化入手。众所周知,任意一个分片可微的向量场f可以分解为一个标量场的梯度和一个向量场的旋度之和,即著名的Helmholtz分解定理:
| $ \begin{array}{l} \mathit{\boldsymbol{f}} = \nabla \phi + \nabla \times \mathit{\boldsymbol{\psi }},\;\;\;\;\nabla \cdot \mathit{\boldsymbol{\psi }} = 0\\ {\nabla ^2}\phi = \nabla \cdot \mathit{\boldsymbol{f}},\;\;\;\;{\nabla ^2}\mathit{\boldsymbol{\psi }} = - \nabla \times \mathit{\boldsymbol{f}} \end{array} $ | (13) |
ϕ和ψ称为f的标量势和向量势。它们代表的流动过程分别称为纵过程和横过程,因此Helmholtz分解也叫纵横分解。如果势函数本身也是可测的物理量,则称此纵横分解为自然的,十分可贵。对于Lamb矢量l = ω × u,Wu等[27]指出它有自然的Helmholtz分解
| $ \begin{array}{l} \mathit{\boldsymbol{l}} = {\mathit{\boldsymbol{l}}_\parallel } + {\mathit{\boldsymbol{l}}_ \bot } = - \nabla \mathit{\boldsymbol{P}} - \nabla \times \left( {\mathit{\boldsymbol{v\omega }}} \right)\\ {\mathit{\boldsymbol{l}}_\parallel } = - \nabla \mathit{\boldsymbol{P}},\;\;\;\;{\mathit{\boldsymbol{l}}_ \bot } = - \nabla \times \left( {\mathit{\boldsymbol{v\omega }}} \right) \end{array} $ | (14) |
可见,纵Lamb矢量l‖与总压梯度平衡,总压就是Lamb矢量的标量势。正因如此,可以将型阻的面积分转换成Lamb的矩的积分.对上述方程两边在Vf中进行积分,将梯度项变换成面积分,并分别在x方向投影得到:
| $ \int_{\partial B} p {\mathit{\boldsymbol{e}}_x}{\rm{d}}S = - \int_{{V_f}} {{\mathit{\boldsymbol{l}}_\parallel }} \cdot {\mathit{\boldsymbol{e}}_x}{\rm{d}}V - \int_W {\left( {P - {P_\infty }} \right){\mathit{\boldsymbol{e}}_x}{\rm{d}}S} $ | (15) |
| $ \int_{\partial B} \mathit{\boldsymbol{\tau }} \cdot {\mathit{\boldsymbol{e}}_x}{\rm{d}}S = - \int_{{V_f}} {{\mathit{\boldsymbol{l}}_ \bot }} \cdot {\mathit{\boldsymbol{e}}_x}{\rm{d}}V $ | (16) |
这里τ =μω × n是切应力。因此,纵Lamb矢量l‖的x分量体积分代表着壁面压差阻力与流场型阻的差。这个体积分也可以写为-Di‖。横Lamb矢量l⊥的体积分完全提供了壁面摩擦力,它又是诱导阻力的横分量。因此,Lamb矢量的纵横部分将壁面的应力与流域/尾流积分的定义简洁而明确的联系起来,如图 6所示。

|
图 6 基于Lamb矢量纵横分解的总阻力及其分量示意图 Fig.6 Longitudinal-transverse decomposition of total drag and its components based on Lamb vector |
Wu等[27]还观察到,Lamb矢量完全由横分量l⊥以及其全场效应所驱动(非定常时还包括历史积累效应)。正是这种非线性的全场效应导致了包括湍流在内的各种旋涡流动的极为复杂的演化。横分量l⊥变化引起了纵分量l‖的被动变化,它类似于压力梯度的行为。然而,与压力本身不同的是,由于l‖=-▽P中包含动能,所以它受扩散方程的控制。该现象与型阻和黏性扩散之间的内禀物理关联一致。
3 空气动力学断层扫描技术第1节指出了传统阻力分解的种种困难,说明只对附着流可以建立合理的中场近似。第2节发现在所有的气动力分量在物理上同源于Lamb矢量的体积分或矩积分,升力以及阻力分量无法分割开来实施优化。若要考虑更加复杂的构型(如全机或崭新气动概念飞行器)的气动设计,就需要突破传统的阻力分解框架,构建新型的技术路线。本节旨在为这个根本性的创新提供一个坚实的基础。
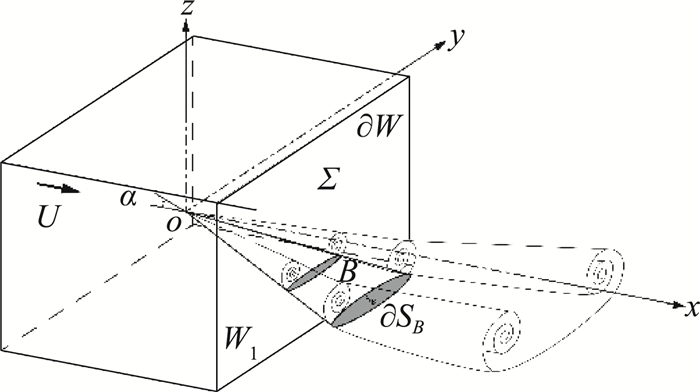
3.1 空气动力学断层扫描诊断的理论基础和对升力来源的认识发展一样,研究阻力也需要突破线性分解、各个击破、线性叠加的传统思维和用速度、动能解释诱导阻力的笼统认识,树立整体的、相互作用的思维,从速度、动能追问到具体的流动结构及其产生机制。基于这一考量,结合CFD/EFD的现实情况可知,非线性近场得到的数据是最为准确的,也是利用有限的CFD/EFD数据进行局部动力学诊断和优化的最佳场所。因此,研究的对象应由速度、动能转变为导致升阻力的紧致Lamb矢量场的纵横部分在近场的非线性演化特性,并追溯其产生机制。如图 7所示,尾流截面甚至可以切入物体内部,将Lamb矢量场及其相关边界量随流向x或展向y的截面积分变化(可拓展到任选方位的截面族)作为诊断和溯源的重要线索。
|
图 7 近场空气动力学CT截面示意图 Fig.7 Sketch of near-field aerodynamic CT |
这种通过扫描、切片得到一系列流动结构的截面数据并进行局部流场结构的动力学分析,并结合边界涡量流追溯其产生机制的技术,我们称为空气动力学断层扫描技术(亦即空气动力学CT技术)。
为此,我们首先写出一般不可压定常黏性流动的空气动力学CT涡力公式为:
| $ \mathit{\boldsymbol{F}} = - \int_{{V_f}} \mathit{\boldsymbol{l}} {\rm{d}}V - \frac{1}{{m - 1}}\int_W \mathit{\boldsymbol{x}} \times (\mathit{\boldsymbol{n}} \times \mathit{\boldsymbol{l}}){\rm{d}}S + {\mathit{\boldsymbol{F}}_\Sigma } + {\mathit{\boldsymbol{F}}_{{S_B}}} $ | (17) |
其中:
| $ {\mathit{\boldsymbol{F}}_\Sigma } = - \frac{\mu }{{m - 1}}\int_{{W_f}} {(\mathit{\boldsymbol{x}} \times \mathit{\boldsymbol{\sigma }} + \mathit{\boldsymbol{\tau }}){\rm{d}}S} $ |
| $ {\mathit{\boldsymbol{F}}_{SB}} = - \frac{1}{{m - 1}}\oint_{\partial {S_B}} p \mathit{\boldsymbol{x}} \times {\rm{d}}\mathit{\boldsymbol{x}} $ |
分别为外边界项以及物面边界项,
若把基于尾流截面积分的气动力公式推广至空气动力学CT中,也会出现相应的边界积分,在此不再赘述。
上述两种理论属于结构层次[9],它只关注流动结构如何决定气动力,并不关注流动结构如何形成。后一个问题涉及复杂的因果关系链条,其最主要和最基本的机理是涡量如何在壁面产生[9],因此还需要考虑基于边界涡量流的合力积分公式,它在三维流中是:
| $ \mathit{\boldsymbol{F}} = - \rho \int_{\partial B} \mathit{\boldsymbol{x}} \times \left( {\frac{1}{2}{\mathit{\boldsymbol{\sigma }}_p} + {\mathit{\boldsymbol{\sigma }}_{{\rm{vis}}}}} \right){\rm{d}}S $ | (18) |
其中:
| $ {\mathit{\boldsymbol{\sigma }}_p} = \mathit{\boldsymbol{n}} \times \nabla p,\;\;\;\;{\mathit{\boldsymbol{\sigma }}_{{\rm{vis}}}} = \mu (\mathit{\boldsymbol{n}} \times \nabla ) \times \mathit{\boldsymbol{\omega }} $ |
边界涡量流σ = σp+ σvis(简写为BVF)衡量了单位面积的壁面在单位时间内由于无滑移条件产生并扩散进入流体内部的涡量大小。它代表着由于黏附性条件而通过切向压力梯度产生涡量的机制,因此也展现了两个基本过程——纵横过程——在边界上的黏性与线性耦合。壁面是产生涡量的地方,因此也是最初形成Lamb矢量的地方。虽然由于黏附条件而在静止边界上有u = 0从而l = 0,但其纵场和横场部分并不分别为0,而是在壁面有:
| $ \rho {\mathit{\boldsymbol{l}}_ \bot } + \mu \nabla \times \mathit{\boldsymbol{\omega }} = {\bf{0}},\;\;\;\;\rho {\mathit{\boldsymbol{l}}_\parallel } + \nabla p = {\bf{0}} $ | (19) |
Wu等[27]已经推导出不可压缩流动的Lamb矢量输运方程。该方程有一个扩散项μ▽2l的体积分,可以转换成边界积分μn ·▽l,该形式与BVF相似且密切相关。可以得到Lamb矢量的纵横分量在壁面上与BVF之间的关系:
| $ \rho \mathit{\boldsymbol{n}} \times {\mathit{\boldsymbol{l}}_ \bot } = - \rho \mathit{\boldsymbol{n}} \times {\mathit{\boldsymbol{l}}_\parallel } = - \mu (\mathit{\boldsymbol{n}} \times \nabla ) \times \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{n}} \times \nabla p = \mathit{\boldsymbol{\sigma }} $ | (20) |
| $ \rho \mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{l}}_ \bot } = - \rho \mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{l}}_\parallel } = - \mu (\mathit{\boldsymbol{n}} \times \nabla ) \cdot \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{n}} \cdot \nabla p $ | (21) |
可见,横向Lamb矢量在壁面的切向分量即为BVF,法向分量为法向压力梯度。在壁面产生的横向Lamb矢量首先通过扩散进入流体内部靠近边界的黏性子层中,因为该区域有着很强的黏性作用。
具体应用空气动力学CT时,可遵循Wu等[9]的建议:面对特定的流动问题,首先考察全局流场,然后更多地关注局部结构和过程,最后查明其物理原因。为了获得流场多层次的视野,需要把所有可能层次的理论有机地结合起来使用,且与CFD/EFD得到的精确数据结合。为了展示空气动力学CT的具体应用,下一节将以第2节中的细长三角翼分离流为例,在相同的计算参数下,对其升阻力进行流场诊断,并据此提出新的概念性的增升减阻方案。
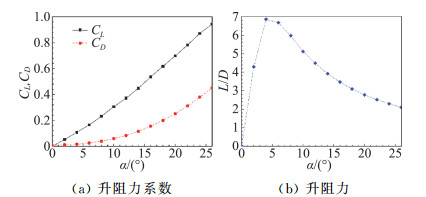
3.2 基于空气动力学CT的流场诊断先从全局流场的角度来检查三角翼在不同攻角情况下升阻力的变化曲线,如图 8所示。图 8(a)表明,升力基本是线性增长,而阻力按二次曲线增长。因此升阻比L/D一开始急剧增长,在α=4°时达到了最大值。此后L/D一直下降并逐渐平缓。
|
图 8 细长三角翼升阻力系数以及升阻比随攻角变化曲线 Fig.8 Curves of lift and drag coefficients and lift-drag ratio vs. angle of attack for slender delta wing |
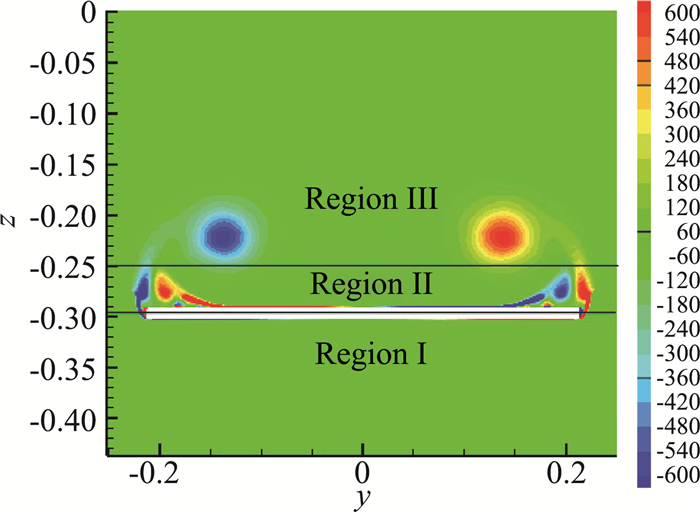
为了定量的探讨气动力随攻角的变化关系,取α=4°以及α=20°两个代表性的算例进行分析。在结构层次的理论中,气动力的变化与涡息息相关。流动结构在空间中并不是均匀分布的,参照Yang等[29]的方法,将流场分为三个区:区域Ⅰ(Region Ⅰ)是下表面以下区域,区域Ⅲ(Region Ⅲ)是脱体涡区,区域Ⅱ(Region Ⅱ)是两者中间的上表面近壁区。
|
图 9 流场分区示意图(背景为α=20°时细长三角翼x/c=0.8截面ωx云图) Fig.9 Sketch of region (the background is the contour of ωx at x/c=0.8 for slender delta wing with α=20°) |
当然更好的方式是将脱体涡单独隔离出来计算。但数值结果表明,只要保证上表面近壁区处于区域Ⅱ中,其值就很稳定。连接集中涡与近壁层的剪切层对升阻力贡献都较小。值得注意的是,这种分区并不意味着各区域的效果是独立的:近壁区产生的涡量从翼尖分离进入流场形成自由剪切层,它进而卷绕成集中的脱体涡;而集中涡又会反过来影响上翼面近壁区的流场,诱导出二次涡。这种涡结构的产生和诱导都是相互的,因此空间上的分解是对结果的描述,而不是原因。真实的物理原因需要进一步采用动理学的公式追溯流场结构产生的因果关系。
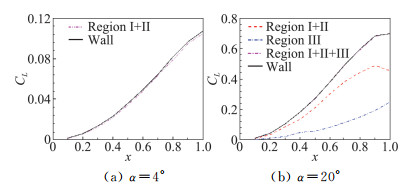
现在采用涡力理论进行分析。图 10显示了近壁区域(Region Ⅰ+Ⅱ)与脱体涡区域(Region Ⅲ)在不同攻角下升力随着流向的变化曲线。图中每个区域的升力采用涡力公式(17)计算,三个区域相加得到的升力与采用壁面积分得到的升力曲线几乎完全一致,充分验证了公式的正确性和计算结果的精确性。
|
图 10 三角翼不同区域涡升力沿流向位置x的变化曲线 Fig.10 Curves of vortex lift in different region vary with x for slender delta wing |
α=4°时,升力系数一直沿流向持续增加,尾缘部分的增速只稍微降低。且由于不存在脱体涡,近壁区域提供了全部升力。α=20°时,升力系数在到达尾缘之前一直持续增加,但在尾缘部分其增速几乎为0。与小攻角不同,脱体涡也提供了一部分升力。x较小时,前缘涡与近壁区比较接近,两个区域对合力的贡献不能完全区分开来。但总体来说,近壁区提供了80%左右的升力,而脱体涡提供了20%左右的升力。随x增大,前缘涡不断加强,提供的升力逐渐线性化并占总升力的更高比例。到了尾缘附近,前缘涡提供的升力仍然稳定增长,而近壁区提供的升力则略有下降。最终前缘涡给整个机翼提供了大约40%的升力,近壁区提供了大约60%的升力。这与Yang等[29]的结论定性上一致。
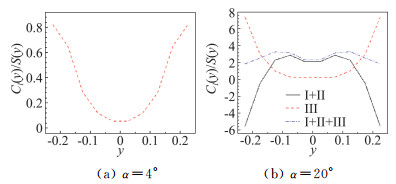
除了沿流向引入不同的横流切片外,还可以沿展向引入不同的流向切片观察升力的展向分布,如将机翼分为宽度为y=0.05的条带,对每条条带进行积分。由于各条带的面积不同,内翼面区域显然积分面积更大,为避免误解,可以考虑单位面积的升力系数Cl(y)/S(y)随y的变化曲线,如图 11所示。
|
图 11 三角翼不同区域单位面积涡升力Cl(y)/S(y)沿流向位置y的变化曲线 Fig.11 The curves of vortex lift Cl(y)/S(y) in different region vary with y for slender delta wing |
α=4°时,单位面积产生的涡升力随着|y|的增大而增大,在外翼面区域达到最大值。但当α=20°时,Cl(y)/S(y)随着|y|的增大先增加后减小,峰值在|y|≈0.1附近,靠近前缘涡的涡心位置。总单位面积涡升力曲线的变化来源于近壁区与脱体涡产生的涡升力之间的竞争。脱体涡产生的Cl(y)/S(y)随着|y|的增大先保持不变,然后急剧增大,并且在外翼面达到最大值。曲线急剧增长的位置与脱体涡的位置是相关的。而近壁区产生的Cl(y)/S(y)随着|y|的增大先轻微变大,然后迅速变小。其曲线变化的位置与脱体涡曲线的变化位置是一致的。
通过解剖两个特征攻角下的流动结构对升力系数贡献沿流向和展向的变化,可以发现造成三角翼升阻比下降的主要流动结构位于尾外翼面处。由于在两个算例中机翼下表面均未发生分离,可以断定上翼面的结构是产生升阻比下降的主要原因。
为了进一步锁定该流动结构,还需考虑尾流截面型的气动力公式。公式(12)中第一项线性升力L0可转换为尾流截面积分形式:
| $ {L_0} = \rho \int_V {{\mathit{\boldsymbol{e}}_z}} \cdot (\mathit{\boldsymbol{U}} \times \mathit{\boldsymbol{\omega }}){\rm{d}}V = \rho U\int_W y {\omega _x}{\rm{d}}S $ | (22) |
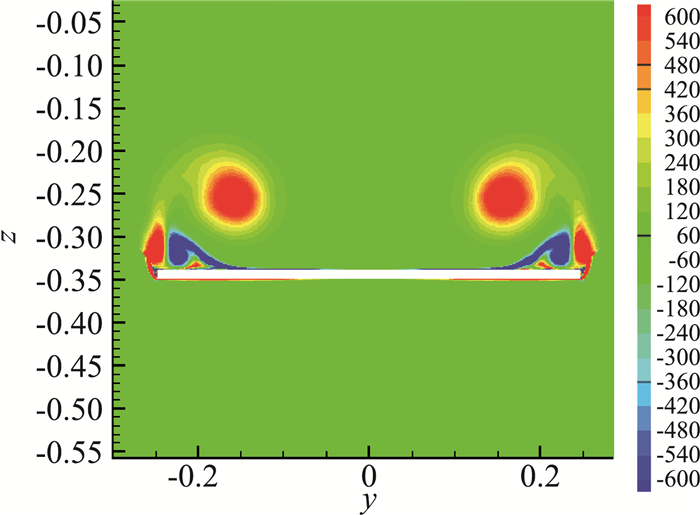
图 12是L0的被积函数在靠近机翼尾缘的横截面上分布的云图。由图可见,上表面的|y|≈0.2处,正是主涡诱导的二次涡结构在近壁区产生负升力的地方,与涡力理论的结果一致。正是由于该结构的存在,使得近壁区的升力不再继续增长。
|
图 12 α=20°, 细长三角翼x/c=0.9处线性升力L0云图 Fig.12 Contour of L0 at x/c=0.9 for the slender wing with α=20° |
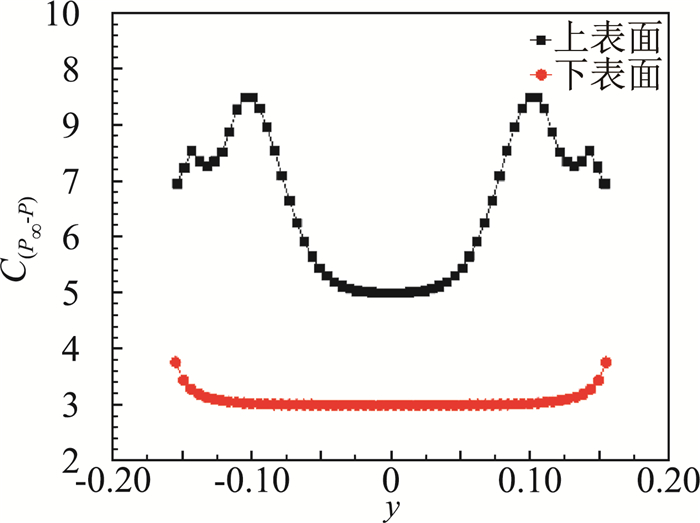
图 13展示了α=20°细长三角翼上表面BVF型公式(18)给出的阻力和升力被积函数云图。显然,二次涡是在壁面上产生负升力的机制,而该二次涡也同样产生了大量阻力。图 14进一步给出代表型阻的总压损失沿展向变化。显然,二次涡不仅产生负升力还造成总压损失的大峰值。
|
图 13 α=20°, 细长三角翼上表面边界涡量型公式(18)阻力和升力被积函数云图 Fig.13 Contour of drag integrand and lift integrand on the upper side of the slender delta wing with α=20° |
|
图 14 型阻总压损失C(P∞-P)在x/c=0.6截面沿机翼边界的分布 Fig.14 Distribution of C(P∞-P) along boundary of the slender delta wing at x/c=0.6 wake plane |
若仅从线性的设计思路出发,要增升减阻只需简单的切掉尾缘附近的翼尖,使得二次涡没有产生的机会。但对于大雷诺数下大攻角分离流来说,壁面上压强产生的力占主导,此时对于任意形状的平板可以很简单的证明如下关系式:
| $ \frac{L}{D} = \cot \alpha $ | (23) |
因此线性设计思路无法帮助我们提高升阻比。
若从非线性的角度来思考如何减少主涡诱导的二次涡结构,则需要考虑减少机翼翼尖压力梯度的构型,并同时考虑
|
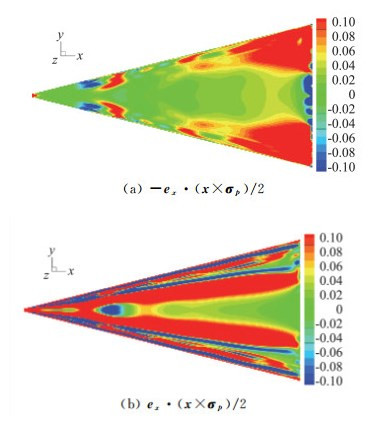
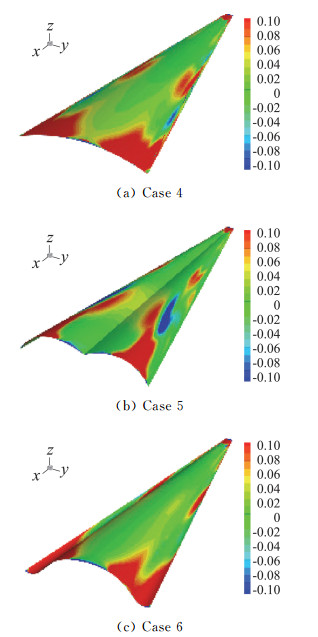
图 15 不同增升减阻曲面三角翼(采用阻力被积函数- ex·(x × σp)/2填色) Fig.15 Three different curve delta wings for increasing lift-drag ratio, colored by - ex·(x × σp)/2 |
|
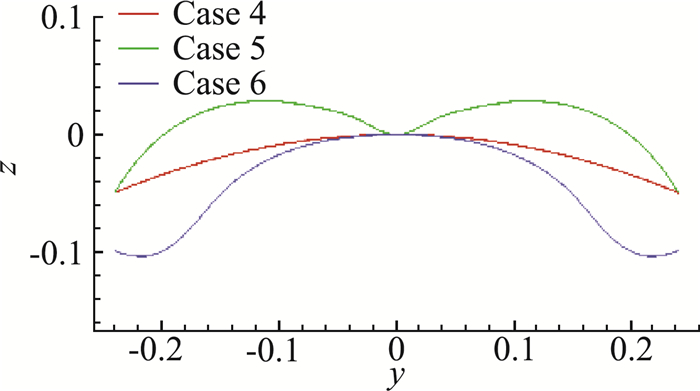
图 16 不同曲面三角翼截面曲线 Fig.16 Section curves of three curve delta wings |
Case 4为圆弧曲线,Case 5采用曲率更大的两个半圆弧拼接,Case 6采用样条曲线。仍按α=20°、Re=5×105的流动参数计算。计算的升阻力系数以及升阻比结果如表 1所示。
| 表 1 不同曲面三角翼气动力系数表 Table 1 Aerodynamic force coefficients for different curve delta wings |
|
|
Case 4的升力增加,阻力有少许增加,升阻比增加了一些,但变化不大,说明这个方法可能有效。Case 5的升力减小了14%,但阻力减少了34%,升阻比提高了31%,这是由于其沿展向的大曲率基本上把将二次涡完全去掉了。这个改进太过激进。我们吸收了Case 4和Case 5的优点,重新设计了Case 6的曲线。可以看出,升力基本没变,但阻力减小了10%,从而使得升阻比也增加了10%。
三个算例的升力基本没变,且σp的贡献远大于σvis,因此可以采用边界型涡力公式来追踪σp以阐述阻力减小导致升阻比增加的原因。图 15同时展示了边界型公式中阻力被积函数- ex·(x × σp)/2的云图。与图 13(a)对比,Case 4的阻力分布变化不大,在尾缘处仍有很大的阻力贡献。虽然机翼前部和中部的阻力减少,但总阻力基本不变。Case 5中的阻力明显减小,只在尾缘部分区域中出现阻力贡献,在尾缘外翼部基本没有阻力。在翼中部还出现了明显的推力,这说明该设计明显减少了σp,从而减少了对阻力的贡献。美中不足的是σp减少的太多,也导致了升力的减小。Case 6中阻力与图 13(a)对比,在尾缘处的阻力贡献区域有所减小,在翼型中段的阻力减少得更多,而且分布更加均匀。这也证明了这种设计能通过减少壁面切向压力梯度沿阻力方向的投影,进而减少阻力。三种翼型下表面均是附着流动,其压力以及压力梯度分布均可用势流解来估计,与原方案的阻力系数差别不大。
当然,以上探索还只是基于对机翼和流场的初步认识,尚未提供优化设计的系统理论方案。这也是今后需要进一步探究和深化的方向。
4 结论传统空气动力学流场诊断和减阻方案往往采用线性分解、各个击破的思路。Zou等[4]发现上述思路并不能有效地处理真实复杂流动。我们发现物体定常运动产生的Lamb矢量场ω×u及其演化,是制约所有气动力分量的关键物理载体。Lamb矢量可自然的分解为纵横两个部分。横Lamb矢量体积分的x分量(即诱导阻力的横分量)完全提供了壁面摩擦力;纵Lamb矢量体积分的x分量(即诱导阻力的纵分量)提供了压差阻力和型阻之差。这意味着采用线性思维,单独减少特定阻力分量的思路,会不可避免的影响其余气动力分量,很难达到优化升阻比的目的。
本文突破传统阻力分解框架,提出面向任意复杂构型的空气动力学CT原理,允许截面切入物体,给出了可切入物体内部的涡力公式和尾流截面公式。通过对大攻角三角翼的流场进行断层扫描,找到了产生负升力和型阻相对应的主要涡结构,并可以追溯到特定壁面区域的边界涡量流。基于以上认识, 提出了概念性的增加升阻比的设计思路与参考构型,并证实了该诊断原理的适用性和合理性。
这个新的设计理念,对于复杂构型流场诊断理论如何在实际工程应用中发挥作用,也有着重要的启发作用。常用的基于压力速度层次的流场优化策略,虽然方便易行,还能与EFD有效结合,但往往无法揭示物理根源;基于结构层次的流场优化策略,对CFD来说是合适的,却由于EFD很难获得三维流场而无法进行验证。看来,需要将几个层次的理论有机结合起来,对CFD数据进行有针对性的挖掘,锁定具体的影响气动力的关键流场结构与壁面物理来源。这个认识也能用于指导EFD对壁面和流场关键区域的测量,反过来佐证CFD计算和理论的正确性,并在此基础上进行下一步的优化设计。这就不仅是建立CFD或EFD与理论的单向连接,而是建立起CFD/EFD/理论的相互双向互动,充分发挥流体力学研究中每种手段的优势,共同进行流场诊断与优化。
应当看到,以近场Lamb矢量为主攻对象的空气动力学CT技术才刚刚起步,还面临新的挑战。以定常不可压缩流动为例,气动力各分量不只取决于尾流中的分布涡量,而是由涡量场及其诱导的速度场共同决定,后者是前者的Biot-Savart积分, 有非局域效应。Lamb矢量场既有散度,又有旋度,比涡量场内容丰富复杂。其线性部分导致的L0和DP0公式仅提供了指导设计的一些基本线索,还需仔细研究其非线性部分的作用。对不同几何构型与流动条件, 有旋有散的非线性Lamb矢量场及其矩的各分量有何特殊分布、相互如何制约、如何优化, 是个崭新课题。
致谢: 非常感谢张锡金教授和张淼博士启发我们进行此项研究,感谢史一蓬教授、苏卫东教授、白鹏研究员、李周复研究员、钱战森研究员、张日葵博士、刘罗勤博士、高安康以及康林林对本研究极为有益的讨论与建议。
| [1] |
MAREC J P. Drag reduction: a major task for research[M]//Aerodynamic Drag Reduction Technologies. Springer, Berlin, Heidelberg, 2001: 17-27.
|
| [2] |
ZHU J Y, ZHU F L, SU W D, et al. Avorticity dynamics view of "effective slip boundary" with application to foil-flow control[J]. Physics of Fluids, 2014, 26(12): 123602. DOI:10.1063/1.4904379 |
| [3] |
CHEN C, SEELE R, WYGNANSKI I. Separation and circulation control on an elliptical airfoil by steady blowing[J]. AIAA Journal, 2012, 50(10): 2235-2247. DOI:10.2514/1.J051538 |
| [4] |
ZOU S F, WU J Z, GAO A K, et al. On the concept and theory of induced drag for viscous and incompressible steady flow[J]. Physics of Fluids, 2019, 31(6): 065106. DOI:10.1063/1.5090165 |
| [5] |
KUSUNOSE K. A wake integration method for airplane drag prediction[M]. Tohoku University Press, 2005.
|
| [6] |
PRANDTL L. Theory of lifting surface. Part Ⅰ[J]. Nachricheten Ges. Wiss. Göttingen, Math.-Phys. Kl., 1918, 1918: 451-477. |
| [7] |
MASKELL E C. Progress towards a method for the measurement of the components of the drag of a wing of finite span[R]. Procurement Executive, Ministry of Defence, Royal Aircraft Establishment. RAE TP 72232, 1972.
|
| [8] |
WU J Z, MA H Y, ZHOU M D. Vorticity and vortex dynamics[M]. Springer, 2006.
|
| [9] |
WU J, LIU L, LIU T. Fundamental theories of aerodynamic force in viscous and compressible complex flows[J]. Progress in Aerospace Sciences, 2018, 99: 27-63. DOI:10.1016/j.paerosci.2018.04.002 |
| [10] |
BETZ A. A method for the direct determination of wing-section drag[R]. NACA-TM-337, 1925.
|
| [11] |
TAYLOR G I. Note on the connection between the lift on anaërofoil in a wind and the circulation round it[J]. Philosophical Transactions of the Royal Society A, 1926, 225: 238-246. |
| [12] |
GLAUERT H. The elements of aerofoil and airscrew theory[M]. Cambridge University Press, 1926.
|
| [13] |
MARONGIU C, TOGNACCINI R, UENO M. Lift and lift-induced drag computation by Lamb vector integration[J]. AIAA Journal, 2013, 51(6): 1420-1430. DOI:10.2514/1.J052104 |
| [14] |
YATES J E, DONALD C D. A fundamental study of drag and an assessment of conventional drag-due-to-lift reduction devices[R]. NASA-CR-4004, 1986.
|
| [15] |
CHAO D D, VAN DAM C P. Wing drag prediction and decomposition[J]. Journal of Aircraft, 2006, 43(1): 82-90. DOI:10.2514/1.12311 |
| [16] |
MÉHEUT M, BAILLY D. Drag-breakdown methods from wake measurements[J]. AIAA Journal, 2008, 46(4): 847-862. DOI:10.2514/1.29051 |
| [17] |
VAN DAM C P. Recent experience with different methods of drag prediction[J]. Progress in Aerospace Sciences, 1999, 35(8): 751-798. DOI:10.1016/S0376-0421(99)00009-3 |
| [18] |
GILES M B, CUMMINGS R M. Wake integration for three-dimensional flow-field computations:theoretical development[J]. Journal of Aircraft, 1999, 36(2): 357-365. DOI:10.2514/2.2465 |
| [19] |
DESTARAC D, VAN DER VOOREN J. Drag/thrust analysis of jet-propelled transonic transport aircraft; definition of physical drag components[J]. Aerospace Science and Technology, 2004, 8(6): 545-556. DOI:10.1016/j.ast.2004.03.004 |
| [20] |
陈真利, 张彬乾. 基于尾迹积分的阻力计算方法研究[J]. 空气动力学学报, 2009, 27(3): 329-334. CHEN Z L, ZHANG B Q. Drag prediction method investigation basing on the wake integral[J]. Acta Aerodynamica Sinica, 2009, 27(3): 329-334. DOI:10.3969/j.issn.0258-1825.2009.03.012 (in Chinese) |
| [21] |
薛榕融, 叶正寅, 王刚, 等. 展向动量测定法与前掠翼流动机理研究[J]. 空气动力学学报, 2018, 36(5): 736-742. XUE R R, YE Z Y, WANG G, et al. Flow mechanism of forward-swept wing with spanwise momentum method[J]. Acta Aerodynamica Sinica, 2018, 36(5): 736-742. DOI:10.7638/kqdlxxb-2016.0146 (in Chinese) |
| [22] |
SPALART P R. On the far wake and induced drag of aircraft[J]. Journal of Fluid Mechanics, 2008, 603: 413-430. DOI:10.1017/S0022112008001146 |
| [23] |
LIU L Q. Unified theoretical foundations of lift and drag in viscous and compressible external flows[M]. Springer, 2018.
|
| [24] |
GAO A K, ZOU S F, SHI Y P, et al. Energy-based drag breakdown in compressible flow by wake-plane integrals[J]. AIAA Journal, 2019, 57(8): 3231-3238. DOI:10.2514/1.J058114 |
| [25] |
KANG L L, RUSSO L, TOGNACCINI R, et al. Aerodynamic force breakdown based on vortex force theory[C]//AIAA Scitech 2019 Forum, 2019: 2122.
|
| [26] |
MOORE D W, SAFFMAN P G. Axial flow in laminar trailing vortices[J]. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 1973, 333(1595): 491-508. DOI:10.1098/rspa.1973.0075 |
| [27] |
WU J Z, ZHOU Y, LU X Y, et al. Turbulent force as a diffusive field withvortical sources[J]. Physics of Fluids, 1999, 11(3): 627-635. DOI:10.1063/1.869934 |
| [28] |
LIU L Q, SHI Y P, ZHU J Y, et al. Longitudinal-transverse aerodynamic force in viscous compressible complex flow[J]. Journal of Fluid Mechanics, 2014, 756: 226-251. DOI:10.1017/jfm.2014.403 |
| [29] |
YANG Y T, ZHANG R K, AN Y R, et al. Steady vortex force theory and slender-wing flow diagnosis[J]. Acta Mechanica Sinica, 2007, 23(6): 609-619. DOI:10.1007/s10409-007-0107-0 |
 2019, Vol. 37
2019, Vol. 37


