过去,人们认为许多数据都是陈旧的、无用的、冗余的,比如:飞机降落后,票价数据是陈旧的;网络上搜索关键词数据是无用的;风洞常规试验中非阶梯稳定时刻的数据是冗余的,所以都被舍弃了[1-3]。
随着大数据的引领,一些互联网公司首先成了大数据的赢家和先行者。通过用户搜索和使用信息数据累积,可以综合分析出用户的喜好,甚至通过关键词搜索的频次和来源地分析,可以获取流感爆发地及爆发规模等重要信息。目前大数据已成了新发明和深刻洞见之源泉。
对大数据的定义,到目前还没有公认的统一的标准,但普遍认为,大数据是指数据规模大且数据类型繁多。以盲人摸象为例:小数据,仅几个盲人摸摸大象的牙鼻身脚等特征部位,综合后只能得出片面再加以猜想的结果;大数据,可采用足够多的盲人摸遍大象全身,再辅以坐标、时间等相关信息,最后通过复杂多样的综合分析就可获得大象全身的、动态的、可精细到每个细节的大象外形结果。
由此,可看出大数据方法带来的四个转变:一是数据不再是随机样本,而是全体数据;二是数据量和数据杂混性增加,导致数据处理复杂度呈指数型增长;三是大数据方便提供准确的相关、概率等关系,可帮助人们明了因果关系[4-5];四是分析结论不再是抽样数据趋势再加推测的结果,而是全面的、可精细到细节的、可与多种信息相关联的分析结果。
我国风洞试验在几十年间积累了大量的阶梯抽样采集的气动试验数据。目前大数据分析在风洞试验方面的应用研究主要集中在对风洞历年生产的气动试验数据的分析挖掘上[6-7]。而运用大数据对风洞试验全过程进行研究方面则几乎还是空白。分析其原因是传统的风洞常规试验采用阶梯采集的方式,一次车只采集十数个阶梯数据,而其它的数据被认为是无用的,直接就舍弃了。当试验出现故障或者试验数据出现异常时,人们很难从这么少的数据中得到更多的信息,定位故障,明确原因,所以只能采用换电源、换采集通道等多次的吹风测试来定位故障,费事费力,浪费能源,且效率不高。
自连续变迎角测力试验技术投入应用,采集到了大量的风洞试验全程的连续数据和信息,每次车的数据及信息量可达数十万。在对这些海量试验数据和信息的研究分析中,我们逐渐发现这些海量数据中富含许多阶梯数据中没有的频率、概率、相关性等信息,可为风洞试验数据和故障的深入分析等提供有力的支持。由此,我们探索开展了大数据在风洞试验方面的应用研究。
1 风洞试验大数据分析的实现要应用大数据方法深入分析风洞试验全程,需要解决三个问题:一是风洞试验全程大数据的采集;二是风洞试验大数据的处理;三是风洞试验大数据的可视化分析。下面简要介绍解决方案。
1.1 风洞试验数据采集新方法过去,风洞常规试验采用阶梯抽样采集方法,即风洞试验时,迎角按照预先设定的阶梯轨迹运行(如:-2°、-1°、0°、1°、2°、4°、6°、8°、10°、12°共10个阶梯),测量只采集阶梯稳定时刻的数据,试验数据点与阶梯数相同,数据少且时序、频率等信息丢失,大数据应用缺少数据和信息的支持。
为此,发明风洞试验“全程连续采集,阶梯时刻标注,连续阶梯两全”的风洞试验数据采集专利技术[8],即:风洞起动前10 s就起动采集系统,以300~2000 Hz的采样率连续采集数据,并记录每点的时序,阶梯稳定时连续采集不变,只对稳定时刻数据点进行阶梯标注,然后继续下一阶梯,直到风洞关车10 s后,结束连续采集,保存该次试验全程的连续试验数据,并从连续试验数据中将标注的全部阶梯数据提取出来组成该次试验的阶梯试验数据并保存。此采集方法即兼容传统的阶梯采集,又采集到试验全程的全部连续数据、时频域信息等,使试验的宏观全貌和各种细微、瞬时的数据信息得以保留,为大数据分析提供了数据支持。另外,此技术还为连续数据和阶梯数据架起了相通的桥梁,使传统的小数据分析和大数据分析可以相辅相成。
在专利技术的指导下,开发了2.4 m跨声速风洞、2 m超声速风洞测力/测压试验采集全数据的采集软件[3],解决了风洞试验应用大数据的数据来源问题。
1.2 风洞杂混大数据多样化处理传统的风洞试验处理程序的设计思想是:先梳理总结出风洞试验数据有限种的处理方法,制定出数据处理规范,然后再依据规范,开发风洞试验标准化的处理程序。按此设计思想开发的风洞试验数据标准化处理程序在小数据时代,数据点和数据类型少、处理方法有限的情况下,是可以满足数据处理需求的。但是,风洞试验采用新采集方法后,数据量、数据类型、信息等大幅增加,数据处理方法亦呈指数型剧增,再沿用上述的程序设计思想,程序将面临处理方法太多而程序不能全部涵盖的困境。
为此,发明了自动识别、自动解析计算的通用风洞试验数据处理程序。基本设计思想为:程序设计前,先制定出识别数据和解析计算方法的规则,然后设计程序实现输入数据和计算方法;依据规则识别数据和解析计算方法;按识别和解析结果对数据进行计算输出。这种设计思想,就像是在人与程序之间建立了一种交流语言,人们可以将能想到的计算方法通过这种语言告诉程序,程序就可以明白并智能的实现人们的要求。采用此设计思想实现了处理程序数据类型和处理方法的无限拓展,为风洞试验大数据任意计算方法的处理分析搭建了基础的计算平台,解决了风洞试验大数据多样化处理的难题。
1.3 风洞试验大数据的可视化分析大数据分析最基本的方法就是数据特征提取和可视化分析,数据特征提取将蕴含在大数据中的特征明显化,而可视化分析则直观的呈现出大数据的特征[9-15]。为此,开发了风洞试验海量杂混大数据显示分析软件,风洞试验大数据频谱分析、相关性分析等计算和显示分析软件。解决了风洞试验大数据的可视化分析问题。
2 典型应用实例 2.1 天平电源故障的分析2009年某型号尾支干扰测力试验(Ma=0.6),天平静态正常,但试验时,数据在小角度范围出现异常跳动见图 1。
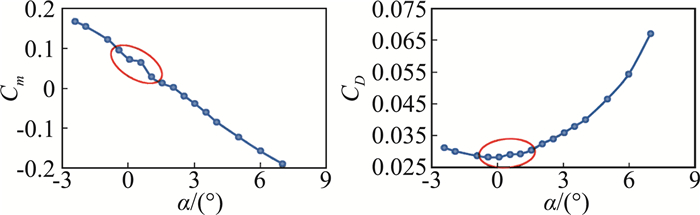
|
图 1 试验数据在小角度范围出现异常跳动 Fig.1 Abnormal runout of test data over a small range of angles |
在传统的小数据(阶梯数据)分析方法中,因只有十余个数据点,无法分析原因。采用大数据可视化分析,将故障车次与正常车次采集的试验全程(包括起动关车前后)全部试验数据按时序显示出来,见图 2,就能从图中的时序关系上看出数据异常是因为风洞起动引起了天平电源异常跳动所致,也即是天平电源的动态特性异常所致。同时,图中细节也可以表现出天平阶梯测值随电源波动的相关性等。更换电源后,数据恢复正常。
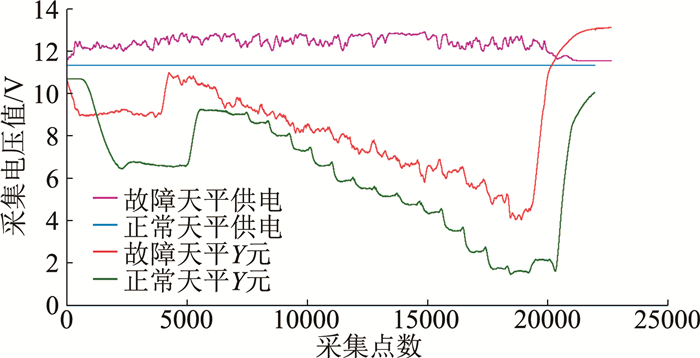
|
图 2 正常和故障情况的全部试验数据对比分析图 Fig.2 Comparison of all experimental data for normal and fault conditions |
此例是利用大数据可视化分析方法,将试验大数据按时序显示在图中,直接从图中的时序关系上找出天平电源异常和恢复的时刻,以及异常时天平电源、天平信号的故障形态的应用实例。
2.2 试验阻力系数的误差原因分析2015年某模型风洞试验Ma=0.96时连续变迎角和阶梯变迎角重复性验证,发现比较车次马赫数差量小于0.002、迎角差量小于0.015°时的阻力系数CD差量却高达0.0024,CD差量达到常规差量的8倍左右。CD曲线对比如图 3(a)。
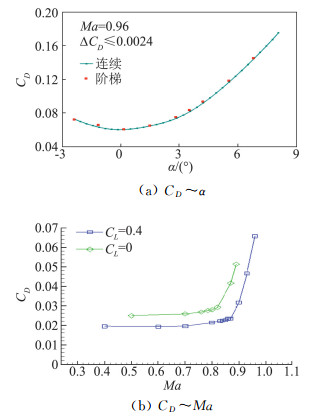
|
图 3 连续和阶梯CD曲线对比、某模型CD随Ma变化曲线 Fig.3 Comparison of continuous and step CD curves and a model of CD with Ma of changes in the curve |
用比较车次全部有效数据的CD差量与试验中所有的其它变量的差量进行相关分析计算,得知CD差量与Ma差量的相关系数最大,即,CD的误差多因马赫数误差引起。计算结果见表 1。
| 表 1 比较车次变量差相关系数计算结果 Table 1 Comparison of calculation results of correlation coefficient |
|
|
有了上述相关分析后,再看该模型CD随Ma的变化曲线(图 3(b))。该模型CD在Ma=0.9处开始发散,因此当Ma>0.9时,Ma的微量变化,将引起CD的大幅变化。这也是该模型试验对Ma>0.9的控制精度要求极高的原因。
此例是利用大数据获取数据间精准的相关关系,再由相关关系指明因果关系的。该例虽然也可以从阶梯数据中获取类似的相关关系,但是,从少量阶梯数据中获取的相关关系的可信度大大降低。
2.3 倾角传感器风洞应用跳数原因的分析近3年来,GWA、WTAS倾角传感器在2 m量级风洞的使用过程中,始终存在静态工作正常但试验状态就出现跳数的现象(跳数误差≤1.5°)。使用了减振、抗噪等措施后问题依然存在,故障原因一直不明确。倾角传感器测量故障曲线见图 4。
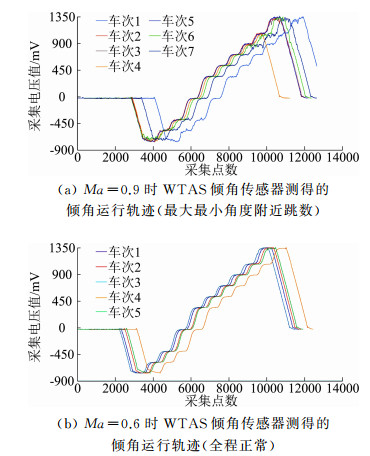
|
图 4 倾角传感器测量故障曲线 Fig.4 Fault curves measured by inclination sensor |
采用大数据分析方法,将3年来所有GWA、WTAS倾角传感器的全部试验数据与试验条件等信息进行概率和相关性分析,得出倾角传感器跳数问题的宏观表现规律:
(1) 问题与马赫数有关。在2.4 m跨声速风洞,当Ma≥0.7,有跳数,且强度和概率与马赫数成正比;而在2 m超声速风洞,当Ma≤2.75,有跳数,但强度和概率与马赫数成反比;相同马赫数,问题相似;
(2) 问题与侧滑角有关,跳数强度和发生概率随倾滑角的增大而降低;
(3) 两种传感器跳数时而同时,时而交错;多数跳数发生时,未见模型有明显振动;
(4) 跳数大多发生在最大、最小角度位置,且角度测值的绝对值始终偏小。
虽然大数据宏观分析得出了倾角传感器跳数问题较为准确的概率和相关性的特征,但是倾角传感器跳数为什么会与马赫数和倾滑角相关仍然是个谜,需要再对大数据进行更加深入的微观分析,明确各种跳数的相关性。
(1) 通过多种相关性分析发现,GWA、WTAS传感器与气流脉动(X)方向的频谱相关性较强,而GWA、WTAS传感器的跳数频率又与风洞气流脉动强度的相关性较强。根据这两个相关性特点,推理出因GWA、WTAS敏感元件摆片正对气流,所以对风洞气流脉动敏感,导致跳数频率和强度随马赫数变化,也即是随脉动强度变化;而当β>0°时,摆片轴线偏离气流脉动轴线,敏感性下降,故障频率也随之下降。传感器摆片结构及倾角传感器频谱与X、Y、Z方向频谱的比较见图 5。
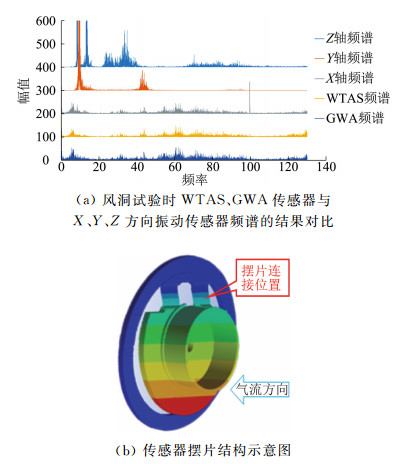
|
图 5 传感器摆片结构及倾角传感器频谱与X、Y、Z方向频谱的比较图 Fig.5 Sensor pendulum mechanism, inclinometer spectrum, and the spectrum comparison of X, Y, Z direction |
(2) GWA、WTAS传感器跳数主要由两种跳数组成(见图 6)。第一种,V字状跳数。模型有可见的振动;跳数误差与振幅成正比;跳数变化缓慢,周期约2.5 s;多个传感器会同步跳;跳数多出现在大位置。第二种,毛刺状跳数。模型无明显振动;跳数误差与干扰信号溢出量成正比;跳数变化迅速,周期约0.4 s;多个传感器同步跳概率低;跳数多出现在最大、最小角度位置。
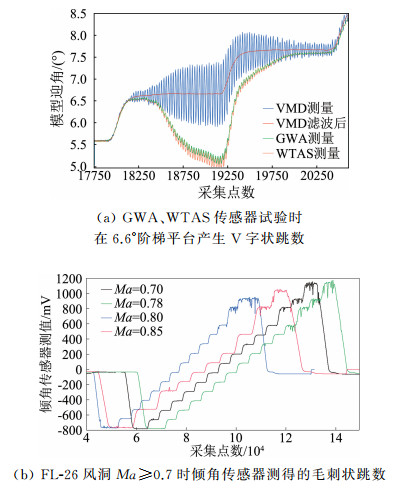
|
图 6 V字状和毛刺状跳数的特征示意图 Fig.6 Characteristics of V-shaped and burr-like hops |
(3) 根据两种跳数相关关系的指引,推理这两种跳数所产生的原因。第一种,V字状跳数是模型和支杆的纵横向振动带动倾角传感器振动,从而对多个倾角传感器的敏感元件摆片带来离心力的影响;第二种,毛刺状跳数是由于轴向的高频脉动耦合上倾角传感器摆片的固有频率从而产生高能量的干扰信号,造成倾角传感器输出信号在最大、最小位置时非对称溢出所致。因多个倾角传感器摆片的固有频率不同,所以此类跳数通常在多个传感器之间交错出现。
有了精确深入的跳数原因的分析后,制定了相应的改进措施。倾角传感器GWA、WTAS在随后的2.4 m跨声速风洞、2 m超声速风洞的多期试验中的取得了全程精准测量无跳数现象的突破,解决了长期存在的问题。
此例是一个较为典型的应用大数据分析的例子,首先是利用历年来大量试验数据获取宏观上的跳数问题与马赫数、侧滑角及流场脉动等参数的概率分布和相关性;再拓展数据源,深入到微观细节去探寻跳数问题与更加广阔其它数据之间的联系和相关性;最后,通过宏观和微观中获得的多种相关性的引领分析,明确各种跳数产生的原因。
上述三个应用实例中使用的分析数据全部是采用风洞试验数据采集新方法采集的试验全程、全部试验数据[16-18]。
3 结论1) 结合大数据分析的基础方法,通过对传统风洞试验采集、处理方法的改进创新,建立了一套集风洞试验数据采集、分析、挖掘及结果展现为一体的风洞试验大数据综合分析处理系统;
2) 在风洞试验中应用大数据分析方法,既可以对试验宏观现象进行精准分析,也可以对试验局部和细节进行精细化微观分析;
3) 从风洞试验大数据中挖掘出的频率、概率、相关关系等数据,可以为试验数据的深入分析、试验故障的准确定位指明方向。
本项研究目前只是风洞试验大数据分析的简易平台,验证了平台建设中的一些关键设计思想,取得了阶段性成果,实现了风洞试验数据采集从传统的阶梯抽样采集的小数据时代到采集试验全程全部试验数据和信息的大数据时代的初步转变。但是,要继续深入进行风洞试验的大数据研究,还需要进一步夯实大数据软硬件基础平台支撑能力。
| [1] |
XIE Y, LI P, WANG R B, et al. An experiment research on dsp technology in wind tunnel[C]//2010 International Conference on Apperceiving Computing and Intelligence Analysis Proceeding, 2010.
|
| [2] |
LI P, RUI W, QIN J H, et al. Development of measurement and operation management system in 2 m×2 m supersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(4): 96-99. |
| [3] |
XIE Y, LI P, JIANG H, et al. The key technique research on continuous sweeping angle of attack test in 2.4 m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(1): 89-93. |
| [4] |
吕长青. 大数据[M]. 北京: 北京工业大学出版社, 2016. LU C Q. Big data[M]. Beijing: Beijing University of Technology Press, 2016. (in Chinese) |
| [5] |
BAKER P.大数据策略[M].于楠, 译.北京: 清华大学出版社, 2016.
|
| [6] |
王文正, 郑鹍鹏, 陈功, 等. 数据挖掘技术在飞行试验数据分析和气动参数辨识中的应用研究[J]. 空气动力学学报, 2016, 34(6): 778-782. WANG W Z, ZHENG K P, CHEN G, et al. Application research of data-mining to flight test data analysis and aerodynamic parameter identification[J]. Acta Aerodynamica Sinica, 2016, 34(6): 778-782. DOI:10.7638/kqdlxxb-2015.0032 (in Chinese) |
| [7] |
袁炳南, 霍朝辉, 白效贤. 飞行试验大数据技术发展及展望[J]. 计算机测量与控制, 2016, 34(6): 778-782. YUAN B N, HUO Z H, BAI X X. Technology development and prospects of big data in flight test[J]. Computer Measurement & Control, 2016, 34(6): 778-782. (in Chinese) |
| [8] |
李平.一种风洞试验数据采集的方法: 中国, 201318003324.7[P]. 2015-02-04.
|
| [9] |
朱明. 数据挖掘[M]. 合肥: 中国科学技术大学出版社, 2008. ZHU M. Data mining[M]. Hefei: Press of University of Science and Technology of China, 2008. (in Chinese) |
| [10] |
王梦雪. 数据挖掘综述[J]. 软件导刊, 2013, 12(10): 135-137. WANG M X. Survey of data mining[J]. Software Uuide, 2013, 12(10): 135-137. (in Chinese) |
| [11] |
JEONG S, SHIMOYAMA K. Review of data mining for multi-disciplinary design optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2011, 225(5): 469-479. DOI:10.1177/09544100JAERO906 |
| [12] |
MONROE U A, FREEMAN K, JONES K I. IT data mining tool uses in aerospace[R]. NASA ARC-E-DAA-TN 4694, 2012.
|
| [13] |
BRYAN M, SANTANU D, KANISHKA B, et al. Discovering anomalous aviation safety events using scalable data mining algorithms[J]. Journal of Aerospace Information Systems, 2014, 11(7): 482-482. DOI:10.2514/1.I010211 |
| [14] |
SHINKYU J, KAZUHISA C, SHIGERU O. Data mining for aerodynamic design space[R]. AIAA 2005-5079, 2005.
|
| [15] |
OYAMA A, VERBURG P C, NONOMURA T, et al. Flow field data mining of pareto-optimal airfoils using proper orthogonal decomposition[R]. AIAA 2010-1140, 2010.
|
| [16] |
MACKMAN T J, ALLEN C B. Aerodynamic data modeling using adaptive sampling[R]. AIAA 2010-9194, 2010.
|
| [17] |
魏志, 谢艳, 吴军强, 等. 连续变迎角测力试验技术在大型暂冲式跨声速风洞中的应用[J]. 实验流体力学, 2011, 25(4): 99-102. WEI Z, XIE Y, WU J Q, et al. Application of continuous sweeping force measuring technology in large intermittent transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 99-102. DOI:10.3969/j.issn.1672-9897.2011.04.019 (in Chinese) |
| [18] |
AMIRI K, SOLTANI M R, HAGHIRI A. Steady flow quality assessment of a modified transonic wind tunnel[J]. Scientia Iranica Transactions B: Mechanical Engineering, 2013, 20(3): 500-507. |
 2019, Vol. 37
2019, Vol. 37

