近些年来,使用非结构混合网格的计算流体力学(Computational Fluid Dynamics, CFD)在工程模拟中得到了广泛的应用。非结构混合网格,没有网格拓扑的限制,能够高效地处理复杂外形问题。网格生成时需要较少的人工干预,网格生成的时间相对于多块结构网格也大大减少,计算前期准备的工作量和所需时间显著减少。非结构网格另一个比较吸引人的特点是便于开展基于流场解的网格自适应[1]。在两个著名的航空标模计算会议、阻力会议和高升力会议上,超过一半的参与者使用基于非结构网格的流场计算器[2-16]。
现有的面向工程应用的非结构网格CFD求解器大多是基于空间二阶精度的有限体积方法。为了达到空间的二阶精度,使用分段线性重构多项式来近似流场变量的分布。梯度求解的精度在很大程度上决定了求解器的整体空间精度。常用的梯度方法主要有格林高斯法和最小二乘法两种方法。
格林高斯法是利用格林高斯定理,将流场变量在体心的梯度转换为变量在单元界面上的积分。格林高斯法最大的优点是它与计算通量的过程相似,因此不需要增加新的数据结构,可以提高计算效率。求解过程中只使用了与当前单元共面的单元信息,计算过程比较紧致,比较容易实现大规律并行计算。但是格林高斯法的缺点也很明显。计算中只使用了共面的单元信息,这样较窄的模板有可能导致较小的数值耗散,影响计算的鲁棒性[17-18]。
为了改善传统格林高斯法的求解精度和鲁棒性问题,有学者提出了节点格林高斯法[17, 19]。这种方法的思路是面心(二维情况下为线中点)的值用该面所有顶点的算术平均得到,而顶点的值又利用它周围所有单元的体心值通过加权平均得到,这样就充分利用了周围控制体的所有已知信息,模板相较传统的格林高斯法更宽。
最小二乘法[18, 20-23]可以认为是一种k-exact重构(k=1),是将流场变量在当前单元体心处做一阶Taylor级数展开,随后将该展开延拓到周围邻近单元(共面或者共点单元),并且要求满足该单元的平均值约束条件。这样得到一个未知量是体心梯度的最小二乘问题。
在现阶段,关于梯度求解方法的文献有很多,但是大多都是从数值测试的方面来评估各种方法的数值表现[17-27],比如Sozer[27]测试了几种常用的梯度求解方法的数值表现,也得到了在任意网格拓扑下能保持一阶精度的梯度求解方法。但是他们没有过多涉及到方法本身的理论精度问题。国内的王年华等[30]在理论分析方面做了一定工作,侧重点在数值测试方面,并对网格质量和网格类型的影响做了一定分析。本文结合前人的工作,重点在理论方面分析了几种常见的梯度求解方法的精度,给出了精度推导的具体过程,并从数值方面对上述理论精度进行了验证。在数值测试过程中,通过以当前单元体心为基准进行坐标局部缩放的做法,保证了在非结构网格上做精度测试时,网格拓扑能够严格保持不变。这些研究内容对非结构网格梯度求解方法的理论分析和对比,具有一定的借鉴意义。本文的分析和数值验证都是基于格心的有限体积法展开的。
1 梯度求解方法的理论精度推导在本节中主要推导了几种常用的梯度求解方法的理论精度,主要有格林高斯法、节点格林高斯法和最小二乘法。首先在二维情况下做了推导,最后将推导推广到三维。
本文的研究考虑了直角坐标系下的Euler方程,控制方程为:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial z}} = 0 $ | (1) |
其中:U为守恒变量,F、G、H为无黏通量, 定义如下:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{l}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ {\rho E} \end{array}} \right],\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} {\rho u}\\ {\rho uu + p}\\ {\rho uv}\\ {\rho uw}\\ {\rho Hu} \end{array}} \right],\mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{l}} {\rho v}\\ {\rho uv}\\ {\rho vv + p}\\ {\rho vw}\\ {\rho Hv} \end{array}} \right],\\ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} {\rho w}\\ {\rho uw}\\ {\rho vw}\\ {\rho ww + p}\\ {\rho Hw} \end{array}} \right] \end{array} $ |
在有限体积法中,将上述控制方程在每个网格单元Ωi内积分,得到:
| $ \frac{{\partial {{\bar U}_i}}}{{\partial t}} + \frac{1}{{{{\mathit{\bar \Omega }}_i}}}\oint_{\partial {\mathit{\Omega }_i}} {{\mathit{\boldsymbol{F}}_n} \cdot \mathit{\boldsymbol{n}}{\rm{d}}s} = 0 $ | (2) |
其中:
在非结构网格中,为了达到空间二阶精度,需要利用守恒变量的平均值信息,完成分段线性重构,即计算出守恒变量在单元体心的梯度。然后利用线性插值得到界面左右两侧的守恒变量,
| $ \begin{array}{l} {U_L} = {{\bar U}_i} + \nabla {U_i} \cdot {\mathit{\boldsymbol{r}}_L}\\ {U_R} = {{\bar U}_j} + \nabla {U_j} \cdot {\mathit{\boldsymbol{r}}_R} \end{array} $ | (3) |
其中:rL、rR分别表示从左右两侧体心到面心的矢量。最后可以使用成熟的Riemann求解器得到界面处的无黏通量Fn(UL, UR, n)。
1.1 格林高斯法对于在单元内部和单元界面上一阶连续的函数f,根据格林高斯公式可以得到:
| $ \iint {\nabla f{\text{d}}s} = \oint {f\mathit{\boldsymbol{n}}{\text{d}}l} $ | (4) |
其中n为控制体界面的外法线方向。定义梯度在单元上的平均值为(
由于单元体心值是单元平均值的二阶精度近似,式(4)可以改写为:
| $ \left( {\nabla f} \right)\left| {_c} \right. = \frac{1}{S}\oint {f\mathit{\boldsymbol{n}}{\text{d}}l} + O\left( {f'''{\Delta ^2}} \right) $ | (5) |
在实际应用过程中,式(5)右端的积分
| $ \oint {f{\text{d}}l} = l{f_{{\text{mid}}}} + O\left( {f''{\Delta ^3}} \right) $ |
代入式(5)得到:
| $ \left( {\nabla f} \right)\left| {_c} \right. = \frac{1}{S}\sum {\mathit{\boldsymbol{n}}l{f_{{\text{mid}}}}} + O\left( \Delta \right) $ | (6) |
因此下面的关键是求得fmid的近似
假定f1和f2分别为界面两侧函数的单元平均值或体心函数值(由于体心值是平均值的二阶精度近似,两者交换使用不影响下文的推导),r1和r2分别为从两侧体心到界面中点的矢径。根据Taylor展开(只取一阶项),若两侧体心和线中点在同一条直线上,即
| $ {{\tilde f}_{{\text{mid}}}} = \frac{{\left| {{\mathit{\boldsymbol{r}}_2}} \right|{{\bar f}_1} + \left| {{\mathit{\boldsymbol{r}}_1}} \right|{{\bar f}_2}}}{{\left| {{\mathit{\boldsymbol{r}}_1}} \right| + \left| {{\mathit{\boldsymbol{r}}_2}} \right|}} = {f_{{\text{mid}}}} + O\left( {f''{\Delta ^2}} \right) $ | (7) |
如果两侧体心和线中点不在同一条直线上,则无论距离权,还是使用面积权或者简单算术平均,都达不到二阶精度。
在很多情况下,特别是网格质量不是特别好的时候,“两侧体心和线中点不在同一条直线上”是经常发生的,这也给计算带来很大的误差。此时,即使对于线性分布的函数,
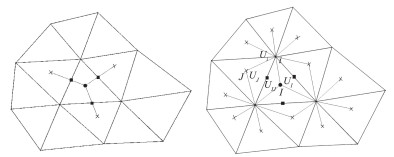
格林高斯法的关键是利用左右单元体心的值来求解线中点的值,这种做法虽然简单,但只使用了与当前单元共面的单元的信息,如图 1左所示,周围其他单元的信息并没有用到。为了改善传统格林高斯法的求解精度和鲁棒性问题,有学者提出了节点格林高斯法。这种方法的思路是线中点的值用该线所有顶点的算术平均得到,而顶点的值又利用它周围所有单元的体心值通过加权平均得到,这样就充分利用了周围控制体的所有已知信息,模板相较传统的格林高斯法更宽,如图 1右所示。
|
图 1 格林高斯法(左)和节点格林高斯法(右)的模板点示意图[28] Fig.1 Stencil illustration for Green-Gauss method (Left) and node-based Green-Gauss method (Right) [28] |
在节点格林高斯法中,线中点的函数值由该线段端点的函数值算术平均得到:
| $ {{\tilde f}_{{\text{mid}}}} = \frac{{{f_1} + {f_2}}}{2} = {f_{{\text{mid}}}} + O\left( {{\Delta ^2}} \right) $ | (8) |
如果f1和f2均有二阶精度,则得到的
对于节点值f1和f2,可以根据周围的节点值通过某种加权算法得到。
| $ \begin{array}{l} {w_i} = 1 + \Delta {w_i}\\ \Delta {w_i} = {\lambda _x}\left( {{x_i} - {x_0}} \right) + {\lambda _y}\left( {{y_i} - {y_0}} \right)\\ {\lambda _x} = \frac{{{I_{xy}}{R_y} - {I_{yy}}{R_x}}}{{{I_{xx}}{I_{yy}} - I_{xy}^2}},{\lambda _y} = \frac{{{I_{xy}}{R_x} - {I_{xx}}{R_y}}}{{{I_{xx}}{I_{yy}} - I_{xy}^2}}\\ {R_x} = \sum\limits_{i = 1}^n {\left( {{x_i} - {x_0}} \right)} ,{R_y} = \sum\limits_{i = 1}^n {\left( {{y_i} - {y_0}} \right)} ,\\ {I_{xx}} = \sum\limits_{i = 1}^n {{{\left( {{x_i} - {x_0}} \right)}^2}} ,\\ {I_{yy}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {y_0}} \right)}^2}} ,\\ {I_{xy}} = \sum\limits_{i = 1}^n {\left( {{x_i} - {x_0}} \right)} \left( {{y_i} - {y_0}} \right) \end{array} $ | (9) |
其中当前节点记为0,邻近体心记为i,(i=1, 2, …,n)。不过需要指出的是,使用这种权函数需要做两次基于节点的循环,计算量至少比使用距离权多了一倍。
1.3 最小二乘法利用最小二乘法来估算体心梯度最早是由Barth[20-21]提出,可以理解为k-exact(k=1)重构[24]。在当前单元及其领域内,假定线性函数分布,该函数分布不仅满足当前单元的平均值约束,也满足邻近单元的平均值约束。二维情况下,当前单元记为0,邻近单元记为i,(i=1, 2, …,N),满足单元0上平均值约束的函数分布可以写为:
| $ f = {{\bar f}_0} + {\left. {{f_x}} \right|_0}\left( {x - {x_0}} \right) + {\left. {{f_y}} \right|_0}\left( {y - {y_0}} \right) $ | (10) |
将其在邻近单元i上积分,满足单元i的平均值约束:
| $ {{\bar f}_i} = {{\bar f}_0} + {\left. {{f_x}} \right|_0}\left( {{x_i} - {x_0}} \right) + {\left. {{f_y}} \right|_0}\left( {{y_i} - {y_0}} \right) $ | (11) |
将xi-x0记为Δxi,yi-y0记为Δyi,得到如下的最小二乘问题
| $ \left[ {\begin{array}{*{20}{c}} {{w_1}\Delta {x_1}}&{{w_1}\Delta {y_1}}\\ {{w_2}\Delta {x_2}}&{{w_2}\Delta {y_2}}\\ \vdots & \vdots \\ {{w_i}\Delta {x_i}}&{{w_i}\Delta {y_i}}\\ \vdots & \vdots \\ {{w_N}\Delta {x_N}}&{{w_N}\Delta {y_N}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde f}_x}}\\ {{{\tilde f}_y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{w_1}\left( {{f_1} - {f_0}} \right)}\\ {{w_2}\left( {{f_2} - {f_0}} \right)}\\ \vdots \\ {{w_i}\left( {{f_i} - {f_0}} \right)}\\ \vdots \\ {{w_N}\left( {{f_N} - {f_0}} \right)} \end{array}} \right] $ | (12) |
其中:wi为权函数,可以取为单元i体心到单元0体心距离的函数。该最小二乘问题可以记为Ax=b。为了避免病态问题,上述最小二乘问题A矩阵使用Gram-Schmidt过程[23]分解为正交矩阵Q和上三角矩阵R的乘积,因此得到x=R-1QTb。亦可以使用奇异值分解,通过矩阵A的广义逆来估算体心梯度。
为了分析最小二乘法的精度,通过式(12)的法方程来分析求解精度[26]。
上述最小二乘问题的法方程为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\sum\limits_i {w_i^2} \Delta x_i^2}&{\sum\limits_i {w_i^2} \Delta {x_i}\Delta {y_i}}\\ {\sum\limits_i {w_i^2} \Delta {x_i}\Delta {y_i}}&{\sum\limits_i {w_i^2} \Delta y_i^2} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde f}_x}\left| {_{{x_0},{y_0}}} \right.}\\ {{{\tilde f}_y}\left| {_{{x_0},{y_0}}} \right.} \end{array}} \right]\\ = \left[ \begin{array}{l} \sum\limits_i {w_i^2} \Delta {x_i}\left( {{f_i} - {f_0}} \right)\\ \sum\limits_i {w_i^2} \Delta {y_i}\left( {{f_i} - {f_0}} \right) \end{array} \right] \end{array} $ | (13) |
将fi-f0在(x0, y0)处做Taylor展开得到,经过简单推导得到:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\tilde f}_x}\left| {_{{x_0},{y_0}}} \right.}\\ {{{\tilde f}_y}\left| {_{{x_0},{y_0}}} \right.} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_x}\left| {_{{x_0},{y_0}}} \right.}\\ {{f_y}\left| {_{{x_0},{y_0}}} \right.} \end{array}} \right] + \\ {\left[ {\begin{array}{*{20}{c}} {\sum\limits_i {w_i^2} \Delta x_i^2}&{\sum\limits_i {w_i^2} \Delta {x_i}\Delta {y_i}}\\ {\sum\limits_i {w_i^2} \Delta {x_i}\Delta {y_i}}&{\sum\limits_i {w_i^2} \Delta y_i^2} \end{array}} \right]^{ - 1}} \cdot \\ \left[ \begin{array}{l} \sum\limits_i {w_i^2} \Delta {x_i}\left( {\frac{1}{2}{f_{xx}}\Delta x_i^2 + \frac{1}{2}{f_{yy}}\Delta y_i^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{f_{xy}}\Delta {x_i}\Delta {y_i} + O\left( {{\Delta ^3}} \right)\\ \sum\limits_i {w_i^2} \Delta {y_i}\left( {\frac{1}{2}{f_{xx}}\Delta x_i^2 + \frac{1}{2}{f_{yy}}\Delta y_i^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{f_{xy}}\Delta {x_i}\Delta {y_i} + O\left( {{\Delta ^3}} \right) \end{array} \right]\\ = \left[ {\begin{array}{*{20}{c}} {{f_x}\left| {_{{x_0},{y_0}}} \right.}\\ {{f_y}\left| {_{{x_0},{y_0}}} \right.} \end{array}} \right] + O\left( {f''\Delta } \right) \end{array} $ | (14) |
可见最小二乘法计算体心梯度达到一阶精度,而且推导过程中不引入近似。对于任意的网格拓扑,都能准确计算线性函数的梯度。
在最小二乘法求解过程中,可以选择与当前单元共面的单元,也可以选择与当前单元共点的单元,这类似于格林高斯法和节点格林高斯法模板集的不同。只使用共面单元,导致模板集过窄,数值耗散较小,工程计算中可能遇到鲁棒性问题。使用全部共点单元,计算量相对大一点,但是模板点更宽,计算的稳定性提高。
在实施过程中,权函数的选择比较关键。在大拉伸比网格上,不加权的最小二乘法产生的左端项矩阵条件数过大。使用距离的倒数作为权重的话,可以有效改善矩阵的条件数问题,在各向异性网格上减轻计算的刚性问题,得到更好的梯度近似。
上面的分析给出了三种梯度求解方法的理论精度。格林高斯法中,只有当单元两侧体心和线中点在同一条直线上并且使用距离权插值到中点上时,计算得到的梯度才有一阶精度。节点格林高斯法计算梯度的精度取决于节点上的函数值是通过何种加权方法得到。如果使用距离的倒数作为权重,计算得到的梯度不到一阶精度。如果使用满足二阶精度的插值方法,计算得到的梯度为一阶精度,能够准确得到线性函数的梯度。但是这样做付出的代价是必须循环两次,计算量增大。对于最小二乘法,不管使用共面单元还是共点单元,不管在何种网格拓扑下,只要邻近单元数目足够,计算得到的梯度为一阶精度,能够准确得到线性函数的梯度。
从上述二维推导很容易扩展到三维。高斯和节点高斯方法中:
| $ \left( {\nabla f} \right)\left| {_c} \right. = \frac{1}{V}\oint {f\mathit{\boldsymbol{n}}{\rm{d}}s} + O\left( {f'''{\Delta ^2}} \right) $ | (15) |
三维情况下,不管单元界面是三角形还是四边形都有:
| $ \oint {f{\rm{d}}s} = S{f_{{\rm{mid}}}} + O\left( {f''{\Delta ^4}} \right) $ | (16) |
因此
最小二乘法的精度分析可以更加直接地从二维推广到三维,具体细节比较简单,本文不再给出。在三维情况下,关于梯度求解方法的理论精度分析与二维情况一致。
2 精度测试在上一节中,对三种梯度求解方法的理论精度做了推导,这一节将首先验证不同梯度求解方法在网格变形情况下对线性函数梯度的求解精度。然后从数值方面在不同网格拓扑情况下对上节推导的理论精度进行验证。最后通过低速无黏翼型绕流问题验证在稍复杂问题下,各种梯度求解方法的表现。
2.1 梯度求解误差分析使用线性解析函数来验证不同梯度求解方法在网格变形情况下预测梯度的能力。考虑了5种梯度的求解方法,分别为格林高斯法(GreenGauss-CellBased),使用距离倒数权插值到节点的节点格林高斯法(GreenGauss-NodeBased-InverseDistance),使用保线性权插值到节点的节点格林高斯法(GreenGauss-NodeBased-LinearPreserving),使用共面单元的最小二乘法(LeastSquare-CellBased)和使用共点单元的最小二乘法(LeastSquare-NodeBased)。两种最小二乘法都使用了距离倒数作为权函数。
在[0, 1]×[0, 1]的二维区域内,生成三角形的初始网格。网格变形方法参考了Cary[18]的处理方法,是通过代码将初始网格点的位置由(xi, yi)平移到(xi+(s-1)yi, yi),s为从1开始连续变化的正整数,称为拉伸比例。在此过程中保持网格拓扑不变。
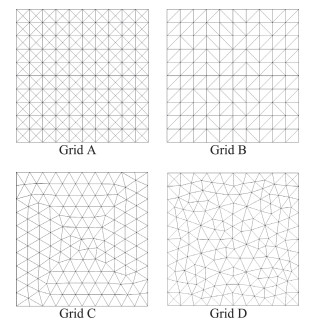
验证过程中考虑了四种不同的网格拓扑,分别记做Grid A、Grid B、Grid C、Grid D,如图 2所示。这里给出的是初始网格的示意图。在网格还没有变形的情况下,就已经有很多“两侧体心和线中点不在同一条直线上”的情况发生。
|
图 2 用来测试线性函数梯度求解的四套网格 Fig.2 Grids used for gradient computation test of linearly varying function |
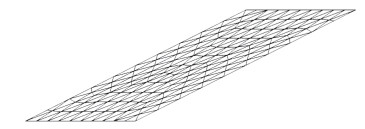
图 3给出了s=3时Grid C变形后的示意图,网格在x方向拉伸严重。
|
图 3 网格x向拉伸示意图 Fig.3 Illustration of grid stretching in x direction |
在测试中主要考虑不同梯度求解方法的影响,没有关注边界的处理。在格林高斯和节点格林高斯法中,在边界附近单元梯度求解时,需要用到边界上线段中点和节点的函数值。这里通过解析函数精确给出。在共面的最小二乘法中,有些边界单元没有足够多的内部共面相邻单元,无法给出预测梯度,在统计误差时,这部分单元忽略。
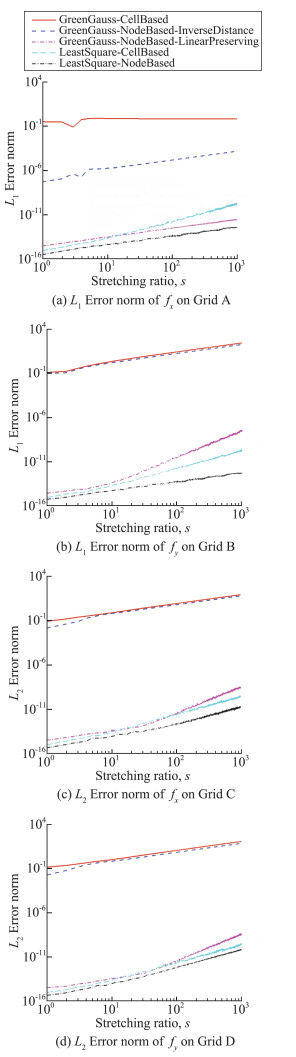
测试使用的是线性函数f=x+sy。通过上面的理论分析可以预测,格林高斯法和使用距离倒数权插值到节点的节点格林高斯法不能准确预测该函数的梯度值,随着网格变形加大,误差更大。其他三种方法都能准确计算该函数梯度。图 4给出了4种网格拓扑下,计算得到的体心梯度误差的1-范数和2-范数误差随着拉伸比例的变化情况,其中fy的误差是除了拉伸比例s后的结果。格林高斯法和使用距离倒数权插值到节点的节点格林高斯法在四套网格上都不能准确预测体心梯度。特别是在Grid B, Grid C和Grid D上,随着网格拉伸加大,误差持续增加。后三种梯度求解方法在四种网格拓扑下,都准确预测了线性函数的体心梯度。随着网格变形的加剧,计算误差均在可以接受的范围内。
|
图 4 不同梯度求解方法对线性函数梯度求解的误差 Fig.4 Gradient computation error for linear function with different methods |
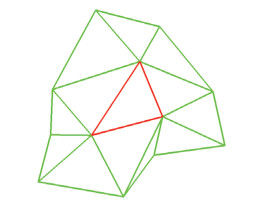
非结构网格加密的过程中,很难保证局部网格的拓扑不变。对于计算域中的某一个参考点,网格加密后其周围的网格拓扑很可能发生改变,这样做数值精度测试是否严格是存疑的。Sozer[27]提出了一种新的思路。在测试过程中,保持网格不变,将测试函数在局部坐标系下进行缩放,以此来验证方法的数值精度。但实施过程中,因为测试函数是定义在局部坐标系下的,过程稍微繁琐。本文提出了一种新的数值精度验证的方法。对于图 5所示的单元0(由红色线段构成),在高斯法和共面最小二乘法中,单元0体心的梯度只与单元0以及与其共面的单元有关,在节点高斯法和共点最小二乘法中,单元0体心的梯度只与单元0以及与其共点的单元有关。将单元0和其相关单元组合在一起,以单元0的体心为基准点来进行局部的坐标缩放,通过单元0体心梯度的预测值和精确值的误差来验证方法的数值精度。在此过程中测试函数保持不变。如果只在计算域中的某一点上通过预测误差来测试精度难免会受到函数分布的影响。在验证过程中,将单元0及其相关单元在计算域内整体均匀平移,通过误差的1-范数和2-范数来测试数值精度。验证使用的测试函数是非线性函数:
|
图 5 完成收敛精度测试的网格示意(Grid E) Fig.5 Illustration of grid used for the order of accuracy test (Grid E) |
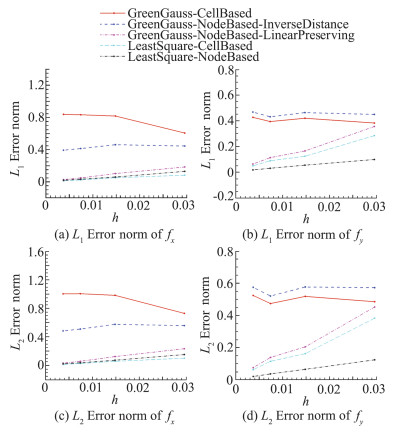
图 6给出了不同的梯度预测方法计算的梯度误差随着网格尺度的变化规律,其中h为当前单元0面积的平方根。使用保线性权插值到节点的节点格林高斯法,使用共面单元的最小二乘法和使用共点单元的最小二乘法这三种方法计算的梯度有着近似线性的网格收敛性,证明了梯度预测的精度为一阶精度。格林高斯法和使用距离倒数权插值到节点的节点格林高斯法,梯度预测的误差与预想的不一致。预计中这两种方法的误差随着网格加密会逐渐减小,但收敛速度慢于其他后面三种方法,即梯度预测的精度低于一阶。
|
图 6 不同梯度求解方法的数值精度验证(Grid E) Fig.6 The order of accuracy for different gradient computation methods on Grid E |
可以简单地从理论上分析这种情况发生的原因。对于格林高斯法,预测的x方向体心梯度从式(3)出发,可以写为:
| $ \begin{array}{l} \widetilde {{{\left. {{f_x}} \right|}_c}} = \frac{{\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}{f_{i,{\rm{mid}}}}} }}{S}\\ \;\;\;\;\;\; = \frac{{\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}\left( {{w_{i1}}{f_0} + {w_{i2}}{f_j}} \right)} }}{S} \end{array} $ | (17) |
其中:i=1, …,N0表示单元0的边界,j表示单元0的共面单元,两者的公共面是i。将fi在当前单元体心0处做Taylor展开,可以得到:
| $ \begin{array}{l} \widetilde {{{\left. {{f_x}} \right|}_c}} = \frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}\left[ {{w_{i1}}{f_0} + {w_{i2}}{f_0} + } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {{w_{i2}}\left( {\nabla f} \right)\left| {_0} \right. \cdot {\mathit{\boldsymbol{r}}_{j0}} + {w_{i2}}O\left( {f''{\Delta ^2}} \right)} \right]\\ \;\;\;\;\;\; = \frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}\left[ {{f_0} + {w_{i2}}\left( {\nabla f} \right)\left| {_0} \right. \cdot {\mathit{\boldsymbol{r}}_{j0}} + } \right.} \\ \;\;\;\;\;\;\left. {{w_{i2}}O\left( {f''{\Delta ^2}} \right)} \right] \end{array} $ | (18) |
由于
| $ \begin{array}{l} \widetilde {{{\left. {{f_x}} \right|}_c}} = \frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}\left[ {{w_{i2}}{f_x}\left| {_0} \right.{x_{j0}} + } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {{w_{i2}}{f_y}\left| {_0} \right.{y_{j0}} + {w_{i2}}O\left( {f''{\Delta ^2}} \right)} \right] \end{array} $ | (19) |
因此:
| $ \begin{array}{l} \widetilde {{{\left. {{f_x}} \right|}_c}} = \left( {\frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}{l_i}{w_{i2}}{x_{j0}}} } \right){f_x}\left| {_0} \right. + \\ \;\;{\left. {\left( {\frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_{ix}}} {l_i}{w_{i2}}{y_{j0}}} \right){f_y}} \right|_0} + O\left( {f''\Delta } \right) \end{array} $ | (20) |
只有当两侧体心和线中点在一条直线上并且使用式(7)的插值权函数时才有:
| $ \begin{array}{l} \frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{l_i}{w_{i2}}{x_{j0}}} = \left( {1,0} \right),\\ \frac{1}{S}\sum\limits_{i = 1}^{{N_0}} {{{\bf{n}}_i}} {l_i}{{\bf{w}}_{i2}}{y_{j0}} = \left( {0,1} \right) \end{array} $ | (21) |
此时
值得注意的是,式(21)也给出了格林高斯法中梯度求解为一阶精度时权函数需要满足的条件。在二维情况下,式(21)给出了四个约束方程,而未知数的个数为与当前单元共面的邻近单元的个数。通过最小二乘法求得wi2(i=1, …,N0)后,可以得到单元体心处的梯度为:
| $ \nabla f\left| {_0} \right. = \frac{{\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{l_i}{w_{i2}}\left( {{f_j} - {f_0}} \right)} }}{S} $ | (22) |
三维情况下有类似的推导。此时约束方程的个数为9个,分别为:
| $ \begin{array}{*{20}{l}} {\frac{1}{V}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{s_i}{w_{i2}}{x_{j0}}} = \left( {1,0,0} \right)}\\ {\frac{1}{V}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{s_i}{w_{i2}}{y_{j0}}} = \left( {0,1,0} \right)}\\ {\frac{1}{V}\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{s_i}{w_{i2}}{z_{j0}}} = \left( {0,0,1} \right)} \end{array} $ | (23) |
同样通过最小二乘法求得wi2后,可以得到单元体心处的梯度为:
| $ \nabla f\left| {_0} \right. = \frac{{\sum\limits_{i = 1}^{{N_0}} {{\mathit{\boldsymbol{n}}_i}{s_i}{w_{i2}}\left( {{f_j} - {f_0}} \right)} }}{V} $ | (24) |
由于上述权函数是通过最小二乘法得到的,因此在一般情况下不能保证该方法得到的梯度精确满足一阶精度。但该权函数使用了当前单元和所有共面单元的几何信息,并不像前面提到的距离加权或者面积加权等方法只使用当前单元和某一个共面单元信息。从式(20)可以推断出,新权函数求解梯度的精度更高。这种在格林高斯法的框架下,使用新权函数求解体心梯度的方法将在我们后续的文章中详细分析。
对于节点格林高斯法,通过类似的推导可以得到,当节点插值函数需要满足式(25),体心的梯度预测才有一阶精度。
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^{{N_0}} {\sum\limits_{m = 1}^{{P_i}} {{\mathit{\boldsymbol{n}}_m}} } {l_m}\sum\limits_{j = 1}^{{N_i}} {{w_j}} \left( {{x_j} - {x_i}} \right) = \left( {0,0} \right)}\\ {\sum\limits_{i = 1}^{{N_0}} {\sum\limits_{m = 1}^{{P_i}} {{\mathit{\boldsymbol{n}}_m}} } {l_m}\sum\limits_{j = 1}^{{N_i}} {{w_j}} \left( {{x_j} - {x_i}} \right) = \left( {0,0} \right)} \end{array} $ | (25) |
其中:i=1, …,N0表示单元0的节点编号,j=1, …,Ni表示拥有节点i的单元编号,m=1, …,Pi表示属于单元0并且拥有节点i的边界编号。当使用保线性权插值到节点上时,权函数满足:
| $ \begin{array}{*{20}{l}} {\sum {{w_i}} \left( {{x_i} - {x_0}} \right) = 0}\\ {\sum {{w_i}} \left( {{y_i} - {y_0}} \right) = 0} \end{array} $ | (26) |
这时有:
|
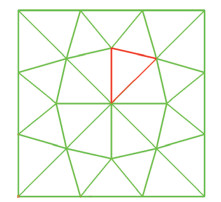
图 7 完成收敛精度测试的网格示意图(Grid F) Fig.7 Illustration of grid used for the order of accuracy test (Grid F) |
| 表 1 梯度求解方法的数值精度验证(Grid F) Table 1 The order of accuracy for different methods on Grid F |
|
|
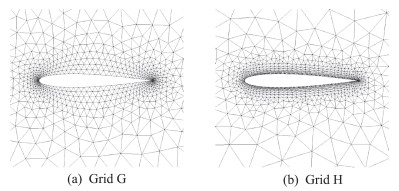
最后一个算例是NACA0012翼型亚声速无黏绕流。计算使用了逐渐加密的网格来验证不同梯度求解方法对流场的模拟能力。计算采用了两套网格,粗网格分别如图 8所示。其中Grid G是近似各向同性的三角形单元,Grid H是将各向异性的四边形单元剖分成三角形单元。在不同的网格拓扑下进行计算可以更全面地验证梯度求解方法的精度。计算的马赫数为0.6,迎角为0°。理论上该算例的阻力系数应该为零,因此在分析中用阻力系数的误差来分析数值精度。在计算中,使用共面单元的最小二乘法遇到了严重的鲁棒性问题,无法得到收敛的结果,因此只给出了其他四种梯度求解方法的结果。
|
图 8 NACA0012翼型绕流网格示意图 Fig.8 Illustration of grids used for simulation of flow around NACA0012 airfoil |
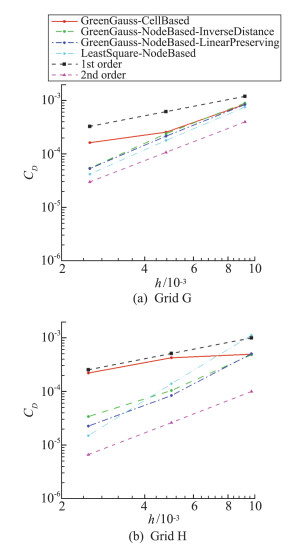
体心梯度的求解精度决定了求解器的整体精度。梯度求解为一阶精度时,求解器整体有二阶精度。梯度求解为零阶精度时,求解器整体只有一阶精度。图 9给出了不同梯度求解方法预测的阻力系数。坐标都是在对数坐标下的表示。横坐标为网格的特征尺度,取为
|
图 9 NACA0012翼型绕流问题预测的阻力系数 Fig.9 Drag coefficient for inviscid transonic flow around NACA0012 airfoil |
| 表 2 梯度求解方法的数值精度验证(Grid G) Table 2 The order of accuracy for different methods (Grid G) |
|
|
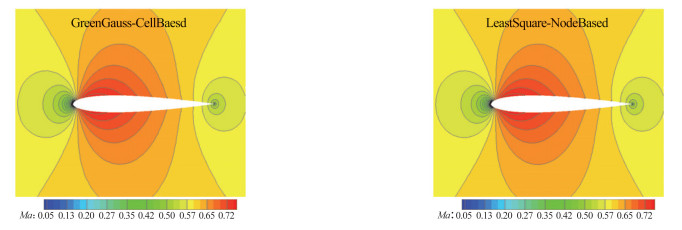
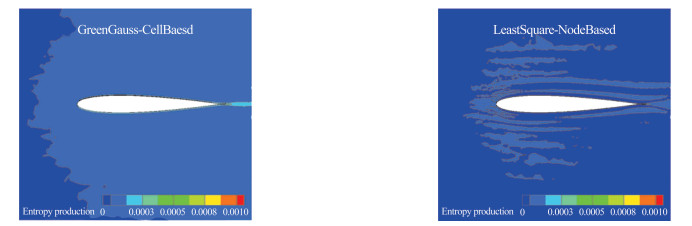
为了进一步判别不同梯度求解方法对流动结构的刻画能力,图 10和图 11分别给出了格林高斯法和使用共点单元的最小二乘法得到的马赫数云图和熵增云图,其中熵增定义为:
|
图 10 NACA0012翼型绕流的马赫数云图 Fig.10 Computed Mach number contours for flow around NACA0012 airfoil |
|
图 11 NACA0012翼型绕流的熵增云图 Fig.11 Computed entropy production contours for flow around NACA0012 airfoil |
| $ \Delta S = \frac{{S - {S_\infty }}}{{{S_\infty }}} = \frac{p}{{{p_\infty }}}{\left( {\frac{{{\rho _\infty }}}{\rho }} \right)^\gamma } - 1 $ | (27) |
在本算例中,流动是等熵的,理论上在计算域的任何位置均有ΔS=0。这里只给出了在Grid H序列中细网格上的结果,在其他网格上的结果与此类似。虽然两种梯度求解方法的收敛精度不同,但从图 10可以看到,两者得到了基本一致的光滑的马赫数分布。图 11的熵增云图可以看出明显的区别。格林高斯法得到的流场中在翼型附近和下游区域熵增明显较大,而使用共点单元的最小二乘法得到的流场中熵增区域显著较小。这与阻力系数的预测一起证明了格林高斯方法求解梯度的误差较最小二乘法偏大。
3 结论本文对二阶精度非结构混合网格求解器中几种常用的梯度求解方法进行了深入的理论分析。从理论精度方面,对几种方法的截断误差精度进行了推导。使用保线性权插值到节点的节点格林高斯法、使用共面单元的最小二乘法和使用共点单元的最小二乘法,不管网格拓扑关系如何,都能保证梯度求解为一阶精度。而格林高斯法和使用距离倒数权插值到节点的节点格林高斯法只有在特定的网格和权函数下,才能有一阶精度。在一般的网格中,只有零阶精度。
在得到上述理论之后,对各种梯度求解方法做了进一步的数值测试。首先验证了不同方法在网格持续拉伸变形情况下,对线性函数梯度求解的误差。格林高斯法和使用距离倒数权插值到节点的节点格林高斯法计算的梯度随着网格拉伸,计算的梯度急剧恶化。而其他三种方法都能准确计算线性函数的梯度。
随后从数值精度方面对上述的理论精度进行了验证。这里提出了一种新的精度测试方法。以当前单元体心为基准点进行局部网格的缩放,可以精确地保持网格加密过程中的网格拓扑不变。数值测试验证了上述推导的理论精度。对于格林高斯法和节点格林高斯法,推导得到了其满足一阶精度要求的权函数与网格尺度的约束关系。从这一约束出发,可以验证某种权函数能否满足一阶精度要求。
最后通过NACA0012翼型亚声速无黏绕流进一步分析了各种梯度求解方法的表现。使用保线性权插值到节点的节点格林高斯法和使用共点单元的最小二乘法求得的体心梯度均为一阶精度,这样解算器的整体精度为二阶精度。使用距离倒数权插值到节点的节点格林高斯法只有在网格各向同性的情况下才有一阶精度的体心梯度求解,否则低于一阶。格林高斯法在一般的网格下体心梯度低于一阶,解算器的整体精度也低于二阶。使用共面单元的最小二乘法因为只使用共面单元,鲁棒性较差,不能得到收敛的结果。
本文只是从梯度求解的精度方面对几种方法进行了分析。在实际工程应用中,计算的鲁棒性、计算量、并行传输的数据量等都是需要仔细考察的因素。后续文章将从这些方面对梯度求解方法进一步分析,并考察在边界层等大拉伸比单元上的表现。文中也提出了一种在格林高斯法的框架下,尽可能提高梯度求解精度的权函数求解方法。在后续的文章中将对这一方法深入研究和分析。
| [1] |
BLAZEK J. Computational fluid dynamics: principles and applications[R]. Oxford: Elsevier Science Ltd, 2001: 1-4.
|
| [2] |
RUMSEY C L, LONG M, STUEVER R A, et al., Summary of the first AIAA CFD high-lift prediction workshop: AIAA-2011-0939[R]. Reston: AIAA, 2011.
|
| [3] |
LONG M, MAVRIPLIS D. NSU3D results for the first AIAA high-lift prediction workshop: AIAA-2011-0863[R]. Reston: AIAA, 2011.
|
| [4] |
PARK M A, LEE-RAUSCH E M, RUMSEY C L. UN3D and CFL3D computations for the first high-lift prediction workshop: AIAA-2011-0936[R]. Reston: AIAA, 2011.
|
| [5] |
CRIPPA S, WILKENDINGY S M, RUDNIK R. DLR Contribution to the first high-lift prediction workshop: AIAA 2011-938[R]. Reston: AIAA, 2011.
|
| [6] |
RUMSEY C L, SLOTNICK J P, LONG M, et al. Summary of the first AIAA CFD high-lift prediction workshop[J]. Journal of Aircraft, 2011, 48(6): 2068-2079. DOI:10.2514/1.C031447 |
| [7] |
RUMSEY C L, SLOTNICK J P. Overview and summary of the second AIAA high-lift prediction workshop[J]. Journal of Aircraft, 2015, 52(4): 1006-1025. DOI:10.2514/1.C032864 |
| [8] |
MURAYAMA M, YAMAMOTO K, IT OY, et al. Japan aerospace exploration agency studies for the second high-lift prediction workshop[J]. Journal of Aircraft, 2015, 52(4): 1026-1041. DOI:10.2514/1.C033158 |
| [9] |
CHEN J T, ZHANG Y B, ZHOU N C, et al. Numerical investigations of the high-lift configuration with MFlow solver[J]. Journal of Aircraft, 2015, 52(4): 1051-1062. DOI:10.2514/1.C033143 |
| [10] |
MAVRIPLIS D, LONG M, LAKE T, et al. NSU3D Results for the second AIAA high-lift prediction workshop[J]. Journal of Aircraft, 2015, 52(4): 1063-1081. DOI:10.2514/1.C033042 |
| [11] |
LEE-RAUSCH E M, RUMSEY C L, PARK M A. Grid-adapted FUN3D computations for the second high-lift prediction workshop[J]. Journal of Aircraft, 2015, 52(4): 1098-1111. DOI:10.2514/1.C033192 |
| [12] |
LEVY D W, ZICKUHR T, VASSBERG J C, et al. Data summary from the first AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2003, 40(5): 875-882. DOI:10.2514/2.6877 |
| [13] |
LAFLIN K R, KLAUSMEYER S M, ZICKUHR T, et al. Data summary from second AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178. DOI:10.2514/1.10771 |
| [14] |
VASSBERG J C, TINOCO E N, MANI M, et al. Abridged summary of the third AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798. DOI:10.2514/1.30572 |
| [15] |
VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the fourth AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1070-1089. DOI:10.2514/1.C032418 |
| [16] |
LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the fifth computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1194-1213. DOI:10.2514/1.C032389 |
| [17] |
KIM S E, MAKAROV B, CARAENI D. A multi-dimensional linear reconstruction scheme for arbitrary unstructured grids[C]//16th AIAA Computational Fluid Dynamics Conference. AIAA 2003-3990, 2003.
|
| [18] |
CARY A W, DORGAN A J, MANI M. Towards accurate flow predictions using unstructured meshes[C]//19th AIAA Computational Fluid Dynamics. AIAA 2009-3650, 2009.
|
| [19] |
ZHANG S J, ZHAO X. Higher order data reconstruction schemes for unstructured grid[C]//36th AIAA Fluid Dynamics Conference and Exhibit. AIAA 2006-3061, 2006.
|
| [20] |
BARTH T J. A 3-D upwind Euler solver for unstructured meshes: AIAA-1991-1548[R]. Reston: AIAA, 1991.
|
| [21] |
BARTH T J. Aspects of unstructured grids and finite volume solvers for the Euler and Navier-Stokes equations[C]//AGARD R-787, Special Course on Unstructured Grid Methods for Advection Dominated Flows. Brussels, Belgium. 1992: 18-22.
|
| [22] |
MAVRIPLISD J. Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes[R]. NASA/CR-2003-212683.
|
| [23] |
WINKLER C M, DORGANY A J, MANIZ M. A reduced dissipation approach for unsteady flows on unstructured grids[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. AIAA 2012-0570, 2012.
|
| [24] |
BARTH T J, FREDERICKSON P O. High-order solution of the Euler equations on unstructured grids using quadratic reconstruction[C]//28th Aerospace Sciences Meeting. AIAA-90-0013, 1990.
|
| [25] |
ANDERSON W K, BONHAUSD L. An implicit upwind algorithm for computing turbulent flows on unstructured grids[J]. Computers Fluids, 1994, 23(1): 1-21. |
| [26] |
SHIMA E, KITAMURA K, FUJIMOTOK. New gradient calculation method for MUSCL Type CFD schemes in arbitrary polyhedra[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. AIAA 2010-1081, 2010.
|
| [27] |
SOZER E, BREHM C, KIRISY C C. Gradient calculation methods on arbitrary polyhedral unstructured meshes for cell-centered CFD solvers[C]//52nd Aerospace Sciences Meeting. AIAA 2014-1440, 2014.
|
| [28] |
张耀冰, 运输机气动特性混合网格数值模拟研究[D], 绵阳: 中国空气动力研究与发展中心, 2010. ZHANG Y B. Numerical simulation of transport aircraft's aerodynamic characteristics using mixed grid[D]. Mianyang: China Aerodynamics Research and Development Center, 2010. (in Chinese) |
| [29] |
RAUSCH R D, BATINA J T, YANG H T Y. Spatial adaptation of unstructured meshes for unsteady aerodynamic flow computations[J]. AIAA Journal, 1992, 30(5): 58-127. |
| [30] |
王年华, 张来平, 马戎, 等. 非结构网格质量对梯度重构及无黏流动模拟精度的影响[J]. 计算力学学报, 2017, 34(5): 555-563. WANG N H, ZHANG L P, MA R, et al. Mesh quality effects on the accuracy of gradient reconstruction and inviscid flow simulation on isotropic unstructured grids[J]. Chinese Journal of Computational Mechanics, 2017, 34(5): 555-563. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


