吸气式超燃冲压发动机允许来流以超声速状态进入燃烧室,是一种新型吸气式动力装置,在未来航空、航天领域中具有广阔的应用前景。在过去的几十年中,人们对超燃冲压发动机技术进行了大量试验、理论及数值计算研究[1]。对超燃冲压发动机设计研究来讲,理解超燃冲压发动机燃烧室内部的流场结构、流动特性是非常重要的。单纯依靠风洞试验难以给出详细的流场细节,而与风洞试验紧密结合的数值模拟在提供流场细节的同时,也有助于减少风洞试验内容,提高风洞试验效率。超燃冲压发动机内部流场数值模拟增加了对组分方程的求解过程,这使得流场模拟的计算量急剧增加。为了降低计算量,提高流场求解效率,除了进一步发展高效算法、采用并行技术外,通常还需要通过简约组分来降低组分守恒方程的规模。此外,在组分方程的求解过程中,为了获得动量、组分以及能量的输运强度,频繁计算组分及混合气体的输运系数,这是造成计算量剧增的主要因素之一。在混合气体输运系数计算方面,混合气体分子黏性系数由各组分的黏性系数表达,混合气体导热系数和扩散系数通常有两种计算方案[2]:1)假设普朗特数、施密特数为常数,由混合气体的分子黏性系数关联相应的导热系数和扩散系数;2)在计算组分的导热系数和扩散系数基础上,利用半经验公式计算混合气体的导热系数和扩散系数。受单个组分的基本输运系数数据匮乏和计算机能力的限制,早期多采用第一类方法计算混合气体导热系数和扩散系数[3],现在针对空气的流场计算仍主要采用该方案[4]。目前,组分基本输运系数有了很大的扩充,计算机能力也有了大幅度的提高,第二类计算方案已成为主流。
第二类计算方案虽然提高了混合气体输运系数计算的准确度,但是却增加了流场的计算量,由此降低了流场求解效率。在大规模、多组分复杂流场计算时,为了提高流场的求解效率,根据流场实际灵活选择导热系数和扩散系数计算方案,这就需要开展混合气体输运系数求解方案对流场计算影响的对比研究。当前,国内外超声速燃烧流场数值技术主要关注数值格式和计算方法[5],均直接采用其中一种方案计算混合气体输运系数,并没有对比研究输运系数各计算方案对流场数值模拟的影响。
因此,为有效运用混合气体输运系数近似计算方案,降低多组分流场数值模拟中对混合气体输运过程的计算量,进一步提高流场求解效率,有必要开展混合气体输运系数近似计算方案对流场计算的影响特点研究。本文基于Burrow和Kurkov实验构型及其实验数据[6],进行了多组分混合气体输运系数计算方案影响数值模拟,对比研究了混合气体分子导热系数、组分扩散系数的不同近似计算方案对边界层及射流剪切层流场计算的影响,以期为在超燃冲压发动机燃烧室流场的数值模拟中有效运用混合气体输运系数求解方案提供技术基础。
1 计算模型及参数定义 1.1 计算模型及来流条件Burrow和Kurkov实验研究了二维后台阶燃烧室中的顺喷氢燃料与来流的混合、燃烧特性,给出了较为详细的燃烧室出口温度、压力及组分分布,该实验已成为常用的验证算例[7-9]。
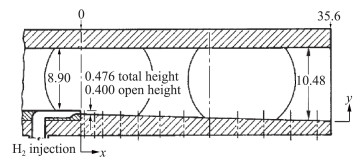
图 1为实验(计算)模型构型示意图。该实验模型在台阶之前为等截面构型,在台阶之后为扩张截面构型,用下壁面的扩张抵消燃烧室下游边界层的影响。实验过程中,模型与燃烧加热风洞的喷管相连,氢气燃料由实验模型下壁面的后台阶以声速注入,喷注压强为一个大气压,氢气燃料出流方向与污染空气来流平行、同向(图中从左至右)。
本文针对纯混合工况开展了数值模拟,其来流条件由表 1给出(纯混合实验时,污染空气来流中没有O2组分,以确保不发生化学反应)。
| 表 1 计算及实验的来流参数 Table 1 Inflow parameters for the CFD and test |
|
|
计算区域如图 1所示,为保证流向后台阶位置的边界层厚度为0.01 m,自后台阶(图中0 m处)向上游延伸0.42 m。网格结点总数为461×161,其中台阶上游部分的网格结点数为201×101,近壁网格的法向距离为1×10-5m,以保证k-ω SST类湍流模型所需的近壁网格雷诺数(y+<2)。本文仅开展相同网格条件下不同近似计算方案对比研究,没有特别考虑网格无关性的影响。同时,由于计算网格同向相邻网格间距比小于1.25,并且受近壁网格雷诺数的限制,因此网格无关性影响相对较小。
在计算中,①壁面边界:根据实验条件,设定模型壁面为等温壁(壁温为298 K),并采用无滑移条件;②来流边界:来流为超声速流动,固定入口截面的来流参数;③喷口边界:固定喷嘴出口截面的喷流参数;④出流边界:核心区的出流为超声速流动,对原始变量进行一阶外推。
1.3 摩阻系数、传热系数定义壁面摩阻系数、传热系数的计算式为[10]:
| $ \begin{array}{l} {C_f}(x) = \frac{{{\tau _w}}}{{\frac{1}{2}{\rho _\infty }V_\infty ^2}}\\ {C_h}(x) = \frac{{{q_w}}}{{{\rho _\infty }{V_\infty }{C_{p\infty }}\left( {{T_{t\infty }} - {T_w}} \right)}} \end{array} $ | (1) |
式中,ρ∞、V∞、Cp∞、Tt∞分别为来流核心区流场的密度、速度、定压比热及总温,τw、qw分别为壁面切应力和热流量,定义为:
| $ \begin{array}{l} {\tau _w} = {\left. {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial u}}{{\partial y}}} \right)} \right|_{y = 0}}\\ {q_w} = {\left. {\left( {\kappa + {\kappa _t}} \right)\left( {\frac{{\partial T}}{{\partial y}}} \right)} \right|_{y = 0}} \end{array} $ | (2) |
式中,μ、μt、κ、κt分别为流场中混合气体的分子黏性系数、涡黏性系数、分子导热系数、湍流导热系数,u、T分别为流场的速度、温度。
2 控制方程和数值方法 2.1 控制方程和计算方法简介计算坐标系下,含k-ω SST湍流模型[11]、组分方程的三维密度平均完全Navier-Stokes方程的守恒形式为:
| $ \frac{{\partial \mathit{\boldsymbol{\tilde Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{\tilde E}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\tilde F}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\tilde G}}}}{{\partial \xi }} = \frac{{\partial {{\mathit{\boldsymbol{\tilde E}}}_v}}}{{\partial \xi }} + \frac{{\partial {{\mathit{\boldsymbol{\tilde F}}}_v}}}{{\partial \eta }} + \frac{{\partial {{\mathit{\boldsymbol{\tilde G}}}_v}}}{{\partial \zeta }} + \mathit{\boldsymbol{S}} $ | (3) |
| $ \mathit{\boldsymbol{\tilde Q}} = {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{Q}} $ | (4) |
| $ \mathit{\boldsymbol{\tilde E}} = {\mathit{\boldsymbol{J}}^{ - 1}}\left( {{\xi _t}\mathit{\boldsymbol{Q}} + {\xi _x}\mathit{\boldsymbol{E}} + {\xi _y}\mathit{\boldsymbol{F}} + {\xi _z}\mathit{\boldsymbol{G}}} \right) $ | (5) |
| $ {{\mathit{\boldsymbol{\tilde E}}}_v} = {\mathit{\boldsymbol{J}}^{ - 1}}\left( {{\xi _x}{\mathit{\boldsymbol{E}}_v} + {\xi _y}{\mathit{\boldsymbol{F}}_v} + {\xi _z}{\mathit{\boldsymbol{G}}_v}} \right) $ | (6) |
这里,Q=(ρ, ρu, ρv, ρw, ρE, ρk, ρω, ρfi)T为守恒变量,其中的E为单位质量总内能; E、F、G、Ev、Fv以及Gv分别为控制方程的对流通量项和扩散通量项; S为湍流及化学源项; J为两坐标系之间的体积变换系数。
计算中,采用Liou[12]的AUSM+-up格式离散控制方程中的无黏项,采用二阶中心差分离散黏性项,采用Jameson[13]的LU-SSOR方法进行隐式求解。不对S进行隐式化处理时,LU-SSOR方法可表示为(去掉了方程中的上标“~”):
| $ \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{U}}\delta {Q_{i,j,k}} = \Delta \tau \left( {\mathit{\boldsymbol{rhs}}} \right)_{i,j,k}^n $ | (7) |
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{I}} + \Delta \tau {\left( {{\sigma _A} + {\sigma _B} + {\sigma _C}} \right)_{i,j,k}}\mathit{\boldsymbol{I}} $ | (8) |
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{D}} - \Delta \tau \left( {\mathit{\boldsymbol{A}}_{i - 1}^{ + n} + \mathit{\boldsymbol{B}}_{j - 1}^{ + n} + \mathit{\boldsymbol{C}}_{k - 1}^{ + n}} \right) $ | (9) |
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{D}} + \Delta \tau \left( {\mathit{\boldsymbol{A}}_{i + 1}^{ - n} + \mathit{\boldsymbol{B}}_{j + 1}^{ - n} + \mathit{\boldsymbol{C}}_{k + 1}^{ - n}} \right) $ | (10) |
| $ \begin{array}{l} (\mathit{\boldsymbol{rhs}})_{i,j,k}^n = - {\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \zeta }}} \right)^n} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{Re}}{\left( {\frac{{\partial {\mathit{\boldsymbol{E}}_v}}}{{\partial \xi }} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial \eta }} + \frac{{\partial {\mathit{\boldsymbol{G}}_v}}}{{\partial \zeta }}} \right)^n} + \mathit{\boldsymbol{S}} \end{array} $ | (11) |
式中,σA=max[|λ(A)|],λ(A)为A=∂E/∂Q的特征值,A±=12[A±σAI],其它从略。
为了适用于计算超声速自由剪切流,需对初始k-ω SST湍流模型进行可压缩性修正,本文采用了Sarkar类型修正[14-15]。计算源项S时,对湍流源项采用隐式处理,对化学源项则采用了预处理[16]。
2.2 输运模型在本文所关心的多组分流场中,气体输运过程主要引起以下三种现象,即:由速度梯度引起动量输运的黏性现象、由温度梯度和组分扩散引起能量输运的导热现象及由浓度梯度引起组分输运的扩散现象。为了获得流场中的动量、组分以及能量输运强度,需要给出组分的分子输运系数,并以此求出混合气体的分子输运系数。在多组分流场中,精细计算混合气体的分子输运系数耗时巨大,通常采用近似计算方法,其常用近似计算公式[17]如下文所述。
2.2.1 混合气体输运系数的近似计算计算混合气体分子黏性系数μ的常用公式为Wilke的半经验关系式,即:
| $ \mu = \sum\limits_{i = 1}^{ns} {\frac{{{X_i}{\mu _i}}}{{\sum\limits_{j = 1}^{ns} {{X_j}} {\phi _{ij}}}}} $ | (12) |
| $ {\phi _{ij}} = \frac{{{{\left[ {1 + \sqrt {\frac{{{\mu _i}}}{{{\mu _j}}}} {{\left( {\frac{{{W_j}}}{{{W_i}}}} \right)}^{\frac{1}{4}}}} \right]}^2}}}{{\sqrt {8\left( {1 + \frac{{{W_i}}}{{{W_j}}}} \right)} }} $ | (13) |
其中,Xi、Wi和μi分别为组分的摩尔分数、摩尔质量(分子量)及分子黏性系数。
计算混合气体的分子导热系数κ的常用近似公式类同Wilke的半经验公式,而较为精确的近似公式则为Brokaw的半经验公式,即:
| $ \kappa = \sum\limits_{i = 1}^{ns} {\frac{{{X_i}{{\kappa '}_i}}}{{\sum\limits_{j = 1}^{ns} {{X_j}} {\psi _{ij}}}}} + \sum\limits_{i = 1}^{ns} {\frac{{{X_i}{{\kappa ''}_i}}}{{\sum\limits_{j = 1}^{ns} {{X_j}} {\varphi _{ij}}}}} $ | (14) |
| $ \frac{{{\psi _{ij}}}}{{{\varphi _{ij}}}} = 1 + \frac{{2.41\left( {{W_i} - {W_j}} \right)\left( {{W_i} - 0.142{W_j}} \right)}}{{{{\left( {{W_i} + {W_j}} \right)}^2}}} $ | (15) |
| $ {\varphi _{ij}} = \frac{{{{\left[ {1 + \sqrt {\frac{{{{\kappa '}_i}}}{{{{\kappa '}_j}}}} {{\left( {\frac{{{W_i}}}{{{W_j}}}} \right)}^{\frac{1}{4}}}} \right]}^2}}}{{\sqrt {8\left( {1 + \frac{{{W_i}}}{{{W_j}}}} \right)} }} $ | (16) |
其中,κ′i为组分i的导热系数中的平动部分,κi″为由转动、振动等自由度产生的附加项。
与流体力学控制方程中组分的平均速度、扩散速度和扩散通量相容,组分i穿过其余混合气体的分子扩散系数Dim的半经验公式为[18]:
| $ \frac{1}{{{D_{im}}}} = \sum\limits_{j \ne i}^{ns} {\frac{{{X_j}}}{{{D_{ij}}}}} + \frac{{{X_i}}}{{1 - {Y_i}}}\sum\limits_{j \ne i}^{ns} {\frac{{{Y_j}}}{{{D_{ij}}}}} $ | (17) |
式中,Yi为组分i的质量分数,Dij为各组分之间的双组元扩散系数。实际计算中,普遍采用下述两个半经验公式计算混合气体分子扩散系数,即:
| $ {D_{im}} = \frac{{1 - {Y_k}}}{{\sum\limits_{j \ne i}^{ns} {\frac{{{X_j}}}{{{D_{ij}}}}} }} $ | (18) |
| $ {D_{im}} = \frac{{1 - {X_k}}}{{\sum\limits_{j \ne i}^{ns} {\frac{{{X_j}}}{{{D_{ij}}}}} }} $ | (19) |
公式(18)导自基于摩尔分数梯度的质量平均速度和扩散通量,公式(19)则导自基于摩尔分数梯度的摩尔平均速度和扩散通量,虽然理论上均与流体力学控制方程存在相容性问题,但因其计算量相对较小,得到了普遍使用,公式(17)虽与流体力学控制方程相容,但是目前鲜见实际应用。
2.2.2 导热系数、扩散系数的关联计算多组分流场中,即使采用了半经验公式,求解混合气体分子输运系数仍是一个耗时运算,还需要在计算效率和计算精度间进行权衡。关联计算方案预设常值普朗特数和施米特数,根据混合气体分子黏性系数计算导热系数和扩散系数,即:
| $ \kappa = \frac{\mu }{{Pr}}{C_p},\;\;\;\;{D_{im}} = \frac{\mu }{{Sc}}{\rho ^{ - 1}} $ | (20) |
该方案计算精度稍逊,但计算效率很高,为提高复杂流场求解效率,仍需研究其适用空间。
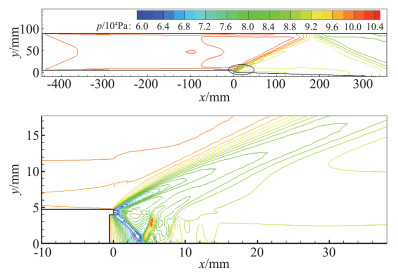
3 结果分析 3.1 基于Burrow & Kurkov实验的验证计算验证计算的来流条件仍由表 1给出,混合气体的输运系数由半经验关系式求解。其中,混合气体分子扩散系数由公式(17)计算。图 2为数值模拟给出的全流场压强等值线,并且给出了基于压强的局部流场波系结构。等直段的流场简单,属于受限平板流。由于氢气燃料的平行、同向喷注,且喷注静压强为一个大气压,后台阶区域的流场结构主要表现为喷口唇口构型所引起的底部流场结构,其中剪切层上缘的左传波系与上壁面作用,其反射波系在与下壁面作用前传出计算域,上缘波系与喷口的喷流波系叠加,经过下壁面反射、底部及射流自由剪切层的透射、反射,形成了喷口近场波系。
|
图 2 压强等值线 Fig.2 Pressure contour |
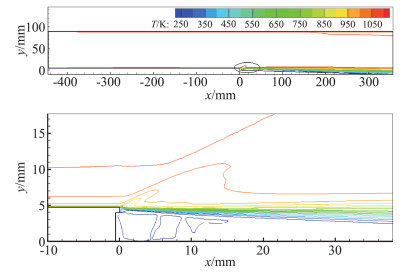
图 3为流场等温度线。由图可见,近壁区域的温度梯度大,掩盖了核心区温度场变化细节,没有刻画出类似压强场给出的波系结构。射流温度接近壁温,射流上缘的温度梯度大,在一定程度上显示了台阶下游区域射流剪切层的发展情况。
|
图 3 温度等值线 Fig.3 Temperature contour |
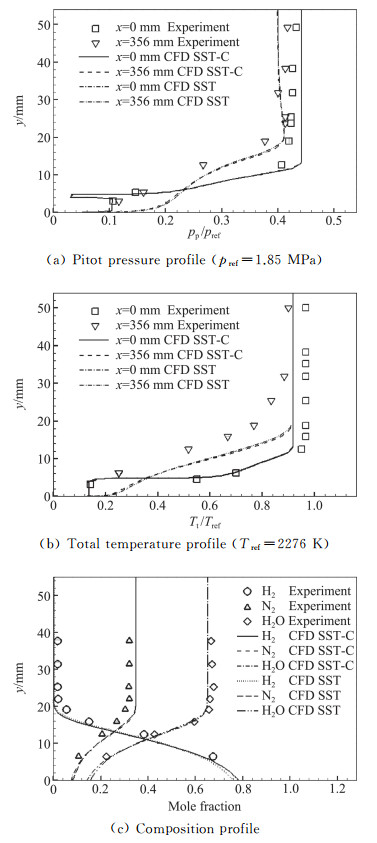
图 4给出了台阶及出口位置的皮托压强、总温和组分剖面。图中Experiment指实验,CFD SST指采用的湍流模型为k-ω SST模型,CFD SST-CC指采用的湍流模型仅对k-ω SST模型的k-ε模型部分进行可压缩性修正。湍流可压缩性效应主要作用于边界层外缘、自由剪切层,对出口流场参数剖面影响较为明显。整体上,计算的皮托压强、总温及组分剖面虽然与实验值有偏差,但是反映了变化规律,表明该数值技术可以用于本文的数值模拟研究。
|
图 4 皮托压强、总温及组分剖面 Fig.4 Profile of Pp, Tt and fi |
根据表 1的来流条件,针对输运系数近似计算方案,开展了湍流/层流状态下的数值模拟,具体的算例由表 2给出。计算中,混合气体分子黏性系数均由公式(12)和公式(13)计算给出,并且作为近似处理其它输运系数的基础。
| 表 2 输运系数近似计算方案 Table 2 Approximate formula for K and Dim |
|
|
根据图 2、图 3所示,台阶上游流场属于受限平板边界层流场,显示了边界层的流动,下游流场包含射流剪切层流动,显示了台阶下游射流剪切层发展情况。由此,本文通过对一个状态的计算可以同时对比输运系数的近似计算方案对边界层、射流剪切层流动的影响特点。
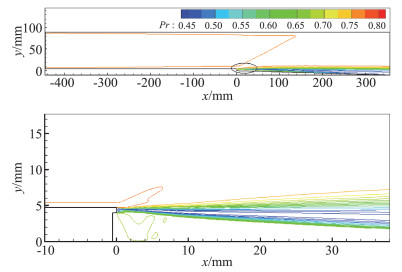
3.2.1 近似计算方案对壁面边界层流动的影响图 5为根据导热系数、黏性系数以及定压比热计算给出的混合气体普朗特数等值线,显示了混合气体普朗特数在流场中的变化特点。计算中,台阶上游没有燃料注入,污染空气来流的实际普朗特数变化较为平缓,且与本文预先给定的普朗特数相差不大(本文给定Pr=0.7)。由于燃料的喷入,台阶下游近壁区域的氢气组分占优,使得该区域的混合气体普朗特数与预设普朗特数相差较大,同时射流上缘区域的普朗特数场梯度大,也可在一定程度上显示台阶下游区域射流剪切层的发展情况。
|
图 5 普朗特数等值线 Fig.5 Prandtl number contour |
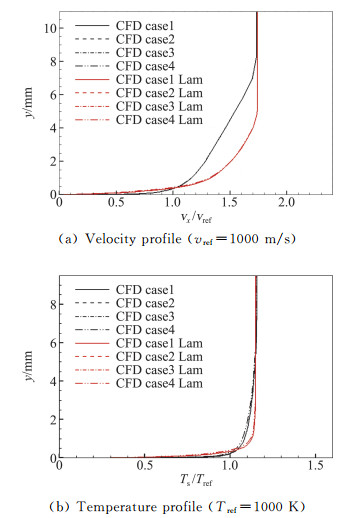
图 6为下壁面在台阶上游10 mm位置的边界层速度和温度剖面。这里,“Lam”表示层流条件下的计算值。因计算混合气体分子黏性系数的公式相同,速度剖面几近相同,算例1、算例2和算例3采用同一公式计算分子导热系数,因此温度剖面相同,算例4采用关联法获得分子导热系数,其温度剖面与其余算例的结果出现差异。
|
图 6 x=-10 mm位置的速度、静温剖面 Fig.6 Profile of Vx and Ts at x=-10 mm |
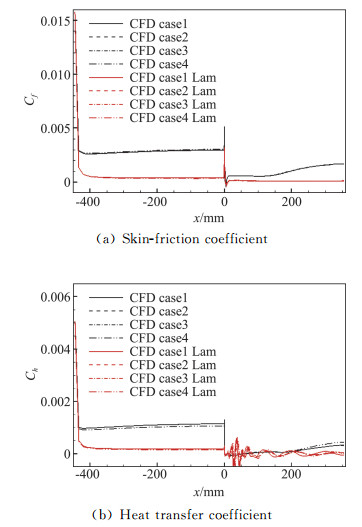
图 7为模型下壁面的壁面摩阻系数、传热系数分布。算例1、算例2和算例3同样有相同的壁面摩阻系数和壁面传热系数,算例4的摩阻系数与其余算例值接近,传热系数则与其余算例的结果有一定的差异。结合图 6所给出的速度、温度剖面可见,分子导热系数的计算方案对边界层温度剖面及壁面传热系数影响较大,通过能量方程间接影响了边界层速度剖面及壁面摩阻系数分布,但是其影响程度相对较小。对比数据的差异表明,虽然混合气体分子导热系数计算方案对边界层速度及温度剖面、壁面摩阻系数及传热系数分布计算产生了影响,但是其偏差仍在可接受的范围。由此,通过预先设定适当普朗特数,由分子黏性系数关联混合气体分子导热系数,在降低计算量的基础上可获得与采用公式计算混合气体分子导热系数的直接计算方案相近的壁面摩阻系数和壁面传热系数。
|
图 7 摩阻系数、传热系数分布 Fig.7 Distribution of Cf and Ch |
由图 3、图 5的参数等值线可见,台阶下游的射流剪切层在发展过程中逐步与壁面边界层产生了流动干扰。为排除其干扰因素的影响,本文在台阶下游选择10、100 mm位置对比输运系数近似计算方案对射流剪切层流动的影响,并同时给出燃烧室出口位置(356 mm)的参数剖面,以对比显示输运系数近似计算方案对综合流场的影响。
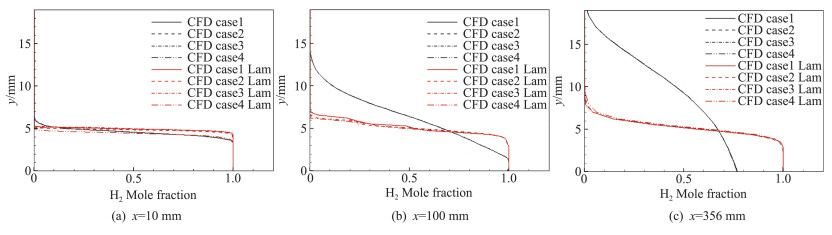
图 8为台阶下游10、100、356 mm位置的流场氢气组分剖面,显示了近似计算方案对射流剪切层区域内氢气组分剖面的影响特点。由图可见,层流状态下,算例1、算例2和算例3的流场组分剖面近乎相同,算例4的组分剖面则与其余算例的结果出现差异;湍流状态下,混合气体“涡黏性”输运效应掩盖了对应的分子输运效应,使各算例(输运系数近似计算方案)给出了相同的组分剖面。
|
图 8 不同x向位置的H2组分剖面 Fig.8 Profile of H2 composition at different x position |
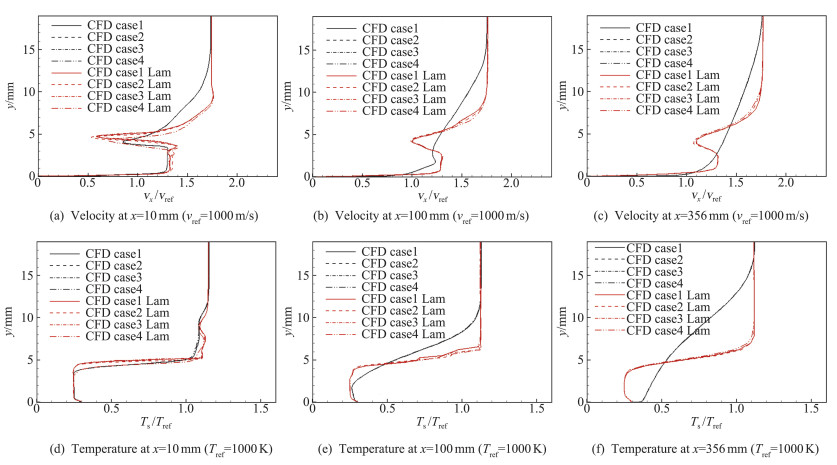
图 9为台阶下游10、100、356 mm位置的流场速度、温度剖面。湍流状态下,各算例给出相同的流场速度、温度剖面;层流状态下,算例1、算例2和算例3的速度、温度剖面非常接近,而算例4的速度、温度剖面则与算例1、算例2以及算例3的对应结果有相对较大的差异。结合图 8可见,随着流场向下游发展,层流流场中组分剖面的差异主要出现在组分扩散波阵面的上升沿,且差异程度逐渐减弱。与此相呼应,层流流场中对应的速度、温度剖面差异程度也随流场向下游的发展而减弱。
|
图 9 不同x向位置的速度、静温剖面 Fig.9 Profile of vx and Ts at different x position |
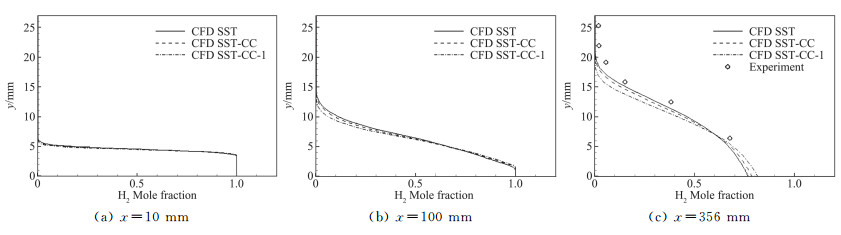
在算例1的基础上,开展了两种可压缩性修正方案下的流场数值模拟,进一步对比显示混合气体的“涡黏性”输运对组分剖面的影响。图 10给出了台阶下游10、100、356 mm位置的流场氢气组分的摩尔分数剖面。图中CFD SST-CC-1指采用的湍流模型对k-ω SST模型中的k-ε和k-ω模型部分进行可压缩性修正。结合图 8、图 9可见,湍流流场中各湍流模型的“涡黏性”输运系数是导致流场组分剖面(包括速度剖面、温度剖面)出现差异的主要因素,此时混合气体分子输运系数近似计算方案对流场数值模拟的影响则退居于次要地位。
|
图 10 不同x向位置的H2组分剖面 Fig.10 Profile of vx and Ts at different x position |
利用Burrow和Kurkov的实验构型及相关研究数据,本文开展了多组分混合气体导热系数、组分扩散系数近似计算方案对流场参数影响的数值模拟研究,获得以下主要结论:
(1) 与采用由相关公式近似计算混合气体导热系数、扩散系数的直接近似计算方案相比,采用由普朗特数、施密特数关联混合气体导热系数、扩散系数的关联近似计算方案,流场的数值模拟在获得合理计算结果的同时,可大为降低计算量。
(2) 抛开相容性问题,混合气体扩散系数直接近似计算方案对流场参数计算影响不明显。
(3) 相对层流计算,湍流计算时边界层/剪切层区域的混合气体湍流输运系数大于相应的分子输运系数,由此弱化了混合气体分子输运系数不同近似计算方案对流场数值模拟差异的影响。
(4) 相对输运系数近似计算方案,湍流可压缩修正模型对组分剖面的影响更为明显。
本文主要对比研究了冷态流场下的混合气体输运系数计算方案对流场参数计算的影响,获得了有一定参考价值的结论。同时,基于分子运动论的气体输运系数理论计算公式表明,施密特数受流场压强、温度和组成等因素的影响较大,因此下一步需要开展化学非平衡状态下的计算研究,以期更加全面地数值模拟对比、分析研究输运系数计算方案对流场参数计算的影响特点。
| [1] |
CURRAN E T, MURTHY S N B. Scramjet propulsion[M]. Washington, D C: AIAA Education Series, 2000.
|
| [2] |
POLING B E, PRAUSNITZ J M, O'CONNELL J P. The properties of gases and liquids[M]. 5th ed.. New York: McGraw-Hill, 2001.
|
| [3] |
BERTIN J J, NEAL D R, STALMACH D D. The effect of the transport property models on the shuttle boundary layer[R]. NASA CR-151748, 1978.
|
| [4] |
谭杰, 孙晓峰, 刘芙群, 等. 高超声速平板/空气舵热环境数值模拟研究[J]. 空气动力学学报, 2019, 37(1): 153-159. TAN J, SUN X F, LIU F Q, et al. Numerical simulation of aerodynamic heating environment of a hypersonic plate/rudder configuration[J]. Acta Aerodynamica Sinica, 2019, 37(1): 153-159. DOI:10.7638/kqdlxxb-2018.0234 (in Chinese) |
| [5] |
DRUMMOND J P. Methods for prediction of high-speed reacting flows in aerospace propulsion[J]. AIAA Journal, 2014, 52(3): 465-485. DOI:10.2514/1.J052283 |
| [6] |
BURROWS M C, KURKOV A P. Analytical and experimental study of supersonic combustion of hydrogen in a vitiated airstream[R]. NASA TM X-2828, 1973.
|
| [7] |
MATTICK S J, FRATE F C, NELSON C C. Progress in validation of wind-US for ramjet/scramjet combustion[R]. AIAA 2005-1000, 2005.
|
| [8] |
ENGBLOM W A, FRANKELY S H. Numerical modeling of supersonic combustion: validation and vitiation studies using FLUENT[R]. AIAA 2005-4287, 2005.
|
| [9] |
BHAGWANDIN V A, ENGBLOM W A, GEORGIADIS N J. Numerical simulation of a hydrogen-fueled dual-mode scramjet engine using wind-US[R]. AIAA 2009-5382, 2009.
|
| [10] |
LACASSE D, TURGEON É, PELLETIER D. On the judicious use of the k-ε model, wall functions and adaptivity[R]. AIAA 2001-0882, 2001.
|
| [11] |
MENTER F R. Zonal two equation k-ω turbulence models for aerodynamic flows[R]. AIAA-93-2906, 1993.
|
| [12] |
LIOU M S. Ten Years in the Making-AUSM-family[R]. AIAA 2001-2521, 2001.
|
| [13] |
YOON S, JAMESON A. An LU-SSOR scheme for the Euler and Navier-Stokes equations[R]. NASA CR-179556, 1986.
|
| [14] |
FORSYTHE J R, HOFFMANN K A, SUZEN Y B. Investigation of modified menter's two equation turbulence models for supersonic applications[R]. AIAA-99-0873, 1999.
|
| [15] |
RUMSEY C L. Compressibility considerations for κ-ω turbulence models in hypersonic boundary layer applications[R]. NASA TM-2009-215705, 2009.
|
| [16] |
王晓栋, 乐嘉陵, 宋文艳. 带支板的冲压燃烧室的燃烧性能研究[J]. 空气动力学学报, 2004, 22(3): 274-278. WANG X D, LE J L, SONGW Y. Study to the combustion performance of a scramjet combustor with struts[J]. Acta Aerodynamica Sinica, 2004, 22(3): 274-278. DOI:10.3969/j.issn.0258-1825.2004.03.006 (in Chinese) |
| [17] |
GORDON S, MCBRIDE B J, ZELEZNIK F J. Computer program for calculation of complex chemical equilbrium compositions and applications: supplement Ⅰ-transport properties[R]. NASA TM-86885, 1984.
|
| [18] |
KEE R J, COLTRIN M E, GLARBORG P. Chemically reacting flow:theory and practice[M]. New Jersey: John Wiley & Sons, 2003.
|
 2019, Vol. 37
2019, Vol. 37