中空长航时无人机追求高续航性能和任务多样化(大部分要求多装载和察打一体化功能),此类飞机通常具有大展弦比、低推重比和较大寄生阻力等技术特点,因而在起飞升力、起飞和巡航升阻比以及结构高度等方面具有很高的要求。首先,由于较大寄生阻力并追求高续航性能,此类无人机需用很大的巡航升力以提高其续航因子[1-3, 8];其次,较小的推重比和短距起降要求无人机具有很高的起飞升力和升阻比;再者,大展弦比和内部装载要求机翼具有一定的结构高度;除此之外,着陆阶段在保持较高升力同时具有较高的阻力,降低着陆距离和提高着陆安全性[4]。两段翼型能保持较长的层流区, 在大升力时维持较小阻力, 同时通过构型的变化适用于不同任务阶段, 具有高升力和多任务适应能力等技术特点。即须由过去单段翼型的高效巡航单设计点设计升级成为起飞高升高升阻比、巡航高效和着陆高升高阻的多设计点设计;同时采用固定转轴(非传统襟翼复杂的传动机构),将襟翼和阻力板功能融合,其结构形式简单满足无人机使用的技术特点。综上所述,能满足多任务适应能力的两段翼型是长航时和短距起降无人机翼型设计的一个重要发展方向[2-6]。
本文在原中空长航时无人机单段翼型设计的基础上开展高升力多任务适应能力的两段翼型设计方法研究和翼型设计。
1 翼型设计思路和生成方法 1.1 两段翼型设计思路本文结合某型无人机在续航和起降特性改进设计需要,为了满足起降和巡航以及结构高度等约束,在单段翼型设计特点的基础上,尽量维持原有翼型的基本几何形状(尤其是上表面,维持原有翼型在低雷诺数条件下层流特性[3]),并在主翼后梁高度和襟翼(第二段翼)前缘半径等关键位置设置控制点,其余部分通过分段可控二次曲线与原始翼型相切过渡。利用控制点加分段二次曲线方法快速生成两段翼型外形,之后通过优化程序使主翼及襟翼外形、缝道参数和转轴位置匹配,使之满足多设计点要求。
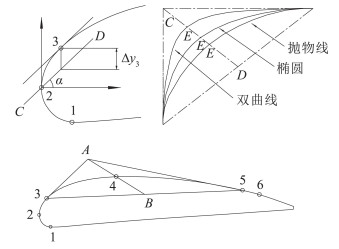
1.2 两段翼型生成方法后缘襟翼生成方法通常参考飞机设计手册或文献[9],在原始翼型的基础上通过切割法生成襟翼外形。为了加强对外形的控制,文献[7]引入了襟翼头部上表面控制点位置偏移量和斜率以及形状控制变量来改变襟翼前缘形状和曲线方程(图 1)。图中右上角部分展现了形状控制变量(
本文研究对象除了需考虑到高升力和多设计点综合设计,还涉及到低雷诺数流动和层流再生成等复杂流动现象。从国外研究结果来看,其主翼和襟翼外形参数和常规襟翼参数分布存在较大的差异[2-3, 12],主翼和襟翼下表面外形也与原始翼型差别较大,文献中虽然提到了翼型分割之后襟翼平移的研究思路,但针对变化较大的外形其未给出生成方法。国内的文献[5]通过“椭圆-控制点”方法生成两段翼型,经研究发现此方法包括文献[7]方法与初始翼型关系较大,会遇到翼型压力分布不合理现象(见后面分析)。本文在文献[5]和文献[7]工作的基础上,借用其部分思想,通过在关键位置增加控制点并结合可控二次曲线生成两段翼型,提高其对原始翼型的适应能力,使其更加适用于优化程序,同时改善流场品质提高翼型性能。
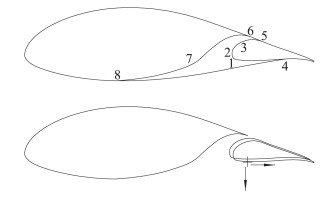
如前所述为了尽量维持原有翼型优良的气动特性,在原有翼型的基础上通过在关键位置增加控制点并结合可控二次曲线和优化方法生成两段翼型。首先,将需要优化的外形分成五部分(图 2所示),即点1~点3曲线段、点3~点5曲线段和点1~点4曲线段,其构成襟翼前缘外形;点6~点7曲线段和点7~点8曲线段构成主翼下翼面后缘外形。其次,选择控制点及其参数,除了一般控制点约束(点4、5、6、8只能在原始翼型上移动), 点1和点2给定坐标(点2处斜率无穷大)用于控制襟翼前缘形状;为了更好的控制主翼后梁高度和后缘形状,点3和点7给定了点坐标与斜率,其值作为优化参数随优化过程而改变。再次,设定曲线的形状控制参数用于进一步控制曲线的形式。此方法控制参数更多, 很大程度上将主翼下表面和襟翼头部外形分开设计,下表面外形对原始翼型依赖性更小;同时结合目标要求对外形参数和缝道参数一并优化设计,从而具有更好的灵活性和适应能力,更适合多目标和多约束下的优化设计。
|
图 2 两段翼型外形生成示意图 Fig.2 Sketch map of two-element airfoil |
二次曲线控制方程表达式为:
| $ y^{2}+a x^{2}+b x y+c x+d y+e=0 $ | (1) |
二次曲线可为椭圆、双曲线和抛物线,根据外形生成的需要, 本文点6~点7和点3~点5曲线段采用可变的形状控制参数控制其二次曲线类型,由优化算法决定形状控制参数Q值;其余曲线段根据初步研究结果采用固定形状控制参数(二次曲线的类型在优化过程中不变)。结合控制点参数和曲线类型能够生成控制段的外形,如通过联合求解点1的坐标、点2和点3的坐标与斜率得到二次曲线系数,从而确定点1~点3曲线段外形方程;其余曲线段外形方程的系数则通过联合求解相应曲线的起点和终点坐标和斜率以及形状控制参数而得到。
2 设计方法及结果分析 2.1 设计方法和条件本文针对中空长航时固定翼无人机在巡航和起飞等状态下的约束进行两段翼型优化设计, 优化参数包括两段翼型外形和缝道参数以及转轴位置。考虑到无人机的使用和保障要求,襟翼形式尽量简单,采用固定转轴(转轴位置设计过程中可变)。除此之外,本文主要目的是验证两段翼型外形生成方法和优化设计方法的有效性,此阶段将巡航状态和起飞状态分开设计,巡航状态以最大升阻比为优化目标(长航时无人机续航性能为首选),优化变量为两段翼型外形和缝道参数;起飞状态以起飞升力为优化目标,以转轴位置为优化参数,并校核优化结果是否满足起降要求。考虑到目标函数与控制参数和约束条件的关系不明确,采用多岛遗传算法进行全局寻优;优化设计程序包含优化算法、翼型生成、网格生成、流场模拟和结果处理五大模块。
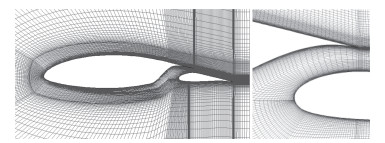
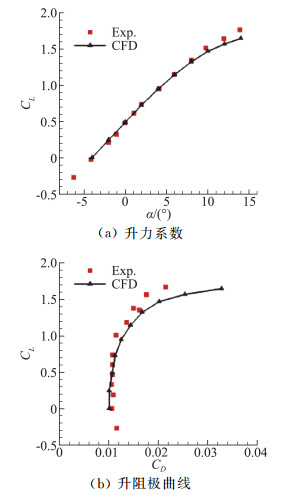
由于涉及到大升力和多段翼型缝道流动,其流场特性包含大量黏性扰流和分离流。为了保证数值模拟的准确性,气动力通过求解RANS方程得到,选用SST κ-ω两方程湍流模型,文献[10, 11]表明此模型在低雷诺数分离流方面和襟翼升力方面都具有很好的模拟能力。来流马赫数Ma=0.15,Re=3.0×106。为了更加准确对流场进行模拟,采用多块C型网格(图 3),并保证每次优化过程网格参数分布一致,以避免因网格对优化结果造成影响。为了验证方法的可靠,开展与本文类型相似的GAW-1翼型在相近条件下(Ma=0.15, Re=6.3×106)的对比分析(详见图 4,试验数据可参见文献[13]),对比结果表明本文采用的方法合理。
|
图 3 计算网格 Fig.3 Computational grid of the flow field |
|
图 4 计算和试验的对比 Fig.4 Comparison of test and computational result |
续航性能对于低速长航时无人机而言是最为重要的指标之一,其很大程度依赖于翼型的升阻比,所以翼型优化设计时以巡航升阻比为目标;考虑不改变飞机基本配平,优化过程中对翼型的俯仰力矩和升力特性进行一定的限制,以不大于原始翼型低头力矩的百分之二和大于初始升力系数为约束,优化变量、变化范围和优化后结果见表 1。
| 表 1 优化参数和优化结果 Table 1 Optimal parameters and their optimal results |
|
|
表 1中δx和δy分别为襟翼向后和向下移动的量,以翼型弦长无量纲化,以点2原始位置为参考点,意义相当于缝道参数。Y1、Y2、Y3、Y7分别为点1、2、3、7在Y方向(高度方向)的位置,其中Y1以点1所在弦向位置原始翼型下翼面点为参考点,以点2与点1的高度差为无量纲化;Y2和Y7以相应位置的翼型高度为无量纲化,以相应位置下翼面点为参考点;Y3以点2和点5高度差为无量纲化,以点2为参考点。K3、K7分别代表点3、7的斜率(以可控角的范围无量纲化)。经初步研究发现,点6~点7段和点3~点5段曲线的线型对优化结果影响较大,采用变化的形状控制参数(即Q67和Q35);其它线段根据初步研究结果采用固定形状控制参数。襟翼外形生成通常做法是在原始翼型的某个位置进行分割,为了更好地控制襟翼上表面局部压力,本文将主翼和襟翼分割点进行分开设计,点6在点5的位置上进行适当调整,形成参数X6(以δx无量纲化)。
遗传优化每代总群体规模数为144,杂交概率0.7,变异概率0.03,最大进化代数40代。
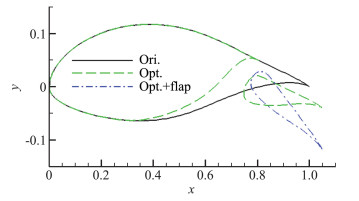
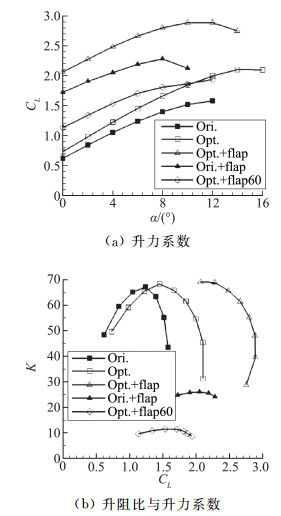
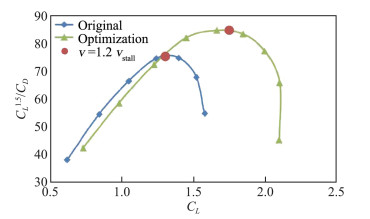
图 5给出了优化翼型和初始翼型的外形(黑色为原始翼型,绿色为改进后的两段翼型,蓝色为偏转状态襟翼);在优化翼型的基础上,对其气动特性进行评估,图 6给出了计算结果。优化结果表明, 相对于原始翼型, 两段翼型升力线性段范围增加, 最大升力系数由1.5增加到2.1,襟翼无偏转情况下最大升力系数增加40%;失速迎角增大, 扩展了无人机的飞行包线,增强其抗风能力。在升阻比方面,滑跑状态下(0°迎角, 襟翼放下)优化后翼型升阻比得到大幅提升, 从约25提升到69;襟翼无偏转状态最大升阻比大于原始翼型(由67.0增加到68.3),但受两段翼型较大零升阻力的影响,较小升力下升阻比略低于原始翼型,在更大升力系数下(大于1.3),升阻比大于原始翼型。文献[2]等研究表明,此类长航时无人机其续航升力系数的选择与零升阻力有很大关系,本文研究对象的无人机最佳续航升力系数应该在1.3以上(Heron-1无人机巡航设计升力系数大于1.5),所以相对于原始翼型,优化后的两段翼型更适合此类飞机。图 7给出了优化前后翼型续航因子与升力系数关系,结合升力曲线,在安全飞行包线内(1.2倍的失速速度),其最大续航因子由优化前的75.5提升到两段翼型的85.0(提升了12.6%),根据文献[2]等研究结果小幅度偏转襟翼后续航因子还能进一步提升。
|
图 5 原始和优化翼型 Fig.5 Geometry between the optimized airfoil and original one |
|
图 6 优化前后翼型气动性能 Fig.6 Geometry between the optimized airfoil and original one |
|
图 7 优化前后续航因子分析 Fig.7 Comparison of endurance factors of airfoil |
针对起飞要求,在相同襟翼偏转下(20°),优化前后最大升力系数得到大幅提升,由原始翼型的2.2提高到2.9。进一步分析发现,升力提升只是一方面,由于原始翼型为了追求巡航升阻比,翼型后缘加载比较严重,襟翼偏转后缘分离严重,在升力受到限制同时阻力急剧增加。过低的升阻比(图 6)严重影响到此类低推重比无人机的滑跑加速度;经研究发现由原始翼型生成的无人机有/无常规襟翼对无人机的滑跑距离影响有限,极大的限制了无人机的使用(如高原和短距起降)。优化设计后的两段翼型则不存在上述问题,在取得大升力同时保持高的升阻比,即在降低离地速度同时还能提升无人机的滑跑加速度;相当于其起飞升力由原始翼型的1.4提升到2.7(由于受阻力影响,原始翼型使用无襟翼数据),改进后两段翼型能极大的提升无人机的起飞性能。除此之外,襟翼的大角度偏转, 在保持一定升力,同时阻力增大(图 5中襟翼偏转60°情况下升阻比降到10左右),其效果相当于阻力板,可以满足着陆过程中的陡下滑和防止长距离飘移的大阻力(保持一定的升力)要求,具有集巡航、起飞和着陆多任务为一体的技术特点。
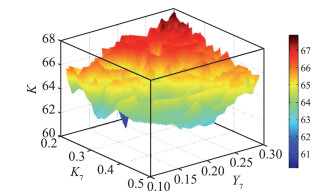
对优化变量进行分析发现,主翼后缘厚度Y7和控制点7斜率K7对两段翼型的升阻比有直接影响,图 8给出了升阻比与这两个参数关系。在目前的参数变化范围内,随着后缘厚度的降低,翼型升阻比提高,体现结构和气动需综合设计。通过厚度参数Y7并配合斜率参数K7变化能找到升阻比优化解,说明设置点7的高度位置和斜率作为控制点参数的合理性,研究表明形状控制参数Q67其能很好适应后面襟翼外形,找到满足要求的缝道外形。
|
图 8 主翼后缘厚度对升阻比影响 Fig.8 Effect of thickness on the lift-to-drag |
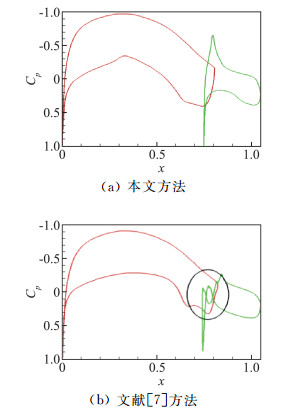
图 9给出设计翼型压力分布, 并与文献[7]所用方法进行对比,如前面翼型生成方法所论述的,由于本文所采用的原始翼型后缘弯度较大,原始翼型大弯度下表面和与其相切的头部曲线会使襟翼头部下表面出现低压值,同时在头部上表面反倒出现高压(简单曲线难以适应缝道流场),影响了翼型的气动特性;文献[5]方法也会出现类似现象,其主要原因与本文的初始翼型外形参数有关。直接切割方法和控制参数少难以使缝道内及襟翼前缘表面同时达到合理的压力分布;而本文采取方法控制点和控制参数更多,控制点和形状控制参数协调工作提高外形的生成能力和对原始翼型适应性能力;于此同时,外形参数和缝道参数同时优化提升翼型的气动性能。
|
图 9 两段翼型压力分布 Fig.9 Pressure distribution of the two-element airfoil |
在巡航状态的基础上,结合襟翼舵机功率(压力分布决定舵机功率)和飞机安装位置的约束给出转轴位置的限制范围,对转轴位置进行优化设计,确定无人机转轴位置和起飞状态构型。优化所用方法与巡航状态优化设计基本一致,表 2给出了优化参数和优化结果,在优化结果的基础上开展起飞状态不同迎角气动性能评估(图 6)。
| 表 2 优化参数和优化结果 Table 2 Optimal parameters and their optimal results |
|
|
在单段翼型的基础上,本文采用控制点加分段可控二次曲线方法构建外形,并对生成外形的控制参数、缝道参数和转轴位置进行优化,完成两段翼型设计和性能评估,主要形成以下结论:
(1) 相比于常规直接切割法,本文采用的方法控制点和控制参数更多,其对原始翼型适应性更好,生成的翼型压力分布更加合理,更适合多目标优化设计;
(2) 相比于原始翼型,新设计两段翼型的续航因子、起飞升力和起飞升阻比得到大幅提升;
(3) 襟翼大角度偏转在保持一定升力同时阻力大幅增加,起到了阻力板作用,利于无人机下滑和着陆减速。
新设计的两段翼型可以满足巡航、短距起降的多设计点要求,对中空长航时无人机设计具有重要意义。
| [1] |
NAGEL A, MISHA S. Development of high-lift UAV wings: AIAA: 2006-3467[R]. Reston: AIAA, 2006.
|
| [2] |
KOSS D, STEINBUCH M, SHEPSHELOVECH M. Development of two-element NLF airfoil for long endurance flight: AIAA-97-0514[R]. Reston: AIAA, 1997.
|
| [3] |
CISTRIANI L. Falco UAV low Reynolds airfoil design and testing at Galileo Avionica[C]. UAV Design Processes/Design Criteria for Structures, RTO-MP-AVT-145: 3. 3. 1-24, 2007.
|
| [4] |
STEINBUCH M, MARCUS B, SHEPSHELOVECH M. Development of UAV wings-Subsonic designs: AIAA 2003-603[R]. Reston: AIAA, 2003.
|
| [5] |
侯成义, 龚志斌, 刘城城, 等.高空长航时无人机高升阻比两段翼型设计研究[J].应用力学学报, 28(2): 148-152, 2011. HOU C Y, GONG Z B, LIU C B, et al. Investigation of the design methodology for the high lift-to-drag ratio two-element airfoil of the high altitude and long endurance UAV[J]. Chinese Journal of Applied Mechanics, 2011, 28(2): 148-152. (in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-YYLX201102010.htm |
| [6] |
刘城城, 李杰, 李鑫, 等. 某螺旋桨长航时无人机气动力改进设计与分析[J]. 飞行力学, 2012, 30(3): 209-212. LIU C B, LI J, LI X, et al. Improved design and analysis on aerodynamics for a propeller-driven long-endurance UAV[J]. Flight Dynamics, 2012, 30(3): 209-212. (in Chinese) |
| [7] |
董斌斌.二维襟翼缝道外形的气动优化设计研究[D].南京: 南京航空航天大学, 2011. DONG B B. Design and optimization of two-element airfoil[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041147.htm |
| [8] |
孔繁美, 华俊, 向锦武, 等. 高升力与失速特性缓和的翼型设计研究[J]. 北京航空航天大学学报, 2011, 28(2): 235-237. KONG F M, HUA J, XIANG JW, et al. Design and research of high-lift mild-stall airfoils[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 28(2): 235-237. (in Chinese) |
| [9] |
SMITH A M O. High lift aerodynamics[J]. Journal of Aircraft, 1975, 12(6): 501-530. DOI:10.2514/3.59830 |
| [10] |
CATALANO P, AMATO M. An evaluation of RANS turbulence modeling for aerodynamic applications[J]. Aerospace Science and Technology, 2003, 7(7): 493-509. DOI:10.1016/S1270-9638(03)00061-0 |
| [11] |
RUMSEY C L, YING S X. Prediction of high lift:review of present CFD capability[J]. Progress in Aerospace Science, 2002, 38(2): 145-180. DOI:10.1016/S0376-0421(02)00003-9 |
| [12] |
WENTZ, OSTOWARI W H. Additional flow field studies of the GA(W)-1 airfoil with 30-percent chord fowler flap including slot-GAP variations and cove shape modifications[R]. NASA CR-3687, 1983.
|
| [13] |
韩忠华, 乔志德, 熊俊涛, 等. Navier-Stokes方程预处理方法及其对翼型绕流数值模拟的应用[J]. 西北工业大学学报, 2006, 24(3): 275-280. HAN Z H, QIAO Z D, XIONG J T, et al. Development of an efficient viscous preconditioning method and its application to numerical simulation of flows over airfoils[J]. Journal of Northwestern Polytechnical University, 2006, 24(3): 275-280. DOI:10.3969/j.issn.1000-2758.2006.03.001 (in Chinese) |
 2019, Vol. 37
2019, Vol. 37